Похожие презентации:
Кривые второго порядка
1.
§12. Кривые второго порядкап.1. Окружность.
Окружность есть геометрическое множество
точек на плоскости, равноудаленных от
данной точки.
2.
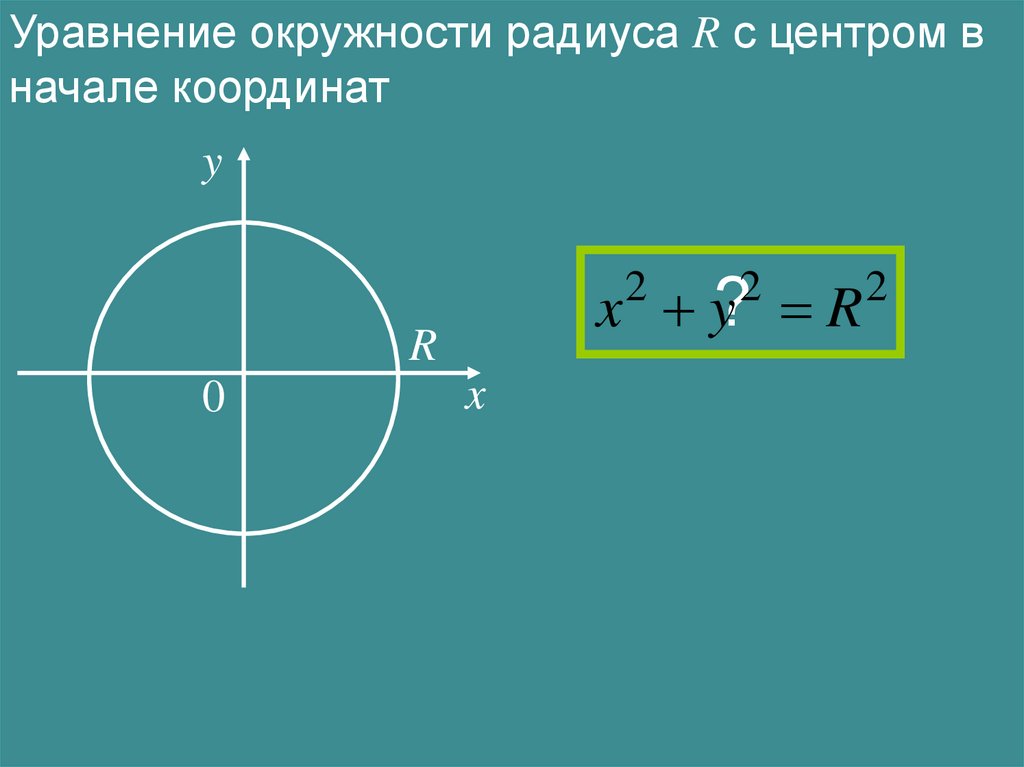
Уравнение окружности радиуса R с центром вначале координат
y
x y? R
2
R
0
x
2
2
3.
Уравнение окружности радиуса R с центром вточке O( x0 ; y0 )
y
( x x0 ) ?( y y0 ) R
2
O
0
x
2
2
4.
п.2. Эллипс.Эллипс есть геометрическое место точек на
плоскости, координаты которых
удовлетворяют уравнению
x
a
2
2
y
b
2
1
,
2
a b 0.
5.
Свойства эллипса1.Симметрия относительно осей координат и
начала координат.
2. | x | a, | y | b.
y
3. I-я четверть:
b
2
x
y b 1 2
a
a
x
6.
yB2
A1
A2
F1
O
F2
x
B1
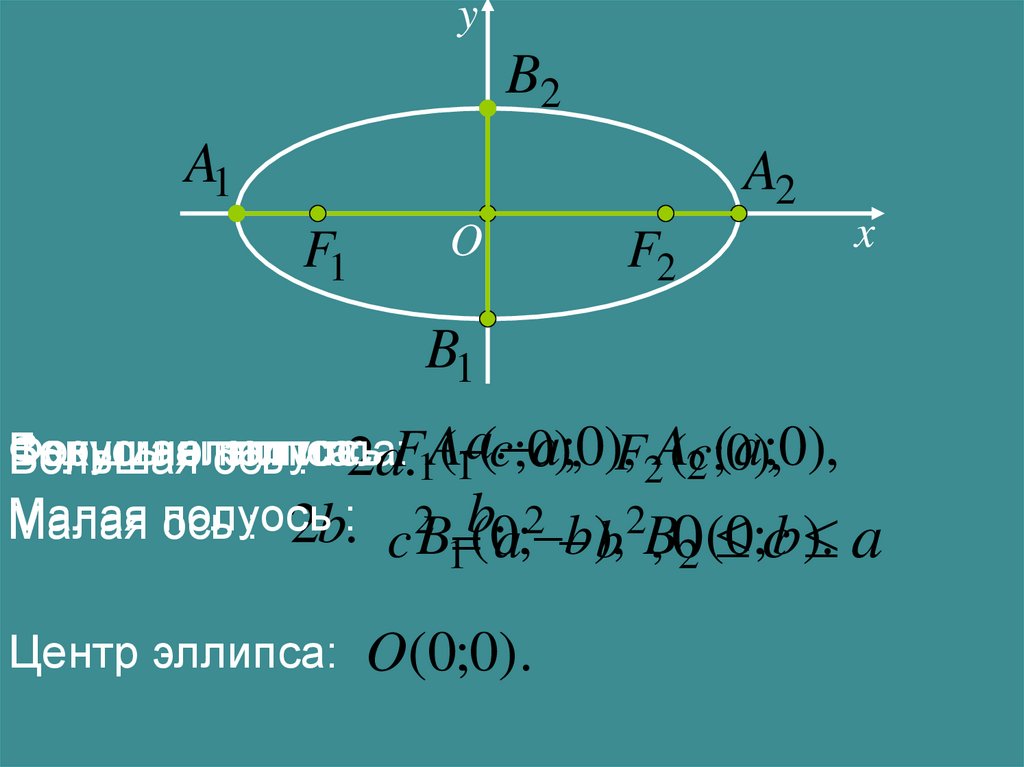
Фокусы эллипса:
Вершины
Большая
полуось
эллипса:
:.1A
(1 a(c. ;0a),;0),F2A(2c;(0a),;0),
ось
: 2aF
Малая ось
полуось
2
: 2b.: 2 b. 2
a
c B1 (0a; b),
bB
, 02 ( 0;cb).
Центр эллипса: O(0;0).
7.
Теорема 1. Точка M плоскости принадлежитэллипсу тогда и только тогда, когда сумма
расстояний от фокусов F1 и F2 до точки M
равна 2a.
y
M ( x; y )
F1
O
F2
x
8.
yM ( x; y )
F1 ( c;0)
MF1 ( x c) y
2
O
2
F2 (c;0)
x
MF2 ( x c) y
2
2
9.
Доказательство.Необходимость.
Пусть точка M ( x; y ) лежит на эллипсе.
Покажем, что MF1 MF2 2a
2
x
y
x
2
2
1
y
1
b
2
2
a2
a
b
2
2
b
2
2 2
b x
a
2
10.
MF1 x 2cx c y2
c a b
2
2
2
2
y b
2
2
2
x 2cx a b b
2
2
2
2
2
b
2
2
x 1 2 2cx a
a
2 2
b x
a
2
2 2
b x
a
2
11.
x2 c
a
2
2
cx
a
2
2
2
c
c
c
x a x a a x
a
a
a
c
MF1 a x
a
12.
cMF2 a x
a
Самостоятельно
c
c
MF1 MF2 a x a x 2a
a
a
13.
Достаточность.MF1 MF2 2a
Покажем, что точка M ( x; y ) лежит на эллипсе.
Пусть
MF1 ( x c) y
2
2
MF2 ( x c) y
2
( x c ) y ( x c ) y 2a
2
2
2
2
2
2 2
( x( x c)c2) 2 y 2y 2 2 a2 a ( x( x c )c2 ) 2
yy
2
2
14.
x 2 2cx c 2 y 2 4a 2 4a ( x c) 2 y 2 x 2 2cx c 2 y 22
2
2
a a ( x( x c)c2) 2 y 2y 2 a 2a
cxcx
a x 2cx c y a 2a cx c x
2
2
2
2
4
2
2 2
a x 2a cx a c a y a 2a cx c x
2 2
2
2 2
2 2
4
2
2 2
15.
a c x a y a a c2
2
c a b
2
2
2
2
2 2
2
2
a c b
2
2
2
2
b x a y a b
2 2
2 2
b x
2 2
a y
2 2
2 2
2 2
2
a b
x
y
2
1
2
2
2 2
2 2
2 2
a
b
a b
a b
a b
Теорема доказана.
16.
c1 ─ эксцентриситет эллипса
a
1
0 b a
17.
Уравнение эллипса с центром в точке O( x0 ; y0 )O
( x x0 )
a
2
2
( y y0 )
b
2
2
1
18.
a bF2 (0; c)
c b a
2
F1 (0; c)
2
2
19.
п.3. Гипербола.Гипербола есть геометрическое место
точек, координаты которых удовлетворяют
уравнению
x
a
2
2
y
b
2
1
,
2
a, b 0.
20.
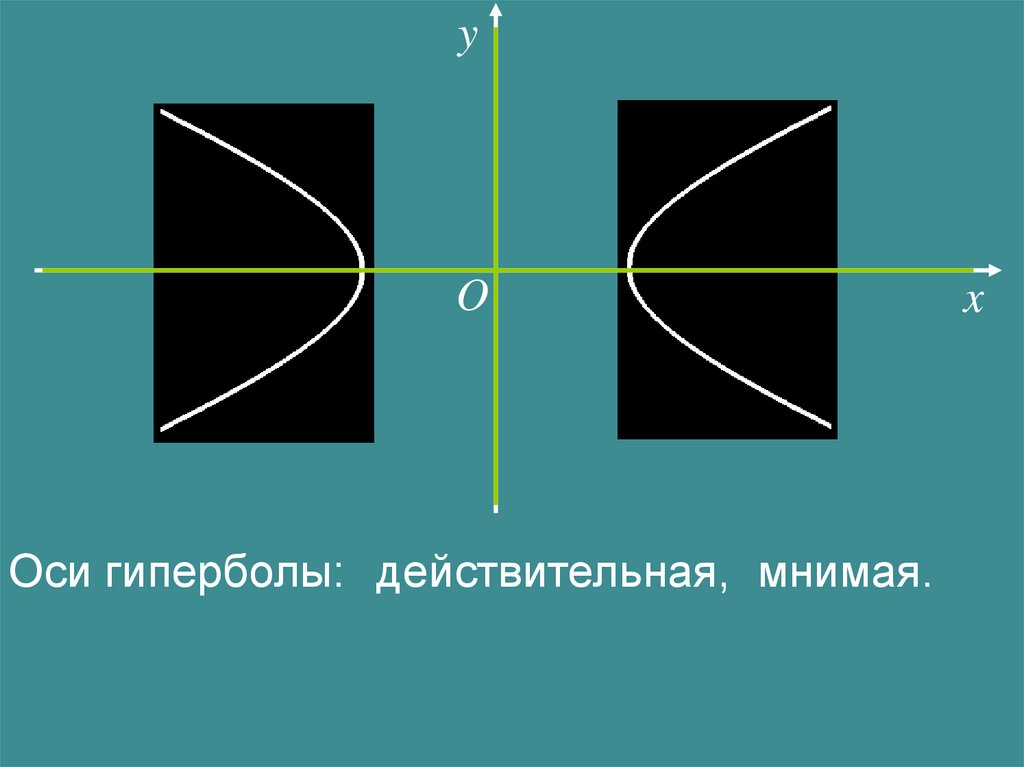
yO
Оси гиперболы: действительная, мнимая.
x
21.
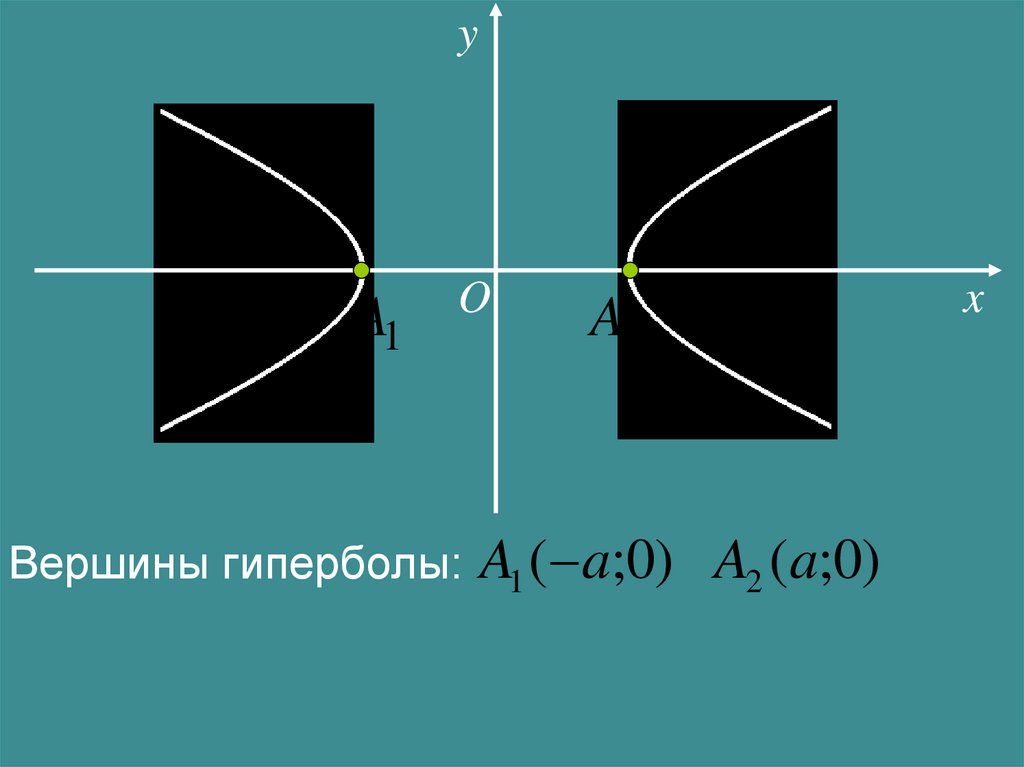
yA1
O
x
A2
Вершины гиперболы: A1 ( a;0)
A2 (a;0)
22.
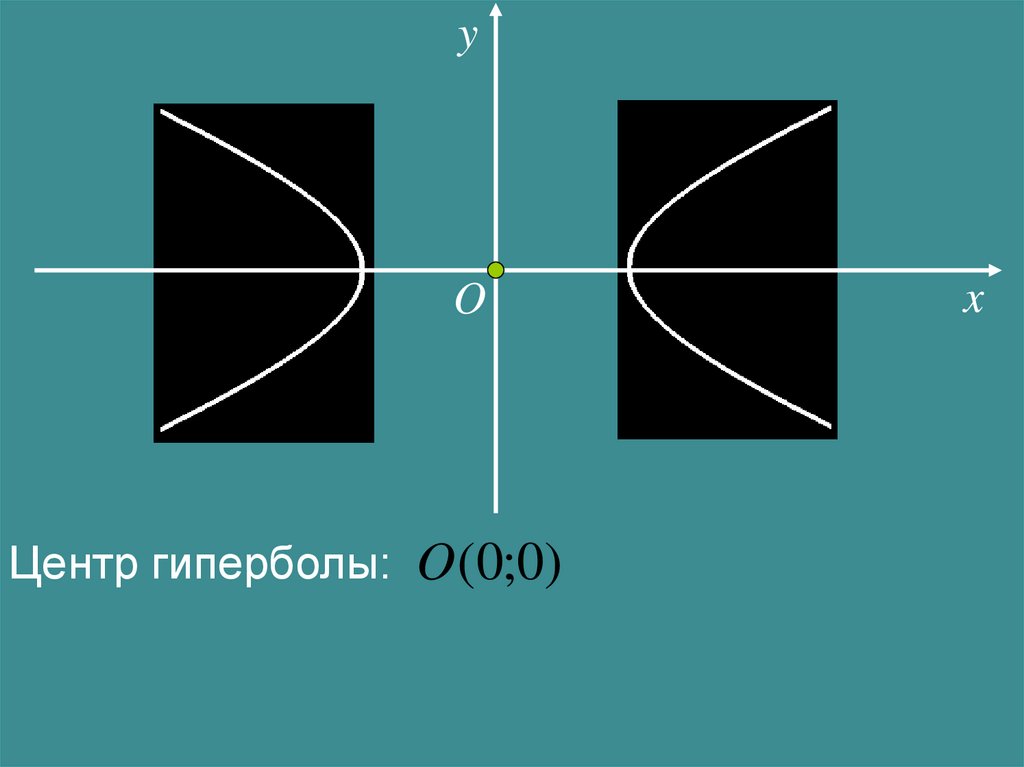
yO
Центр гиперболы: O (0;0)
x
23.
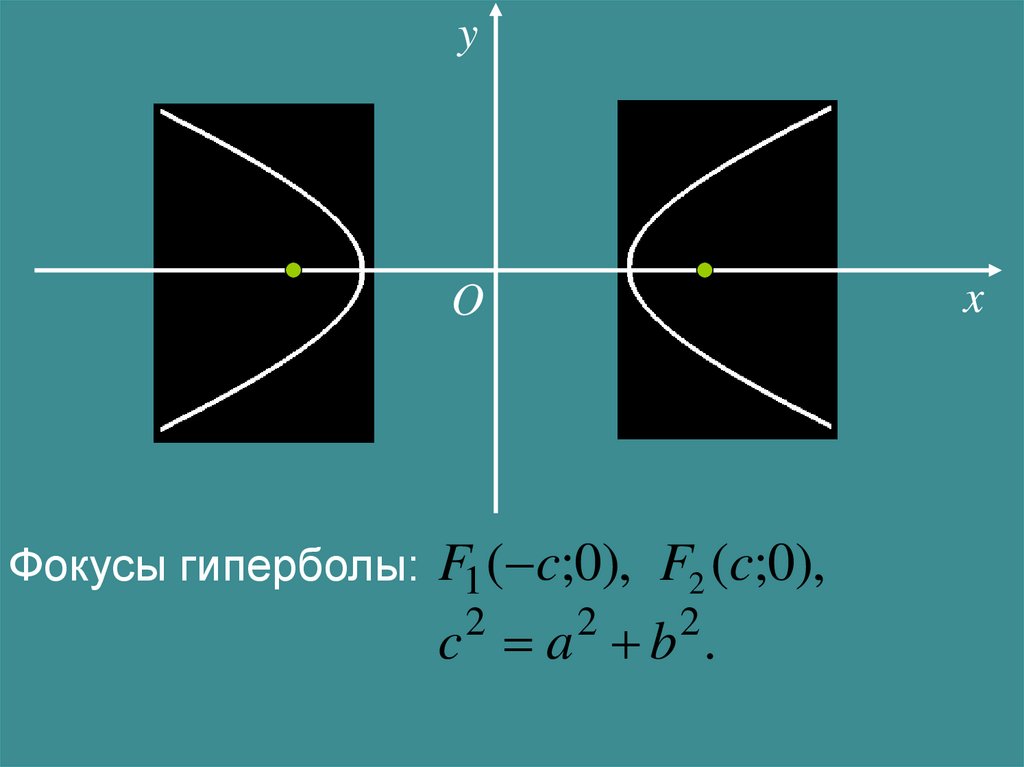
yF1
O
F2
Фокусы гиперболы: F1 ( c;0), F2 (c;0),
c a b .
2
2
2
x
24.
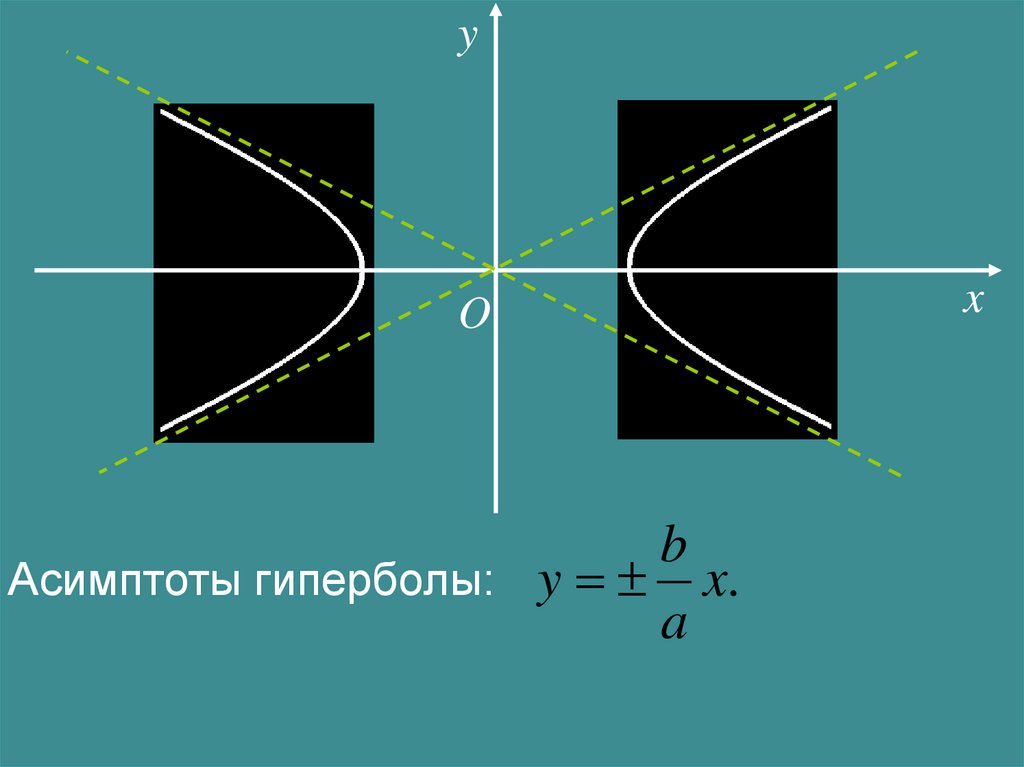
yO
b
Асимптоты гиперболы: y x.
a
x
25.
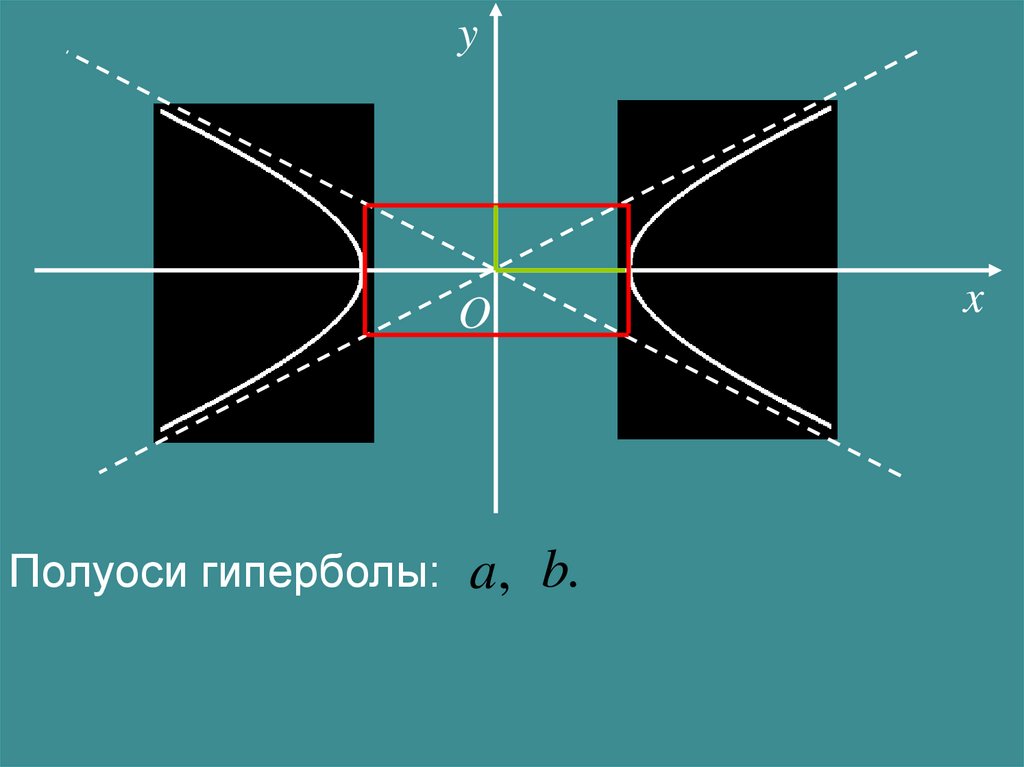
yO
Полуоси гиперболы: a, b.
x
26.
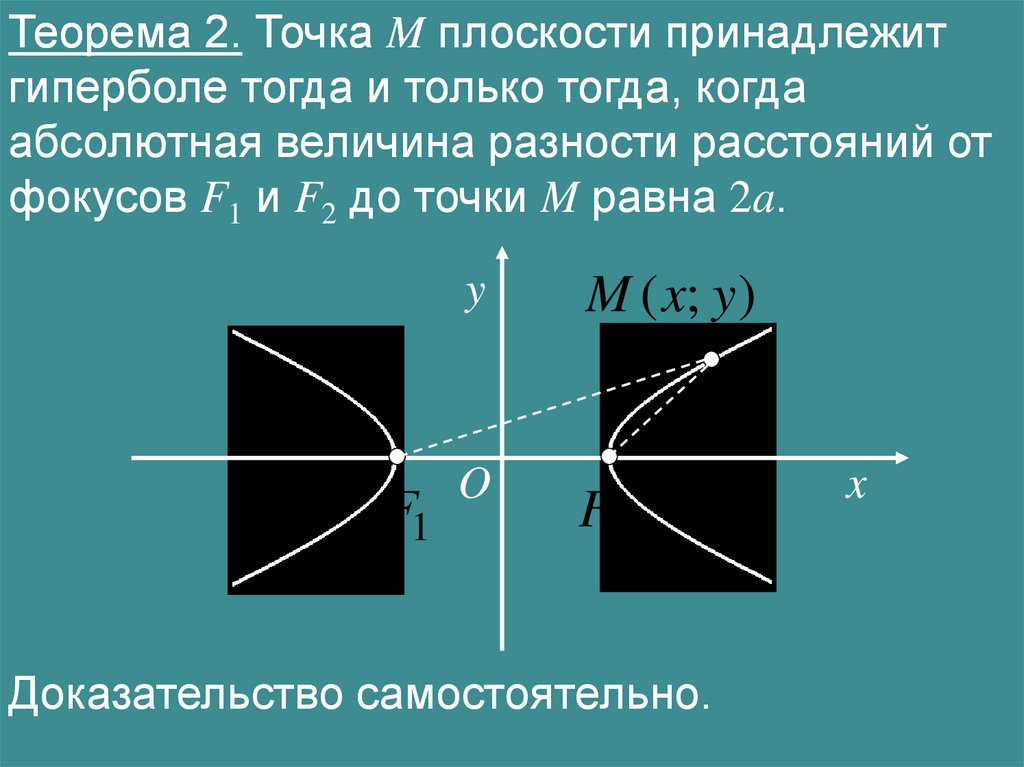
Теорема 2. Точка M плоскости принадлежитгиперболе тогда и только тогда, когда
абсолютная величина разности расстояний от
фокусов F1 и F2 до точки M равна 2a.
y
F1
O
M ( x; y )
F2
Доказательство самостоятельно.
x
27.
Свойства гиперболы1. Симметрия относительно осей координат и
начала координат.
2. Не пересекает ось Oy.
3. | x | a.
4.
a c.
5.
a b ─ равнобочная гипербола.
6. График гиперболы насколько угодно близко
приближается к асимптотам.
28.
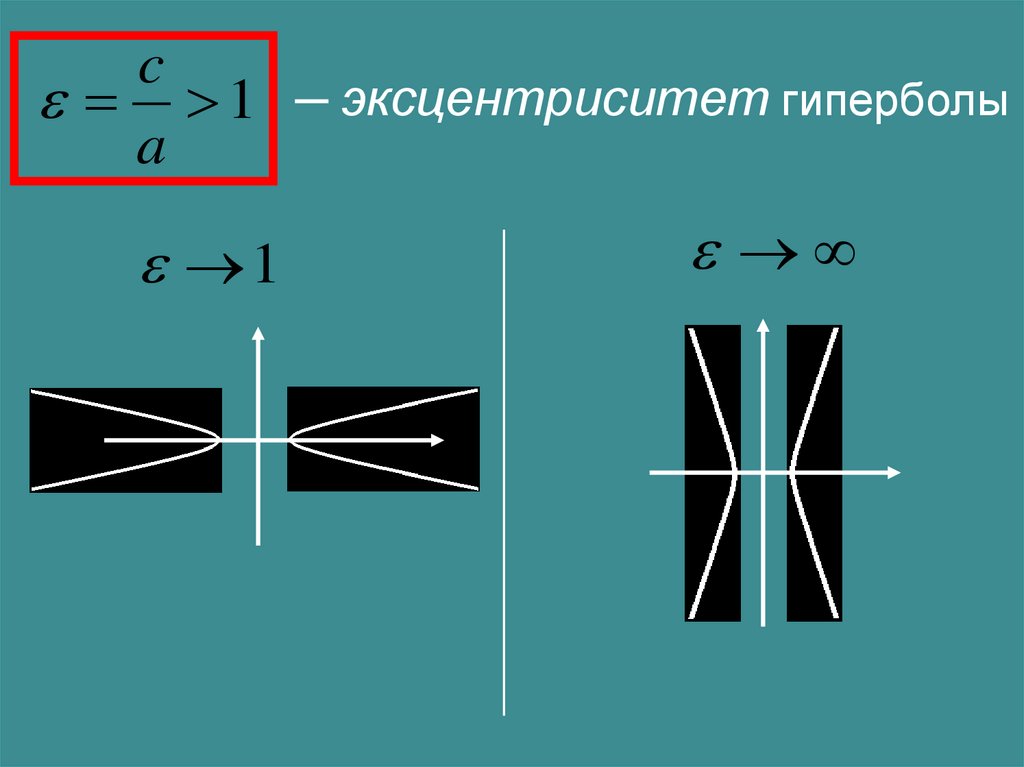
c1 ─ эксцентриситет гиперболы
a
1
29.
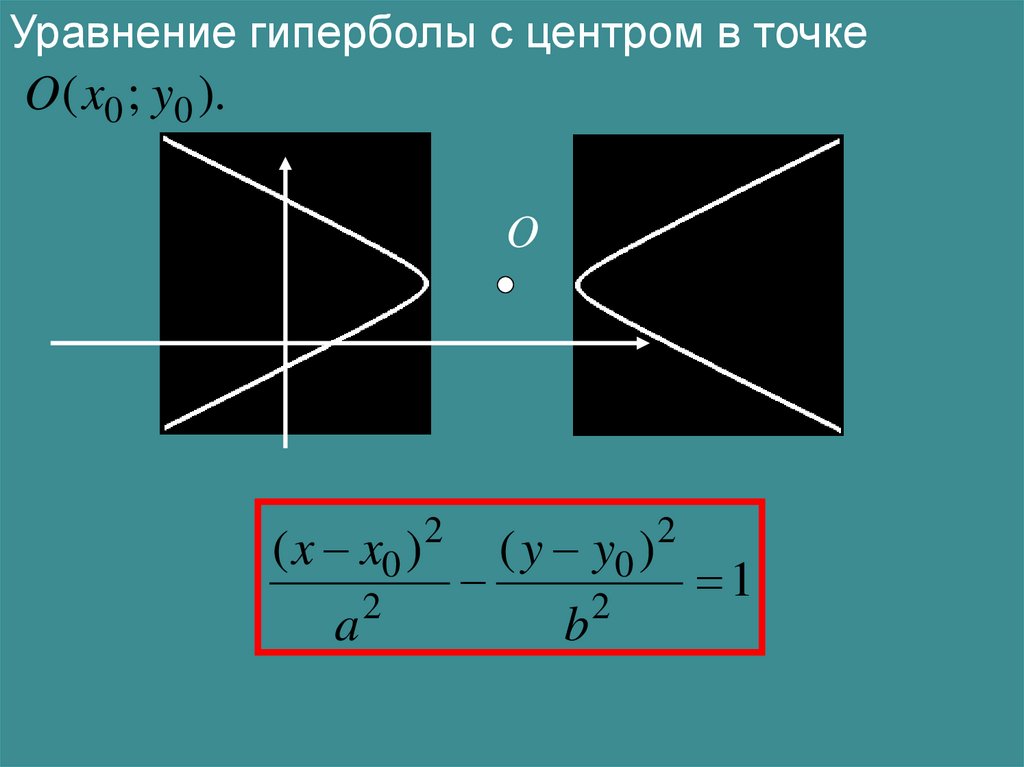
Уравнение гиперболы с центром в точкеO ( x0 ; y0 ).
O
( x x0 )
a
2
2
( y y0 )
b
2
2
1
30.
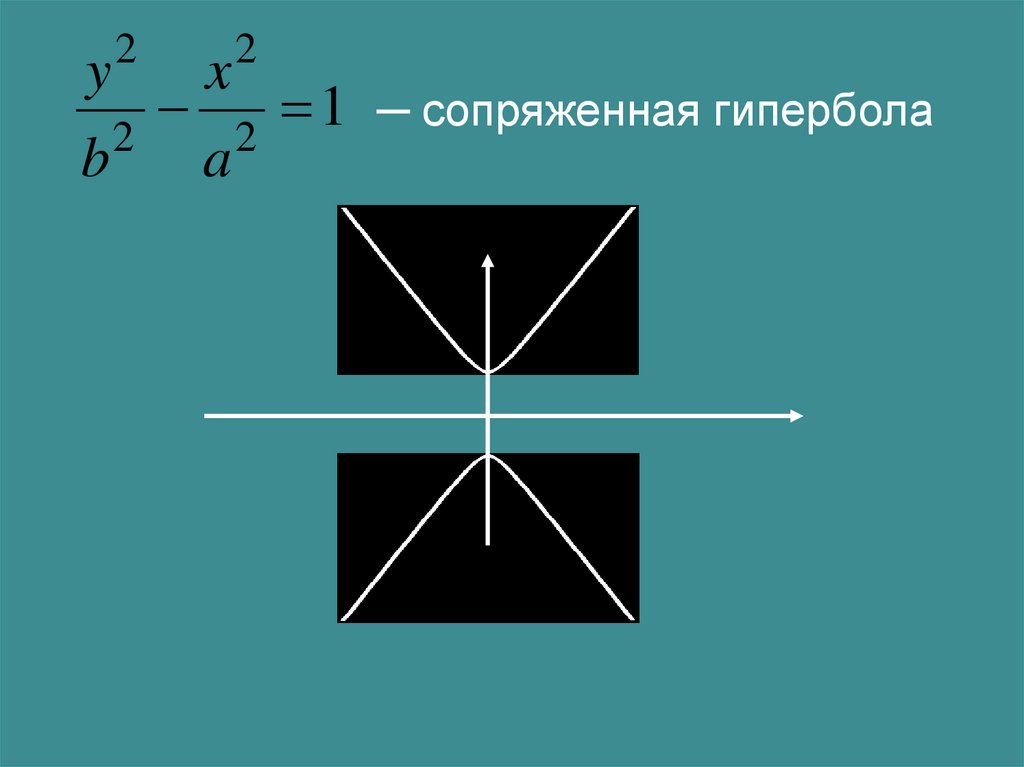
yb
2
2
x
a
2
1
─ сопряженная гипербола
2
31.
п.4. Парабола.Парабола есть геометрическое место
точек, координаты которых удовлетворяют
уравнению
y 2 px,
2
p 0.
32.
px
2
y
O
F
x
Ось параболы: Ox.
Вершина параболы: O(0;0).
p
Фокус: F ,0 .
2
p
Директриса: L : x .
2
Расстояние от фокуса до директрисы: p.
33.
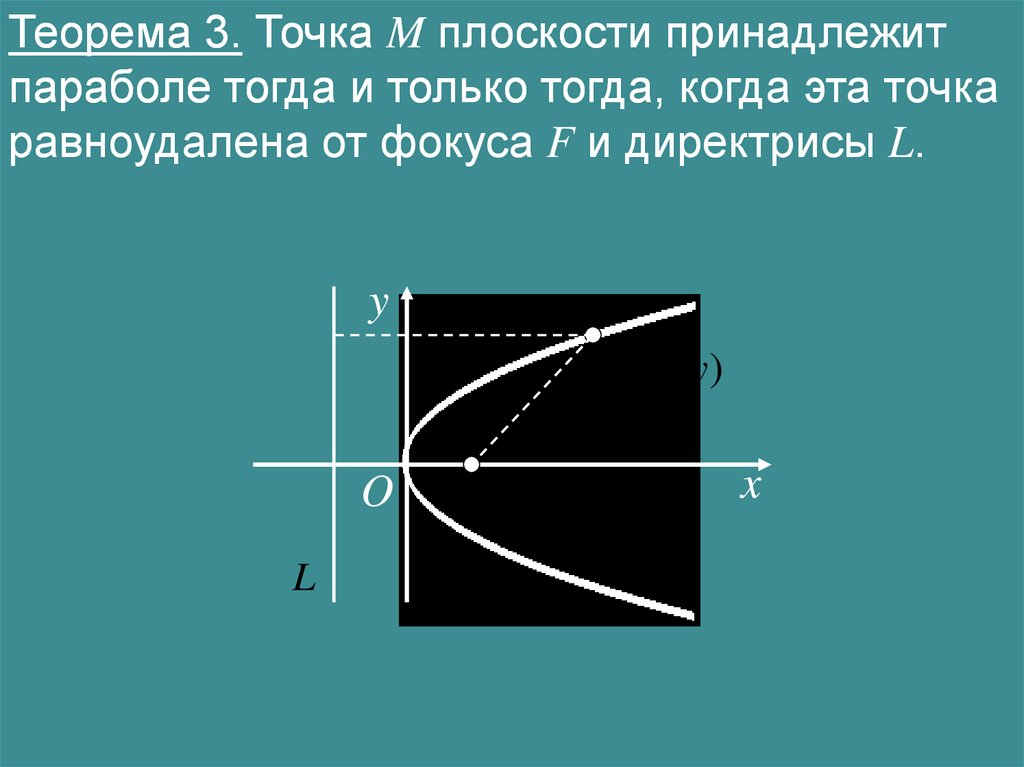
Теорема 3. Точка M плоскости принадлежитпараболе тогда и только тогда, когда эта точка
равноудалена от фокуса F и директрисы L.
y
M ( x; y )
O
L
F
x
34.
pN ; y
2
y
M ( x; y )
O
x
p
F ;0
2
L
2
p
2
MF x y
2
p
MN x
2
Доказательство самостоятельно.
35.
Свойства параболы1. Симметрия относительно оси Ox.
2. x 0.
3. Проходит через начало координат.
36.
Уравнение параболы с центром в точкеO ( x0 ; y0 ).
y
O
x
( y y0 ) 2 p( x x0 )
2
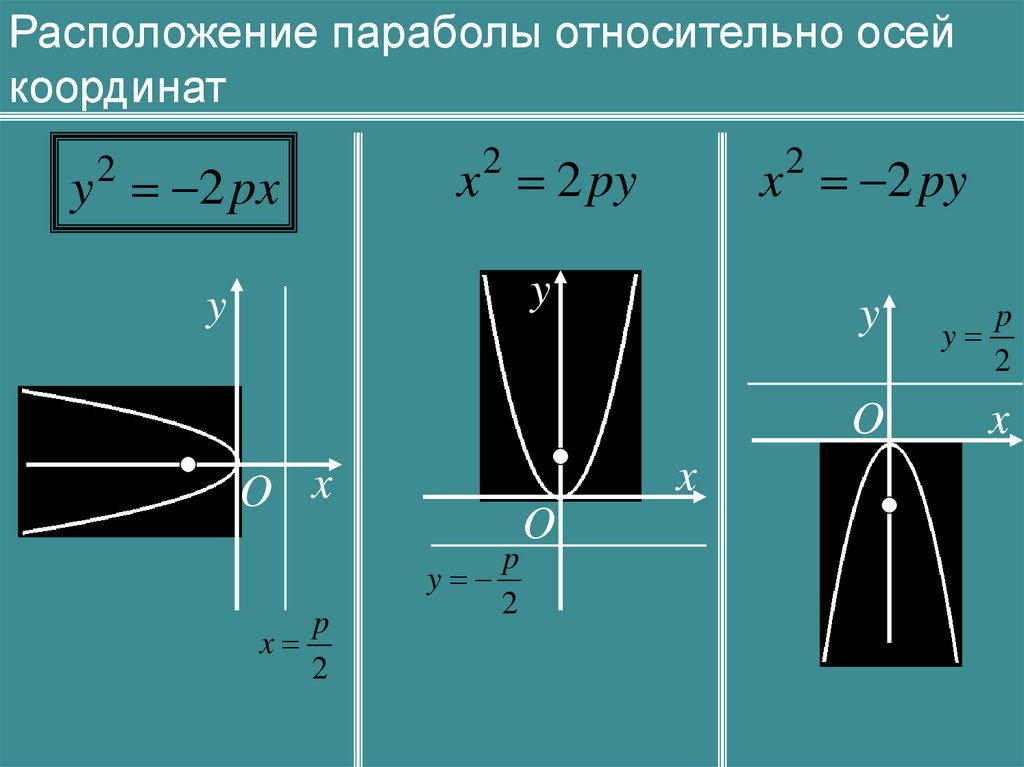
37.
Расположение параболы относительно осейкоординат
x 2 py
x 2 py
2
y 2 px
2
2
y
y
y
O
F
F
x
O x
x
p
2
p
y
2
O
F
y
p
2
x







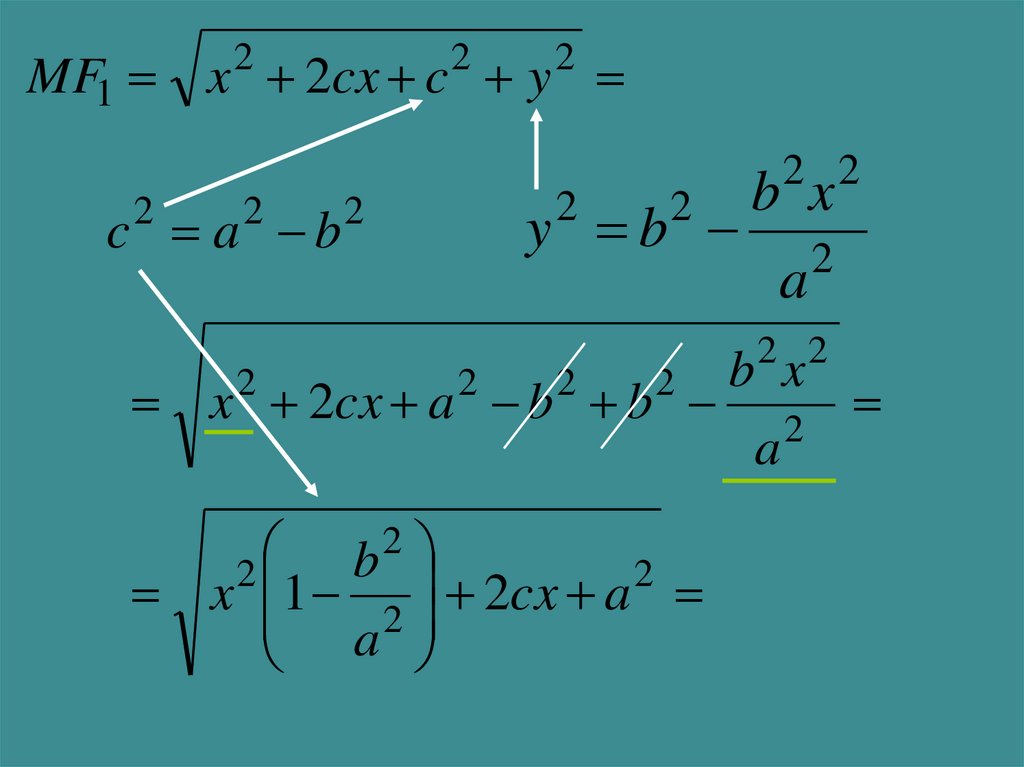
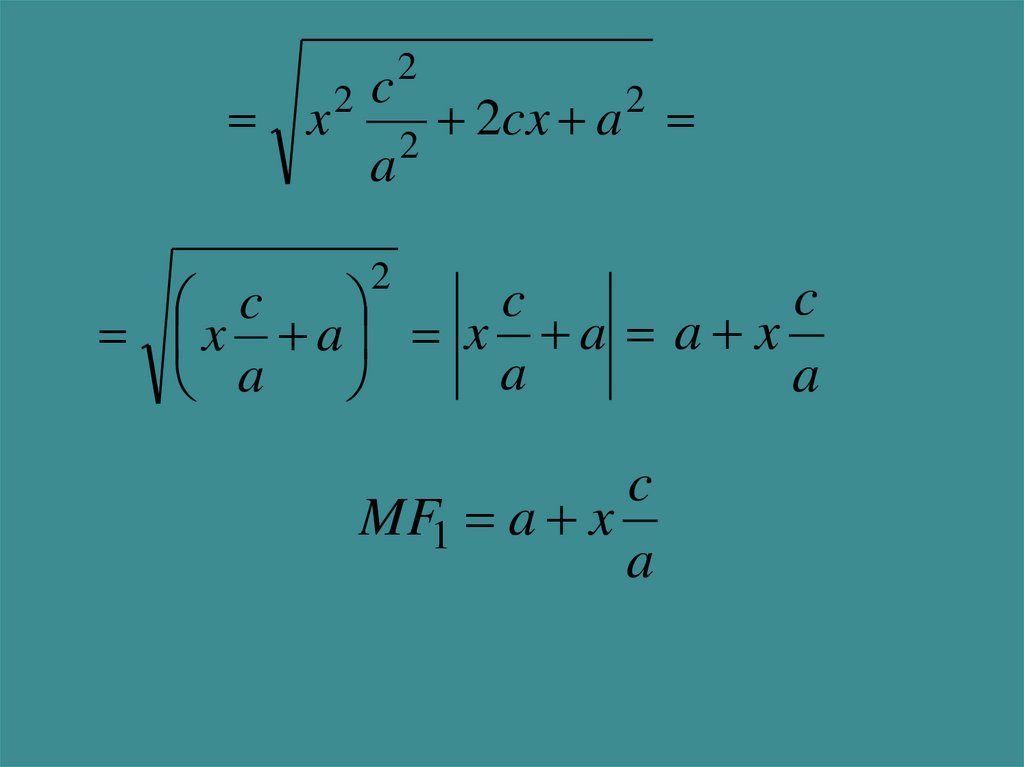


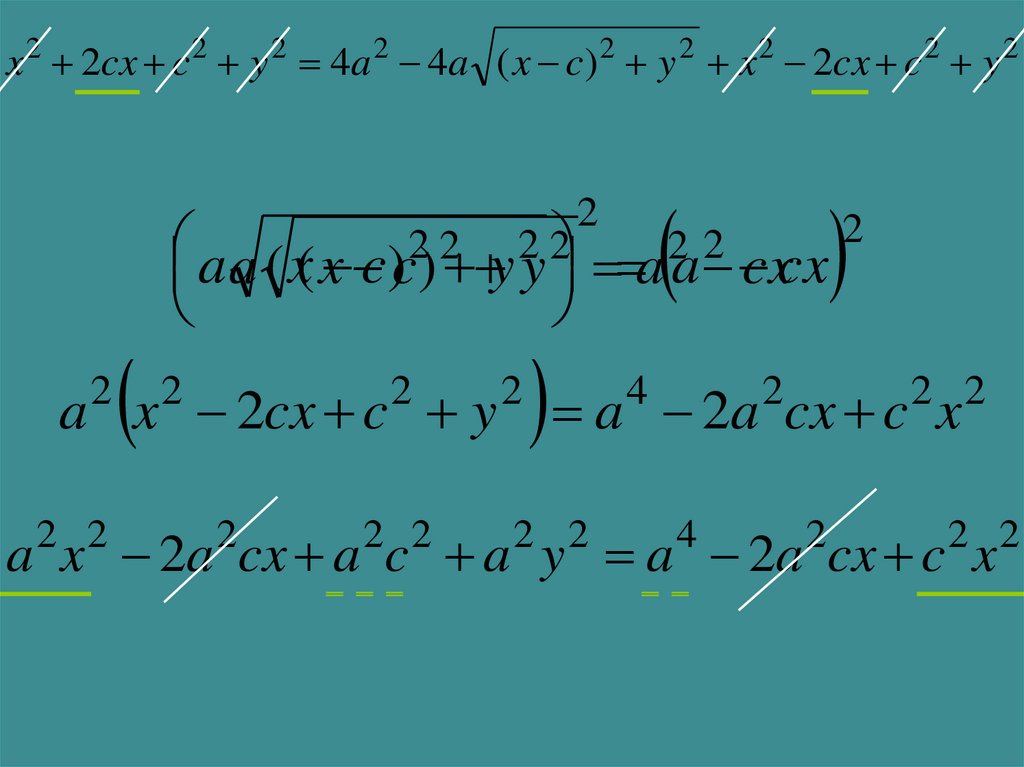



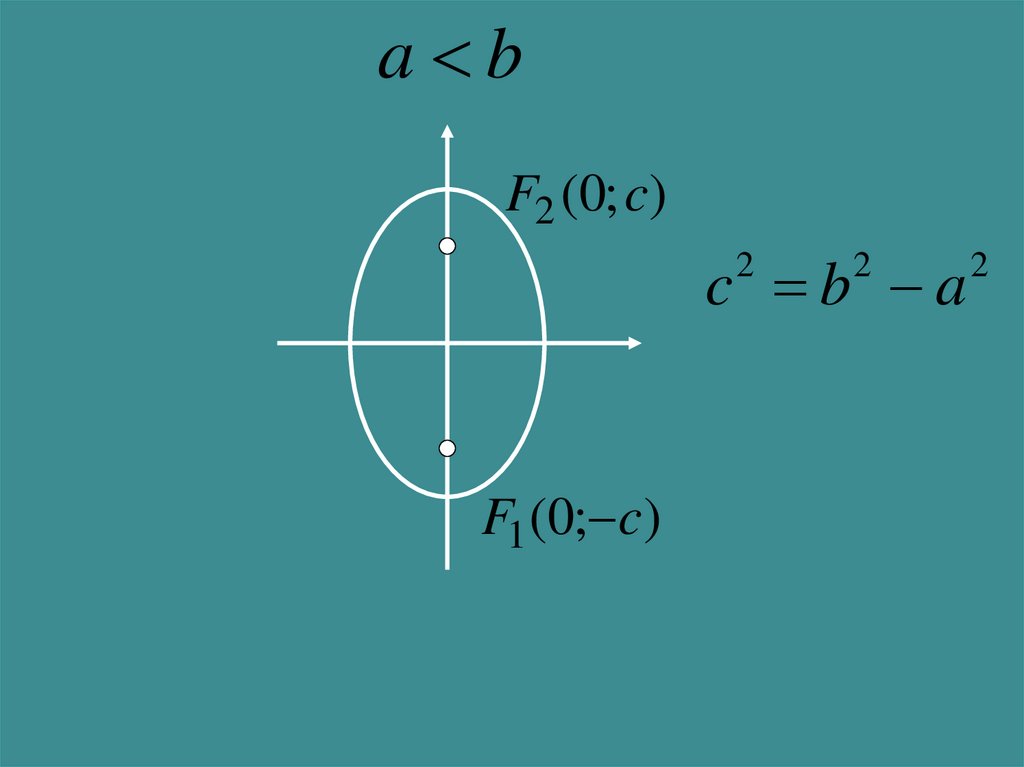







 Математика
Математика








