ЛЕКЦИЯ 3.3 информатика ИСП

1.

МК
АРИФМЕТИЧЕСКИЕ
ОПЕРАЦИИ
В ПОЗИЦИОННЫХ
СИСТЕМАХ СЧИСЛЕНИЯ
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ

2.

МК
Сложение чисел в системе счисления
с основанием q
Чтобы в системе счисления с основанием q получить сумму
S двух чисел A и B, надо просуммировать образующие их
цифры по разрядам i справа налево:
+
Aq
Bq
Sq
1
+
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
sn … si+1 si … s1 s0 q
ai + bi ≥ q
s i = ai + bi - q
a i + bi < q
s i = ai + bi
• если ai + bi < q, то si = ai + bi,
старший (i + 1)-й разряд не изменяется
• если ai + bi ≥ q, то si = ai + bi – q,
старший (i + 1)-й разряд увеличивается на 1

3.

МК
?
Сложение чисел в системе
счисления с основанием q
№ 1.
1 1
b)
1 2 1 1 0 13
+
2 2 23
1 2 2 1 0 03
1
1 2 3 4 5 68
+
1 2 3 48
c)
112+14+17+21=2 2=3 8≥4 3≥ 3
+
D 2 1 B 1 16
CA F E16
DECA F16
1–-–+3331====0012под
< 31-м
записываем
записываем
записываем
3
3
4
под
под
2-м
3-м
разрядом,
разрядом,
разрядом,
записываем
2
под
4-м
разрядом
а 2-й
3-й разряд увеличиваем на 1
4-й
1
+
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
sn … si+1 si … s1 s0 q
ai + bi ≥ q
s i = ai + bi - q
a i + bi < q
s i = ai + bi
Реши сам
а)
1 1 1
?

4.

МК
Решите самостоятельно
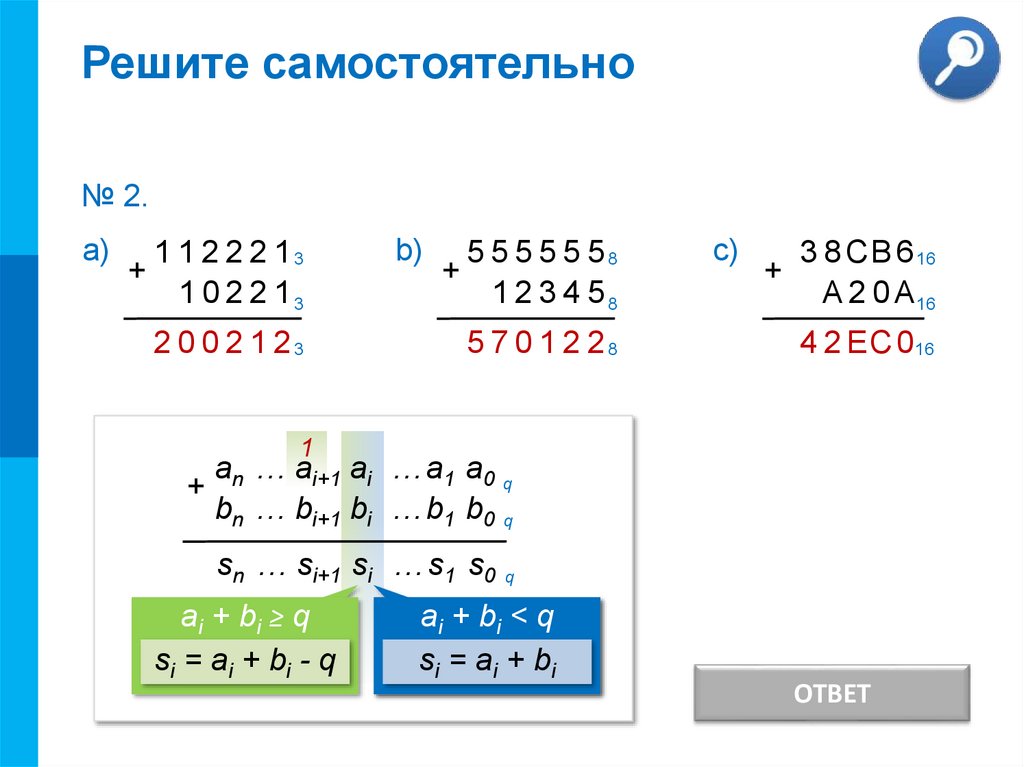
№ 2.
а)
1 1 2 2 2 13
+
1 0 2 2 13
2 0 0 2 1 23
b)
5 5 5 5 5 58
+
1 2 3 4 58
5 7 0 1 2 28
c)
+
3 8 CB 6 16
A 2 0 A16
4 2 EC 0 16
1
+
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
sn … si+1 si … s1 s0 q
ai + bi ≥ q
s i = ai + bi - q
ai + bi < q
s i = ai + bi
ОТВЕТ

5.

МК
Вычитание чисел в системе счисления
с основанием q
Чтобы в системе счисления с основанием q получить
разность R двух чисел A и B, надо вычислить разности
образующих их цифр по разрядам i справа налево:
–
Aq
Bq
Rq
–
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
rn … ri+1 ri … r1 r0 q
ai < bi
ri = q + a i – b i
ai ≥ bi
ri = ai – bi
• если ai ≥ bi, то ri = ai – bi,
старший (i + 1)-й разряд не изменяется
• если a i < b i , то ri = q + ai – bi ,
старший (i + 1)-й разряд уменьшается на 1

6.

МК
?
Вычитание чисел в системе
счисления с основанием q
№ 3.
●
b)
1 0 1 1 0 13
–
1 0 2 1 03
2 0 1 2 13
6 5 4 3 2 18
–
5 6 3 4 1 28
c)
7 0 7 00 7< 812
–
DECA F 16
CA F E16
D 2 1 B 1 16
1
01
≥
===02
записываем
записываем
3
3
+
+
0
0
–
2
1
12
под
под
5-м
3-м
2-м
разрядом,
разрядом,
записываем
записываем
1
0
0
=
под
1
под
4-м
1-м
разрядом
разрядом
делая
делая заем
заем вв 6-м
4-м
3-м разряде
разряде
–
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
rn … ri+1 ri … r1 r0 q
ai < bi
ri = q + a i – b i
ai ≥ bi
ri = a i – b i
Реши сам
а)
?

7.

МК
Решите самостоятельно
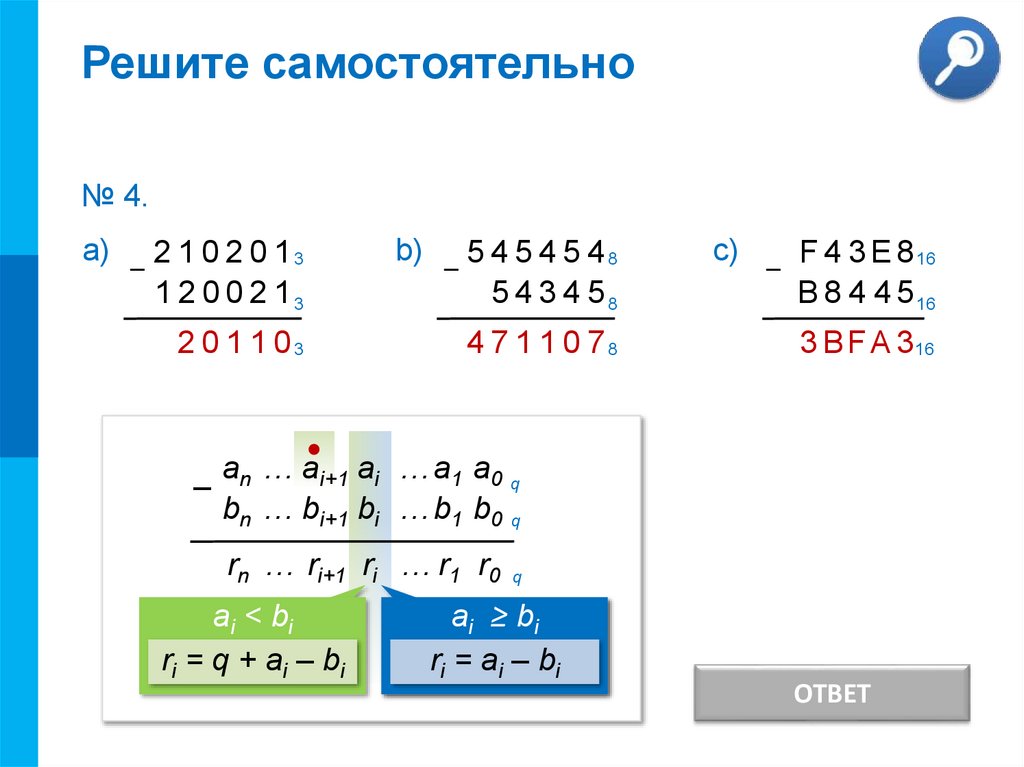
№ 4.
а)
–
b)
2 1 0 2 0 13
1 2 0 0 2 13
2 0 1 1 03
–
5 4 5 4 5 48
5 4 3 4 58
4 7 1 1 0 78
c)
–
F 4 3 E 8 16
B 8 4 4 5 16
3 B F A 3 16
–
an … ai+1 ai … a1 a0 q
bn … bi+1 bi … b1 b0 q
rn … ri+1 ri … r1 r0 q
ai < bi
ri = q + a i – b i
ai ≥ bi
ri = a i – b i
ОТВЕТ

8.

МК
Умножение многозначного числа на
однозначное в системе счисления q
Чтобы в системе счисления q получить произведение M
многозначного числа A и однозначного числа b, надо
вычислить произведения b и цифр числа A по разрядам i :
ai · b div q
Aq
х
Bq
Mq
an … ai+1 ai … a1 a0 q
x
b q
mn …mi+1 mi …m1 m0 q
ai · b ≥ q
mi = ai · b mod q
ai · b < q
mi = ai · b
• если ai · b < q, то mi = ai · b,
старший (i + 1)-й разряд не изменяется
• если ai · b ≥ q, то mi = ai · b mod q,
старший (i + 1)-й разряд увеличивается на ai · b div q

9.

МК
?
Умножение чисел в системе
счисления с основанием q
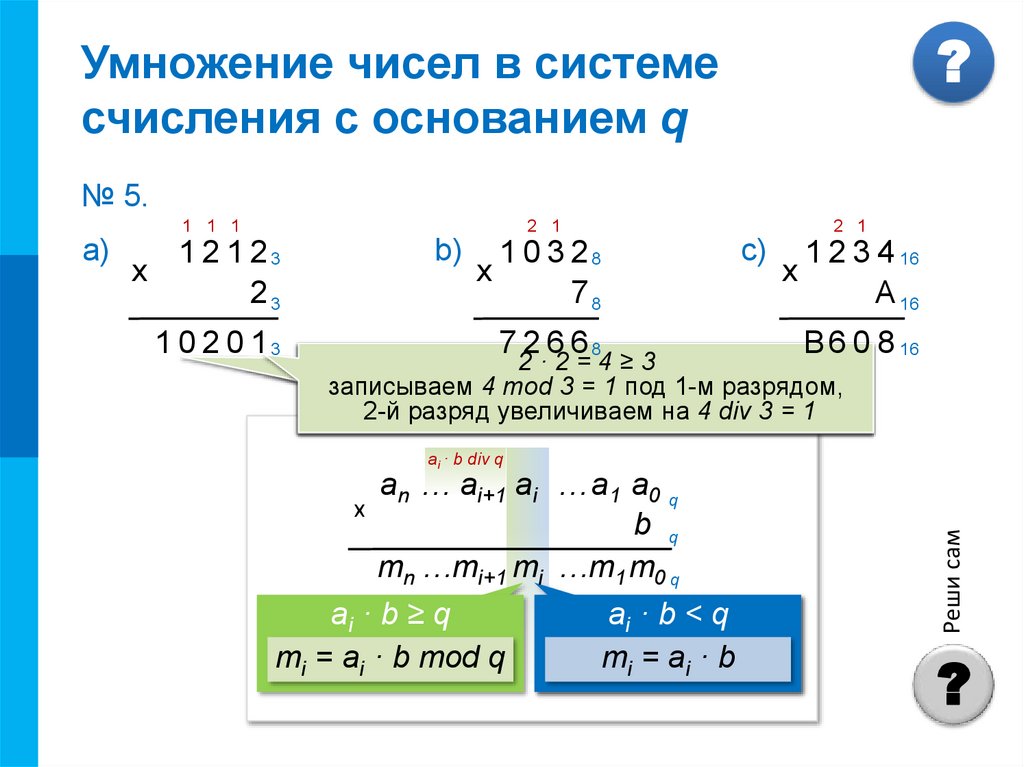
№ 5.
2 1
1 2 1 23
х
23
1 0 2 0 13
b)
1 0 3 28
х
78
7 2 6 68
с)
2 1
х
1 2 3 4 16
А 16
В 6 0 8 16
2 ·2 1
1
2=
1=
4≥
33
≥3
2· +
записываем
записываем 4
33 mod
mod 33 == 1
00 под
под 1-м
2-м
4-м разрядом,
разрядом
5
2
3-м
и2-й
3-й
в 5-й
разряд
записываем
3 div
4-й
разряд
увеличиваем
на 34
5
div 33 == 11
ai · b div q
an … ai+1 ai … a1 a0 q
x
b q
mn …mi+1 mi …m1 m0 q
ai · b ≥ q
ai · b < q
mi = ai · b mod q
mi = ai · b
Реши сам
а)
1 1 1
?

10.

МК
Решите самостоятельно
№ 6.
а)
2 1 0 23
х
23
1 1 2 1 13
b)
2 0 58
х
58
1 2 3 18
с)
х
А 1 В 2 16
5 16
3 2 8 7 А 16
ai · b div q
an … ai+1 ai … a1 a0 q
x
b q
mn …mi+1 mi …m1 m0 q
ai · b ≥ q
ai · b < q
mi = ai · b mod q
mi = ai · b
ОТВЕТ

11.

МК
Деление чисел в системе счисления
с основанием q
Деление нельзя свести к поразрядным операциям над
цифрами, составляющими число.
Деление чисел в системе счисления с произвольным
основанием q выполняется так же, как и в десятичной
системе счисления.
А значит нам понадобятся правила умножения и вычитания
чисел в системе счисления с основанием q.

12.

МК
Делениесамостоятельно
чисел в системе
Решите
счисления с основанием q
?
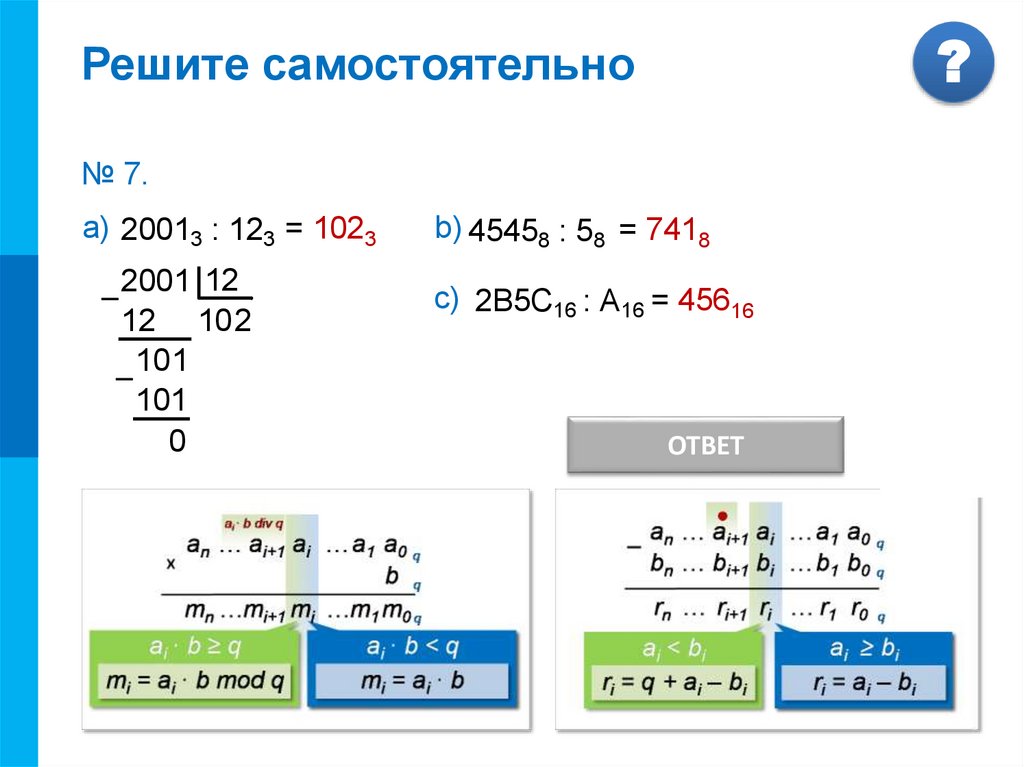
№ 7.
2001 12
12 102
10 1
–
101
0
–
b) 45458 : 58 = 7418
с) 2В5С16 : А16 = 45616
ОТВЕТ
Реши сам
а) 20013 : 123 = 1023
?

13.

МК
Двоичная арифметика
Таблица
сложения
Таблица
вычитания
Таблица
умножения
+
0
1
–
х
0 1
0 1
1 10
0
1
№ 8.
а)
1 1 1 1 1
1 1 1 1 12
+
12
1 0 0 0 0 02
b)
0
0
1
1
11
0
0
1
●
2 2 2
1 0 0 02
–
12
1 1 12
0
0
1
1
1
1
● 2
2 0 2
c)
10101 0 2
–
11 1 2
100011 2

14.

МК
В КОНСПЕКТЕ ДОЛЖНО БЫТЬ …
• СЛОЖЕНИЕ ЧИСЕЛ В СИСТЕМЕ СЧИСЛЕНИЯ С ОСНОВАНИЕМ
Q. АЛГОРИТМ. ПРИМЕРЫ.
• ВЫЧИТАНИЕ
ЧИСЕЛ
В
СИСТЕМЕ
СЧИСЛЕНИЯ
С
ОСНОВАНИЕМ Q. АЛГОРИТМ. ПРИМЕРЫ.
• УМНОЖЕНИЕ
ЧИСЕЛ
В
СИСТЕМЕ
СЧИСЛЕНИЯ
С
ОСНОВАНИЕМ Q. АЛГОРИТМ. ПРИМЕРЫ.
• ДЕЛЕНИЕ ЧИСЕЛ В СИСТЕМЕ СЧИСЛЕНИЯ С ОСНОВАНИЕМ
Q. АЛГОРИТМ. ПРИМЕРЫ.
• ДВОИЧНАЯ АРИФМЕТИКА. ПРИМЕРЫ.