Лекция №5 (3)

1.

Лекция №5
Математический аппарат для построения
компьютерных сетей

2.

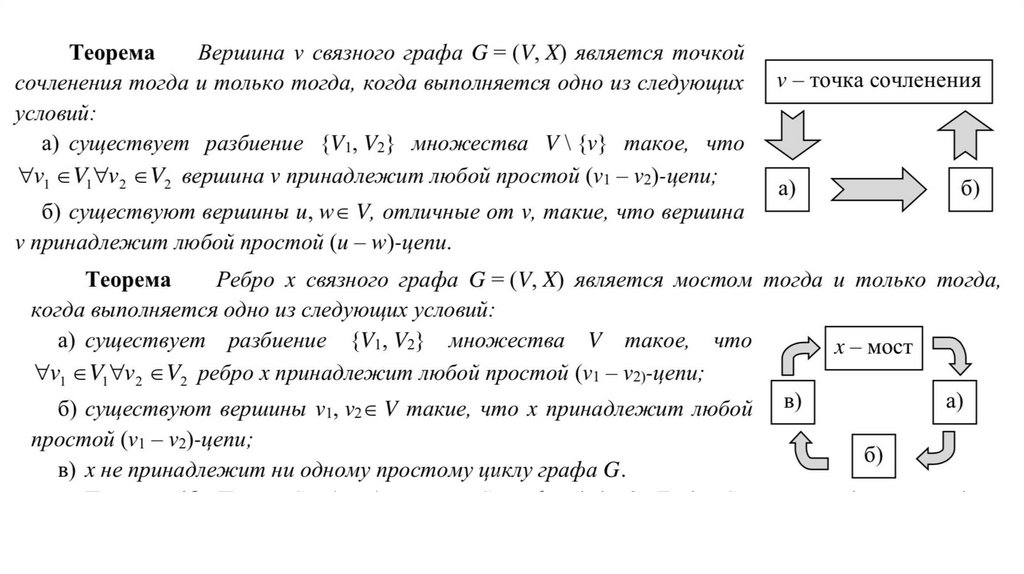
Точки сочленения, мосты и блоки
• Точка сочленения графа G = (V, X) – такая его вершина v, при
удалении которой получается граф G – v с числом компонент
большим, чем у графа G.
• Мост графа – его ребро x, удаление которого увеличивает число
компонент.
Граф неразделимый, если он связный, непустой и без точек
сочленения, иначе – разделимый.
• Блок графа – его максимальный неразделимый подграф.

3.

4.

5.

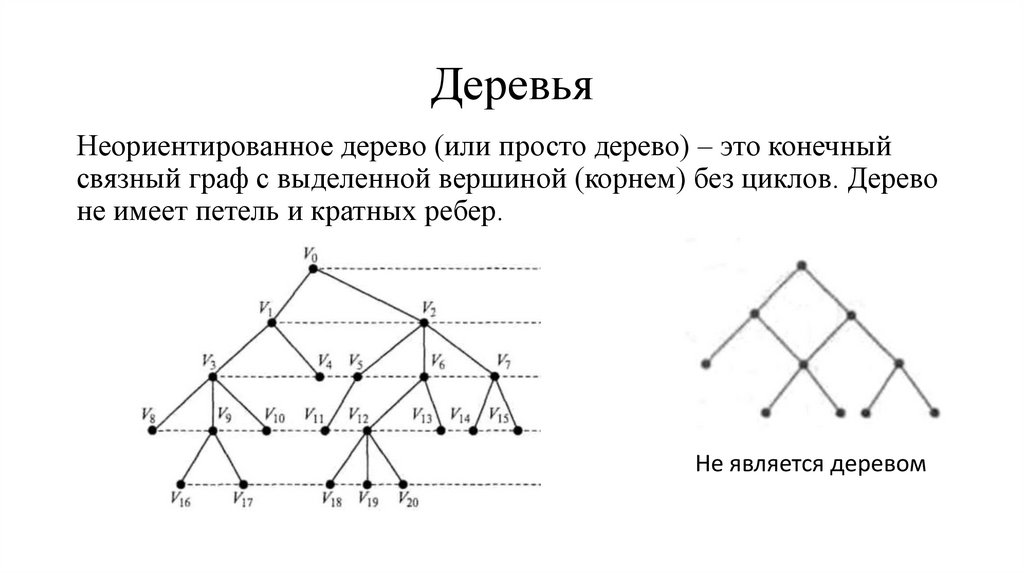
Деревья
Неориентированное дерево (или просто дерево) – это конечный
связный граф с выделенной вершиной (корнем) без циклов. Дерево
не имеет петель и кратных ребер.
Не является деревом

6.

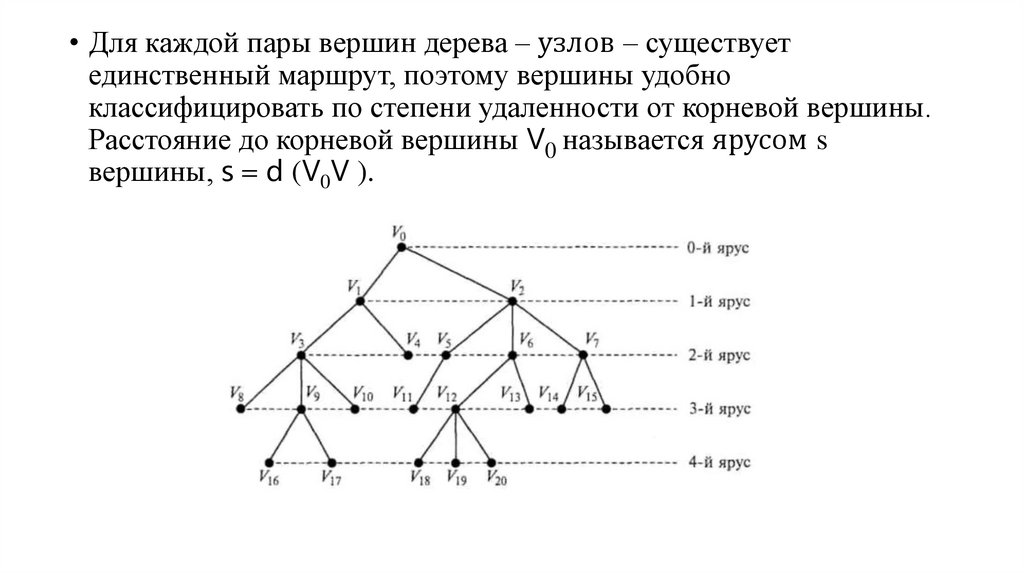
• Для каждой пары вершин дерева – узлов – существует
единственный маршрут, поэтому вершины удобно
классифицировать по степени удаленности от корневой вершины.
Расстояние до корневой вершины V0 называется ярусом s
вершины, s d (V0V ).

7.

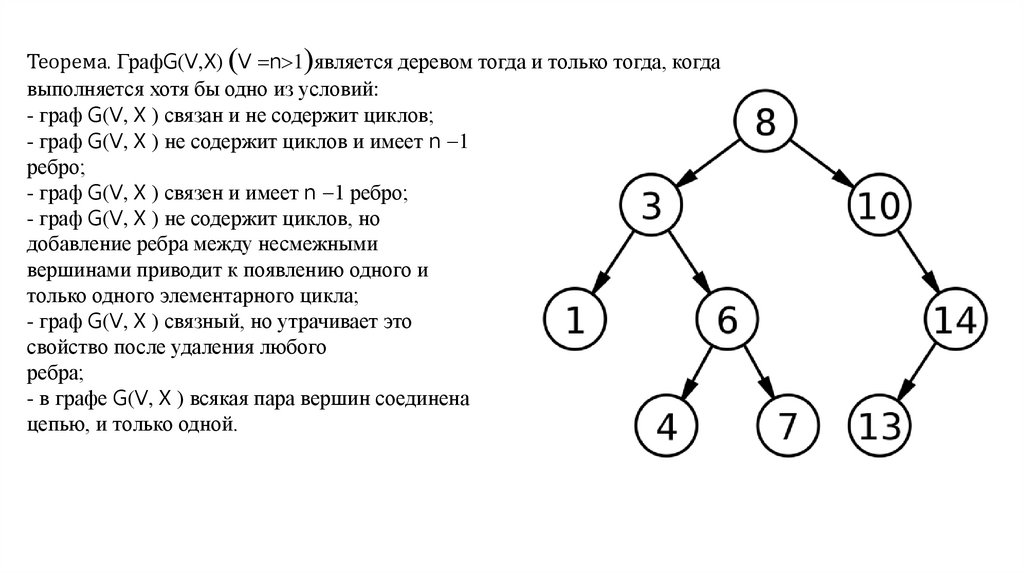
Теорема. ГрафG(V,X) V n 1 является деревом тогда и только тогда, когда
выполняется хотя бы одно из условий:
- граф G(V, X ) связан и не содержит циклов;
- граф G(V, X ) не содержит циклов и имеет n 1
ребро;
- граф G(V, X ) связен и имеет n 1 ребро;
- граф G(V, X ) не содержит циклов, но
добавление ребра между несмежными
вершинами приводит к появлению одного и
только одного элементарного цикла;
- граф G(V, X ) связный, но утрачивает это
свойство после удаления любого
ребра;
- в графе G(V, X ) всякая пара вершин соединена
цепью, и только одной.

8.

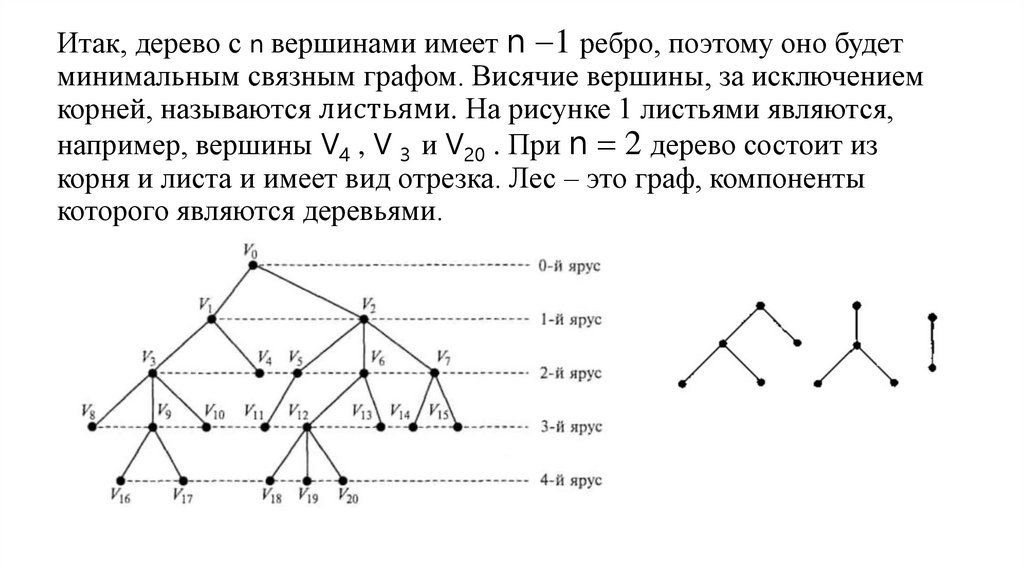
Итак, дерево с n вершинами имеет n 1 ребро, поэтому оно будет
минимальным связным графом. Висячие вершины, за исключением
корней, называются листьями. На рисунке 1 листьями являются,
например, вершины V4 , V 3 и V20 . При n 2 дерево состоит из
корня и листа и имеет вид отрезка. Лес – это граф, компоненты
которого являются деревьями.

9.

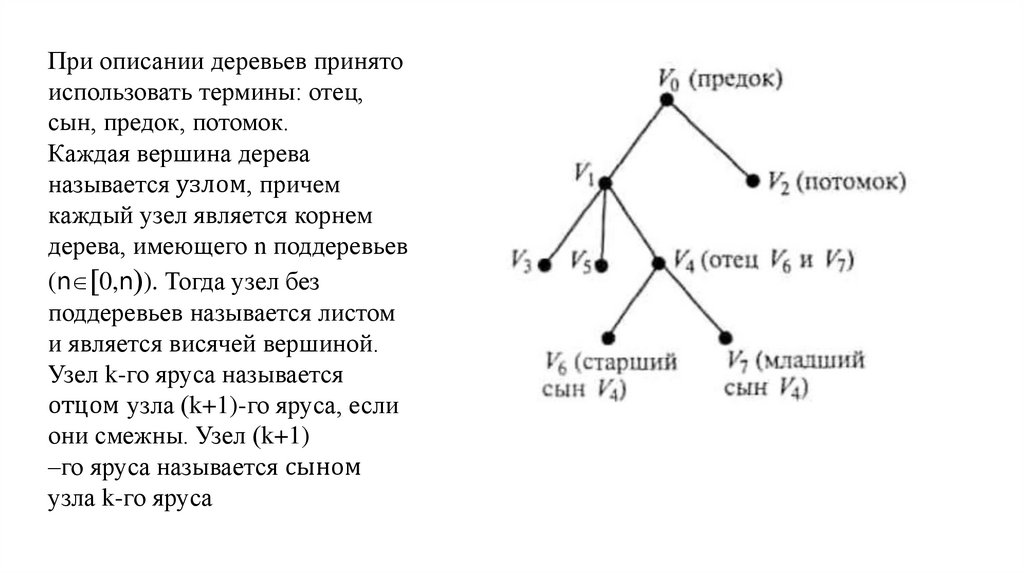
При описании деревьев принято
использовать термины: отец,
сын, предок, потомок.
Каждая вершина дерева
называется узлом, причем
каждый узел является корнем
дерева, имеющего n поддеревьев
(n 0,n ). Тогда узел без
поддеревьев называется листом
и является висячей вершиной.
Узел k-го яруса называется
отцом узла (k+1)-го яруса, если
они смежны. Узел (k+1)
–го яруса называется сыном
узла k-го яруса

10.

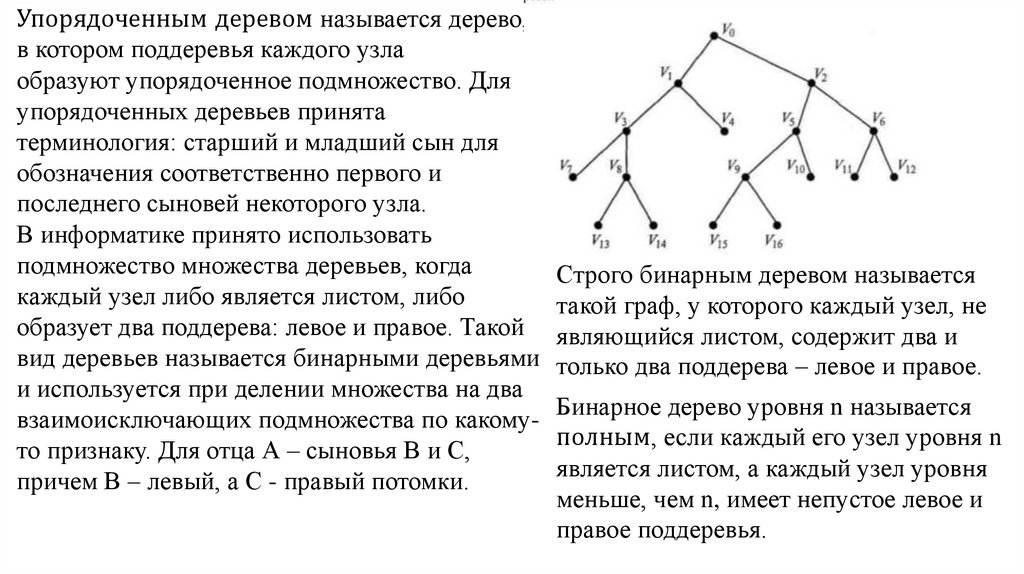
Упорядоченным деревом называется дерево,
в котором поддеревья каждого узла
образуют упорядоченное подмножество. Для
упорядоченных деревьев принята
терминология: старший и младший сын для
обозначения соответственно первого и
последнего сыновей некоторого узла.
В информатике принято использовать
подмножество множества деревьев, когда
Строго бинарным деревом называется
каждый узел либо является листом, либо
такой граф, у которого каждый узел, не
образует два поддерева: левое и правое. Такой являющийся листом, содержит два и
вид деревьев называется бинарными деревьями только два поддерева – левое и правое.
и используется при делении множества на два
взаимоисключающих подмножества по какому- Бинарное дерево уровня n называется
полным, если каждый его узел уровня n
то признаку. Для отца А – сыновья В и С,
является листом, а каждый узел уровня
причем В – левый, а С - правый потомки.
меньше, чем n, имеет непустое левое и
правое поддеревья.

11.

Цикломатическое число графа
Пусть задан неориентированный граф G.
Цикломатическим числом графа называется число v(G) m(G) c(G) n(G), где
m(G) число его ребер; c(G) число связных компонент графа; n(G) число вершин.
Цикломатическое число дерева равно нулю. Цикломатическое число леса равно сумме
цикломатических чисел составных связных компонент – деревьев и, следовательно,
тоже равно нулю. Для остальных графов цикломатические числа – положительные.
Например, для полного графа К5 (имеющего пять вершин и 10 ребер) цикломатическое
число равно v 10 1 5 6.

12.

Алгоритмы поиска кратчайшего пути
В задаче о кратчайшем пути (shortest-paths problem) задается взвешенный
ориентированный граф G = (V, Е) с весовой функцией w : Е —> R, отображающей ребра
на их веса, значения которых выражаются действительными числами. Вес (weight) пути р
= (Vo, Vi,..., Vk) равен суммарному весу входящих в него ребер.
Вес кратчайшего пути (shortest-path weight) из вершины и в вершину v определяется
соотношением
Тогда по определению кратчайший путь (shortest path) из вершины и в вершину v —
это любой путь, вес которого удовлетворяет соотношению w (р) = delta(u, v).
Вес каждого из ребер можно интерпретировать не как расстояние, а как другую
метрику.

13.

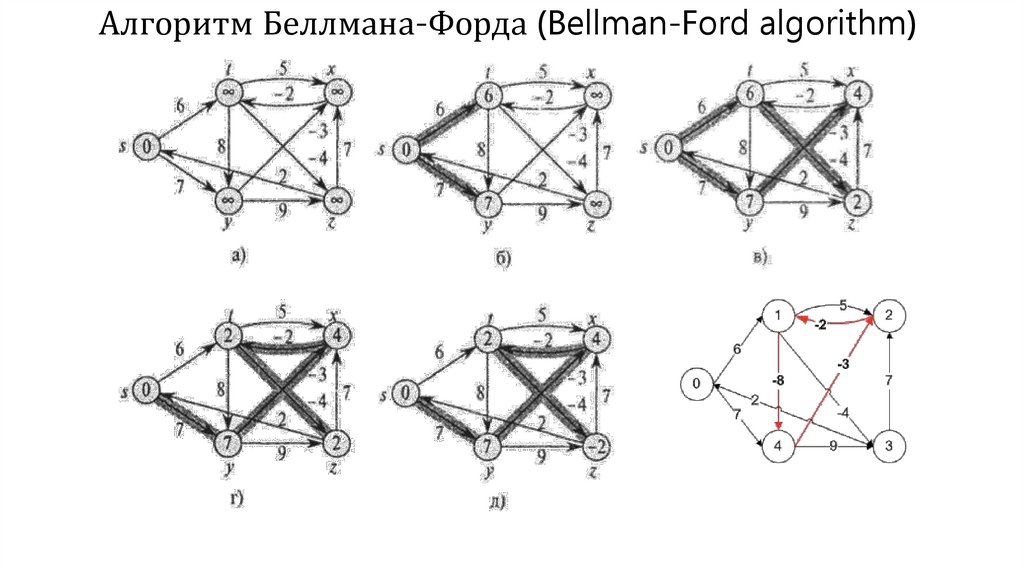
Алгоритм Беллмана-Форда (Bellman-Ford algorithm)
Алгоритм Беллмана-Форда позволяет решить задачу о кратчайшем пути из одной
вершины в общем случае, когда вес каждого из ребер может быть отрицательным.
Для заданного взвешенного ориентированного графа G = (V, Е) с истоком s и
весовой функцией w: Е —» R алгоритм Беллмана-Форда возвращает логическое
значение, указывающее на то, содержится ли в графе цикл с отрицательным весом,
достижимый из истока.

14.

Алгоритм Беллмана-Форда (Bellman-Ford algorithm)

15.

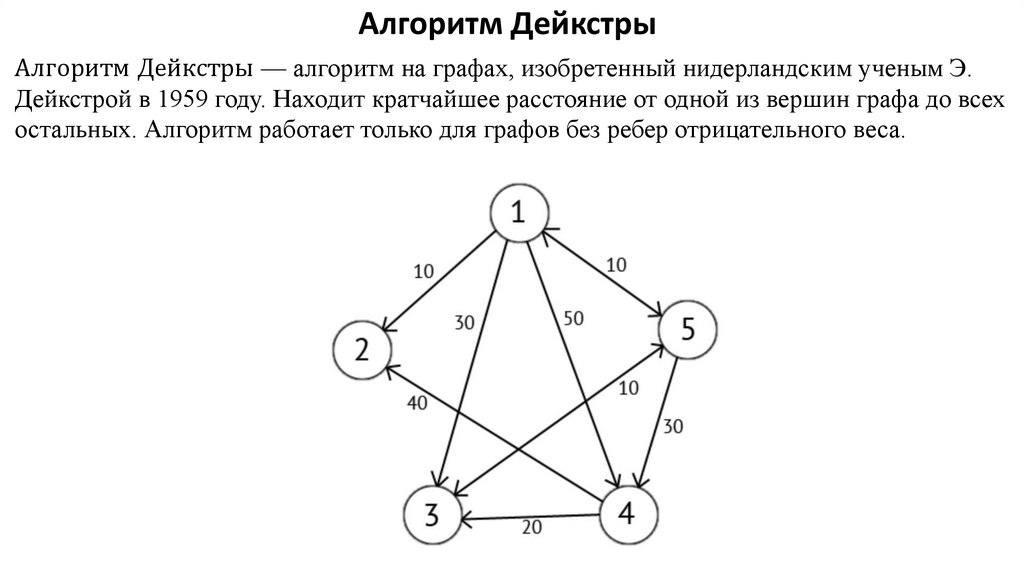
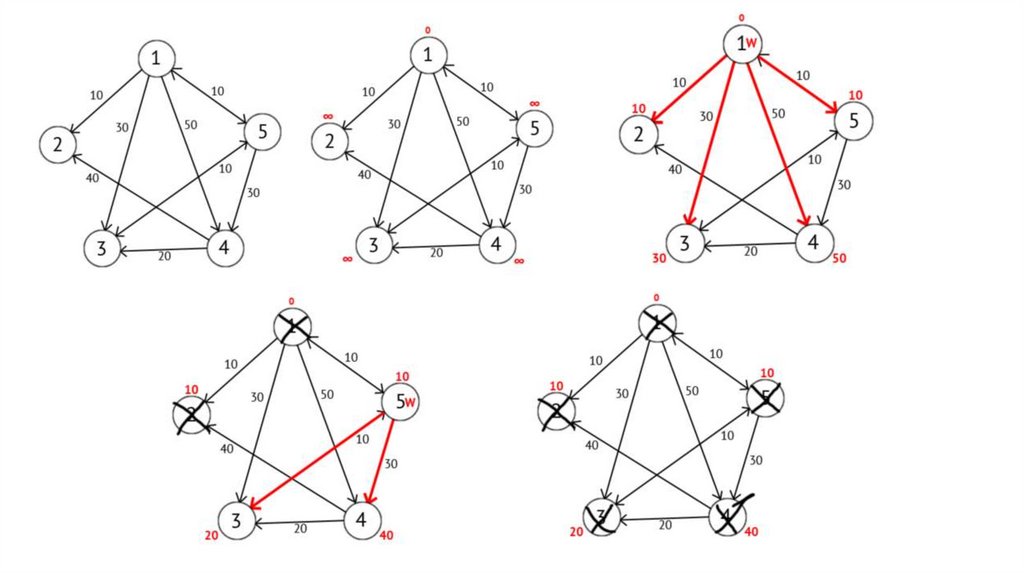
Алгоритм Дейкстры
Алгоритм Дейкстры — алгоритм на графах, изобретенный нидерландским ученым Э.
Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех
остальных. Алгоритм работает только для графов без ребер отрицательного веса.

16.

17.

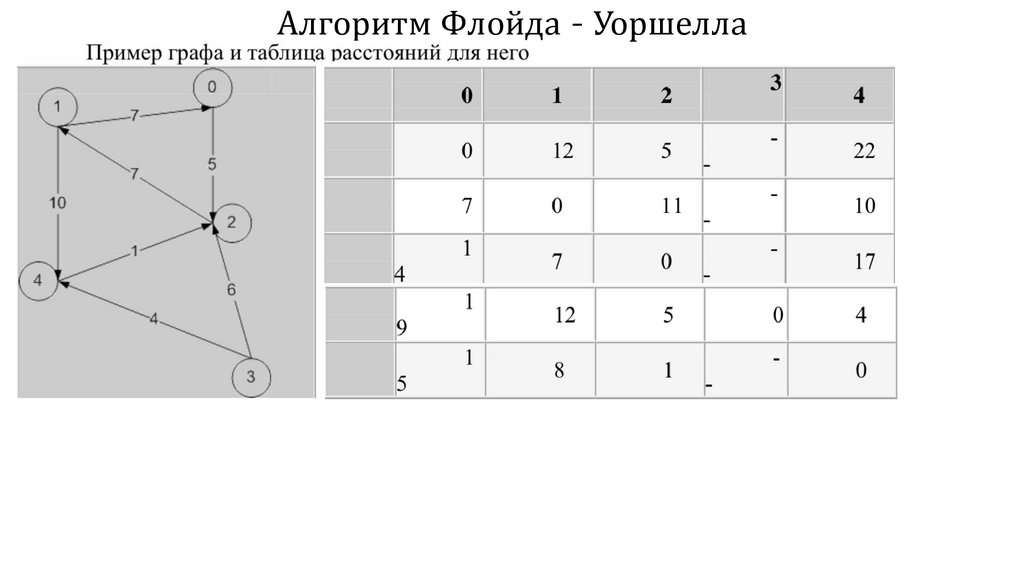
Алгоритм Флойда - Уоршелла
Динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами
взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и
Стивеном Уоршеллом.
Более строгая формулировка этой задачи следующая:
есть ориентированный граф G = (V, Е) каждой дуге v -> w этого графа сопоставлена
неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей
заключается в нахождении для каждой упорядоченной пары вершин v, w любого пути от
вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к
w.

18.

Алгоритм Флойда - Уоршелла