Похожие презентации:
Вокруг проблемы четырех красок
1.
Бугаев Иван, 6 «В» классГУО «Средняя школа
им. Я. Купалы №19 г. Минска»
Научный
руководитель:
Карневич Лариса
Геннадьевна
2.
Математики Френсис Гутри (слева), которыйпредположил, что любую карту можно
раскрасить в четыре цвета, и Артур Кэли,
который представил эту задачу Лондонскому
математическому обществу
2024/10/20
3.
С 1970 по 1976 год математикиКеннет Аппель и Вольфганг
Хакен из Иллинойского
университета в УрбанаШампейн с помощью
компьютера путем перебора
многих тысяч вариантов
окончательно доказали:
«Четырех цветов
достаточно».
Это событие приобрело
такую важность
2024/10/20
4.
исследование теоремы о четырехцветах и возможностей ее
практического применения
1.
Изучить
историю
возникновения
проблемы четырёх красок, варианты ее
доказательств.
2. Провести исследование по данной
тематике на примере плоскостных карт и
правильных многогранников.
3.
Изготовить
макеты
правильных
многогранников с применением теоремы о
четырех цветах для их раскраски.
4. Разработать пособие
«4 цвета» с
заданиями – раскрасками для плоскостных карт.
2024/10/20
5.
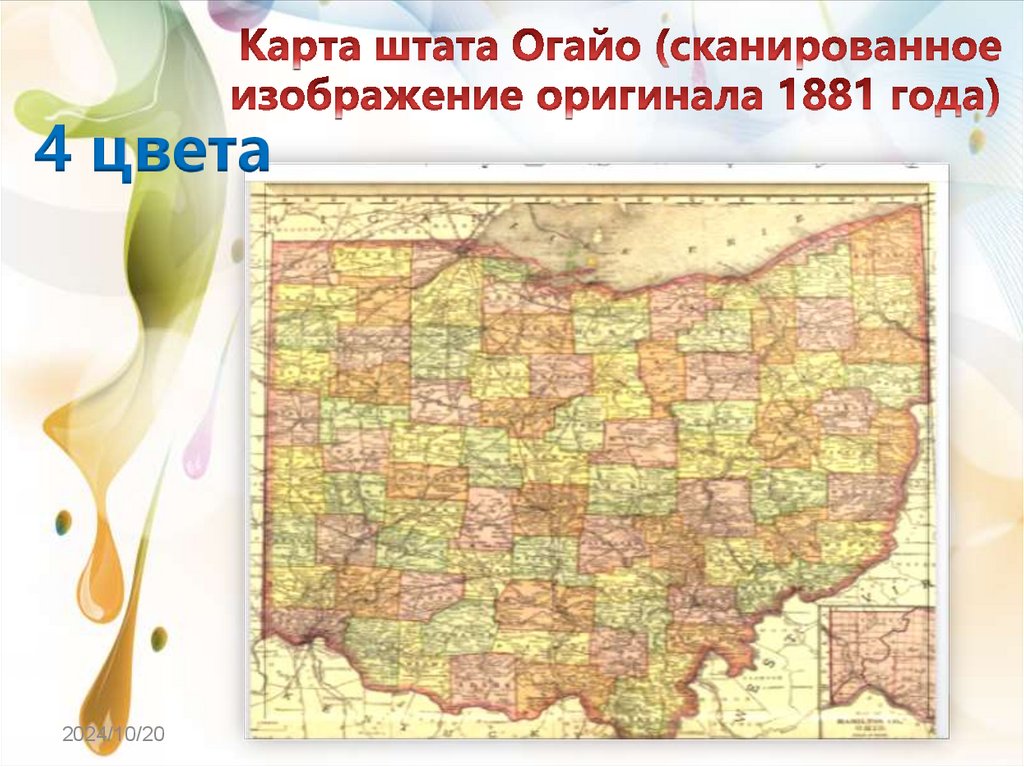
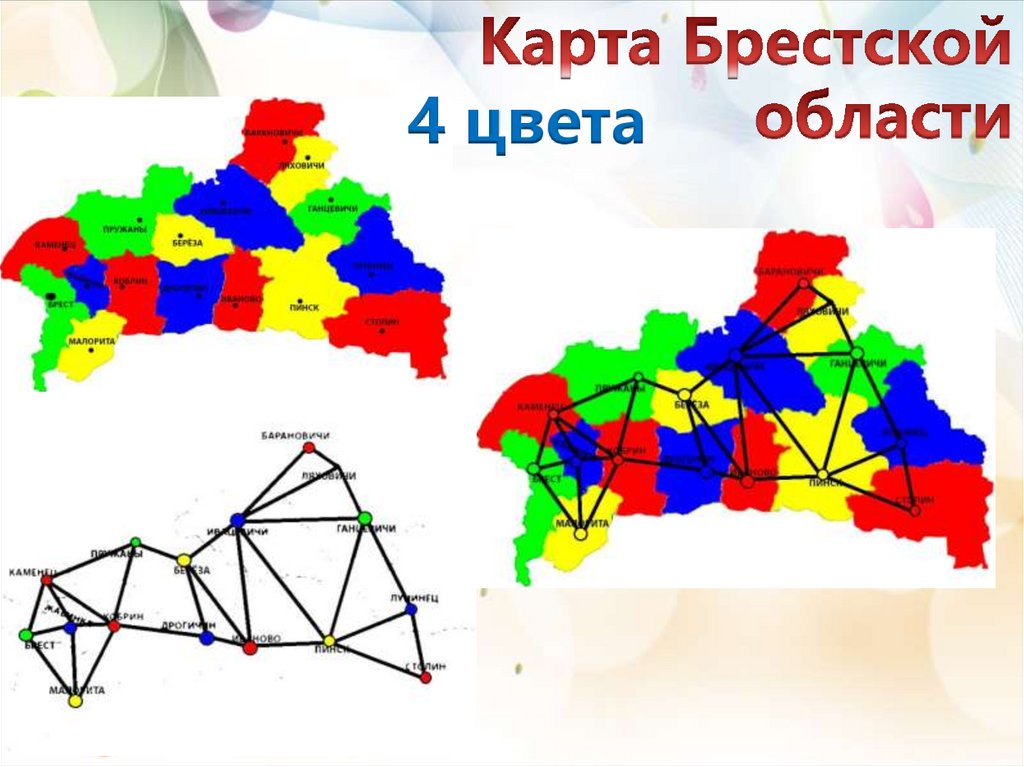
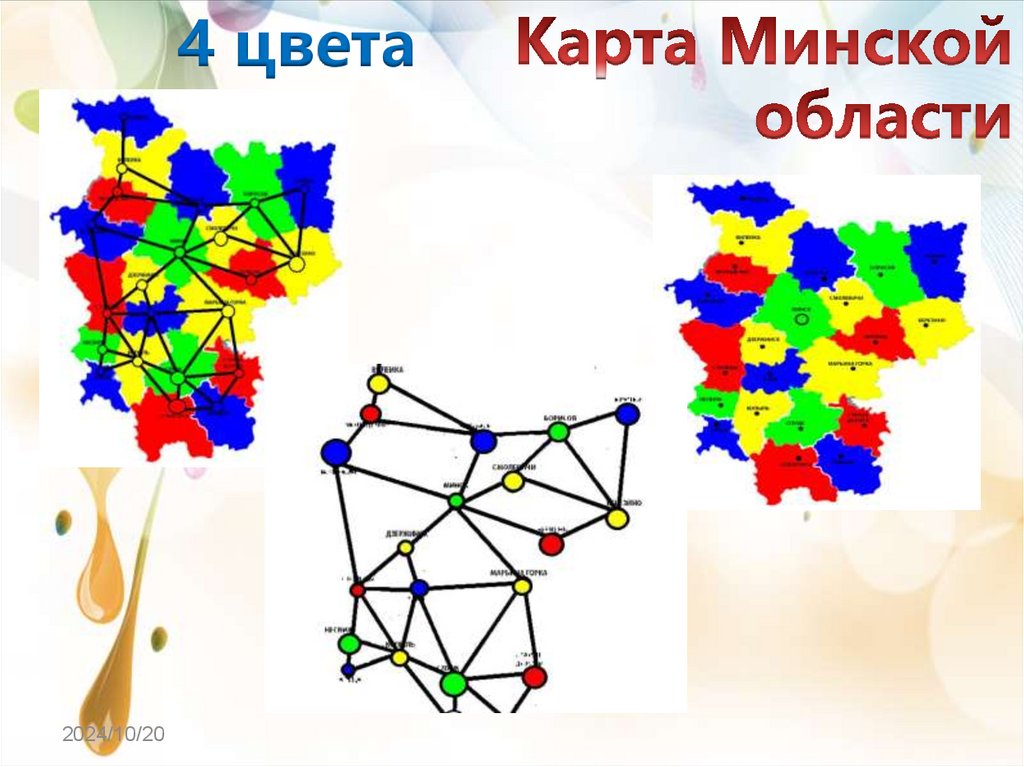
4 цвета2024/10/20
6.
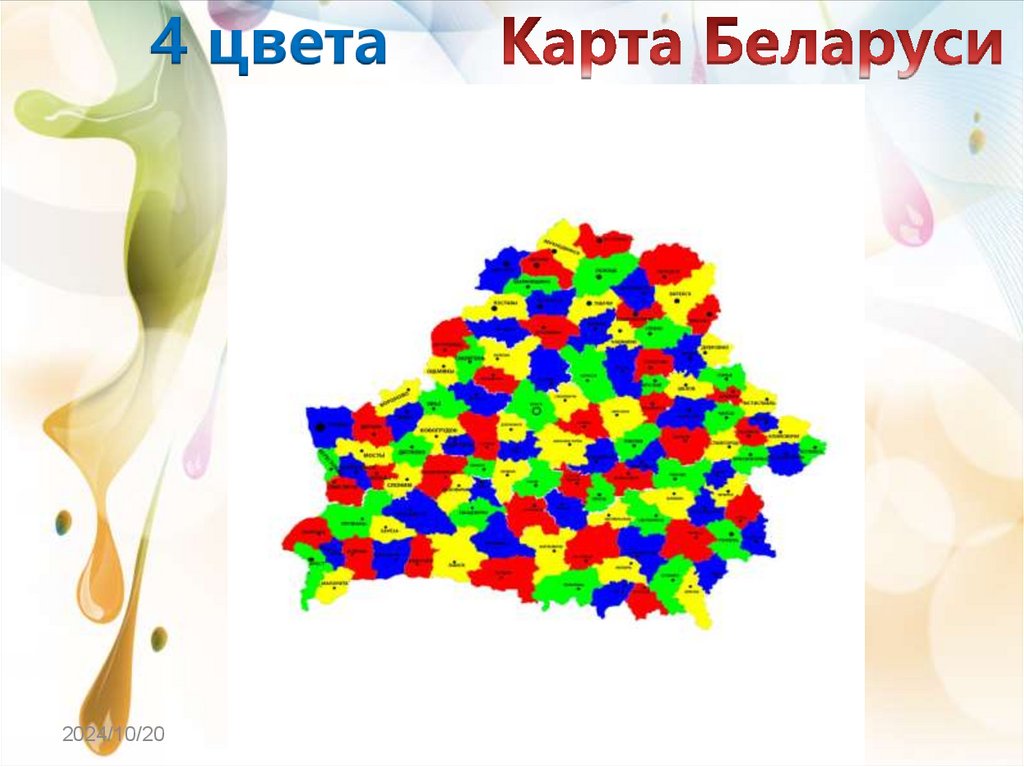
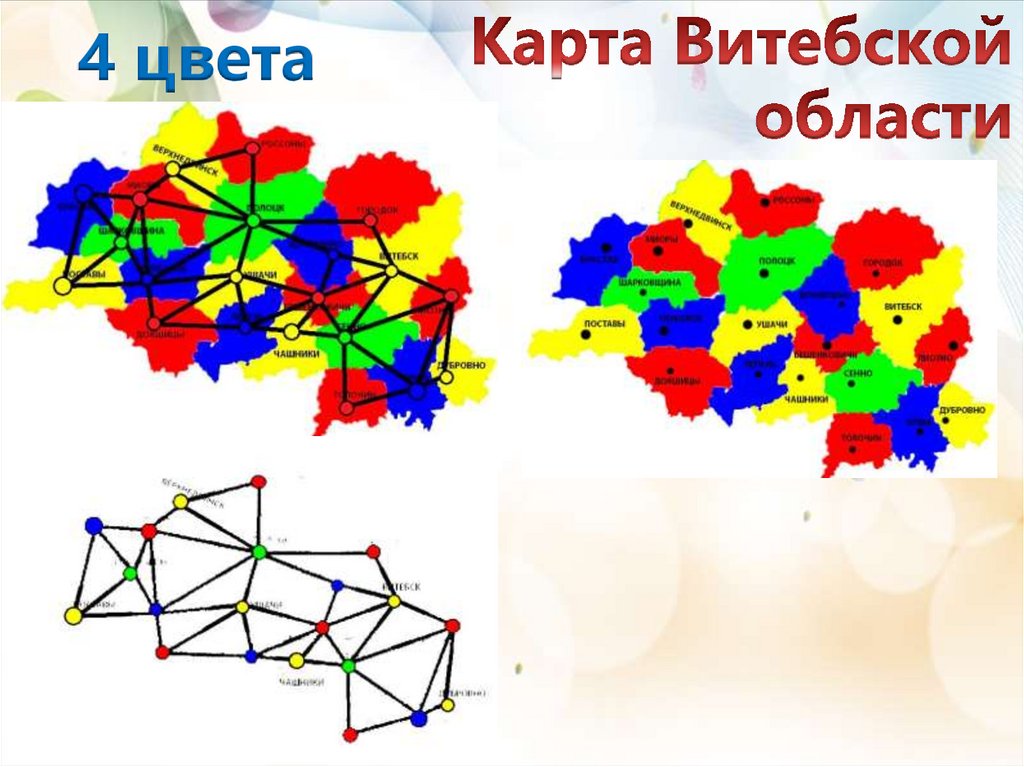
4 цвета2024/10/20
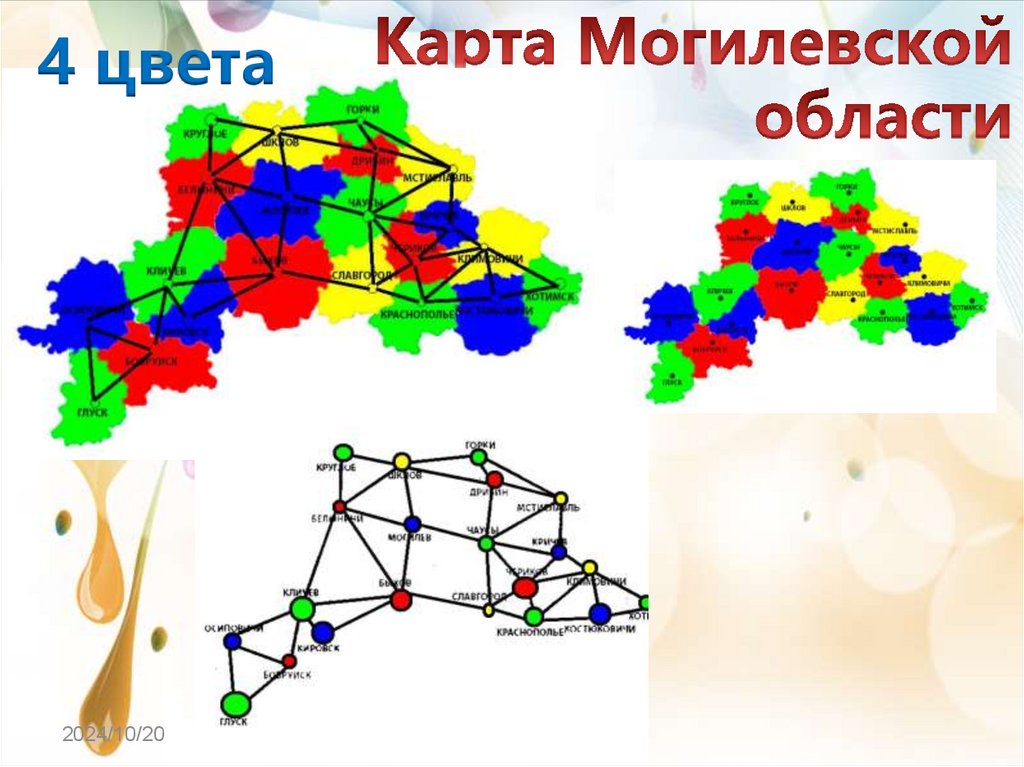
7.
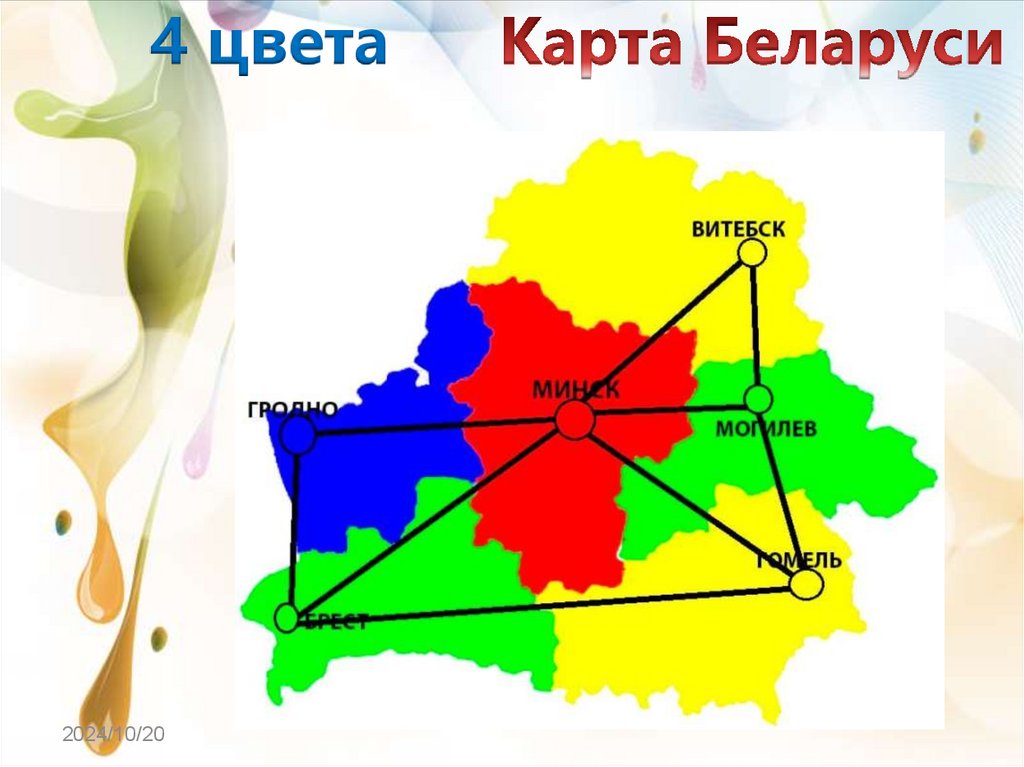
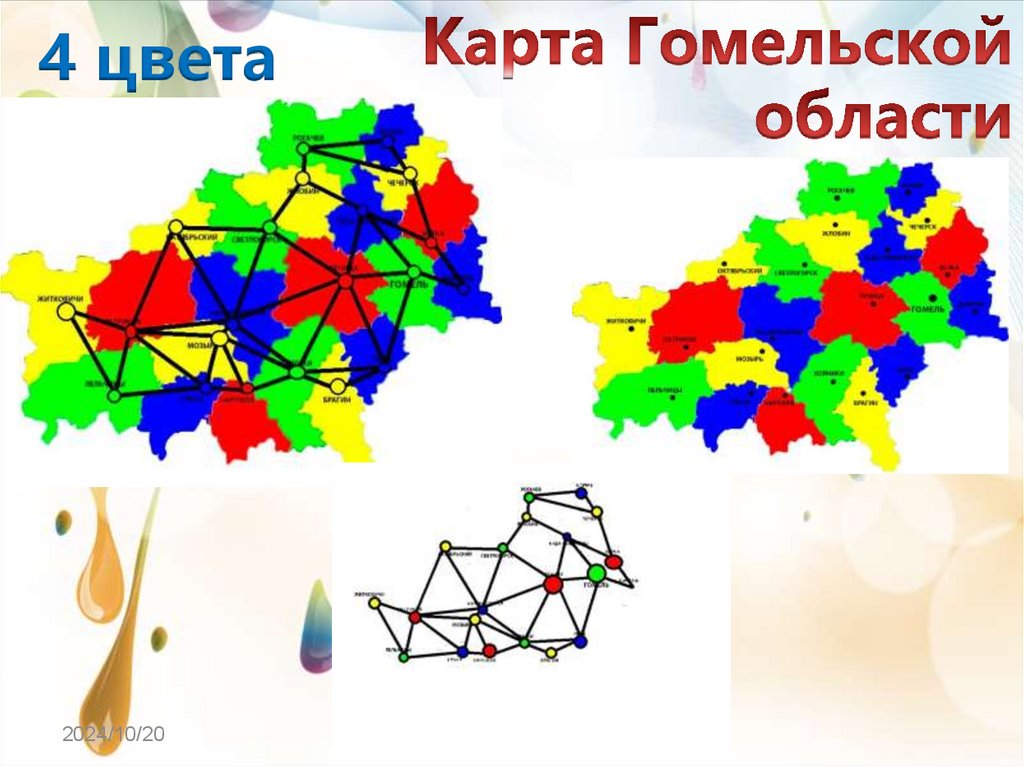
4 цвета2024/10/20
8.
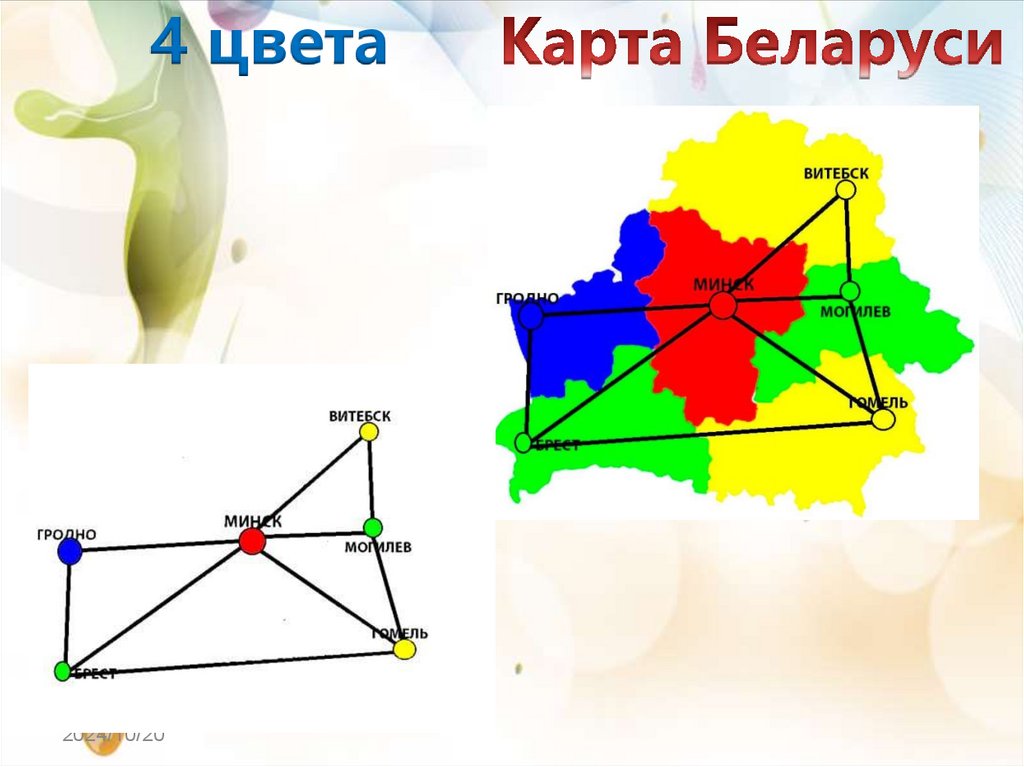
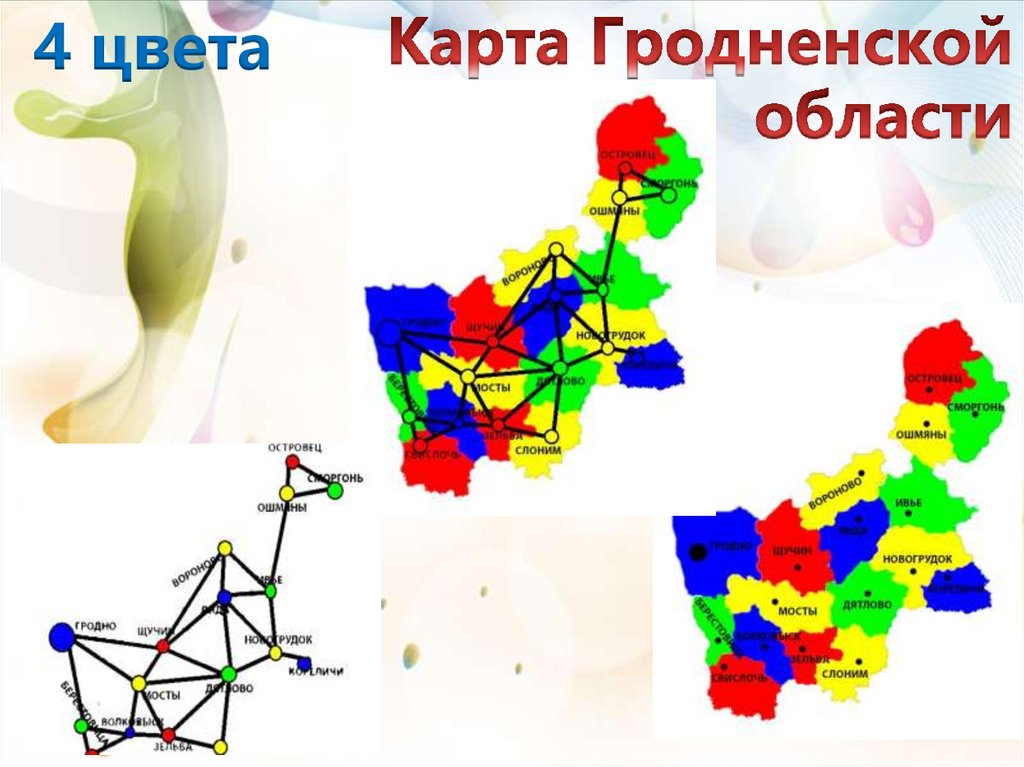
4 цвета2024/10/20
9.
4 цвета2024/10/20
10.
4 цвета2024/10/20
11.
4 цвета2024/10/20
12.
4 цвета2024/10/20
13.
4 цвета2024/10/20
14.
4 цвета2024/10/20
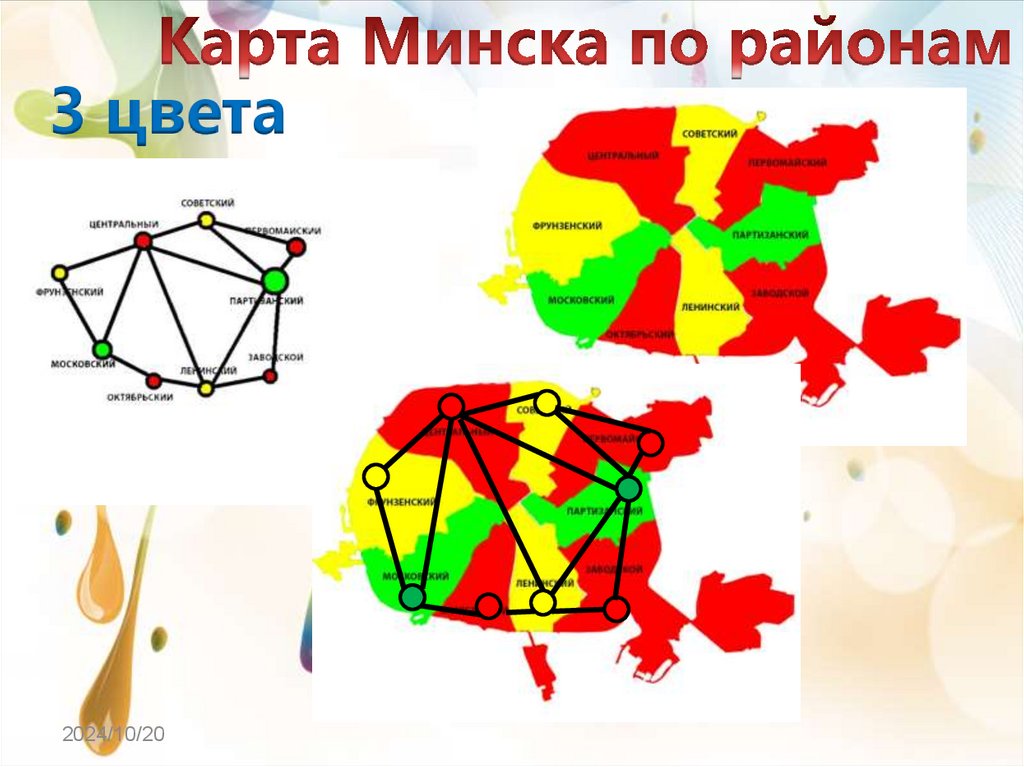
15.
3 цвета2024/10/20
16.
2 цвета2 цвета
3 цвета
4 цвета
карта разбита
если во
Если n
n разбиений
линией прямой,
внутренней
разбиений
нечетно (для
волнистой, вершине карты четно(концентр
концентрическ
овалом, сходится четное
окружностям
число сторон
ические
их
окружности) и
окружностей)
(стран) (нечетное число
стран при
вершине)
2024/10/20
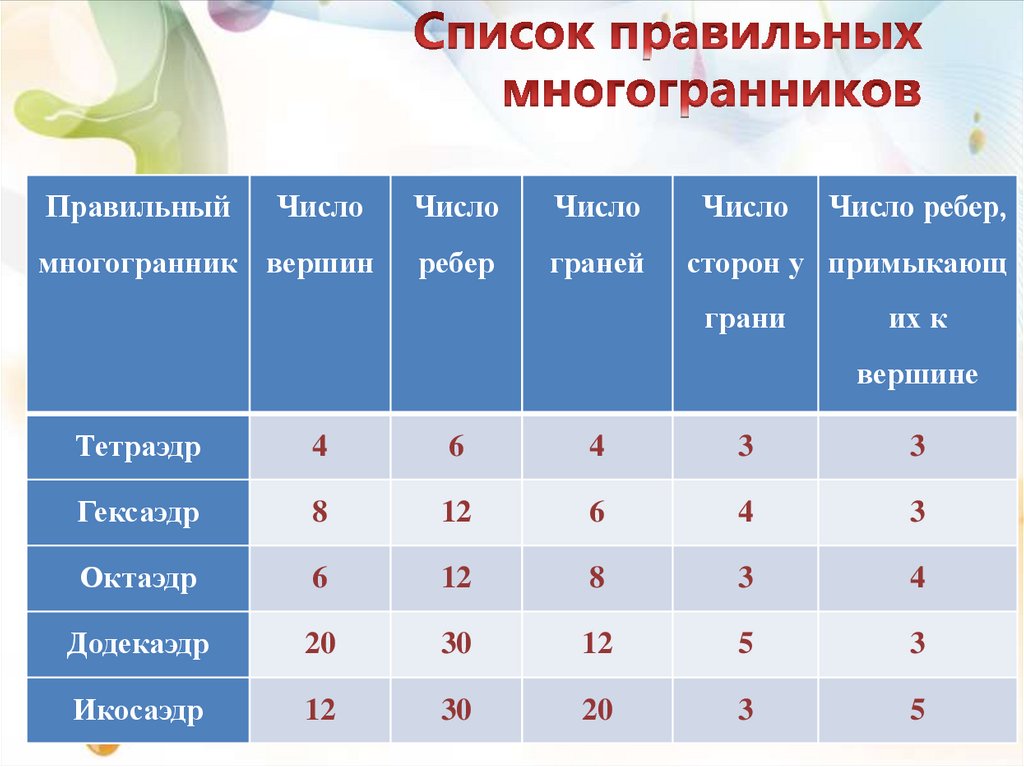
17.
ПравильныйЧисло
Число
Число
Число
многогранник вершин
ребер
граней
сторон у примыкающ
грани
Число ребер,
их к
вершине
Тетраэдр
4
6
4
3
3
Гексаэдр
8
12
6
4
3
Октаэдр
6
12
8
3
4
Додекаэдр
20
30
12
5
3
Икосаэдр
12
30
20
3
5
2024/10/20
18.
4 цвета3 цвета
2 цвета
3 цвета
2024/10/20
4 цвета
19.
2 цветаесли в каждой
3 цвета
3 цвета
если в каждой если в каждой
вершине
вершине
сходится 4
сходится 3
ребра
ребра, каждая
вершине
если в каждой
вершине
сходится сходится 3 ребра,
нечетное
грани имеют
грань имеет
количество четное +нечетное
четное число
рёбер >3, и
сторон
число
грани имеют сторон=нечетное
нечетное
число сторон
2024/10/20
4 цвета
число сторон
20.
Пособие «4 цвета» с заданиями –раскрасками для различных карт
2024/10/20
21.
Рассмотрена проблема четырех красок.Проведено практическое исследование
теоремы на примерах плоскостных карт
и
правильных
многогранников
и
сделаны выводы.
Изготовлены
макеты
правильных
многогранников
с
применением
теоремы о четырех цветах для их
раскраски.
Разработано пособие
«4 цвета» с
заданиями
–
раскрасками
для
различных карт.
2024/10/20










 Искусство
Искусство








