МД и СУБД(Л3)

1.

МД и СУБД
Реляционная алгебра
Реляционная алгебра – это теоретический язык операций, которые на основе одного или
нескольких отношений позволяют создавать другое отношение.
Операндами операций реляционной алгебры являются отношения фиксированной
арности. Операции, применяемые к одному отношению, называются унарными,
применяемые к паре отношений, называются бинарными.
Отношения, участвующие в выполнении бинарных операций, в ряде случаев должны быть
совместимы по структуре, что означает совместимость имен атрибутов и типов
соответствующих доменов.
К основным операциям относятся следующие операции:
объединение отношений;
разность отношений;
пересечение отношений;
декартово произведение отношений;
проекция;
выборка;
деление отношений;
-соединение отношений; естественное соединение; внешнее соединение отношений;
полусоединение отношений.

2.

МД и СУБД
Объединение отношений R и S, обозначаемое как R S, представляет собой множество всех
таких кортежей, каждый из которых принадлежит R или S или обоим сразу. Операция
объединения применяется только к совместимым отношениям одной арности, поэтому все
кортежи в объединении имеют одинаковое число компонент.
Разностью отношений R и S, обозначаемой R\S, называется множество всех кортежей,
принадлежащих R, но не принадлежащих S. Здесь также требуется, чтобы R и S имели одну
и ту же арность и были совместимы.
Пересечение. R S обозначает множество всех кортежей, принадлежащих одновременно R
и S. Ясно, что R и S должны иметь одинаковую арность и быть совместимы. Очевидно, что
R S=R\(R\S)=S\(S\R).
A B C
Примеры.
A B C
R= 1 2 3
S= 2 7 1
4
1
6
3
2
4
4
A
B
C
R S = 1
4
2
3
6
1
A
B
C
A
B
C
3
2
4
R\S = 1
2
3
R S = 4
1
6
2
7
1
3
2
4
1
6

3.

МД и СУБД
Декартово произведение. Пусть R и S – отношения арности г и s соответственно. Тогда
декартовым произведением RxS отношений R и S называется множество всех кортежей
длины r+s, таких что, первые г компонент образуют кортежи, принадлежащие R, а
последние s – кортежи, принадлежащие S.
Примеры.
A D E
A B C
R=
S= 2 7 1
1 2 3
4 1 6
4 1 6
3
2
4
RxS =
R.A
B
C
S.D
D
E
1
2
3
2
7
1
4
1
6
2
7
1
3
2
4
2
7
1
1
2
3
4
1
6
4
1
6
4
1
6
3
2
4
4
1
6

4.

МД и СУБД
Проекция. Сущность этой операции заключается в том, что в исходном отношении
удаляются некоторые компоненты (атрибуты) и (или) переставляются оставшиеся. Пусть R –
отношение арности г. Обозначим i1, i2, …, im(R), где ij – целые числа в диапазоне от 1 до г,
проекцию R на компоненты i1, i2, …, im, то есть множество m-ок, таких, что существует
некоторый принадлежащий R кортеж b1, b2, …, br, удовлетворяющий условию aj=bij ,
R=
A
B
C
A
C
1
2
3
1
3
4
1
6
4
6
3
2
4
3
4
A,C(R )=
Выборка. Пусть F – формула, образованная:
операндами, являющимися константами или номерами компонент (атрибутами);
операциями сравнения: <, =, >, , ;
логическими операциями (И – конъюнкция), \/ (ИЛИ – дизъюнкция), (НЕТ – отрицание).
В этом случае F(R) есть множество всех таких кортежей t, принадлежащих R, что при
подстановке i-го компонента вместо всех вхождений i (или соответствующего атрибута) в
формулу F она станет истинной.
A B C
B=’2’(R )=
1 2 3
3
2
4

5.

МД и СУБД
Деление. Пусть R и S отношения арности r и s соответственно, причем r>s и S .
Предположим, что R определено на множестве атрибутов A, а S на множестве атрибутов B и
B A. R S (частное) есть множество кортежей t длины r-s, таких, что для всех кортежей u S,
кортеж tu принадлежит R ( здесь tu означает кортеж полученный приписыванием справа к
кортежу t компонент кортежа u).
R=
A
B
C
D
1
2
3
4
1
2
5
6
2
3
5
6
5
4
3
4
5
4
5
6
1
2
4
5
C
D
A
B
S= 3
4
R S = 1
2
5
6
5
4

6.

МД и СУБД
-соединение. -соединение отношений R и S по столбцам i и j, записываемое R i jS, где
– операция сравнения ( = , < и т. д. ), есть краткая запись выражения: i j(RxS). Таким
образом, -соединение R и S представляет собой множество всех таких кортежей в
декартовом произведении R и S, что i-й атрибут R находится в отношении с j-м атрибутом
отношения S. Если является операцией “=”, то эта операция называется эквисоединением.
R=
A
B
C
1
2
3
4
5
6
7
8
9
R B<D S =
S=
A
B
C
D
E
1
2
3
3
1
1
2
3
6
2
4
5
6
6
2
D
E
3
1
6
2

7.

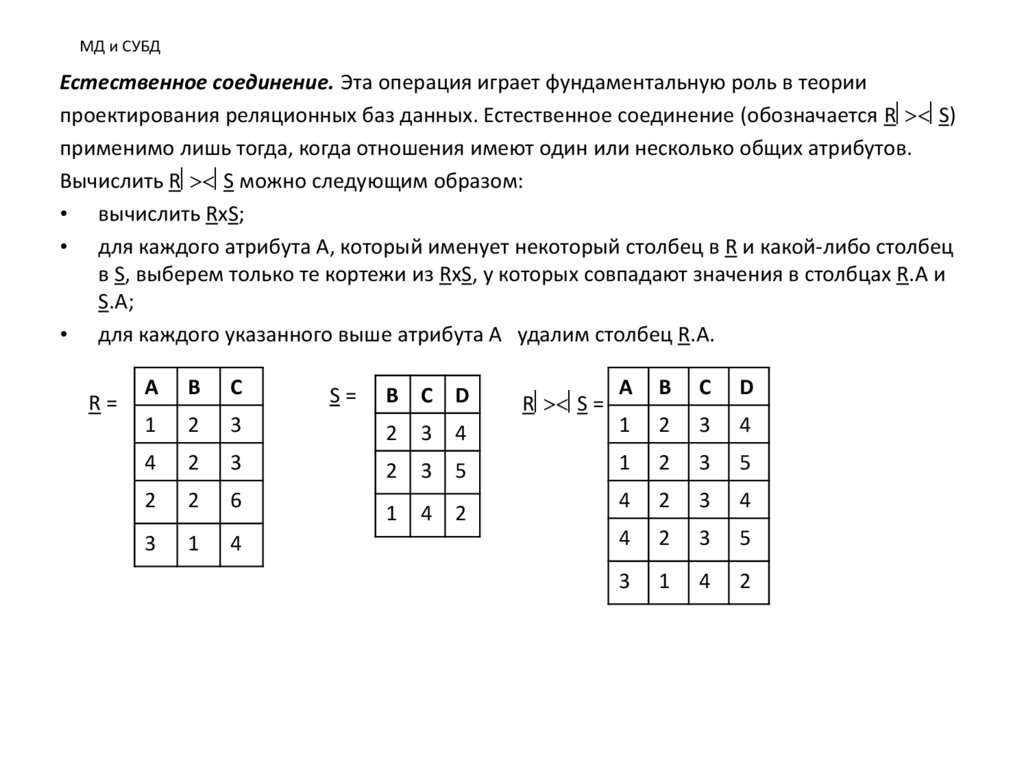
МД и СУБД
Естественное соединение. Эта операция играет фундаментальную роль в теории
проектирования реляционных баз данных. Естественное соединение (обозначается R S)
применимо лишь тогда, когда отношения имеют один или несколько общих атрибутов.
Вычислить R S можно следующим образом:
• вычислить RxS;
• для каждого атрибута А, который именует некоторый столбец в R и какой-либо столбец
в S, выберем только те кортежи из RxS, у которых совпадают значения в столбцах R.A и
S.A;
• для каждого указанного выше атрибута А удалим столбец R.A.
R=
A
B
C
1
2
3
2
3
4
2
3
2
2
2
6
1
3
1
4
S=
A
B
C
D
4
1
2
3
4
3
5
1
2
3
5
4
2
4
2
3
4
4
2
3
5
3
1
4
2
B C D
R S =

8.

МД и СУБД
Внешнее соединение. Левым внешним соединением R S отношений R и S называется
отношение, содержащее все кортежи отношения R S, а также кортежи R, не имеющие
совпадающих значений в общих столбцах с отношением S. Для обозначения отсутствующих
значений во втором отношении используется определитель NULL.
Аналогично вводится операция правого внешнего соединения R S. Существует также
полное внешнее соединение R S, в результирующем отношении которого помещаются
все кортежи из обоих отношений и в котором для обозначения несовпадающих значений
кортежей используются определите ли NULL.
R=
A
B
C
1
2
3
4
2
2
3
B C D
A
B
C
D
2
3
4
2
3
5
3
4
3
S= 2
2
3
5
R S = 1
1
2
6
1
4
2
4
2
3
4
1
4
3
5
4
4
2
3
5
3
1
4
2
2
2
6
NULL

9.

МД и СУБД
R=
A
B
C
1
2
3
4
2
2
3
R S=
B C D
A
B
C
D
2
3
4
2
3
5
3
4
3
S= 2
2
3
5
R S = 1
1
2
6
1
4
2
4
2
3
4
1
4
3
5
4
4
2
3
5
3
1
4
2
NULL
3
5
4
A
B
C
D
1
2
3
4
1
2
3
5
4
2
3
4
4
2
3
5
3
1
4
2
2
2
6
NULL
NULL
3
5
4

10.

МД и СУБД
Полусоединение. Эту операцию можно определить с помощью операций “проекция” и
“ соединение”. А именно R i jS= u(R i jS). Здесь u это набор всех атрибутов отношения
R.
Аналогично определяются полусоединение по эквивалентности (когда есть равенство) и
полуестественное соединение R S.
R=
R=
A
B
C
1
2
3
4
5
4
3
2
3
2
2
7
1
1
2
6
A
B
C
B
C
D
7
3
1
S= 4
3
1
2
4
1
4
1
2
S=
D E
R C<DS=
R S=
A
B
C
1
2
3
4
3
2
2
7
1
A
B
C
2
4
1