Похожие презентации:
Тіла обертання
1. Епіграф: “Без звички працювати, без уміння долати труднощі, без дисципліни праці нема людини”
2. Пригадайте!
1. Які прямі в просторі називаютьсяпаралельними?
2. Які площини називаються паралельними?
3. Сформулюйте означення
перпендикулярності прямої до площини.
4. Що таке коло? Радіус? Хорда ? Діаметр?
О
3.
5. Що таке круг? Чим відрізняється круг відкола?
6. Відтворіть формули:
Ск=
Sк=
Ск=2 R
Sк= R2
4. Тіла обертання
5. Тіла обертання. Циліндр.
План1. Циліндр, його елементи. Властивості
циліндра.
2. Перерізи циліндра.
3. Бічна і повна поверхня циліндра.
6. Мета:
• ввести поняття циліндра і йогоелементів: основи, твірні, вісь, висота,
радіус;
• ввести поняття перерізів циліндра;
• вивести формули для обчислення
площі бічної та повної поверхні
циліндра; розглянути типові задачі.
7. “ЦИЛІНДР НАВКОЛО НАС”
Виконала студентка групи В-22Кузьменко Катерина
8. Використання циліндрів
9. Найбільш широко використовуються циліндри у машино-будівництві.
Найбільш широковикористовуються
циліндри у машинобудівництві.
Це основна частина
двигуна внутрішнього
згоряння.
10. Циліндри в деревообробній промисловості
11. Метало - обробна промисловість
12. Військова промисловість
13.
14. Архітектурні споруди середньовіччя
15. Будівництво криниць
16.
Циліндрична архітектура17. Сучасні архітектурні споруди
18.
Ракетна галузь19.
ПРИРОДА20. Хімія та медицина
21. Історичні вікриття та знахідки
• Древнійаптекарський
посуд
22. Історичні вікриття та знахідки
Циліндрифараона
23. Товари широкого вжитку
24.
Циліндрична гастрономія25.
26. Дякую за увагу!!!
27.
AA1
A
B
B
B1
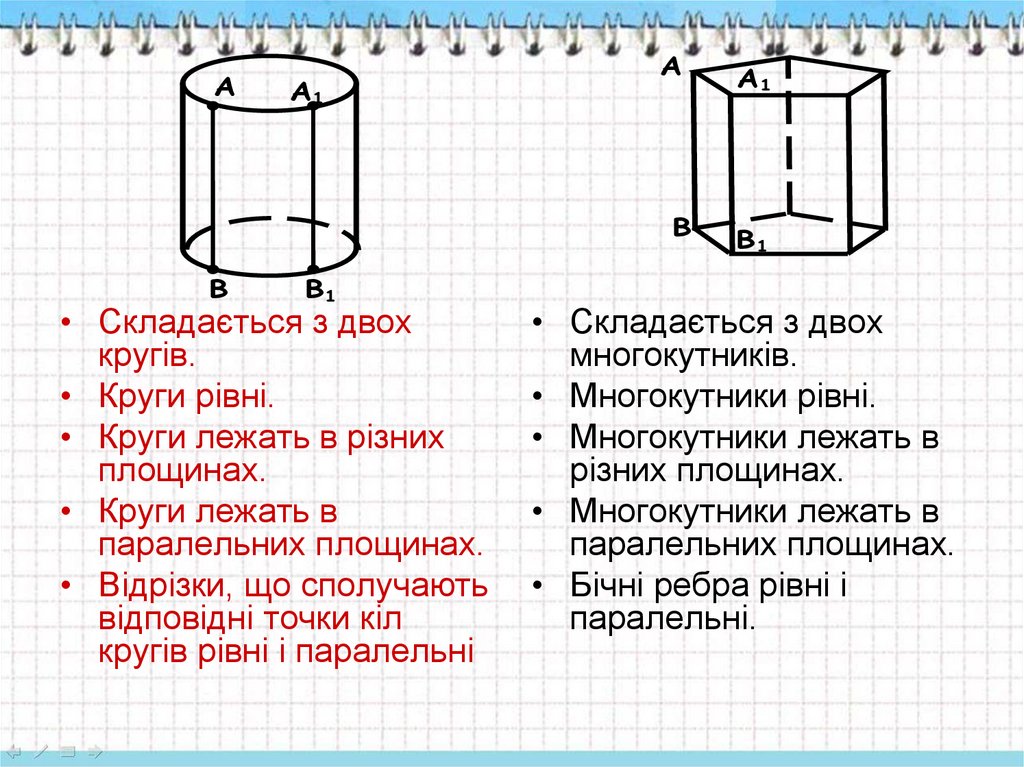
• Складається з двох
кругів.
• Круги рівні.
• Круги лежать в різних
площинах.
• Круги лежать в
паралельних площинах.
• Відрізки, що сполучають
відповідні точки кіл
кругів рівні і паралельні
A1
B1
• Складається з двох
многокутників.
• Многокутники рівні.
• Многокутники лежать в
різних площинах.
• Многокутники лежать в
паралельних площинах.
• Бічні ребра рівні і
паралельні.
28.
Циліндром (круговим циліндром) називається тіло, щоскладається з двох кругів, які не лежать в одній площині і
суміщаються паралельним перенесенням, і всіх відрізків,
що сполучають відповідні точки цих кругів.
верхня основа
О1
радіус R
висота H
твірна L
нижня основа
О
вісь OO1
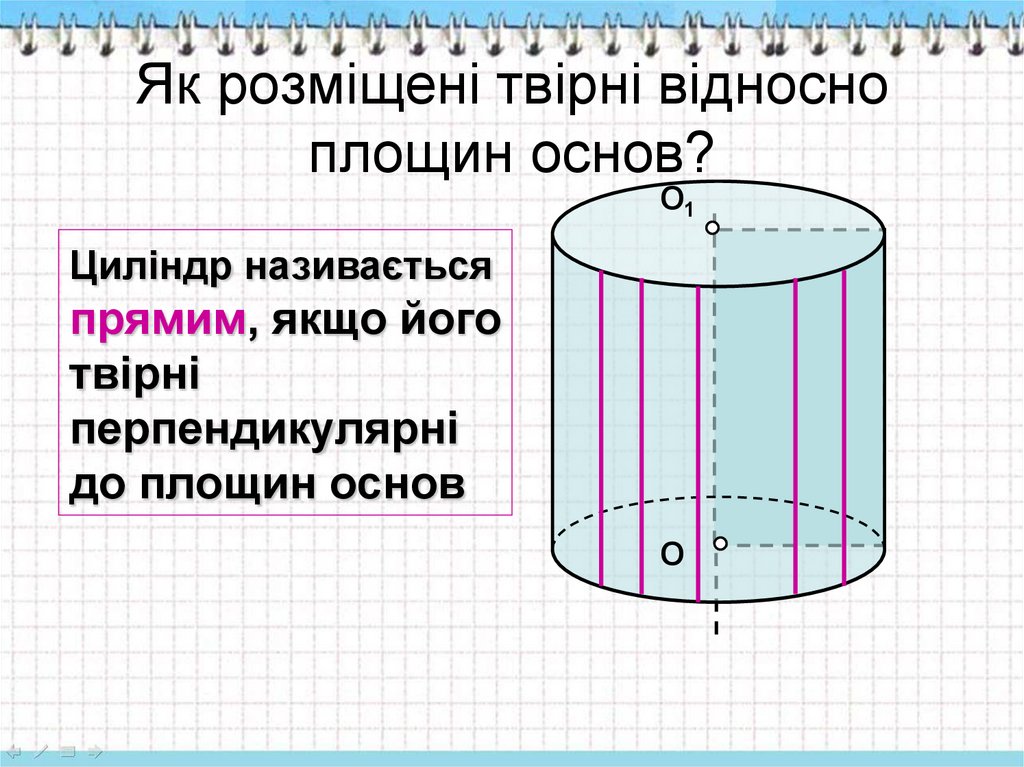
29. Як розміщені твірні відносно площин основ?
О1Циліндр називається
прямим, якщо його
твірні
перпендикулярні
до площин основ
О
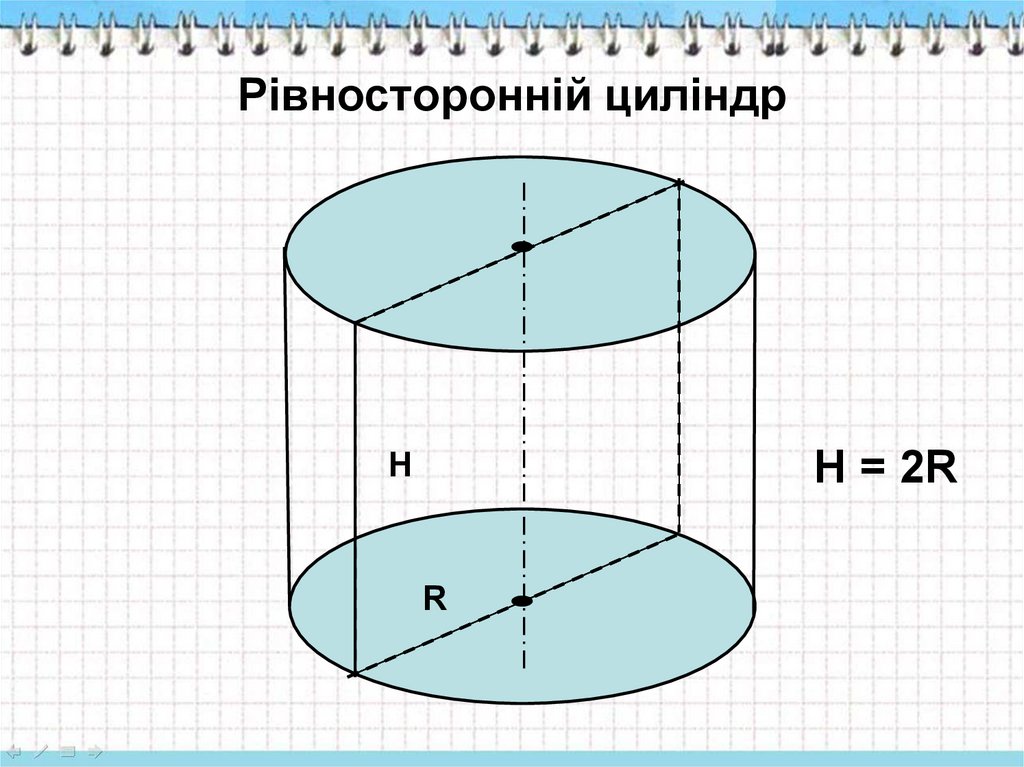
30. Рівносторонній циліндр
H = 2RH
R
31.
Похилий циліндркруг
Н
32. Сформулюйте властивості основ і твірних циліндра
• Основи циліндра рівні• Основи циліндра лежать у паралельних
площинах
• Твірні циліндра паралельні і рівні
33.
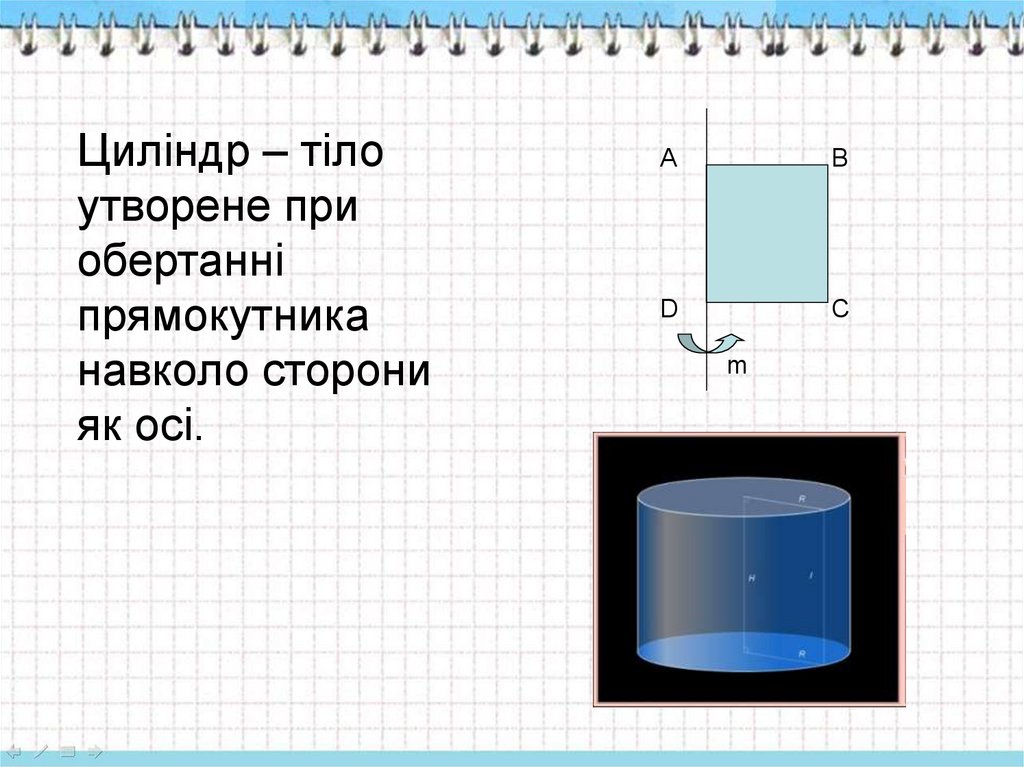
Циліндр – тілоутворене при
обертанні
прямокутника
навколо сторони
як осі.
A
B
D
C
m
34.
Переріз циліндраплощиною
паралельною осі
О1
Переріз циліндра
площиною
перпендикулярною осі
О1
А1
О2
О
О
А
35.
Осьовий переріз - прямокутникО
H
О
2R
36.
Розгортка циліндраС 2 R
R
О1
О1
H
Sк R
2
Sб 2 R H
О
S п 2 R H 2 R 2 R ( H R)
2
О
R
37. Контроль
BO
A
C
O1
K
1. AK –
а) твірна циліндра;
б) радіус циліндра;
в) діаметр основи
циліндра;
г) вісь циліндра;
д) інша відповідь
2. АО –
а) твірна циліндра;
б) радіус циліндра;
в) діаметр основи
циліндра;
г) вісь циліндра;
д) інша відповідь
3. ОО1 –
а) твірна циліндра;
б) радіус циліндра;
в) діаметр основи циліндра;
г) вісь циліндра;
д) інша відповідь
4. АBCK –
а) твірна циліндра;
б) радіус циліндра;
в) діаметр основи циліндра;
г) вісь циліндра;
д) інша відповідь
38. Перевір себе!
Відповідіа
б
в
г
д
Запитання
1
2
3
4
+
+
+
+
39.
Задача 1. Знайдіть площу поверхні капелюха,розміри якого в сантиметрах зображені на
рисунку.
Розв’язок
1) Якщо дно капелюха опустити до
нижніх полів, то отримаємо круг
радіуса
R = r1+ 10 = 20 cм.
r1=10
10
10
2) Площа цього круга
Sк R 2 400 (см2 )
3) Знайдем площу бічної поверхні циліндричної частини
Sб Ск h 2 r1 h 2 10 10 200 (см 2 )
4) Знайдем площу шляпи
Sшляпи Sк Sб 400 200 600 (см 2 )
Відповідь: 600 (см2).
40. Задача 2 (підручник №1(с.95))
СВ
D
А
Дано: циліндр, r=2 м,
h=3 м
З-ти:АС
Розв’язок
1.Осьовий переріз – прямокутник.
2.З прямокутного ADC:
АС2=AD2+CD2
АС2=42+32=16+9=25
АС=5 (м)
Відповідь:5 м.
41. Задача 3 (лови помилку!!!) Осьовий переріз циліндра прямокутник зі сторонами 6 см і 8 см. Знайти площу основи циліндра та площу
Задача 3 (лови помилку!!!) Осьовий переріз циліндрапрямокутник зі сторонами 6 см і 8 см. Знайти площу
основи циліндраСта площу бічної поверхні.
В
8
D
6
А
Дано: циліндр, ABCD-осьовий
переріз, АВ=8 см, АD=6 см.
З-ти: Sосн., Sбіч.
Розв’язок
1. Sосн.= R2=36 (см2)
Sосн.= R2=9 (см2)
2. Sбіч.= RH=6*8 =48 (см2)
Sбіч.=2 RH=2*3*8 =48 (см2)
Відповідь: 9 см2, 48 см2.
42. Продовжте речення
• Відстань між основами циліндраназивається…
• Осьових перерізів можна провести в
циліндрі…
• Переріз циліндра площиною, що
проходить паралельно до його основ …
43.
• Як утворюється таке тіло обертання, якпрямий круговий циліндр?
• Виключити елементи, які не входять в
циліндр: висота, вісь, осьовий переріз,
основа, апофема, квадрат, катет.
• Виберіть правильну відповідь: яка
фігура являється осьовим перерізом
циліндра? Еліпс, прямокутник,
трапеція, квадрат, круг.
44.
• Що на занятті було головним?• Чому навчилися?
• Чи зможете пояснити одногрупникам,
яких не було на занятті цей матеріал?
45.
Домашнє завданняПогорєлов О.В ,Геометрія 10-11 клас:
§6 ст.82-84, п.52, 53, Задача №4; 8
§8 ст.116, 117.
46. ДОДАТОК
Додаткові завдання47.
Задача 4. Осьовий переріз циліндра – квадрат,діагональ якого дорівнює 20 см. Знайдіть: а) висоту
циліндра; б) So циліндра
Розв’язок.
B
C
1. Проведем діагональ АС перерізу
АВСD.
2. ADC – рівнобедренний,
прямокутний, АD=DC, h = 2r,
45
20
CAD = ACD=45 , тоді
2
h AC cos 45 20
10 2 .
2
3. Знайдемо радіус основи
45
A
D
4. Знайдемо площу основи
Відповідь:
а)10 2 ;
h 10 2
r
5 2.
2
2
2
So r 5 2 50 .
б )50 .
2
48.
Задача 5. Площа осьового перерізу циліндра дорівнює10 м2, а площа основи – 5 м2. Знайдіть висоту циліндра.
Розв’язок.
C
1. Площа основи – круг,
B
So r 2 , тоді
r
S
5
.
2. Площа перерізу – прямокутник,
S пер. AB BC h 2r , тоді
D
A
r
h
Sпер.
2r
10 2
Відповідь:
5
5
5 .
5
5 .
49.
Задача 6. Кінці відрізка АВ лежать на різних основах циліндра. Радіусциліндра дорівнює r, його висота – h, відстань між прямою АВ і віссю
циліндра дорівнює d. Знайти: висоту, якщо r = 10, d = 8, AB = 13.
В
Розв’язок.
1. Будуємо відрізок АВ.
2. Проведем радіус АО.
3. Будуємо відрізок d.
4. Відрізок ОК – шукана відстань.
5. З прямокутного АОК знайдем:
a
AK r 2 d 2 100 64 6,
С
К
А
тоді АС = 12.
6. З прямокутного АВС знайдем:
d r
ВС АВ 2 АС 2 169 144 5.
r
Отже, h = 5.
Відповідь: 5.












































 Математика
Математика








