Медиана, биссектриса и высота треугольника

1. Медиана, биссектриса и высота треугольника

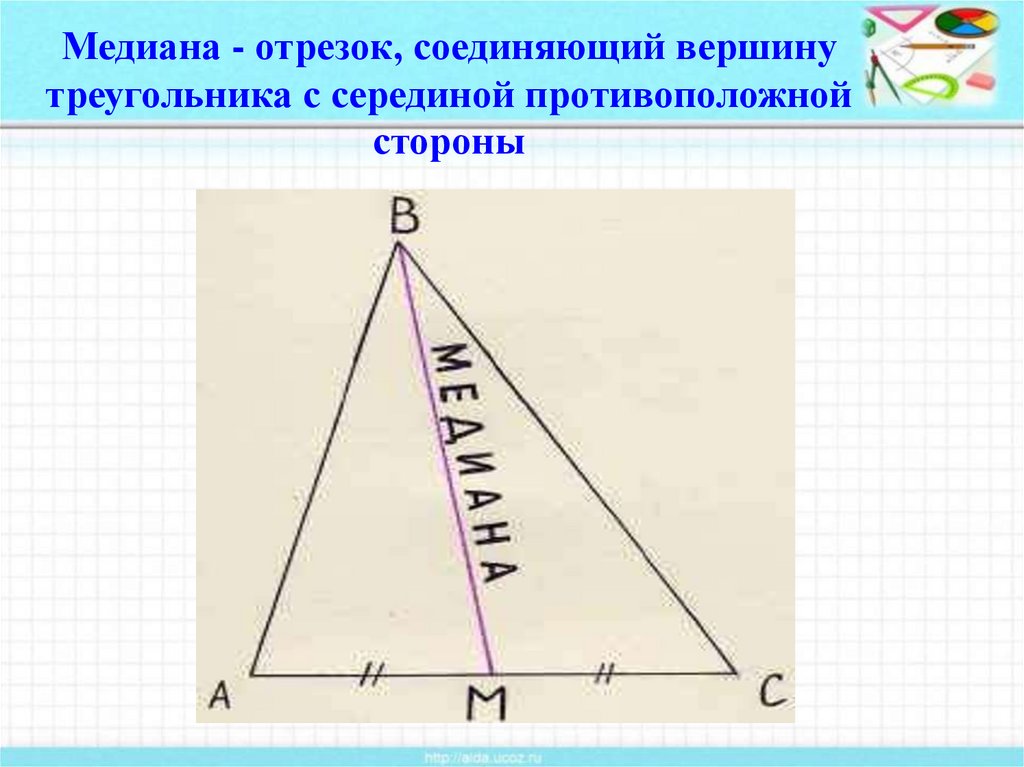
2. Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны

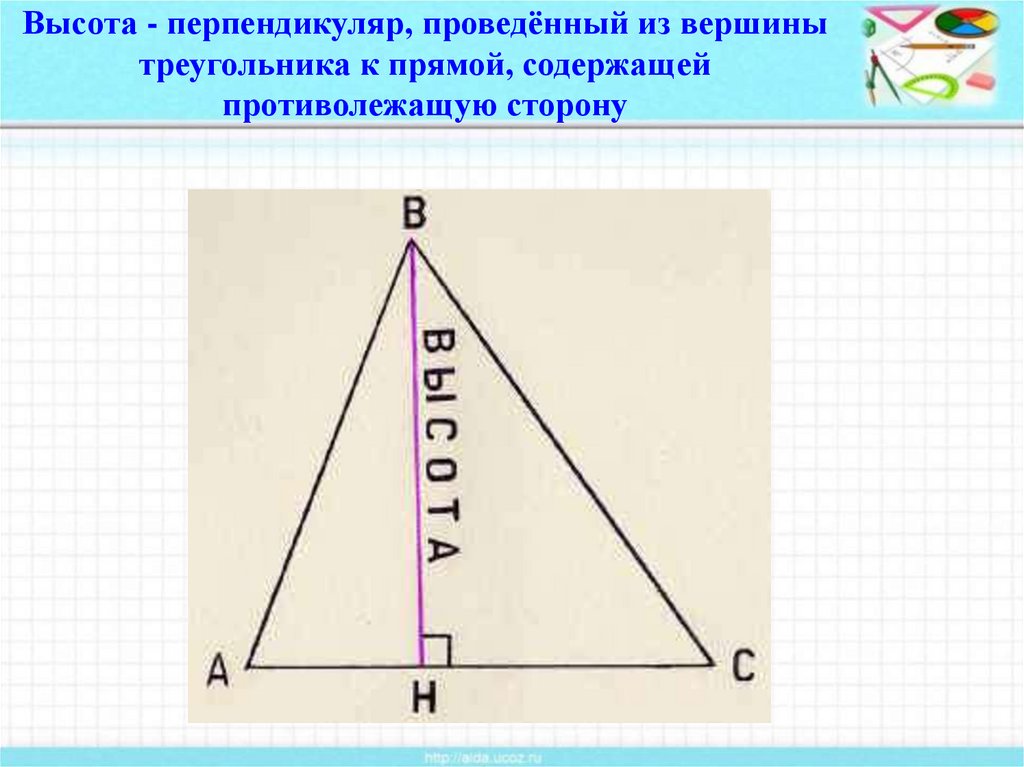
3. Высота - перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону

4. Биссектриса - отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны

треугольника

5. Вопрос-ответ

• Как называется
отрезок, проведенный
из вершины
треугольника к
противолежащей
стороне и делящий эту
сторону пополам?
• А) медиана;
• Б) высота;
• В) биссектриса.
21.10.2024
• Укажите, какое из
перечисленных ниже
утверждений верное.
• А) Медиана всегда делит
пополам один из углов
треугольника.
• Б) В каждом треугольнике
можно провести три
биссектрисы.
• В) В прямоугольном
треугольнике можно провести
только одну высоту.
5

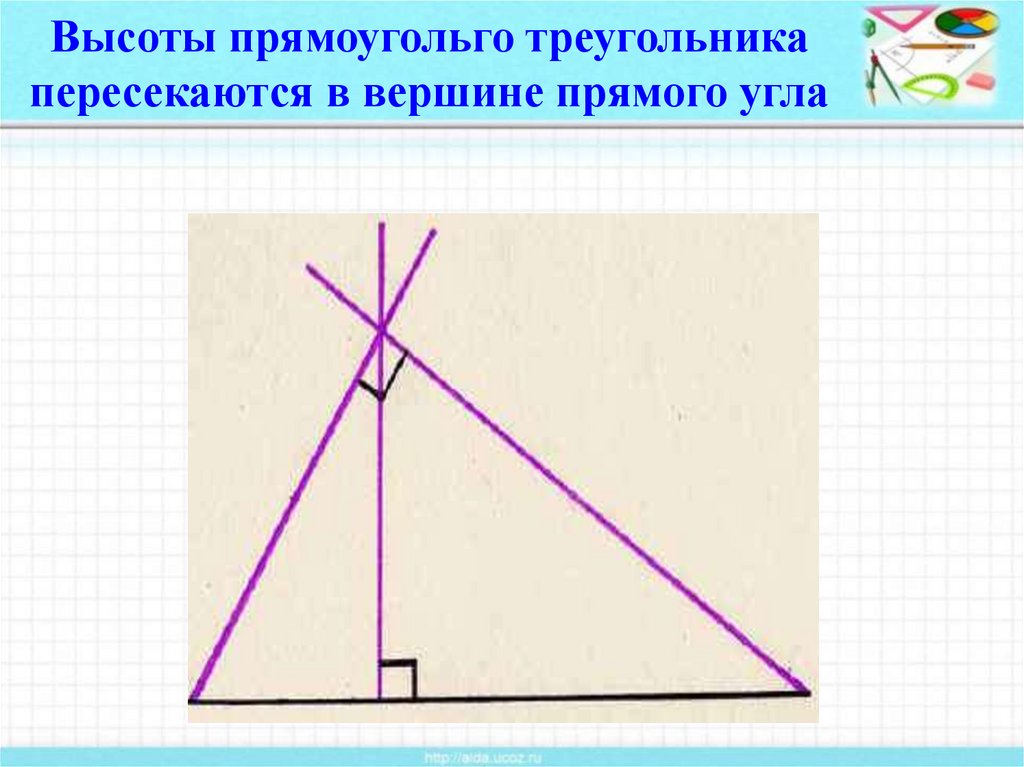
6. Высоты прямоугольго треугольника пересекаются в вершине прямого угла

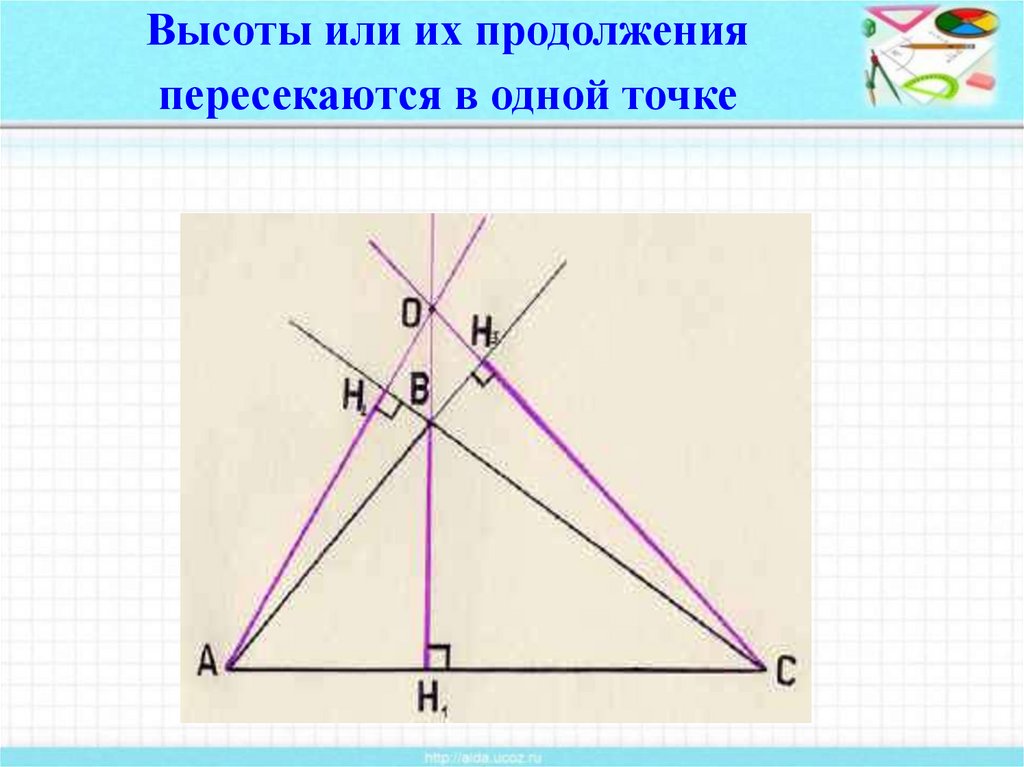
7. Высоты или их продолжения пересекаются в одной точке

8. Вопрос-ответ

• Сколько медиан имеет
любой треугольник
• А) 1;
• Б) 2;
• В) 3.
21.10.2024
• Какое понятие не
относится к
треугольнику?
• А) высота;
• Б) медиана;
• В) луч.
8

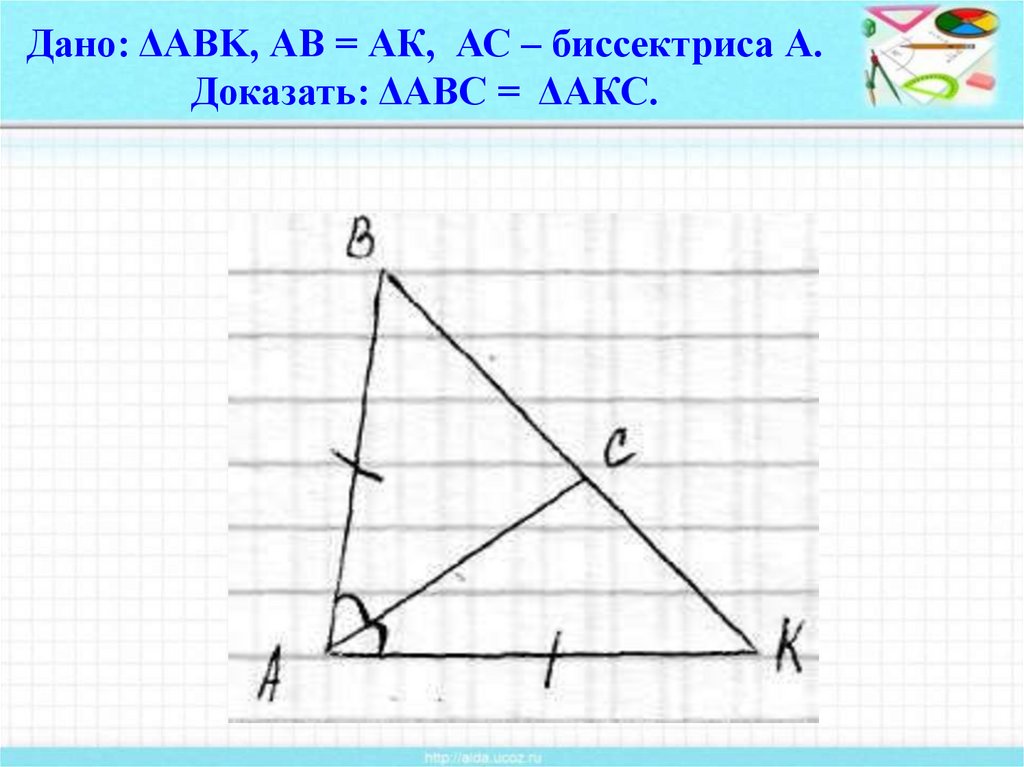
9. Дано: ΔАВK, АВ = АК,  АС – биссектриса А. Доказать: ΔАВС =  ΔАКС.

Дано: ΔАВK, АВ = АК, АС – биссектриса А.
Доказать: ΔАВС = ΔАКС.

10. Задача 1

• В треугольнике