457.99K

Похожие презентации:

Циклы. Цикл с фиксированным числом операций for

Лекция 2. Организация циклических программ

Решение вычислительных задач на компьютере

Программирование на алгоритмическом языке. Массивы. (Часть 2. Тема 1. 8 класс)

Школьный алгоритми́ческий язык

Язык Python. Решение вычислительных задач на компьютере

Решение вычислительных задач на компьютере

Решение вычислительных задач на компьютере (язык С++)

Решение вычислительных задач на компьютере

Операторы и функции

lecture 1_10_2024_______

1.

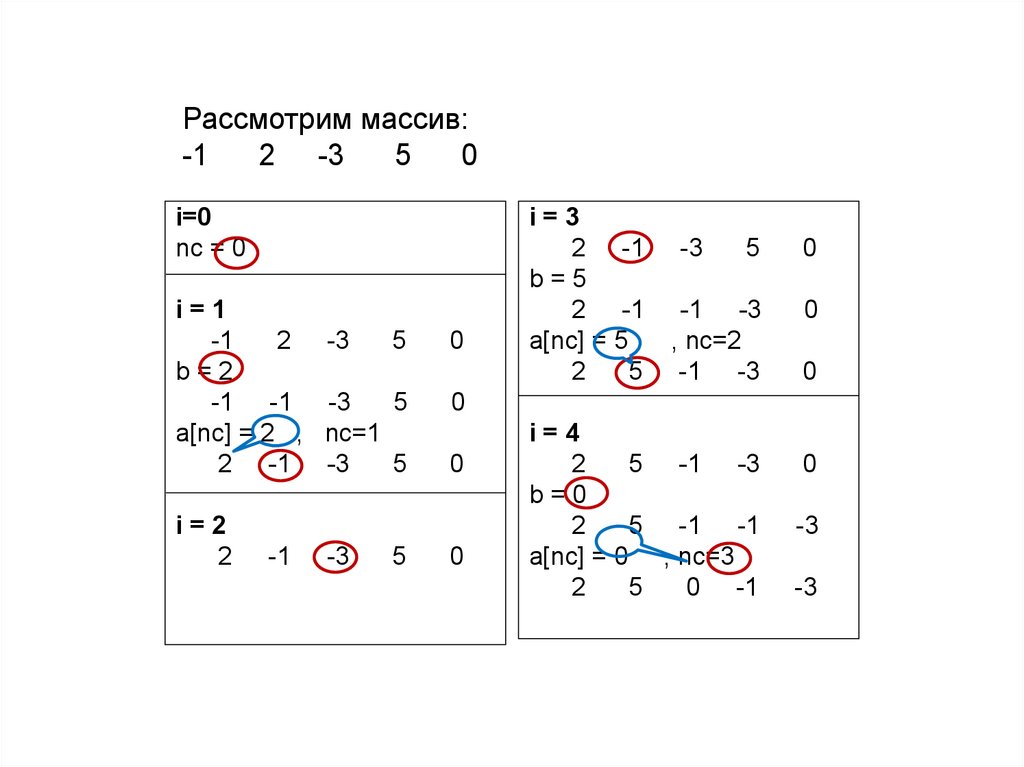
Задача 5. Дан массив. Переставить его элементы так, чтобы сначала
расположились все неотрицательные элементы, а затем отрицательные.
Порядок среди отрицательных и неотрицательных элементов должен быть
сохранён. Дополнительный массив не использовать.
nc:=-1 //начало цепочки отрицательных элементов
цикл от i:=0 до n-1
если a[i]>=0 то
если nc<>-1 то /* уже есть отрицательные */
b:=a[i]
цикл от j:=i до nc+1 шаг -1
/* сдвиг неотрицательных вправо, т.е. освобождение места в конце
последовательности неотрицательных */
a[j]:=a[j-1]
кц
a[nc]:=b
nc:=nc+1
всё
иначе
если nc=-1 то
nc:=i всё
всё
кц

2.

Рассмотрим массив:
-1
2 -3
5
0
i=0
nc = 0
i=1
-1
2
b=2
-1 -1
a[nc] = 2 ,
2 -1
i=2
2
-1
-3
5
-3
5
nc=1
-3
5
-3
5
0
i=3
2 -1
b=5
2 -1
a[nc] = 5
2
5
-3
5
0
-1 -3
, nc=2
-1 -3
0
0
0
0
0
i=4
2
5 -1 -3
b=0
2
5 -1 -1
a[nc] = 0 , nc=3
2
5
0 -1
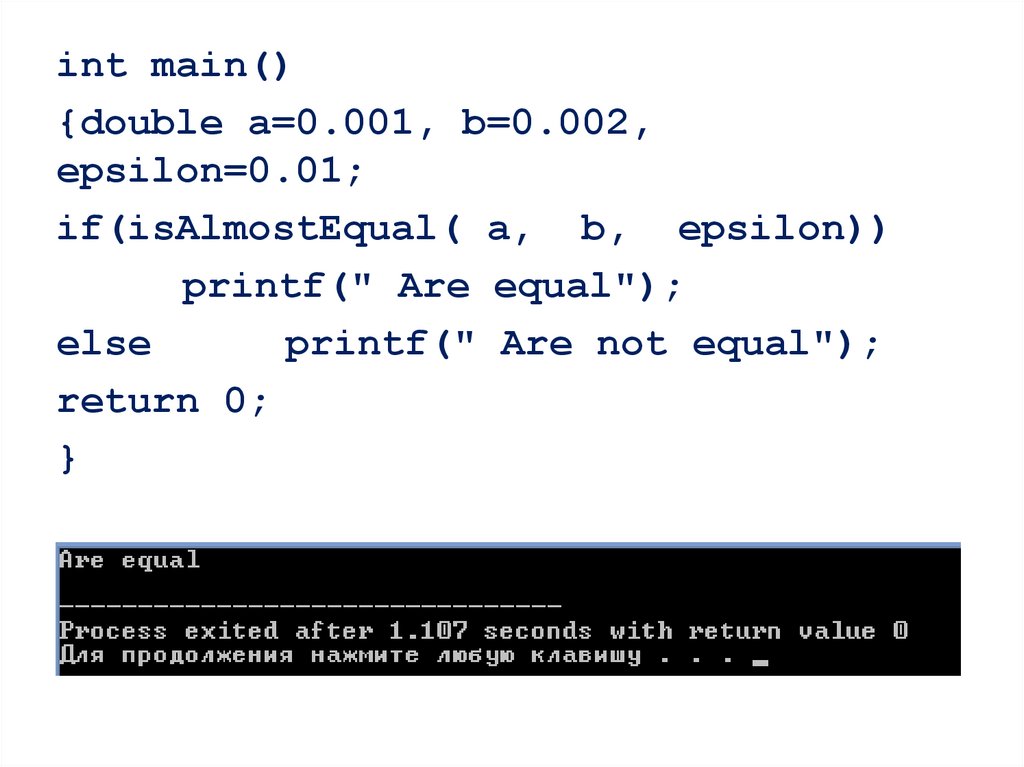
0
-3
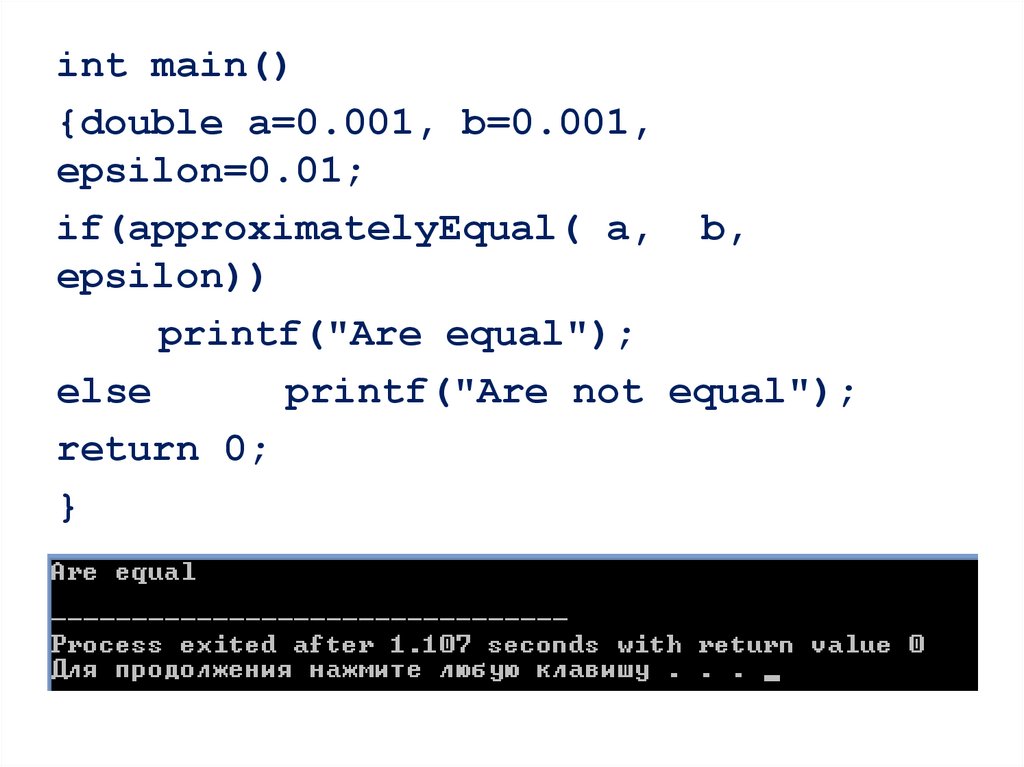
-3

3.

#include <iostream> //для setlocale
#include <stdio.h> //стандартный ввод и вывод
//используем прототип функции перестановки
void sort(int n,int a[]);
int main()
{setlocale(LC_ALL, ".1251");
int a[50], n, i;
printf("Введите 0<n<=50 n = "); scanf("%d", &n);
printf("Введите элементы массива\n");
for (i=0; i<n; i++) scanf("%d", a+i);
sort(n,a); //вызов функции сортировки
printf("Преобразованный массив:\n");
for (i=0; i<n; i++) printf("%7d", a[i]);
printf(‘\n’);
return 0; //признак успешного завершения программы
}

4.

void sort(int n, int a[])
{ int b, i, nc=-1, j;
//функция сортировки
//описание переменных
for (i=0; i<n; i++)
if (a[i]>=0)
{
if (nc!=-1) /* сдвиг вправо, начиная с последнего */
{
for (b=a[i], j=i; j>=nc+1; j--)
a[j]=a[j-1];
a[nc++]=b;
}
}
else
if (nc==-1) nc=i;
}

5.

Задача . Написать программу для
вычисления числа Фибоначчи с
заданным номером. Вычисления
оформить в виде рекурсивной функции,
ввод номера числа и вывод результата –
в главной программе.
Числа Фибоначчи вычисляются по формуле:
1, n 1, n 2
F ( n)
F (n 1) F (n 2), n 2, n N

6.

#include <stdio.h>
#include <limits.h>
float fib(int n)
{
if(n==1||n==2) return 1;
else return fib(n-1)+fib(n-2);
}
int main()
{
float r;
int n;
do{
printf("enter n");
scanf("%f",&r);
}while (r<=0||r>INT_MAX||r!=(int)r);
n=(int)r;
printf("Fibonacci(%d)=%10.0f \n",n,fib(n));
return 0;
}

7.

Итерационные алгоритмы

8.

9.

Итерационные алгоритмы
• Итерация (лат. iteratio — повторение) в
математике - одно из ряда повторений какойлибо математической операции,
использующее результат предыдущей
аналогичной операции.
• Итерация в программировании - это
организация обработки данных, при которой
действия повторяются многократно, не
приводя при этом к вызовам самих себя (т.е.
нет рекурсии).

10.

11.

Задача 1. Вычислить сумму членов ряда
cos( nx)
cos( 2 x)
,
...
z cos( x)
2
n
4
cos( nx)
Eps.
до тех пор, пока не выполнится условие
2
n

12.

Задача 1. Вычислить сумму членов ряда
cos( nx)
cos( 2 x)
,
...
z cos( x)
2
n
4
cos( nx)
Eps.
до тех пор, пока не выполнится условие
2
n
Дано: x – вещ., Eps – вещ.

13.

Задача 1. Вычислить сумму членов ряда
cos( nx)
cos( 2 x)
,
...
z cos( x)
2
n
4
cos( nx)
Eps.
до тех пор, пока не выполнится условие
2
n
Дано: x – вещ., Eps – вещ.
Результат: z – вещ.

14.

Задача 1. Вычислить сумму членов ряда
cos( nx)
cos( 2 x)
,
...
z cos( x)
2
n
4
cos( nx)
Eps.
до тех пор, пока не выполнится условие
2
n
Дано: x – вещ., Eps – вещ.
Результат: z – вещ.
При : Eps>0, x≠0

15.

16.

Алгоритм

17.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)

18.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}

19.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл

20.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл
slag:=cos(ix)/i2 {слагаемое}

21.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл
slag:=cos(ix)/i2 {слагаемое}
z:=z+slag {вычисление
суммы}

22.

Алгоритм
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл
slag:=cos(ix)/i2 {слагаемое}
z:=z+slag {вычисление
суммы}
i:=i+1 {увеличение номера
шага}

23.

24.

25.

Трассировка
алг “итерация “
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл
slag:=cos(ix)/i2 {слагаемое}
z:=z+slag {вычисление
суммы}
i:=i+1 {увеличение номера
шага}
до slag≤Eps
кц
вывод(z)
кон
Z=0

26.

Трассировка
алг “итерация 1”
нач
ввод(x, Eps)
z:=0 {сумма членов ряда}
i:=1 {номер слагаемого}
цикл
slag:=cos(ix)/i2 {слагаемое}
z:=z+slag {вычисление
суммы}
i:=i+1 {увеличение номера
шага}
до slag≤Eps
кц
вывод(z)
кон
Z=0
i=1

27.

28.

29.

30.

31.

32.

33.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2

34.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2
Здесь формула для члена ряда не дана. Выведем ее:

35.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2
Здесь формула для члена ряда не дана. Выведем ее:
1 n 1
1 n 2
y1 x ; y2 x ; y3 x ;
2
3
n

36.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2
Здесь формула для члена ряда не дана. Выведем ее:
1 n 1
1 n 2
y1 x ; y2 x ; y3 x ;
2
3
n
1 n i 1
yi x
;
i

37.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2
Здесь формула для члена ряда не дана. Выведем ее:
1 n 1
1 n 2
y1 x ; y2 x ; y3 x ;
2
3
n
1 n i 1
1 n i 2
yi x
; yi 1
x
.
i
i 1

38.

Задача 2. Вычислить сумму членов ряда
y xn
1 n 1
1
1
1 1
x ... x
x ..., до yi Eps.
2
n
n 1 n 2
Здесь формула для члена ряда не дана. Выведем ее:
1 n 1
1 n 2
y1 x ; y2 x ; y3 x ;
2
3
n
1 n i 1
1 n i 2
yi x
; yi 1
x
.
i
i 1
Для того, чтобы выразить слагаемое через предыдущее:

39.

40.

41.

42.

43.

44.

Дано: x- вещ., Eps – вещ., n –
цел.
Результат: y – вещ.
При : Eps>0, x≠0
Связь:.
1 n 1
1
1
1 1
y x x ... x
x ..., до yi Eps.
2
n
n 1 n 2
n

45.

алг “итерация 2”
нач
ввод (x, Eps, n)

46.

алг “итерация 2”
нач
ввод (x, Eps, n)
y:=xn {сумма членов ряда}
slag:=y {слагаемое}
i:=2 {номер слагаемого}

47.

алг “итерация 2”
нач
ввод (x, Eps, n)
y:=xn {сумма членов ряда}
slag:=y {слагаемое}
i:=2 {номер слагаемого}
цикл

48.

алг “итерация 2”
нач
ввод (x, Eps, n)
y:=xn {сумма членов ряда}
slag:=y {слагаемое}
i:=2 {номер слагаемого}
цикл
slag:=slag*(i-1)/(ix) {слагаемое}

49.

алг “итерация 2”
нач
ввод (x, Eps, n)
y:=xn {сумма членов ряда}
slag:=y {слагаемое}
i:=2 {номер слагаемого}
цикл
slag:=slag*(i-1)/(ix) {слагаемое}
y:=slag+y {вычисление суммы}

50.

алг “итерация 2”
нач
ввод (x, Eps, n)
y:=xn {сумма членов ряда}
slag:=y{ слагаемое}
i:=2 {номер слагаемого}
цикл
slag:=slag*(i-1)/(ix) {слагаемое}
y:=slag+y {вычисление суммы}
i:=i+1 {увеличение номера шага}

51.

52.

53.

Задача 3. Вычислить сумму членов ряда
2
4
2n
x
x
x
n
z 1 ... ( 1)
,
2! 4!
(2n)!
До тех пор пока не выполнится условие:
где
ai ai 1 Eps,
2i
x
ai ( 1)i
,
(2i)!
используя цикл с предусловием и цикл с постусловием.

54.

Выведем рекуррентное отношение

55.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1)i
; ai 1 ( 1)i 1
( 1)i 1
(2i)!
(2(i 1))!
(2i 2)!

56.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1) i
; ai 1 ( 1) i 1
( 1) i 1
(2i )!
(2(i 1))!
(2i 2)!
ai
ai 1

57.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1)i
; ai 1 ( 1)i 1
( 1) i 1
(2i )!
(2(i 1))!
(2i 2)!
ai
( 1)i x 2i
(2i 2)!
ai 1
(2i )!
( 1)i 1 x 2i 2

58.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1)i
; ai 1 ( 1)i 1
( 1) i 1
(2i )!
(2(i 1))!
(2i 2)!
ai
( 1)i x 2i
(2i 2)!
x 2 (2i 2)!
i 1
2i 2
ai 1
(2i )!
( 1) x
(2i )!

59.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1)i
; ai 1 ( 1)i 1
( 1) i 1
(2i )!
(2(i 1))!
(2i 2)!
ai
( 1)i x 2i
(2i 2)!
x 2 (2i 2)!
i 1
2i 2
ai 1
(2i )!
( 1) x
(2i )!
x 2 1 2 ... (2i 2)
1 2 ... (2i 2)( 2i 1)( 2i )

60.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
ai ( 1)i
; ai 1 ( 1)i 1
( 1) i 1
(2i )!
(2(i 1))!
(2i 2)!
ai
( 1)i x 2i
(2i 2)!
x 2 (2i 2)!
i 1
2i 2
ai 1
(2i )!
( 1) x
(2i )!
x 2 1 2 ... (2i 2)
x2
1 2 ... (2i 2)( 2i 1)( 2i )
(2i 1)( 2i )

61.

Выведем рекуррентное отношение
2i
2 ( i 1)
2i 2
x
x
x
i
i 1
i 1
ai ( 1)
; ai 1 ( 1)
( 1)
(2i )!
(2(i 1))!
(2i 2)!
ai
( 1) i x 2i
(2i 2)!
x 2 (2i 2)!
i 1
2i 2
ai 1
(2i )!
( 1) x
(2i )!
x 2 1 2 ... (2i 2)
x2
1 2 ... (2i 2)( 2i 1)( 2i )
(2i 1)( 2i )
2
x
ai ai 1 (
)
(2i 1)( 2i )

62.

Алгоритм
алг “постусловие”
нач
ввод(x, eps)
z:=1 {сумма}
curr:=1 {текущее слагаемое}
i:=1 {номер члена ряда}
цикл
pred:=curr {предыдущее слагаемое}
x2
curr : pred
2i(2i 1)
z:=z+curr
i:=i+1
до |curr+pred|<eps
кц
вывод(z)
кон

63.

Трассировка
алг “постусловие”
нач
ввод(x, eps)
z:=1 {сумма}
curr:=1 {текущее слагаемое}
i:=1 {номер члена ряда}
цикл
pred:=curr {предыдущее слагаемое}
x2
curr : pred
2i(2i 1)
z:=z+curr
i:=i+1
до |curr+pred|<eps
кц
вывод(z)
кон

64.

65.

66.

67.

Трассировка
алг “постусловие”
нач
ввод(x, eps)
z:=1 {сумма}
curr:=1 {текущее слагаемое}
i:=1 {номер члена ряда}
цикл
pred:=curr {предыдущее слагаемое}
x2
curr : pred
2
i
(
2
i
1
)
z:=z+curr
i:=i+1
до |curr+pred|<eps
кц
вывод(z)
кон
z=1;
curr=1;
i=1
pred=curr=1;

68.

69.

70.

71.

72.

73.

алг “предусловие”
нач
ввод(x, eps)
z:=1-x2/2 {сумма}
pred:=1 {предыдущее слагаемое}
curr:=-x2/2 {текущее слагаемое}
i:=2 {номер члена ряда}
цикл-пока |curr+pred|≥ eps
pred:=curr
x2
curr : pred
2i(2i 1)
z:=z+curr
i:=i+1
кц
вывод(z)
кон

74.

Сравнение значений с плавающей
точкой
#include <stdio.h>
int main()
{ double d1=100.0-99. 999999999999998;
// должно быть 0.000000000000002
double d2=100.0-99. 999999999999999;
// должно быть 0.000000000000001
if (d1 == d2)
printf("d1 == d2" );
else
if (d1 > d2) printf(" d1 > d2" );
else
if(d1 < d2) printf(" d1 < d2" ); return
0; }

75.

Если требуется высокий уровень точности, сравнение
значений с плавающей запятой с использованием
любого из операторов отношения может быть
опасным. Это связано с тем, что значения с
плавающей запятой неточны, а небольшие ошибки
округления в операндах с плавающей запятой могут
привести к неожиданным результатам.
Поскольку даже самая маленькая ошибка округления
приведет к тому, что два числа с плавающей запятой
не будут равны, операторы == и != имеют высокий риск
возврата false, когда можно было бы ожидать true.

76.

Как можно корректно сравнить два операнда с
плавающей точкой, чтобы увидеть, равны ли они?
Самый распространенный метод обеспечения
равенства с плавающей запятой включает
использование функции, которая
проверяет, почти ли равны два числа. Если они
«достаточно близки», то мы называем их равными.
Значение, используемое для обозначения
«достаточно близко», традиционно
называется эпсилон. Эпсилон обычно определяется
как небольшое положительное число (например,
0,00000001, иногда пишется 1e-8).

77.

Рассмотрим следующую программу.
#include <stdio.h>
#include <math.h> // для fabs()
// эпсилон - абсолютное значение
int isAlmostEqual(double a, double b, double
epsilon)
{ // если расстояние между a и b меньше
эпсилон, тогда a и b "достаточно близки"
if( fabs(a - b) <= epsilon) return 1;
else return 0;
}

78.

int main()
{double a=0.001, b=0.002,
epsilon=0.01;
if(isAlmostEqual( a, b, epsilon))
printf(" Are equal");
else
printf(" Are not equal");
return 0;
}

79.

Хотя эта функция работает, но она не очень хороша.
Эпсилон 0.00001 подходит для входных значений
около 1.0, но слишком велико для входных значений
около 0.0000001 и слишком мало для входных
значений, таких как 10000. Это означает, что каждый
раз, когда мы вызываем эту функцию, мы должны
выбирать эпсилон, подходящий для наших входных
данных. Если мы знаем, что нам придется
масштабировать эпсилон пропорционально нашим
входным данным, мы могли бы изменить функцию
так, чтобы она делала это за нас.
Дональд Кнут, в своей книге «Искусство
программирования, том 2: Получисленные
алгоритмы» предложил следующий метод.

80.

#include <stdio.h>
#include <math.h>
// для abs
/* возвращаем истину, если разница
между a и b находится в пределах
эпсилон-процента от большего из a и b
*/
int approximatelyEqual(double a,
double b, double epsilon)
{
double
max=(fabs(a)>fabs(b))?fabs(a):fabs(b)
; if(fabs(a - b) <= max*
epsilon)return 1;else return 0;}

81.

int main()
{double a=0.001, b=0.001,
epsilon=0.01;
if(approximatelyEqual( a, b,
epsilon))
printf("Are equal");
else
printf("Are not equal");
return 0;
}

82.

В этом случае, вместо абсолютного значения, эпсилон
теперь зависит от величины a или b.
Левая часть оператора <= (т.е. fabs(a - b)) сообщает
нам расстояние между a и b как положительное число.
В правой части оператора <= нам нужно вычислить
наибольшее значение «достаточно близко», которое
мы готовы принять. Для этого алгоритм выбирает
большее из a и b (в качестве приблизительного
показателя общей величины чисел), а затем умножает
его на эпсилон. В этой функции эпсилон представляет
собой процент. Например, если мы хотим сказать
«достаточно близко» означает, что a и b находятся в
пределах 1% от большего из a и b, мы передаем
эпсилон 0.01 (1% = 1/100 = 0,01).

83.

Чтобы выполнить сравнение на неравенство (!=)
вместо равенства, просто вызовите эту функцию
и используйте оператор логического отрицания
(!), чтобы инвертировать результат:
if (!approximatelyEqual(a, b, 0.001))
printf("%10.5 f not equal %10.5
f\n",a,b);
Обратите внимание, что хотя функция
approximatelyEqual() в большинстве случаев
будет работать, она не идеальна, особенно когда
числа близки к нулю.

84.

int main()
{/* a действительно близко к 1.0, но
имеет ошибки округления, поэтому оно
немного меньше 1.0*/
double a= 0.1 + 0.1 + 0.1 + 0.1 + 0.1 +
0.1 + 0.1 + 0.1 + 0.1 + 0.1 ;
// сначала сравним "почти 1.0" с 1.0
printf("%d\n",napproximatelyEqual(a
, 1.0, 1e-8) );
/* а теперь сравним a-1.0 (почти 0.0) с
0.0 (точное 0.0) ñ 0.0 */
printf("%d\n",
approximatelyEqual(a-1.0, 0.0, 1e-8));
return 0;}

85.

Получаем результат
Второй вызов не сработал, как ожидалось.
Наши расчеты неверны при приближении почти
до нуля.
Один из способов избежать этого –
использовать как абсолютный эпсилон (как мы
делали в первом примере), так и
относительный эпсилон (как мы делали в
подходе Кнута).

86.

/* возвращаем 1, если разница между a
и b меньше, чем absEpsilon, или в
пределах процента relEpsilon от
большего значения a и b */
int approximatelyEqualAbsRel(double
a, double b, double absEpsilon,
double relEpsilon)
{ // Проверяем, действительно ли
числа близки - необходимо при
сравнении чисел, близких к нулю */
double diff=fabs(a - b) ;
if (diff <= absEpsilon) return true;

87.

/* В противном случае возвращаемся к
алгоритму Кнута */
return (diff <= (max(abs(a), abs(b))
* relEpsilon));
}
Проверим работу полученной функции

88.

int main() { /* a близко к 1.0, но имеет
ошибки округления */
double a= 0.1 + 0.1 + 0.1 + 0.1 + 0.1 +
0.1 + 0.1 + 0.1 + 0.1 + 0.1;
// сравниваем "почти 1.0" с 1.0
cout << approximatelyEqual(a, 1.0, 1e-8)
<< '\n';
// сравниваем "почти 0.0" с 0.0 cout <<
approximatelyEqual(a-1.0, 0.0, 1e-8) <<
'\n';
// сравниваем "почти 0.0" с 0.0
cout << approximatelyEqualAbsRel(a-1.0,
0.0, 1e-12, 1e-8) << '\n'; return 0;}

English Русский Правила