Похожие презентации:
Логические основы компьютеров
1. Логические основы компьютеров
1Логические
основы
компьютеров
Логика и компьютер
2. Логика, высказывания
2Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы,
доказывать утверждения.
Формальная логика отвлекается от
конкретного содержания, изучает только
истинность и ложность высказываний.
Аристотель
(384-322 до н.э.)
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
или ложно.
3. Высказывание или нет?
3Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
4. Логика и компьютер
4Логика и компьютер
Двоичное кодирование – все виды информации кодируются с помощью 0 и 1.
Задача – разработать оптимальные правила обработки таких данных.
Почему «логика»?
Результат выполнения операции можно представить как истинность (1) или ложность (0)
некоторого высказывания.
Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра
логики, булева алгебра).
Ограничения: 1) Величина должна принимать два возможных состояния, но не более того.
2) В любой момент времени величина не может принимать оба состояния одновременно.
3) В любой момент времени величина не может принимать ни одного состояния.
4) Если рассматриваются несколько таких величин, то допускается, чтобы каждая из них
принимала одно из двух состояний независимо.
5) Не допускается применять одну пару состояний для одной величины, а для другой другую.
5. Логические основы компьютеров
5Логические
основы
компьютеров
Логические операции
6. Обозначение высказываний
6Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
}
простые высказывания
(элементарные)
! Любое высказывание может быть ложно (0)
или истинно (1).
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если … то», «тогда и только тогда» и др.
AиB
Сейчас идет дождь и открыта форточка.
A или не B
Сейчас идет дождь или форточка закрыта.
если A, то B
Если сейчас идет дождь, то форточка открыта.
A тогда и только
тогда, когда B
Дождь идет тогда и только тогда, когда открыта
форточка.
7. Операция НЕ (инверсия)
7Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
также A , A ,
А
не А
0
1
1
0
Таблица истинности логического
выражения Х – это таблица, где в
левой части записываются все
возможные комбинации значений
исходных данных, а в правой –
значение выражения Х для каждой
комбинации.
not A (Паскаль),
! A (Си)
таблица
истинности
операции НЕ
8. Операция И
8Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В
Операция, выражаемая связкой «и»,
называется конъюнкцией (conjunctio
- соединение) или логическим
умножением и обозначается точкой
«.»(может также обозначаться
знаками ∧, &, and, ∩, И).
9. Операция И (логическое умножение, конъюнкция)
9Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также: A·B, A B,
A and B (Паскаль),
A && B (Си)
A B
конъюнкция – от лат.
conjunctio — соединение
10. Операция ИЛИ (логическое сложение, дизъюнкция)
10Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда истинно
А или B, или оба вместе. Операция, выражаемая
связкой «или» (в неисключающем смысле этого слова),
называется дизъюнкцией (disjunctio - разделение) или
логическим сложением и обозначается знаком ∨, ∪, OR,
ИЛИ, ||, | ).
A
B
A или B
220 В
11. Операция ИЛИ (логическое сложение, дизъюнкция)
11Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Паскаль),
A || B (Си)
дизъюнкция – от лат. disjunctio — разъединение
12.
1213. Задачи
13Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый
сервер по каждому запросу. Для обозначения логической
операции «ИЛИ» в запросе используется символ |, а для
логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
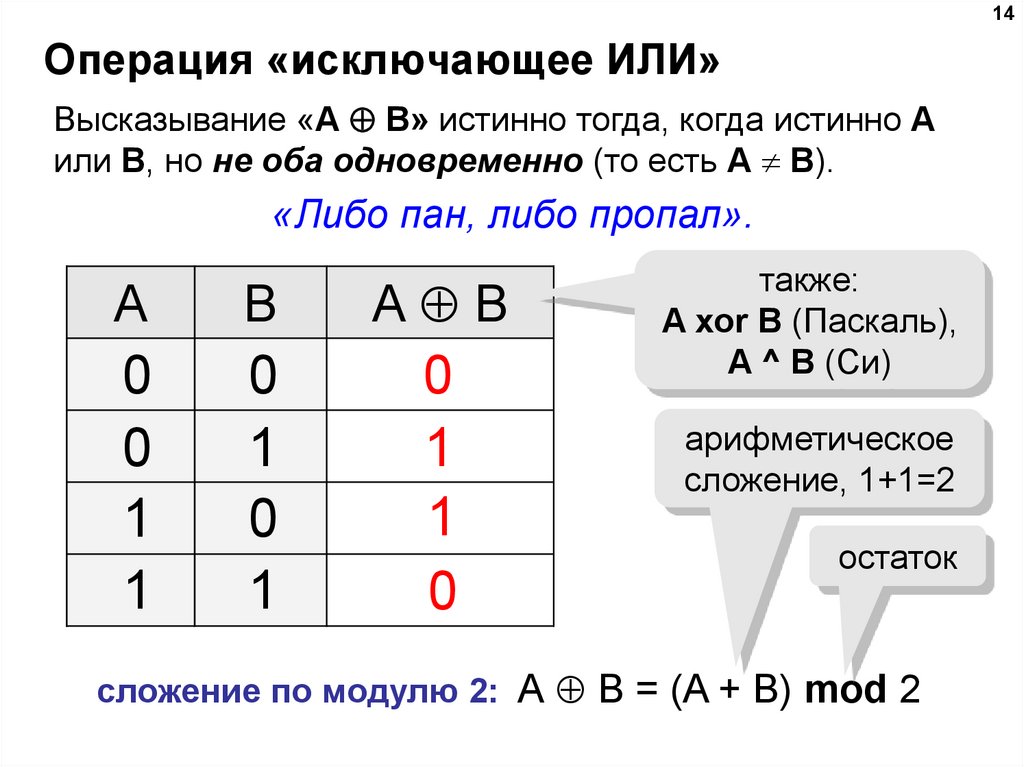
14. Операция «исключающее ИЛИ»
14Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (то есть A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
также:
A xor B (Паскаль),
A ^ B (Си)
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2
15. Свойства операции «исключающее ИЛИ»
15Свойства операции «исключающее ИЛИ»
A A= 0
(A B) B = ?
A 0= A
A 1= A
A B A B A B
A
0
0
1
1
B
0
1
0
1
A B
A B A B A B А B
0
0
1
0
0
1
0
0
0
1
1
0
0
1
1
0
16. Импликация («если …, то …»)
16Импликация («если …, то …»)
Высказывание «A B» истинно, если не
исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
А B
1
1
0
1
A B A B
17. Импликация («если …, то …»)
17Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит дома».
A – «Вася идет гулять».
A
B
А
B
B – «Маша сидит дома».
A B 1
? А если Вася не идет
гулять?
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
0
0
1
1
0
1
0
1
1
1
0
1
18.
Логическое следование соответствует высказываниюне A или B
Сравним таблицы истинности:
A
B
A B
A
B
¬A
¬A˅B
0
0
1
0
0
1
1
0
1
1
0
1
1
1
1
0
0
1
0
0
0
1
1
1
1
1
0
1
Логические выражения, у которых последние столбцы
истинности совпадают, называются равносильными.
18
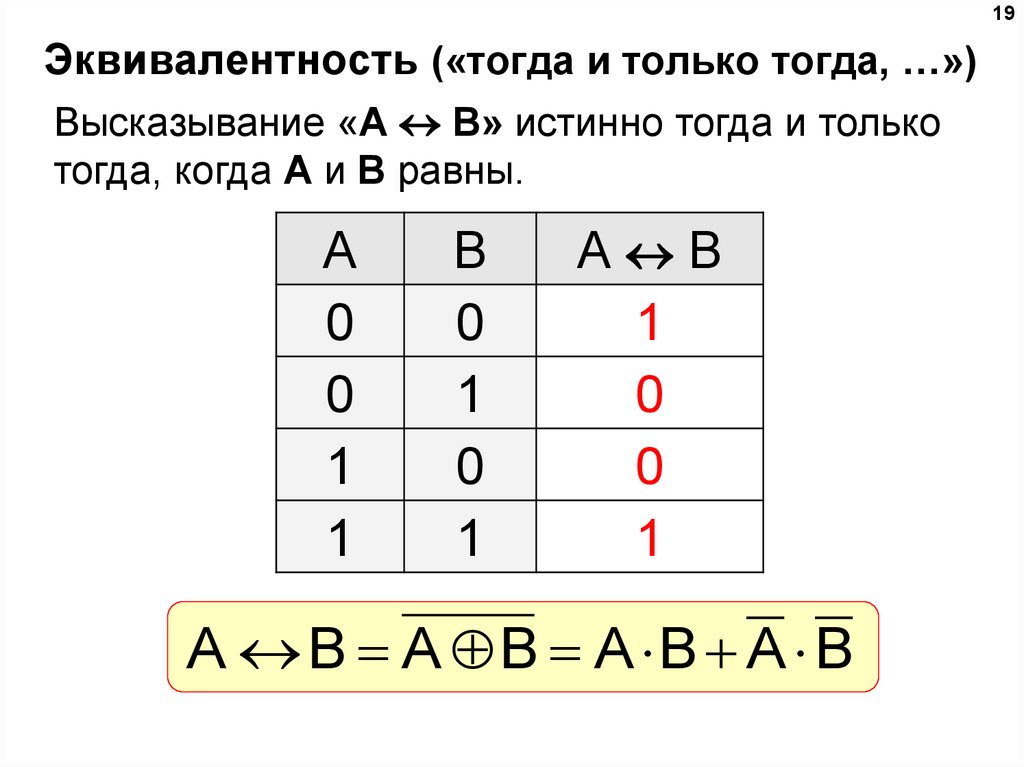
19. Эквивалентность («тогда и только тогда, …»)
19Эквивалентность («тогда и только тогда, …»)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
A B A B A B A B
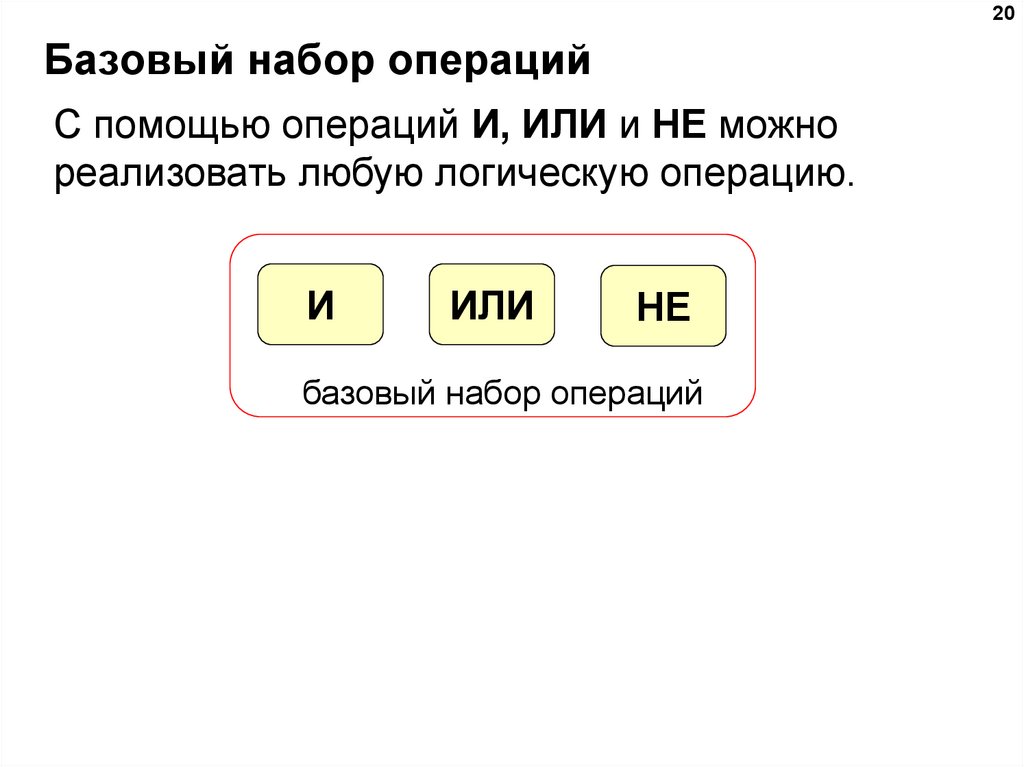
20. Базовый набор операций
20Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно
реализовать любую логическую операцию.
И
ИЛИ
НЕ
базовый набор операций
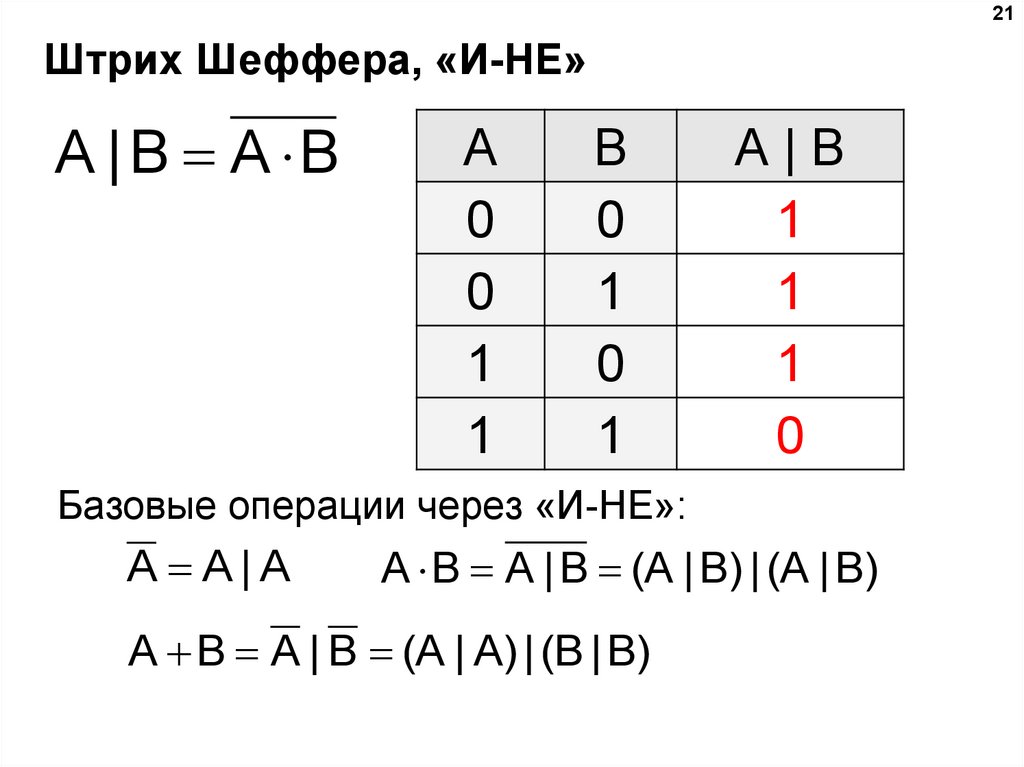
21. Штрих Шеффера, «И-НЕ»
21Штрих Шеффера, «И-НЕ»
A | B A B
A
0
0
1
1
B
0
1
0
1
А|B
1
1
1
0
Базовые операции через «И-НЕ»:
A A|A
A B A | B (A | B) | (A | B)
A B A | B (A | A) | (B | B)
22. Стрелка Пирса, «ИЛИ-НЕ»
22Стрелка Пирса, «ИЛИ-НЕ»
A B A B
A
0
0
1
1
B
0
1
0
1
Базовые операции через «ИЛИ-НЕ»:
А↓B
1
0
0
0
23. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
В основе булевой алгебры лежат 16 основных функций. Наиболее частоприменяемые из них:
логическое отрицание (инверсия) – «не»; ¬ ; ¯ ;
логическое умножение (конъюнкция) – «и»; &; ^ ; • ;
логическое сложение (дизъюнкция) – «или»; +; ;
логическое следование (импликация) –
логическая операция эквивалентности – ~ ; ; ;
функция Вебба (отрицание дизъюнкции) – ИЛИ-НЕ;
функция Шеффера (отрицание конъюнкции) – И-НЕ;
сложение по модулю 2 (М2).
23
24. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Приведенные функции можно свести в таблицу истинности:Функции
Аргументы
A B A B
A
B
¬A
¬B
A^B
A B ИЛИНЕ
ИНЕ М2
0
0
1
1
0
0
1
1
1 1
0
0
1
1
0
0
1
1
0
0 1
1
1
0
0
1
0
1
0
0
0 1
1
1
1
0
0
1
1
1
1
0 0
0
24
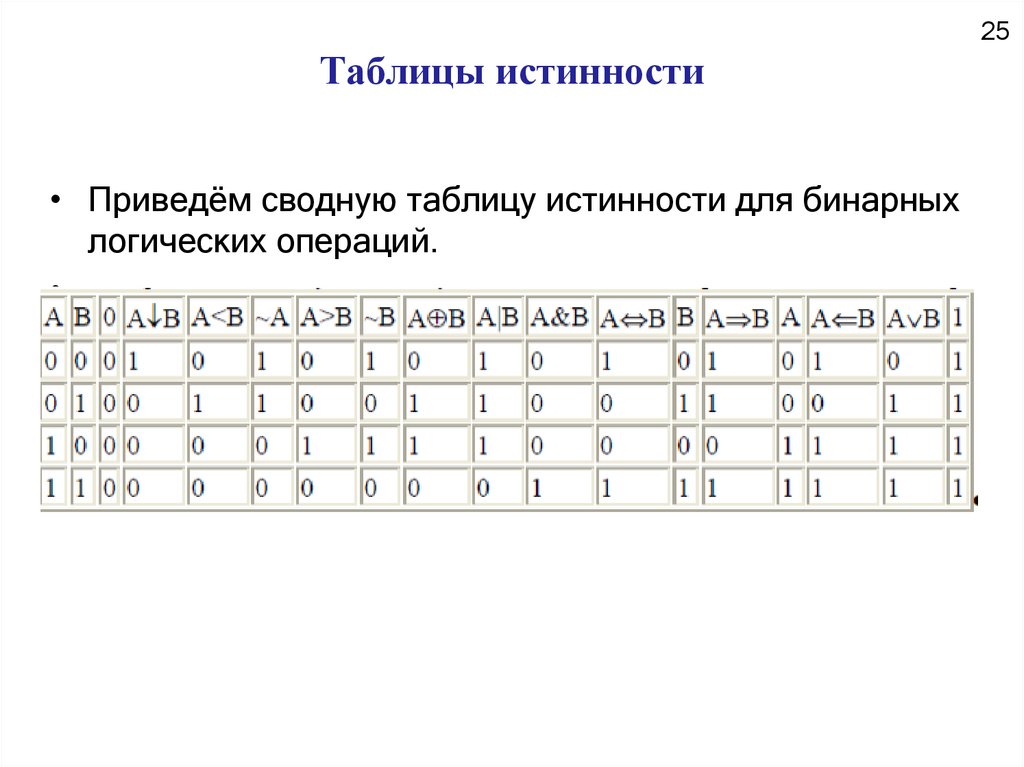
25. Таблицы истинности
25Таблицы истинности
• Приведём сводную таблицу истинности для бинарных
логических операций.
26. Формализация
26Формализация
Прибор имеет три датчика и может работать, если два из
них исправны. Записать в виде формулы ситуацию
«авария».
A – «Датчик № 1 неисправен».
B – «Датчик № 2 неисправен».
Формализация – это
переход к записи на
C – «Датчик № 3 неисправен».
формальном языке!
Аварийный сигнал:
X – «Неисправны два датчика».
X – «Неисправны датчики № 1 и № 2» или
«Неисправны датчики № 1 и № 3» или
«Неисправны датчики № 2 и № 3».
логическая
формула
X A B A C B C
!
27. Вычисление логических выражений
27Вычисление логических выражений
1
4
2
5
3
X A B A C B C
+
Порядок вычислений:
•скобки
•НЕ
•И
•ИЛИ, исключающее ИЛИ
•импликация
•эквивалентность
+
A
B
A
B
С
C
28. ТАБЛИЦЫ ИСТИННОСТИ
Таблица истинности определяет истинность или ложность логическойфункции при всех возможных комбинациях исходных значений простых
высказываний.
Правила построения таблиц истинности.
1)Подсчитать количество переменных n в логическом выражении.
2)Определить количество строк в таблице, которое равно
m=2n
3)Подсчитать количество операций в логическом выражении и определить
количество столбцов в таблице:
k = количество переменных (n) + количество операций.
4)Ввести названия столбцов таблицы в соответствии с последовательностью
выполнения логических операций с учетом скобок и приоритетов.
5)Заполнить столбцы логических переменных наборами значений.
6)Провести заполнение таблицы истинности по столбцам, выполняя базовые
логические операции
в
соответствии
с
установленной в
п. 4 последовательностью.
28
29. ТАБЛИЦЫ
ИСТИННОСТИПример. Определить истинность формулы
F=((C B) B)^ (A^ B) B
Формула
является тождественно истинной, если все
значения строк результирующего столбца будут равны 1.
1шаг. Определяем количество строк в таблице:
m=23=8
2шаг. Определяем количество столбцов в таблице:
k=3+5=8
29
30. Пример. Составить таблицу истинности сложного логического выражения D = не A& (B+C) А, В, С - три простых высказывания, поэтому
Пример. Составить таблицу истинности сложного логического выраженияD = не A& (B+C)
А, В, С - три простых высказывания, поэтому :
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элеманта А, В, С)
количество столбцов : 1) А 2) В 3) С 4) не A это инверсия А (обозначим Е) 5) B+
C это операция дизъюнкции (обозначим F) 6) D = неA& (B+C ), т.е. D = E&F это
операция конъюнкции
1
2
3
4
5
6
А
В
С
E = не А (не 1)
F = В+С (2+3)
D = E&F (4*5)
1
1
1
0
1
0
1
1
0
0
1
0
1
o
1
0
1
0
1
o
0
0
0
0
0
1
1
1
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
0
0
1
0
0
30
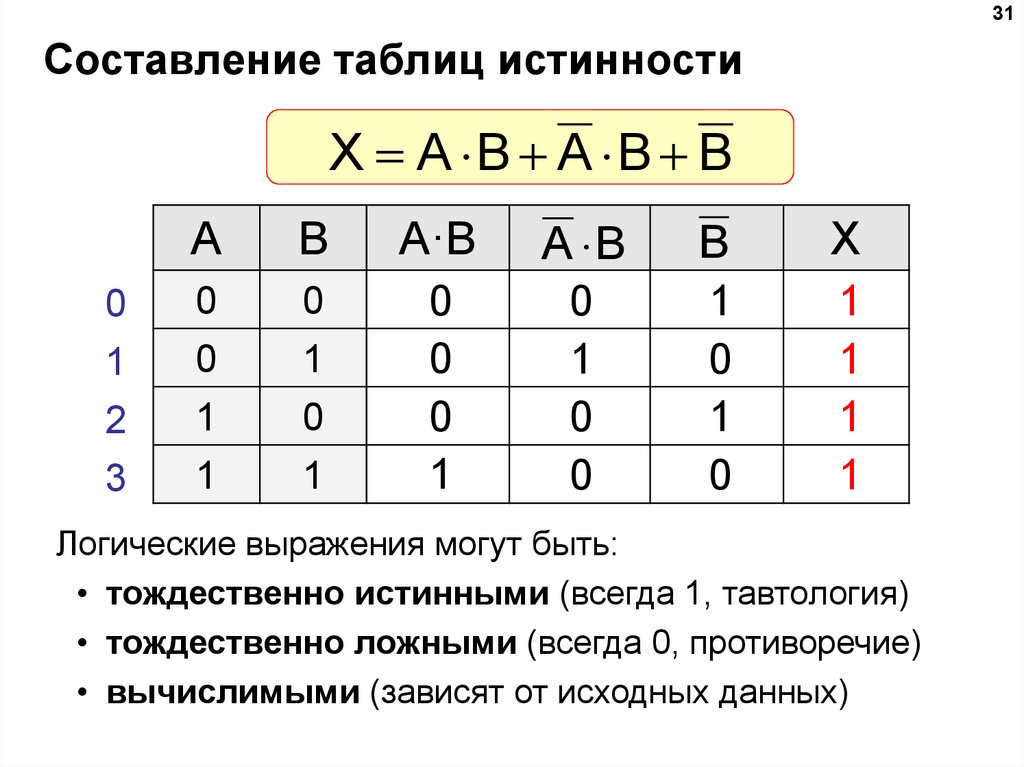
31. Составление таблиц истинности
31Составление таблиц истинности
X A B A B B
0
1
2
3
A
B
A·B
A B
B
X
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
1
1
Логические выражения могут быть:
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)
32. Составление таблиц истинности
32Составление таблиц истинности
X A B A C B C
0
1
2
3
4
5
6
7
A
B
C
A∙B
A∙C
B∙C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
33. Задачи (таблица истинности)
33Задачи (таблица истинности)
Символом F обозначено одно из
указанных ниже логических выражений
от трех аргументов: X, Y, Z. Дан
фрагмент таблицы истинности
выражения F. Какое выражение
соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z
X
1
0
1
Y
0
0
1
Z
0
0
1
F
1
1
0
34. Логические основы компьютеров
34Логические
основы
компьютеров
Диаграммы
35. Диаграммы Венна (круги Эйлера)
35Диаграммы Венна (круги Эйлера)
A
A
A
B
B
A·B
A
A+B
A
A
A
B
B
A B
A B
B
A B
36. Диаграмма с тремя переменными
36Диаграмма с тремя переменными
Хочу
Могу
3
2
1
5
6
4
7
8
1 M X H
5 M X H
2 M X H
6 M X H
3 M X H
7 M X H
4 M X H
8 M X H
Надо
3 4 M X H M X H
3 4 X H
! Логические выражения можно упрощать!
37.
37САМОСТОЯТЕЛЬНАЯ РАБОТА
1.
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что
большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и
«Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику.
Причем трем среди них нравятся еще и «Волк и теленок», шестерым - «Губка Боб Квадратные
Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13
фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же
шестиклассникам нравится «Губка Боб Квадратные Штаны».
2.
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4
прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри
Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг.
Сколько книг прочитал только Рон?
3.
Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу – 8
человек, спортивную школу – 12 человек, музыкальную и художественную школу– 3,
художественную и спортивную школу– 2, музыкальную и спортивную школу– 2, все три школы
посещает 1человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в
чем себя не развивают?
38. Задачи
38Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
огурцы
помидоры
огурцы & помидоры
Количество сайтов
100
200
50
Сколько сайтов будет найдено по запросу
огурцы | помидоры
39. Задачи
39Задачи
A
B
NA|B = NA+ NB
50
огурцы & помидоры
A
B
NA|B = NA+ NB – NA&B
огурцы | помидоры
огурцы
помидоры
100
200
40. Задачи
40Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак & Рубин
! Общее условие с & можно отбросить !
41. Задачи
41Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
Динамо
Спартак
Динамо | Спартак
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак
42. Задачи
43Задачи
Некоторый сегмент сети Интернет состоит из 1000
сайтов. Поисковый сервер в автоматическом режиме
составил таблицу ключевых слов для сайтов этого
сегмента. Вот ее фрагмент:
Ключевое слово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если по трем следующим запросам найдено:
принтер | сканер
– 450 сайтов,
принтер & монитор
– 40 сайтов
сканер & монитор
– 50 сайтов.
43. Задачи
44Задачи
(принтер | сканер) & монитор = ?
А (сканер)
B (принтер)
450
принтер | сканер
0
NA|B = NA+ NB – NA&B
сканер
200
принтер
250
принтер
сканер
принтер & монитор = 40
50
40
сканер & монитор = 50
монитор
40 + 50 = 90
44. Задачи
45Задачи
Перед началом Турнира Четырех болельщики
высказали следующие предположения по поводу своих
кумиров:
А) Макс победит, Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков
был прав только в одном из своих прогнозов. Какое место на турнире
заняли Джон, Ник, Билл, Макс? (В ответе перечислите подряд без
пробелов места участников в указанном порядке имен.)
A
Джон
Ник
Билл
Макс
2
1
B
C
1
1
3
4
45. Задачи
46Задачи
На одной улице стоят в ряд 4 дома, в каждом из них живет
по одному человеку. Их зовут Василий, Семен, Геннадий и
Иван. Известно, что все они имеют разные профессии:
скрипач, столяр, охотник и врач. Известно, что
(1) Столяр живет правее охотника.
(2) Врач живет левее охотника.
(3) Скрипач живет с краю.
(4) Скрипач живет рядом с врачом.
(5) Семен не скрипач и не живет рядом со скрипачом.
(6) Иван живет рядом с охотником.
(7) Василий живет правее врача.
(8) Василий живет через дом от Ивана.
Определите, кто где живет, и запишите начальные буквы
имен жильцов всех домов слева направо. Например, если бы
в домах жили (слева направо) Кирилл, Олег, Мефодий и
Пафнутий, ответ был бы КОМП.







































 Информатика
Информатика








