Похожие презентации:
Ассиметричные криптографические алгоритмы
1.
МИНОБРНАУКИ РОССИИФедеральное государственное бюджетное образовательное учреждение
высшего образования
«МИРЭА – Российский технологический университет»
РТУ МИРЭА
Институт искусственного интеллекта
Кафедра Компьютерной и информационной безопасности
Тема занятия:
«Ассиметричные криптографические
алгоритмы»
Преподаватель: Афанасьев Дмитрий Михайлович
Москва, 2023 г.
2.
В отличие от симметричного шифрования, в которомвсё шифруется и расшифровывается одним и тем же ключом,
асимметричное устроено сложнее. В нём уже два ключа, и
один из них публичный.
Принцип работы:
Асимметричное шифрование основано на парах чисел.
Одно из этих чисел — открытый ключ, который доступен
всем. С помощью этого числа кто угодно может зашифровать
сообщение. Но расшифровать его с помощью этого же числа
не получится.
Для расшифровки берут второе число — закрытый
ключ. Он должен быть секретным.
3.
Это не могут быть два случайных ключа. Открытыйи закрытый ключ всегда связаны между собой алгоритмом,
который их выдаёт. Смысл в том, что внутри этого алгоритма
есть третье, тоже секретное, число, которое связано с обоими
ключами.
Самый простой способ установить такую связь — взять
два больших простых числа и перемножить их. Получится
ещё большее число, которое и будет лежать в основе
алгоритма. А внутри этого алгоритма будет такая математика,
которая зависит от разложения чисел на множители. Если не
знать ни одно из первоначальных простых чисел, то
разложить на множители такое огромное число будет очень
сложной задачей.
4.
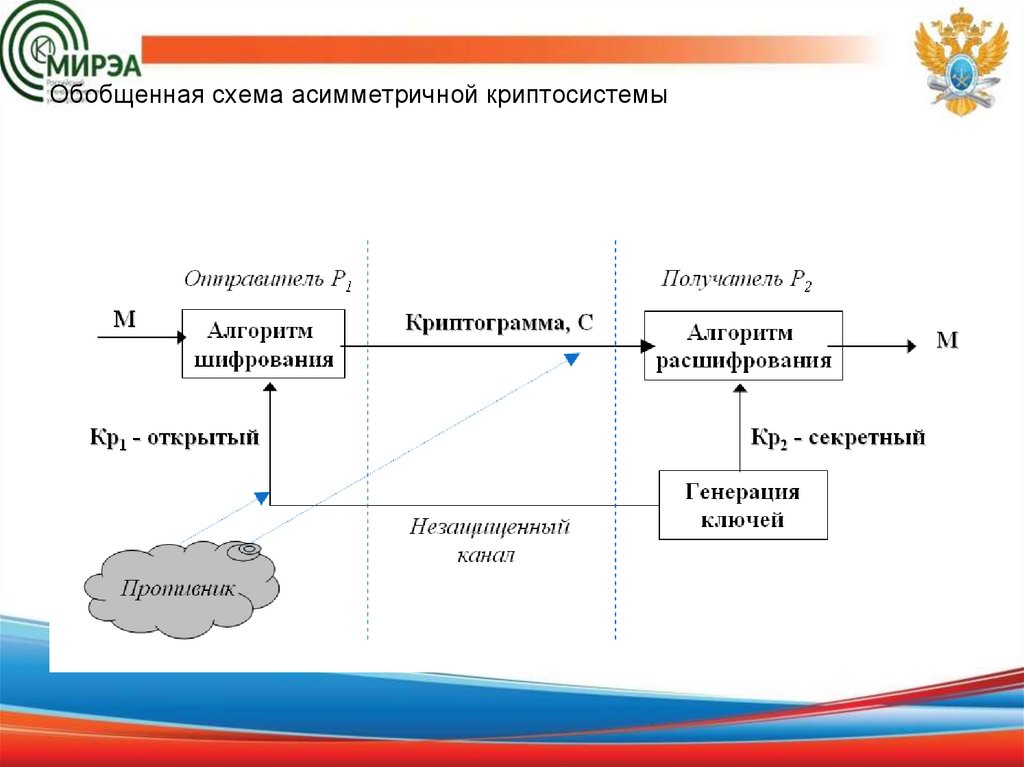
Обобщенная схема асимметричной криптосистемы5.
Передача ключа по открытым каналам была большой проблемойкриптографии XX века. Но эту проблему удалось решить после появления
алгоритма Диффи — Хеллмана. Схема открытого распределения ключей,
предложенная Диффи и Хеллманом, произвела настоящую революцию в
мире шифрования.
Открытое распространение ключей Диффи — Хеллмана
позволяет паре пользователей системы выработать общий секретный
ключ, не обмениваясь секретными данными.
Основы
криптографии
с
открытыми
ключами
были
выдвинуты
Уитфилдом
Диффи
(Whitfield
Diffie)
и
Мартином
Хеллманом (Martin Hellman), а также независимо от них Ральфом
Мерклом (Ralph Merkle).
6.
Их вкладом в криптографию было убеждение, что ключи можноиспользовать парами — ключ зашифрования и ключ расшифрования —
при условии, что исключается возможность определения содержимого
ключа для расшифрования исходя из содержимого открыто
передаваемого ключа для зашифрования.
Диффи и Хеллман впервые представили эту идею на
Национальной компьютерной конференции 1976 года, а через несколько
месяцев была опубликована их основополагающая работа «New
Directions in Cryptography» («Новые направления в криптографии»)
Хоть алгоритм и известен как алгоритм Диффи — Хеллмана, но в
патенте в качестве создателей данного алгоритма указано три автора —
Хеллман, Диффи и Меркл.
7.
Алгоритм Диффи-ХеллманаАлгоритм Диффи-Хеллмана (Diffie-Hellman) использует функцию
дискретного возведения в степень. Сначала генерируются два больших
простых числа n и q. Эти два числа не обязательно хранить в секрете.
Далее один из партнеров P1 генерирует случайное число x и
посылает другому участнику будущих обменов P2 значение
A = qx mod n
По получении А партнер P2 генерирует случайное число у и
посылает участнику обмена P1 вычисленное значение
B = qy mod n
8.
Партнер P1, получив В, вычисляета партнер P2 вычисляет
Kx = Bx mod n,
Ky = Ay mod n.
Алгоритм гарантирует, что числа Ky и Kx равны и могут быть
использованы в качестве секретного ключа для шифрования. Ведь даже
перехватив числа А и В, трудно вычислить Kx или Ky.
Схематично, работа алгоритма Диффи-Хеллмана представлена на рис. 2
9.
Рис.2. Схема работы алгоритма Диффи-Хеллмана10.
Вычислим Kx и Ky, если известно:1) n = 7; q = 3; x = 3; y = 2;
2) n = 5; q = 3; x = 3; y = 2;
3) n = 11; q = 3; x = 3; y = 4;
10
11.
Однонаправленные хэш-функцииХэш-функция предназначена для сжатия подписываемого
документа М до нескольких десятков или сотен бит. Хэш-функция h(.)
использует в качестве аргумента сообщение М произвольной длины и
возвращает хэш значение h(M)=H фиксированной длины. Обычно
хэшированная информация является сжатым двоичным представлением
основного сообщения произвольной длины. Следует отметить, что
значение хэш-функции h(M) зависит от документа M и не позволяет
восстановить сам документ M.
12.
Хэш-функция должна удовлетворять целому ряду условий:
должна быть чувствительна к всевозможным изменениям в тексте М;
должна обладать свойством необратимости, т.е. задача подбора
документа М1, который обладал бы требуемым значением
хэшфункции, должна быть вычислительно неразрешима;
вероятность того, что значения хэш-функции двух различных
документов совпадут, должна быть ничтожно мала.
13.
Большинствохэш-функций
строится
на
основе
однонаправленной функции f(.) , которая образует выходное значение
длиной n при заданых двух входных значений длиной n. Этими входами
являются блок исходного текста Мi и хэш-значение Hi-1 предыдущего
блока текста.
14.
Криптосистема Эль-ГамаляДля генерации пары ключей сначала выбирается
простое число p и два случайных числа, g и x, оба
меньше p. Затем вычисляется
y = gx mod p.
15.
Шифрование:выбираем случайное k, которое
взаимно простое с p–1;
a (шифротекст) =gk mod p,
b (шифротекст)= M (yk mod p).
16.
Дешифрирование:M (открытый текст) = b/ax mod p.
Приведем пример использования метода Эль-Гамаля для
шифрования сообщения 2, 5, 7. Для простоты вычислений будем
использовать маленькие числа (на практике используются числа
существенно большие).
17.
Пример1. Выбирается простое число p=19; g=5 (g <p); k=13; x=11.
2. Вычисляется y =gx mod p=511mod 19=6.
3. Шифруется сообщение a=gk mod p=513 mod 19=17,
b1= M1 (yk mod p)=2 (613 mod 19)=8,
b2= M2 (yk mod p)=5 (613 mod 19)=20,
b3= M3 (yk mod p)=7 (613 mod 19)=28.
18.
4. Дешифрование сообщенияM1 = b1/(ax mod p)=8/(1711mod 19)=8/4=2,
M2 = b2/(ax mod p)=20/(1711mod 19)=20/4=5,
M3 = b3/(ax mod p)=28/(1711mod 19)=28/4=7.





















 Информатика
Информатика








