Лекция (СиАОД ч.2) 4

1.

1
Структуры и алгоритмы обработки данных
(часть 2)
Лекция 4
Москва 2022

2.

2
Алгоритм Бойера Мура
Алгоритм Бойера-Мура разработан двумя учеными —
Бойером (Robert S. Boyer) и Муром (J. Strother Moore) в 1977
году.
Считается наиболее быстрым среди алгоритмов общего
назначения, предназначенных для поиска подстроки в строке.
Важная особенность алгоритма - выполняет сравнения в
шаблоне справа налево в отличие от многих других
алгоритмов.
Алгоритм Бойера-Мура считается наиболее эффективным
алгоритмом поиска шаблонов (образцов) в стандартных
приложениях и командах, таких как Ctrl+F в браузерах и
текстовых редакторах.

3.

3
Алгоритм Бойера Мура
Правила алгоритма:
Совмещается начало текста (строки) и образца, проверка начинается с последнего
символа шаблона.
Если все символы образца совпали с наложенными символами строки, значит,
подстрока найдена, и поиск окончен.
Если же какой-то символ образца не совпадает с соответствующим символом строки,
образец сдвигается на несколько символов вправо, и проверка снова начинается с
последнего символа.
Эти «несколько» вычисляются по двум эвристикам (правилам):
1. Эвристика (правило) стоп-символа (эвристика плохого характера, правила плохих
персонажей);
2. Эвристика (правило) хорошего суффикса (эвристика безопасного суффикса,
хорошие суффиксные правила)

4.

4
Алгоритм Бойера Мура
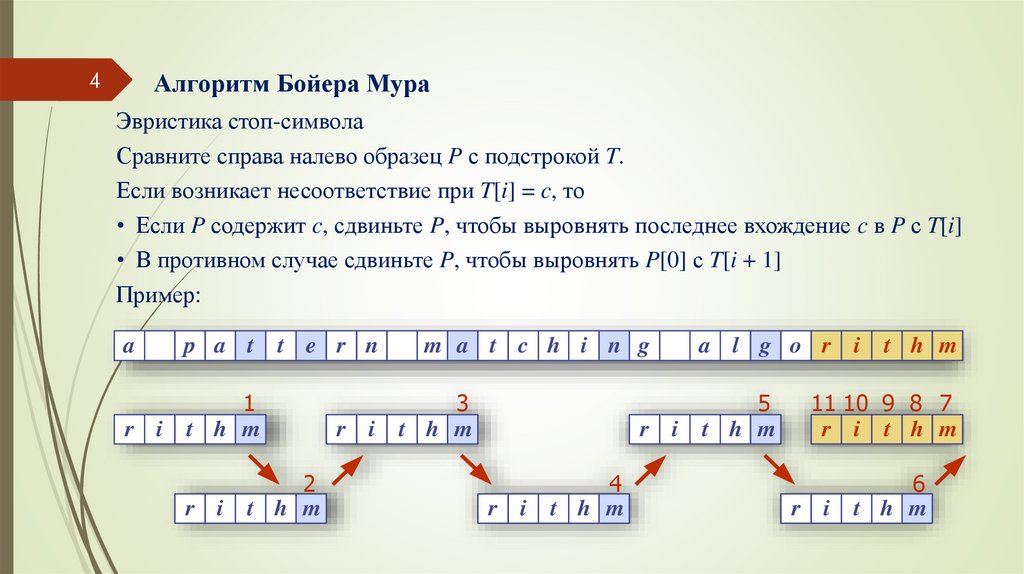
Эвристика стоп-символа
Сравните справа налево образец P с подстрокой T.
Если возникает несоответствие при T[i] = c, то
• Если P содержит c, сдвиньте P, чтобы выровнять последнее вхождение c в P с T[i]
• В противном случае сдвиньте P, чтобы выровнять P[0] с T[i + 1]
Пример:
a
p a t
r i
1
t h m
r i
t e r n
2
t h m
r
i
m a t c h i n g
3
t h m
r
r
i
4
t h m
a l g o r
i
5
t h m
i
t h m
11 10 9 8 7
r i t h m
r
i
6
t h m

5.

5
Алгоритм Бойера Мура
Таблица стоп-символов
Обе эвристики требуют предварительных вычислений — в зависимости от шаблона
поиска заполняются две таблицы. Таблица стоп-символов по размеру соответствует
алфавиту (например, если алфавит состоит из 256 символов, то её длина 256);
таблица суффиксов — искомому шаблону.
При поиске таблица стоп-символов позволит быстро определить величину сдвига
образца до ближайшего слева от точки несовпадения в нём стоп-символа.
В разных реализациях алгоритма БМ:
• нумерация может быть с 0 или с 1;
• индексирование в образце может вестись с его левого края или с правого;
• признаком отсутствия стоп-символа в образце может быть либо начальный
индекс - 1 (будет -1 или 0), либо конечный индекс + 1 (т.е. заведомо
несуществующий индекс);

6.

6
Алгоритм Бойера Мура
Таблица стоп-символов
В таблице стоп-символов указывается последняя позиция в образце P (исключая
последнюю букву) каждого из символов алфавита. Для всех символов, не вошедших
в образец P, пишем 0 (для нумерации с 0 — соответственно, −1).
Например, если P = «abcdadcd», таблица стоп-символов будет выглядеть так.

7.

7
Алгоритм Бойера Мура
a
b
c
x
a
b
c
d
e
*
4
5
6
3
4
5
6
7
-1
-1
Если несовпадение произошло на позиции i символа в образце, а стопсимвол «c», то значение величины сдвига будет равно i-StopTable[c] .

8.

8
Создание таблицы стоп-символов

9.

9
Анализ правила сдвига по стоп-символу
• Наибольший эффект при несовпадениях, близких к правому концу
шаблона поиска
• Дополнительная память О(|А|) и время на подготовку шаблона О(|А|),
где |А| – длина алфавита
• Нет эффекта, если стоп-символ в шаблоне справа от точки несовпадения
(сдвиг не может быть отрицательным, т.е. влево)
Решения:
• Расширенное правило стоп-символа (см. Д.Гасфилд)
• Эвристика (правило) хорошего суффикса.

10.

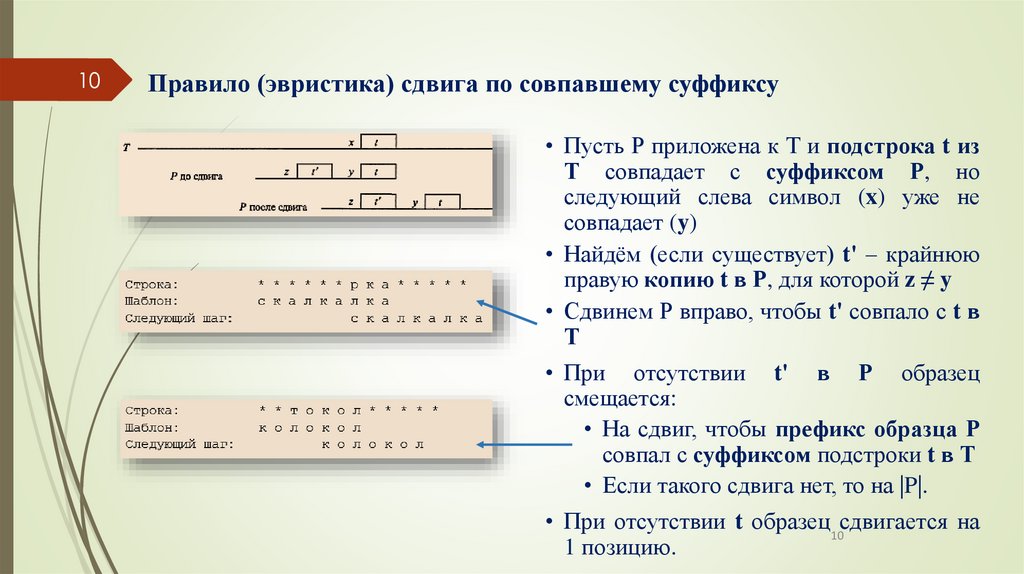
10
Правило (эвристика) сдвига по совпавшему суффиксу
• Пусть Р приложена к Т и подстрока t из
Т совпадает с суффиксом Р, но
следующий слева символ (x) уже не
совпадает (y)
• Найдём (если существует) t' – крайнюю
правую копию t в Р, для которой z ≠ y
• Сдвинем Р вправо, чтобы t' совпало с t в
Т
• При отсутствии t' в Р образец
смещается:
• На сдвиг, чтобы префикс образца Р
совпал с суффиксом подстроки t в Т
• Если такого сдвига нет, то на |P|.
• При отсутствии t образец10сдвигается на
1 позицию.

11.

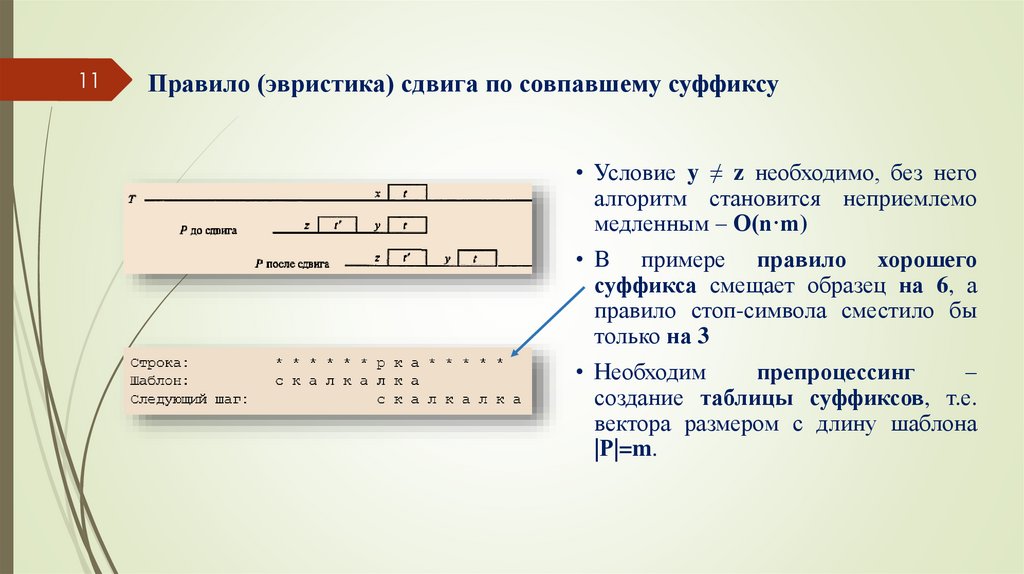
11
Правило (эвристика) сдвига по совпавшему суффиксу
• Условие y ≠ z необходимо, без него
алгоритм становится неприемлемо
медленным – О(n·m)
• В примере правило хорошего
суффикса смещает образец на 6, а
правило стоп-символа сместило бы
только на 3
• Необходим
препроцессинг
–
создание таблицы суффиксов, т.е.
вектора размером с длину шаблона
|Р|=m.

12.

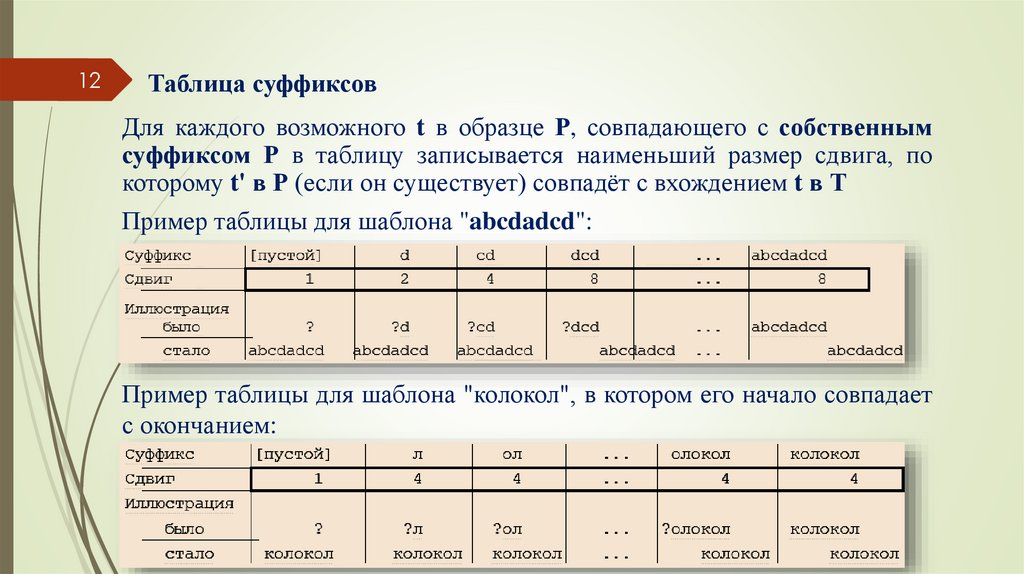
12
Таблица суффиксов
Для каждого возможного t в образце Р, совпадающего с собственным
суффиксом Р в таблицу записывается наименьший размер сдвига, по
которому t' в Р (если он существует) совпадёт с вхождением t в Т
Пример таблицы для шаблона "abcdadcd":
Пример таблицы для шаблона "колокол", в котором его начало совпадает
с окончанием:

13.

13
Алгоритм Бойера Мура. Пример
Рассмотрим общий пример
Первый шаг:
Обнаружено, что S и E не
совпадают,
применяется
эвристика стоп-символа, и сдвиг
составляет 6 - (- 1) = 7 позиций.
Второй шаг:
Обнаружено, что P и E не
совпадают,
применяется
эвристика стоп-символа, и сдвиг
составляет 6 - 4 = 2 позиции.

14.

14
Алгоритм Бойера Мура. Пример
Рассмотрим общий пример
Третий шаг:
Сравнивая
по
очереди,
обнаружено, что I и A не
совпадают,
применяется
эвристика хорошего суффикса,
которое дает перемещение на 6
позиций.
Применение эвристики стопсимвола дало бы перемещение
только на 3 позиции.

15.

15
Алгоритм Бойера Мура. Пример
Рассмотрим общий пример
Четвертый шаг:
Обнаружено, что P и E не
совпадают,
применяется
эвристика стоп-символа, и сдвиг
составляет 6 - 4 = 2 позиции.
Пятый шаг:
Обнаружено,
полное
совпадение. Образец обнаружен
в строке

16.

16
Создание таблицы суффиксов с помощью Z-функции

17.

17
Процедура БМ-поиска

18.

18
Основная программа БМ-поиска

19.

19
Анализ алгоритма БМ
• Использование только правила («плохого») стопсимвола даст наихудшее время О(n·m),
в среднем случае (в т.ч. в текстах на естественных
языках) время сублинейно – О(n+m).
• Использование только правила совпавшего
(«хорошего») суффикса даст наихудшее время:
• Без модификаций – сублинейное О(n+m)
• С модификациями – линейное O(m) – согласно
оценке Р. Коула 3·m сравнений.

20.

20
Анализ алгоритма БМ
• В целом, использование полного алгоритма БМ в
наихудшем случае даст:
•Без модификаций – сублинейное время О(n+m)
•С модификациями – линейное O(m), например, до
2·m сравнений в алгоритме Апостолико-Джанкарло
•Дополнительная память О(|А|+m).
• Эффективен для естественных языков, снижение
замечено только на специально подобранных примерах
• На больших алфавитах (ASCII) растёт ёмкостная
сложность БМ-поиска
• На малых алфавитах (ДНК) ухудшается время БМпоиска.

21.

21
Алгоритм Бойера-Мура-Хорспула (упрощённый БМ-поиск)
• Модификация
–
упрощённый
вариант
алгоритма БМ с одной изменённой эвристикой
стоп-символов
• На случайных текстах показывает время лучше
• Прост в реализации
• Использует стандартную функцию сравнения
участков
памяти,
оптимизированную
на
ассемблерном уровне под конкретный процессор
• Стабильнее на больших алфавитах.

22.

22
Алгоритм Рабина-Карпа
Суть алгоритма: берем хеш образца, берем хеш куска текста равного по длине, сравниваем их.
Если равны, то проверяем их посимвольно, в противном случае — идем дальше.
Рассмотрим пример. В качестве хэш-функции возьмем
полиномиальный хеш (подойдет любая кольцевая хешфункция)
Есть двоичный алфавит, где a = 0, b = 1
Вычислим хеш образца:
Вычислим хеш подстроки T[0, 4].
Они не совпадают, значит двигаем образец на символ правее. Вычислим хеш подстроки T[1, 5]
Хеши подстроки и образца снова не совпадают, значит двигаем образец еще на символ правее.
Вычислим хеш подстроки T[2, 6]
Хеши совпали, значит проверяем этот участок посимвольно.

23.

23
Алгоритм Рабина-Карпа
• 1987 – М. Рабин и Р. Карп
• Алгоритм поиска подстроки с использованием хеширования
• В худшем случае O(n·m), в лучшем и среднем – до O(n)
• Главная особенность – способен в среднем за время O(n) найти любую из k образцов
одинаковой длины независимо от количества k
• Поэтому используется для поиска не одиночного шаблона, а множественных шаблонов
одинаковой длины
• Пример – поиск плагиата.
• Предыдущие алгоритмы настроены на оптимизацию величины сдвига образца
• РК-алгоритм пытается ускорить процесс сравнения текста с образцом
• Хеш-функция преобразует символьную последовательность (строку) в числовое значение –
хеш-значение (хеш)
• В РК-алгоритме хеш шаблона поиска сравнивается с хешами текста
• Неравенство хешей гарантирует отсутствие шаблона в тексте → можно посимвольно не
сравнивать
• Равенство хешей указывает на возможность присутствия (ложные совпадения) → необходимо
сравнить посимвольно.

24.

24
Алгоритм Рабина-Карпа
Проблема 1 – ложное совпадение хешей
• Между двумя строками (частью текста и образцом) может произойти коллизия — совпадение их
хешей
• Тогда необходимо посимвольно проверять совпадение самих строк → много времени, если
строки имеют большУю длину
• Проверка не нужна, если ложные срабатывания допустимы → в среднем время поиска О(n)
• «Алгоритм хорош настолько, насколько хороша его хеш-функция»:
• При использовании достаточно хороших хеш-функций коллизии случаются крайне редко (в
среднем до О(n)).

25.

25
Алгоритм Рабина-Карпа
Полиномиальный хеш и модульная арифметика
• Низкую вероятность коллизий и эффективное вычисление сочетает в себе полиномиальный
хеш:
• Во избежание переполнения целочисленной разрядной сетки в памяти при больших Н:
Выбор b и Q:
• Метод авторов: фикс. b=2, Q – простое случ. из [2..n3], тогда вероятность коллизии не
превосходит 1/n;
• Модификация (Дитзфелбингер и др.): фикс. простое Q (напр., простые числа Мерсенна, 231-1,
261-1, 232-5, 264-59), b – случ. из [0..Q-1], тогда при Q>nc для какого-то с>2 вероятность коллизии
не превосходит 1/nc-2.

26.

26
Алгоритм Рабина-Карпа
Проблема 2 – многократный пересчёт хеша подстрок в тексте при сдвиге образца
• При наивном пересчёте хеша сложность РК-поиска сравняется с более простыми алгоритмами в
худшем случае – O(n·m)
• Приём – кольцевой (скользящий) хеш, когда при сдвиге на +1 позицию в тексте новый хеш
вычисляется на основе старого:
• убрав из подсчёта первый символ предыдущей подстроки и
• добавив в подсчёт новый символ справа;
• В случае полиномиального хеша:

27.

27
Алгоритм Рабина-Карпа
Поиск одиночного образца:
Поиск множества образцов: