Лекция (СиАОД ч.2) 5

1.

1
Структуры и алгоритмы обработки данных
(часть 2)
Лекция 5
Москва 2023

2.

2
Бинарное дерево поиска
Бинарное дерево поиска — это бинарное дерево, с дополнительными
свойствами по упорядоченности вставки узлов:
• у всех узлов левого поддерева произвольного узла Х значения ключей
данных меньше, чем значение ключа данных самого узла Х;
• у всех узлов правого поддерева произвольного узла Х значения ключей
данных не меньше, чем значение ключа данных самого узла Х;
• оба поддерева – левое и правое же являются бинарными деревьями поиска.
В бинарном дереве поиска, ключи в пределах набора элементов данных,
должны быть уникальны.

3.

3
Бинарное дерево поиска
Более простое определение бинарного дерева поиска — это бинарное дерево,
узлы которого упорядочены по значениям ключей по правилу:
• в левом поддереве любого узла (кроме листьев) расположены узлы со
значением ключа меньшим, чем значение ключа в родительском узле;
• в правом поддереве любого узла (кроме листьев) расположены узлы со
значением ключа большим, чем значение ключа в родительском узле.

4.

4
Трассировка процесса построения бинарного дерева поиска
Построение дерева включает две операции над бинарным деревом поиска:
поиск узла, поддеревом которого должен стать новый узел, и
непосредственно установление связи родительского узла с новым узлом –
вставка узла в дерево. Новый узел всегда вставляется в левое или правое
поддерево как лист.
Пример.
Построение бинарного дерева поиска для списка ключей:
12 10 25 8 5 22 28 14 44 1.

5.

5
Вырожденное бинарное дерево поиска
Дерево бинарного поиска может быть вырождено в список, т.е. может
иметь только одно поддерево: только левое или только правое.
Пример. Включение в бинарное дерево поиска
ключей, упорядоченных по убыванию.
Пример. Включение в бинарное дерево поиска
ключей, упорядоченных по возрастанию.
Дан список записей с ключами: 10 8 7 5 4.
Изобразить дерево, включая ключи в
указанном порядке.
Дан список записей с ключами: 4, 5, 7, 8, 10.
Изобразить дерево, включая ключи в
указанном порядке.

6.

6
Реализация бинарного дерева поиска
Бинарное дерево поиска можно реализовать:
• на векторном представлении: на массиве родителей; на списках левых сыновей и
правых братьев; на таблице, со ссылками на сыновей; на курсорах;
• на связанном представлении, с явно реализующем иерархическую структуре, в
которой отношения между узлами (поддеревьями) явно реализуются посредством
указателей.
Так как дерево поиска применяется к динамическим таблицам данных, т.е. таким, в
которых при выполнении поиска требуется удалять записи по ключу и вставлять
записи в определенном порядке, то и само дерево удобнее реализовать как
связанную динамическую структуру, связывая родительские узлы с дочерними
поддеревьями на основе указателей, так как время выполнения операций вставки и
удаления узлов выполняется со сложностью O(1).

7.

7
Связанное размещение элементов дерева в динамических областях памяти
Рассмотрим два способа организации бинарного дерева поиска и
отношений между его элементами
Способ 1. Узел содержит: информационную часть узла (или ссылка на
данные в другой структуре данных) и указатели на левое и правое
поддеревья.
Структура узла бинарного дерева поиска для рассматриваемого способа,
реализуемого на связанной структуре, имеет вид:
Где lefttree – указатель на левое поддерево, righttree – указатель на правое поддерево.

8.

8
Связанное размещение элементов дерева в динамических областях памяти
Информационная часть узла может содержать:
• для некоторых приложений только ключ (значение, которое требуется
для организации дерева), например, сортировать список значений целого
типа;
• для других узел может хранить ключ и связанные с ним данные,
например, номер зачетной книжки и анкетные данные студента;
• для третьих узел может хранить ключ и ссылку на данные в другой
структуре хранения.

9.

9
Связанное размещение элементов дерева в динамических областях памяти
Пример программной реализации структуры узла
struct Node{
unsigned int key;
string Name;
Node *lefttree, *righttree;
};
Node *Root;
//указатель на корень дерева
Где ключ (key) определяется как целочисленное значение; данные, которые
идентифицирует ключ, строкового типа; ссылки на левое (lefttree ) и правое
(lefttree ) поддеревья - указатели на узел. Согласно структуре узла дерево
однородное.

10.

10
Связанное размещение элементов дерева в динамических областях памяти
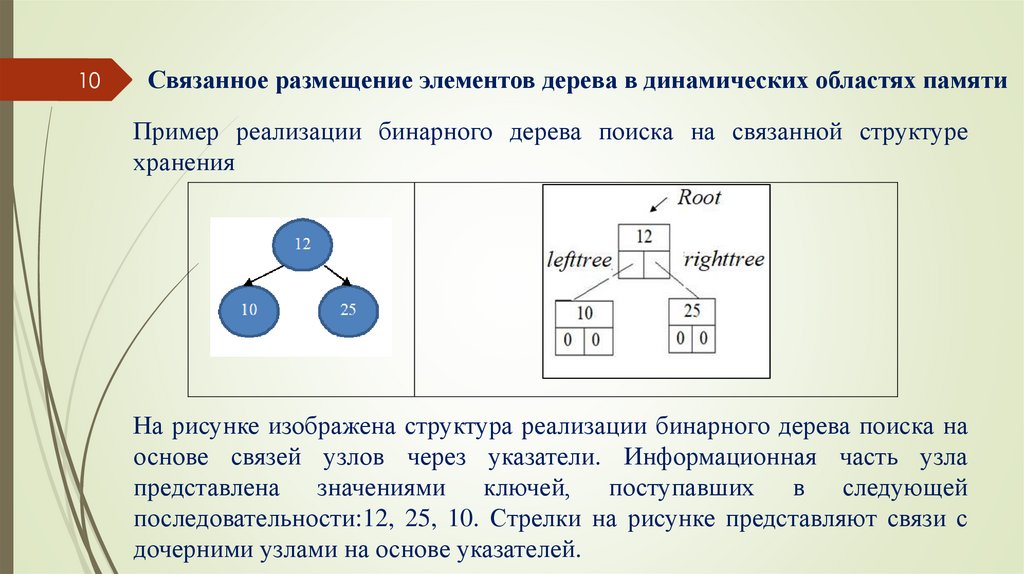
Пример реализации бинарного дерева поиска на связанной структуре
хранения
На рисунке изображена структура реализации бинарного дерева поиска на
основе связей узлов через указатели. Информационная часть узла
представлена значениями ключей, поступавших в следующей
последовательности:12, 25, 10. Стрелки на рисунке представляют связи с
дочерними узлами на основе указателей.

11.

11
Связанное размещение элементов дерева в динамических областях памяти
Способ 2. Хранение ссылки на родителя и правое и левое поддеревья узла
Узел содержит: информационную часть узла и указатели на левое и правое
поддеревья и указатель на родительский узел.
Структура узла бинарного дерева поиска для рассматриваемого способа,
реализуемого на связанной структуре, имеет вид:
Информационная часть узла Ссылка на родительский
узел parent
Ссылка на левое поддерево Ссылка
на
правое
lefttree
поддерево righttre
Где lefttree – указатель на левое поддерево, righttree – указатель на правое поддерево,
parent – указатель на родительский узел.

12.

12
Связанное размещение элементов дерева в динамических областях памяти
Пример программной реализации структуры узла для способа 2.
struct Node{
int key;
string Name;
Node *lefttree, *righttree;
Node *parent;
};
Node *Root;//указатель на вершину дерева

13.

13
Связанное размещение элементов дерева в динамических областях памяти
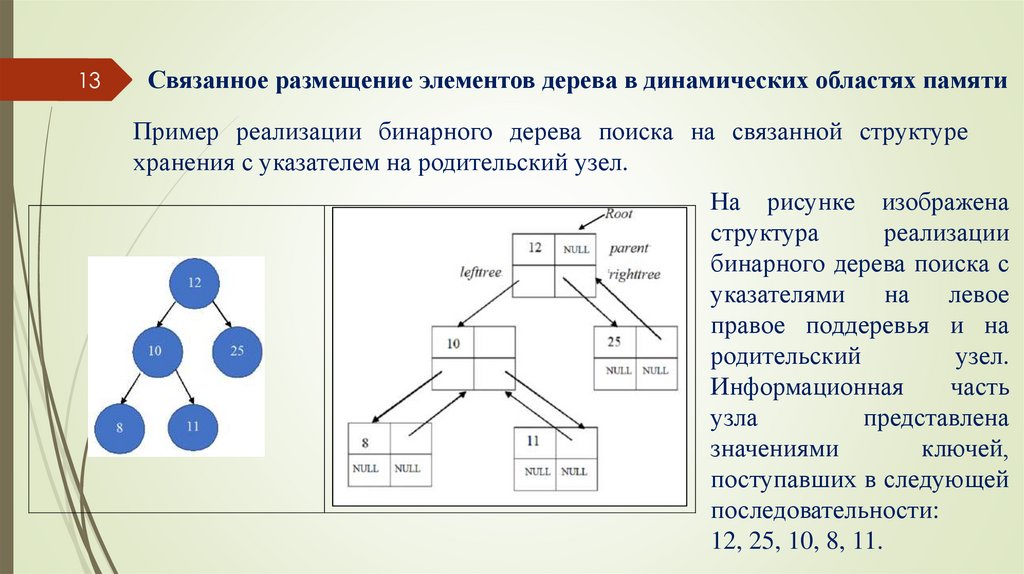
Пример реализации бинарного дерева поиска на связанной структуре
хранения с указателем на родительский узел.
На рисунке изображена
структура
реализации
бинарного дерева поиска с
указателями
на
левое
правое поддеревья и на
родительский
узел.
Информационная
часть
узла
представлена
значениями
ключей,
поступавших в следующей
последовательности:
12, 25, 10, 8, 11.

14.

14
Алгоритмы операций над бинарным деревом поиска
1.
2.
3.
4.
5.
6.
Обход бинарного дерева поиска методом в глубину.
Обход бинарного дерева поиска методом в ширину.
Создание узла бинарного дерева
Вставка узла в бинарное дерево поиска
Удаление узла из бинарного дерева поиска
Поиск узла, содержащего заданный ключ

15.

15
Абстрактный тип данных для бинарного дерева поиска
Приведем АТД для бинарного дерева поиска, с базовым набором операций,
для удобства описания алгоритмов.
АТД BinSearchTree
{
Данные
Root – корень дерева
key – ключ узла типа Tkey
data – информационная часть узла дерева типа Tdata
leftTree – левое поддерево
rightTree - правое поддерево
node - узел дерева

16.

16
Абстрактный тип данных для бинарного дерева поиска
Операции
//Создание узла node дерева
createNode(key,data) – возвращает созданный узел node дерева
//Вставка ключа в дерево
insertKeyBinSearchTree(T, key) – вставяет ключ в бинарное дерево поиска
//Вставка узла в дерево
insertBinSearchTree(T, node) – вставляет узел node в бинарное дерево
поиска
//Удаление узла со значением key из дерева
deleteBinSearchTree(T, key) – удаляет узел с ключом key из дерева

17.

17
Абстрактный тип данных для бинарного дерева поиска
//Получить значение ключа узла node
getKey(node)
//Получить левое поддерево дерева Т
getLeftTree(Т) - возвращает корень левого поддерева дерева Т
//Получить правое поддерево дерева Т
getRightTree(Т)
//Пусто ли дерево
isEmpty(T) – возвращает true если дерево пусто и false, если не пусто
//Сделать дерево пустым
MakeNull(T)
}

18.

18
Алгоритмы операций над бинарным деревом поиска
Алгоритмы операций АТД бинарного дерева реализуем на связанном
представлении бинарного дерева поиска.
Структура узла
typedef string Tdata;
typedef int Tkey;
struct Node{
Tkey key;
Tdata data;
Node *lefttree, *righttree;
};

19.

19
Алгоритмы операций над бинарным деревом поиска
1. Алгоритм операции создания узла
Принимает входные данные: key – ключ, data – данные, идентифицируемые
ключом. Создает в динамической памяти узел c типом Node, заполняет
значениями и возвращает созданный узел
Node* createNode(int key, Tdata data){
Node * node=new Node;
node->key=key; node->data=data;
node->lefttree=0; node->righttree=0;
return node;
}

20.

20
Алгоритмы операций над бинарным деревом поиска
2. Алгоритм операции вставки ключа в бинарное дерево поиска
Исходные данные алгоритма: указатель на вершину дерева (Root) и значение ключа.
Результат: измененное по содержанию дерево, в него добавлен новый узел.
1. Если дерево не пустое, то алгоритм выполняет поиск узла, спускаясь либо по левому,
либо по правому поддереву, в зависимости от значения ключа:
1.1. если значения вставляемого ключа меньше значения ключа текущего узла дерева,
то алгоритм выполняется для левого поддерева текущего узла (передается ссылка на
левое поддерево текущего узла, т.е. указатель на узел);
1.2. если значения вставляемого ключа больше значения ключа текущего узла дерева,
то алгоритм выполняется для правого поддерева текущего узла (передается ссылка на
правое поддерево текущего узла, т.е. указатель на узел).
2. Если дерево пустое, т.е. значение переданного указателя NULL, то на этом указателе
создается узел и в него помещается ключ и данные, и алгоритм завершается. Этот пункт
выполняется как при первичном вызове алгоритма вставки, так и при достижении
листового узла, к которому и прикрепиться новый узел. При первом вызове алгоритма
вставки, дерево пусто и указатель на вершину NULL, узел становится корнем дерева и
алгоритм завершается.

21.

21
Алгоритмы операций над бинарным деревом поиска
Реализация алгоритма на псевдокоде.
//предусловие: T – корень дерева (указатель на узел в вершине), node –
//указатель на заполненный данными узел
//постусловие: вставляет узел node в дерево Т
void insertBinSearchTree(Node * T, Tkey key,Tdata data){
if (isEmpty(T ))
T=createNode(key,data);
else
if (key<getKey(T))
insertBinSearchTree(getLeftTree(T),key,data)
else
if (key>getKey(T))
insertBinSearchTree(getRightTree(T), key,data)
}

22.

22
Алгоритмы операций над бинарным деревом поиска
Протестируем функцию insertBinSearchTree, для этого разработаем
приложение создания дерева с слайда 13. Ниже представлен код главной
функции приложения.
int main(){
Node &Root; // корень дерева
//Создание дерева
insertBinSearchTree(Root, 12);
insertBinSearchTree(Root, 25);
insertBinSearchTree(Root, 10);
insertBinSearchTree(Root, 8);
insertBinSearchTree(Root,11);
//вывод дерева
printBinTree(Rooy,0,5);
}

23.

23
Алгоритмы операций над бинарным деревом поиска
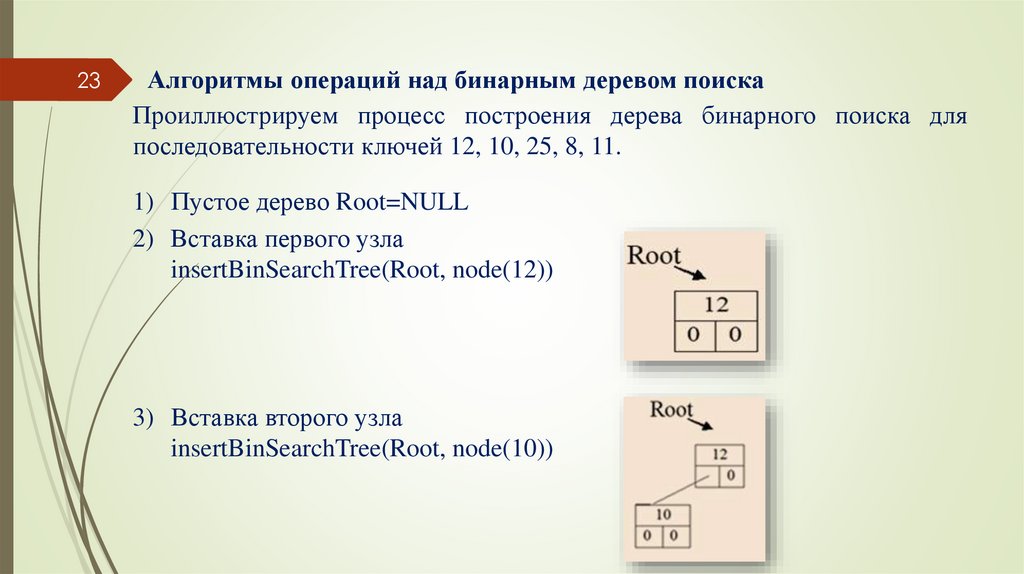
Проиллюстрируем процесс построения дерева бинарного поиска для
последовательности ключей 12, 10, 25, 8, 11.
1) Пустое дерево Root=NULL
2) Вставка первого узла
insertBinSearchTree(Root, node(12))
3) Вставка второго узла
insertBinSearchTree(Root, node(10))

24.

24
Алгоритмы операций над бинарным деревом поиска
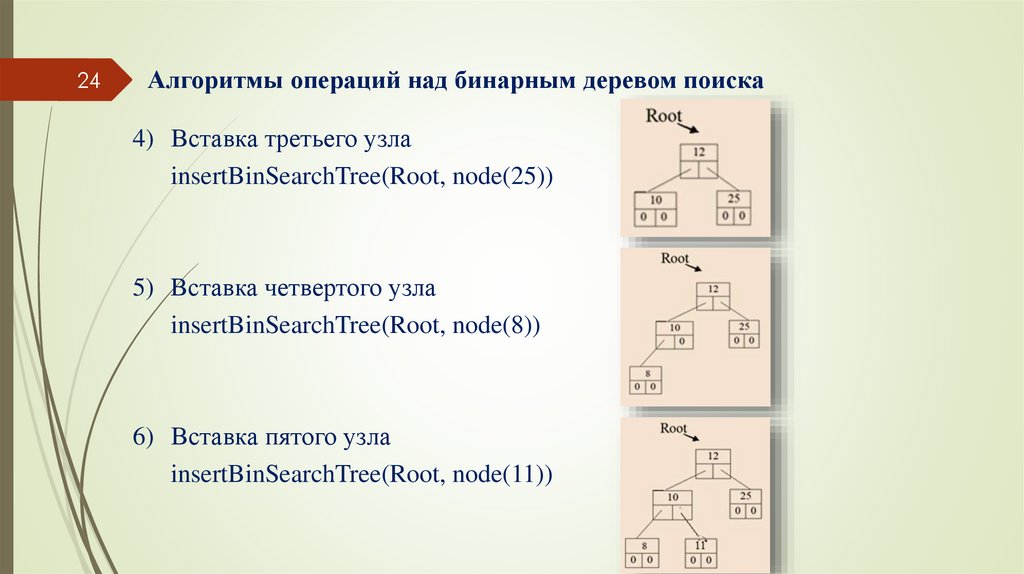
4) Вставка третьего узла
insertBinSearchTree(Root, node(25))
5) Вставка четвертого узла
insertBinSearchTree(Root, node(8))
6) Вставка пятого узла
insertBinSearchTree(Root, node(11))

25.

25
Алгоритмы операций над бинарным деревом поиска
3. Алгоритм поиска ключа в бинарном дереве поиска
Поиск ключа в бинарном дереве осуществляется на основе алгоритмов
обхода.
Исходные данные алгоритма: указатель на корень дерева, значение
искомого ключа.
Результат: при успешном поиске алгоритм возвращает указатель на узел,
содержащий искомый ключ или NULL, если ключ не найден.
В бинарном дереве поиска, в связи со свойством упорядоченности, поиск
осуществляется либо в правом, либо в левом поддереве любого текущего
узла.

26.

26
Алгоритмы операций над бинарным деревом поиска
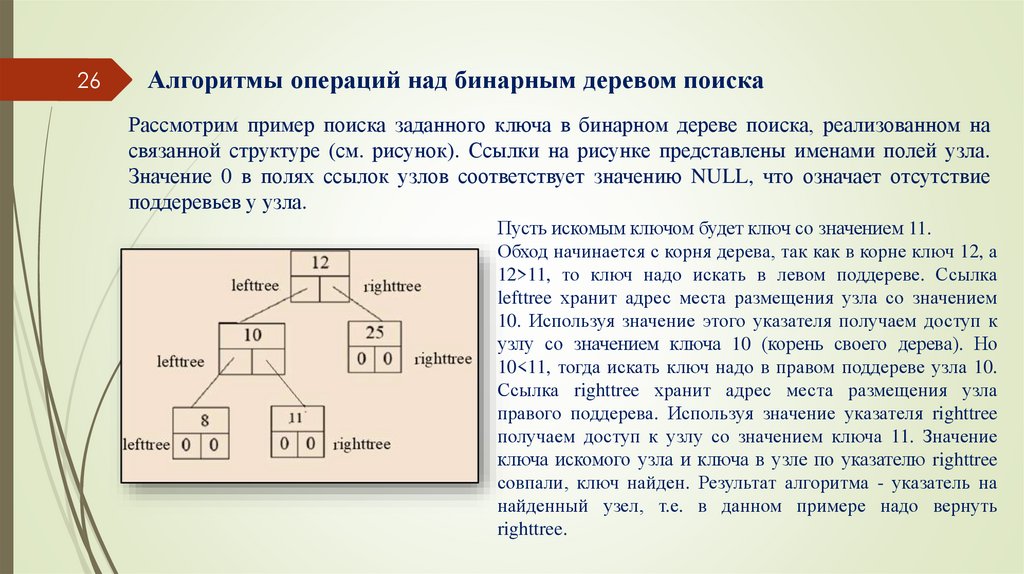
Рассмотрим пример поиска заданного ключа в бинарном дереве поиска, реализованном на
связанной структуре (см. рисунок). Ссылки на рисунке представлены именами полей узла.
Значение 0 в полях ссылок узлов соответствует значению NULL, что означает отсутствие
поддеревьев у узла.
Пусть искомым ключом будет ключ со значением 11.
Обход начинается с корня дерева, так как в корне ключ 12, а
12>11, то ключ надо искать в левом поддереве. Ссылка
lefttree хранит адрес места размещения узла со значением
10. Используя значение этого указателя получаем доступ к
узлу со значением ключа 10 (корень своего дерева). Но
10<11, тогда искать ключ надо в правом поддереве узла 10.
Ссылка righttree хранит адрес места размещения узла
правого поддерева. Используя значение указателя righttree
получаем доступ к узлу со значением ключа 11. Значение
ключа искомого узла и ключа в узле по указателю righttree
совпали, ключ найден. Результат алгоритма - указатель на
найденный узел, т.е. в данном примере надо вернуть
righttree.

27.

27
Алгоритмы операций над бинарным деревом поиска
Рекурсивная реализация алгоритма.
//предусловие: Т – корень дерева, key – ключ поиска
//постусловие: результат – указатель на узел с заданным ключом при успешном
поиске, и значение NULL при безуспешном поиске
Node* SearchBinSearchTree(Node* T, Tkey key){
1. if (isEmpty(T)) return NULL;
2. if(key==getKey(T)) return Т;
3. if(key<getKey(T)) SearchBinSearchTree (getLeftTree(T),key)
4. if(key)>getKey(T)) SearchBinSearchTree (getRightTree(T), key);
}
int main(){
Node *Root; // корень дерева
Функция main содержит алгоритм построения бинарного
//Создание дерева
дерева поиска на ключах: 12, 25, 10, 8, 11, для этого
insertBinSearchTree(Root, 12);
используется
операция
insertBinSearchTree,
которая
insertBinSearchTree(Root, 25);
insertBinSearchTree(Root, 10);
вставляет узлы с данными в дерево. В результате будет
insertBinSearchTree(Root, 8);
получено дерево, представленное на предыдущем слайде.
insertBinSearchTree(Root,11);
//Поиск ключа в дереве
Tkey key=8;
Node *ptr= SearchBinSearchTree(Root, key);
}

28.

28
Алгоритмы операций над бинарным деревом поиска
4. Алгоритмы обхода бинарного дерева поиска
Так как дерево бинарное, то алгоритмы обхода, рассмотренные для
бинарных деревьев по методам в глубину и в ширину, применимы и к
бинарным деревьям поиска.
Особенность бинарного дерева поиска в свойстве упорядоченности его
узлов. Если обойти бинарное дерево поиска, содержащего ключи,
алгоритмом симметричного обхода, то получим упорядоченную
последовательность ключей.
Пример. Применение бинарного дерева
поиска для сортировки списка значений.
Дано бинарное дерево поиска, узлы
которого содержат целые числа. Надо
сформировать
упорядоченную
по
возрастанию последовательность чисел.

29.

29
Алгоритмы операций над бинарным деревом поиска
5. Алгоритм удаления узла с заданным значением ключа из дерева
Исходные данные: бинарное дерево поиска, значение ключа удаляемого
узла.
Результат: модифицированное дерево, не содержащее узел с искомым
ключом.
Удаление узла из дерева сводиться к операциям:
1) Найти узел в дереве по значению ключа (получить на него ссылку)
2) Удалить найденный узел. Алгоритм различает 4 случая:
2.1 Удаляемый узел – лист.
2.2 Удаляемый узел имеет правое поддерево, но не имеет левого.
2.3 Удаляемый узел имеет только левое поддерево, но не имеет правого.
2.4 Удаляемый узел имеет два поддерева.

30.

30
Алгоритмы операций над бинарным деревом поиска
5. Алгоритм удаления узла с заданным значением ключа из дерева
После удаления узла упорядоченность дерева должна сохраниться.
Идея алгоритма: подобрать в дереве замещающий узел, который бы
заменил удаляемый узел и при этом свойство упорядоченности дерева
бинарного поиска не нарушилось.
Введем обозначения:
D – указатель на удаляемый узел
R – указатель на замещающий узел (узел, на
который будет заменяться удаляемый узел в
некоторых указанных случаях)
P – указатель на родителя удаляемого узла
Pr –указатель на родителя замещающего узла

31.

31
Алгоритмы операций над бинарным деревом поиска
Случай 1. Удаляемый узел – лист
Пусть удаляется узел со значением ключа 130 - этот узел лист D.
Алгоритм удаления ключа 130
1) Спуск по дереву алгоритмом поиска с сохранением ссылки на родителя в Р
удаляемого узла D.
2) Необходимо просто у родителя этого узла установить в NULL ссылку на правое
(в примере так) поддерево:
P -> right = NULL.
Замещающий узел в этом случае
не используется.
3) Удаление узла D.
Обобщенно алгоритм
можно представить так:
P -> right = NULL
delete D
удаления

32.

32
Алгоритмы операций над бинарным деревом поиска
Случай 2. Удаляемый узел имеет левое поддерево, но не имеет правого
Пусть удаляется узел со значение ключа 19.
Алгоритм удаления узла с ключом 19
1) Поиск узла со значением ключа удаляемого узла. Сохранить ссылку на найденный узел в D.
2) Проверить что у него одно поддерево - левое.
3) Сохранить ссылку на родителя удаляемого узла
в Р.
4) Сохранить ссылку на замещающий узел – это
узел левого поддерева удаляемого узла:
R= D->left ;
5) Заменить значение ссылки на правое поддерево
в родительском узле удаляемого узла на ссылку на
замещающий узел: P->right=R.
6) Удалить узел D.
Обобщенно алгоритм замещения можно представить так:
R= D->left
P->right=R

33.

33
Алгоритмы операций над бинарным деревом поиска
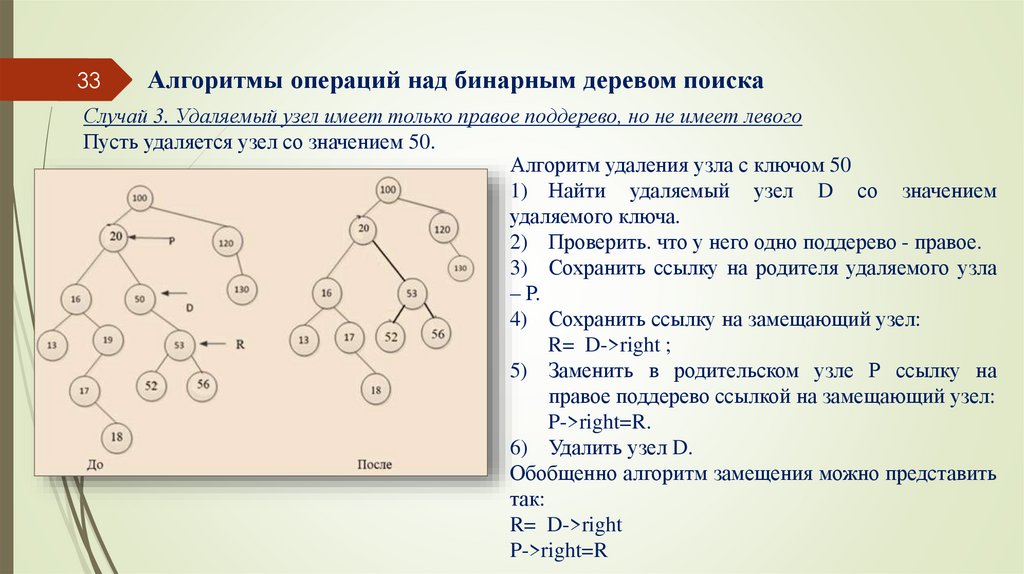
Случай 3. Удаляемый узел имеет только правое поддерево, но не имеет левого
Пусть удаляется узел со значением 50.
Алгоритм удаления узла с ключом 50
1) Найти удаляемый узел D со значением
удаляемого ключа.
2) Проверить. что у него одно поддерево - правое.
3) Сохранить ссылку на родителя удаляемого узла
– Р.
4) Сохранить ссылку на замещающий узел:
R= D->right ;
5) Заменить в родительском узле Р ссылку на
правое поддерево ссылкой на замещающий узел:
P->right=R.
6) Удалить узел D.
Обобщенно алгоритм замещения можно представить
так:
R= D->right
P->right=R

34.

34
Алгоритмы операций над бинарным деревом поиска
Случай 4. Удаляемый узел имеет два поддерева
Пусть удаляется узел содержащий ключ 20.
При поиске замещающего узла можно использовать один из 2-х подходов:
Подход 1. Замещающий узел – это узел с максимальным значением ключа в левом
поддереве удаляемого узла, т.е. самый правый в левом поддереве удаляемого узла;
Подход 2. Замещающий узел – это узел с минимальным значением ключа правого
поддерева удаляемого узла, т.е. самый левый правого поддерева удаляемого узла.

35.

35
Алгоритмы операций над бинарным деревом поиска
Алгоритм удаления Подход 1
1. Найти удаляемый узел D и проверить, что у него два поддерева.
2. Найти замещающий узел R, спускаясь по левому поддереву удаляемого узла и найти
самый правый узел.
Результат поиска предполагает 2 случая:
А) Правое поддерево не пусто, тогда проход завершается узлом, имеющим только левое
поддерево или листом, если R лист.
B) Правое поддерево пусто.
Тогда замещающим R будет корень левого поддерева удаляемого узла.

36.

36
Алгоритмы операций над бинарным деревом поиска
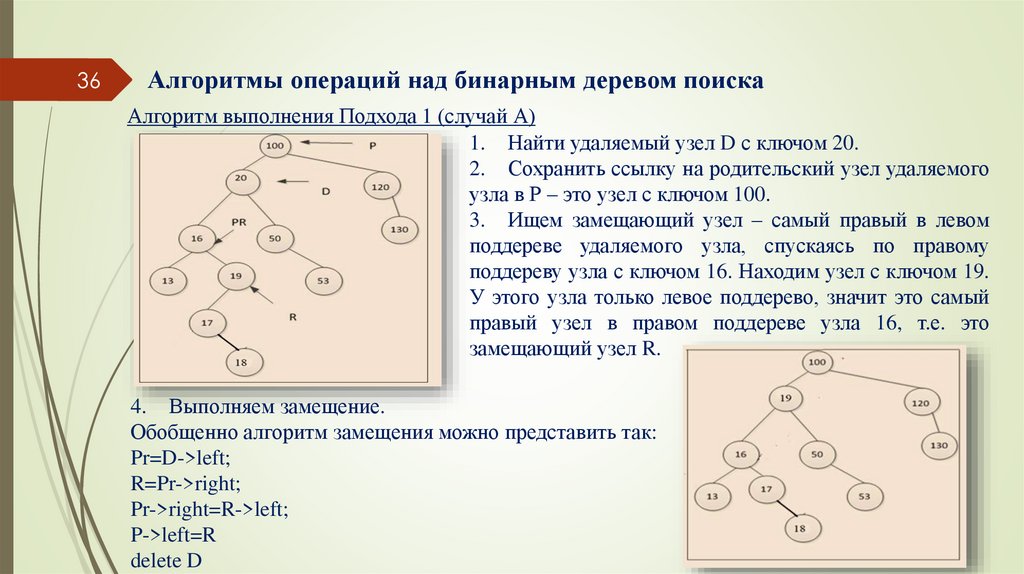
Алгоритм выполнения Подхода 1 (случай А)
1. Найти удаляемый узел D с ключом 20.
2. Сохранить ссылку на родительский узел удаляемого
узла в Р – это узел с ключом 100.
3. Ищем замещающий узел – самый правый в левом
поддереве удаляемого узла, спускаясь по правому
поддереву узла с ключом 16. Находим узел с ключом 19.
У этого узла только левое поддерево, значит это самый
правый узел в правом поддереве узла 16, т.е. это
замещающий узел R.
4. Выполняем замещение.
Обобщенно алгоритм замещения можно представить так:
Pr=D->left;
R=Pr->right;
Pr->right=R->left;
P->left=R
delete D

37.

37
Алгоритмы операций над бинарным деревом поиска
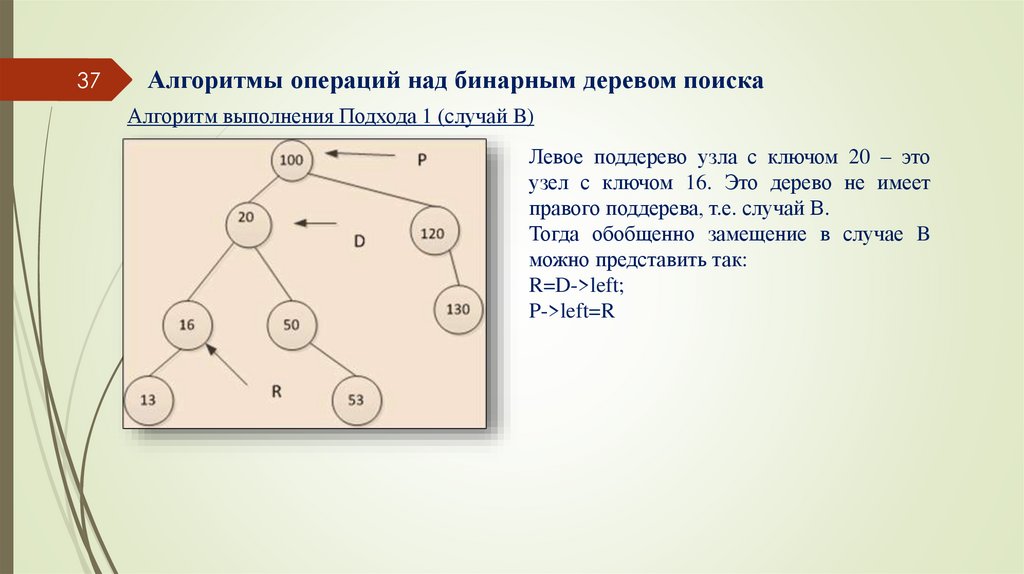
Алгоритм выполнения Подхода 1 (случай B)
Левое поддерево узла с ключом 20 – это
узел с ключом 16. Это дерево не имеет
правого поддерева, т.е. случай В.
Тогда обобщенно замещение в случае B
можно представить так:
R=D->left;
P->left=R

38.

Алгоритмы операций над бинарным деревом поиска
38
Обобщенный алгоритм операции удаления
1.
2.
Найти удаляемый узел и запомнить на него ссылку в D.
Определить, есть ли у него поддеревья:
-Одно правое. Ищем замещающий узел R и выполняем перестройку дерева.
-Одно левое. Ищем замещающий узел R и выполняем перестройку дерева.
-Нет поддеревьев — это лист. Заменяем у родителя соответствующую ссылку на NULL.
-Если два поддерева, то выбираем один из вариантов поиска замещающего узла:
Подход 1. самый правый в левом поддереве удаляемого узла,
Подход 2. либо самый левый в правом поддереве удаляемого узла.
Для обоих подходов рассматриваются два случая:
А) Либо дерево, в котором ищем замещающий узел не пусто, тогда тоже два
случая: либо поддерево (для случая а) завершается листом если R лист, либо,
завершается узлом, имеющим только одно поддерево (левое если Подход 1, правое
– если подход 2).
В) Либо пусто, тогда замещающий узел: при подходе 1 - узел левого поддерева
удаляемого узла, при подходе 2 – узел правого поддерева удаляемого узла.

39.

39
Алгоритмы операций над бинарным деревом поиска
Реализация алгоритма удаления узла из бинарного дерева поиска
int deleteNodeTREE(Tkey x, Node* &r)
{ Node* q;
if (r == NULL)return 1;
if (r)
{if (x < r->key) DELTREE(x, r->left);
else{if (x > r->key) DELTREE(x, r->right);
else
// delete - нашли узел для удаления
{q = r;
if (q->right == NULL ) // случаи 1 и 2
r=q->left; // при 1 r=NULL при 2 r – ссылка
else
if (q->left == NULL)
//при 3
r = q->right;
else
//поиск замещающего узла случай 4
DEL(q->left,q);
}delete q;
return 0;}
}
//Алгоритм поиска замещающего узла
DEL( Node* &r, Node* &q)
{
if (r->right)
DEL( r->right,q);
else {
q->key = r->key;
q = r;
r = r->left; //левое п.д., исключение
// узла, который самый правый, его
//заменяет левый, узел т.к. правого нет
}
}

40.

40
Анализ алгоритмов поиска, вставки, удаления ключа в дереве поиска
Операция
Средний
случай
Худший
случай
Вставить элемент
O(log n)
O(n)
Найти элемент
O(log n)
O(n)
Удалить элемент
O(log n)
O(n)
Найти максимальный ключ
O(log n)
O(n)
Найти минимальный ключ
O(log n)
O(n)
Емкостная сложность алгоритма поиска O(n*объем памяти одного узла).