Похожие презентации:
Действительные числа и операции над ними
1.
ingacademy.ruДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
И ОПЕРАЦИИ НАД НИМИ
План лекции
>Системы счисления
>Теория множеств
>Математическая логика
>Действительные числа
>Аксиоматика действительных чисел
>Операции с действительными числами
>Числовая прямая
2.
ingacademy.ruСИСТЕМЫ
СЧИСЛЕНИЯ
3.
ingacademy.ruМатематика для IT
НЕПОЗИЦИОННЫЕ
ЧТО ЭТО ТАКОЕ
В непозиционных системах
счисления величина,
обозначаемая цифрой, не
зависит от её положения в
числе. Однако такая система
может требовать, чтобы цифры
располагались, например, в
порядке убывания.
ПРИМЕР
К наиболее распространённым
сегодня непозиционным
системам счисления относятся
СИСТЕМЫ
СЧИСЛЕНИЯ
АРАБСКАЯ
и РИМСКАЯ ЗАПИСЬ
1-I
2 - II
3 - III
4 - IV
5-V
6 - VI
7 - VII
8 - VIII
9 - IX
10 – X
11 - XI
12 - XII
13 - XIII
14 - XIV
15 - XV
16 - XVI
17 - XVII
18 - XVIII
19 - XIX
20 – XX
30 – XXX
40 – XL
50 – L
60 – LX
70 – LXX
80 – LXXX
90 – XC
100 - C
ИСЧИСЛЕНИЕ
6 = 5 + 1 = V + I = VI
17 = 10 + 7 = X + VII = XVII
14 = 10 - 1 + 5 = X I V = XIV
35 = 30 + 5 = XXX + V = XXXV
81 = 50 + 30 + 1 = L + XXX + I = LXXXI
3
4.
ingacademy.ruМатематика для IT
ПОЗИЦИОННЫЕ
СИСТЕМЫ
СЧИСЛЕНИЯ
ЧТО ЭТО ТАКОЕ
В позиционных системах счисления значение одной и той же цифры
зависит от её положения в числе. Чем дальше цифра от начала, тем
больше её значение.
ПРИМЕР
Позиционная система счисления была изобретена шумерами и
вавилонянами, а позже усовершенствована индусами, что оказало
огромное влияние на развитие цивилизации.
Одной из таких систем является
,
возникшая благодаря счёту на пальцах.
В средневековую Европу она попала через итальянских
купцов, которые заимствовали её у арабов.
ЦИФРЫ
0 ,1 , 2 , 3 , 4 , 5 , 6 , 7, 8 , 9
9 7 4 5
тысячи сотни десятки единицы
4
5.
ingacademy.ruТЕОРИЯ МНОЖЕСТВ
6.
ingacademy.ruМатематика для IT
ПОНЯТИЕ
>>>
>>>
МНОЖЕСТВА
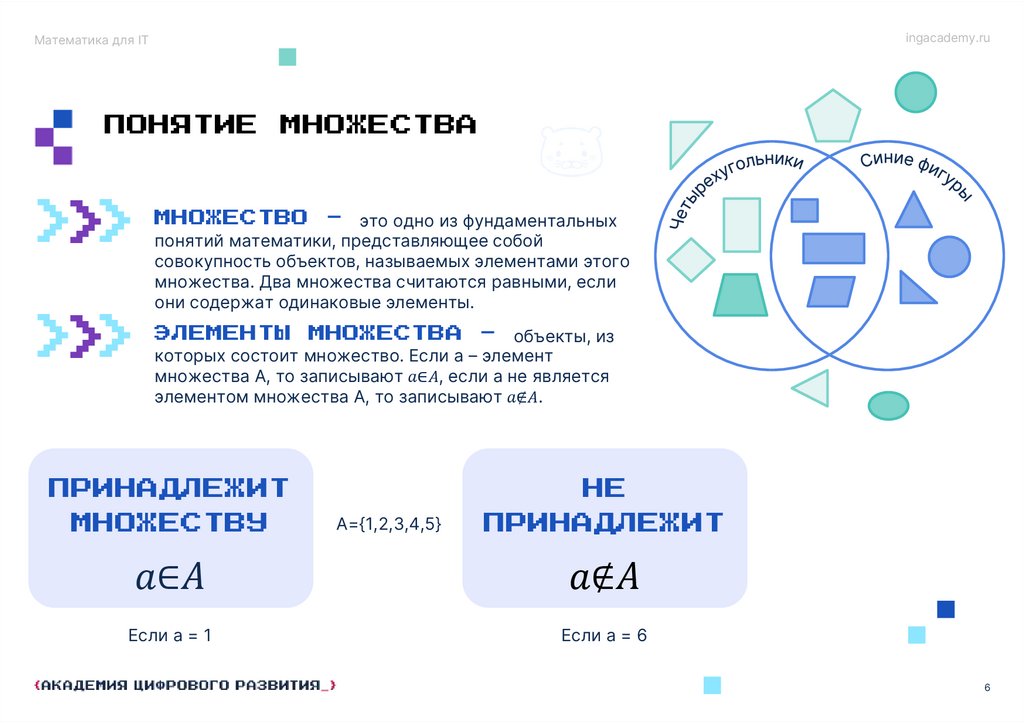
МНОЖЕСТВО - это одно из фундаментальных
понятий математики, представляющее собой
совокупность объектов, называемых элементами этого
множества. Два множества считаются равными, если
они содержат одинаковые элементы.
ЭЛЕМЕНТЫ МНОЖЕСТВА - объекты, из
которых состоит множество. Если a – элемент
множества A, то записывают


























 Математика
Математика








