Похожие презентации:
Теория систем и системный анализ
1.
Теория систем и системный анализАндрей Евгеньевич Петров,
профессор кафедры АПД,
доктор технических наук
Группы БИВТ-22-ИВ-1, БИВТ-22-ПАУ-1,2 и БИВТ-22-ИСАД-1,2,3
МИСИС осень 2024
1
2.
Процессы и структура в теории системСложность систем в технике, экономике, биологии постоянно растет.
Это требует разделения сложных систем на более простые задачи и расчета
по частям с применением суперкомпьютеров.
Для этого необходимо применять сетевые модели, которые способны
представить процессы и структуру сложных систем.
Системы состоят из элементов, и структуры связей, которые соединяют
элементы их границами.
Процессы протекают в элементах системы как потоки измеримых величин с
воздействиями, сопротивлением элементов и откликами.
Соединение элементов между собой есть структура, которая связывает
элементы в единую систему.
В элементах возникают потоки, измеряемые одними величинами, вызванные
воздействиями, измеряемыми другими величинами. Их связывают свойства
материи элементов, метрика. Потоки представляют собой потоки энергии.
Процессы описывают уравнения вида e = Z i
Мир состоит из структуры – молекулы из атомов, атомы из ядра и оболочек
электронов, ядро из протонов и нейтронов, и т.д.
Возможно, бозон Хиггса, Higgs boson определяет массу, материю. Но это не
точно – он и сам может из чего-то состоять.
В структуре протекают потоки энергии. Сложную систему, состоящую из
большого числа элементов и структуры связей между ними для расчета и
анализа следует декомпозировать, т.е. разделять на части. Затем возникает
задача агрегировать – т.е. получить решение целого из решений его частей.
.
3.
Декомпозиция и агрегирование в системном анализеВ любом системном исследовании есть две процедуры, которые могут
повторяться неоднократно – это декомпозиция и агрегирование. Процесс
разложения целого на части называется декомпозицией. А процесс
объединения частей в целое – агрегацией.
Основание декомпозиции системы – это модель рассматриваемой системы.
Операция декомпозиции – это процесс сопоставления частей исходной
системы элементам модели. Число частей, которые получатся в результате
декомпозиции равно числу элементов такой модели.
В качестве основания декомпозиции можно брать модель системы, или ее
надсистемы или модель ее подсистемы. Иногда целесообразно за основание
декомпозиции взять модель другой системы, связанной с исследуемой.
Типов моделей систем: черный ящик, модель состава, модель структуры,
белый ящик, каждая в статическом и динамическом варианте. Итого –
восемь типов. Содержательная модель-основание конкретизирует
формальную модель.
.
– Модель «черного ящика» состоит из двух множеств: входов системы и
выходов системы. Она выражает обособленность системы от окружающей
среды.
– Модель состава системы описывает из каких подсистем и элементов эта
система состоит
– Модели структуры системы описывают, как между собой связаны элементы
– Обычно модели состава, структуры системы и «черного ящика»
рассматривают совместно. Все они вместе образуют структурную схему
системы. Известную также как модель «белого ящика».
4.
Декомпозиция и агрегирование в системном анализеВ полной формальной модели перечислены все возможные элементы
системы-оригинала. Благодаря абстрактности и формальности удается
добиться полноты таких моделей
Примером полной формальной модели является общая модель
деятельности.
Полнота формальной модели является необходимым, но не является
достаточным условием полноты декомпозиции. Она указывает на то,
что может являться элементами реальной системы.
В содержательную модель основания декомпозиции рекомендуется
вводить элемент «все остальное». Он будет напоминать исследователю
на более поздних этапах декомпозиции, что модель основание
декомпозиции могла быть неполна.
Полнота и простота декомпозиции часто исключают друг друга.
Поскольку число элементов результата декомпозиции совпадает с
числом элементов модели основания, то, полнота или простота
декомпозиции системы зависит от полноты и простоты основания
декомпозиции.
Таким образом, эксперт ищет компромисс между полнотой и
простотой основания декомпозиции. То есть, в модель следует
включать только существенные элементы исходной системы. А какие
элементы системы следует считать существенными должен определить
эксперт.
.
5.
Декомпозиция и детализацияПроцесс декомпозиции обычно итеративен. То есть, после декомпозиции
системы в соответствии с некоторой моделью-основанием, возможна
детализация, если не все существенные элементы системы были получены.
Затем повторяется этап декомпозиции в соответствии с уточненной моделью.
Такой итеративный процесс декомпозиции можно представить в виде дерева.
Пример: Рассмотрим четыре последовательных этапа уточнения модели
основания атома водорода. Пусть остановились на модели основании
состоящей из двух верхних кварков, одного нижнего кварка некоторого числа
глюонов и одного электрона. Однако, если декомпозиция проводилась
химиком, он скорее всего остановился бы уже на этапе протона.
Физик мог бы уточнить модель-основание и продолжить декомпозицию.
Например, попытаться оспорить элементарность кварков. Что гарантирует
полноту декомпозиции? Формальной моделью в данном случае можно
считать физику элементарных частиц.
.
– В физике элементарных частиц глюо́ны (англ. glue — клей) — это
элементарные частицы, обеспечивающие взаимодействия кварков.
Типы сложности декомпозиции систем: нет достаточной информации; нет
понимания. Первый тип - знаний одного эксперта оказывается недостаточно.
Требуется привлечь других специалистов для завершения декомпозиции.
Однако, иногда дальнейшая декомпозиция невозможна независимо от того,
сколько экспертов вы пригласите. Такая неустранимая сложность называется
сложностью непонимания. Тогда декомпозиция не улучшает понимание
исходной системы, но показывает, что именно нам о ней неизвестно.
6.
Алгоритмы решения проблемВ системном анализе решение проблем, возникающих в теории
систем, занимает центральное место. Существует ряд подходов к
декомпозиции жизненного цикла проблем, которые по сути являются
алгоритмами решения проблем.
Декомпозиция, Стэнфорд Л. Оптнер (Системный анализ для решения
деловых и промышленных проблем), 1969
1. Идентификация симптомов
2. Определение актуальности проблемы
3. Определение целей
4. Определение структуры системы и ее дефектов
5. Определение возможностей
6. Нахождение альтернатив
7. Оценка альтернатив
8. Выработка решения
9. Признание решения
10. Запуск процесса решения
11. Управление процессом реализации решения
12. Оценка реализации и ее последствий
.
7.
Алгоритмы решения проблемДекомпозиция по С. Янгу:
1. Определение цели организации
2. Выявление проблемы
3. Диагностика системы (где именно возникла проблема)
4. Поиск решения
5. Оценка и выбор альтернативы
6. Согласование решения
7. Утверждение решения
8. Подготовка к вводу в действие
9. Управление применением решения
10. Проверка эффективности
Декомпозиция по Н. П. Федоренко (1917-2006):
1. Формулирование проблемы
2. Определение целей
3. Сбор информации
4. Разработка максимального количества альтернатив
5. Отбор альтернатив
6. Построение модели в виде уравнений, программ или сценария
7. Оценка затрат
8. Испытание чувствительности решения (параметрическое исследование)
.
8.
Алгоритмы решения проблемДекомпозиция по Спартаку Петровичу Никанорову
(1923 —2015)
.
• (первым понял и оценил идею П.Г. Кузнецова в отношении
космической миссии человечества и конструктивного
мировоззрения):
1. Обнаружение проблемы
2. Оценка актуальности проблемы
3. Анализ ограничений проблемы
4. Определение критериев
5. Анализ существующей системы
6. Поиск альтернатив
7. Выбор альтернативы
8. Обеспечение признания
9. Принятие формальной ответственности за решение
10. Реализация решения
11. Определение результатов решения
9.
Алгоритмы решения проблем. Декомпозиция по Ю. И. Черняку:
1. Анализ проблемы
2. Определение системы
3. Анализ структуры системы
4. Формулирование общей цели и набора критериев
5. Декомпозиция цели, выявление потребностей в ресурсах,
композиция целей
6. Выявление ресурсов
7. Прогноз и анализ будущих условий
8. Оценка целей и средств
9. Отбор вариантов
10. Диагноз существующей системы.
11. Построение комплексной программы развития
12. Проектирование организации для достижения целей
10.
Алгоритмы решения проблемШаги алгоритма :
1. Объектом декомпозиции может стать любая система. Часто, когда анализ
необходим для решения больших и сложных задач, даже систему – объект,
декомпозиция которого помогла бы решить поставленную задачу системного
анализа, определить непросто.
2. Прежде чем перейти собственно к декомпозиции необходимо определить
«заинтересованную» систему.
3. Выбор формальной модели, - базы определения содержательной моделиоснования декомпозиции- либо брать из библиотеки известных полных
формальных моделей, либо привлекать экспертов.
4. На основе формальной модели и целевой системы, определенных на
предыдущих шагах алгоритма, строится содержательная модель-основание
декомпозиции.
5. – 7. Эти блоки соответствуют одной итерации процесса декомпозиции.
8. После того, как были получены «фрагменты» - кандидаты на элементы
системы, проверка, действительно ли очередной фрагмент элементарен. Если
все фрагменты элементарны, декомпозиция завершена. В противном случае,
итерация декомпозиции повторяется.
9. – 10. Если возникла необходимость совершить новую итерацию
декомпозиции, проверяется наличие новых формальных моделей, и
соответствующих им новых содержательных моделей. Если они имеются, то
новая итерация декомпозиции возможна. Иначе процесс декомпозиции
остановим ввиду сложности непонимания. Тогда результатом декомпозиции
будет указание на то, что именно вызывает непонимание в системе.
.
11.
АгрегированиеОперацией, противоположной декомпозиции является агрегирование, оно
позволяет объединить разрозненные элементы в целое.
Результат агрегирования называют агрегатом – он определяется некоторой
моделью исследуемой или проектируемой.
С этим связано понятие эмерджентности – это свойство агрегирования,
которое проявляется в возникновении у агрегата качественно новых свойств,
которые не могли быть присущи исходным элементам до их объединения.
Например. Свойства автомобиля не являются простой суммой свойств его
частей, так как никакая его часть не обладает свойством «перевозить
пассажира по заданному маршруту и с заданной скоростью».
Модели состава определяют какие элементы должны войти в агрегат. А модели
структуры описывают, как эти элементы будут между собой связаны.
Не имеет смысла пытаться описать все возможные типы агрегатов, которые
возникают в процессе агрегирования.
Однако есть небольшое число наиболее важных агрегатов, которые часто
используются в системном анализе.
12.
Агрегат конфигураторЭто агрегат, состоящий из качественно различных языков описания системы, и при этом
число этих языков минимально, но необходимо для заданной цели.
Примеры: a. Конфигуратором для задания точки в n-мерном пространстве является
совокупность ее координат. Каждая координата – это описание системы на языке оси,
которой эта координата соответствует. Однако, для однозначного задания точки в таком
пространстве нам необходимо определить все n координат.
b. Конфигуратор пространственной перспективы (различий в направлениях и
удаленностях источников сигналов от наблюдателя) – запись сигнала (видео, или аудио),
сделанная в двух различных точках пространства. Чтобы человек мог определять
направление звука и расстояние между предметами, у него два уха и два глаза.
c. Конфигуратором для описания трехмерных поверхностей на языке плоскостей
является совокупность трех ортогональных проекций.
d. Конфигуратором радиотехнического устройства является совокупность трех схем.
Блок схема прибора описывает его в терминах радиодеталей. Принципиальная схема –
на языке функциональных единиц (усилитель, приемник, блок питания). Они могут и не
иметь определенной локализации в пространстве. Монтажная схема описывает
размещение деталей прибора в некотором корпусе.
Состав конфигуратора определяется целью исследования. Если цель - сбыт
радиоаппаратуры, то в конфигуратор придется включить и язык рекламы.
Агрегат-оператор объединяет множества исходных элементов, чтобы получить
подсистемы исходной системы, что уменьшает размерность исходной задачи.
Простейшим видом агрегата-оператора является классификация.
13.
Физические величины описания системФизической величиной называют свойство, общее в качественном
отношении для многих физических объектов, но в количественном
отношении индивидуальное для каждого объекта. Например: длина,
время, сила электрического тока, .
Размер физической величины – количественное содержание в данном
объекте свойства, соответствующего понятию физическая величина.
Единица физической величины – физическая величина фиксированного
размера, которая применяется для количественного выражения
однородных физических величин. Например: 1 м – единица длины, 1А –
силы электрического тока.
Система единиц физических величин – совокупность основных и
производных единиц физических величин, образованная для заданной
системы физических величин. Международная система единиц (СИ),
принятая в 1960 г. В системе единиц физических величин выделяют
основные единицы (в СИ – метр, килограмм, секунда, ампер, кельвин).
Существует LT система, в которой все физические величины выражаются
через длину (L - length) и время (T – time).
13
14.
Размерность физической величиныРазмерность физической величины dim Q – выражение, составленное из произведений
символов основных физических величин в различных степенях и отражающее
связь данной величины с принятыми в данной системе за основные:
Впервые «размерность» как физико-математическая категория встречается в
Форономии Я. Германа в 1716 году для установления связи телесных
(геометрических) и без телесных величин. Фурье в 1822 году ввел понятие
размерность в физику для выделения границ однородных групп (качеств), а в 1855
году Дж. Максвелл ввел квадратные скобки, подчеркивая качественное различие
величин, определяемое их размерностью и единицей.
Величина без квадратных скобок выражает количественную определенность,
численное значение величины, определяемое её отношением к единице
измерения.
Существуют разные системы размерности, в которых все известные физические
величины выражаются через основные величины.
В системе СИ используют семь основных величин (длина, время, масса, сила
электрического тока, термодинамическая температура, количество вещества, сила
света). В системе СГС – три величины: длина, масса и время.
Существует LT система Бартини-Кузнецова, в которой все физические величины
выражаются через пространство (длина) и время. для анализа аналогий между
величинами, разных предметных областей, с помощью сравнения их физических
размерностей.
14
15.
Выражение физических величин черезпространство (длину) и время
Возможность выразить массу через длину и время показал Дж. Максвелл в
1867 г. [29], а затем Кельвин, Эддингтон и другие. Разработал систему
физических величин Б. Браун в 1941 году и независимо от него в 1966 году Р.Л.
Бартини [30]. Система представлена таблицей LT, (L – длина, T – время) в
клетках которой расположены физические величины, в соответствии с их
размерностью, выраженной в единицах длины и времени. Фрагмент таблицы
LT, опубликованной в [29, 31], показан на рисунке 4.1.
Выражение физических величин через длину и время предполагает тождество
гравитационной и инертной массы. «В принципе ниоткуда не следует, что
масса, создающая поле тяготения, определяет и инерцию того же тела. Опыт
показал, что инертная и гравитационная массы пропорциональны друг другу (а
при обычном выборе единиц измерения численно равны).
Этот фундаментальный закон называется принципом эквивалентности,
который экспериментально подтвержден с высокой точностью» (Физический
Энциклопедический Словарь, с 393). Сама таблица LT опирается на
справедливость принципа эквивалентности.
15
16.
LT таблица размерностей физических величинВремя, T-1 (сек.)-1
L3 T-6
L4 T-6
Изменение
мощности
Поверхнос
тная
мощностьL
3
T-5
Поверхн.
натяжение
L3 T-4
Скорость
изменения
силы L4 T-5
Мощнос
ть
L5 T-5
Сила
L4 T-4
Ток
Скорость
смещения
заряда
Импульс
L4 T-3
Момент
силы
Энергия
L5 T-4
Момент
импульса
Действие
L5T-3
T-5
L1 T-5
Изменение
давления
L2 T-5
T-4
Изменение
плотности
тока L1 T-4
Давление
L2 T-4
Скорость
массы
Плотность
тока L1T-3
Напряженность
электромагн. поля
Вязкость
L2 T-3
Напряжение, химич.
потенциал
L2 T-2
Масса,
Колич-во
магнетизма
Заряд L3 T-2
Магнитный
момент L4
T-2
Момент
инерции L5
T-2
Скорость.
изменения
площади
L2T-1
Площадь
L2
Скорость
изменения
объема
L3T-1
Объем
L3
Скорость
смещения
объема
L4 T-1
4-Объем L4
L5 T-1
5-Объем L5
L3
L4
L5
T-3
Гидравлич.
сопротивле
ние
L-1 T-3
Изменение
углового
ускорения
T-3
T-2
Изменение
объемной
плотности
T-1
L-1 T-1
Массовая
плотность
Угловое
ускорение
T-2
Частота
T-1
T0
Изменение
проводимости
Безразмерные
константы
Изменение
магнитной
проницаемости
Магнитная
проницаемость
L-2 T3
Текучесть
Электрич.
проводимость
L-1 T1
L-1 T2
Период
L-2
L-1
T1
T2
T3
L-1 T3
Поверхность
времени
Объем
времени
L0
Линейное
ускорени
е L1T-2
Скорость
Электрич.
сопротивл.
L1 T-1
Длина
Емкость
Самоиндукция L
Длительность
расстояния
Массовы
й расход
L3 T-3
Скорость
передачи
мощности
Скорость
передачи
энергии
Скорость
передачи
действия
Момент
действия
L2T1
L 1 T2
Гидравлич.
проводимость
L 1 T3
L1
L2
L6
Длина L, м
17.
Примеры размерностей физических величинОбозначим длину через L, время через T, а размерность квадратными
скобками, которые ввел Максвелл. Тогда размерность площади [r2] = L2,
размерность ускорения [a] = L1 T–2.
Чтобы выразить массу через длину и время, Максвелл приравнял
выражения силы в законе гравитации Ньютона F = m2/r2 и втором законе
Ньютона F = m a. Тогда, поскольку F = F, получим, что m2/r2 = m a. Согласно
принципу эквивалентности, полагая, что гравитационная и инертная массы
есть одна величина, получим m = r2 a, а размерность массы: [m] = L3 T–2, и она
выражена через длину и время.
Электрический заряд (размерность следует из закона Кулона),
количество магнетизма попадают в ту же клетку таблицы, что и масса. Все они
являются мерой взаимодействия воздействия и отклика. Количество движения
(импульс) p имеет размерность в терминах длины и времени как произведение
массы и скорости:
[p] = [m] [v] =L3 T–2 L1 T-1 = L4 T–3.
Электрический ток i, как заряд в единицу времени, имеет размерность [i]
= L3 T–3. Напряжение e имеет размерность [e] = L2 T–2.
Мощность P (power) равна произведению тока и напряжения, ее
размерность, следовательно, [P] = L5 T–5.
18.
Продольные и поперечные величиныСуществует связь между физической величиной внешних и внутренних
воздействий и структурой системы. В сети разомкнутые и замкнутые пути
являются независимыми. Для внешних потоков базисом являются разомкнутые
пути, а для внутренних потоков базисом являются замкнутые пути.
Воздействия и отклики в открытых и замкнутых системах отличаются по
способу их измерения.
По способу измерения величины воздействия и отклика, определяющие
поток энергии, делятся на два типа: измеряемые в одной точке и в двух точках.
Величины, которые измеряют в одной точке. Например,
электрический ток в ветви, сила, приложенная к точке; их называют
«продольные» (along) величины;
Величины, которые измеряют как разность значений в двух
пространственно различных точках; их называют «поперечные» (across)
величины. Поперечными величинами являются, например: электрическое
напряжение, измеряемое как разность потенциалов между двумя узлами сети;
или скорость, измеряемая как разность между двумя положениями тела в
единицу времени.
Напряжение является разностью потенциалов между двумя
поверхностями равного потенциала, эквипотенциальными поверхностями.
19.
Воздействия и отклики в разных системах. В разных предметных областях воздействие и отклик, составляющие
поток энергии, представлены продольной и поперечной величинами.
Физическая размерность произведения пары продольных и поперечных
величин воздействия и отклика всегда равна мощности [P] = L5 T–5. Например,
ток и напряжение в электротехнике, сила и скорость в механике, давление и
поток жидкости в гидравлике, и т.д.
Интересно, что значения размерностей в каждой паре различное, но
произведение величин имеет размерность мощности.
Например, размерность электрического тока, как было показано [i] = L3
T–3, а напряжения – [e] = L2 T–2; их произведение есть мощность с
размерностью [P] = L5 T–5.
В гидродинамике давление p имеет размерность [p] = L2 T–4, а поток
жидкости g (скорость изменения объема) – [g] = L3 T–1.
В механике сила F (приложена в точке) и скорость v (разность положения
тела в двух точках в единицу времени); сила имеет размерность [F] = L4
T–4, а скорость – [v] = L1 T–1
Аналогично получается для потока тепла и температуры; потока массы и
концентрации (химического потенциала) и т.д.
20.
Отличие замкнутых и открытых систем.Отличие замкнутых и открытых систем. Продольные и
поперечные
величины
в
системах
могут
быть
как
воздействиями, так и откликами, в зависимости от того,
является ли система замкнутой или открытой.
В открытой системе продольная величина является
воздействием, а поперечная величина – откликом. В
замкнутой системе, наоборот, поперечная величина является
воздействием, а продольная величина – откликом.
Это вызвано тем, что продольные и поперечные
величины в открытых и замкнутых путях ведут себя
двойственно.
Базисом для процессов в открытой системе являются
разомкнутые пути. Поскольку поток протекает в контуре, то в
открытой системе потоки замкнуты вне сети. Поток
(продольная величина) входит в сеть извне через один узел,
проходит по сети, а выходит из другого узла, покидая сеть.
При этом потенциалы (поперечная величина) меняются от
узла к узлу в соответствии с метрикой элементов, как оклик
на поток от максимального значения на входе до
минимального (нулевого) значения на выходе.
21.
Отличие замкнутых и открытых системБазисом для процессов в замкнутой системе являются контуры. Потоки
протекают внутри сети по замкнутым путям. Для этого в контуре необходимо
создать разность потенциалов, которая вызывает поток. Поток в каждом
контуре остается постоянным. Разность потенциалов на источнике, которая
задает воздействие, понижается при прохождении метрики ветвей, так что
сумма по контуру равна нулю.
Таким образом, физические величины воздействий и откликов по типу
измерения (продольные и поперечные) для открытых и замкнутых систем
меняются местами. Отношения между этими понятиями представлены в табл.
4.1
Воздействия и отклики в открытых и замкнутых системах
Тип системы
Воздействие
Отклик
Закрытая система, базис
определяют замкнутые
пути
Поперечная
величина
Продольная
величина
Открытая система, базис
определяют разомкнутые
пути
Продольная
величина
Поперечная
величина
В качестве примера рассмотрим электрическую цепь. Внутренние воздействия,
источники напряжения (поперечная величина) расположены в ветвях самой
цепи. Отклики, токи (продольная величина) протекают в замкнутых путях.
21
22.
Методология создания сетевых моделей систем• Система состоит из элементов, характеристики которых определяют
физические, информационные свойства системы и связей между
ними. При воздействии на систему, в ней возникают процессы –
потоки одних величин под действием других величин.
• При внешнем воздействии базисом для потоков являются
разомкнутые пути, при внутреннем воздействии базисом для
потоков являются замкнутые пути.
• Создание сетевых моделей технических, физических, экономических
систем состоит в поиске аналогий между элементами и структурой, а
также между величинами процессов предметной области и сети.
Установление аналогий между системой и сетевой моделью нельзя
полностью автоматизировать.
• Создание сетевой модели требует интуиции, творческого подхода,
воображения. В каждом случае это остается скорее искусством, чем
наукой.
• Для создания сетевой модели необходимо установить аналогии
одновременно между процессами и структурой. Двойственные сети
представляют процессы в структуре, в ортогональных
подпространствах замкнутых и разомкнутых путей.
22
23.
Размерности воздействия, сопротивления и откликадля потока жидкости в скважине
•Таблица 1. LT-таблица размерностей физических величин Бартини-Кузнецова
•Время, T-1 (сек.)-1
L1 T-5
T-5
Изменение
давления L2 T-5
L3 T-6
L4 T-6
Изменение
мощности
Скорость
передачи
мощности
Поверх-ностная
мощностьL3 T-5
Скорость изменения
силы L4 T-5
Мощность
Скорость
передачи
энергии
L5 T-5
Гидравлич.
сопротивлен.
T-3
L-1 T-3
Поверхн. натяжение
L3 T-4
Сила
L4 T-4
Момент силы
Энергия
L5 T-4
Скорость
передачи
действия
Напряжен.
электро-магн. поля
Вязкость
L2 T-3
Ток Массовый
расход
L3 T-3
Скорость смещения
заряда Импульс
L4 T-3
Момент импульса
Действие L5T-3
Момент
действия
Изменение
плотности тока L1
T-4
Давление
Изменение
углового
ускорения T-3
Скорость массы
Плотность тока
L1T-3
T-4
L2 T-4
T-2
Изменение
объемной
плотности
Массовая
плотность Угловое
ускорение T-2
Линейное
ускорение L1T-2
Напряжение
(разность
потенциалов) L2
T-2
Масса, Колич-во
магнетизма Заряд
L3 T-2
Магнитный момент
L4 T-2
Момент инерции
L5 T-2
T-1
L-1 T-1
Частота
T-1
Скорость
Электрич.
сопротивл.
L1 T-1
Скорость
изменения
площади L2T-1
Скорость
изменения
объема L3T-1
Скорость смещения
объема
L4 T-1
L5 T-1
T0
Изменение
проводимости
Безразмер-ные
константы
Длина Емкость
Самоин-дукция L
Площадь L2
Объем
L3
4-Объем L4
5-Объем L5
L2T1
T1
Изменение
магнитной проницаемости
Электрич.
проводи-мость
L-1 T1
Период
Длитель-ность
расстояния
T2
Магнитная проницаемость
L-1 T2
Поверх-ность
времени
L 1 T2
T3
L-2 T3 Текучесть
L-1 T3
Объем времени
Гидравлич.
проводим.
L-2
L-1
L0
Длина
L, м
L 1 T3
L1
L2
L3
L4
L5
L6
23
24.
Моделирование• Моделирование — исследование объектов познания на их
моделях; построение и изучение моделей реально существующих
объектов, процессов или явлений с целью получения объяснений
этих явлений, а также для предсказания явлений, интересующих
исследователя.
• Моделирование – метод исследования объектов познания на их
моделях; построение и изучение моделей реально существующих
предметов и явлений (органич. и неорганич. систем,
инженерных устройств, разнообразных процессов —
физических, химических, биологических, социальных) и
конструируемых объектов для определения либо улучшения их
характеристик, рационализации способов их построения,
управления ими и т. п.
• Формы моделирования разнообразны и зависят от используемых
моделей и сферы применения моделирования.
• По характеру моделей выделяют предметное и знаковое
(информационное) моделирования.
24
25.
Процессы как потоки в элементах системСистема представляет собой совокупность элементов, которые определяют
свойства протекающих в них процессов и соединяющей их структуры
связей. Эти свойства присущи материи в целом.
Причиной изменения положения или состояния материи является
воздействие. Реакцией на приложенное воздействие является отклик
системы.
Мерой сопротивления воздействию является инерция материи. В
технических и физических системах это могут быть масса, сопротивление,
теплоемкость, вязкость, магнитная проницаемость. В экономических
системах это могут быть коэффициенты прямых затрат, ставки привлечения
и размещения денежных средств, доходность финансовых инструментов на
фондовых рынках.
Отклик на приложенное воздействие проявляется в изменении положения
или состояния материи системы; появлении или изменении протекающих в
ней потоков. Вместе это составляет суть процессов, которые протекают в
элементах материи.
Процессы в логистических системах – это передача и преобразование
потоков материи, энергии, информации.
25
26.
Замкнутые и открытые пути, поступательное ивращательное движение
• Любое движение состоит из поступательного движения
(переноса) и вращательного движения .
• Вращение и перенос не зависят друг от друга, и дополняют
друг друга. Это два различных качества движения.
• Пути в пространстве могут быть или замкнутые или
разомкнутые.
• Вращение происходит по замкнутым путям, перенос - по
открытым, разомкнутым путям.
• Системы и взаимодействуют, и не взаимодействуют с
другими системами в окружающем пространстве.
• Потоки энергии от внутренних источников протекают в
замкнутых путях.
• Потоки энергии от внешних источников протекают в
разомкнутых путях.
26
27.
Технология применения тензорного метода• Все системы одного класса рассматриваются как одна «обобщенная»
система, тензор, а системы разных предметных областей – как
проекции в частные системы координат. Для них применяется один
метод исследования, расчета, анализа.
• Процессы и структура являются неразрывными сторонами состояния
сложных систем разных предметных областей.
• Структура играет роль пространства, в котором процессы являются
объектами. Объект остается тождественным самому себе при взгляде
на него с разных точек зрения.
• Необходимо определить, какие измеримые величины,
характеристики системы, являются необходимыми и достаточными
для получения желаемых результатов моделирования, а какие
являются избыточными, и их можно не рассматривать.
• Достаточно ли средств сети, ее понятий, для моделирования системы?
Если нет, то, как дополнить недостающие понятия, например,
используя независимость потоков в замкнутых или разомкнутых
путях?
• Может ли понятийный аппарат сети оказаться шире, чем исследуемая
система, так, что топология сети генерирует и предоставить новое
знание об исследуемой системе, которое расширит возможности ее
анализа и управления.
28.
Межотраслевой баланс (МОБ) экономической системыМОБ обеспечивает анализ хозяйственных связей на уровне
предприятий, отраслей, регионов, государств.
Возможен расчет вариантов производства продуктов и
потребления ресурсов для управления, структурных реформ.
Расчет последствий разделения экономической системы на
части или создания союзов и т.д.
Рассмотрим сетевую модель межотраслевого баланса в
экономике, который основан на таблицах затраты-выпуск.
Задача состоит в расчете производства отраслей,
обеспечивающих спрос, ресурсы, и поставки.
Модель открытая - любую отрасль можно сделать ресурсом
(и наоборот).
Можно добавить или исключить отрасли; с изменением
состава поставок и ресурсов, провести структурные
преобразования.
28
29.
Метод затраты-выпуск• Метод затраты-выпуск вырос из разработанного ЦСУ России
межотраслевого баланса народного хозяйства страны за 1923-1924 гг.,
базировавшегося на уравнениях Дмитриева (1909), описывающих
материально-финансовые связи в процессе производства.
В России метод применялся Госпланом. В России расчеты проводятся
Министерством экономического развития (есть расчеты затраты-выпуск от
2003 года). В СССР – на родине метода межотраслевого баланса –
разрабатывалось в год до 12 тысяч межотраслевых балансов.
Метод был воспринят в развитых странах: в США в год рассчитывается до 40
тысяч межотраслевых балансов, во Франции – до 25 тысяч. Дубна, календарь
от 2016 года.
В экономической теории впервые идея исследования и анализа
межотраслевых связей была предложена советскими экономистамистатистиками при составлении баланса народного хозяйства за 1923-1924
хозяйственный год. В этом пионерском балансе содержалась информация о
связях основных отраслей экономики и направления производственного
использования продукции.
29
30.
Межотраслевой балансМежотраслевой баланс бывает двух видов: баланс потоков продуктов (материальный
баланс) и баланс потоков денежных средств (финансовый баланс). Этим двум видам потоков
соответствуют две разные сети, которые по своей структуре являются двойственными по
отношению друг к другу.
Математически задача МОБ имеет вид уравнений потоков продуктов. Система
хозяйства состоит из n отраслей, которые производят продукты с валовым выпуском X (где
= 1, ..., n), чтобы обеспечить план (спрос) y и поставки x . При этом сами потребляют
ресурсы и поставки. На выходе отраслей это представляет система уравнений распределения
валового выпуска [3а, 4б]:
n
X x y .
1
(6.1)
Межотраслевые поставки задают коэффициенты прямых затрат (КПЗ), которые
обозначают a . Значения КПЗ численно равны количеству продукта отрасли , которое
необходимо для производства единицы продукта отрасли .
Определение Росстата. Коэффициенты прямых затрат представляют собой затраты одного
продукта на производство другого продукта (например, расход угля на производство
электроэнергии) и рассчитываются в рублях на 1000 рублей продукции
31.
Коэффициенты прямых и полных затратЗначения поставок продуктов между отраслями выражаются уравнением:
x = a X .
(6.2)
Матрица КПЗ обозначается a = A. Потребление ресурсов определяется
аналогичными коэффициентами прямых затрат ресурсов b , численно равными
количеству ресурса для производства одной единицы продукта отрасли , что выражается
уравнениями:
r = b X .
(6.3)
Таким образом, коэффициенты a и b устанавливают пропорции между
воздействиями, в виде валового выпуска, и откликом, в виде потока поставки или ресурса.
Коэффициенты полных затрат учитывают затраты, связанные с производством того
или иного продукта не только прямо, но и косвенно через другие продукты, участвующие в
производстве данного продукта.
Например, для определения полных затрат электроэнергии на производство станков
учитываются не только прямые затраты на их производство, но и расход электроэнергии на
выплавку стали, обработку металлов и производство других материалов, из которых
изготавливаются станки; на выработку топлива для производства станков; на доставку
материалов с мест первичного производства до предприятий-потребителей и т. д. Итак,
полные затраты электроэнергии на производство станков должны учесть весь ее расход по
всей цепи технологических связей станкостроения с другими отраслями экономики.
32.
Обращение матрицы ЛеонтьеваПодставляя (6.2) в (6.1) и преобразуя, получим систему уравнений:
y ( a ) X ,
(6.4)
где ( – a ) = (I – A) – так называемая экономическая матрица, или матрица Леонтьева (
= I – единичная матрица). Уравнение баланса в матричной форме имеет вид X = A X + Y.
Обращение экономической матрицы дает решение задачи:
X = (I – A)-1 Y.
(6.5)
Для реальных задач порядок экономической матрицы может составлять тысячи строк и
столбцов, тогда время решения может превышать плановый период. Это затрудняет
управление экономикой. Обращение экономической матрицы можно выполнить
вычислением суммы степенного ряда:
(I – A)–1 = I + A + A2 + A3 + ...
(6.6)
поскольку коэффициенты в матрице a меньше, и даже много меньше, единицы и норма
матрицы ( – a ) меньше единицы. Элементы обратной экономической матрицы
называют коэффициентами полных затрат.
В отличие от КПЗ, являющихся составной частью издержек производства данного вида
продукции, коэффициенты полных затрат охватывают элементы издержек производства
других продуктов, косвенно связанных с производством данного вида продукции.
Коэффициенты полных затрат показывают потребности в выпуске для производства 1000
рублей продукции данного вида, конечной продукции другого вида
33.
Баланс потоков продуктов на входе отраслиБаланс потоков продуктов представляет закон сохранения потоков в узлах на выходе
отраслей подобно первому закону Кирхгофа в электрической цепи. Формулы (6.2) и (6.3)
подобны метрическим, где элементы метрической матрицы – это коэффициенты прямых
затрат для поставок a и ресурсов b . Они аналогичны законам Ома в цепи. Другие
соотношения обычно не используют. Однако, как можно видеть на рис. 6.1, существует
связь между потоками в узлах входов отраслей. Эту связь можно записать в виде системы
уравнений:
X = x + r = a X + b X = ( a + b ) X .
(6.7)
Потоки ресурсов r и поставок x пропорциональны величине выпуска X . В формуле
(6.7) слева и справа стоит численно один и тот же вектор, поэтому:
a + b = 1.
(6.8)
Физически это означает: для выпуска единицы данного продукта должны быть
обеспечены все необходимые поставки и ресурсы – условие очевидное, а потому обычно не
используемое. Однако это условие обеспечивает полноту описания потоков в сети и
позволяет привести уравнения к тензорному виду.
Нетрудно видеть, что отсюда следует равенство суммы спроса на выходе отраслей
сумме потоков ресурсов на входе в систему: r = y .
34.
Двойственная модель ЛеонтьеваДвойственной к модели Леонтьева является следующая
р = Аt р + v
где p — вектор цен отраслей,
v — вектор добавленных стоимостей на единицу продукции,
Аt р — вектор затрат отраслей на единицу выпуска.
Соответственно, p – Аt р — вектор чистого дохода на единицу
выпуска, который и приравнивается к вектору добавленных
стоимостей.
Тогда решение двойственной модели
р = (I – Аt)-1 v
Совокупный выпуск всех отраслей состоит из двух
компонент – выпуск для конечного потребления и выпуск
межотраслевого потребления для обеспечения выпуска
продукции других отраслей.
35.
Декомпозиция на части сетевой моделиэкономической системы и МОБ
• Расчет по частям ускоряет расчеты и позволяет
решить для МОБ проблему больших данных
• Для расчета по частям сетевую модель делим на
подсистемы; их решения затем соединяем в
решение всей системы.
• Такой алгоритм обеспечивает многократное
снижение объема вычислений, ускоряя плановые
расчеты
35
36.
Пример сетевой модели экономической системыДобыча полезных ископаемых
X3
X7
X6
X4
Обрабатывающие
производства
Транспорт
X5
Производство и распределение
электроэнергии, газа и воды
Строительство
X1
Оптовая
и
розничная торговля
Сельское хозяйство,
охота и лесное хозяйство
Спрос (план) на произведенные продукты
Экономическая матрица (I – A):
3
(I – A) =
3
4
5
6
7
1
1
-0,1
-0,1
-0,1
0
0
4
-0,2
1
-0,1
-0,1
0
0
5
-0,1
-0,2
1
0
0
0
6
-0,1
-0,2
0
1
-0,2
0
7
1
0
0
0
-0,1
1
-0,2
0
0
0
0
-0,1
1
(2.16)
36
37.
Пример расчета МОБ по частямr2,3 = 118,17304
X3 = 147,7163
X6 = 140,018
G
0,8
r2,4 = 155,0971
r2,5 = 25,84985
A
3
4
r2,1 = 5,1435
L
x7,6 = 28,0036
M
X7 = 28,575
x4,5 = 7,38567
1
X1 = 5,715
7
6
D
x7,1 = 5,715
X5 = 36,9284
5
x3,4 = 44,3135
x4,3 = 14,7716
r2,7 = 20,0025
K
C
B
x3,5 = 3,6928
x5,4 = 22,1567
x5,3 = 14,7716
R
r2,6 = 112,0144
x6,7 = 2,8575
x1,7 = 125,8118
O
X4 = 221,5673
N
y3 = 99,71
y5 = 0
P
Сеть
y7 = 02
F
y4 = 199,41
E
r2,6 = 432,0378
r2,6 = 802,4004
0,9
Сеть 1
y1 = 0
y6 = 137,16
0,7
r2,6 = 697,94186
0,9
B
3
X3 = 891,556
K
x6,3 = 89,1156
A
x6,4 = 48,0042
0,1
0,1
0,2
6
X6 = 997,0598
x3,6 = 99,70598
4
D
X4 = 480,042
y3 = 791,85
0,1
0,1
x4,6 = 199,41196
0,1
N
E
y4 = 280,63
y6 = 859,9
Сеть пересечений после первого этапа расчета
Рис. 2.7. Потоки в подсистемах (2.28–2.29) и сети пересечений (2.26) после завершения
первого этапа расчета по частям
37
38.
Таблицы затраты-выпуск по КазахстануПродукция
сельского
хозяйства,
охоты и
связанные с
этим услуги
Продукция
лесного
хозяйства,
лесозаготовок
и услуги в этих
областях
Рыба и
продукция
рыболовства
прочая, услуги
в этих
областях
Уголь
каменный и
лигнит; торф
Нефть сырая и
газ природный;
Услуги в
области
добычи нефти
и газа, кроме
работ
изыскательских
Руды
металлические
Прочие
отрасли
горнодобывающей
промышленности 8-12
Производство
пищевых
продуктов,
включая
напитки 13-21
Табачные
изделия
Текстильное
производство
23-25
Производство
одежды;
выделка и
крашение меха
Сельское
хозяйство,
охота и
предоставление услуг в
этих
областях
Лесное
хозяйство и
предоставление услуг в
этой области
Рыболовство,
рыбоводство
и
предоставление услуг в
этих
областях
Добыча
угля,
лигнита
и
торфа
Добыча
сырой
нефти и
попутного
газа
Добыча
природного
газа и
предоставление услуг по
добыче
нефти
и
газа
Добыча
металлических
руд
Прочие
отрасли
горнодобывающей
промышленности
Производство
пищевых
продуктов,
включая
напитки
Производство
табачных
изделий
Текстильное
производство
Производство
одежды;
выделка и
крашение
меха
Производс
кожи,
изделий
из кожи и
производс
обуви
1
2
3
4
5
6
7
8
9
10
11
12
0,15520
0,00015
0,00001
0,00000
0,00000
0,00000
0,00000
0,00005
0,12269
0,01215
0,00628
0,00203
0,00
0,05579
0,01912
0,00005
0,00389
0,00188
0,00085
0,01604
0,00020
0,00000
0,00000
0,00000
0,00000
0,00
0,00214
0,00000
0,08807
0,00000
0,00003
0,00000
0,00000
0,00000
0,09819
0,00000
0,00000
0,00000
0,00
0,00482
0,00002
0,00048
0,22960
0,00000
0,00000
0,02540
0,00040
0,00000
0,00000
0,00000
0,00000
0,00
0,00011
0,00000
0,00000
0,00000
0,22438
0,00045
0,00084
0,00000
0,00035
0,00000
0,00001
0,00000
0,00
0,00000
0,00000
0,00000
0,00000
0,75994
0,15882
0,01019
0,00000
0,00000
0,00000
0,00000
0,00000
0,00
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,25338
0,00000
0,00000
0,00000
0,00000
0,00000
0,00
0,00021
0,00000
0,00014
0,00160
0,00304
0,00102
0,00097
0,05222
0,00316
0,00001
0,00047
0,00001
0,00
0,04204
0,00000
0,00009
0,00014
0,00007
0,00000
0,00008
0,00030
0,16082
0,00069
0,00017
0,00001
0,00
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,00003
0,05116
0,00000
0,00000
0,00
0,03102
0,00048
0,00337
0,00032
0,00033
0,00210
0,00187
0,00485
0,05301
0,00021
0,21986
0,07046
0,00
0,02642
0,00008
0,00131
0,00193
0,03969
0,01851
0,01710
0,00041
0,00756
0,00050
0,00173
0,05053
38
0,00
39.
Пример расчета МОБ для Казахстанаматрица КПЗ A для макромодели отраслей
Сельское
хозяйство, 1-3
Добыча
ископаемых, 4-8
Электроэнергия,
газ, вода, 32-33
Обработка передел 1, 17-22
Готовая
продукция передел 2, 14-16,
23-29
ТНП и услуги, 913,30,38,49,5153,55,56
Транспорт и
связь, 39-43, 47
Торговля,35-37
Строительство,
управление,
финансы,34,4446,48,50,54
Сельское Добыча
Электроэнергия, Обработка Готовая
хозяйство, ископаемых, газ, вода, 32-33 - передел продукция
1-3
4-8
1, 17-22
- передел
2, 14-16,
23-29
1
2
3
4
5
0,15391
0,00027
0,00020
0,00022
0,00819
ТНП и услуги, Транспорт Торговля,359и связь,
37
13,30,38,49,51- 39-43, 47
53,55,56
Строительство,
управление,
финансы,34,4446,48,50,54
6
0,16030
7
0,01634
8
0,00000
9
0,00319
0,00025
0,25841
0,02985
0,10036
0,00073
0,00611
0,01705
0,00000
0,01097
0,01615
0,04789
0,06023
0,05344
0,02477
0,07244
0,06089
0,01299
0,05584
0,02278
0,06657
0,00752
0,27994
0,05334
0,07128
0,08035
0,00329
0,29451
0,04280
0,10416
0,04660
0,10542
0,14427
0,12605
0,12740
0,01496
0,24964
0,01292
0,14966
0,00209
0,01163
0,00584
0,24326
0,02250
0,05551
0,09199
0,01781
0,10201
0,00414
0,00807
0,00579
0,04623
0,17056
0,08343
0,10010
0,04734
0,00284
0,00241
0,01903
0,00004
0,00191
0,00242
0,00721
0,00440
0,00249
0,04838
0,01452
0,01847
0,01945
0,09640
0,01882
0,01242
0,10188
39
40.
Агрегирование МОБ для Казахстана3. Расчет сводного баланса по трем секторам экономики:
Добывающий сектор
Обрабатывающий
сектор
Производство товаров для
населения
1. Расчет сводной межотраслевой матрицы поставок (Матрица КПЗ 3X3), тыс. тенге
Добывающий Обрабатывающий Производство товаров
сектор
сектор
для населения
1
2
3
1 Добывающий сектор
1648850151
684050490
306855054
2 Обрабатывающий сектор
599484304
1552273247
1559825582
Производство товаров
3 для населения
653970912
267236803
1908872886
3, Расчет сводной межотраслевой матрицы коэффициентов прямых затрат (Матрица КПЗ 3X3)
Добывающий Обрабатывающий Производство товаров
сектор
сектор
для населения
1
2
3
1 Добывающий сектор
0,25649
0,10641
0,04773 0,41063
2 Обрабатывающий сектор
0,11878
0,30757
0,30907 0,73542
Производство товаров
3 для населения
0,08188
0,03346
0,23901 0,35436
1,50041
40
41.
Структура сети потоков продуктов в социальноэкономической системеПРИРОДА
Энергетические
ресурсы
rb
Сырьевые ресурсы
Утилизация
Добыча ресурсов
ra
Производство продуктов
Xa
Горная
промышленность
Сельское хозяйство
Энергия, газ, тепло
Xb
Транспорт
Строительство
yb
Спрос (план) на продукты
ya
Оптовый рынок
Торговля
Розничный рынок
Потребление
Работники
Пенсионеры
Дети, учащиеся
Отходы,
экология
41
42.
Финансовая система – двойственная сеть• Финансовая система имеет двойственную структуру по
отношению к сети производства. Здесь деньги играют
роль токов, а продукты – роль напряжений.
• Создание продукта порождает деньги, которые потекут в
уплату за него уже сейчас, при этом ожидается
получение результата от использования данного товара в
будущем, когда он принесет новые деньги и даст новую
свободную энергию.
• Каждому открытому пути жизненного цикла изделия
здесь соответствует замкнутый цикл, контур оборота
потока денег.
• Работает схема деньги-товар-деньги.
42
43.
Структура сети потоков денег в социальноэкономической системеЭнергетические
ресурсы
Банк ресурсов
Сырьевые ресурсы
Оплата ресурсов
Налоги
Xa
Банк промышленности
Оплата поставок
Промышленность
Сельское хозяйство
Транспорт
Бюджет
Энергия, газ, тепло
Доход предприятий
Зарплаты
Оптовый рынок
Торговля
Розничный рынок
Государственное
управление
Работники
Пенсионеры
Дети, учащиеся
43
44.
Решение задачи МОБ• Определение Росстата. Отрасль представляет собой
совокупность предприятий и организаций, принадлежащих
соответствующей отрасли. Продукт – совокупность
однородных товаров и услуг данного вида, произведенных в
различных отраслях экономики [3а].
• В качестве «отраслей» в задаче могут фигурировать
предприятия, технологические линии, страны, регионы. Задача
баланса потоков продуктов в системе производства достаточно
универсальна и существует в технике, биологии, и т.д.
• Задача состоит в расчете объема производства (валового
выпуска) каждой отрасли и ресурсов, обеспечивающих спрос и
поставки.
• Если ресурсы ограничены, то возникает задача максимизации
общего выпуска, или обеспечения выпуска приоритетных
отраслей («остаточный» принцип планирования) и т.д.
45.
Потоки продуктов как токи• Применяется двойственность потоков в замкнутых и разомкнутых путях
в сети. Эти потоки вызваны двойственными источниками воздействия,
которые не зависят друг от друга.
• Отклики на них дополняют друг друга, поэтому их можно использовать
для создания суммарных потоков в сети, соответствующих потокам
продуктов.
• Для этого будем так задавать двойственные компоненты вектора
воздействий (в данном случае – в замкнутых путях), чтобы отклики от
них последовательно, шаг за шагом, дополняли отклики в разомкнутых
путях до величин, соответствующих потокам продуктов в каждой ветви
сетевой модели.
• То есть в ветвях, соответствующих отраслям, поставкам и ресурсам.
• Будем задавать источники напряжения так, чтобы отклики-токи на них
дополняли отклики-токи на источники тока до таких величин, которые
равны потокам продуктов.
46.
Потоки продуктов как токи• Рассмотрим, где должны располагаться дополнительные источники и
какие иметь значения.
• Получим формулы, которые выражают величины потоков продуктов
через величины сети, что и составит саму модель задачи баланса.
• Допустим, что сначала заданы только узловые токи (представляющие
спрос ya), обозначим их как Ia.
• Эти токи заданы на ветвях отраслей.
• Проводимости ветвей Yab - аналогия коэффициентов прямых затрат aab
для поставок и bgb для ресурсов.
• Если отрасли не потребляют свою продукцию, то Yaa = aaa = 1, т.е.
диагональные элементы экономической матрицы равны единицам.
• Решая полученную сеть, получим отклики – узловые токи в ветвях Iac.
Величины откликов в ветвях отраслей, поставок и ресурсов
обозначим как Iaca, Iacq, Iacr.
• Индекс a перечисляет ветви данной сети: сначала отрасли от 1 до n,
затем поставки от n + 1 до n + q, затем ресурсы от n + q + 1 до N = n + q
+ r, где N – полное число ветвей.
• Как надо расположить источники напряжения, чтобы они обеспечили
выполнение этих условий? Общее число узлов J = 2n + k, где k
показывает, сколько в данной системе есть разных типов ресурсов.
47.
Источники напряжения в контурах• Возможны два типа ресурсов, k = 2. Это могут быть материальные и
энергетические ресурсы. Чтобы с помощью воздействий получать
любые значения откликов в ветвях сети, надо задать столько
источников, сколько есть независимых путей данного типа.
• Они составят базис, в котором можно задать вектор потока с любыми
необходимыми значениями откликов в ветвях сети.
• Всего ветвей в данной сети N = n + q + r. Если каждую отрасль
снабжает ресурс одного типа, то r = n, тогда N = 2n + q. Из структуры
сетей ясно, что все такие ветви выходят из одного узла (заземленного
на окружающую среду).
• Тогда общее число узлов в сети составит J = 2n + 1, а число
независимых разомкнутых путей равно: j = J – 1 = 2n, т.е. сумме
ветвей отраслей и ресурсов.
• Число независимых контуров: m = N – j = q, т.е. равно числу ветвей
поставок. Если в поставках расположить источники напряжения eqa,
как показано кружками на рис. 5.4.а, то можно подобрать их значения
так, что отклики в ветвях сети будут иметь любые заданные значения.
Например, допустим, что заданы источники напряжения в замкнутых
путях, определяемых ветвями поставок, eqa, такие, что отклики-токи на
них в ветвях, т.е. iaс, примут те значения, которые нам необходимы. То
есть такие значения, которые дополнят токи отклика в ветвях Iaс (от
источников тока Ia) до любой заданной или необходимой величины.
48.
Первый этап расчета• Процесс дополнения узловых токов контурными токами для
того, чтобы представить этой комбинацией токов сети потоки
продуктов, выполним за несколько итераций.
• Сначала допустим, что источники ea1 таковы, что отклики ia1, (по
отраслям, поставкам, ресурсам – ian1, iam1, iar1), вместе с
откликами на Ia составят величины, равные начальным
значениям потоков продуктов при вычислении суммы ряда
(5.6), т.е. будут соответствовать его первому члену. Получим
формулы представления потоков продуктов токами на первом
этапе:
• Xa1 = Ian + ian1 = ya + xab1 = ya;
• xab1 = Iam + iam1 = 0;
• rgb1 = Iar + iar1 = ya.
• То есть, на этом этапе отрасли производят столько, чтобы
удовлетворить спрос и потребляют необходимые для этого
ресурсы, не обмениваясь взаимными поставками. С точки
зрения экономики, это соответствует ремесленным
производствам, когда каждый производитель сам производит
товар от сырья до прилавка.
49.
Второй этап расчета• Допустим, что источники ea2 таковы, что отклики на них, ia2, (по
отраслям, поставкам, ресурсам – ian2, iam2, iar2), вместе с откликами на
источники Ia и откликами на источники ea1, составят величины, равные
значениям потоков продуктов при вычислении второго члена суммы
ряда (5.6). Получим формулы для выражения потоков продуктов
токами на втором этапе:
• Xa2 = Ian + ian1 + ian2 = ya + S xab2 = ya + S aab yb;
• xab2 = Iam + iam1 + iam2 = xab1 + aab Xa1 = aab yb;
• rga2 = Iar + iar1 + iar2 = ya + S aab yb – S aba ya = bga ya + S aab yb.
• При этом значения ресурсов rga2 связаны с Xa2 и xab2 соотношениями
(5.7), выражающими закон Кирхгофа для узлов входа отраслей.
Покажем, что этот закон выполняется в узлах входов отраслей при
выборе источников напряжения, которые дают приращения токов в
ресурсах и с учетом соотношения (5.8), связывающего коэффициенты
bga и aab.
50.
Потоки продуктов, как контурные и узловые токи• Электрическая цепь рассеивает энергию, не усиливает
мощность. Экономическая система, как живая система,
усиливает мощность, дает свободную энергию.
• Токи в замкнутых или разомкнутых путях цепи не могут
представить потоки продуктов. В сетевой модели
дополнение токов в замкнутых и разомкнутых путях
позволяет представить потоки продуктов.
• Продолжим выбирать значения источников так, чтобы
они обеспечили в ветвях на каждом этапе такую сумму
узловых и контурных токов, которая равна потокам
продуктов в сети отраслей при решении балансовой
задачи.
• Тогда получим для p-ого этапа расчета следующие
двойственные отклики (токи) замкнутых и разомкнутых
путей, которые численно равны потокам продуктов.
• В совокупности они представляют компоненты, из
которых состоят потоки продуктов в ветвях сети.
51.
Двойственные воздействия в контурах сетиПунктирные кружки - размещение источников
ЭДС в ветвях отраслей и ресурсов
G
0,7
4
5
A
0,8
0,8
6
B
0,3
0,2
1
1,0
C
2
0,1
3
0,1
1,0
1,0
D
7
10
8
9
E
10
F
3
5
Кружки - размещение источников ЭДС в
ветвях поставок
Спрос (план) – двойные стрелки
Схема контурной части сетевой модели потоков продуктов
Кружки представляют два варианта размещения источников ЭДС, которые дают одинаковое
распределение потоков продуктов, соответствующее нулевому этапу расчета
51
52.
Сетевая модель потоков продуктовДля дополнения узловых токов до потоков продуктов вводим источники ЭДС в
контурах. Их величину определяют поставки между отраслями.
Двойственность дает процессы в живой системе экономики комбинацией
контурных и узловых токов в неживой электрической цепи и представляет
потоки продуктов:
Для валовых выпусков в ветвях отраслей получим:
p
p 1
X I i (a ) y y a y (a ) 2 y ... (a ) p 1 y ,
p
n
1
n
1
в поставках между отраслями:
p
p 1
1
1
x p I m im (a ) y
ресурсов, потребляемых отраслями:
p
p 1
r I i b ( y (a ) y )
p
r
1
r
0
Суммы двойственных контурных и узловых токов численно равны потокам
продуктов в отраслях, поставках и ресурсах. Напряжения на ветвях сети
пропорциональны добавленной стоимости, а потенциалы узлов задают цены
производителей.
52
53.
Сетевая модель потоков продуктовЭлектрическая цепь рассеивает энергию, не усиливает мощность.
Экономическая система, как живая система, усиливает мощность, увеличивает
свободную энергию.
Токи в замкнутых или разомкнутых путях цепи не могут представить потоки
продуктов. В сетевой модели дополнение токов в замкнутых и разомкнутых
путях позволяет представить потоки продуктов.
Для этого вводятся источники ЭДС в контурах. Их величину определяют
поставки между отраслями.
Двойственность дает процессы в живой системе экономики комбинацией
контурных и узловых токов в неживой электрической цепи и представляет
потоки продуктов: в отраслях; в поставках между отраслями; в ресурсах,
потребляемых отраслями.
Суммы двойственных контурных и узловых токов численно равны потокам
продуктов в отраслях, поставках и ресурсах. Напряжения на ветвях сети
пропорциональны добавленной стоимости, а потенциалы узлов задают цены
производителей.
53
54.
Проблема больших данных при расчете МОБГосплан рассчитывал 4000 показателей. Вычислительная техника
обеспечивала обращение матрицы порядка 1000 строк примерно за
неделю. За это время возможен сбой аппаратуры, поэтому проводили
повторный расчет. Если результаты не совпадали, то проводили третий
расчет и брали два совпадающих результата.
Такой расчет занимал примерно месяц. Время обращения матрицы
пропорционально кубу числа строк (переменных).
Обращение матрицы порядка 4000 строк будет требовать 4х4х4 = 64
месяца, что равно как раз пятилетнему периоду планирования.
Это только один вариант плана, а для оптимизации необходимо
рассчитать несколько вариантов. Возможности ЭВМ возросли, но
проблемы расчета балансового планирования остались.
54
55.
Декомпозиция сетевой модели МОБ ирасчет по частям
• Расчет по частям ускоряет расчеты и позволяет
решить для МОБ проблему больших данных
• Для расчета по частям сетевую модель делим на
подсистемы; их решения затем соединяем в
решение всей системы.
• Такой алгоритм обеспечивает многократное
снижение объема вычислений, ускоряя плановые
расчеты
55
56.
Алгоритм расчета МОБ по частямПростой путь обеспечивает снижение объемов вычислений по сравнению с
традиционным способом расчета межотраслевого баланса; в результате получаем
только значения потоков продуктов (это и есть решение задачи МОБ).
Простой алгоритм. Разделить сеть на подсети, рассчитать каждую из них как обычную
задачу баланса – обращая матрицу (I – A) или вычисляя сумму ряда (2.6), а затем
соединить решения подсетей, используя сеть соединения (сеть пересечения связей).
Алгоритм такой схемы блочного расчета матрицы (I – A), к которому приводится метод
расчета эквивалентной сети баланса продуктов по частям (6.3), состоит в следующем:
Разделение сетевой модели системы производства на подсети. В результате этой
декомпозиции выделяются блоки вдоль диагонали экономической матрицы такого
размера, который соответствует выбранному размеру подсистемы. Эти блоки
обращаются независимо друг от друга последовательно или с применением
параллельных вычислений.
Выделение сети соединения подсетей (сети пересечений). Все ненулевые элементы вне
выбранных блоков образуют сеть пересечений. Из этих элементов выбираем все
элементы их строк и столбцов вместе с расположенными на главной диагонали
элементами. Полученная матрица соответствует сети, составленной из разорванных
при декомпозиции ветвей поставок, а также отраслей, которые связывают эти поставки.
Расчет независимых подсетей – получение валовых выпусков на нулевом этапе.
Получение воздействия подсетей на сеть пересечений. Полученные решения – валовые
выпуски подсетей – рассматриваются как воздействие-спрос на отрасли сети
пересечений.
57.
Алгоритм расчета МОБ по частямРасчет сети пересечений с воздействиями от независимых подсетей. Получаются
отклики-выпуски отраслей сети пересечений. Приращения этих выпусков, по сравнению
с теми, которые заданы со стороны подсистем, играют роль дополнительных обратных
воздействий сети пересечений на подсистемы.
Расчет обратного воздействия сети пересечений на независимые подсети (взаимное
воздействие подсетей).
Расчет подсетей с найденными взаимными воздействиями (пункт 3). Производим
расчет подсистем при новых воздействиях. Полученные результаты играют роль новых
дополнительных воздействий на сеть пересечений.
Получение полного выпуска отраслей: сумма выпуска в подсетях и приращений
выпусков от сети пересечений (или сумма совокупности значений от предыдущих
этапов и приращения выпуска от очередного этапа расчета).
Проверка на достижение заданной точности решения. Повторяем этот вычислительный
процесс до тех пор, пока получаемые приращения не станут меньше наперед заданного
порога точности расчета. Если разность между предыдущим и последующим
приращениями меньше заданного значения, то решение получено. Результат является
решением задача межотраслевого баланса производства продуктов. Если нет, то:
Получение приращений выпусков – новых воздействий подсетей на сеть пересечений,
и повторяются этапы расчета 4–8.
Окончательная проверка: получить значения потоков поставок и ресурсов; проверить
баланс всех потоков в узлах входа и выхода каждой отрасли в сетевой модели.
Проверить равенство суммы ресурсов сумме спроса. Это и есть межотраслевой баланс.
58.
Пример расчета МОБ методом декомпозицииИсходные данные
1
2
3
0,2
0,4
0,2
0,3
0,1
Y1=200
0,1
Y2=200
Y3=300
Y4=300
Матрица Леонтьева (экономическая):
коэффициенты прямых затрат direct cost factors
(I –
1
-0,2
0
0
-0,1
1
0
-0,4
4
0
-0,3
1
-0,2
0
0
-0,1
1
A) =
59.
Расчет полной сетиРешение задачи
2.1 Расчет полной сети
Матрица коэффициентов полных затрат:
(I –
1,020666 0,10333193 0,031632 0,003163
0,206664 1,03331927 0,316322 0,031632
0,008435 0,0421763 1,033319 0,103332
0,084353 0,42176297 0,333193 1,033319
A)-1 =
Отсюда получим значения валовых выпусков отраслей:
X I a y
1
1,020666 0,10333193 0,031632 0,003163
= 0,206664 1,03331927 0,316322 0,031632
0,008435 0,0421763 1,033319 0,103332
0,084353 0,42176297 0,333193 1,033319
*
200
200
300
300
=
235,238
352,383
351,118
511,177
60.
Потоки продуктов в полной сети производстваРасчет поток продуктов в полной сети производства.
Входящие ресурсы:
R1 = 0,8 * 235,238 = 188,19;
R2 = 0,5 * 352,383 = 176,19;
R3 = 0,5 * 351,118 = 175,56;
R4 = 0,9 * 511,177 = 460,06.
Поставки продукции между отраслями:
X12 = 0,1 * 352,383 = 35,24;
X21 = 0,2 * 235,238 = 47,05;
X23 = 0,3 * 351,118 = 105,34;
X34 = 0,1 * 511,177 = 51,12;
X42 = 0,4 * 352,383 = 140,95;
X43 = 0,2 * 351,118 = 70,22.
Далее проводится проверка выполнения баланса спроса, поставок, выпуска
продукции и потребления ресурсов в каждом узле сетевой модели.
61.
Расчет по частям подсистема 1Энергетические
ресурсы
0,9
0,8
8
0,2
X1
0,1
Промышленность
Y1=200
X2
АПК
Y2=200
Спрос (план) на произведенные продукты
Подсеть 1
62.
Расчет подсети 1Матрица коэффициентов прямых затрат:
(I -
1
-0,2
-0,1
A)1 =
1
Матрица коэффициентов полных затрат:
(I -
1,020408 0,102041
A)1 -1 =
0,204082 1,020408
1,020408 0,102041
0,204082 1,020408
Значения валовых выпусков отраслей:
200
200
224,4898
244,898
X 1
Далее при необходимости проводится расчет потоков поставок и ресурсов.
Заметим, что коэффициенты прямых затрат ресурсов в отдельных подсетях
(представляющих отдельные цеха, предприятия, регионы) меняются, поскольку в этом
случае необходимо потреблять больше собственных ресурсов, хозяйственные связи,
реализующие разделение труда и специализацию, разорваны.
*
=
63.
Подсеть 2Подсистема 2 из отраслей 3 и 4
0,8
8
3
0,9
0,2
4
8
8
0,1
8
Y3=300
Y4=300
Матрица коэффициентов прямых затрат:
(I -
1
-0,2
-0,1
A)2 =
1
Матрица коэффициентов полных затрат:
(I -
1,020408 0,102041
0,204082 1,020408
A)2 -1 =
Значения валовых выпусков отраслей:
1,020408 0,102041
0,204082 1,020408
300
300
336,7347
367,3469
X 2
*
=
64.
Сеть пересеченийЗдесь роль спроса играют соответствующие валовые выпуски отраслей.
0,6
2
3
4
0,7
8
1
8
0,4
8
8
0,3
8
y2 p = 244,898
y 3 p = 336,7347
Матрица коэффициентов прямых затрат:
(I-
1
0
-0,4
-0,3
1
0
0
0
1
A)p =
y4 p = 367,3469
65.
Расчет сети пересеченийМатрица коэффициентов полных затрат:
(I-A)p
1
0
0,4
0,3
1
0,12
0
0
1
-1
=
Значения валовых выпусков отраслей сети пересечений:
1
X p = (I – A)p -1 y p =
1
0
0,4
0,3
1
0,12
0
0
1
*
244,898
336,7347
367,3469
345,9184
336,7347
505,7143
=
66.
Реакция на подсетиПостроение обратных воздействий от сети пересечений на подсистемы:
345,9184
336,7347
505,7143
244,897959
336,734694
367,346939
101,0204
0
138,3673
1 p
y s=
–
Расчет воздействия сети пересечений на подсети
Подсеть 1. Значения дополнительных выпусков отраслей для подсети 1:
1
X 1 = (I-A)1 -1 * 1y p1 =
1,020408 0,1020408
0,204082 1,0204082
0
101,0204
=
10,3082
103,082
=
14,11912
141,1912
Подсеть 2. Значения дополнительных выпусков отраслей для подсети 2:
1
X 2 = (I-A)2 -1 * 1y p1 =
1,020408 0,1020408
0,204082 1,0204082
0
*
138,3673
Полученные значения прибавляются к выпускам отраслей.
1
X X 1 X 1, 2
10,3082
103,082
14,11912
141,1912
224,489796
+244,897959
336,734694
367,346939
234,798
= 347,98
350,8538
508,5381
=
67.
Проверка расчета по частямВходящие ресурсы:
R1 = 0,8 * 234,798 = 187,84;
R2 = 0,5 * 347,98 = 173,99;
R3 = 0,5 * 350,8538= 175,43;
R4 = 0,9 * 508,5381 = 457,68.
Поставки:
X12 = 0,1 * 347,98 = 34,80;
X21 = 0,2 * 234,798 = 46,96;
X23 = 0,3 * 350,8538= 105,26;
X34 = 0,1 * 508,5381 = 50,85;
X42 = 0,4 * 347,98 = 139,19;
X43 = 0,2 * 350,8538= 70,17.
Отклонение результата расчета задачи МОБ по частям от точного решения
полной задачи (сети) после первого этапа вычислений.
234,798
347,98
350,8538
508,5381
235,238
352,383
351,118
511,177
–
-0,440
-4,403
-0,264
-2,639
=
В
целом
получилось
удовлетворительное приближение результата расчета по частям к решению задачи
как единого целого. Наибольшее отклонение получилось для отрасли 2. На
следующих этапах отклонения должны уменьшаться до необходимой точности
вычислений.
68.
Пример расчета МОБ по частямr2,3 = 118,17304
X3 = 147,7163
X6 = 140,018
G
0,8
r2,4 = 155,0971
r2,5 = 25,84985
A
3
4
r2,1 = 5,1435
L
x7,6 = 28,0036
M
X7 = 28,575
x4,5 = 7,38567
1
X1 = 5,715
7
6
D
x7,1 = 5,715
X5 = 36,9284
5
x3,4 = 44,3135
x4,3 = 14,7716
r2,7 = 20,0025
K
C
B
x3,5 = 3,6928
x5,4 = 22,1567
x5,3 = 14,7716
R
r2,6 = 112,0144
x6,7 = 2,8575
x1,7 = 125,8118
O
X4 = 221,5673
N
y3 = 99,71
y5 = 0
P
Сеть
y7 = 02
F
y4 = 199,41
E
r2,6 = 432,0378
r2,6 = 802,4004
0,9
Сеть 1
y1 = 0
y6 = 137,16
0,7
r2,6 = 697,94186
0,9
B
3
X3 = 891,556
K
x6,3 = 89,1156
A
x6,4 = 48,0042
0,1
0,1
0,2
6
X6 = 997,0598
x3,6 = 99,70598
4
D
X4 = 480,042
y3 = 791,85
0,1
0,1
x4,6 = 199,41196
0,1
N
E
y4 = 280,63
y6 = 859,9
Сеть пересечений после первого этапа расчета
Рис. 2.7. Потоки в подсистемах (2.28–2.29) и сети пересечений (2.26) после завершения
первого этапа расчета по частям
68
69.
Простая сетевая модель из двух отраслейЭто баланс потоков продуктов на выходе отраслей, которые производят
продукты с валовым выпуском X, обеспечивая план (спрос) y и поставки xij.
n
X x y .
(6.1)
1
Поставки задают коэффициенты (КПЗ), aij. Это количество продукта
отрасли i, для производства единицы продукта отрасли j. Уравнение баланса X
= A X + Y. Решение дает обращение экономической матрицы:
X = (I – A)-1 Y.
(6.5)
Обращение можно выполнить вычислением суммы степенного ряда:
(I – A)–1 = I + A + A2 + A3 + ...
поскольку aij меньше единицы и норма матрицы (I – A) меньше единицы.
Добыча полезных ископаемых
b2 = 0,8
b1= 0,9
Отрасль 1
a21 = 0,1
Отрасль 2
Выпуск X1
Выпуск X2
a12 = 0,2
Спрос Y1 = 100
Y2 = 200
Система из двух отраслей, двух поставок и двух ресурсов
(6.6)
70.
Уравнения баланса модели из двух отраслейСистему производства в простейшем виде представляют
уравнения баланса на выходе двух отраслей
Преобразуя, получим
X1 = Y1 + a12 X2
X2= Y2 + a21 X1
Y1 = X1 - a12 X2
Y2 = X2 - a21 X1
Решение получаем из обращения матрицы
X1= (Y1 + a12 Y2) / (1 - a12 a21)
X2= (a21 Y1 + Y2) / (1 - a12 a21)
71.
Решение простой задачи МОБЭкономическая матрица I – A =
1
2
1
1 -0,2
2
-0,1
1
b
0,9
0,8
Коэффициенты прямых затрат ресурсов b
Полные затраты дают валовые выпуски Х = (I – A)-1 Y =
1
2
1 1,020408 0,204082
2 0,102041 1,020408
*
Y
100
200
=
Х
142,8572
214,2857
Это валовые выпуски Х – решение задачи.
Далее вычисляем поставки, ресурсы и проверяем выполнение
баланса потоков продуктов по всем узлам.
72.
Расчета матрицы Леонтьева степенным рядомИли вычисляем степенной ряд (I – A)–1 = I + A + A2 + A3 +:
I
A
1,00
0,00
0,00
1,00 +
A
0,00
0,10
0,00
0,10
0,20
0,00
0,02
0
0
0,02
0
0,002
0,004
0
0,20
0,00
0
0,1
A2
0,2
0
A
0
0,1
A3
0,2
0
A2
+
1
0,1
0,20
0,00 =
A
A
I+A
0,00
0,10
0,2
1
+
0,02
0
0
0,0004
A3
+
0
0,002
0
0,02
1
I + A + A2 + A3 + A4 =
I+A
1,00
0,10
A2
0,02
0,00
A3
0
0,002
A4
0,0004
0
0,20
1,00
0,00
0,02
0,004
0
0,004
0
A4
0,0004
0
0
0,0004
(I – A)–1
2
1
1,0204
0,204
1,02041 0,20408
2
0,102
1,0204
0,10204 1,02041
73.
Обращение матрицы• Обращение матрицы состоит из 5 шагов
• Найти определитель матрицы
• Заменить каждый элемент его алгебраическим
дополнением, минором. Это определитель
матрицы, получаемой при вычеркивании
строки и столбца данного элемента.
• Умножить каждый элемент матрицы на минус
единицу в степени суммы его строки и
столбца.
• Транспонировать полученную матрицу
• Разделить каждый элемент полученной
матрицы на определитель
74.
Расчет сетевой модели баланса по полному алгоритмуА именно, рассчитаем сетевую модель как физическую систему, как
электрическую сеть с полным набором токов и напряжений от внешних источников и
внутренних источников по формулам (5.22–5.27).
Для такого расчета задачи баланса потоков продуктов и денежных средств
рассмотрим сетевую модель из трех отраслей, связывающих их поставок и ресурсов.
Эта сетевая модель представлена на рисунке 5.16, где нумерация ветвей дает их более
удобное расположение в подматрицах замкнутых и разомкнутых путей.
Стрелки – узловые токи в сети на входе и
выходе ветвей отраслей и ресурсов
представляют спрос
G
0,7
A
4
5
0,8
0,8
B
6
0,3
0,2
C
1
1,0
2
0,1
0,1
1,0
3
1,0
D
7
8
9
10
E
y1 = 10
F
y2 = 5
Спрос (план) – двойные стрелки
Рис. 5.16. Структура сети потоков продуктов в отраслях
Стрелки представляют спрос и узловые токи модели
y3 = 3
75.
Матрица преобразования прямого базиса путейМатрица преобразования прямого базиса путей данной сети, если ветви 1-6 определяют
разомкнутые пути, а ветви 7–10 определяют замкнутые пути, имеет вид:
1
C=
1`
2`
3`
4`
5`
6`
7`
8`
9`
10`
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
1
-1
1
1
1
-1
1
1
-1
1
1
-1
1
1
1
j
j
j
j
j
j
m
m
m
m
Контуры в этой сети выбраны как естественные пути от ресурса через отрасль, поставку и
как противодействие другому ресурсу. Т.е. поставки из других отраслей снижают
необходимость потребления ресурсов самой отраслью (регионом).
76.
Нулевой этап расчетаНулевой этап расчета (выпуски отраслей равны спросу). Узловая сеть. Для этого
расчета применяется подматрица преобразования открытых путей матрицы взаимного
базиса (или замкнутых путей двойственной сети). Эта подматрица имеет вид:
1
1`
2
5
6
7
8
9
10
j
j
j
j
j
j
-1
1
-1
3`
A=
4
1
2`
j
3
-1
1
-1
4`
1
5`
1
6`
-1
1
1
-1
1
-1
1
1
-1
Расчет сети производим по обычным формулам решения сети из главы 2:
контурной сети – используя (2.70): mdс = mCt (mC Z mCt) –1 mC md0,
узловой сети по формуле: jdс = jAt (jA Y jAt) –1 jA jd0, где опущены текущие индексы.
В соответствии со схемой зададим вектор источников узлового (открытого)
воздействия, который должен иметь указанные значения на ветвях отраслей, и равные им
значения в ветвях ресурсов, чтобы обеспечить компенсацию в узлах входа отраслей.
I =y =
1
10
2
5
3
3
4
10
5
5
6
3
7
0
8
0
9
0
10
0
Дело в том, что спрос в экономике задан только на выходе отраслей, а источник тока в сети
задают на входе ветви отрасли, и на выходе из нее.
77.
Расчет связанной узловой сетирасчет связанной узловой сети. Выполняя перемножения матриц в скобках формулы
расчета узловой сети, т.е., умножая последовательно jA Y jAt, получим:
j
j
A Y At =
1
2
3
4
5
6
1
1,1
0
0
0,1
-0,1
0
2
0
1,5
0
-0,3
0,5
-0,2
3
0
0
1,1
0
-0,1
0,1
4
0,1
-0,3
0
1,1
-0,4
0
5
-0,1
0,5
-0,1
-0,4
1,5
-0,3
6
0
-0,2
0,1
0
-0,3
1,1
Обратная матрица имеет вид (jA Y jAt) –1:
j
j
–1
( A Y At) =
1
2
3
4
5
6
1
0,9206
-0,0315
0,0042
-0,0724
0,0546
0,0088
2
-0,0315
0,7753
-0,0268
0,1387
-0,2080
0,0867
3
0,0042
-0,0268
0,9211
0,0141
0,0599
-0,0723
4
-0,0724
0,1387
0,0141
1,0430
0,2463
0,0911
5
0,0546
-0,2080
0,0599
0,2463
0,8468
0,1877
6
0,0088
0,0867
j
-0,0723
0,0911
0,1877
0,9826
Полученную матрицу умножим на A справа и слева, получим Zс = jAt (jA Y jAt) –1 jA
78.
Сумма узловых и контурных токовВ таблице показана сумма узловых и контурных токов (представляющих потоки
продуктов) в ветвях на каждом этапе расчета, а также изменение этой суммы при переходе
от одного этапа к следующему.
Сумма узловых и контурных токов в ветвях и их приращения по этапам расчета
Ветви
Сумма узловых и контурных токов в ветвях
Этап 0
Приращения суммы токов по этапам
Этапы 0-1
Этапы 0-2
Этапы 0-3
Этапы 0-4
Этап 1 - 0
Этап 2 - 1
Этап 3 - 2
Этап 4 - 3
1 отрасль
10,000
10,500
10,860
10,8847
10,9027
0,500
0,360
0,025
0,018
2 отрасль
5,000
8,600
8,850
9,0302
9,0422
3,600
0,250
0,180
0,012
3 отрасль
3,000
3,500
3,860
3,885
3,903
0,500
0,360
0,025
0,018
4 ресурс
10,000
7,500
7,710
7,6266
7,6366
-2,500
0,210
-0,083
0,01
5 ресурс
5,000
7,599
7,129
7,2594
7,2354
2,600
-0,470
0,130
-0,024
6 ресурс
3,000
2,900
3,160
3,113
3,126
-0,100
0,260
-0,047
0,013
7 поставка
0,000
0,500
0,860
0,8847
0,9027
0,500
0,360
0,025
0,018
8 поставка
0,000
3,000
3,150
3,2581
3,2651
3,000
0,150
0,108
0,007
9 поставка
0,000
0,600
0,700
0,7721
0,7771
0,600
0,100
0,072
0,005
10 поставка
0,000
0,500
0,860
0,885
0,903
0,500
0,360
0,025
0,018
Быстрое уменьшение значений приращений в правых четырех столбцах таблицы
показывает, что сумма токов в ветвях сходится к некоторым предельным значениям. Эти
значения должны представлять потоки продуктов в сбалансированной сети отраслей,
поставок и ресурсов, т.е. в системе производства.
79.
Результаты расчета сетевой модели балансаВ таблице дана сумма токов за четыре этапа расчета. Затем даны точные
значения потоков продуктов, полученные при расчете самой задачи баланса. В
последнем столбце – разность между суммой токов в модели и потоками
продуктов в отраслях, поставках и ресурсах.
Результаты расчета сетевой модели баланса продуктов
Сумма токов представляет потоки продуктов в отраслях, поставках и ресурсах
Этап 1
Этап 2
Этап 3
Этап 4
Контурная
сеть
0,360
Контурная
сеть
0,025
Контурная
сеть
0,018
Сумма
узловых и
контурных
токов за
этапы 0-4
10,9027
10,9053
Отклонения
токов в
ветвях от
потоков
продуктов
-0,0026
9,0422
9,0526
-0,0104
0,018
3,903
3,9053
-0,0023
-0,083
0,010
7,6366
7,6337
0,00289
-0,470
0,130
-0,024
7,2354
7,2421
-0,00668
-0,100
0,260
-0,047
0,013
3,126
3,1242
0,00176
1,3637
0,500
0,360
0,025
0,018
0,9027
0,9053
-0,00256
0,2739
-0,2739
3,000
0,150
0,108
0,007
3,2651
3,2716
-0,00649
9 поставка
-1,1863
1,1863
0,600
0,100
0,072
0,005
0,7771
0,7811
-0,00396
10 поставка
-0,1051
0,1051
0,500
0,360
0,025
0,018
0,903
0,9053
-0,00226
Токи в ветвях
Ветви
Нулевой этап
Узловая
сеть
Контурная
сеть
1 отрасль
8,6363
1,3637
Контурная
сеть
0,500
2 отрасль
4,0876
0,9124
3,600
0,250
0,180
0,012
3 отрасль
2,8949
0,1051
0,500
0,360
0,025
4 ресурс
8,3624
1,6376
-2,500
0,210
5 ресурс
5,5564
-0,5564
2,600
6 ресурс
4,0812
-1,0812
7 поставка
-1,3637
8 поставка
Точный
расчет
потоков
продуктов
Отклонение суммы контурных и узловых токов в сетевой модели от потоков
продуктов в сети хозяйства, которые получены в результате расчета задачи
баланса, за 4 этапа вышло на уровень заданной точности вычислений. Это
показывает, что сетевая модель в данной предметной области правильно
представляет систему связанных отраслей.
80.
Напряжения - распределение денежных потоковСумма напряжений показывает пропорции распределения
воздействий (денежных средств) в отраслях, поставках и ресурсах.
полных
Напряжения в ветвях отраслей, поставок и ресурсов по этапам расчета
Напряжения в ветвях и контурах сети
Ветви
1 отрасль
Нулевой этап
Узловая
Контурная
сеть, Eс
сеть, me с
8,6363
1,3637
Этап 1
Контурная
сеть
0,500
Этап 2
Контурная
сеть
0,360
Этап 3
Контурная
сеть
0,025
Этап 4
Контурная
сеть
0,018
Сумма
контурных
напряжений
за 4 этапа
Сумма
узловых и
контурных
напряжений
за этапы 0-4
Сумма
контурных
токов за 4
этапа
0,903
10,903
0,903
2 отрасль
4,0876
0,9124
3,600
0,250
0,180
0,012
4,042
9,042
4,042
3 отрасль
2,8949
0,1051
0,500
0,360
0,025
0,018
0,903
3,903
0,903
4 ресурс
11,9462
2,3395
-3,572
0,300
-0,119
0,015
-3,376
10,910
-2,363
5 ресурс
6,9455
-0,6955
3,250
-0,588
0,162
-0,029
2,795
9,045
2,236
6 ресурс
5,1015
-1,3515
-0,125
0,325
-0,059
0,016
0,157
3,907
0,126
7 поставка
-13,6370
13,6370
5,000
3,600
0,250
0,180
9,030
9,030
0,903
8 поставка
0,9131
-0,9131
10,000
0,500
0,360
0,025
10,884
10,884
3,265
9 поставка
-5,9316
5,9316
3,000
0,500
0,360
0,025
3,885
3,885
0,777
10 поставка
-1,0509
1,0509
5,000
3,600
0,250
0,180
9,030
0,903
21,798
0,903
Контур 7
0
18,036
-1,3215
4,848
-0,006
0,242
9,030
Сумма ЭДС
за 4 этапа
3,762
Контур 8
0
-3,036
20,4205
-0,138
0,821
-0,007
21,097
18,061
3,265
Контур 9
0
7,498
9,975
-0,163
0,761
-0,008
10,566
18,064
0,777
Контур 10
0
0,5
2,125
4,873
Мощность в
284,9803
34,3769
67,6495
3,46256
сети
Мощность в свободных ветвях: 284,9803 + 34,3769 = 319,3572
0,054
0,244
7,295
7,795
0,903
0,00863
87,0786
ЭДС в контурах
0,14466
162,5901
Мощность в узловой и контурной сети за этапы 0-4: 406,4358
81.
Home work, coursework 11. Source data
1
2
3
0,2
0,4
0,2
4
0,1
0,3
0,1
Y1=200
0,1
0,1
Y2=200
Demand (plan) for manufactured products
Y3=300
Y4=300
Y4=300
82.
Home work, coursework 21. Source data
1
3
2
0,3
0,2
4
0,3
0,3
0,1
0,2
0,1
Y2=200
6
0,4
0,2
0,2
Y1=100
5
Y3=200
0,2
0,1
Y4=100
Demand (plan) for manufactured products
Y5=300
0,1
Y6=200
83.
Home work 31. Source data
1
3
2
0,2
5
4
0,1
0,5
0,1
0,1
Y1=200
Y2=300
0,3
0,2
0,1
Y3=100
Y4=500
Demand (plan) for manufactured products
0,4
Y5=400
84.
Home work 4Source data
1
2
0,2
0,3
3
4
0,2
0,3
5
6
0,1
0,1
0,2
0,3
0,1
0,1
Y1=400
Y2=100
0,4
0,1
Y3=300
Y3=600
Demand (plan) for manufactured products
Y5=100
Y6=300
85.
Home work 5rk6
0,2
X3
0,2
0,3
0,2
X1
0,1
0,1
X6
0,4
0,1
0,3
X2
Y1 = 600
0,2
100
Y3 = 600
0,3
400
Demand (plan) for manufactured products
Structure of the network of product flows in industries
0,1
600
0,2
500
86.
Home work 6rk5
0,1
x21 = 0,3
X3
0,3
0,4
X5
X1
x23 = 0,1
0,1
X2
0,1
300
0,2
0,5
0,2
Y3 = 100
Y1 = 200
500
Demand (plan) for manufactured products
Structure of the network of product flows in industries
400
87.
Home work 7rk6
0,2
X2
0,3
X3
0,4
0,4
X6
0,3
X1
0,1
0,1
Y1 = 1000
800
0,2
Y3 = 600
0,2
700
Demand (plan) for manufactured products
Structure of the network of product flows in industries
300
500
88.
Величины для описания системы - страны1. Валовой внутренний продукт - ВВП.
2. Доля продукта страны в мировом ВВП:
Доля (ВВП) = ВВП (страны) / ВВП (мира).
3. Население страны - НАС.
Доля населения страны в мировом населении:
Доля (НАС) = НАС (страны) / НАС (мира).
4. Эффективность деятельности населения страны:
ЭФФ (страны) = Доля (ВВП) / Доля (НАС)
Если эффективность равна единице, то страна среднего уровня развития. Если
больше единицы - развитие страны выше среднего.
Пример: в 1981 году мировой ВВП составлял 12279 млрд. долл., ВВП СССР
составлял 1212 млрд. долл.; при этом население планеты составляло 4,5 млрд.,
а население СССР - 280 млн. чел.
Доля СССР в ВВП - 10%, в населении - 6%. Следовательно, эффективность равна:
ЭФФ (СССР-81) = 10% / 6% = 1,5, т.е. в полтора раза выше среднего мирового
уровня. (В 1998 г. ВВП США составил 8000 млрд. долл., а ВВП РФ 2650 млрд.
руб., или 130 млрд. долл. по среднему курсу декабря 20,65 рубля за 1 доллар.)
Весь ВВП страны делится на две части: А и Б.
5. А - часть продукта, уходящая на экспорт и внутри страны не потребляемая.
6. Б - часть продукта, потребляемая внутри страны.
88
89.
Показатели системы страныУровень жизни равен продукт Б плюс импорт (в энергоэквиваленте) на население
• 7. Уровень ориентации на внешний рынок: А/Б.
• 8. Внешний продукт на потребление внутри И - импорт, зависимость от поставок извне.
• 9. Выпущенный в прошлом году продукт, потребляемый в текущем году - Д.
• 10. Продажа систем оружия страны вовне - внешнее воздействие - А1.
• 11. Покупка страной оружия - И1.
• 12. Потребление систем оружия внутри страны - А21, в том числе:
• системы оружия для внешних воздействий (армия) - А211;
• системы оружия для внутренних воздействий - МВД, ФСБ - А212;
• 13. Ориентированные на экспорт средства производства - А111.
• 14. Направленные на экспорт предметы потребления - поток на выход из страны А112.
• Данные показатели характеризуют экономико-политический портрет страны. Их
постоянство говорит о постоянном политическом курсе. Их изменение говорит об
изменении политического курса. Данные показатели и отношения между ними могут
служить основой составления бюджета и проведения экономической политики.
• За показателем (элементы матриц уравнений внешнего и внутреннего экономикополитических балансов страны) стоят те общности людей, которые заинтересованы в
росте своей доли в распределении продукта. Лоббирование интересов каждой группы
представляет собой желание изменить доли распределения.
89
90.
Динамика ВВП мира и семеркиОсновные показатели развития в странах «семерки», и в мировой экономике в
целом, в те годы, когда формировалась концепция Устойчивого развития,
одобренная ООН в 1987 г.
Динамика ВВП (GNP)
1972
1981
1983
1987
1988
$
Доля в
$
Доля в
$
Доля в $ млрд. Доля в
$
Доля в
млрд. мировом млрд. мировом млрд. мировом
мировом млрд. мировом
продукте
продукте
продукте
продукте
продукте
Англия
145
4,0%
510
4,2%
506
3,40%
593
3,9%
730
4,09%
Италия
107
2,9%
391
3,2%
358
2,91%
597
3,9%
765
4,29%
Канада
97
2,7%
276
2,2%
300
2,44%
390
2,5%
437
2,45%
США
1167
32%
2946 24,0% 3292 26,8%
4486
29,3%
4863 27,28%
Франция 187
5,1%
658
5,4%
569
4,62%
715
4,7%
899
5,04%
ФРГ
209
5,7%
830
6,8%
702
5,71%
880
5,7%
1131
6,34%
Япония
248
6,8%
1180
9,6%
1204 9,79%
1926
12,6%
2576 14,45%
7 стран
2160
59%
6791
55%
6930 56,35% 9587
63%
11401
55%
Мир
3652
12279
12298
15330
18070
91.
Спец. стандарт распространения данных ССРД МВФНоминальный объем произведенного ВВП
- в структуре видов экономической деятельности по ОКВЭД
в текущих ценах, млрд. рублей
2002
Раздел A
Сельское хозяйство, охота и
лесное хозяйство
2003
2004
2005
2006
2007
2008
2009
615,5
730,1
850,5
962,4
1 102,9
1 223,0
1 528,9
1 535,8
Раздел B Рыболовство, рыбоводство
29,6
61,0
62,5
65,5
69,1
63,3
63,5
74,7
Раздел C Добыча полезных ископаемых
650,6
785,0
1 426,9
2 084,9
2 528,6
2 890,8
3 332,5
3 158,6
Раздел D
Обрабатывающие
производства
1 690,9
1 976,3
2 687,6
3 521,0
4 272,8
5 248,4
6 461,2
5 495,7
Раздел E
Производство и распределение
электроэнергии, газа и воды
359,6
428,0
566,5
632,5
755,2
895,9
1 071,6
1 167,7
Раздел F
Строительство
522,6
716,2
863,1
1 012,0
1 231,8
1 680,4
2 281,7
1 970,7
2 207,7
2 589,5
3 040,3
3 649,4
4 726,1
5 821,2
7 471,4
6 831,5
Раздел H Гостиницы и рестораны
89,0
95,1
141,6
170,6
211,2
293,3
370,1
352,7
Раздел I
Транспорт и связь
993,7
1 261,6
1 662,0
1 925,1
2 283,8
2 796,7
3 274,6
3 378,9
Раздел J
Финансовая деятельность
298,0
397,6
511,4
759,0
1 050,1
1 353,4
1 673,7
1 672,4
Оптовая и розничная торговля;
ремонт
автотранспортных
Раздел G средств, мотоциклов, бытовых
изделий и предметов личного
пользования
92.
Классификатор отраслей ВВП по ССРД МВФГостиницы и рестораны
89,0
95,1
141,6
170,6
211,2
293,3
370,1
352,7
Раздел I
Транспорт и связь
993,7
1 261,6
1 662,0
1 925,1
2 283,8
2 796,7
3 274,6
3 378,9
Раздел J
Финансовая деятельность
298,0
397,6
511,4
759,0
1 050,1
1 353,4
1 673,7
1 672,4
Операции
с
недвижимым
Раздел K имуществом,
аренда
и
предоставление услуг
1 029,0
1 259,3
1 421,4
1 848,2
2 311,1
3 138,6
4 148,3
4 430,8
Государственное управление и
обеспечение
военной
Раздел L
безопасности;
обязательное
социальное обеспечение
488,8
651,3
802,5
959,1
1 189,2
1 466,4
1 884,7
2 112,5
Раздел M Образование
280,3
318,5
400,8
494,1
620,5
771,6
971,0
1 062,8
322,3
376.7
473.9
566.3
767.6
953.2
1 195.4
1 323.0
Предоставление
прочих
Раздел О коммунальных, социальных и
персональных услуг
183,1
220.0
276.0
326.0
422.2
526.9
604.2
557.0
Косвенно измеряемые услуги
финансового посредничества
-179,3
-211.6
-307.1
-442.9
-578.6
783.1
1 132.8
1 197.6
Итого добавленная стоимость
по
видам
экономической
деятельности
(в основных ценах)
9 581,3
11 654.8
14 879.7
18 533.3
22 963.6
28 339.9
35 200.0 33 927.0
Чистые налоги на продукты
1 249,2
1 588.5
2 168.4
3 092.1
3 939.9
4 763.0
6 056.0
Валовой внутренний продукт
(в рыночных ценах)
10 830,5
13 243.2
17 048.1
21 625.4
26 903.5
33 102.9
41 256.0 39 016.1
Здравоохранение
Раздел N предоставление
услуг
и
социальных
Источник – Росстат (www.gks.ru).
В состав отрасли «Транспорт и связь» входят информационные продукты. Все
отрасли имеют средства сбора, поддержания и хранения информации. Это не
выделяет информацию, а также средства ее производства в отдельную отрасль
5 089.1
93.
ВВП - сумма добавленных стоимостейРасчет ВВП по производству продукции – суммируются стоимости,
добавленные на каждом предприятии, каждым хозяйствующим субъектом. Т.е.
это совокупная стоимость всех товаров и услуг, произведенных в течение года
на территории страны. Создание ВВП не сводится только к производству
продукции. Одно из определений создания ВВП представлено формулой:
ВВП = СДС + ЧНП,
где СДС – сумма добавленных стоимостей (денежная оценка энергетической
стоимости производства), а ЧНП – чистые налоги на продукты (по сути своей,
это начисление на добавленную стоимость производства, которое возникает в
двойственной финансовой подсети). Налоги не входят в состав потоков
собственно сети производства продукции, т.е. они формируются вне
энергетической стоимости производства. По этой причине налоги назначаются
в сети потоков денежных средств и служат для регулирования распределения и
использования произведенной продукции. В том числе для расходов бюджета
на непроизводственные отрасли (оборону, образование, здравоохранение и
т.д.).
94.
Использование ВВПРаспределение использованного ВВП в 1995–2009 гг. представлено в
таблице по данным Росстата. Порядок публикации определен ССРД МВФ.
Номинальный объем использованного ВВП
в текущих ценах, млрд. руб., до 1998 г. – трлн. руб.
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
1428,5
2007,8
2342,5
2629,6
4823,2
7305,6
8943,6
10817,5
13243,2
17048,1
21625,4
26903,5
33102,9
41256,0
39016,1
1016,6
1435,9
1776,1
2003,8
3285,7
4476,8
5886,8
7448,8
9024,7
11401,5
14318,9
17629,7
21717,8
27106,7
29131,1
домашних
хозяйств
719,8
1007,8
1235,2
1462,3
2526,2
3295,2
4318,1
5408,4
6540,1
8405,6
10590,0
12887,9
15837,3
19752,8
20979,5
государственного
управления
272,5
391,4
493,5
492,6
703,2
1102,5
1469,9
1913,3
2330,6
2847,5
3590,7
4589,2
5698,2
7142,0
7922,7
некоммерческих
организаций,
обслуживающих
домашние
хозяйства
24,3
36,7
47,4
48,9
56,3
79,1
98,8
127,1
154,0
148,4
138,2
152,6
182,3
211,9
228,9
Валовое
накопление
363,4
475,2
514,8
393,5
715,3
1365,7
1963,1
2170,5
2755,1
3558,9
4338,7
5748,8
8032,8
10536,1
7002,1
валовое
накопление
основного
капитала1)
301,1
401,6
428,5
424,7
693,9
1232,0
1689,3
1938,8
2432,3
3130,5
3836,9
4980,6
6983,2
9200,3
7863,2
изменение
запасов
материальных
оборотных
средств
62,3
73,6
86,3
-31,2
21,4
133,7
273,8
231,7
322,8
428,4
501,8
768,2 1049,6 1335,8 -861,1
Валовой
внутренний
продукт
в том числе:
Расходы
конечное
потребление
на
Чистый экспорт
48,5
84,8
51,6
175,4
822,2
1463,1
1133,7
1167,5
1502,0
2086,5
2959,0
3422,5
2847,2
3793,4
2855,8
Экспорт
418,4
523,5
579,3
821,0
2084,6
3218,9
3299,6
3813,7
4655,9
5860,4
7607,3
9079,3
10032,8
12926,8
10861,8
Импорт
369,9
438,7
527,7
645,6
1262,4
1755,8
2165,9
2646,2
3153,9
3773,9
4648,3
5656,8
7185,6
9133,4
8006,0
0,0
11,9
0,0
56,9
0,0
0,0
-40,0
30,7
-38,6
1,2
8,8
102,5
505,1
-180,2
27,1
Статистическое
расхождение
1)
включая чистое приобретение ценностей
95.
Распределение при использовании ВВПиспользование
ВВП
в
социально-экономической
Использование ВВП (распределение) представлено формулой:
системе.
ВВП = КП + ВН + ЧЭ.
В состав данной формулы входят:
расходы на конечное потребление КП = ДХ + ГУ + НКООДХ, которые
включают в себя:
o ДХ – расходы домашних хозяйств,
o ГУ – расходы государственного управления,
o НКООДХ
–
расходы
некоммерческих
организаций,
обслуживающих домашние хозяйства (эта величина сравнительно
мала).
валовое накопление ВН = ВНОК + ЗМОС включает в себя:
o ВНОК – валовое накопление основного капитала,
o ЗМОС – изменение запасов материальных оборотных средств;
чистый экспорт ЧЭ = Э – И, включает в себя:
o Э – экспорт, И – импорт.
Здесь возникает проблема измерителей, поскольку в действующей отчетности операции
ВЭД выражены в иностранной валюте (долларах США), а все предыдущие – в национальной
валюте (рублях). Работа транспорта выражается в тонно-километрах, что также нельзя
суммировать с рублевыми показателями. Отечественными учеными предложена единица
измерения работы транспорта, названная «тран», учитывает скорость и стоимость
транспортировки. Это позволяет сравнивать результаты работы транспорта с другими
отраслями
96.
Формирование ВВП по источникам доходовФормирование ВВП по источникам доходов — суммируются доходы
населения, корпораций, проценты по сбережениям, доходы государства от
предпринимательской деятельности, а также в виде налогов на производство и
импорт, амортизационные отчисления. Пример ВВП России по источникам
доходов представлен в таблице по данным Росстата.
Формирование ВВП по источникам доходов
в текущих ценах – млрд. рублей
2002
2003
2004
2005
2006
2007
2008
2009
10830,5
13243,2
17048,1
21625.4
26903.5
33102.9
41256.0
39016.1
5065,1
6231,4
7845,0
9474.3
11985.9
15452.8
19510.6
20222.4
на производство и импорт
1845,8
2110,2
2872,7
4244.5
5381.8
6334.3
8180.3
6529.5
валовая прибыль экономики
и
валовые
смешанные
доходы
3919,6
4901,6
6330,4
7906.6
9535.8
11315.8
13565.1
12264.2
Валовой
продукт
внутренний
в том числе:
оплата
труда
наемных
работников
(включая
скрытые оплату труда и
смешанные доходы)
чистые налоги
Источник – Росстат (www.gks.ru).
97.
Скорость оборота денег в экономике России1996 г.
1997 г.
1998 г.
1999 г.
2000 г.
2001 г.
2002 г.
2003 г.
2004 г.
2005 г.
2006 г.
2007 г.
2008 г.
2009 г.
2010 г.
2011 г.
2012 г.
2013 г.
2014 г.
2015 г.
2016 г.
2017 г.
2018 г.
ВВП,
млрд. руб.,
до 1998 г.
– трлн.
руб.
Денежная
масса
(M2), на
конец года
Скорость
оборота
M2
Наличные
деньги
(МО)
2008
2343
2630
4823
7306
8944
10831
13208
17027
21610
26917
33248
41277
38807
46308,5
55967,2
68163,9
73133,9
79199,7
83101,1
86010,2
92089,3
103626,6
288,3
374,1
453,7
714,6
1154,4
1612,6
2134,5
3212,6
4363,3
6044,7
8995,8
13272,1
13493,2
15267,6
20011,9
24483,1
27405,4
31404,7
31 615,7
35 179,7
38 418,0
42 442,2
47 108,1
6,965
6,263
5,797
6,749
6,329
5,546
5,074
4,111
3,902
3,575
2,992
2,505
3,059
2,542
2,314
2,438
2,442
2,261
2,427
2,257
2,239
2,170
2,200
103,8
130,4
187,7
266,1
418,9
583,8
763,2
1147,0
1534,8
2009,2
2785,2
3702,2
3794,8
4038,1
5062,7
5938,6
6430,1
6985,6
7171,5
7239,1
7 714,8
8 446,0
9 339,0
Скорость
оборота
МО
Безналичн
ые
денежные
средства
M2 - МО
Скорость
оборота
M2 - МО
19,345
17,968
14,012
18,125
17,441
15,320
14,192
11,515
11,094
10,756
9,664
8,981
10,877
9,610
9,147
10,053
10,408
10,166
10,869
11,162
11,149
10,903
11,096
184,5
243,7
266
448,5
735,5
1028,8
1371,3
2065,6
2828,5
4035,5
6210,6
9569,9
9698,4
11229,5
14949,2
18544,5
20975,3
24419,1
24 444,2
27 940,6
30 703,2
33 996,2
37 769,1
10,883
9,614
9,887
10,756
9,933
8,694
7,899
6,394
6,020
5,355
4,334
3,474
4,256
3,456
3,098
3,219
3,191
2,908
3,125
2,828
2,801
2,709
2,744
Внешний
долг, на
конец
года,
млрд.
долл.
153,0
182,8
188,4
177,7
159,9
146,3
152,3
186,0
213,5
257,2
313,2
463,9
480,5
467,2
488,9
545,2
636,4
728,9
599,9
518,5
511 752
518 103
453 749
Доля
внешнего
долга в
ВВП, %,
на конец
года
42,36%
46,50%
147,93%
99,48%
61,63%
49,30%
44,69%
41,37%
34,75%
33,88%
30,79%
34,24%
41277
38807
46309
55800
62599
Основные показатели экономики: ВВП, денежная масса, внешний долг, экспорт и
импорт, золотовалютные резервы, инфляция, курсы валют оказывают влияние на
возможности развития производства. Рассмотрим на примере реальных значений
показателей в новейшей истории России.
97
98.
ВВП стран по паритету покупательной способности• ВВП по ССРД МВФ используется для международных
сопоставлений.
• Для этих целей рассчитывается реальный объём ВВП
разных стран (по паритету покупательной способности,
в долларах США) или ВВП по ППС.
• В экономической теории ППС означает, что
покупательная способность некоторой суммы на одном
рынке должна быть равна покупательной способности
этой же суммы на рынке другой страны, если перевести
данную сумму по текущему обменному курсу в
иностранную валюту.
• Приведение к одной валюте показывает, какой
реальной стоимости (выраженной в измеримых
величинах, например в энергетических показателях)
соответствует произведенная в стране продукция.
99.
Развитие наук и циклы Кондратьева• Развитие творческой деятельности и научной мысли привело к
тому, что наука стала основной движущей силой научнотехнического прогресса и развития всей современной
цивилизации.
• Особое значение здесь имеют научные достижения,
определившие направления развития мирового сообщества.
• Развитие наук идет по прагматичному пути, что существенно
повышает практическую роль исследований в деятельности
человека.
• Сейчас настало время широкого использования достижений
самых различных научных отраслей знаний, которые были
получены при дифференцированном развитии наук.
• Это приводит к интеграции научных дисциплин, обусловившей
возникновение таких наук, как теория систем, теория
управления, кибернетика, бионика, инноватика и др.
• Именно на стыке наук и в интегрированных областях знаний все
чаще делаются новые научные открытия.
100.
Циклы Кондратьева• Процессы дифференциации и интеграции наук и объективная
необходимость внедрения в реальную действительность достижений
науки наиболее ярко отражают научную и практическую роль
исследований в деятельности человека на Земле.
• В совокупности результаты научных исследований, оказывают
влияние на всю цивилизацию, геополитику, безопасность стран,
социальную, экономическую и техническую политику государств,
общественное, социальное и профессиональное положение людей.
• Результаты познавательной деятельности определили реализацию в
мировой экономике соответствующих технологических укладов —
циклов, существенно изменявших человеческую жизнь на планете.
• На основе теории длинных волн Н. Кондратьева ряд ученых выделяет
следующие циклы развития научно-технического прогресса,
связанные с внедрением в практику результатов научных
исследований.
• Первый цикл (1785—1835) — промышленный переворот в
Великобритании, обусловленный внедрением новых технологий в
текстильной промышленности и использованием гидроэнергии
(пруды и плотины).
101.
Циклы КондратьеваВторой цикл (1830—1890) — создание парового двигателя и последующее
использование и развитие на его базе железнодорожного и водного
транспорта, механического и машиностроительного производства.
Третий цикл (1885—1940) — изобретение электродвигателя, производство и
использование в промышленности и в быту электроэнергии. Возникла
тяжелая электроэнергетическая и электротехническая, сталелитейная и
другие виды промышленности. Открытия в области химии позволили
выделить самостоятельный раздел — неорганическую химию, а изобретения
в области двигателей внутреннего сгорания способствовали созданию
автомобиля, радиосвязи, телеграфа, самолетов и соответствующих отраслей
промышленности. В крупных странах стали развиваться банковское дело и
концентрироваться финансовые капиталы.
Четвертый цикл (1935—1990) — использование нефти и продуктов ее
переработки, газа, развитие энергетики, дизелей и двигателей внутреннего
сгорания и их массовое изготовление, прогресс производства синтетических
материалов, космических средств связи. В этот период становится массовым
производство автомобилей, тракторов, самолетов, радиолокаторов, ракет,
вооружения (в том числе атомного), атомная энергия используется в мирных
целях, появляются мощные транснациональные компании, осуществляющие
прямые инвестиции в экономику различных стран.
102.
Циклы КондратьеваПятый цикл (1985—2035) — научно-технические достижения в
микроэлектронике, информатике и электронных сетях Интернета, инноватике,
биотехнологии, генетике, материаловедении, авиакосмонавтике и в области
освоения космического пространства, спутниковых телекоммуникаций, тонких
химических технологий, термоядерного синтеза, экологии; гуманизация
образования; социально-ориентированная организация предпринимательства (с
использованием различных форм собственности, интеграции в мировое
хозяйство), управления, производства (на основе его индивидуализации для
достаточно обеспеченных потребителей и массовости для населения
развивающихся стран) и т.п.
Среди основных составляющих, определяющих пятый технологических цикл,
важнейшими являются достижения в области организации управления, при
обеспечении успеха которых первостепенную роль играют результаты
фундаментальных и прикладных исследований СУ.
Законы рынка формируют в настоящее время жесткую конкуренцию, в условиях
которой от менеджеров организаций требуется принятие новых эффективных
управленческих решений, связанных, как правило, с управлением инновациями
и соответственно проведением работ исследовательского характера.
При этом количество принимаемых решений постоянно увеличивается, что
обязывает менеджеров приобретать знания и умения по исследованию СУ и
широко использовать их в своей практической деятельности.
103.
Интеллектуальная собственность• Джо Стиглиц, лауреат Нобелевской премии: Интеллектуальная
собственность является одним из важнейших вопросов
глобализации, в условиях, когда мир движется к экономике знаний.
• Главное значение интеллектуальной собственности состоит в
распределении выгоды от работы в новой экономике.
• Венецианский патентный статут от 19 марта 1474 года установил в
Венецианской республике первую законную патентную систему в
Европе и считается самой ранней кодифицированной патентной
системой в мире.
• «В этом городе, из-за его величия и изобилия приходят люди из
разных мест и самых творческих умов, способные придумывать и
изобретать всевозможные гениальные изобретения.
• И если будет обеспечено, что изобретенные ими дела и
изобретательства, другие, увидев их, не смогут сделать их, люди
такого рода будут направлять свои мысли, изобретать и делать
вещи, которые будут не малой полезности и пользы нашему
государству.
103
104.
Интеллектуальная собственность, история• 22.05.2021
• Поэтому принято решение, что по согласию Совета каждый
человек, который совершит в этом городе какое-либо новое
гениальное изобретение, не совершенное до сих пор в нашем
государстве, как только оно будет доведено до совершенства,
чтобы его можно было использовать, должен уведомить об этом.
• Запрещено любому другому лицу на любой территории и в
любом месте создавать любые другие приспособления в форме и
подобии этого без согласия и лицензии автора в течение десяти
лет.
• Между 1474 и 1788 годами венецианский Сенат выдал около 2000
патентов: 28 между 1474 и 1500, 593 между 1500 и 1600, 605
между 1600 и 1700 и 670 между 1700 и 1788.
• Венецианские патенты были предоставлены бесплатно, «что
объясняет их относительно высокое количество». Чтобы сравнить
это с современными патентами, USPTO получил 615 243
патентных заявки только в 2014 году.
104
105.
Без денег цивилизация существовать не может• Последствия сокращения американской денежной массы после
Гражданской войны сравнили с гибелью Римской империи:
• "Катастрофический по своим последствиям развал Древнего Рима и
приход Темного Средневековья был вызван снижением денег в
обращении и падением цен... Без денег цивилизация существовать
не может. С сокращением предложения денег она начинает угасать, и
если беде не помочь, может и вовсе погибнуть...
• В начале первого тысячелетия металлические деньги всей Римской
империи равнялись денежному эквиваленту US$1.000.000.000. К
концу XV столетия денежная масса всей Европы составляла всего
US$200.000.000... История не знает другого такого катастрофического
спада от просвещения к варварству, чем от Римской Империи к
Раннему Средневековью".
• Несмотря на сигналы Комиссии по серебру, Конгресс не предпринял
никаких мер. В 1877 году в США, от Питсбурга до Чикаго, начались
голодные мятежи. Факелы голодающих вандалов вспыхнули до небес
• . В этой ситуации банкиры недолго решали, что делать, - они решили
подождать еще. Теперь, когда денежная система страны до
определенной степени находилась под их контролем, спешить было
некуда.
106.
Денежная система страны• Теперь, когда денежная система страны до определенной степени находилась под их
контролем, спешить было некуда. В том же 1877 году на собрании Американской
Банковской Ассоциации (АБА) они порекомендовали всем ее членам сделать все
возможное, чтобы люди и думать забыли о "зеленых спинках".
• Секретарь АБА Джеймс Бьюэл написал всем членам письмо с призывом подкупать
не только Конгресс, но и прессу: "Желательно делать все,, чтобы поддерживать те
ежедневные и еженедельные издания, особенно сельскохозяйственные и религиозные,
которые будут протестовать против возрождения бумажных денег - "зеленых спинок".
• А также предпринять все возможное, чтобы лишить вашего покровительства
издания, не желающие бороться с правительственной точкой зрения по поводу выпуска
бумажных денег...
• Повторение трюка с выпуском банкнот или эмиссией правительством собственных
денег может обеспечить народ деньгами - и поэтому серьезно подорвет нашу доходную
базу как банкиров и кредиторов... Сейчас же свяжитесь с вашими знакомыми
конгрессменами и заручитесь их поддержкой с тем, чтобы мы могли контролировать
законодательный процесс".
• В результате на Конгресс началось политическое давление с требованием
изменений. В газетах открылась целая PR-кампания. Например, газета New York Tribune
писала 10 января 1878 года следующее: "У нашей страны, наконец, появилась столица.
Сейчас мы проверим, сможет ли Конгресс работать в поте лица". Однако ожидания
банкиров не оправдались.
107.
Кризисы
Конечно, все эти разговоры можно списать на необоснованную
панику, вызванную нестабильностью. Можно предположить,
что разговоры об обвале доллара - всего лишь "утка",
запущенная в интернет с целью ослабить американскую
валюту. Или все-таки слухи имеют под собой основание?
• Кризис дотком компаний (или *.com companies, например,
American.com, и другие) в 90-е годы привел сначала к
небывалому взлету акций интернет компаний, (индекс Nasdac
достиг значения 5030 в марте 2000 г.), а затем обрушился.
• Потери инвесторов (в том числе, обладателей нефтедолларов)
составили до 7 трлн. долларов США к 2001 г. Это случайно
сопровождалось атакой террористов, выходцев с Ближнего
Востока, на башни-близнецы 11 сентября 2001 г.
• Задачей концентрации капиталов было создание
постиндустриального общества. Цикл развития и разрешения
этого кризиса составил около 12 лет. Вместе с тем концентрация
капиталов дала толчок к развитию интернет торговли и других
видов электронной коммерции, что позволило создать
фундамент цифровой экономики.
108.
Кризисы• Следующий цикл возник на базе ипотечных кредитов в США, с
эмиссией ценных бумаг, обеспеченных такими кредитами. Широкая
продажа этих ценных бумаг инвесторам, в том числе в странах ЕС,
поддерживалась высшими рейтингами от авторитетных агентств.
Потери мировой экономики от падения рынка ипотечных ценных
бумаг США оценены суммой более 12 трлн. в 2008-2012 гг.
• В частности, расходы США на преодоление последствий кризиса к
2010 г. оцениваются в 11 трлн. долларов, но около половины
составляют не прямые расходы, а инвестиции, гарантии по займам,
выкуп финансовых активов (ипотечные и коммерческие бумаги), с
целью повысить ликвидность рынков.
• Падение производства и безработица в странах ЕС нанесло удар и по
экономике России, что рассматривалось выше. Задачей этой
концентрации капиталов могло быть создание экономики знаний для
непреодолимого технологического отрыва США от остального мира.
Возможно, что этого пока не получилось.
• Цикл развития и разрешения ипотечного кризиса составил 10-12 лет.
109.
КризисыВ настоящее время заканчивается очередной цикл бурного развития рынка ценных
бумаг, на этот раз на базе достижений генной инженерии и нанотехнологий.
Прошедшие кризисы и тот, который на подходе, укладываются в периоды 10-12 лет, с
учетом последействия. Это соответствует циклам солнечной активности, циклу китайского
гороскопа, и т.д., давая почву для нумерологических и физических теорий.
Источник: http://moneymakerfactory.ru/spravochnik/krizis-ssha-2008/
Цикл развития и разрешения текущего роста также может составить 10-12 лет. Таким
110.
Кризисы• Цифровая экономика может рассматриваться как начало очередного
цикла, который будет, безусловно, способствовать внедрению
достижений научно-технического прогресса в устойчивое развитие
страны и внедрение цифровых продуктов во все сферы жизни на
основе экономики знаний.
• Однако могут возникнуть неожиданные последствия, которые
следовало бы заранее предвидеть, подготовить ответы, ресурсы и
мероприятия.
• В соответствии со сложившейся периодичностью, очередной кризис
возникнет в 2029-2030 гг. Вам эти даты ничего не напоминают?
• Венчурный капитализм
• Истоки венчурного капитализма можно отыскать в первой половине
XX века: предприниматели США вкладывали деньги в проекты
(термина «стартап» еще не было), имеющие шансы на прибыльность
не сегодня и не завтра, а в будущем.
• Этим занимались Рокфеллеры, Вандербильты, Уитни, Варбурги. Но
профессиональный венчурный капитализм возник лишь после
принятия в США закона 1958 года «Об инвестициях в малый бизнес».
На основе этого закона специальная администрация начала
лицензировать «инвестиционные компании для малого бизнеса».















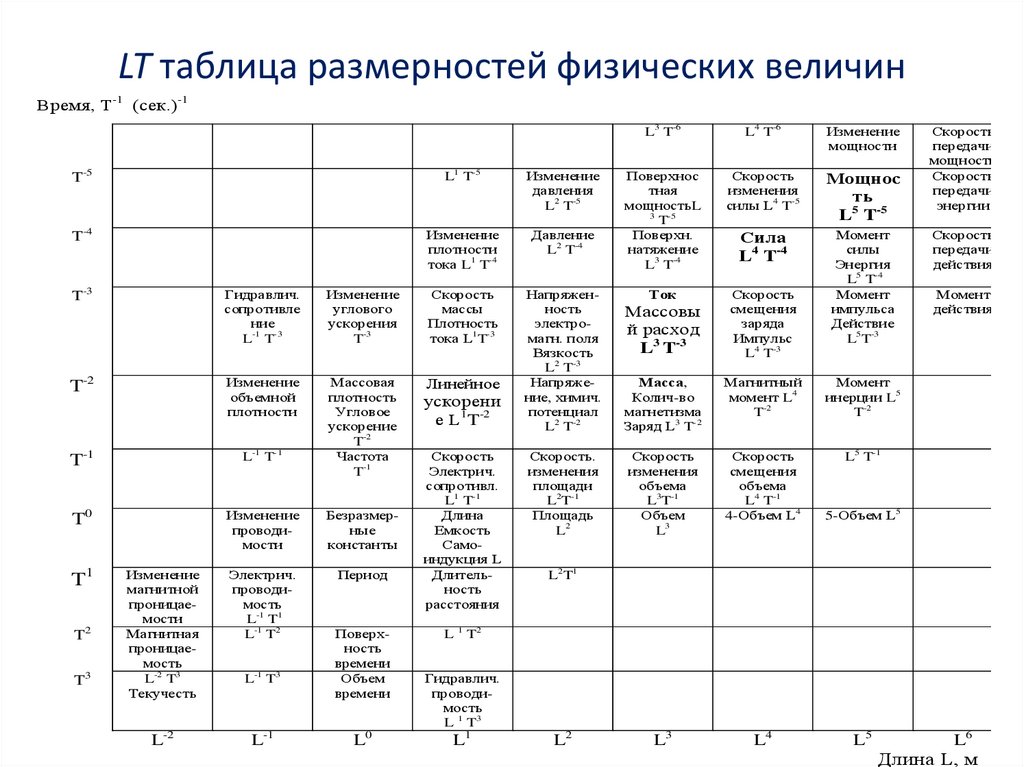






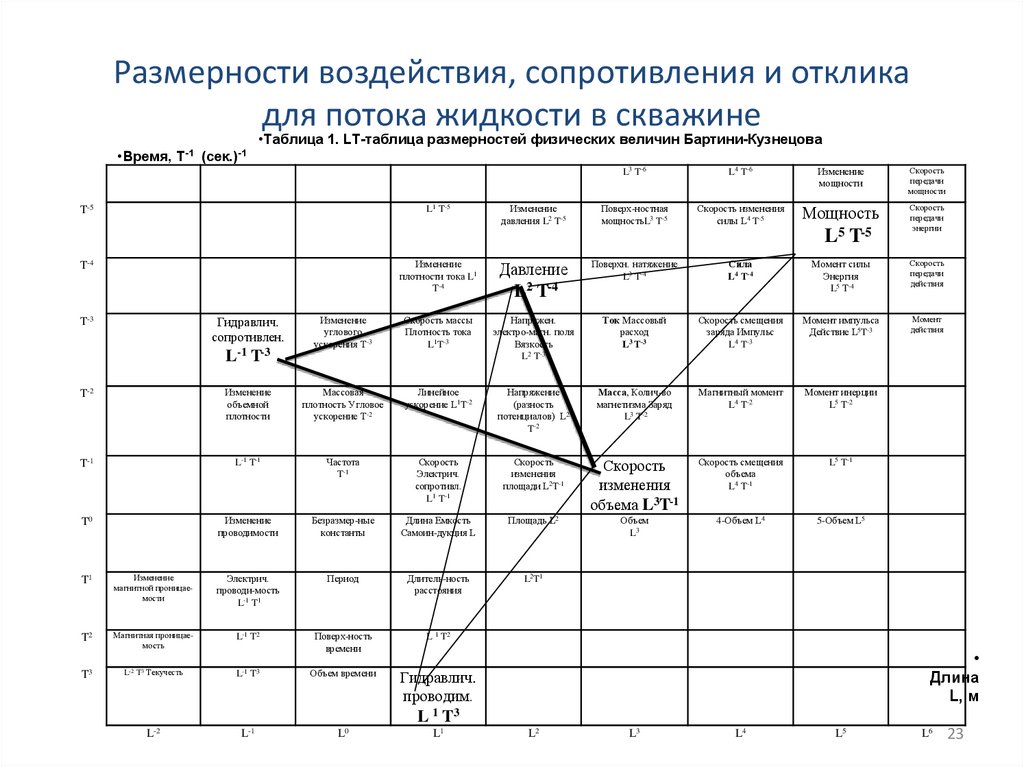












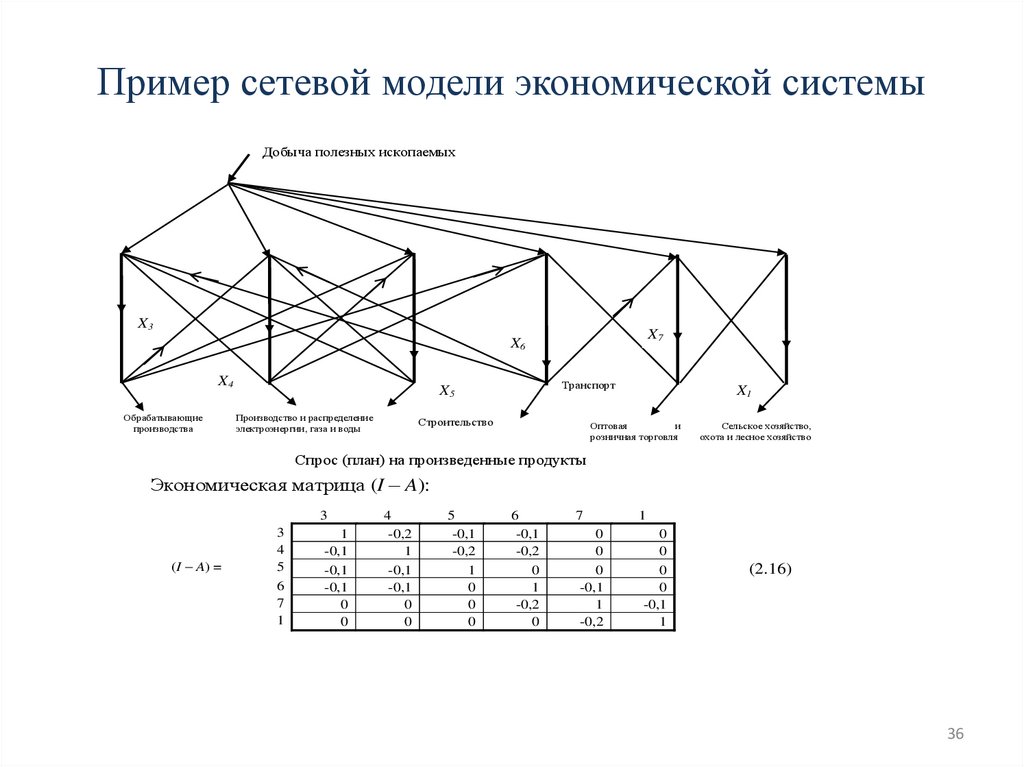
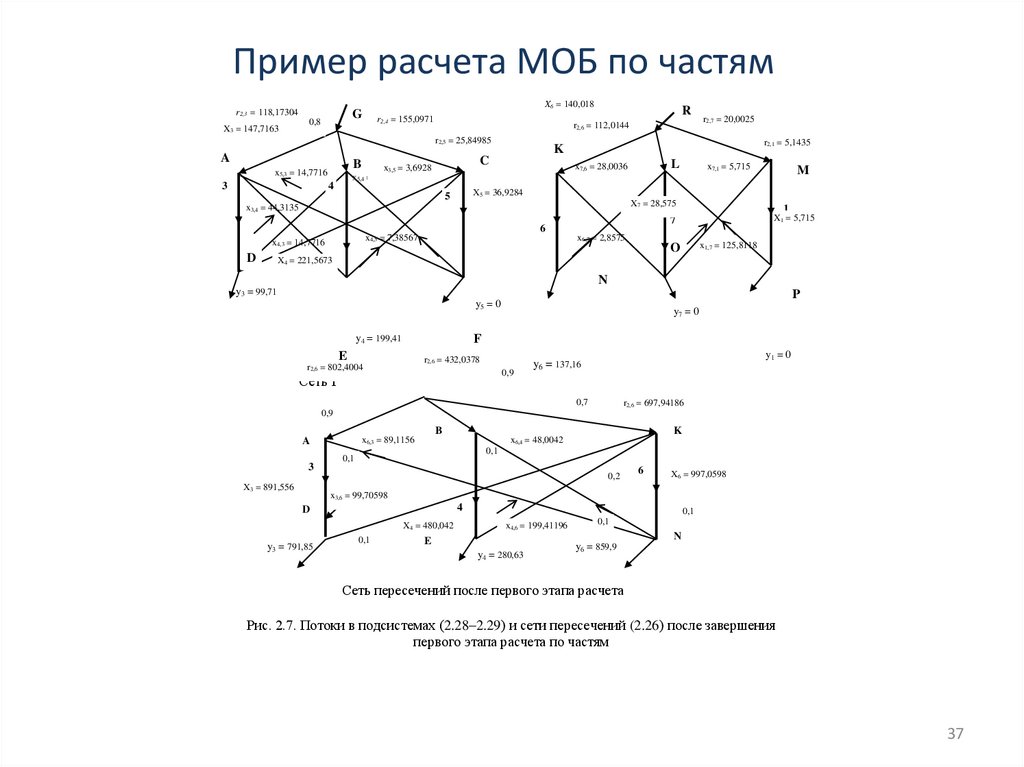
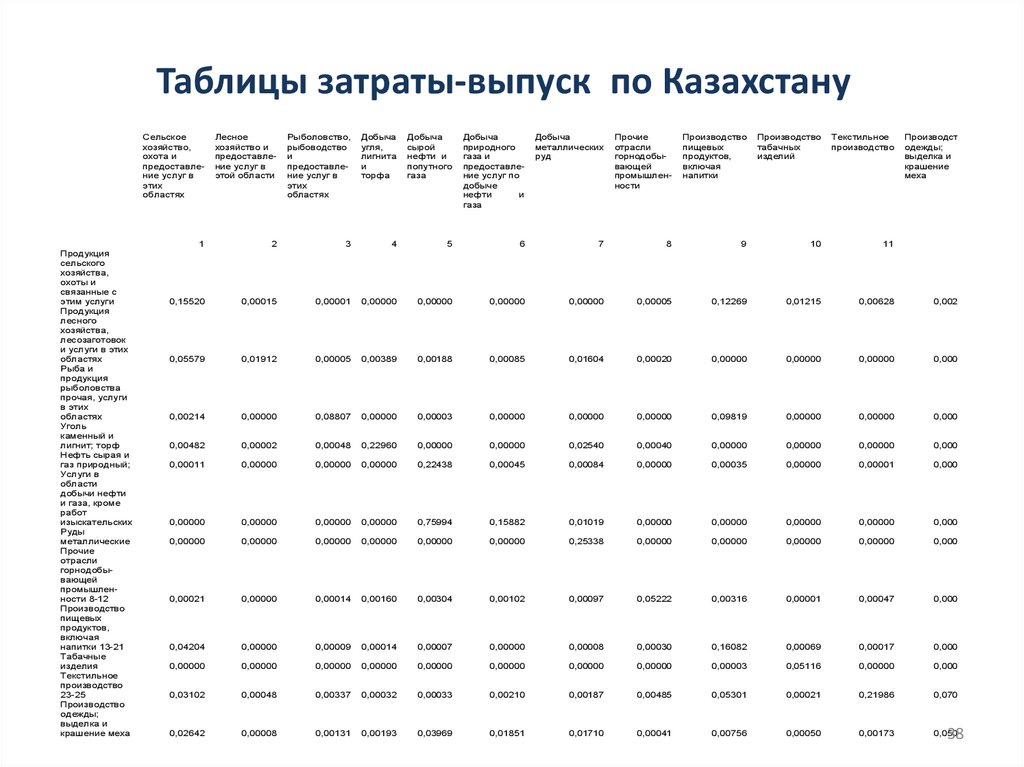
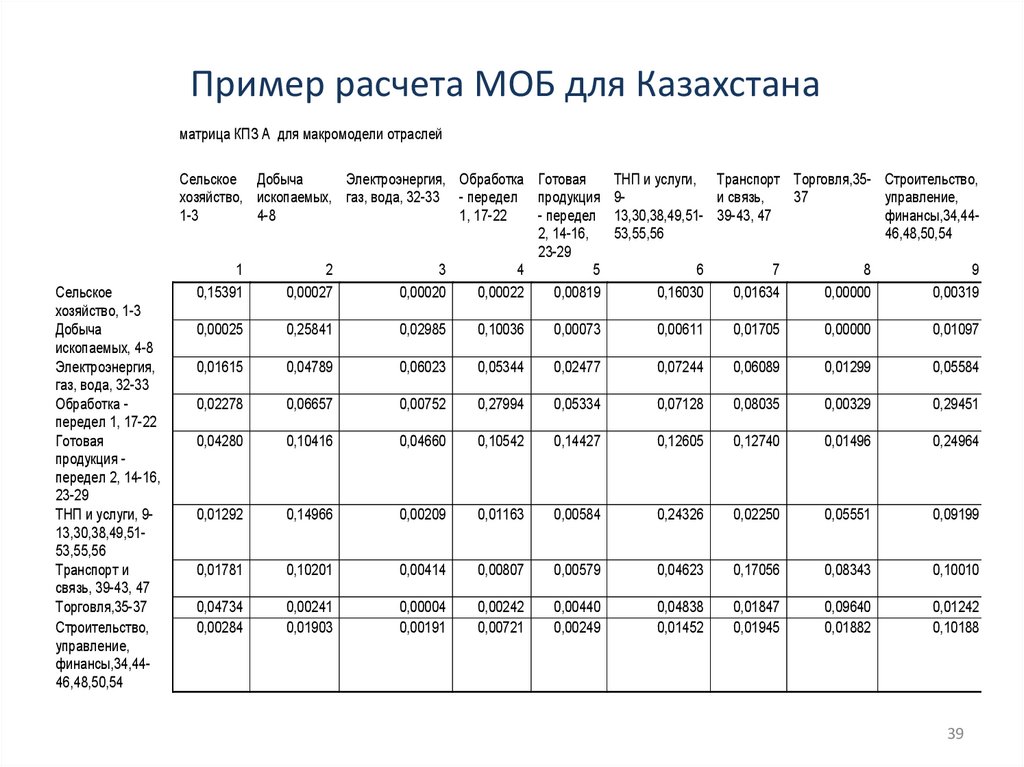
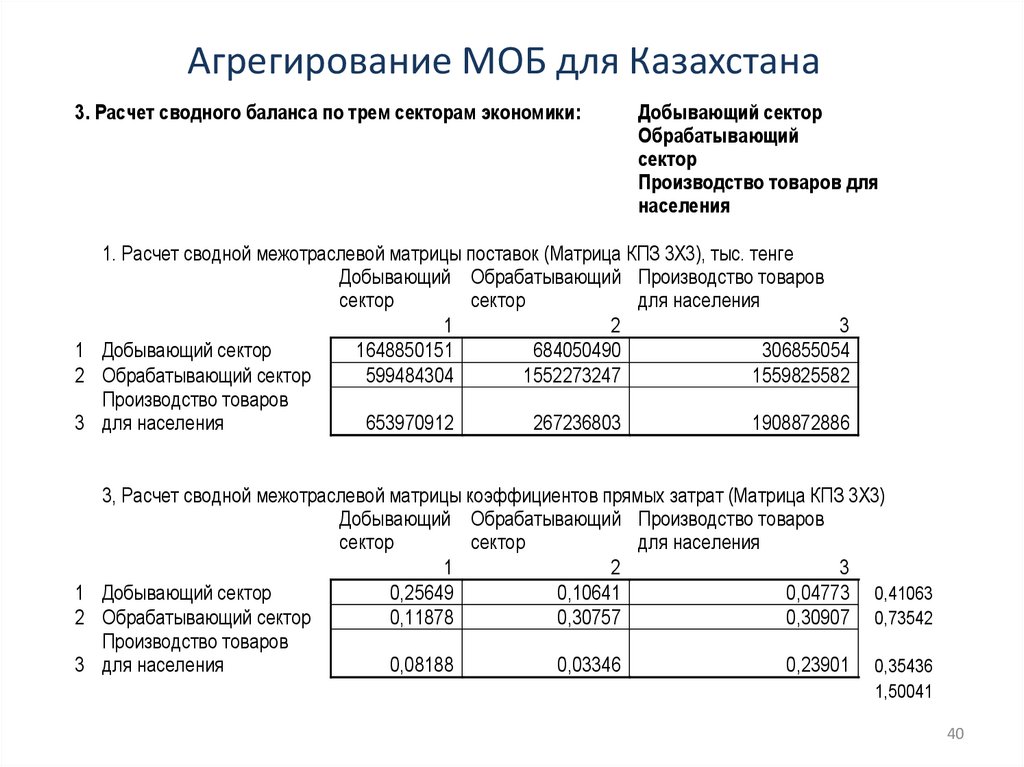
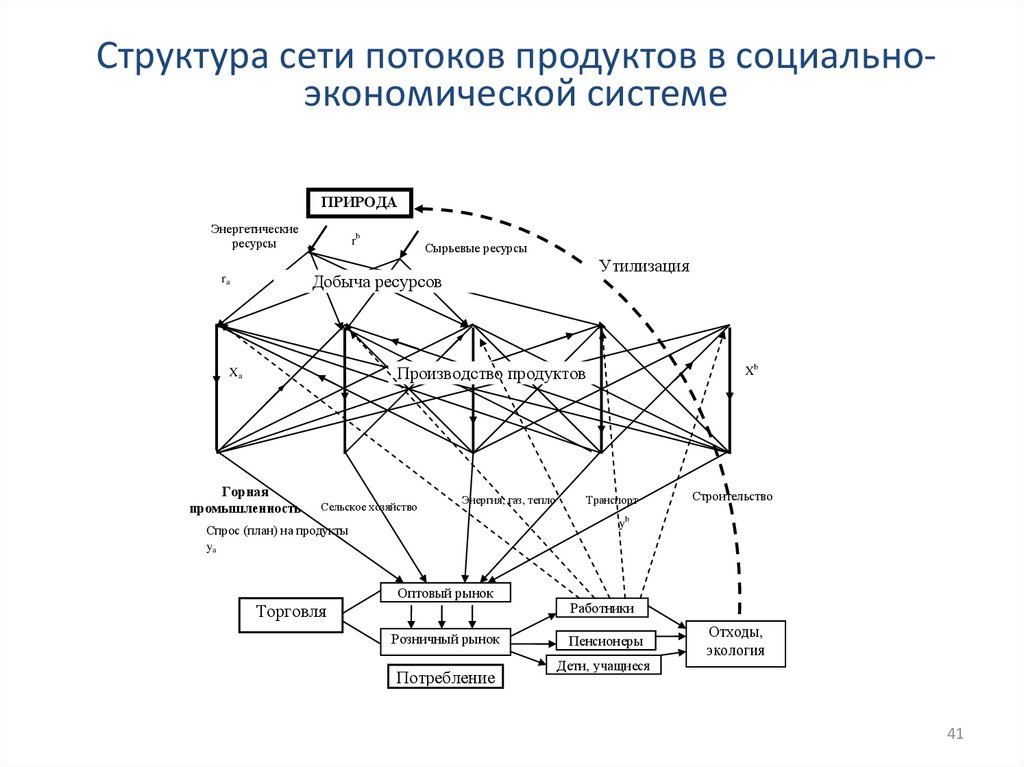

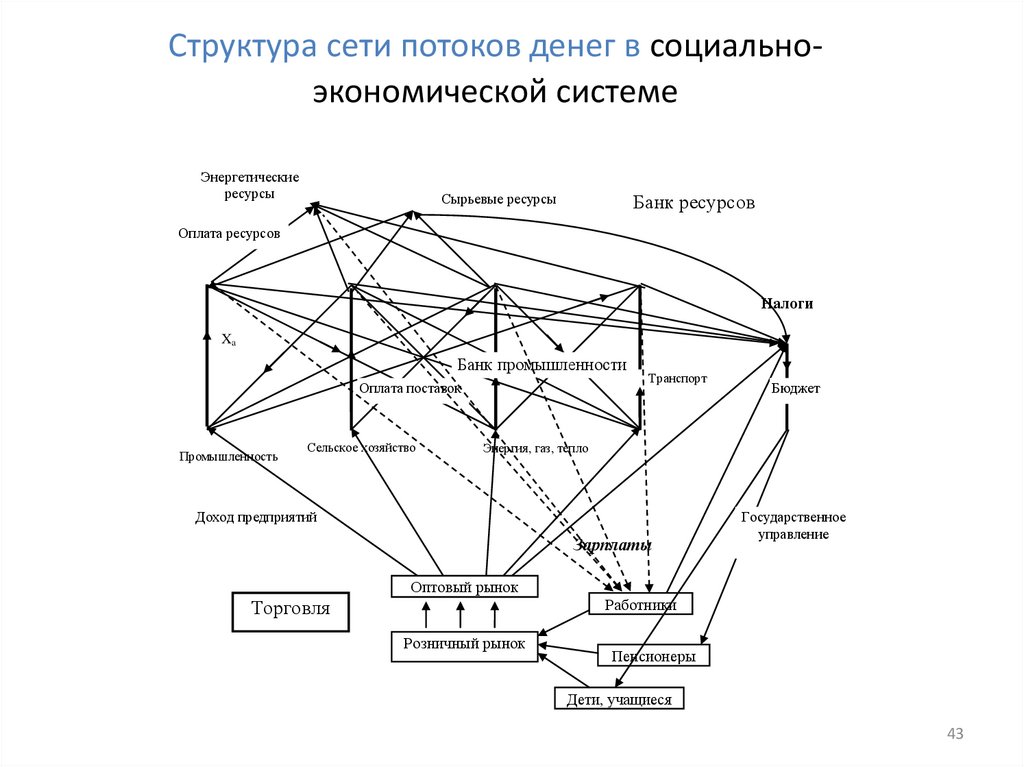







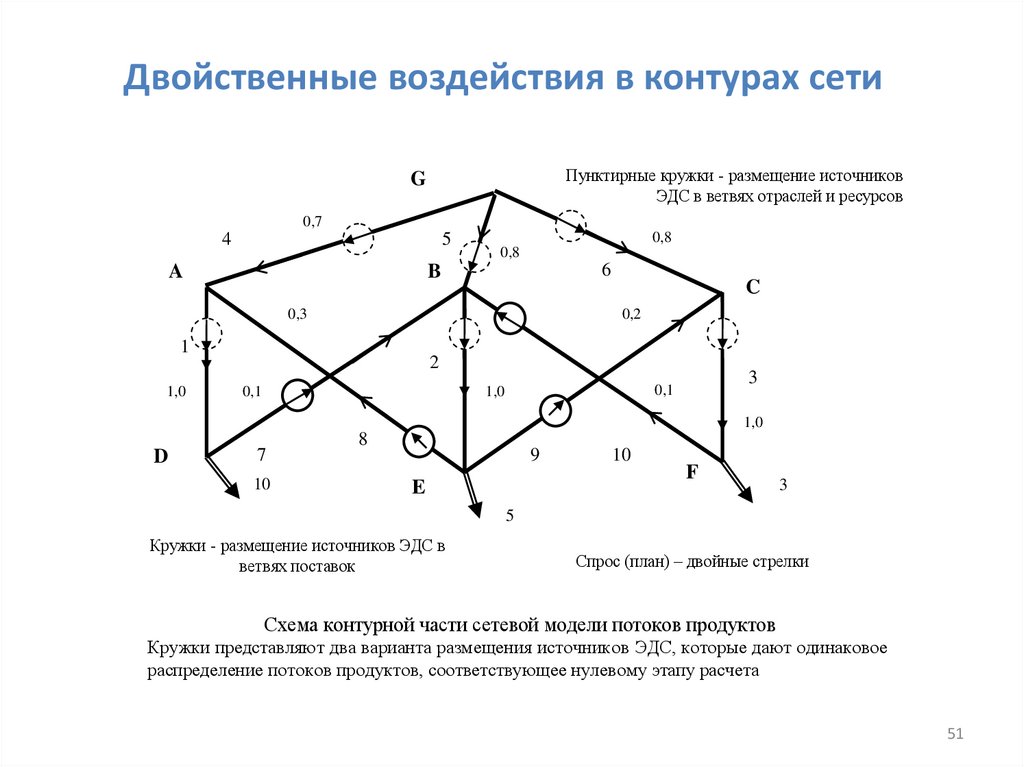






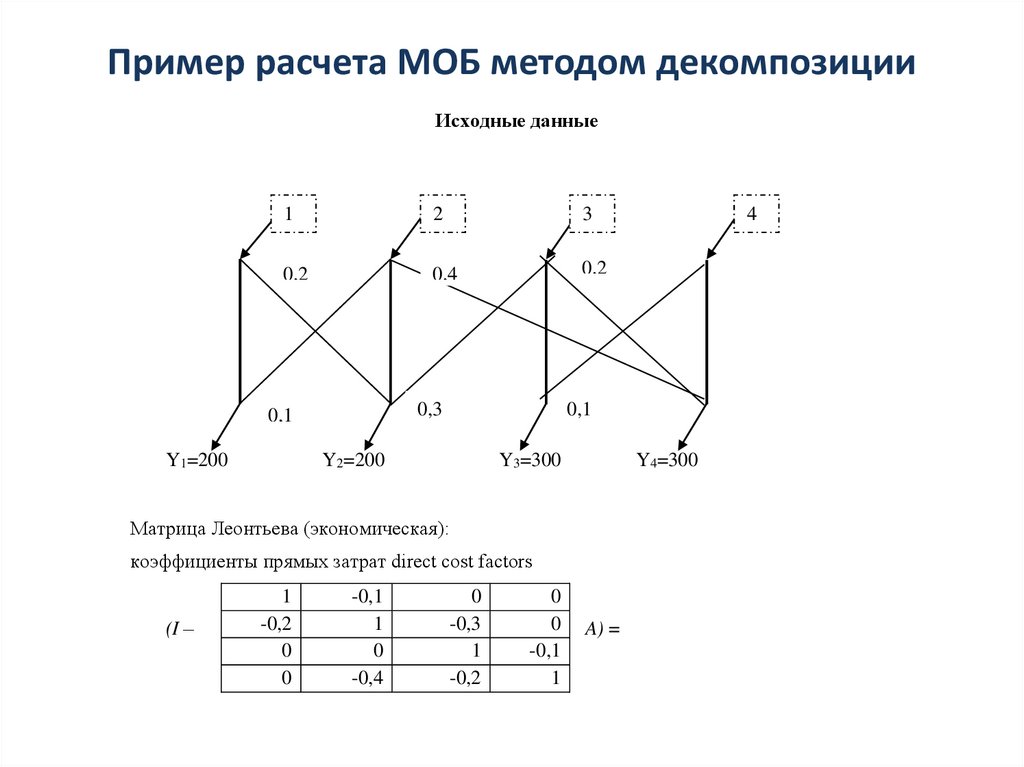


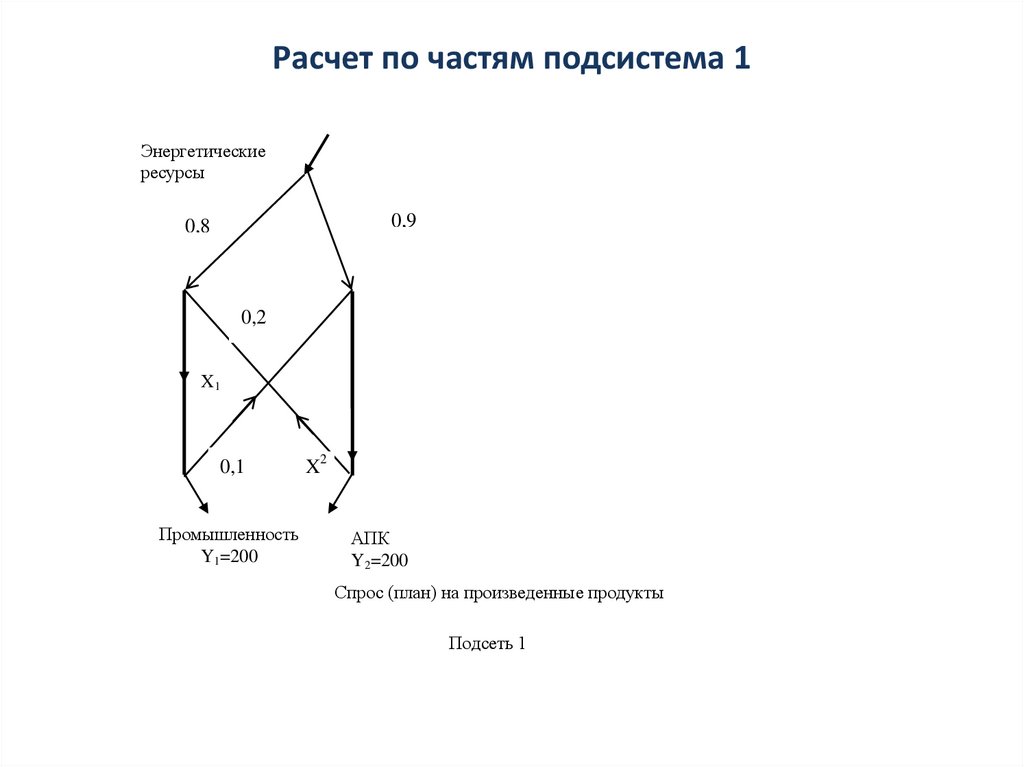

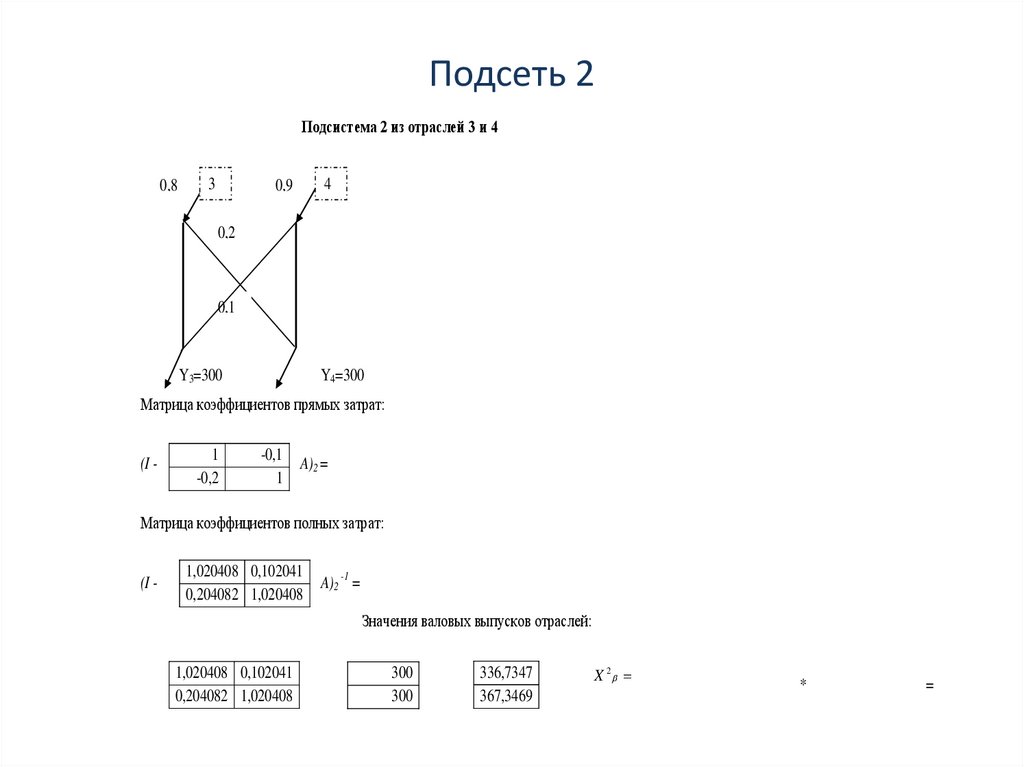
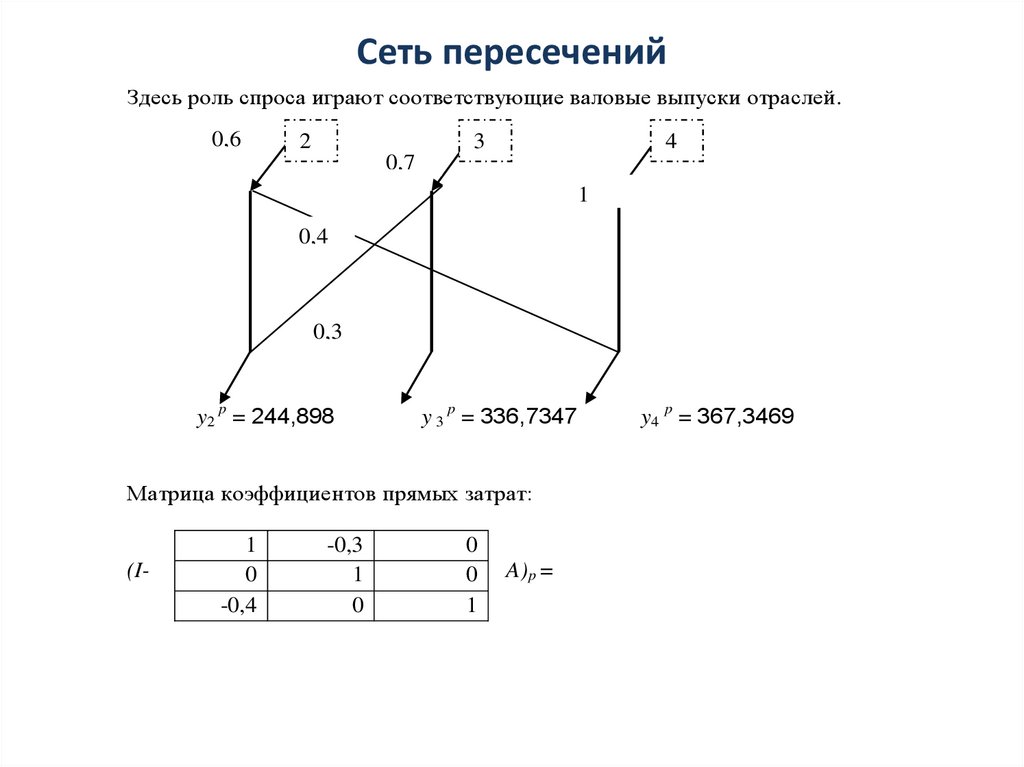



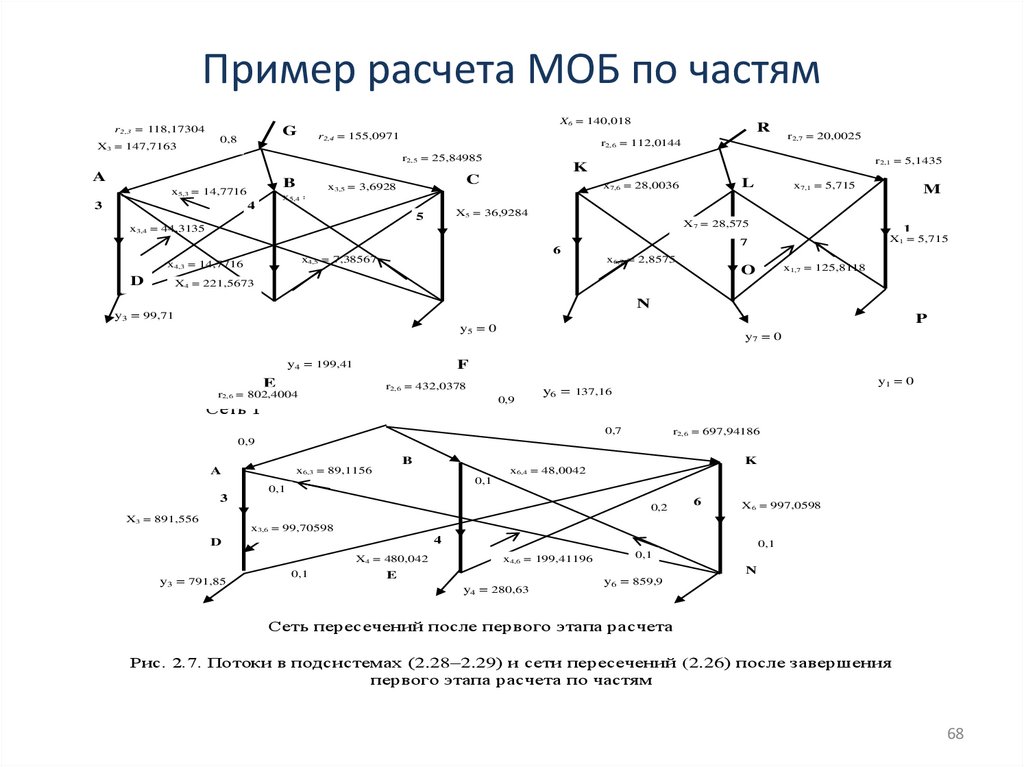






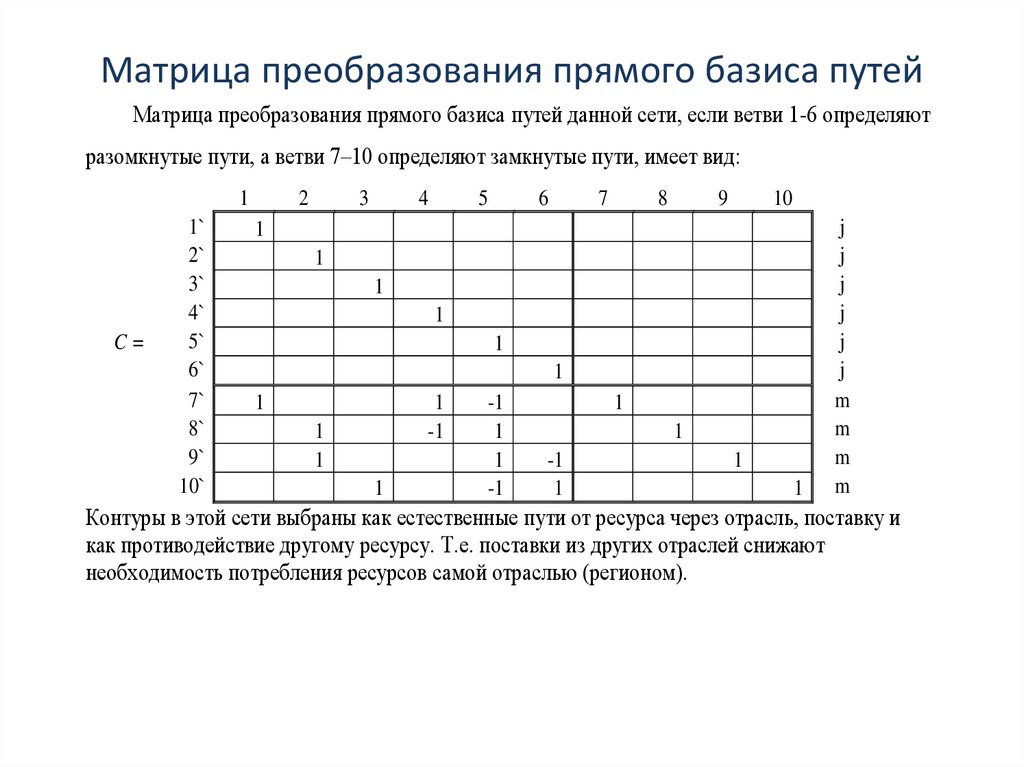



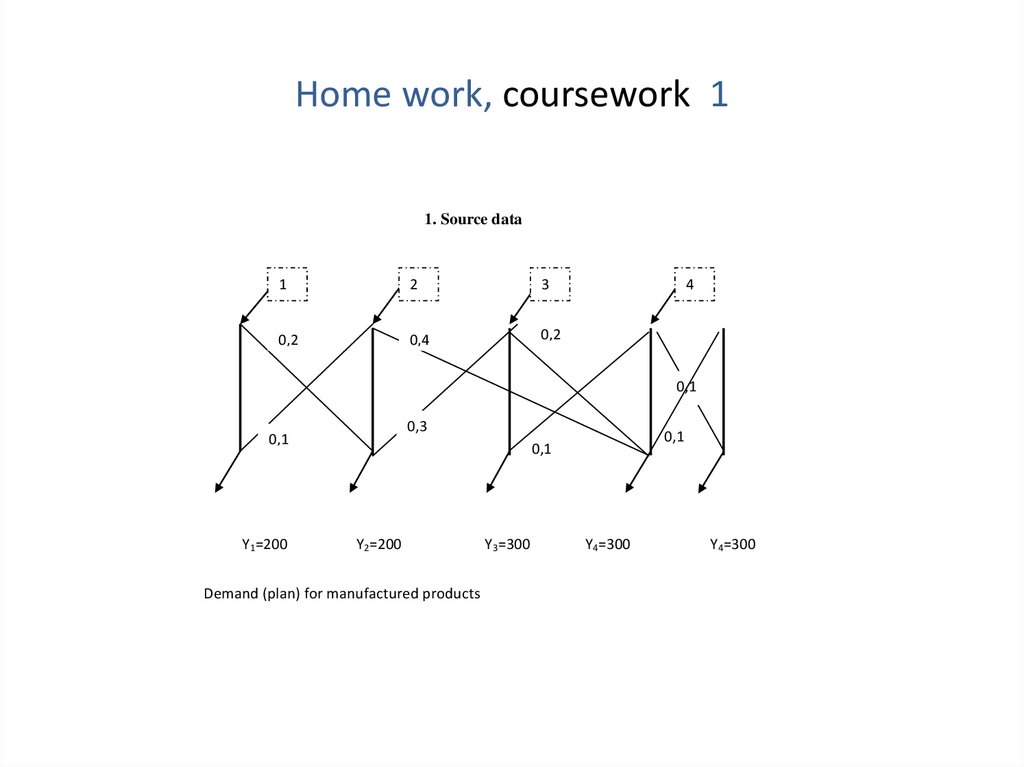
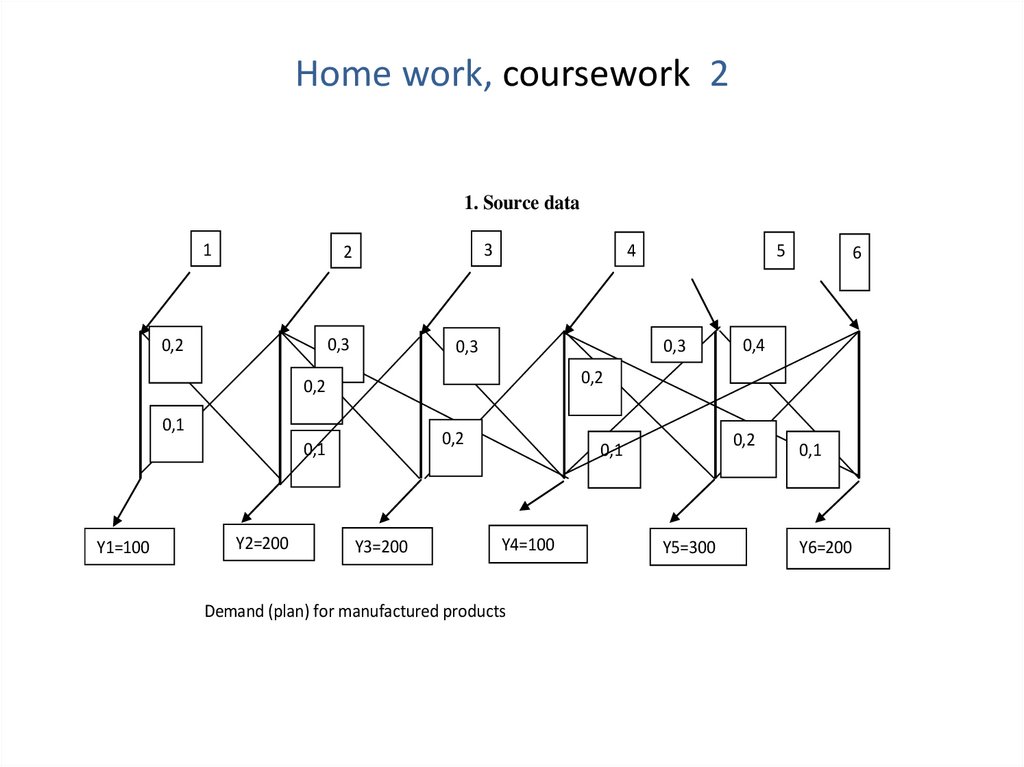
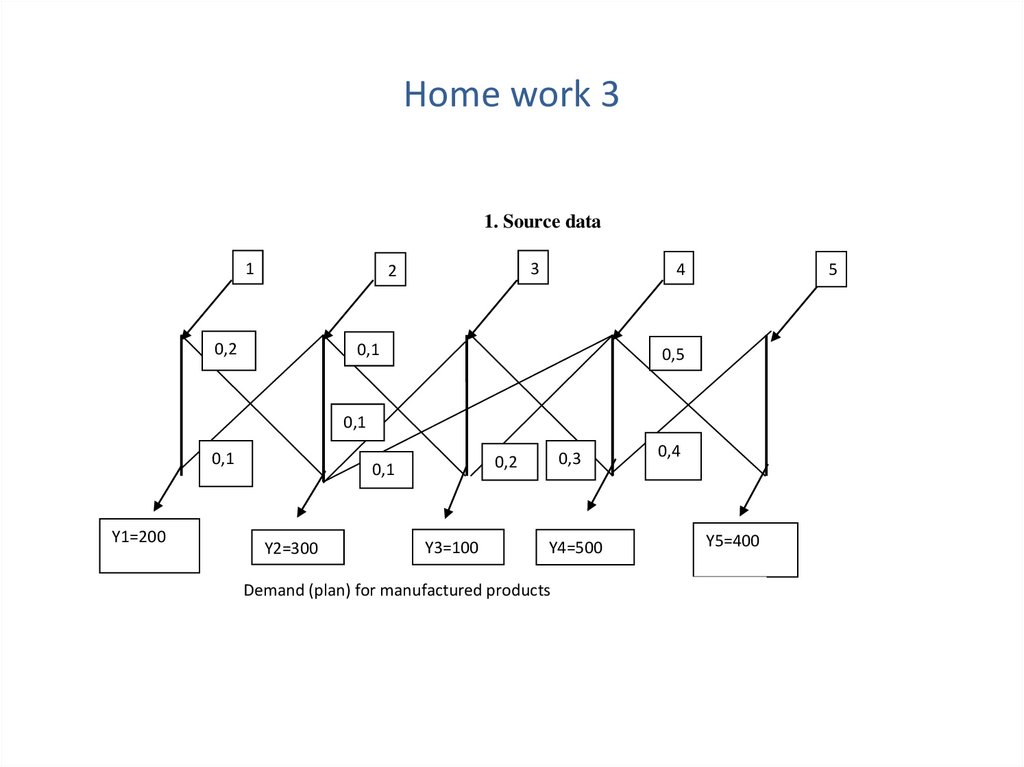
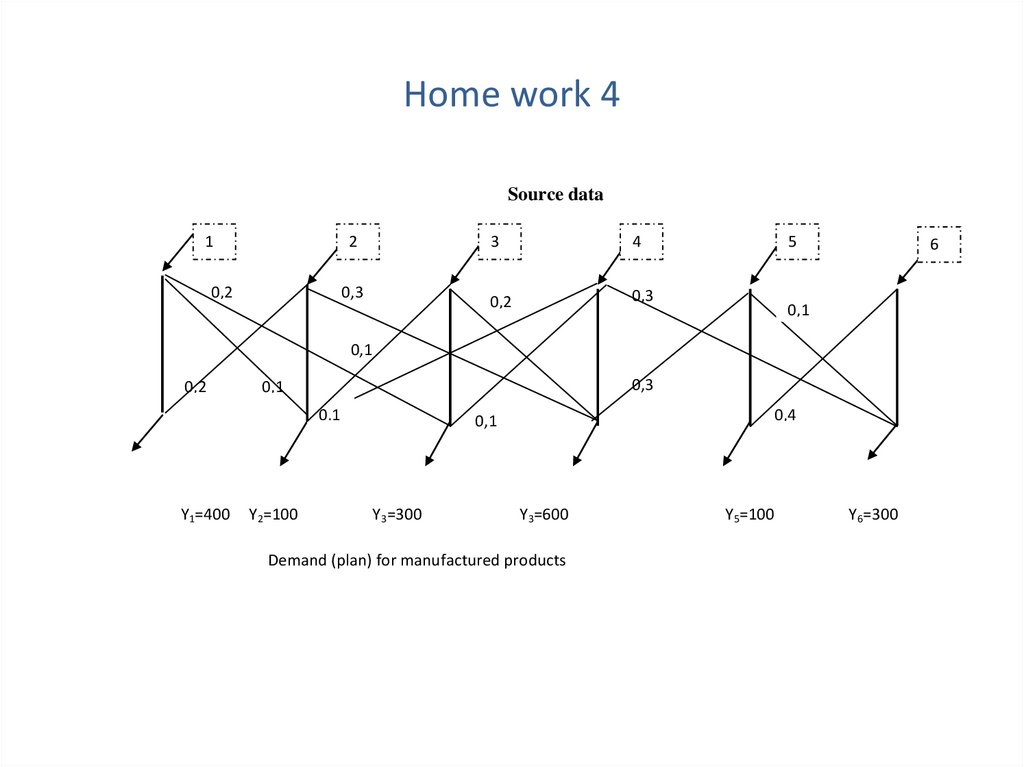
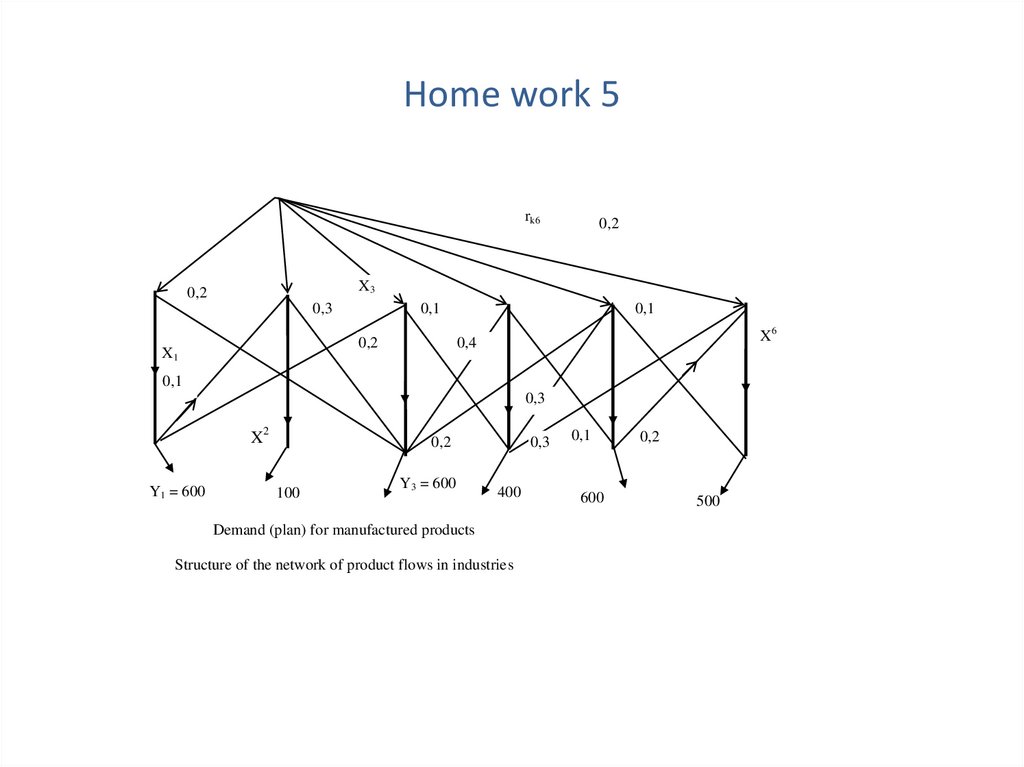
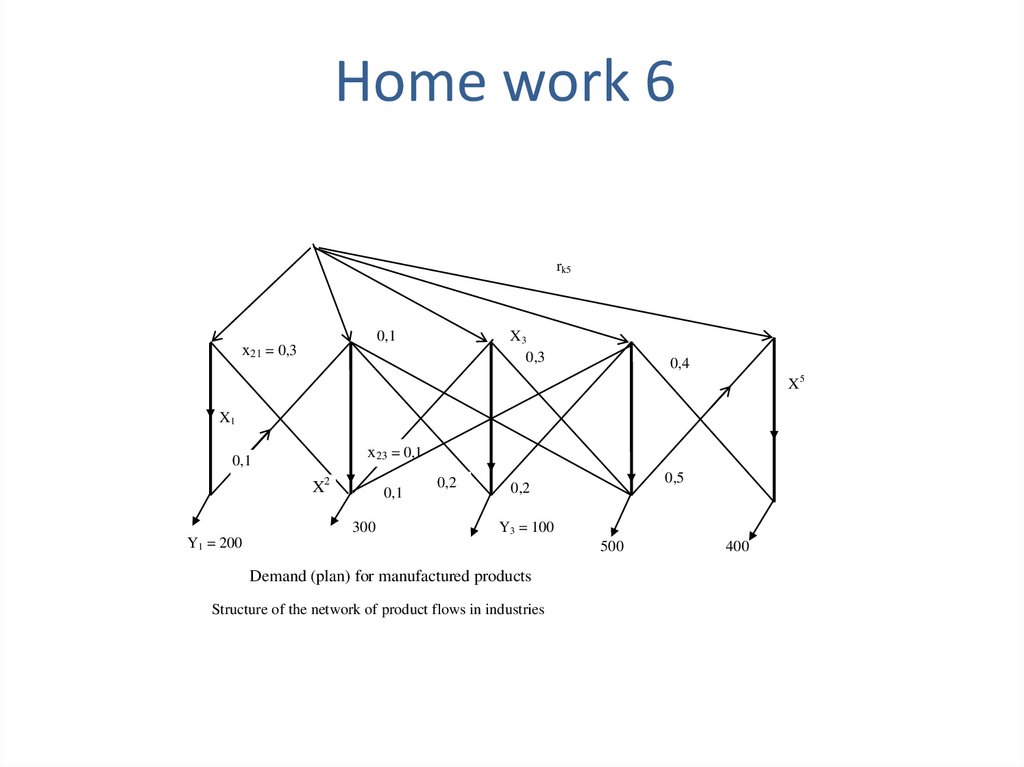
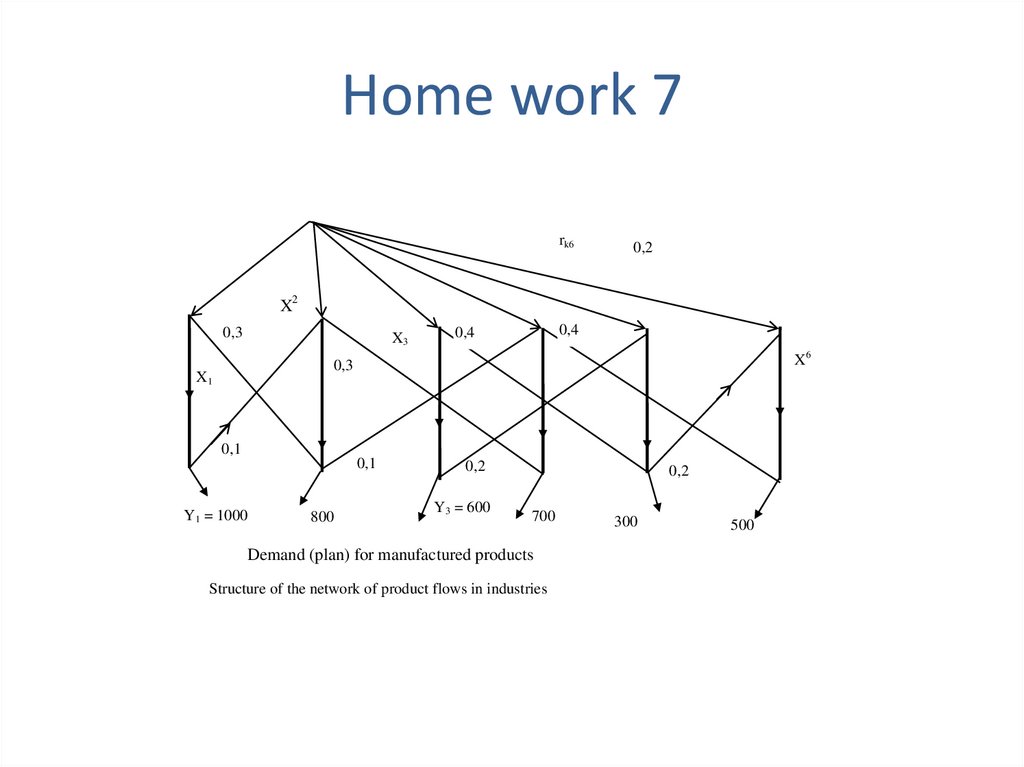


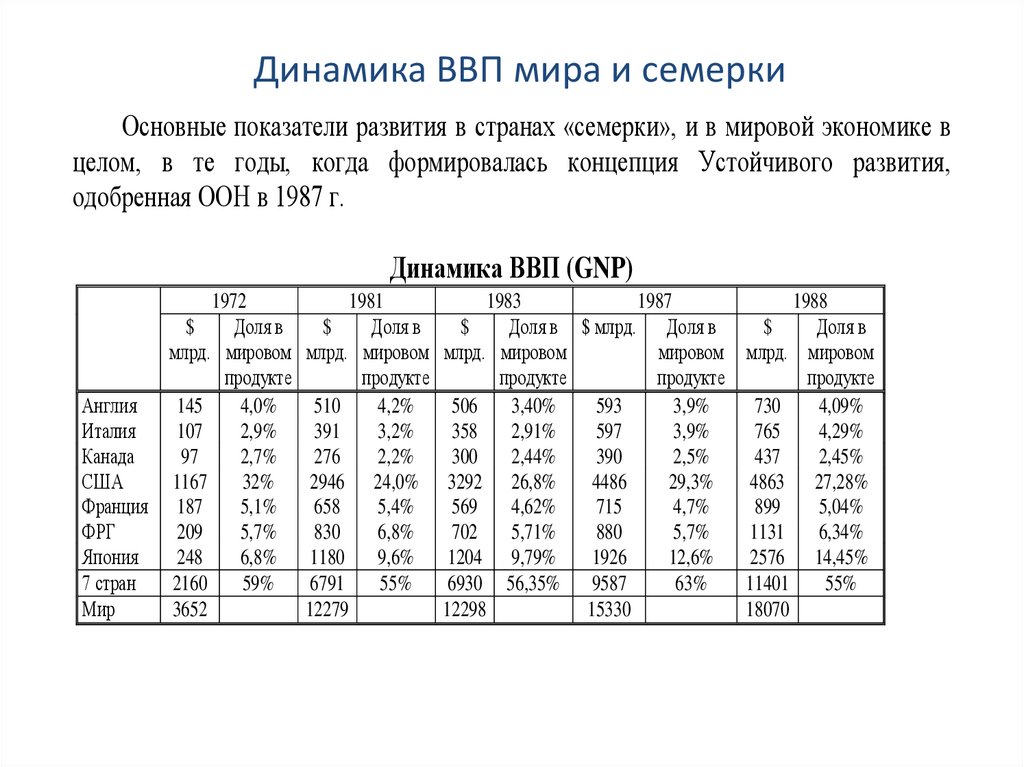
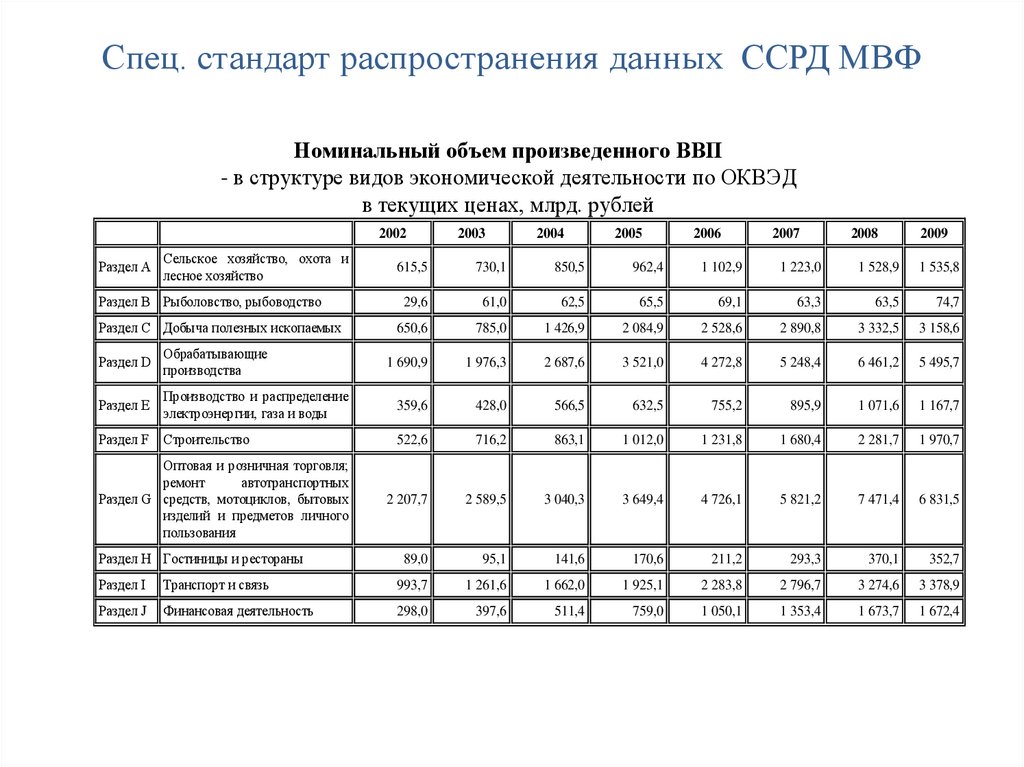
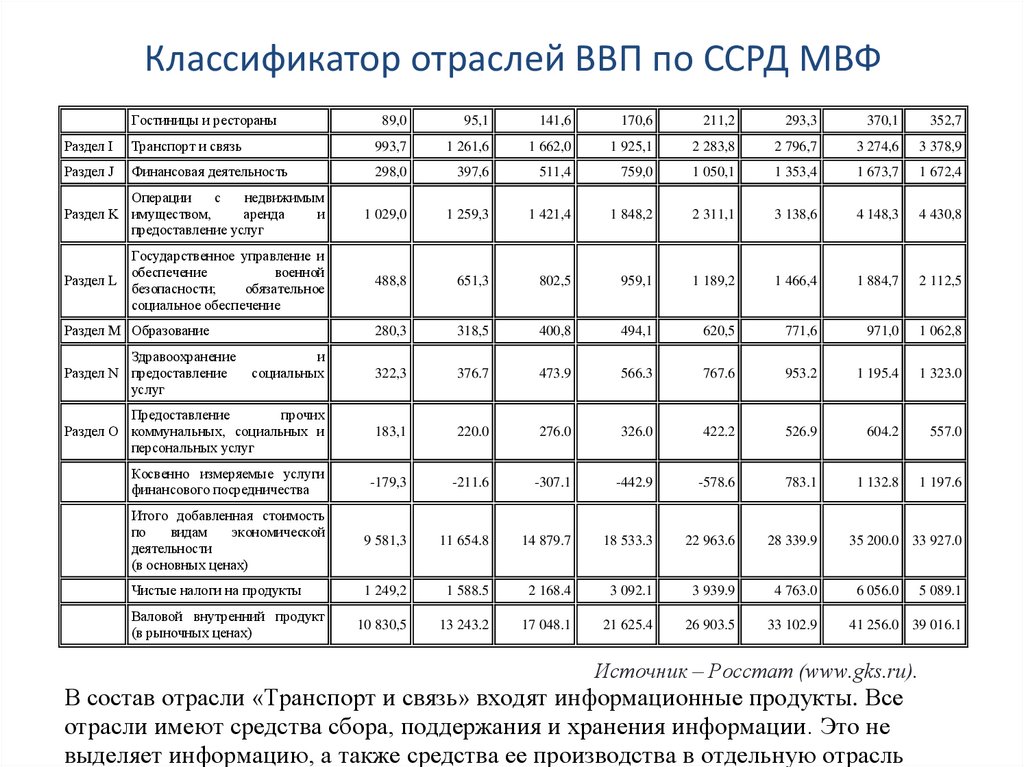

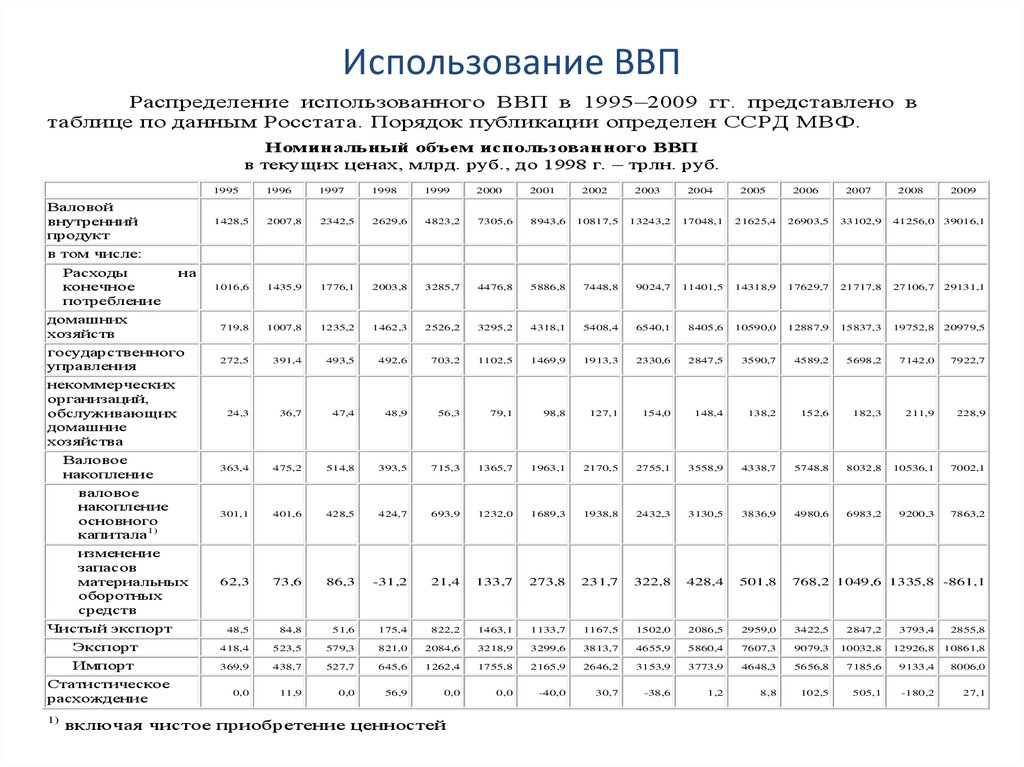

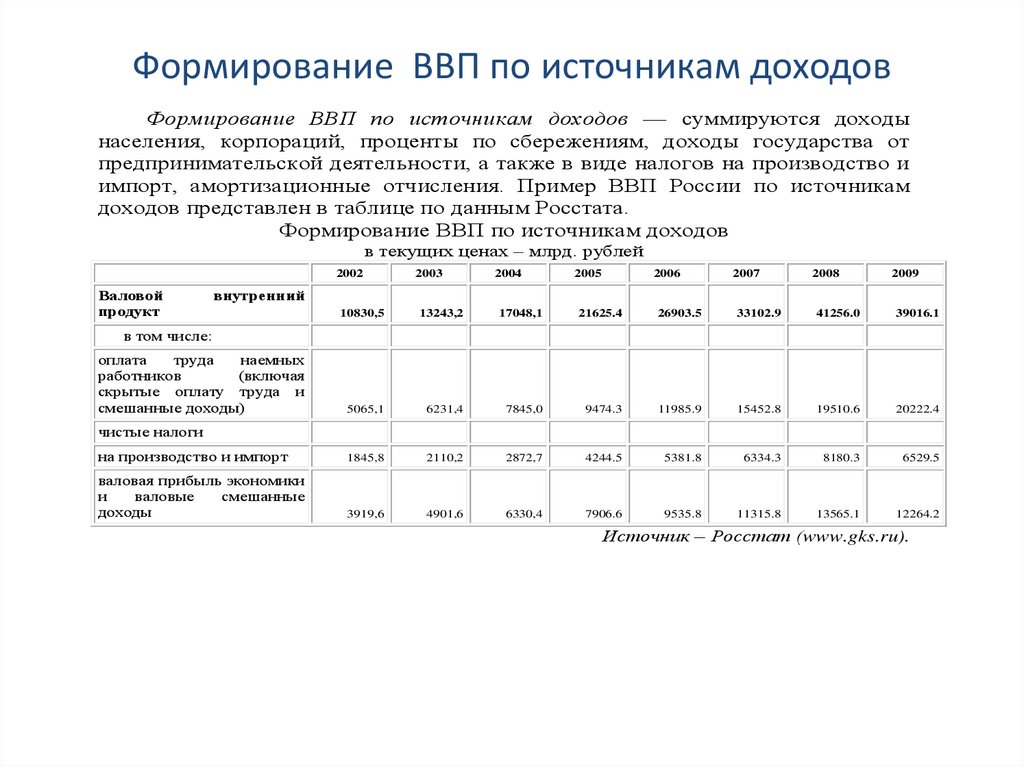
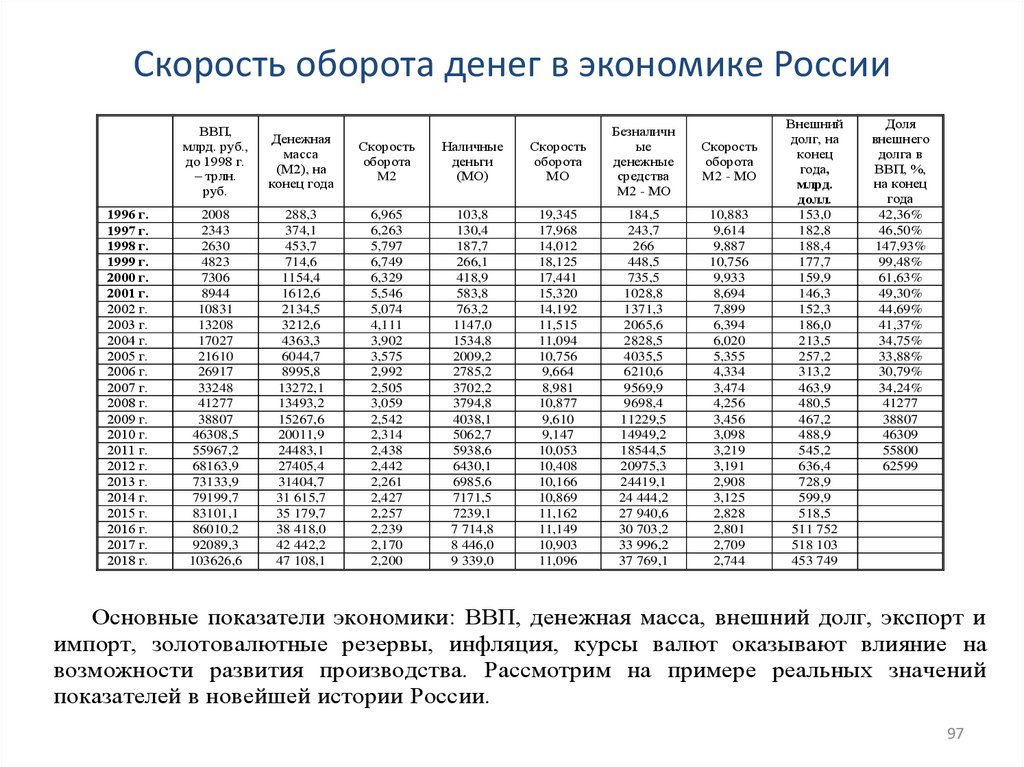












 Экономика
Экономика