Похожие презентации:
Сложные задачи. Кубики
1.
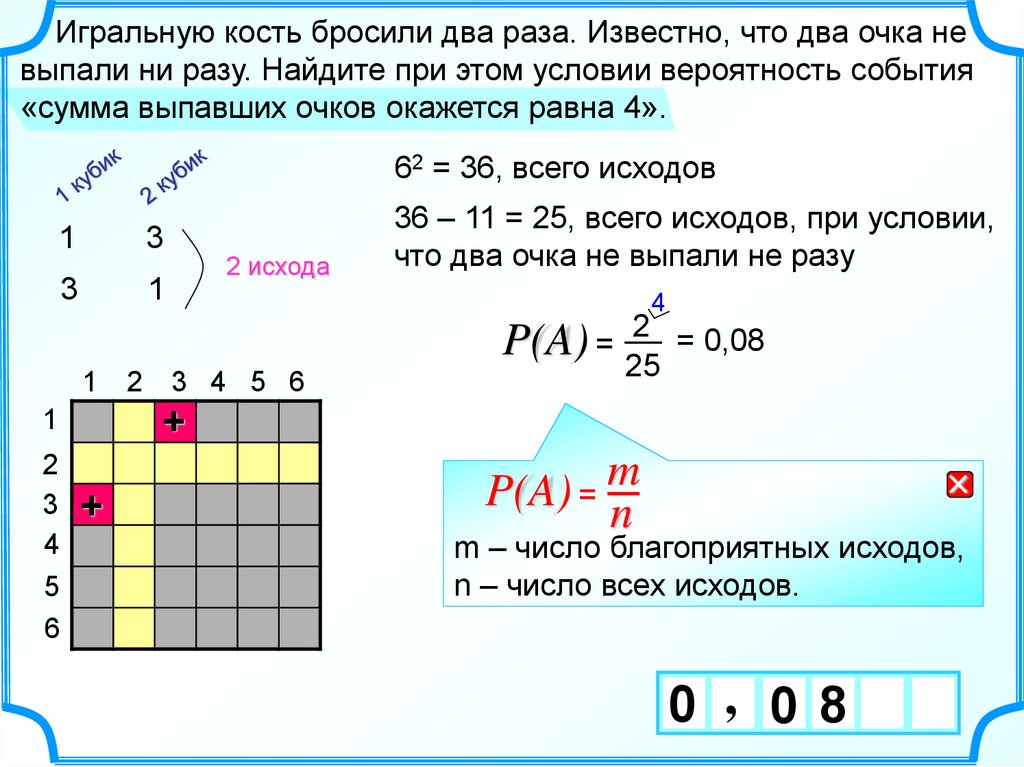
Игральную кость бросили два раза. Известно, что два очка невыпали ни разу. Найдите при этом условии вероятность события
«сумма выпавших очков окажется равна 4».
62 = 36, всего исходов
1
3
3
1
1 2
1
2
3 +
4
5
6
2 исхода
36 – 11 = 25, всего исходов, при условии,
что два очка не выпали не разу
4
3 4 5 6
2 = 0,08
P(A) = 25
+
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 0 8
2.
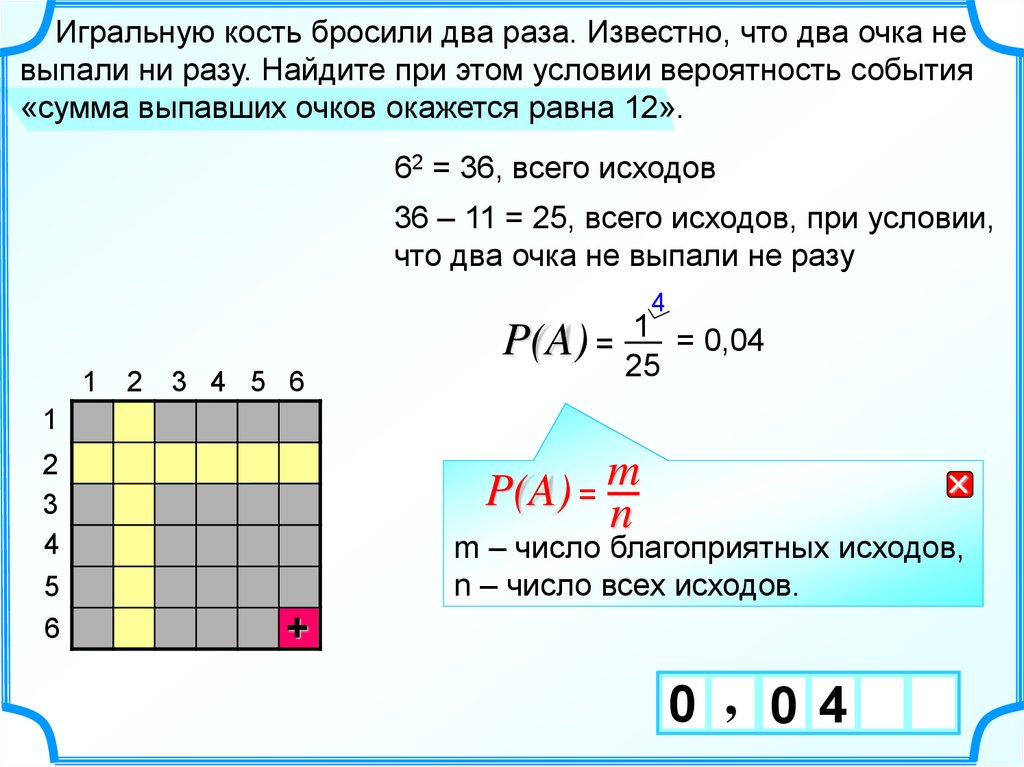
Игральную кость бросили два раза. Известно, что два очка невыпали ни разу. Найдите при этом условии вероятность события
«сумма выпавших очков окажется равна 12».
62 = 36, всего исходов
36 – 11 = 25, всего исходов, при условии,
что два очка не выпали не разу
4
1 2
3 4 5 6
1 = 0,04
P(A) = 25
1
2
3
4
5
6
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
+
0 , 0 4
3.
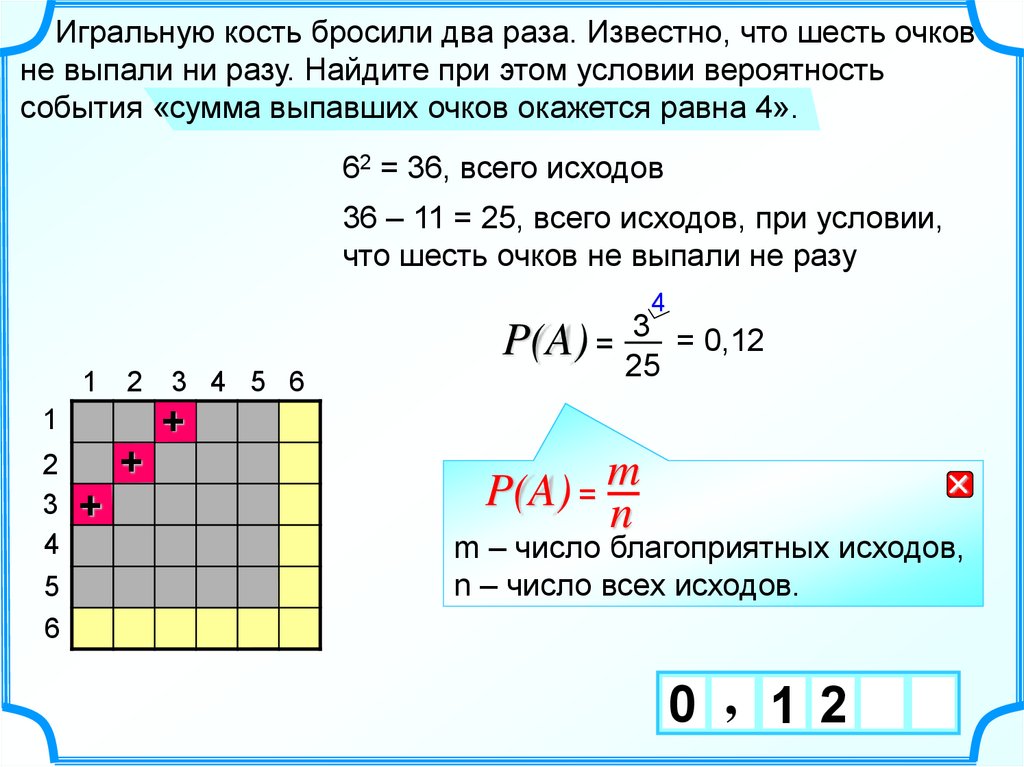
Игральную кость бросили два раза. Известно, что шесть очковне выпали ни разу. Найдите при этом условии вероятность
события «сумма выпавших очков окажется равна 4».
62 = 36, всего исходов
36 – 11 = 25, всего исходов, при условии,
что шесть очков не выпали не разу
4
1 2
1
2
+
3 +
4
5
6
3 4 5 6
3 = 0,12
P(A) = 25
+
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 1 2
4.
Игральную кость бросили два раза. Известно, что пять очковне выпали ни разу. Найдите при этом условии вероятность
события «сумма выпавших очков окажется равна 7».
62 = 36, всего исходов
36 – 11 = 25, всего исходов, при условии,
что пять очков не выпали не разу
4
1 2
3 4 5 6
+
1
2
3
4
5
6 +
4 = 0,16
P(A) = 25
+
+
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 1 6
5.
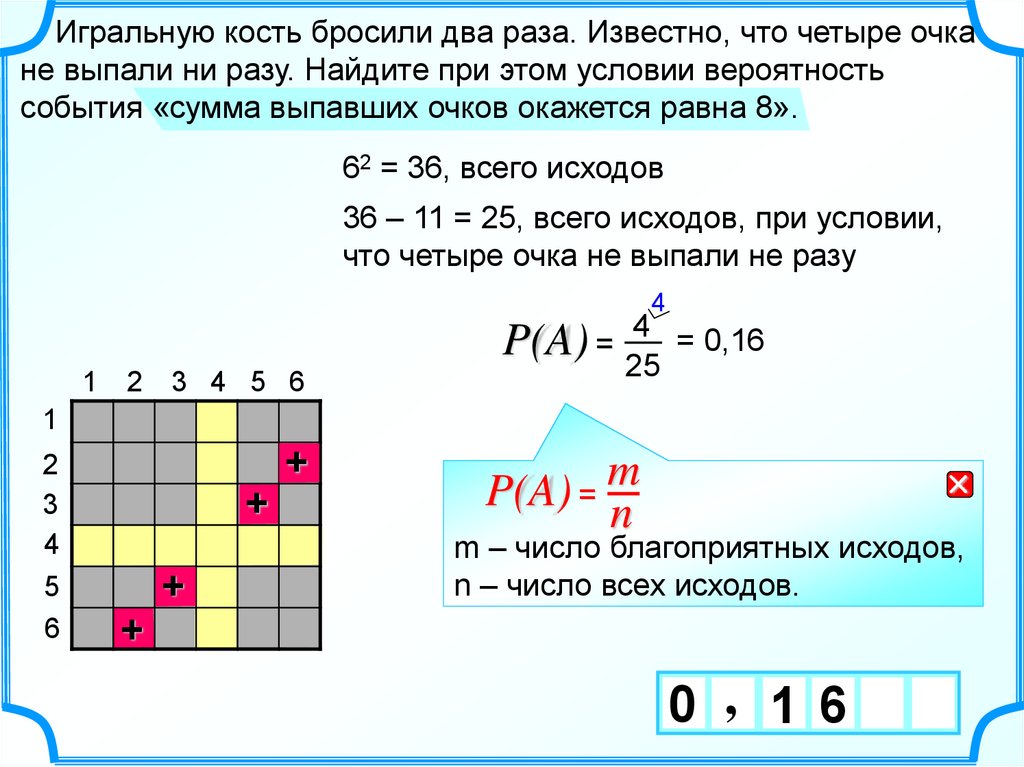
Игральную кость бросили два раза. Известно, что четыре очкане выпали ни разу. Найдите при этом условии вероятность
события «сумма выпавших очков окажется равна 8».
62 = 36, всего исходов
36 – 11 = 25, всего исходов, при условии,
что четыре очка не выпали не разу
4
1 2
3 4 5 6
4 = 0,16
P(A) = 25
1
2
3
4
5
6
+
+
+
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
+
0 , 1 6
6.
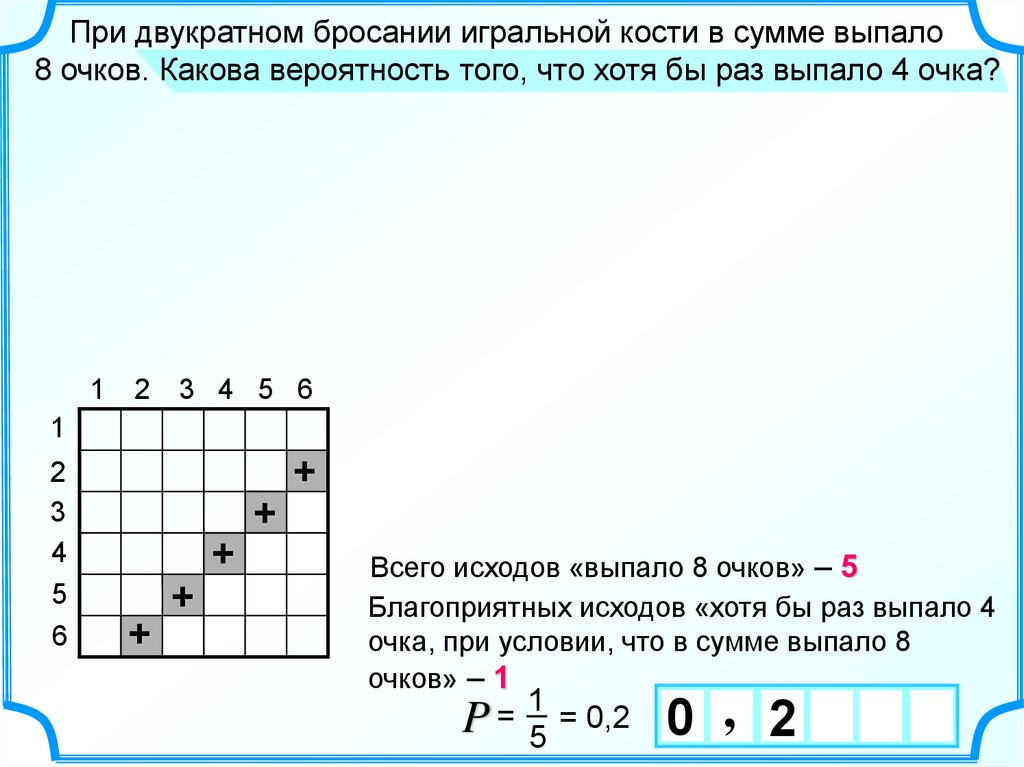
При двукратном бросании игральной кости в сумме выпало8 очков. Какова вероятность того, что хотя бы раз выпало 4 очка?
1 2
3 4 5 6
1
2
3
4
5
6
+
+
+
+
+
Всего исходов «выпало 8 очков» – 5
Благоприятных исходов «хотя бы раз выпало 4
очка, при условии, что в сумме выпало 8
очков» – 1
P=
1
= 0,2
5
0 , 2
7.
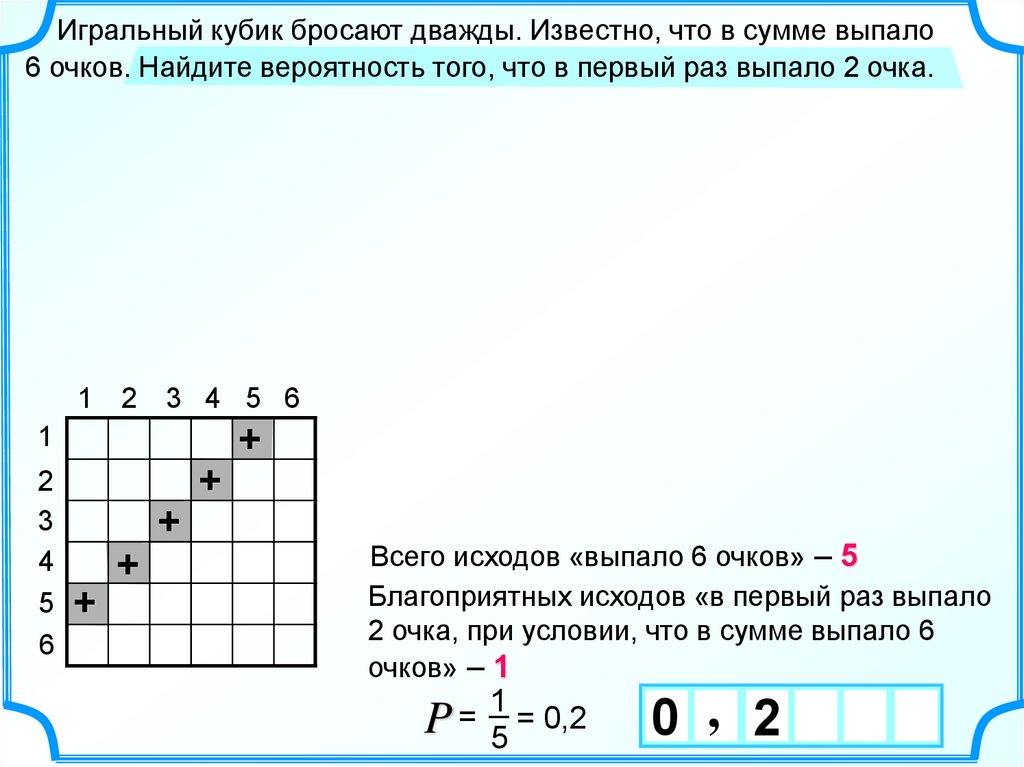
Игральный кубик бросают дважды. Известно, что в сумме выпало6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.
1 2
3 4 5 6
1
2
+
3
+
4
+
5 +
6
+
Всего исходов «выпало 6 очков» – 5
Благоприятных исходов «в первый раз выпало
2 очка, при условии, что в сумме выпало 6
очков» – 1
P=
1
= 0,2
5
0 , 2
8.
Симметричную игральную кость бросили 3 раза. Известно,что в сумме выпало 6 очков. Какова вероятность события
«хотя бы раз выпало 3 очка»?
9.
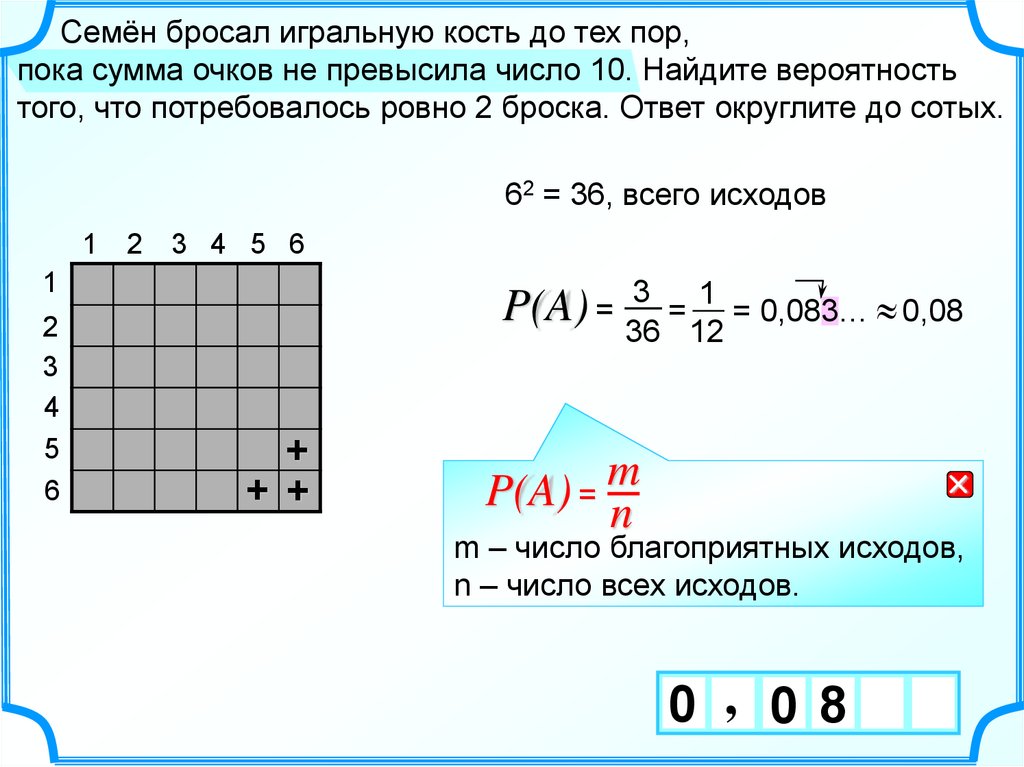
Семён бросал игральную кость до тех пор,пока сумма очков не превысила число 10. Найдите вероятность
того, что потребовалось ровно 2 броска. Ответ округлите до сотых.
62 = 36, всего исходов
1 2
3 4 5 6
1
2
3
4
5
6
3
1
P(A) = 36
= = 0,083… 0,08
12
+
+ +
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 0 8
10.
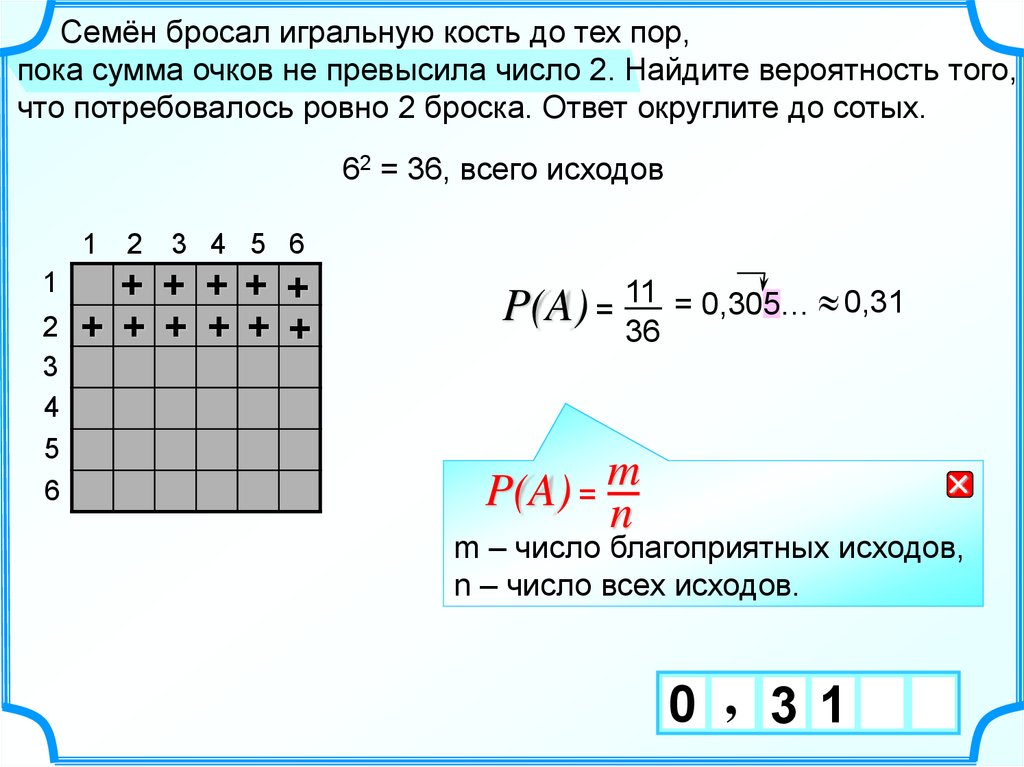
Семён бросал игральную кость до тех пор,пока сумма очков не превысила число 2. Найдите вероятность того,
что потребовалось ровно 2 броска. Ответ округлите до сотых.
62 = 36, всего исходов
1 2
3 4 5 6
+ + + + +
2 + + + + + +
1
3
4
5
6
= 0,305… 0,31
P(A) = 11
36
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 3 1
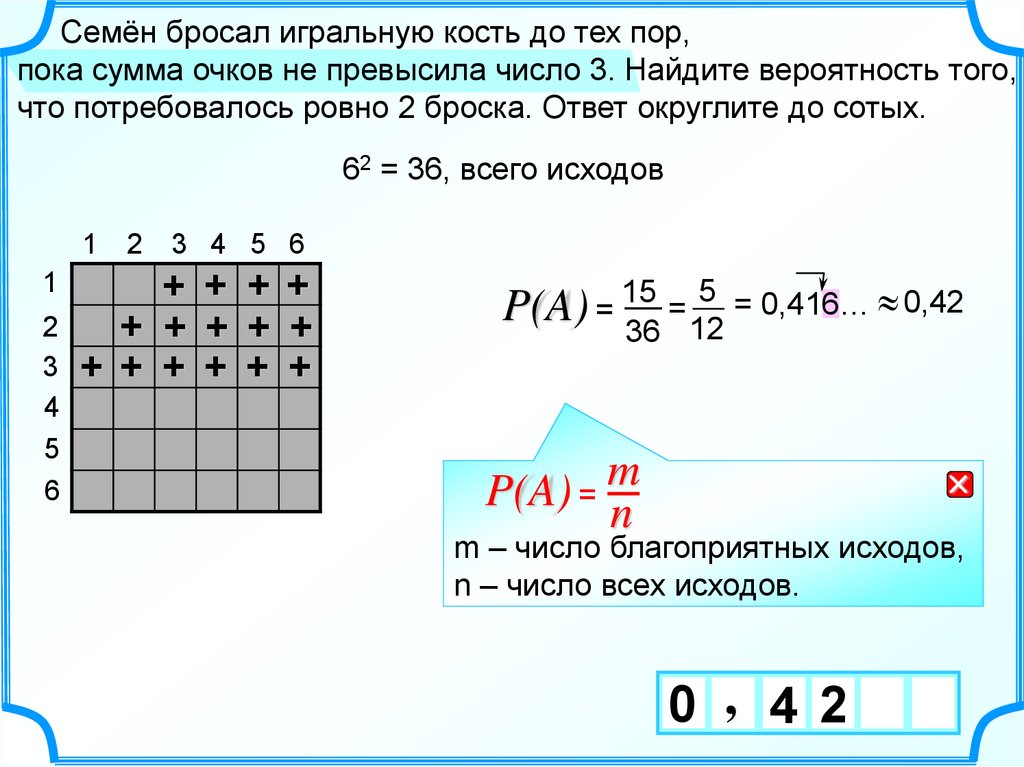
11.
Семён бросал игральную кость до тех пор,пока сумма очков не превысила число 3. Найдите вероятность того,
что потребовалось ровно 2 броска. Ответ округлите до сотых.
62 = 36, всего исходов
1 2
3 4 5 6
+ + + +
2
+ + + + +
3 + + + + + +
1
4
5
6
5 = 0,416… 0,42
=
P(A) = 15
36 12
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 4 2
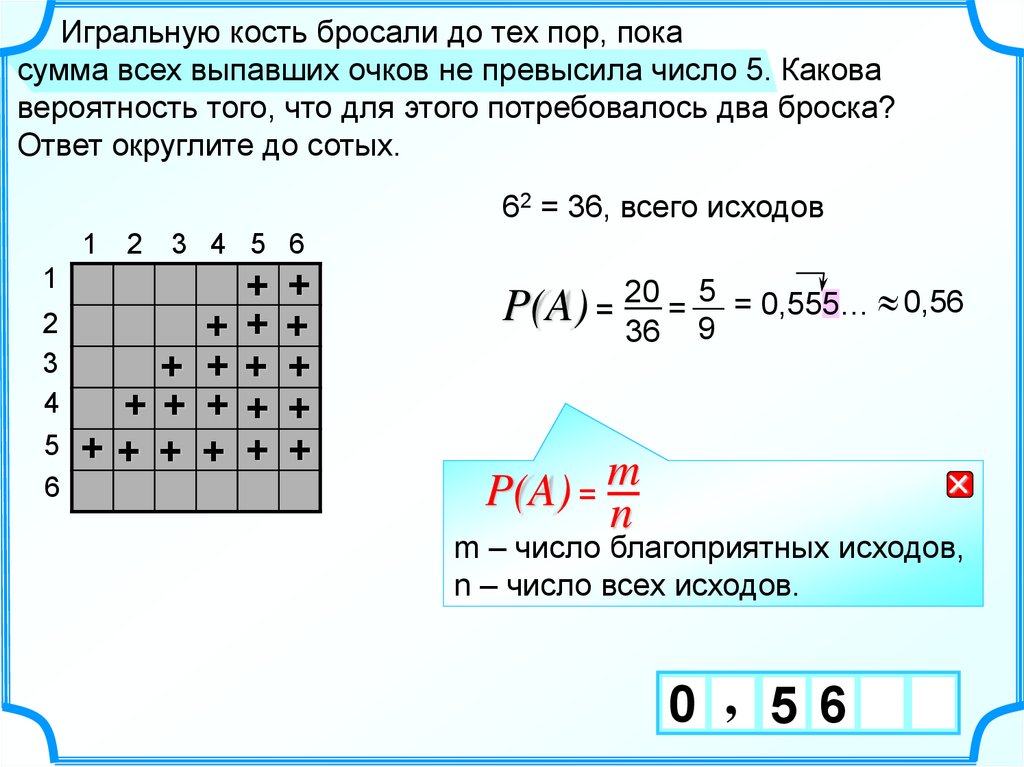
12.
Игральную кость бросали до тех пор, покасумма всех выпавших очков не превысила число 5. Какова
вероятность того, что для этого потребовалось два броска?
Ответ округлите до сотых.
62 = 36, всего исходов
1 2
1
3 4 5 6
+ +
2
+ + +
3
+ ++ +
4
+ + + + +
5 + + + + + +
6
5 = 0,555… 0,56
=
P(A) = 20
36 9
P(A) = m
n
m – число благоприятных исходов,
n – число всех исходов.
0 , 5 6
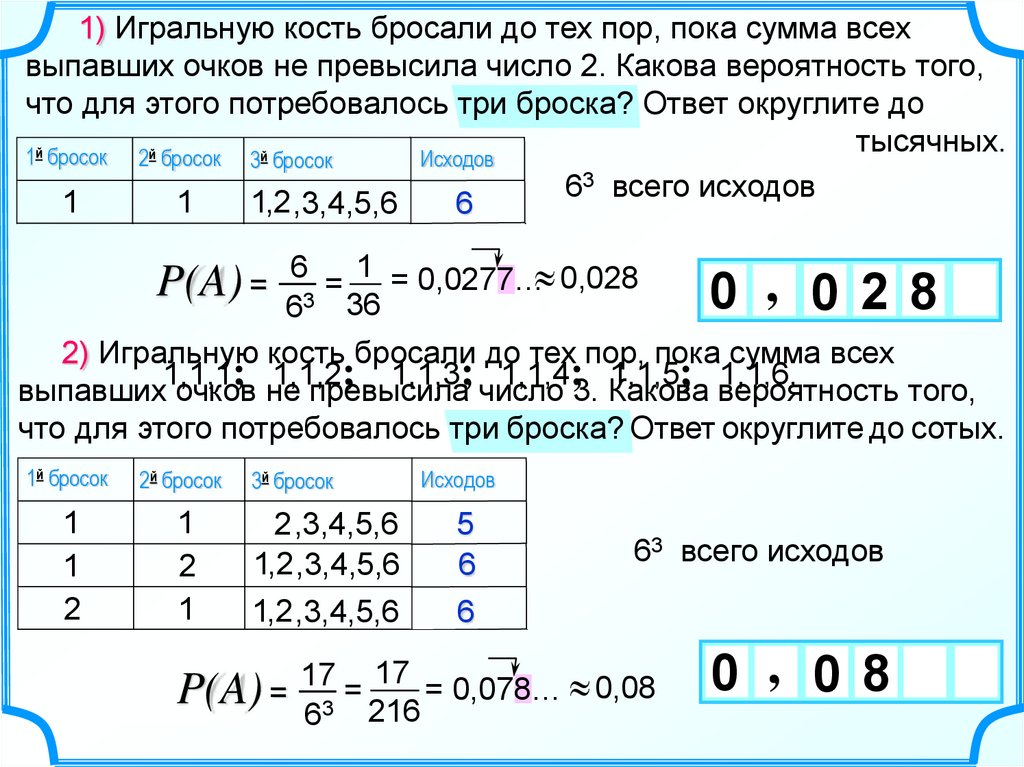
13.
1) Игральную кость бросали до тех пор, пока сумма всехвыпавших очков не превысила число 2. Какова вероятность того,
что для этого потребовалось три броска? Ответ округлите до
тысячных.
1й бросок 2й бросок 3й бросок
Исходов
63 всего исходов
1
1
1,2 ,3,4,5,6
6
1
2
1 = 0,0277… 0,028
6
=
P(A) = 63 36
0 , 0 28
2) Игральную кость бросали до тех пор, пока сумма всех
1,1,1; 1,1,2; 1,1,3; 1,1,4; 1,1,5; 1,1,6.
выпавших очков не превысила число 3. Какова вероятность того,
что для этого потребовалось три броска? Ответ округлите до сотых.
1й бросок
2й бросок
1
1
2
1
2
1
3й бросок
2,3,4,5,6
1,2 ,3,4,5,6
1,2 ,3,4,5,6
Исходов
5
6
63 всего исходов
6
17 = 17 = 0,078… 0,08
P(A) = 63 216
0 , 0 8
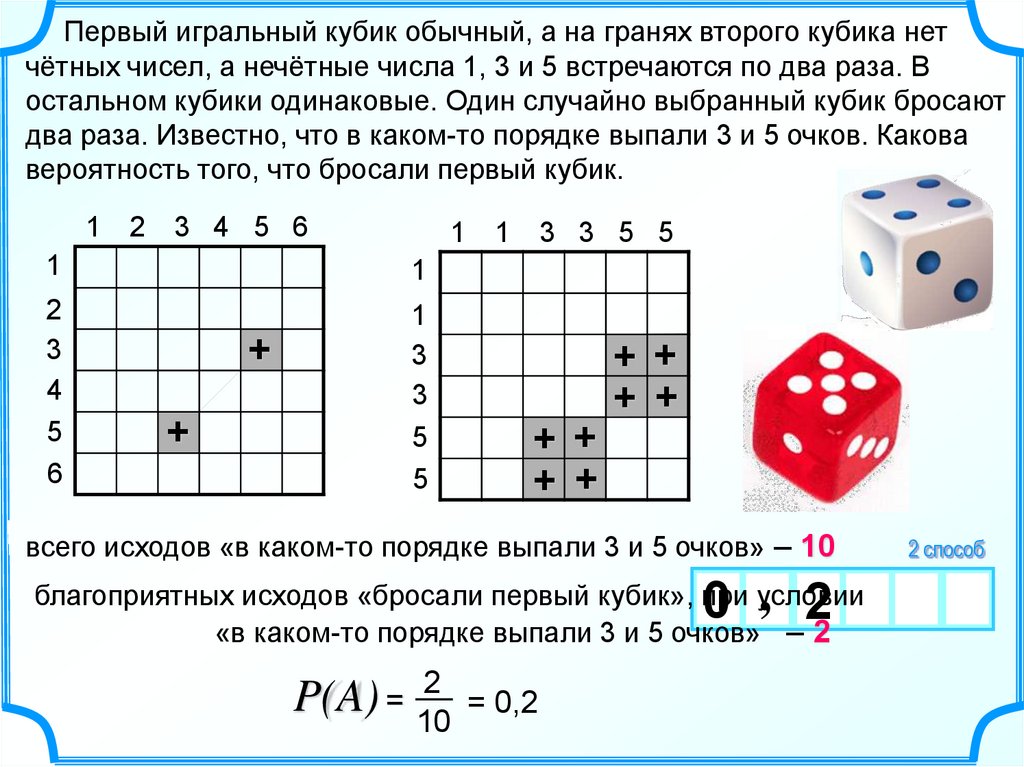
14.
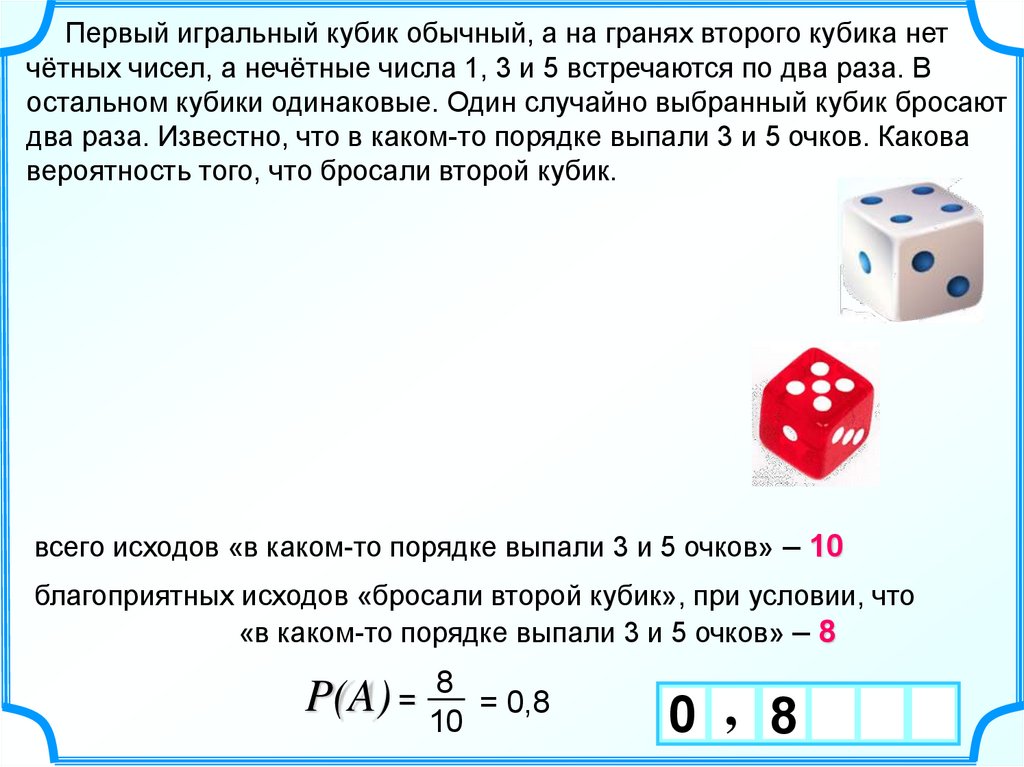
Первый игральный кубик обычный, а на гранях второго кубика нетчётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В
остальном кубики одинаковые. Один случайно выбранный кубик бросают
два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова
вероятность того, что бросали первый кубик.
1 2
3 4 5 6
1 1
1
1
2
3
4
5
6
1
3
3
5
5
+
+
3 3 5 5
+ +
+ +
+ +
+ +
1 2выпали 3 и 5 очков» – 10
всего исходов «в каком-то порядке
2
1 способ
2 способ
36
2 кубик», при условии
P(AB)
благоприятных
исходов
«бросали
первый
=
= 0,2
P(A|B) =
; P(A|B) =
10
10 выпали 3 и 5 очков» – 2
P(B) «в каком-то порядке
0 , 2
72
2
Найдите вероятность
того,=что бросали
P(A)
= 0,2 первый кубик , A
10
при условии, что в каком-то
порядке выпали 3 и 5 очков B
15.
Первый игральный кубик обычный, а на гранях второго кубика нетчётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В
остальном кубики одинаковые. Один случайно выбранный кубик бросают
два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова
вероятность того, что бросали второй кубик.
1 2
3 4 5 6
1 1
1
1
2
3
4
5
6
1
3
3
5
5
+
+
3 3 5 5
+ +
+ +
+ +
+ +
всего исходов «в каком-то порядке выпали 3 и 5 очков» – 10
благоприятных исходов «бросали второй кубик», при условии, что
«в каком-то порядке выпали 3 и 5 очков» – 8
8
P(A) = 10
= 0,8
0 , 8
16.
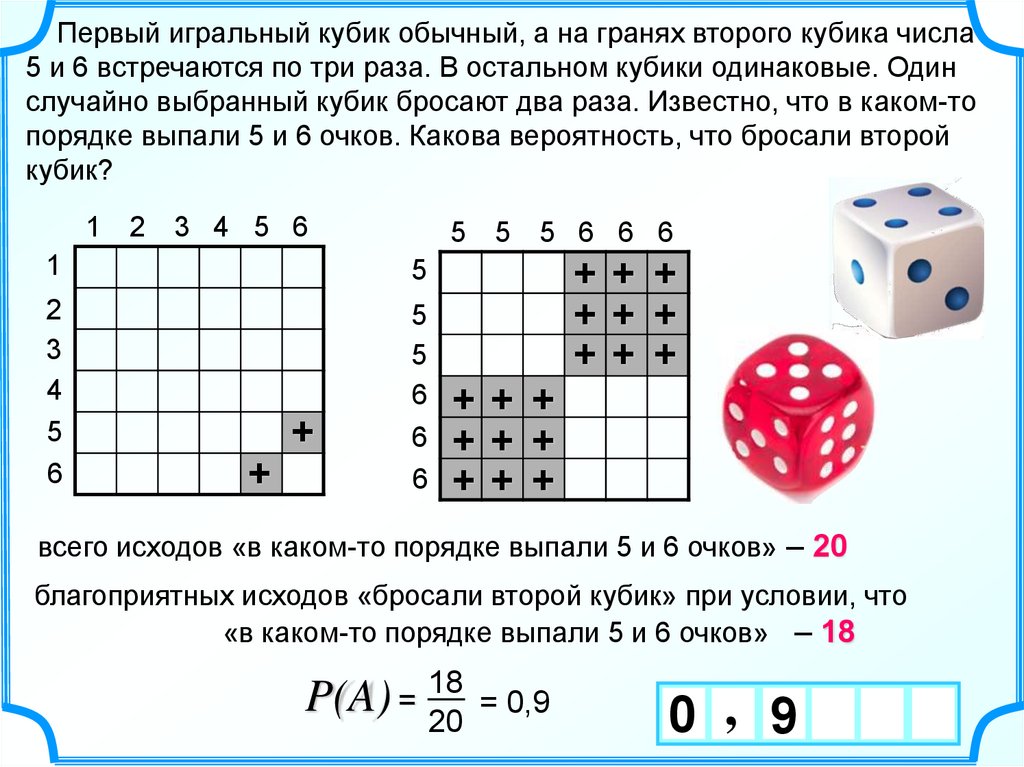
Первый игральный кубик обычный, а на гранях второго кубика числа5 и 6 встречаются по три раза. В остальном кубики одинаковые. Один
случайно выбранный кубик бросают два раза. Известно, что в каком-то
порядке выпали 5 и 6 очков. Какова вероятность, что бросали второй
кубик?
1 2
3 4 5 6
5 5
1
5
2
3
4
5
6
5
5
6
6
6
+
+
5 6 6 6
++ +
++ +
++ +
++ +
++ +
++ +
всего исходов «в каком-то порядке выпали 5 и 6 очков» – 20
благоприятных исходов «бросали второй кубик» при условии, что
«в каком-то порядке выпали 5 и 6 очков» – 18
P(A) = 18
= 0,9
20
0 , 9
17.
Игральный кубик бросили один или несколько раз. Оказалось,что сумма всех выпавших очков равна 3. Какова вероятность
того, что было сделано два броска? Ответ округлите до сотых.
Исходы «сумма
Число
бросков выпавших очков
равна 3»
1 бросок
3
2 броска
1; 2 ; 2; 1
3 броска
1; 1; 1
P
1
6
2
62
1
63
(a +b)2 = a 2 + 2ab + b2
62
6
1 2 1 (6+1)2
+ + = 3
6
6 62 63
0 , 24
18.
Вячеслав бросает кубик один или несколько раз – до тех пор,пока сумма очков при всех бросках не превысит число 2. Вышло так,
что сумма всех очков в результате равнялась 5. Какова вероятность
того, что Вячеслав сделал два броска? Ответ округлите до сотых.
Исходы «сумма
Число
бросков выпавших очков
равна 5»
1 бросок
2 броска
3 броска
4 броска
P
1
5
6
2
1; 4 ; 4; 1
2; 3 ; 3; 2 62
1
1; 1; 3 ; 1; 3;
2; 1
2
63
1;1;1;2
(a +b)2 = a 2 + 2ab + b2
62
6
1 2 1 (6+1)2
+ 2+ 3= 3
6
6 6 6
0 , 24
19.
Игральную кость бросили один или несколько раз. Оказалось,что сумма всех выпавших очков равна 4. Какова вероятность
того, что был сделан один бросок? Ответ округлите до сотых.
Исходы «сумма
Число
бросков выпавших очков
равна 4»
1 бросок
2 броска
3 броска
4 броска
P
1
4
6
3
1;3; 3;1; 2;2 62
1;1;2;
3
1;2;1; 2;1;1 63
1
1;1;1;1
64
(a +b)3 = a 3 + 3a 2b + 3ab 2+ b 3
63
62
6
3
(6+1)
1 3 3 1 =
+ + +
64
6 62 63 64
0 , 63
20.
Борисбросает
кубик
один или
несколько
раз – до
техОказалось,
пор пока
Игральную
кость
бросили
один
или несколько
раз.
сумма
очковвсех
при выпавших
всех бросках
не превысит
число 3.
Оказалось, что
что сумма
очков
равна 4. Какова
вероятность
сумма
всех
очков
в результате
равнялась
Какова вероятность
того, что
было
сделано
три броска?
Ответ4.округлите
до сотых.
того,
чтовероятность
Борис сделал
ровно
три броска?
Ответ округлите до сотых.
P(A)
того, что
«сделано
три броска»
Исходы «сумма
Число
бросков выпавших очков
равна 4»
1 бросок
2 броска
3 броска
4 броска
P
1
4
6
3
1;3; 3;1; 2;2 62
1;1;2;
3
1;2;1; 2;1;1 63
1
1;1;1;1
64
(a +b)3 = a 3 + 3a 2b + 3ab 2+ b 3
63
62
6
3
(6+1)
1 3 3 1 =
+ + +
64
6 62 63 64
0 , 05






 Математика
Математика








