kvadratnye_neravenstva

1.

• 06.11.2024

2.

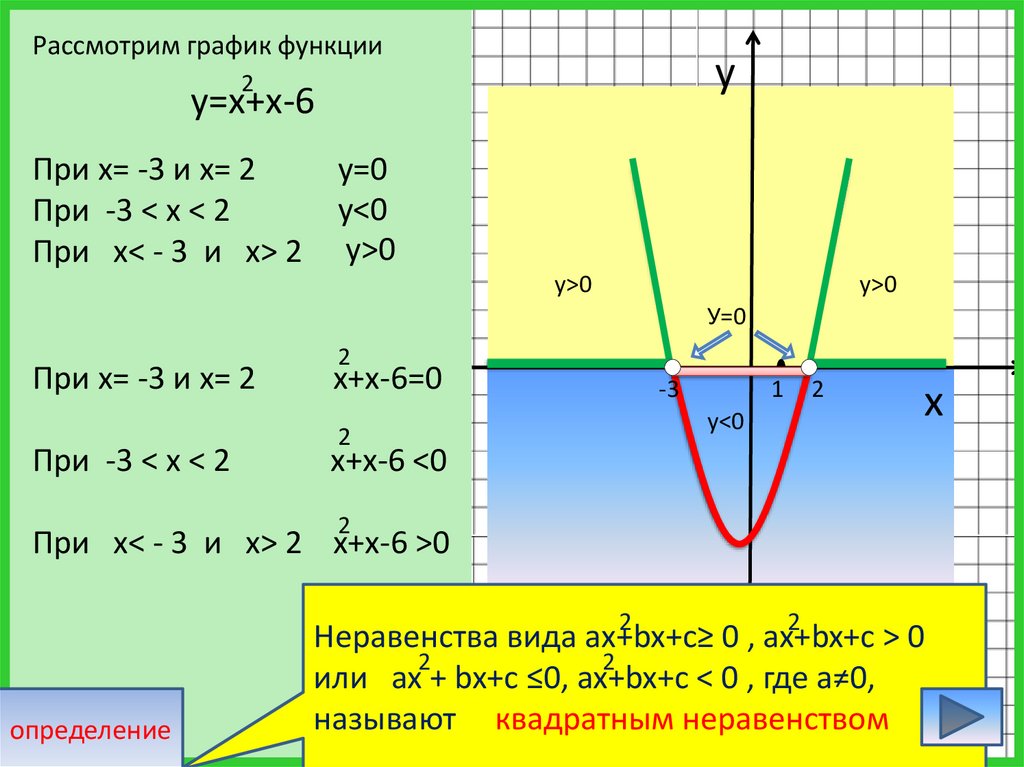
Рассмотрим график функции
у
2
у=х+х-6
При х= -3 и х= 2
При -3 < х < 2
При х< - 3 и х> 2
у=0
у<0
у>0
у>0
у>0
У=0
При х= -3 и х= 2
При -3 < х < 2
2
х+х-6=0
-3
1
2
у<0
2
х
х+х-6 <0
2
При х< - 3 и х> 2 х+х-6 >0
2
определение
2
Неравенства вида ах+bx+c≥ 0 , ах+bx+c > 0
2
2
или ах + bx+c ≤0, ах+bx+c < 0 , где а≠0,
называют квадратным неравенством

3.

Алгоритм решения квадратного
неравенства
Рассмотреть функцию у=ах2 + bx +c
1. Найти нули функции (решить уравнение
2.
ах2 + bx +c=0
Определить направление ветвей параболы
3. Схематично построить график функции.
4. Учитывая знак неравенства, выписать ответ.

4.

Расположение графика квадратичной функции
у=aх2+bx+c
относительно
оси
абсцисс
в
зависимости от дискриминанта и коэффициента а
D>0
D=0
D<0
а>0
x
x
x
x
а <0
x
x

5.

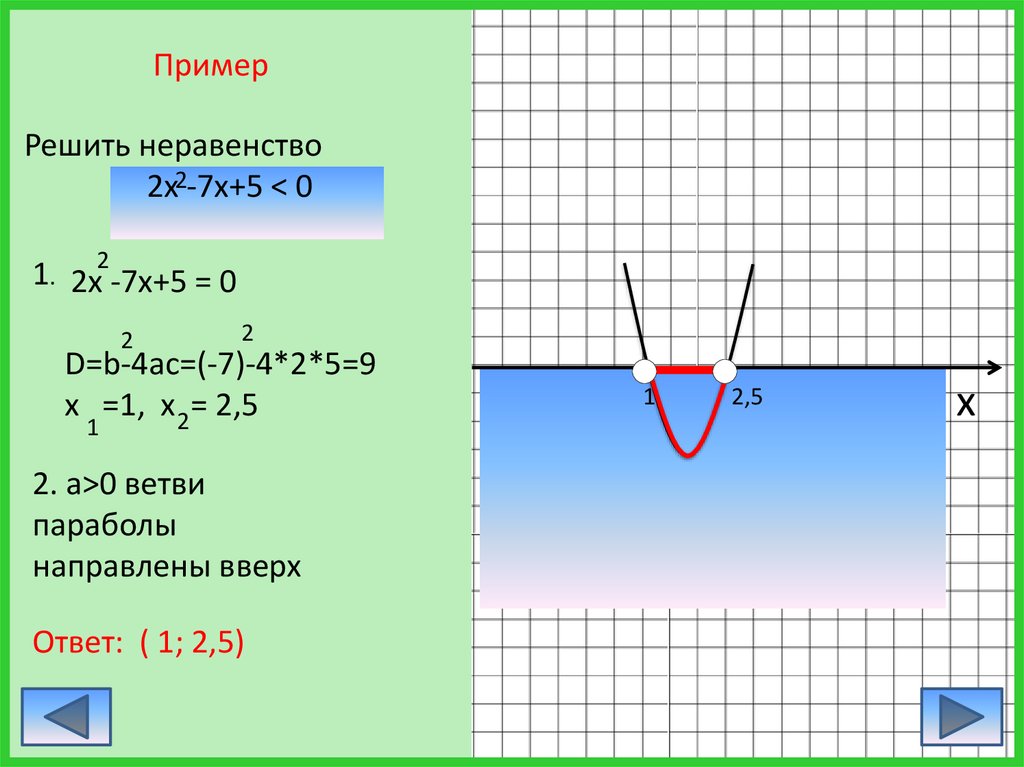
Пример
Решить неравенство
2х2-7х+5 < 0
1. 2х2-7х+5 = 0
2
2
D=b-4ac=(-7)-4*2*5=9
х =1, х 2= 2,5
1
2. а>0 ветви
параболы
направлены вверх
Ответ: ( 1; 2,5)
1
2,5
х

6.

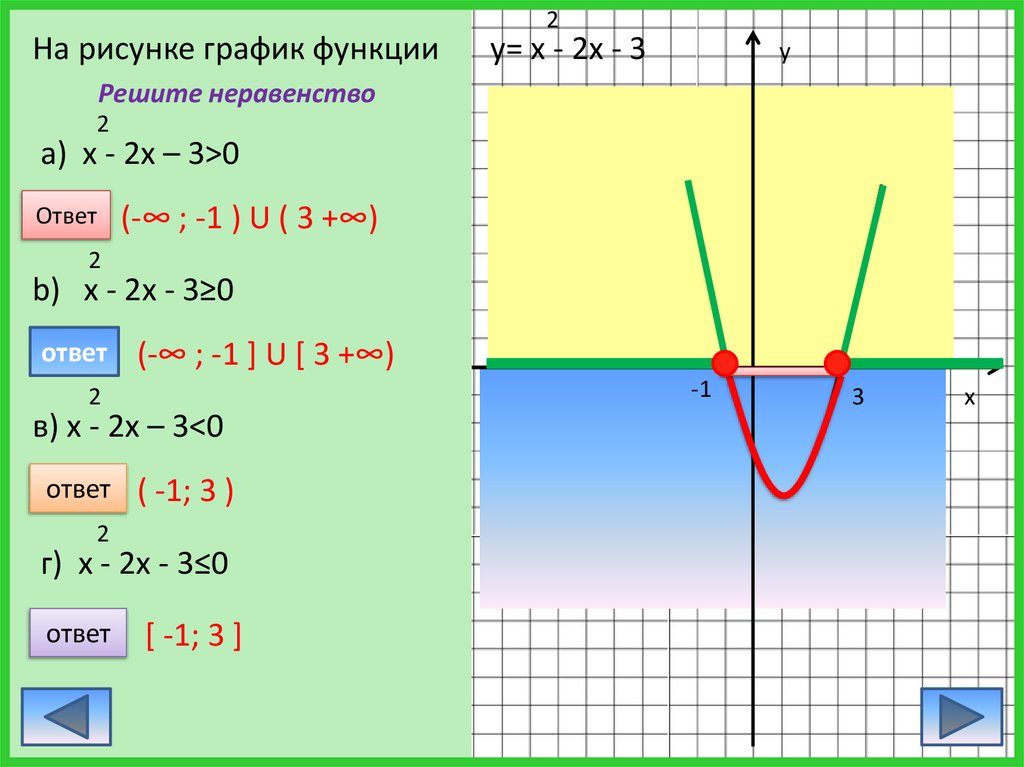
На рисунке график функции
2
у= х - 2х - 3
y
Решите неравенство
2
a) х - 2х – 3>0
Ответ
(-∞ ; -1 ) U ( 3 +∞)
2
b) х - 2х - 3≥0
ответ
(-∞ ; -1 ] U [ 3 +∞)
-1
2
в) х - 2х – 3<0
ответ ( -1; 3 )
2
г) х - 2х - 3≤0
ответ
[ -1; 3 ]
3
x

7.

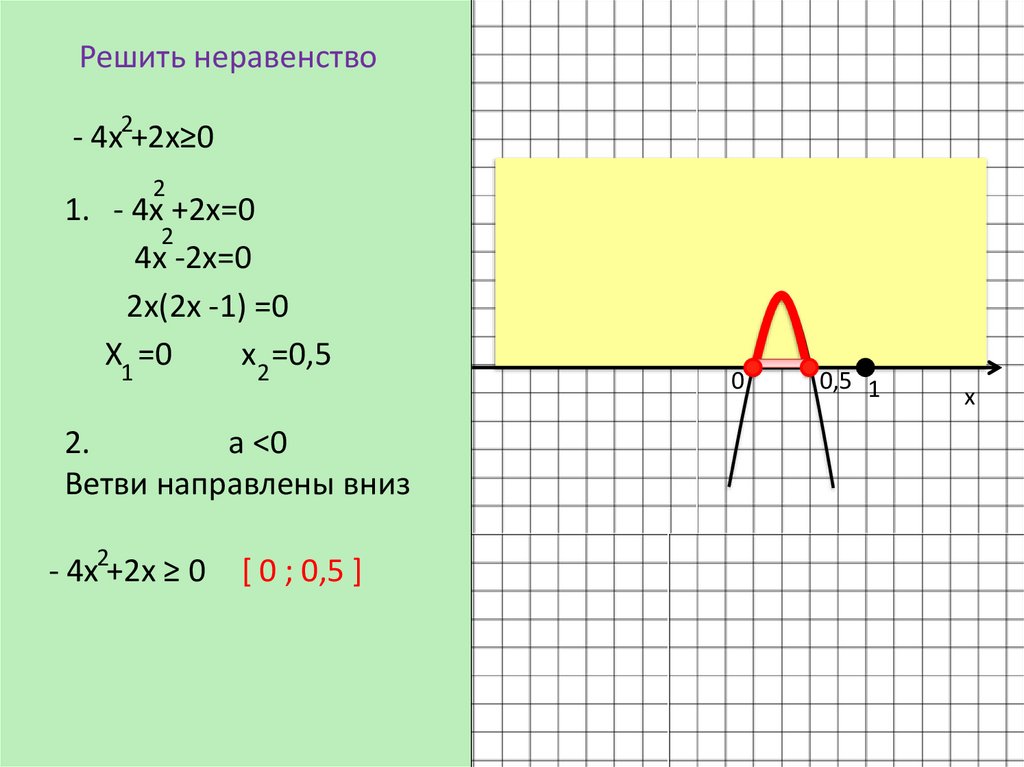
Решить неравенство
- 4х2+2х≥0
2
1. - 4х +2х=0
2
4х -2х=0
2х(2х -1) =0
Х1 =0
х2 =0,5
2.
а <0
Ветви направлены вниз
- 4х2+2х ≥ 0
[ 0 ; 0,5 ]
0
0,5 1
x