INF_L3_Predstavlenie_chisel

1. ИНФОРМАТИКА

Курс лекций
Доцент кафедры Прикладной математики
Шеметова Анастасия Дмитриевна

2. Машинное представление целых чисел в ЭВМ

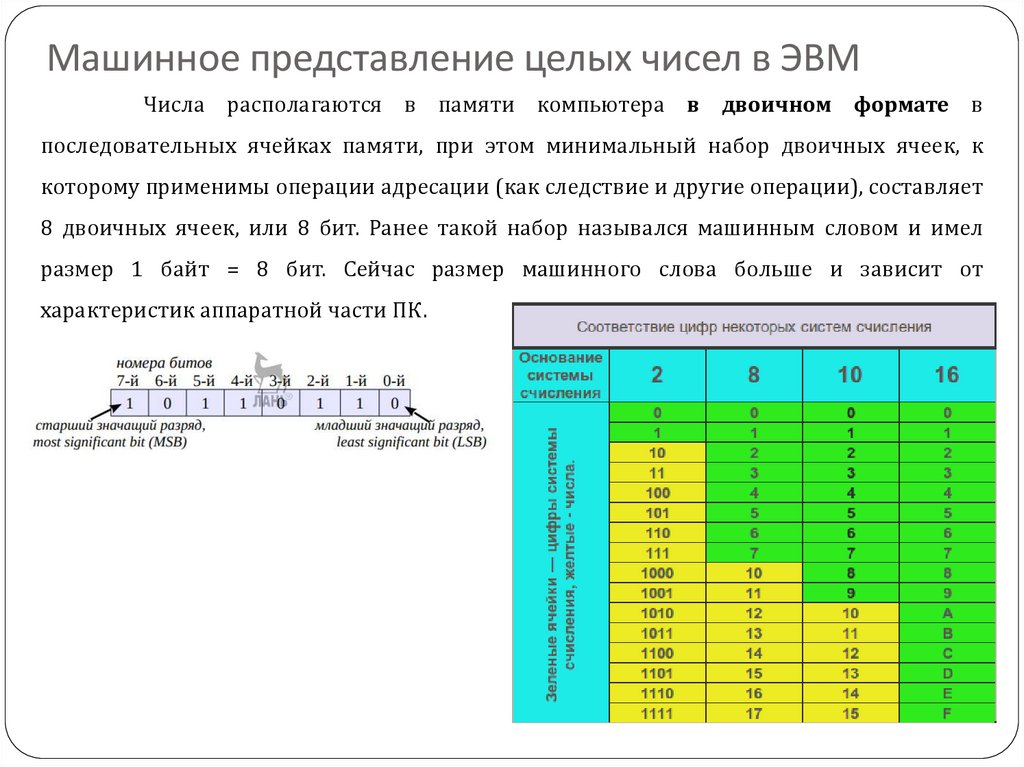
Числа располагаются в памяти компьютера в двоичном формате в
последовательных ячейках памяти, при этом минимальный набор двоичных ячеек, к
которому применимы операции адресации (как следствие и другие операции), составляет
8 двоичных ячеек, или 8 бит. Ранее такой набор назывался машинным словом и имел
размер 1 байт = 8 бит. Сейчас размер машинного слова больше и зависит от
характеристик аппаратной части ПК.

3.

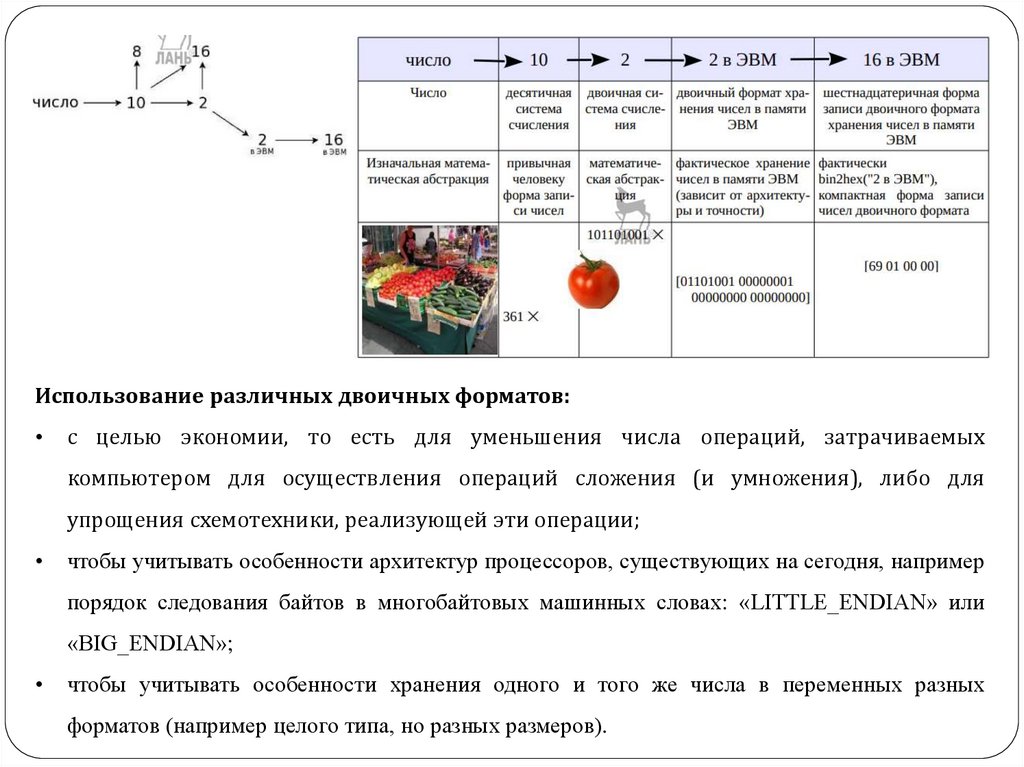
Использование различных двоичных форматов:
с целью экономии, то есть для уменьшения числа операций, затрачиваемых
компьютером для осуществления операций сложения (и умножения), либо для
упрощения схемотехники, реализующей эти операции;
чтобы учитывать особенности архитектур процессоров, существующих на сегодня, например
порядок следования байтов в многобайтовых машинных словах: «LITTLE_ENDIAN» или
«BIG_ENDIAN»;
чтобы учитывать особенности хранения одного и того же числа в переменных разных
форматов (например целого типа, но разных размеров).

4. Прямой код

5. Отрицательные числа

Как записать отрицательное число (а именно «минус») в памяти компьютера?
Если мы задействуем дополнительный бит для знака, то получим числа
размером в 8 + 1 = 9 бит, 32 + 1 = 33 бита и 64 + 1 = 65 бит, где будет
записаны знак и модуль числа, что не очень удобно с точки зрения записи
чисел в памяти и операций над ними (особенно с разными знаками). Также
мы получим ситуацию, когда у нас будет два нуля, «+0» и «−0».
Удобство хранения чисел в таком формате, с точки зрения человека, приведёт
к излишним преобразованиям при сложении чисел компьютером. Если вы
не поленились и постарались ответить на вопросы выше, то заметили, что
обычные правила арифметики (ⴲ – сложение по модулю 2), когда мы
складываем числа с разными знаками «в столбик» работать не будут.

6. Дополнительный код

1. При хранении в переменной чисел обоих знаков в двоичной форме записи этой
переменной самый левый (старший) бит отводится под знак («знаковый бит»).
Первое правило: если он равен 0, то, значит, мы имеем дело с положительным
числом, если в знаковом бите стоит «1», то мы имеем дело с отрицательным
числом. Далее, в зависимости от этого бита, действуют разные алгоритмы. С
положительными числами всё просто, а вот для отрицательных существует
несколько различных схем, упрощающих человеку их преобразование в
«машинный формат» представления

7. Дополнительный код положительных чисел

2. Лучший способ– это хранить числа в дополнительном коде (формате
дополнения «до двух). Этот способ основывается на базовом принципе
арифметики, что число a, сложенное со своим отрицанием −a, должно давать в
сумме 0.
Дополнительный код для положительных и отрицательных чисел
высчитывается по-разному. В случае положительных чисел спереди от
числа, преобразованного в двоичный вид, дописываются незначащие
нули, чтобы общая длина двоичной записи числа соответствовала
размеру отводимой под него памяти. Иными словами, дополнительный код
положительного числа «совпадает» с этим числом.
Например, если взять «число 52», то на следующем этапе, мы берём это число
в десятичной системе счисления 5210, после чего преобразуем его в двоичный
вид 1101002, а затем дописываем спереди нули. В случае хранения числа в
одном байте памяти дописываем нули до 8 разрядов, то есть для «2 в ЭВМ»
получим «00110100», а для случая использования типа integer (занимаемый
объём 4 байта) придётся дописать на 24 нуля больше.

8. Дополнительный код отрицательных чисел

Данный способ базируется на двух основных свойствах: на том, как
компьютер осуществляет сложение, и на факте, что число −a есть то
число, которое вы должны добавить к a, чтобы получить 0. Например,
если а = 3, то −a = −3, так как 3 + (−3) = 0, и если а = −4, то тогда −a = 4,
так как −4 + 4 = 0.
Возьмём два числа 00110100 и 11001100, произведём их сложение «в
столбик», в результате чего получим 0. Последний (левый) 9-й бит
«переноса» мы отбросили, так как сумма должна поместиться в 8 битах.
битовая комбинация 11001100, использовавшаяся нами при
сложении с первым числом, есть дополнительный код (для 8битового представления) для числа −52, так как −52 + 52 в сумме даёт 0.
Как его получить?

9. Алгоритм поиска дополнительного кода числа −m (m > 0):

Алгоритм поиска дополнительного кода
числа −m (m > 0):
Найдите
двоичное представление модуля рассматриваемого
десятичного числа. (Дословно отбросьте знак и переведите в
двоичную систему счисления. Например, для m = 52 получим
110100.)
В двоичном написании дополните это число спереди нулями до n-
разрядного представления. 3. Инвертируйте его запись, заменив все
«0» в записи на «1», а «1» на «0».
Прибавьте к числу 1.
Отбросьте выходящий за пределы n-разрядов результат (n = 8).

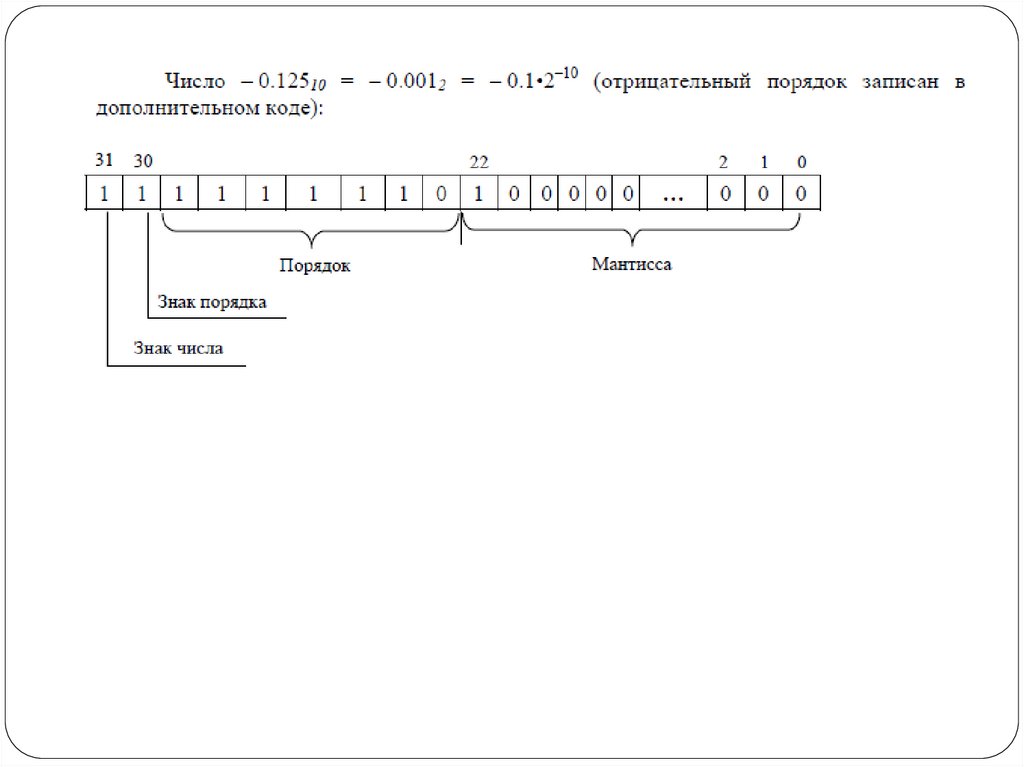
10. Числа с плавающей точкой/запятой

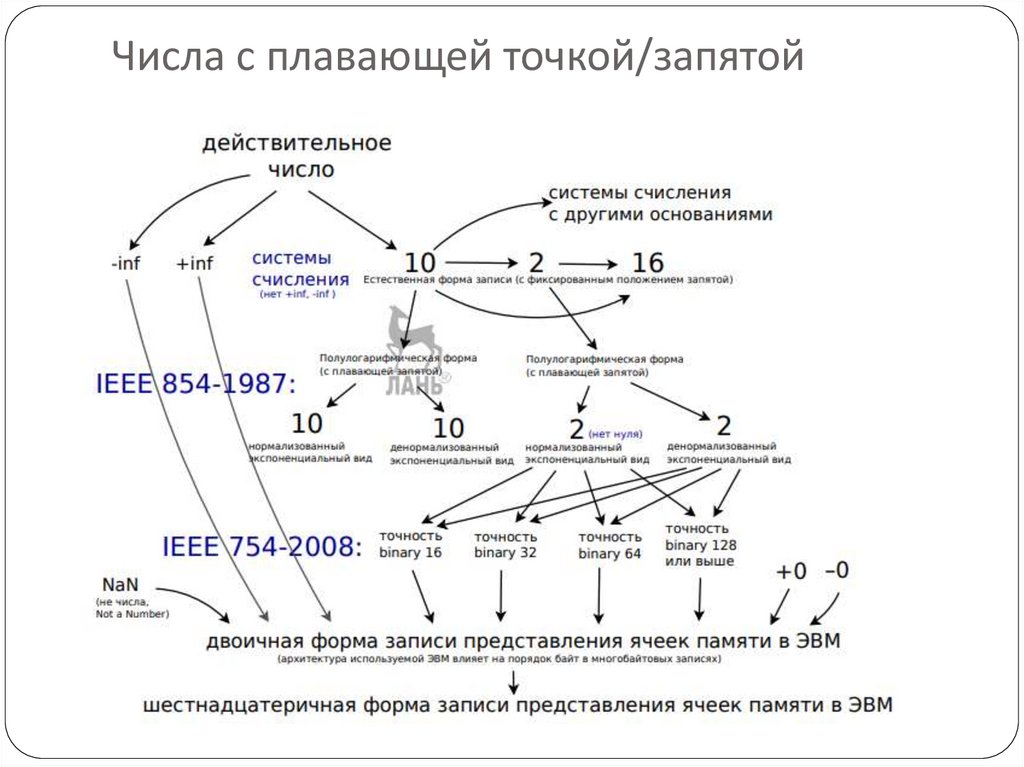
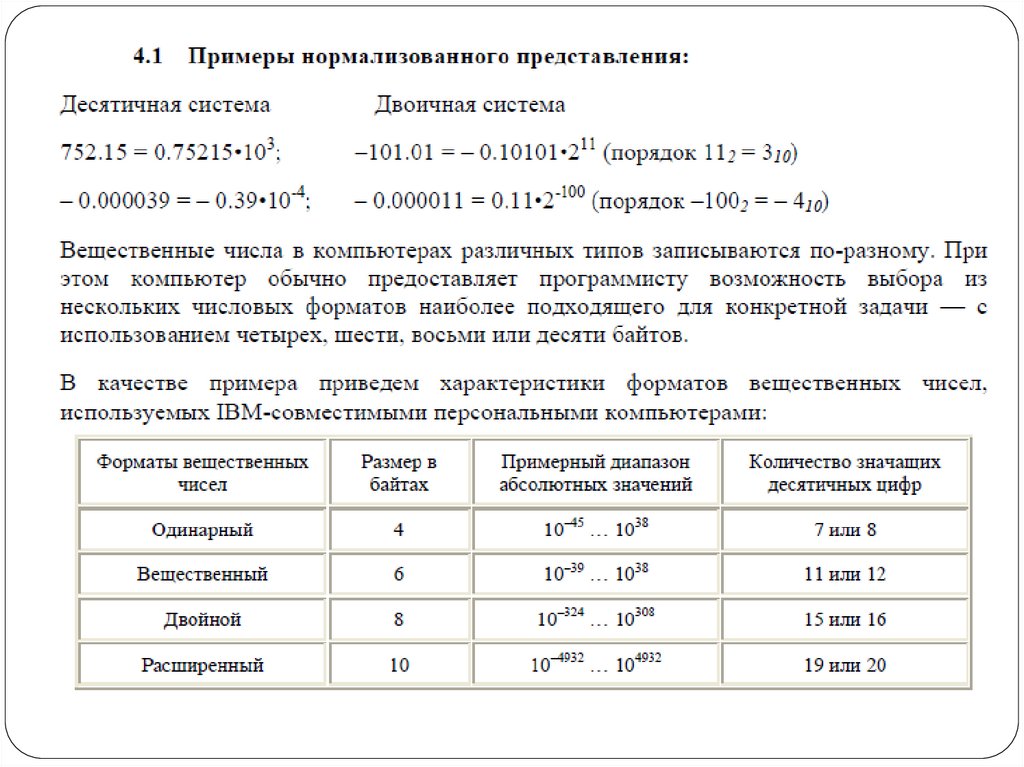
Для представления действительных чисел в компьютерах используется формат с
плавающей запятой (точкой). Актуальными являются два стандарта для
машинной арифметики с плавающей точкой.
IEEE 754-2008 IEEE Standard for Floating-Point Arithmetic определяет
представление и операции для чисел с плавающей точкой в компьютерных
системах.
Рассматривает форматы хранения, правила арифметики, стандартные и
расширенные функции для типов одинарной (single), двойной (double),
расширенной (extended) и расширяемой (extendable) точности, а также
рекомендует форматы для обмена данными. Определяет: как представлять
нормализованные положительные и отрицательные числа с плавающей запятой;
как представлять денормализованные положительные и отрицательные числа с
плавающей запятой; как представлять «нулевые» числа; как представлять
специальные величины «плюс бесконечность» и «минус бесконечность» (±Infinity,
±∞); как представлять специальные величины «Не число» (NaN, NaNs, not a
number).
IEEE 854-1987 IEEE Standard for Radix-Independent Floating-Point Arithmetic описывает числа с
основаниями 2 и 10, но, в отличие от IEEE 754-2008, не описывает точное
представление таких чисел по битам в памяти ЭВМ.

11. Числа с плавающей точкой/запятой

12. Числа с плавающей точкой/запятой

13. Числа с плавающей точкой/запятой

числа с плавающей запятой в общем случае можно представить в
экспоненциальном виде: v=F=M*qp,
где M – мантисса,
q – основание системы счисления,
p – показатель степени или порядок числа v (или F).
Например в десятичной системе счисления будет верно:
0,123·106 = 1,23·105 = 12,3·104 = 123·103 = 1230·102 = 123000 =
1230000·10−1 = …
Аналогично для двоичной системы счисления: 0,110100·26 = 1,10100·2 5
= 11, 0100·2 4 = 110100·20 = 1101000,0·10-1 = 11010000·10−2
выделенное жирным – нормализованная форма записи!
Воспользуемся двоичной нормализованной записью, так как она
наиболее легко преобразуется к 32-битному формату IEEE 754.
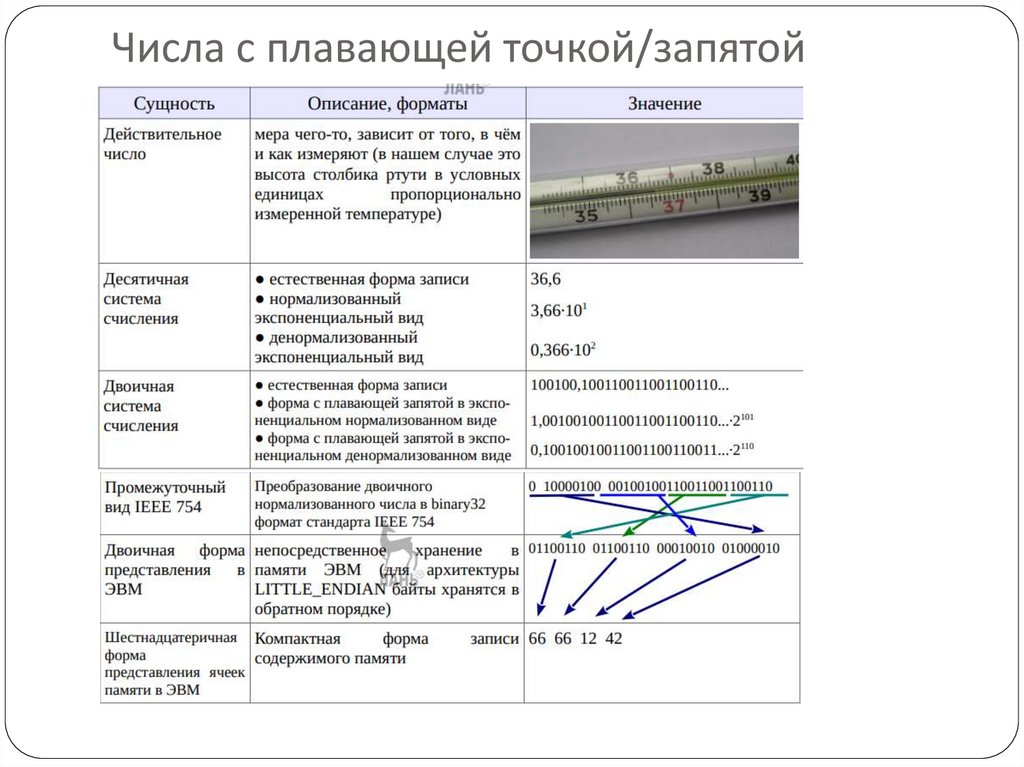
36,610≈100100,1001100110011001102=
=1,00100100110011001100110·25= =1,00100100110011001100110·2101

14. Числа с плавающей точкой/запятой

1. Определяемся со знаком числа. Если знак «+», то первый (он же самый
старший) бит 32-битной записи числа в памяти ЭВМ будет равен 0. Если
знак числа «−», запишем «1». Получим [0xxx xxxx xxxx xxxx xxxx xxxx xxxx
xxxx].
2. Смотрим в таблицу, взятую из стандарта, и определяем, сколько бит
отведено под хранение степени. Из таблицы получаем 8 разрядов. Число,
находящееся в степени, может быть как числом со знаком «+», так и со
знаком «−». Согласно стандарту, для определения знака не отводят
отдельного бита, а используют хранение в формате «со смещением»
Смещение также определяется из таблицы. Численно оно равно «половине»
от 8 бит, отведённых под число, то есть +12710(0111 11112). В нашем
примере степень p=1012=+510, следовательно, после смещения получим
E=+5 + 127 = 13210 = 100001002. Полученное «смещённое значение»
записывают в отведённые 8 битовых позиций. Получим [x100 0010 0xxx xxxx
xxxx xxxx xxxx xxxx].

15. Числа с плавающей точкой/запятой

3. Оставшиеся 23 бита отводят для хранения битов мантиссы. Хранятся не
все биты мантиссы, а лишь их часть. Из записи выбрасывается первый бит,
поскольку у нормализованной двоичной мантиссы он всегда равен 1, так
как число лежит в диапазоне 1 ≤ M < 2.
Нет смыла каждый раз записывать первую единицу в отведённых 23
разрядах и использовать только оставшиеся 22 разряда, лучше «отдать
первый разряд под точность», записывая 2.1. Если оставшиеся биты
мантиссы (после отброса первой единицы) занимают меньше 23 разрядов, то
последние дополняются нулями.
Получим [xxxx xxxx x001 0010 0110 0110 0110 0110].
В результате десятичное число 36,6, представленное в формате IEEE 754 c
одинарной точностью (binary32), равно 66661242 (hex).

16. ИТОГИ: