Методология и методы научных исследований_КМ

1.

Методология и
методы научных
исследований
Лекция 4

2.

Понятие математического моделирования
моделирования
1
2
3
4

3.

Понятия метода и методологии.
Классификация методов научного познания
Понятие метод (от греческого слова «методос» - путь к чему-либо) означает
совокупность приемов и операций практического и теоретического освоения
действительности. Метод вооружает человека системой принципов, требований,
правил, руководствуясь которыми он может достичь намеченной цели. Владение
методом означает для человека знание того, каким образом, в какой
последовательности совершать те или иные действия для решения тех или иных
задач, и умение применять это знание на практике. область знания, которая
специально занимается изучением методов и которую принято именовать
методологией. Методология дословно означает «учение о методах» (ибо происходит
этот термин от двух греческих слов: «методос» - метод и «логос» - учение). Изучая
закономерности человеческой познавательной деятельности, методология
вырабатывает на этой основе методы ее осуществления. Важнейшей задачей
методологии является изучение происхождения, сущности, эффективности и других
характеристик методов познания.
Всеобщие методы в истории познания
диалектический
метафизический

4.

Понятия метода и методологии.
Классификация методов научного познания
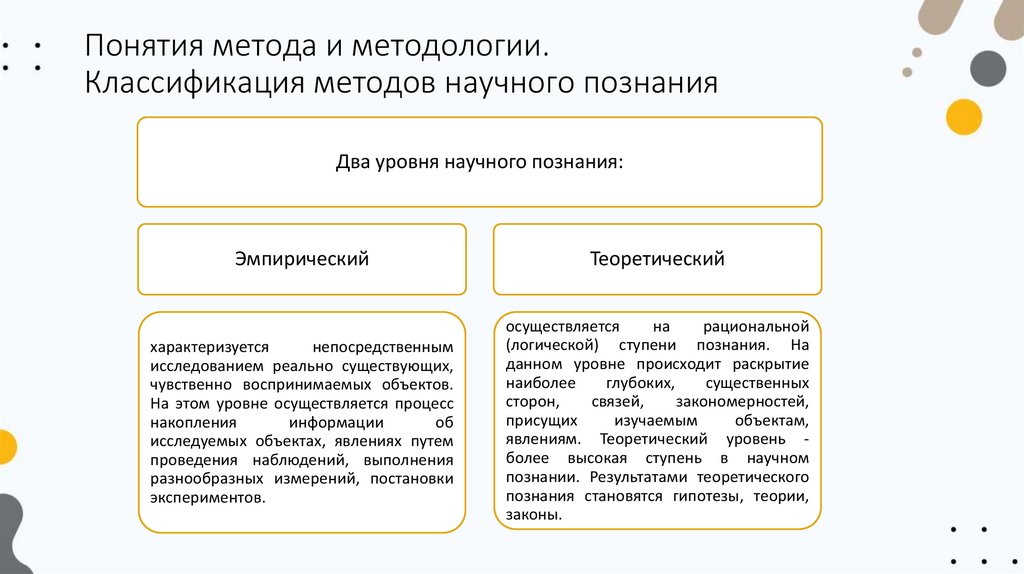
Два уровня научного познания:
Эмпирический
Теоретический
характеризуется
непосредственным
исследованием реально существующих,
чувственно воспринимаемых объектов.
На этом уровне осуществляется процесс
накопления
информации
об
исследуемых объектах, явлениях путем
проведения наблюдений, выполнения
разнообразных измерений, постановки
экспериментов.
осуществляется
на
рациональной
(логической) ступени познания. На
данном уровне происходит раскрытие
наиболее
глубоких,
существенных
сторон,
связей,
закономерностей,
присущих
изучаемым
объектам,
явлениям. Теоретический уровень более высокая ступень в научном
познании. Результатами теоретического
познания становятся гипотезы, теории,
законы.

5.

Понятия метода и методологии.
Классификация методов научного познания
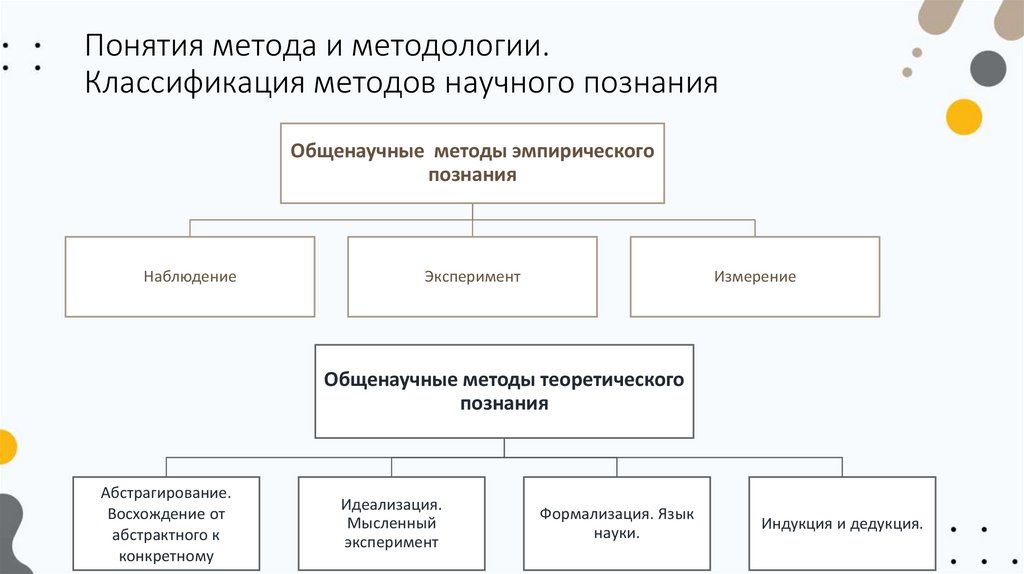
Общенаучные методы эмпирического
познания
Наблюдение
Эксперимент
Измерение
Общенаучные методы теоретического
познания
Абстрагирование.
Восхождение от
абстрактного к
конкретному
Идеализация.
Мысленный
эксперимент
Формализация. Язык
науки.
Индукция и дедукция.

6.

Понятия метода и методологии.
Классификация методов научного познания
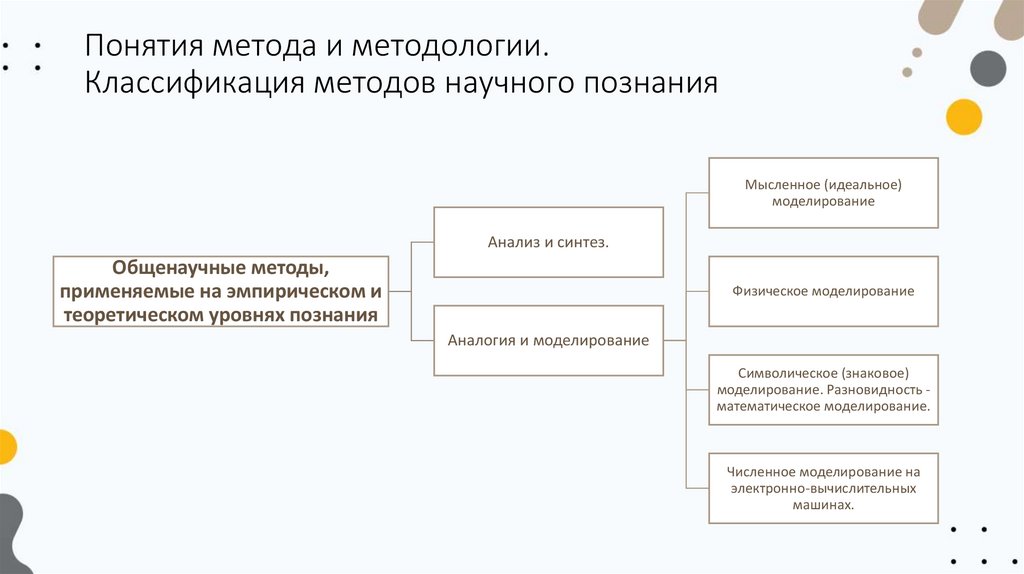
Мысленное (идеальное)
моделирование
Анализ и синтез.
Общенаучные методы,
применяемые на эмпирическом и
теоретическом уровнях познания
Физическое моделирование
Аналогия и моделирование
Символическое (знаковое)
моделирование. Разновидность математическое моделирование.
Численное моделирование на
электронно-вычислительных
машинах.

7.

Понятие модели и моделирования
Модель в широком смысле - это любой образ, аналог
мысленный или установленный изображение, описание,
схема, чертеж, карта и т. п. какого-либо объема, процесса
или явления, используемый в качестве его заменителя
или представителя. Сам объект, процесс или явление
называется оригиналом данной модели.
Моделирование - это исследование какого-либо объекта
или системы объектов путем построения и изучения их
моделей. Это использование моделей для определения
или уточнения характеристик и рационализации
способов построения вновь конструируемых объектов

8.

Понятие модели и моделирования
Слово «модель» произошло от латинского слова «modulus», означает «мера»,
«образец». Его первоначальное значение было связано со строительным
искусством, и почти во всех европейских языках оно употреблялось для
обозначения образа или прообраза, или вещи, сходной в каком-то отношении с
другой вещью. Например, перед строительством здания, сооружения делали
его уменьшенную копию для обсуждения, улучшения, утверждения проекта.
Моделирование в научных исследованиях стало применяться еще в глубокой древности
и постепенно захватывало все новые области научных знаний: техническое
конструирование, строительство и архитектуру, астрономию, физику, химию, биологию
и, наконец, общественные науки. Большие успехи и признание практически во всех
отраслях современной науки принес методу моделирования ХХ век. Однако
методология моделирования долгое время развивалась отдельными науками
независимо друг от друга. Отсутствовала единая система понятий, единая
терминология. Лишь постепенно стала осознаваться роль моделирования как
универсального метода научного познания.

9.

Понятия модели и моделирования
Модель выступает как своеобразный инструмент познания, который
исследователь ставит между собой и объектом, и с помощью которого изучает
интересующий его объект. Именно эта особенность метода моделирования
определяет специфические формы использования абстракций, аналогий,
гипотез, других категорий и методов познания.
В самом общем случае при построении модели исследователь отбрасывает те
характеристики, параметры объекта-оригинала, которые несущественны для
изучения объекта. Выбор характеристик объекта-оригинала, которые при этом
сохраняются и войдут в модель, определяется целями моделирования. Обычно
такой процесс абстрагирования от несущественных параметров объекта
называют формализацией. Более точно, формализация - это замена реального
объекта или процесса его формальным описанием.
Основное требование, предъявляемое к моделям – это их адекватность
реальным процессам или объектам, которые замещает модель.

10.

Понятия модели и моделирования
Модель - это такой материальный или мысленно представляемый, то есть
информационный объект, который в процессе исследования замещает объекторигинал, обладая его существенными информационными свойствами (качественнологическими и количественно-математическими), то есть характером отношений
между элементами изучаемого объекта и его отношений к другим объектам
физической реальности, так, что изучение модели дает новые знания об объектеоригинале. Более строго, по сути модель представляет собой вид информационной
системы, копирующей целевые системы (информационные, энергетические,
вещественные), и предназначенной для изучения свойств последних. По форме
модель может быть воплощена на любом физическом носителе: вещественном
изделии, компьютерной программе, мозге животных.
Моделирование - процесс построения, изучения и применения моделей. Оно тесно
связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс
моделирования обязательно включает и построение абстракций, и умозаключения по
аналогии, и конструирование научных гипотез. Главная особенность моделирования в
том, что это метод опосредованного познания с помощью объектов-заместителей.

11.

Понятие модели и моделирования
Цели создания
математических
моделей
1.
Модели помогают выделить суть или объединить и
выразить с помощью нескольких параметров важные разрозненные
свойства большого числа уникальных наблюдений, что облегчает
исследователю анализ рассматриваемого процесса или проблемы.
2.
Модели выступают в качестве "общего языка", с помощью
которого может быть описано каждое уникальное явление, и
относительные свойства таких явлений становятся более понятными.
3.
Модель может служить образцом "идеального объекта" или
идеализированного поведения, при сравнении с которым можно
оценивать и измерять реальные объекты и процессы.
4.
Модели действительно могут пролить свет на реальный
мир, несовершенными имитациями которого они являются.

12.

Понятия модели и моделирования
Два подхода в
моделировании:
натурное и
абстрактное
моделирование.
Натурная модель, физическая модель - это модель копия объекта, выполненная из другого материала, в
другом масштабе, с отсутствием ряда деталей.
Например, это игрушечный кораблик, домик из
кубиков, деревянная модель самолета в натуральную
величину, используемая в авиаконструировании и др.
Абстрактная модель, информационная модель - это
модель отображающая реальность путем не
вещественных, а информационных связей - словесным
описанием в свободной форме, описанием,
формализованным
по
каким-то
правилам,
математическими соотношениями и т.п.

13.

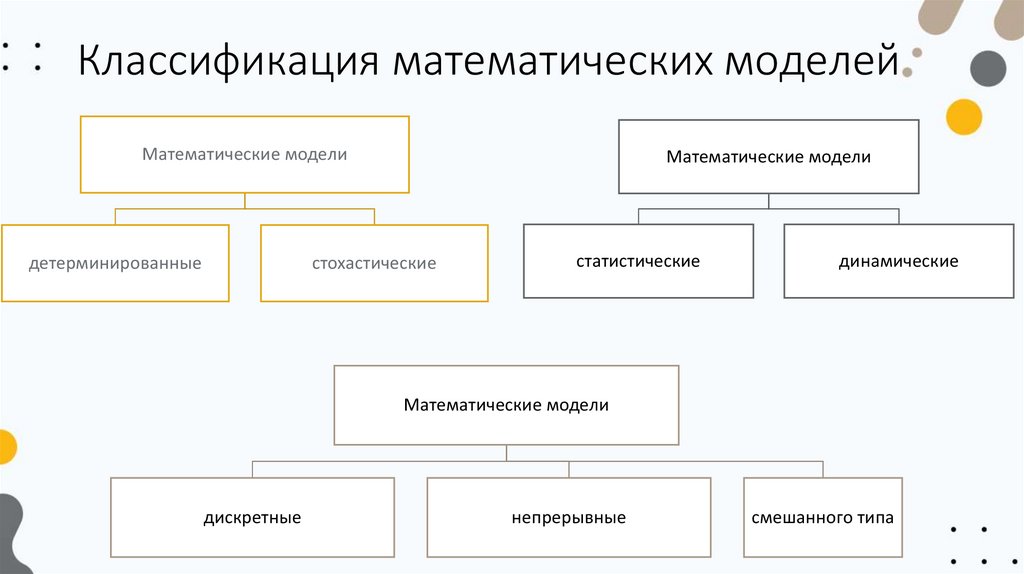
Классификация математических моделей
Математические модели
детерминированные
Математические модели
стохастические
статистические
динамические
Математические модели
дискретные
непрерывные
смешанного типа

14.

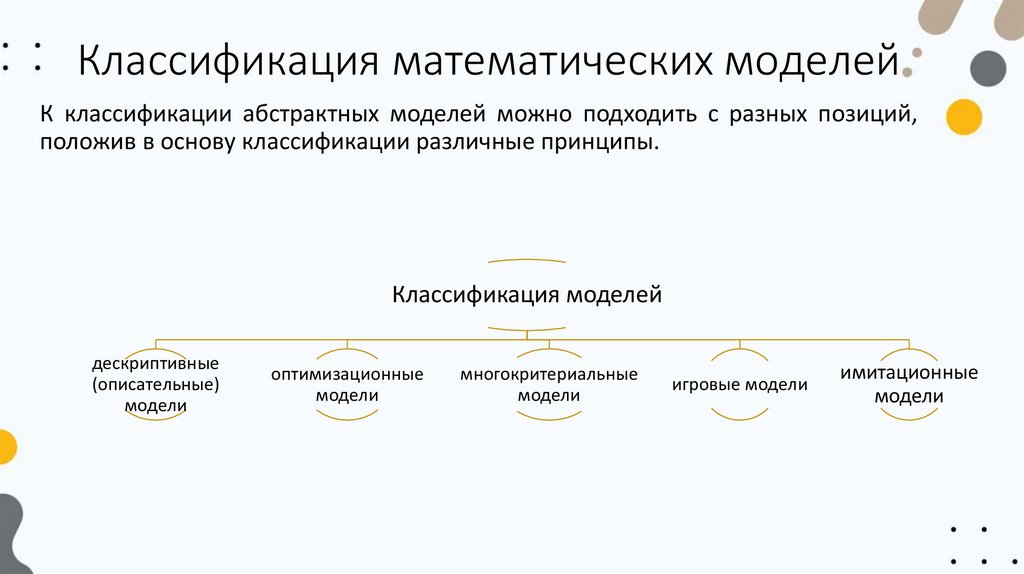
Классификация математических моделей
К классификации абстрактных моделей можно подходить с разных позиций,
положив в основу классификации различные принципы.
Классификация моделей
дескриптивные
(описательные)
модели
оптимизационные
модели
многокритериальные
модели
игровые модели
имитационные
модели

15.

Классификация абстрактных моделей
Классификация абстрактных моделей
детерминированные
стохастические
(вероятностные)
В детерминированных моделях входные параметры поддаются
измерению однозначно и с любой степенью точности, т.е. являются
детерминированными величинами. Соответственно, процесс
эволюции такой системы детерминирован.
В стохастических моделях значения входных параметров известны
лишь с определенной степенью вероятности, т.е. эти параметры
являются стохастическими; соответственно, случайным будет и
процесс эволюции системы. При этом, выходные параметры
стохастической модели могут быть как величинами
вероятностными, так и однозначно определяемыми.

16.

Классификация абстрактных моделей
Непрерывные детерминистские модели
системы с сосредоточенными
параметрами
системы с распределенными
параметрами
Системы с сосредоточенными параметрами описываются с помощью
конечного числа обыкновенных дифференциальных уравнений для
зависящих от времени переменных. Пространство состояний имеет здесь
конечную размерность (число степеней свободы системы конечно).
Под системами с распределенными параметрами понимают системы,
описываемые конечным числом дифференциальных уравнений в частных
производных. Здесь переменные состояния в каждый момент времени
есть функции одной или нескольких пространственных переменных.
Пространство состояний имеет в этом случае бесконечную размерность,
т.е. система обладает бесконечным числом степеней свободы.

17.

Классификация абстрактных моделей
Вербальные модели, словесные, текстовые модели - эти модели используют последовательности
предложений на формализованных диалектах естественного языка для описания той или иной области
действительности (примерами такого рода моделей являются ГОСТы, протоколы, договоры, правила
дорожного движения). Отличительной особенностью таких моделей является их удобная для понимания и
действия людей форма, но часто отсутствие необходимого уровня формализма для автоматизированной и
автоматической обработки данных.
Математические модели, численные модели - очень широкий класс знаковых моделей (основанных на
формальных языках над конечными алфавитами), использующих те или иные математические методы.
Например, математическая модель маятника будет представлять собой систему уравнений, описывающих
движение массы, происходящее в под воздействием внешней силы и механических связей, ограничивающих
движение массы. Отличительной особенностью численно-математических моделей является их способность
дать точную информацию о количественных характеристиках процесса, происходящего в модели и
практически полная неспособность решать качественно-логические задачи.
Информационно-коммуникационные модели - класс знаковых моделей, описывающих информационные
процессы (получение, передачу, обработку, хранение и использование информации) в системах самой
разнообразной природы. Примерами таких моделей могут служить OSI - семиуровневая модель
взаимодействия открытых систем в компьютерных сетях, или машина Тьюринга - универсальная
алгоритмическая модель.

18.

Классификация абстрактных моделей
Виды
абстрактных
моделей:
чисто аналитические
математические модели, не
использующие компьютерных
средств;
информационные модели,
имеющие приложения в
информационных системах;
вербальные языковые модели;
компьютерные модели, которые
могут использоваться для:
численного математического моделирования;
визуализации явлений и процессов (как для
аналитических, так и для численных моделей);
специализированных прикладных технологий,
использующих компьютер (как правило, в режиме
реального времени) в сочетании с измерительной
аппаратурой, датчиками и т.п.

19.

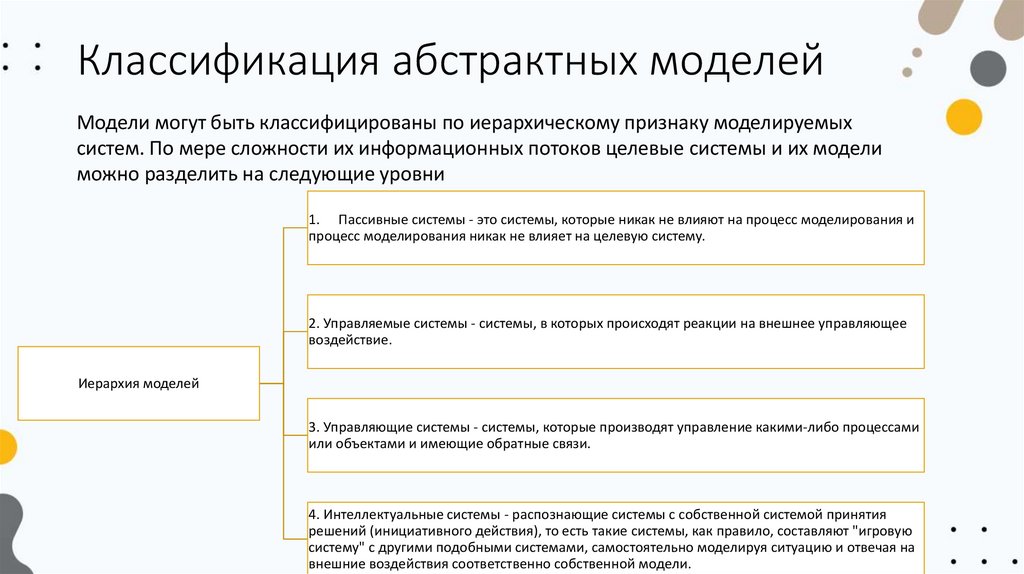
Классификация абстрактных моделей
Модели могут быть классифицированы по иерархическому признаку моделируемых
систем. По мере сложности их информационных потоков целевые системы и их модели
можно разделить на следующие уровни
1. Пассивные системы - это системы, которые никак не влияют на процесс моделирования и
процесс моделирования никак не влияет на целевую систему.
2. Управляемые системы - системы, в которых происходят реакции на внешнее управляющее
воздействие.
Иерархия моделей
3. Управляющие системы - системы, которые производят управление какими-либо процессами
или объектами и имеющие обратные связи.
4. Интеллектуальные системы - распознающие системы с собственной системой принятия
решений (инициативного действия), то есть такие системы, как правило, составляют "игровую
систему" с другими подобными системами, самостоятельно моделируя ситуацию и отвечая на
внешние воздействия соответственно собственной модели.

20.

Принципы моделирования
Основные принципы моделирования
Принцип
информационной
достаточности
При полном отсутствии
информации об объекте
построить модель
невозможно. При
наличии полной
информации
моделирование лишено
смысла. Существует
уровень
информационной
достаточности, при
достижении которого
может быть построена
модель системы.
Принцип
осуществимости
Создаваемая модель
должна обеспечивать
достижение
поставленной цели
исследования за
конечное время.
Принцип
множественности
моделей
Любая конкретная
модель отражает лишь
некоторые стороны
реальной системы. Для
полного исследования
необходимо построить
ряд моделей
исследуемого процесса,
причем каждая
последующая модель
должна уточнять
предыдущую.
Принцип системности
Исследуемая система
представима в виде
совокупности
взаимодействующих
друг с другом
подсистем, которые
моделируются
стандартными
математическими
методами. При этом
свойства системы не
являются суммой
свойств ее элементов.
Принцип
параметризации
Некоторые
подсистемы
моделируемой
системы могут быть
охарактеризованы
единственным
параметром:
вектором, матрицей,
графиком, формулой.

21.

Понятие компьютерной модели
Компьютерная модель - компьютерная программа, работающая на отдельном
компьютере, суперкомпьютере или множестве взаимодействующих компьютеров
(вычислительных узлов), реализующая абстрактную, то есть информационную
модель некоторой системы. Компьютерные модели стали обычным инструментом
численно-математического моделирования и применяются в физике, астрофизике,
механике, химии, биологии, экономике, социологии, метеорологии, других науках и
прикладных задачах в различных областях радиоэлектроники, машиностроения,
автомобилестроения и проч. Компьютерные модели используются для получения
новых знаний о моделируемом объекте или для приближенной оценки поведения
систем, слишком сложных для логико-аналитического исследования.

22.

Понятие компьютерной модели
Компьютерное моделирование является одним из эффективных методов изучения
сложных систем. Компьютерные модели проще и удобнее исследовать в силу их
возможности проводить так называемые "вычислительные эксперименты", которые
на самом деле экспериментами не являются, так как информация берется не из
физического эксперимента, физической реальности, а из модельного представления
о ней, проводят в тех случаях, когда реальные эксперименты затруднены из-за
финансовых или физических препятствий или могут дать непредсказуемо опасный
результат. В случае корректной логики и корректной формализации на этапе
создания компьютерных моделей имеется возможность выявить основные факторы,
определяющие количественные свойства изучаемого объекта-оригинала (или целого
класса объектов), в частности, исследовать отклик моделируемой физической
системы на изменения ее параметров и начальных условий.

23.

Понятие компьютерной модели
Важнейшая
особенность
модели
состоит
в
возможности
неограниченного накопления специализированных знаний без потери
целостного взгляда на объект исследования. Моделирование процессов
в обществе, природе и технических системах - это основная компонента
системного подхода к познанию этих процессов и управлению ими.
Адекватность модели объекту исследований всегда ограничена и
зависит от цели моделирования. Всякая модель не учитывает некоторые
свойства оригинала и поэтому является его абстракцией. Смысл
абстрагирования
заключается
в
отвлечении
от
некоторых
несущественных в данном контексте свойств предмета и
одновременном выделении существенных свойств.

24.

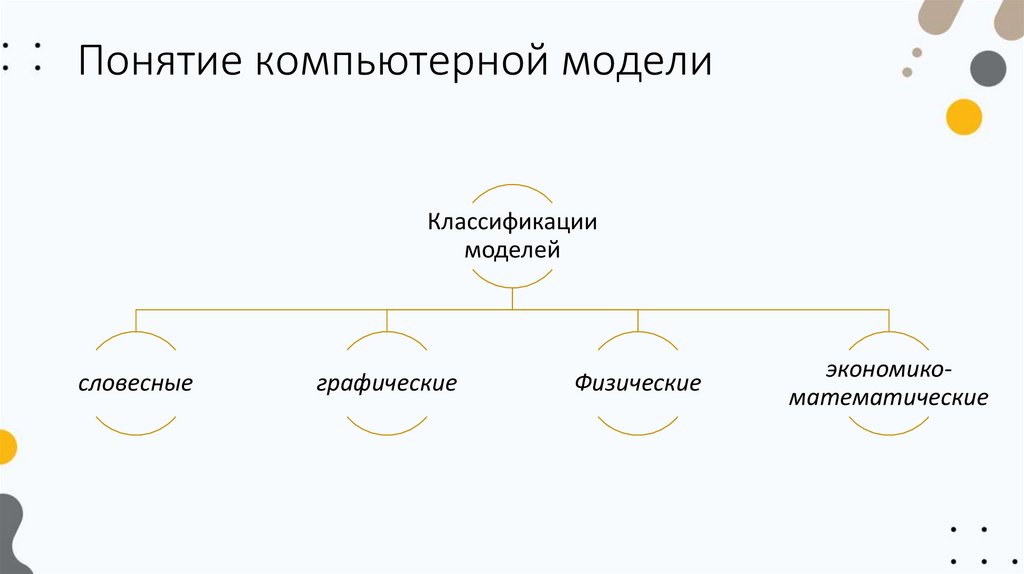
Понятие компьютерной модели
Классификации
моделей
словесные
графические
Физические
экономикоматематические

25.

Понятие компьютерной модели
Словесная, или монографическая, модель представляет собой
словесное описание объекта, явления или процесса. Очень часто она
выражается в виде определения, правила, теоремы, закона или их
совокупности.
Графическая модель создается в виде рисунка, географической карты
или чертежа.
Физические,
или
вещественные
модели
создаются
для
конструирования пока еще несуществующих объектов.
Экономико-математические
модели
отражают
наиболее
существенные свойства реального объекта или процесса с помощью
системы уравнений.

26.

Понятие компьютерной модели
По цели создания и
применения
различают модели:
• балансовые;
• эконометрические;
• оптимизационные;
• сетевые;
• систем массового обслуживания;
• имитационные (экспертные).
По учету фактора
неопределенности
различают модели:
• детерминированные (с однозначно определенными результатами);
• стохастические (с различными вероятностными результатами).
По типу
математического
аппарата различают
модели:
• линейного и нелинейного программирования;
• корреляционно-регрессионные;
• матричные;
• сетевые;
• теории игр;
• теории массового обслуживания и т.д.

27.

Основные этапы математического моделирования
1. Постановка задачи. Определение цели анализа и пути ее достижения и выработки общего подхода к исследуемой проблеме. На
этом этапе требуется глубокое понимание существа поставленной задачи. Иногда, правильно поставить задачу не менее сложно
чем ее решить. Постановка - процесс не формальный, общих правил нет.
2. Изучение теоретических основ и сбор информации об объекте оригинала. На этом этапе подбирается или разрабатывается
подходящая теория. Если ее нет, устанавливаются причинно-следственные связи между переменными описывающими объект.
Определяются входные и выходные данные, принимаются упрощающие предположения.
3. Формализация. Заключается в выборе системы условных обозначений и с их помощью записывать отношения между
составляющими объекта в виде математических выражений. Устанавливается класс задач, к которым может быть отнесена
полученная математическая модель объекта. Значения некоторых параметров на этом этапе еще могут быть не
конкретизированы.
4. Выбор метода решения. На этом этапе устанавливаются окончательные параметры моделей с учетом условия
функционирования объекта. Для полученной математической задачи выбирается какой-либо метод решения или разрабатывается
специальный метод. При выборе метода учитываются знания пользователя, его предпочтения, а также предпочтения
разработчика.
5. Реализация модели. Разработав алгоритм, пишется программа, которая отлаживается, тестируется и получается решение
нужной задачи.
6. Анализ полученной информации. Сопоставляется полученное и предполагаемое решение, проводится контроль погрешности
моделирования.
7. Проверка адекватности реальному объекту. Результаты, полученные по модели сопоставляются либо с имеющейся об объекте
информацией или проводится эксперимент и его результаты сопоставляются с расчётными.