3.1. Статические структуры данных (1)

1. Статические структуры данных

Множество
Вектор
Массив
Запись
Таблица
1

2. Свойства статических структур

• Рассматриваемые структуры (множества, векторы
массивы, записи, таблицы) характеризуются
следующими свойствами:
– Постоянство структуры в течение всего времени ее
существования
– Смежность элементов и непрерывность области памяти,
отводимой сразу для всех элементов структуры
– Простота и постоянство отношений между элементами
структуры, позволяющие исключить информацию об
этих отношениях и хранить ее в компактной форме в
дескрипторах.
• В силу перечисленных свойств такие элементы
называются часто статическими.
2

3. Вектор

• Одна из простейших структур данных, имеющаяся
во всех алгоритмических языках
• Вектор (одномерный массив) - конечное
упорядоченное множество простых данных, или
скаляров одного и того же типа, называемых
элементами вектора.
• Элементы вектора находятся друг с другом в
единственно возможном отношении-отношении
непосредственного следования.
• Строгая упорядоченность элементов вектора
позволяет пронумеровать их последовательными
целыми числами, которые называются индексами
3
элементов.

4. Логическая структура вектора

• В языках программирования описывается с
помощью соответствующих декларативных
предложений, полностью определяется
числом и типом элементов вектора.
• При описании логической структуры вектора
ему обычно присваивается имя
(идентификатор), указываются минимальное
и максимальное значения индекса и,
возможно, размер памяти для каждого из
элементов.
4

5. операции над вектором

• Операция доступа:
– принадлежности
– извлечения,
– изменения,
– включения
– исключения.
• Арифметические операции над векторами:
– сложение
– вычитание
– умножение
– деление
• Дополнительные операции:
– операции определения нижней и верхней границ индекса по
заданному имени вектора,
– операция, позволяющая получить описание элемента
вектора (например тип и длину).
5

6. Физическая структура вектора

• представляется в машинной памяти
последовательностью одинаковых по
длине участков памяти, называемых
полями или слотами, каждый из
которых предназначен для хранения
одного элемента вектора.
• Слот может иметь размер минимальной
адресуемой ячейки памяти или
соответствовать целой группе
последовательных ячеек памяти.
6

7. дескриптор

• Нередко физической структуре ставится в
соответствие дескриптор или заголовок, который
содержит общие сведения о физической структуре.
Дескриптор необходим, например в том случае,
когда граничные значения индексов элементов
массива неизвестны на этапе компиляции. Другие
названия дескриптора -допвектор,
информационный вектор и определяющий
вектор.
• Дескриптор состоит из полей, характер, число и
размеры которых зависят от той структуры,
которой поставлен в соответствие дескриптор.
• Кроме того, дескриптор обычно содержит
специальное кодовое поле,
7

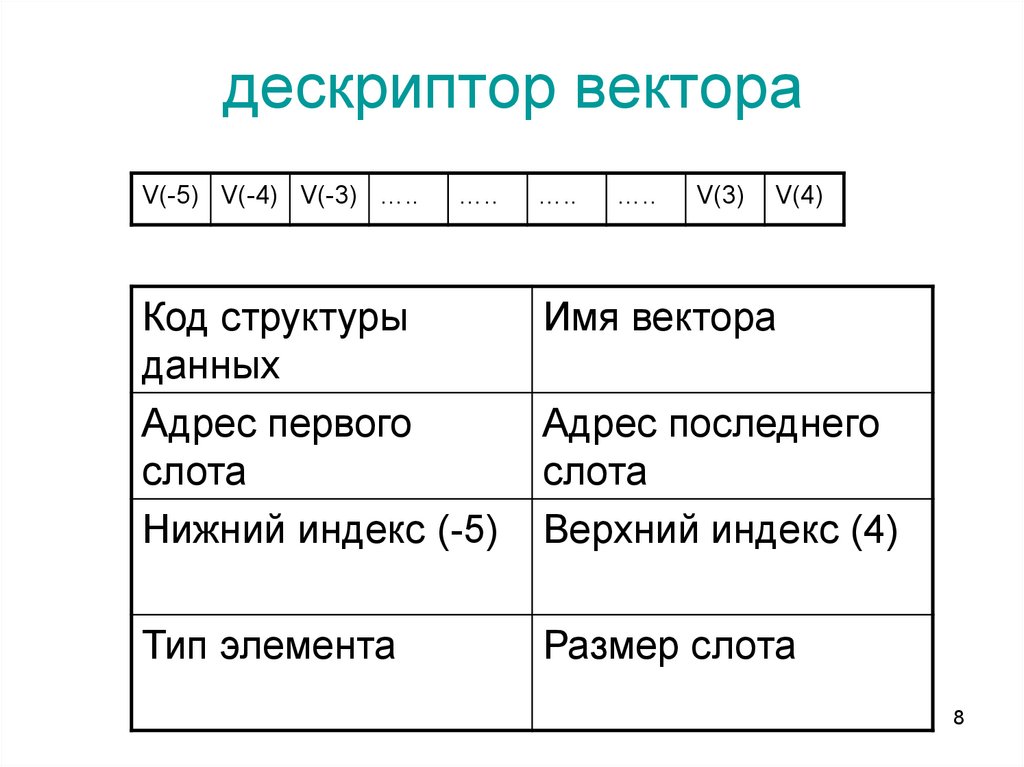
8. дескриптор вектора

V(-5) V(-4) V(-3) …..
…..
…..
…..
V(3)
V(4)
Код структуры
данных
Адрес первого
слота
Нижний индекс (-5)
Имя вектора
Тип элемента
Размер слота
Адрес последнего
слота
Верхний индекс (4)
8

9. Массив

• Массивом называется такой вектор,
каждый элемент которого - вектор. В свою
очередь, элементы вектора, являющиеся
элементами массива, могут быть векторами.
• Если массив состоит из векторов,
элементами которых являются простые
данные (скаляры), то логическая структура
такого массива может быть представлена
прямоугольной матрицей, у которой первый
индекс задает номер строки, а второй номер
столбца.
9

10. Логическая структура массива

• В языках программирования описывается с
помощью декларативных предложений.
• Доступ к его любому элементу
осуществляется с помощью имени массива
и упорядоченного набора индексов,
однозначно идентифицирующих элемент.
10

11. Преобразование логической структуры массива в физическую структуру

• на практике обычно используют два способа:
отображение строками и отображение столбцами.
• Преобразование логической структуры массива в
физическую структуру реализуется с помощью
подходящей функции упорядочения.
• Например: B(j1 , j2, ...., jn) - произвольный элемент nмерного массива
B(i1 , i2 , ...., in)- первый элемент массива
• Если длина слота равна 1-ой ячейке памяти, то адрес
произвольного элемента массива равен:
AD (B(j1 , j2 , ... , jn)) = AD(B(i1 , i2 , ... , in) )- 1 im Dm
+1 jm Dm , где Dm зависит от способа отображения
массива В.
• Для ускорения доступа к каждому элементу массива
можно заранее вычислить индексные множители 1Dm 11
для m=1,2,...,n и заполнить их в дескрипторе массива.

12. Дескриптор массива

Дескриптор массива отличается от дескриптора вектора.
Например дескриптор трехмерного массива
МАТR(2:3,4:6,1:5) с элементами целого типа по 2 байта
на каждый элемент имеет вид:
A-условный код массива
MATR-имя массива
AD(MATR(2,4,1)) адрес начала массива
AD(MATR(3,6,5)) адрес конца массива
3-размерность массива
Начальное знач. индекса(2,4,1)
конечное знач. индекса (3,6,5)
Знач. 30 e1D1Индекса 10 e2D2Множит.2 e3 D3
INTEGER тип данных
2
кол-во байтов
12

13. Вспомогательные дескрипторы для массива

• Из примера видно, что вычисление адреса элемента
многомерного массива может занять много времени,
поскольку при этом должны выполняться операции
сложения и умножения, число которых пропорционально
размерности массива. Операцию умножения можно
исключить, если применять следующий метод.
• Кроме основного дескриптора организуется несколько
уровней вспомогательных дескрипторов, называемых
векторами Айлиффа. Каждый вектор Айлиффа
определенного уровня содержит указатель Айлиффа
следующего, более низкого уровня, а векторы Айлиффа
самого нижнего уровня содержат указатели групп
элементов отображаемого массива. В этом случае
устраняется необходимость выполнения операций
умножения при определении адреса элемента массива,
приводит в то же время к увеличению суммарного объема
13
памяти, требуемого для представления массива.

14. Разновидности массива

• Разреженный массив - большинство
элементов которого равны нулю, так что
хранить в памяти необходимо лишь
небольшое число ненулевых значений
остальных элементов.
• Подходящей физической структурой
разреженного массива является не
вектор, а связный список.
14

15. Запись

• Запись- конечное упорядоченное
множество элементов, характеризующихся
в общем случае различным типом данных.
Часто элементы записи называются
полями.
• Запись - такое обобщение понятия вектора
(или одномерного массива), при котором
не требуется однотипность или
однородность.
15

16. простая запись

• Дескриптор записи может содержать:
– имя записи,
– число входящих элементов,
– имена и типы элементов,
– длины соответствующих полей,
– указатели значений элементов.
• Такая запись называется простой записью.
Для нее характерно то, что каждый элемент
является простым данным или цепочкой
простых данных одного и того же типа.
16

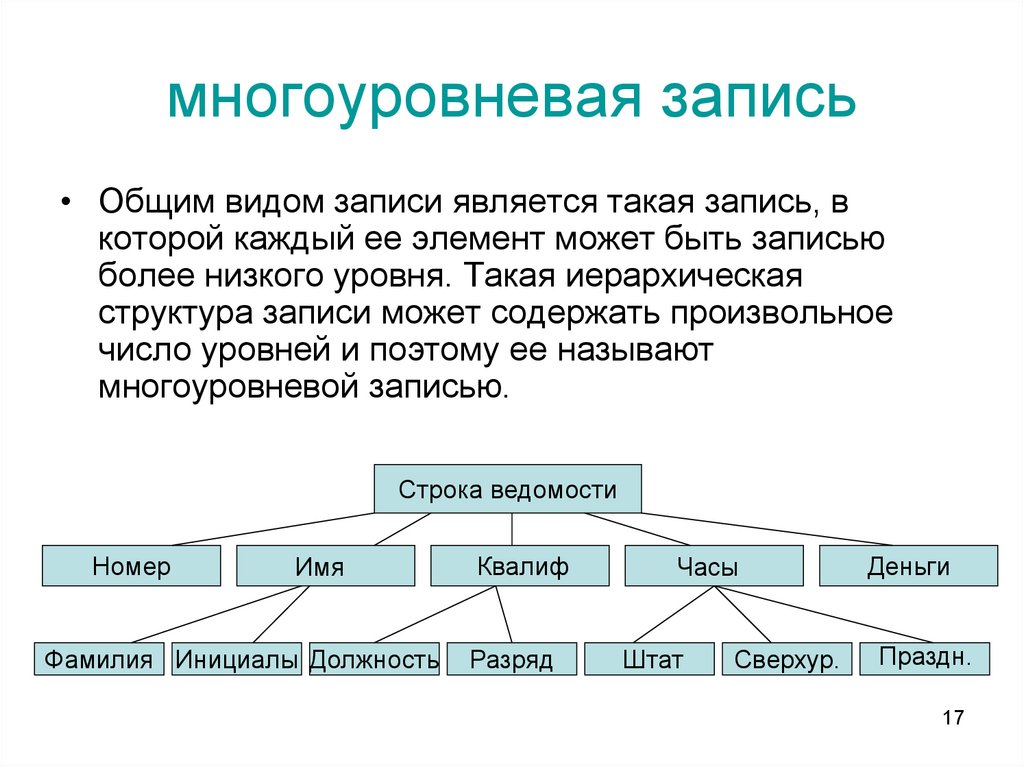
17. многоуровневая запись

• Общим видом записи является такая запись, в
которой каждый ее элемент может быть записью
более низкого уровня. Такая иерархическая
структура записи может содержать произвольное
число уровней и поэтому ее называют
многоуровневой записью.
Строка ведомости
Номер
Имя
Фамилия Инициалы Должность
Квалиф
Разряд
Часы
Штат
Сверхур.
Деньги
Праздн.
17

18. Дескриптор трехуровневой записи с именем ”Строка ведомости”

• кроме информации и
простой записи, может
содержать сведения об
элементах
промежуточных уровней
и о числе элементов
более низкого уровня,
подчиненного элементу
промежуточного уровня.
• REC-признак записи
Указатель
REС
I
строка ведомости
2
REС
Номер
Имя
S
10 Фамилия
S
4
2
Инициалы
REС
Квалификация
S
Должность
I
Разряд
REС
5
Часы
R
4
Штатные
R
4
Сверхурочные
R
4
Праздничные
R
4
Деньги
2
3
18

19. Таблица

• Конечное множество записей, имеющих одну и
ту же организацию называется таблицей.
• Каждая запись входящая в таблицу, называется
элементом таблицы.
• Таблица представляет собой такое обобщение
понятия двухмерного массива, в котором
свойство однотипности элементов массива
требуется лишь для элементов, расположенных
в одном и том же столбце.
19

20. Типичные операции над таблицей

– Доступ к каждому элементу таблицы осуществляется не с
помощью индексов (как для массива), а с помощью ключа,
причем целью служит не отдельное данное, а целая запись.
– включение нового элемента,
– поиск заданного элемента
– исключение заданного элемента из таблицы.
• Скорость выполнения этих операций зависит от числа
элементов таблицы, а также от выбранного способа
поиска заданного элемента таблицы.
• В том случае, когда таблица невелика и частота
обращения к ней мала, применяется последовательный
просмотр таблицы с начала до нахождения элемента с
заданным ключом.
20

21. Алгоритмы над статическими структурами

• Рассмотрим задачу выполнении
различных операций над многочленами
в символьной форме (сложение,
вычитание, умножение, деление,
дифференцирование и т. д.).
• Пусть, например, требуется составить
программу вычитания многочлена
x2+3xy+y2+y-x из 2x2+5xy+y2 ,
21

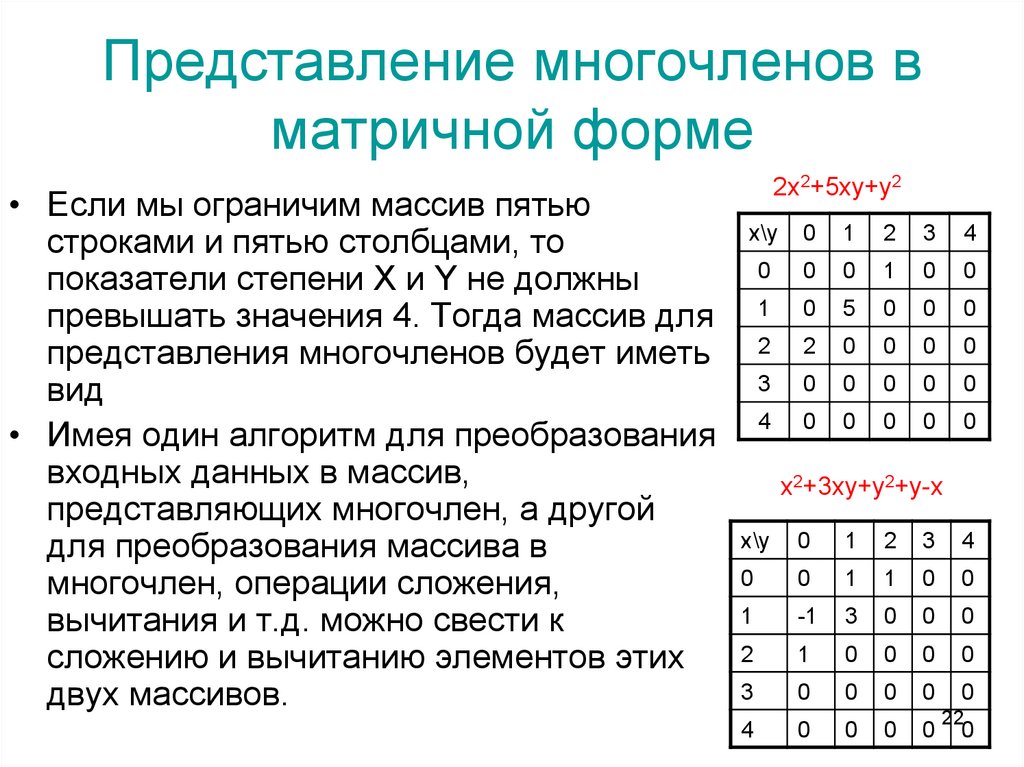
22. Представление многочленов в матричной форме

• Если мы ограничим массив пятью
строками и пятью столбцами, то
показатели степени X и Y не должны
превышать значения 4. Тогда массив для
представления многочленов будет иметь
вид
• Имея один алгоритм для преобразования
входных данных в массив,
представляющих многочлен, а другой
для преобразования массива в
многочлен, операции сложения,
вычитания и т.д. можно свести к
сложению и вычитанию элементов этих
двух массивов.
2x2+5xy+y2
x\y
0
1
2
3
4
0
0
0
1
0
0
1
0
5
0
0
0
2
2
0
0
0
0
3
0
0
0
0
0
4
0
0
0
0
0
x2+3xy+y2+y-x
x\y
0
1
2
3
4
0
0
1
1
0
0
1
-1
3
0
0
0
2
1
0
0
0
0
3
0
0
0
0
0
4
0
0
0
0
22
0

23. Анализ

• Здесь очевиден ряд недостатков
– массив содержит много нулей
– величина показателя степени ограничена.
• Возможны альтернативные алгоритмы
для представления многочленов и
операций над ними на основе других
структур.
23