9-Презентация+ДЗ-В-8

1.

Множество,
подмножество
Теория вероятностей-8

2.

В алгебре мы изучаем множество натуральных чисел, множество
целых чисел, в геометрии — множество точек на прямой,
множество многоугольников, в жизни мы сталкиваемся со
множеством событий, слов, окружающих предметов. Множества
также могут состоять из множества.
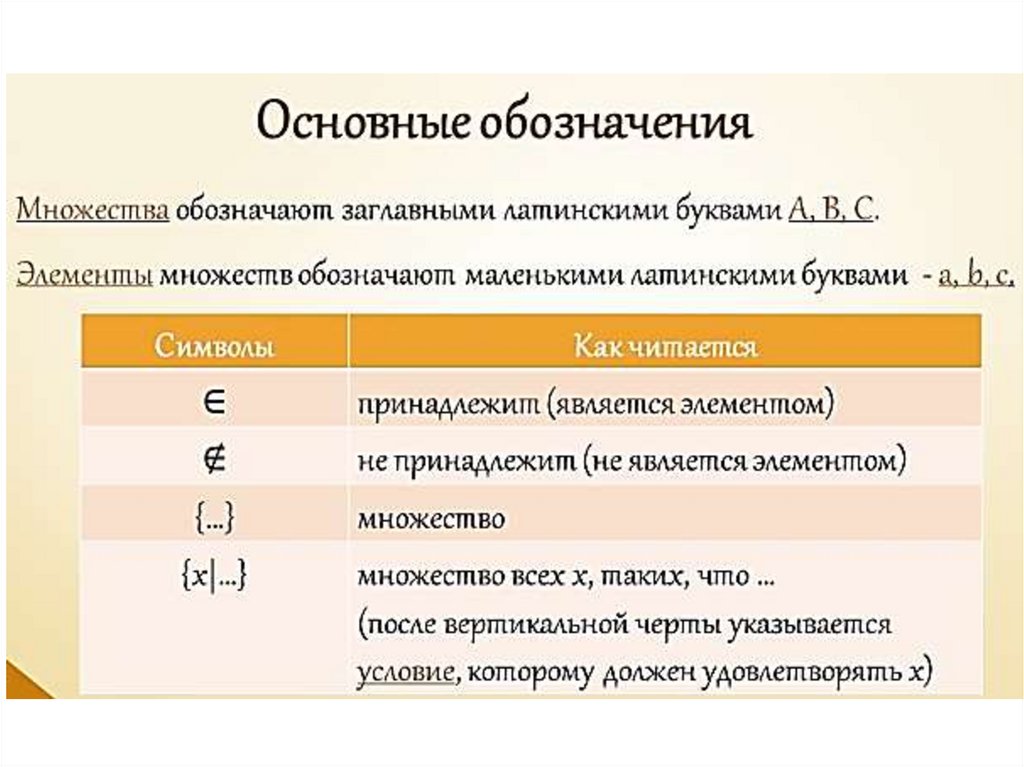
Объекты множества — это элементы множества.
Принадлежность элемента множеству обозначается
значком ∈.

3.

Пример:
Пусть A — это множество
однозначных натуральных чётных чисел.
Математическая запись данного
множества будет
следующей: A={2,4,6,8}.
Принадлежность числа 2
множеству A запишем 2∈A.
Число 3 не принадлежит множеству A,
математическая запись данного факта
— 3∉A.

4.

Множество, состоящее из конечного количества
элементов, называется конечным.
Множество, имеющее бесконечное количество
элементов, называется бесконечным.
Есть множество, состоящее из одного элемента.
Множество может и не иметь элементов.
Множество, не имеющее элементов,
называется пустым множеством.

5.

Пример:
A={2,4,6,8} — конечное множество
натуральных чётных однозначных
чисел;
B={5} — множество, состоящее из
одного элемента;
C=∅ — пустое множество;
D={1,2,3,4,5...} — бесконечное
множество натуральных чисел.

6.

Множество Y называется подмножеством X,
если любой элемент множества Y принадлежит
множеству X.
Математическая запись: Y⊂X.
ПРИМЕР:
множество A={2,4,6,8} является
подмножеством D={1,2,3,4,5...}.
Математическая запись: A⊂D.
Любое множество является подмножеством самого
себя, X⊂X.
Пустое множество является подмножеством любого
множества ∅⊂X.

7.

Множества равны (X=Y), если равны их элементы.
Любой элемент множества X принадлежит
множеству Y, а любой элемент
множества Y принадлежит множеству X.
ПРИМЕР:
{a,b,c,d}={d,c,b,a}.
Порядок расстановки элементов в
множествах неважен.
В числовых множествах принято элементы
записывать в порядке возрастания.

8.

Из множества множеств можно образовывать другие
множества.
В множестве растений содержится множество цветов.
Из множества вкусной еды и множества
полезных продуктов можно составить множество
полезно-вкусных блюд.
Множество ручек, множество карандашей, множество
линеек составляют множество канцелярских
принадлежностей.
Процесс образования дополнительных множеств
называют операциями над множествами.
Операции над множествами позволяют получать
новые множества.

9.

10.

1. Множества могут содержать одинаковые элементы.
Эти элементы образуют новое множество,
называемое пересечением данных множеств.
Пересечение обозначается значком ∩.
Пересечение множеств X и Y (X∩Y) —
это множество, содержащее элементы,
принадлежащие и множеству X, и
множеству Y.
Пример:
Множество домашних животных включает в себя элементы из
множества собак и множества кошек.
Множество законов математики, множество цифр, множество
математических обозначений пересекаются во множестве
формул.

11.

2. При объединении множеств в одно получим новое
объединение множеств.
Объединение обозначается значком ∪.
Объединение множеств X и Y (X∪Y) — это
множество, содержащее все элементы,
принадлежащие хотя бы одному из
множеств X и Y.
При объединении множеств общие элементы учитываются один раз.
Пример:
Множество треугольников, множество четырёхугольников,
множество замкнутых ломаных объединяются во множество
многоугольников.
Множество учащихся состоит из множества школьников и
множества студентов.

12.

3. Множества можем вычитать.
Разностью множеств X и Y называется множество,
содержащее все элементы множества X, но не
принадлежащие множеству Y. Математическая
запись разности множеств: X\Y.
Пример:
Если из множества грибов исключить множество ядовитых
грибов, то останется множество съедобных грибов.
При исключении из множества натуральных чисел множества
нечётных чисел получим множество чётных чисел.

13.

4. Любое множество можем дополнить элементами и
получим новое множество.
Под универсальным множеством понимают максимальное множество,
содержащее все возможные элементы.
Пример:
Множество всех чисел — уникальное множество.
Если к множеству растений добавим множество
животных, получим универсальное множество живой
природы.

14.

Пример:

15.

Задание 1
Даны два
множества X={6,16,26,32,40}, Y={10,16,22,32,40}.
Укажи элементы множества X∩Y.

16.

Задание 2
X — множество букв в слове «корень», Y — множество
букв слова «степень». Заполни таблицу.

17.

Задание 3

18.

Задание 4
Укажи множество корней уравнения −12,5x−8x2=0.
Решение уравнения начинай с вынесения общего
множителя за скобки.

19.

Задание 5
Укажи произведение элементов множества объединения
корней уравнений
(−6−x)(x+2)(2x−20)(11−x)=0 и 2x=x2.
(При решении второго уравнения собери все компоненты
слева, затем вынеси общий множитель.)

20.

Задание 6
Даны два множества
X={−3,11,32,34,49}, Y={8,11,24,34,49}.
Укажи элементы множества X∪Y.

21.

Задание 7
Множество C = {−4,4,12,16},
множество D = {−10,−4,6,12,16}.
Заполни пропуски, располагая числа в порядке
возрастания.

22.

Среди перечисленных ниже множеств укажите
конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.

23.

24.

множество
Множество
четырехугольников
Пространственные тела
Натуральные числа
Квадраты чисел
элемент
Трапеция, параллелограмм, ромб,
квадрат, прямоугольник
Шар, прямоугольный
параллелепипед, призма, пирамида,
октаэдр
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
Цифры десятичной
системы счисления
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
10, 12, 14, 16 … 96, 98

25.

Домашнее задание
Задание 1
Дано множество {−51;−30;−12;−4;11;37;56}, выбери его
подмножество, содержащее целые числа, кроме
натуральных.

26.

Домашнее задание
Задание 2
Даны два
множества X={4,16,27,33,38}, Y={13,16,20,33,38}.
Укажи элементы множества X∩Y.

27.

Домашнее задание
Задание 3
X — множество букв в слове «геометрия»,
Y — множество букв слова «алгебра».
Установи соответствие.