Вводная преза учителя системы и совокупности

1.

Системы и
совокупности
Вариант учителя
Выполнил: Пискунов Олег
Группа: 3121з

2.

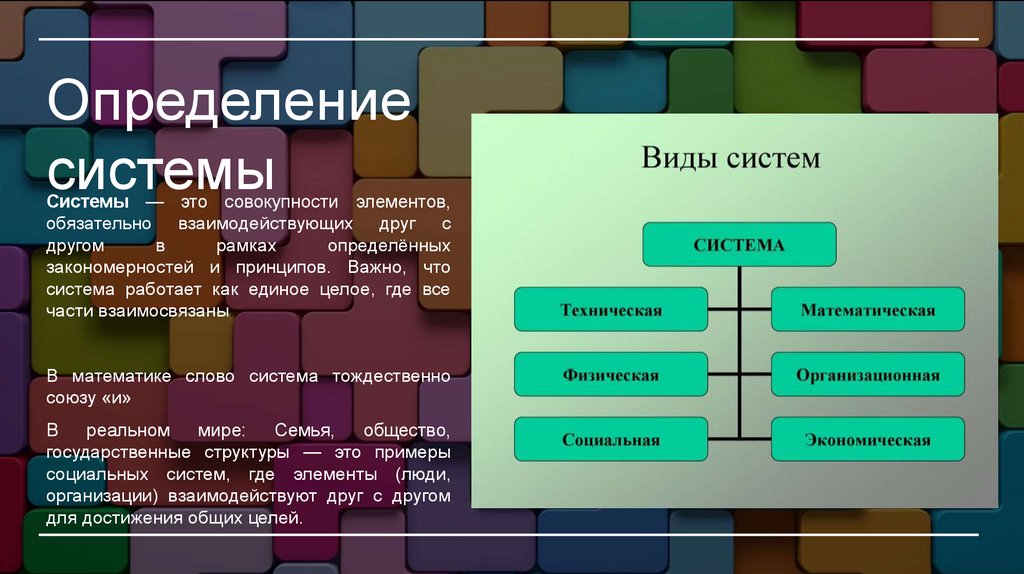
Определение
системы
Системы — это совокупности элементов,
обязательно взаимодействующих друг с
другом
в
рамках
определённых
закономерностей и принципов. Важно, что
система работает как единое целое, где все
части взаимосвязаны.
В математике слово система тождественно
союзу «и»
В
реальном
мире:
Семья,
общество,
государственные структуры — это примеры
социальных систем, где элементы (люди,
организации) взаимодействуют друг с другом
для достижения общих целей.

3.

Что такое совокупности?
Слово "совокупность" - это абстрактный
термин,
который
сам
зачастую
используется в определениях.
По своей сути совокупность - это некое
количество или множество чего-либо объектов или признаков объекта - и их
объединяет некий абстрактный признак.
При этом совокупностью чаще всего
называют количества или множества
абстрактных объектов.

4.

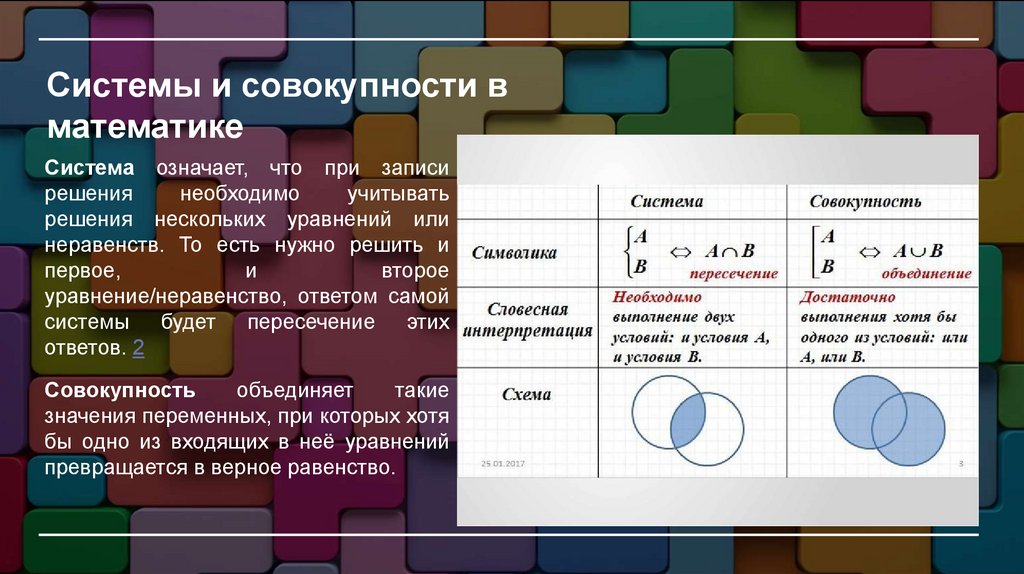
Системы и совокупности в
математике
Система означает, что при записи
решения
необходимо
учитывать
решения нескольких уравнений или
неравенств. То есть нужно решить и
первое,
и
второе
уравнение/неравенство, ответом самой
системы будет пересечение этих
ответов. 2
Совокупность
объединяет
такие
значения переменных, при которых хотя
бы одно из входящих в неё уравнений
превращается в верное равенство.

5.

Математика как язык для
описания систем
•Математические модели: Математика позволяет строить модели, которые
описывают поведение систем. Например, системы уравнений могут описывать
взаимодействие различных элементов системы, таких как в экономике, физике
или биологии.
•Анализ систем с помощью чисел и формул: Математика предоставляет
инструменты для количественной оценки взаимодействий в системах. Например,
использование статистики позволяет анализировать большие данные и выявлять
закономерности в социальных или экономических системах.
•Алгоритмы и оптимизация: В математике существуют алгоритмы, которые
помогают находить оптимальные решения для сложных систем. Например, в
логистике и транспортных системах, где необходимо минимизировать время
доставки или затраты.
•Дифференциальные уравнения: Математические уравнения, такие как
дифференциальные, позволяют моделировать процессы, которые меняются во
времени, например, рост популяций в экосистемах или изменения в экономике.

6.

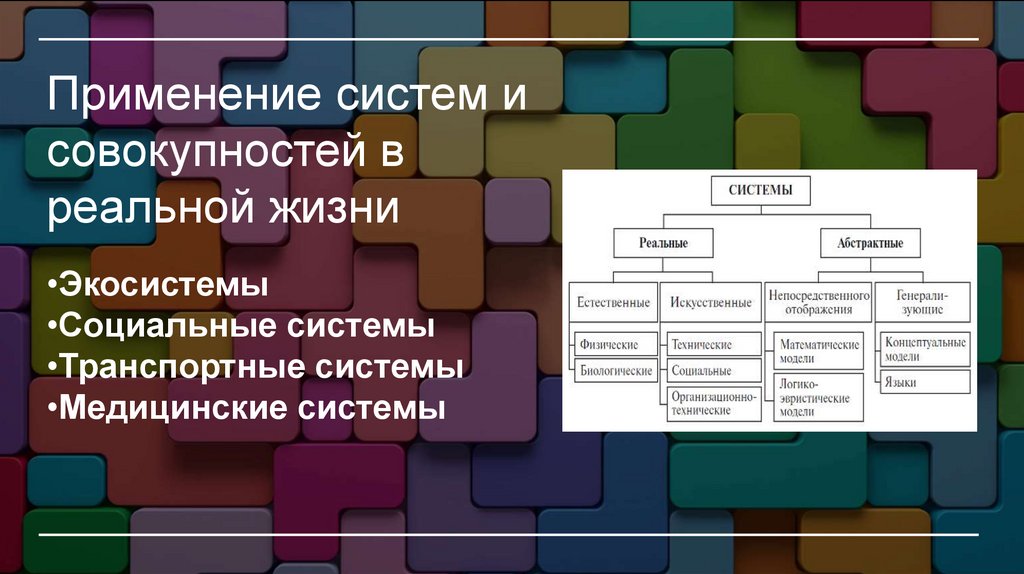
Применение систем и
совокупностей в
реальной жизни
•Экосистемы
•Социальные системы
•Транспортные системы
•Медицинские системы

7.

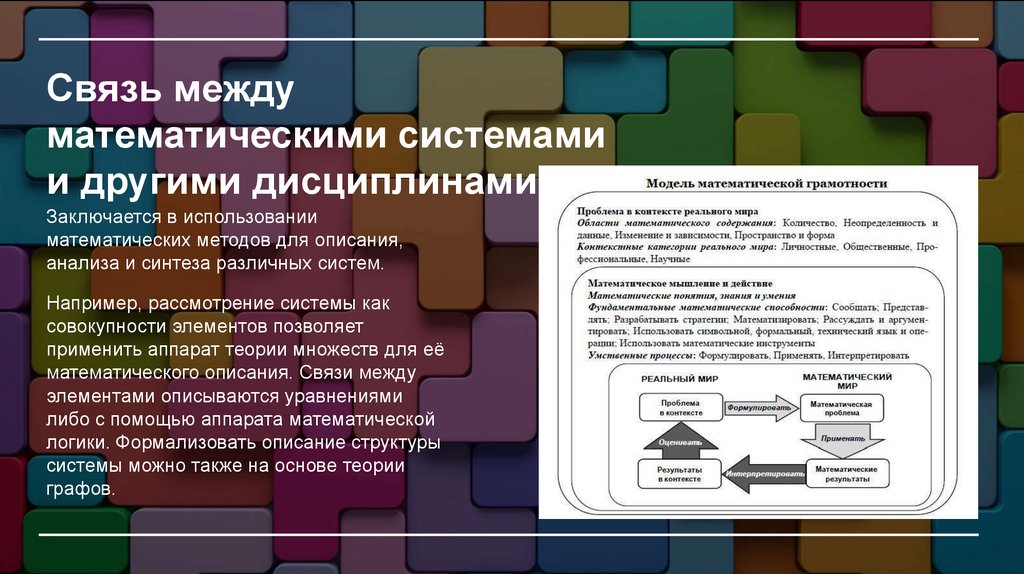
Связь между
математическими системами
и другими дисциплинами
Заключается в использовании
математических методов для описания,
анализа и синтеза различных систем.
Например, рассмотрение системы как
совокупности элементов позволяет
применить аппарат теории множеств для её
математического описания. Связи между
элементами описываются уравнениями
либо с помощью аппарата математической
логики. Формализовать описание структуры
системы можно также на основе теории
графов.

8.

Заключение
•Как можно описать поведение социальных систем с
помощью математики?
•Какие математические модели можно применить для
анализа экосистем?
•В чем заключаются основные отличия между системой и
совокупностью?
•Как математика помогает нам предсказывать будущее
развитие различных систем?