Тема 9.1. Алгебра логики. Таблицы истинности

1.

ИНФОРМАТИКА
МОДУЛЬ 3 Применение средств алгебры логики для описания функционирования персонального
компьютера
Лекция на тему:
АЛГЕБРА ЛОГИКИ
Лектор:
старший преподаватель
кафедры электроэнергетики и автоматики
Анисимова З.Г.

2.

Три основные смысла логики
Объективный
смысл –
закономерности в
изменении и
развитие вещей и
явлений
объективного мира.
Субъективный
смысл – как
совокупность правил,
которым подчиняется
процесс мышления.
Как наука – о правилах
рассуждений, о способах
и формах мышления,
которая изучает
абстрактное мышление
как средство познания
объективного мира.

3.

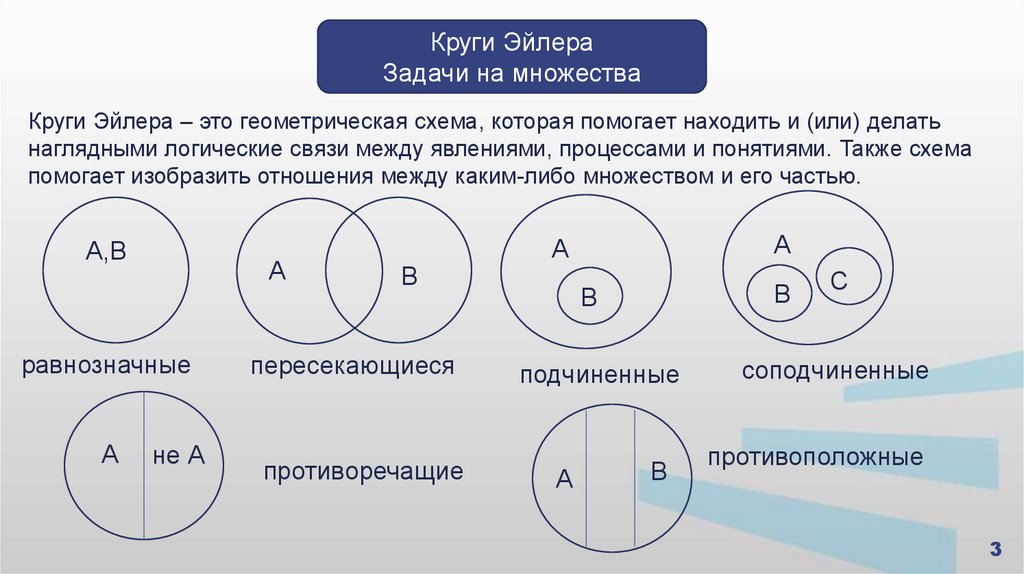
Круги Эйлера
Задачи на множества
Круги Эйлера – это геометрическая схема, которая помогает находить и (или) делать
наглядными логические связи между явлениями, процессами и понятиями. Также схема
помогает изобразить отношения между каким-либо множеством и его частью.
А,В
А
равнозначные
А
не А
В
А
А
В
В
пересекающиеся
подчиненные
противоречащие
В
А
С
соподчиненные
противоположные
3

4.

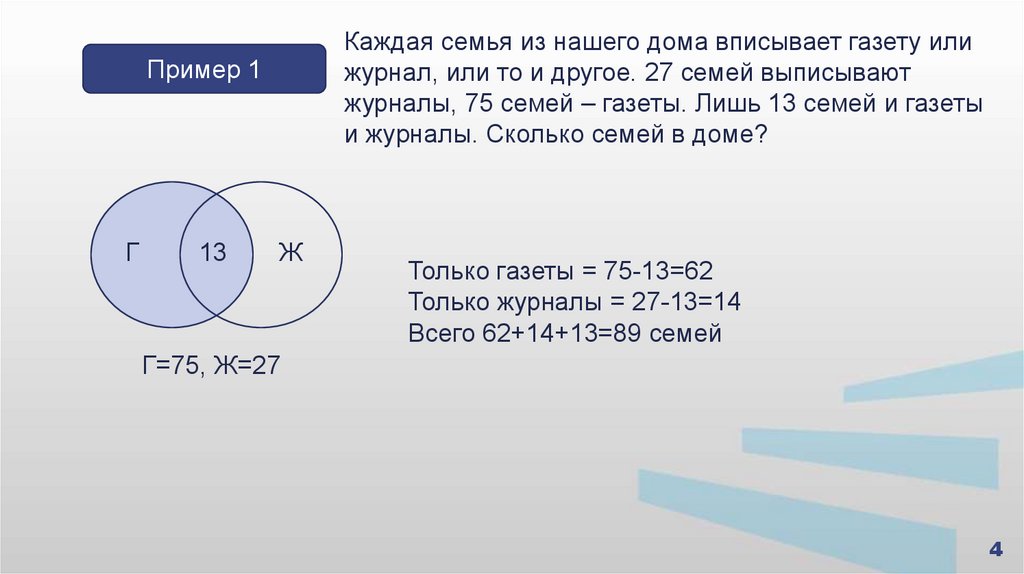
Каждая семья из нашего дома вписывает газету или
журнал, или то и другое. 27 семей выписывают
журналы, 75 семей – газеты. Лишь 13 семей и газеты
и журналы. Сколько семей в доме?
Пример 1
Г
13
Ж
Только газеты = 75-13=62
Только журналы = 27-13=14
Всего 62+14+13=89 семей
Г=75, Ж=27
4

5.

Пример 2
Поток из 100 студентов сдавал экзамен. 85 студентов сдали
английский язык, 73 студента сдали немецкий язык, 10 студентов
не сдали ни одного экзамена. Какое количество студентов сдало
экзамены и по английскому, и по немецкому языкам?
Так как 10 не сдавало, то всего сдавало 100-10=90
А
х
А=85, Н=27
Н
Только английский = 85-х
Только немецкий = 73-х
Всего (85-х)+(73-х)+х=90
Ответ х=68
5

6.

Пример 3
А
12-х
К
х
10-х
Ф
9-х
В группе 30 человек. 20 из них читают книги, 15 – слушают аудиокниги, 23
– смотрят фильмы, снятые по книгам, 10 – и читают книги и смотрят
фильмы, снятые по книгам; 12 – и читают книги и слушают аудиокниги; 9 –
и смотрят фильмы, снятые по книгам и слушают аудиокниги. Сколько
человек и читают книги, и слушают аудиокниги, и смотрят фильмы,
снятые по книгам.
К-читают книги
А-слушают аудиокниги
Ф-смотрят фильмы, снятые по книгам
Пусть Х-неизвестное кол-во человек, которые и читают книги, и слушают
аудиокниги, и смотрят фильмы, снятые по книгам.
Тогда читают книги и смотрят фильмы, снятые по книгам – (10-х) чел.,
Только слушают аудиокниги и смотрят фильмы, снятые по книгам – (9-х)
чел.,
Только читают книги и слушают аудиокниги – (12-х) чел.
6

7.

Х-6
А
12-х
Х-2
К
х
9-х
10-х
Ф
Х+4
Найдем, сколько человек читают только книги (К):
20-(12-х)-(10-х)-х=х-2
Аналогично получаем, слушают только аудиокниги (А):
15-(12-х)-(9-х)-х= х-6
смотрят только фильмы, снятые по книгам (Ф):
23-(10-х)-(9-х)-х=х+4
Так как всего 30 человек, составляем уравнение:
х+(12-х)+(9-х)+(х+4)+(х-2)+(х-6)=30
Получаем х=3.
7

8.

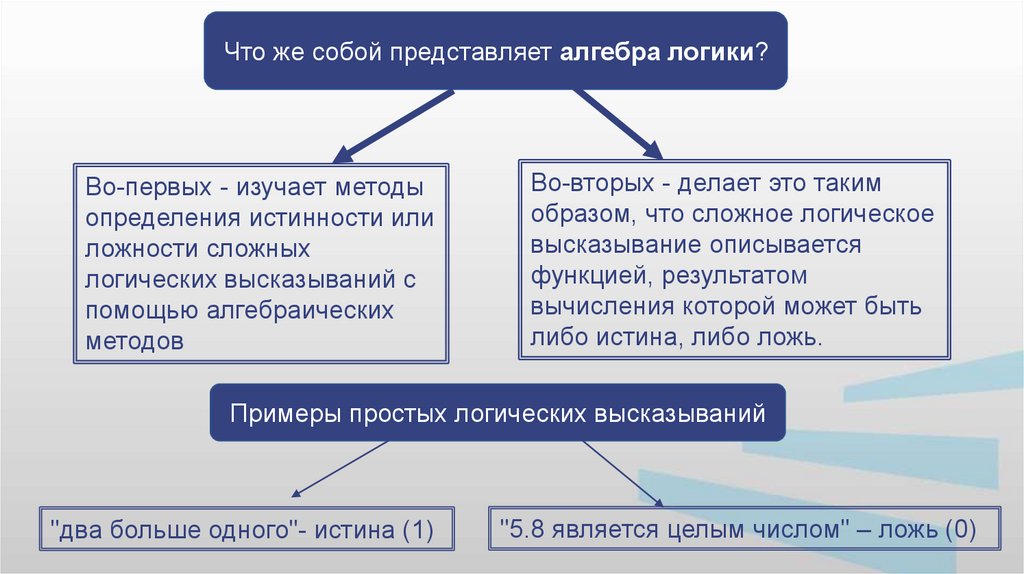
Что же собой представляет алгебра логики?
Во-первых - изучает методы
определения истинности или
ложности сложных
логических высказываний с
помощью алгебраических
методов
Во-вторых - делает это таким
образом, что сложное логическое
высказывание описывается
функцией, результатом
вычисления которой может быть
либо истина, либо ложь.
Примеры простых логических высказываний
"два больше одного"- истина (1)
"5.8 является целым числом" – ложь (0)

9.

Логическое высказывание – это любое повествовательное
предложение, про которое можно однозначно сказать, истинно оно
или ложно
"5 не равно 6"
"у него есть знания и навыки"
"она приедет во вторник, либо в среду"
"я буду смотреть телевизор, когда наступит вечер"

10.

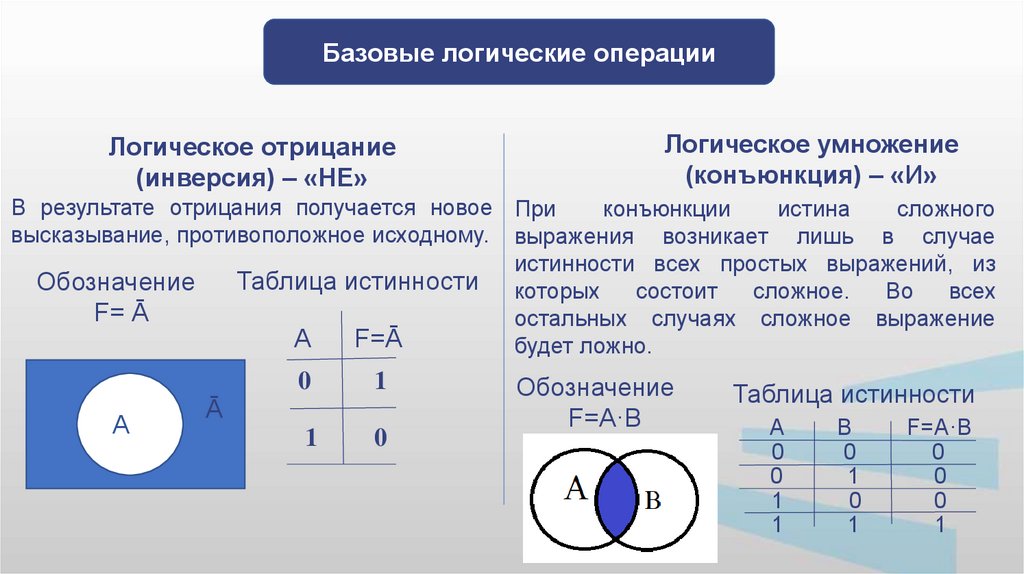
Базовые логические операции
Логическое отрицание
(инверсия) – «НЕ»
Логическое умножение
(конъюнкция) – «И»
В результате отрицания получается новое При
конъюнкции
истина
сложного
высказывание, противоположное исходному. выражения возникает лишь в случае
истинности всех простых выражений, из
Таблица истинности которых состоит сложное. Во всех
Обозначение
F= Ā
остальных случаях сложное выражение
F=Ā
А
будет ложно.
А
Ā
0
1
1
0
Обозначение
F=А·В
Таблица истинности
А
0
0
1
1
В
0
1
0
1
F=А·В
0
0
0
1

11.

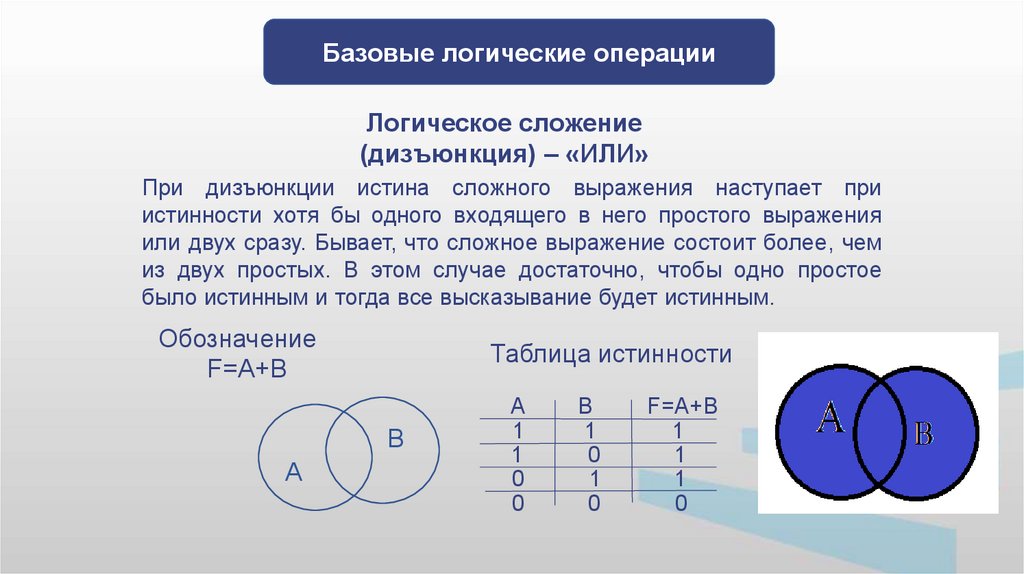
Базовые логические операции
Логическое сложение
(дизъюнкция) – «ИЛИ»
При дизъюнкции истина сложного выражения наступает при
истинности хотя бы одного входящего в него простого выражения
или двух сразу. Бывает, что сложное выражение состоит более, чем
из двух простых. В этом случае достаточно, чтобы одно простое
было истинным и тогда все высказывание будет истинным.
Обозначение
F=А+В
Таблица истинности
В
А
А
1
1
0
0
В
1
0
1
0
F=А+В
1
1
1
0

12.

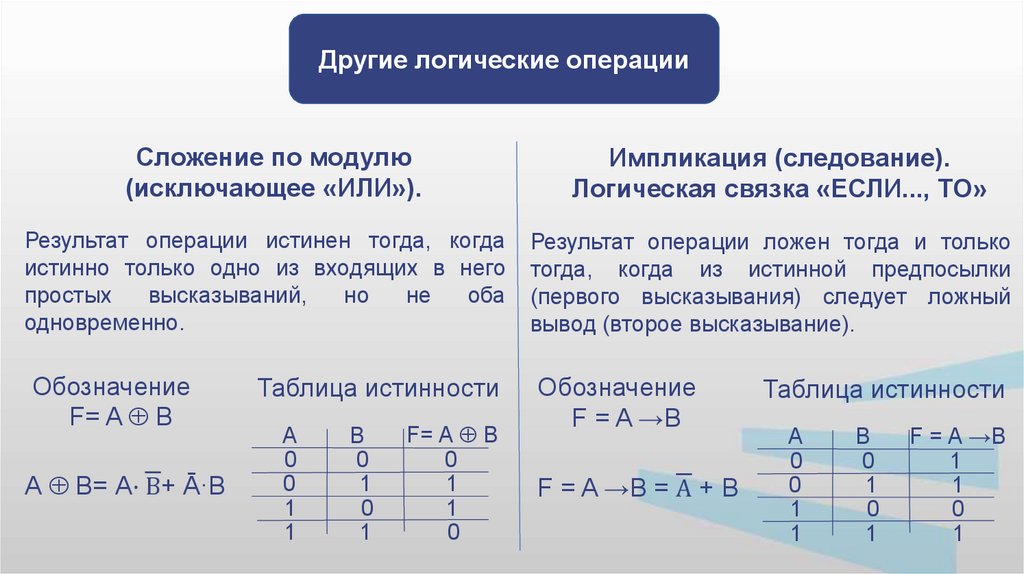
Другие логические операции
Сложение по модулю
(исключающее «ИЛИ»).
Импликация (следование).
Логическая связка «ЕСЛИ..., ТО»
Результат операции истинен тогда, когда
истинно только одно из входящих в него
простых
высказываний,
но
не
оба
одновременно.
Результат операции ложен тогда и только
тогда, когда из истинной предпосылки
(первого высказывания) следует ложный
вывод (второе высказывание).
Обозначение
F= A B
Обозначение
F = A →B
А В= А· В+ Ā·В
Таблица истинности
А
0
0
1
1
В
0
1
0
1
F= A B
0
1
1
0
F = A →B = А + B
Таблица истинности
А
0
0
1
1
В
0
1
0
1
F = A →B
1
1
0
1

13.

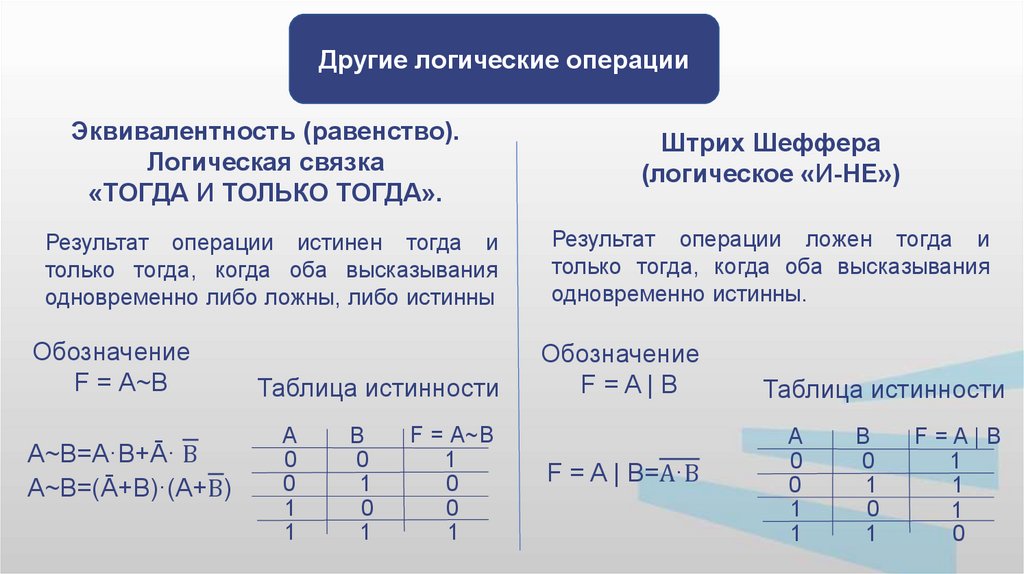
Другие логические операции
Эквивалентность (равенство).
Логическая связка
«ТОГДА И ТОЛЬКО ТОГДА».
Штрих Шеффера
(логическое «И-НЕ»)
Результат операции истинен тогда и
только тогда, когда оба высказывания
одновременно либо ложны, либо истинны
Результат операции ложен тогда и
только тогда, когда оба высказывания
одновременно истинны.
Обозначение
F = А~В
Обозначение
F=A|B
А~В=А·В+Ā· В
А~В=(Ā+В)·(А+В)
Таблица истинности
А
0
0
1
1
В
0
1
0
1
F = А~В
1
0
0
1
F = A | B=А·В
Таблица истинности
А
0
0
1
1
В
0
1
0
1
F=A|B
1
1
1
0

14.

Другие логические операции
Стрелка Пирса (логическое «ИЛИ-НЕ»).
Результат операции истинен тогда и только тогда, когда
оба высказывания одновременно ложны.
Обозначение
F=A B
F=A B=А + В
Таблица истинности
А
0
В
0
F=A B
1
0
1
0
1
0
0
1
1
0

15.

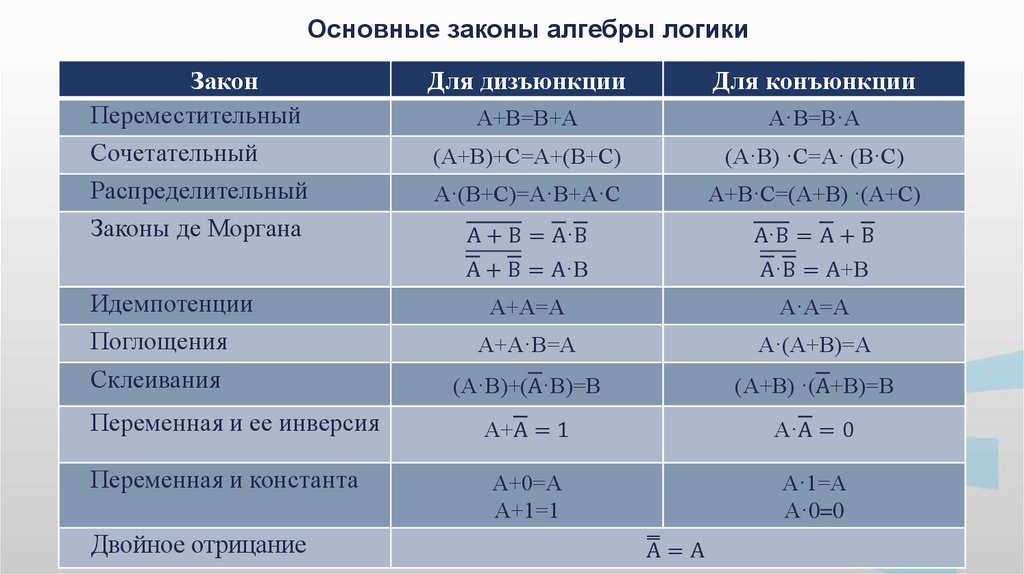
Основные законы алгебры логики
Закон
Переместительный
Сочетательный
Распределительный
Законы де Моргана
Для дизъюнкции
Для конъюнкции
А+В=В+А
А·В=В·А
(А+В)+С=А+(В+С)
(А·В) ·С=А· (В·С)
А·(В+С)=А·В+А·С
А+В·С=(А+В) ·(А+С)
А + В = А·В
А·В = А + В
А + В = А·В
А·В = А+В
А+А=А
А·А=А
А+А·В=А
А·(А+В)=А
(А·В)+(А·В)=В
(А+В) ·(А+В)=В
Переменная и ее инверсия
А+А = 1
А·А = 0
Переменная и константа
А+0=А
А+1=1
А·1=А
А·0=0
Идемпотенции
Поглощения
Склеивания
Двойное отрицание
ന=А
А

16.

Пример 4
«Поиск информации в Интернет».
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» (объединение) используется символ «|», а для
логической операции «И»(пересечение) – символ «&»
Запрос
Телефон | ноутбук
Телефон & ноутбук
Телефон
Найдено страниц
(в тысяч)
3400
900
2100
Какое количество страниц ( в тысячах)
будет найдено по запросу Ноутбук?
Считается, что все запросы
выполнялись практически
одновременно, так что набор страниц,
содержащих все искомые слова, не
изменялся за время выполнения
запросов.
16

17.

Решение: пусть Ф- количество страниц ( в тысячах) по запросу Телефон;
Э- количество страниц ( в тысячах) по запросу Ноутбук;
А- количество страниц ( в тысячах) по запросу , в котором упоминается
Телефон и не упоминается Ноутбук;
В- количество страниц ( в тысячах) по запросу , в котором упоминается
Ноутбук и не упоминается Телефон.
Построим диаграммы Эйлера для каждого запроса:
Согласно диаграммам имеем:
1. А+900+В=Ф+В=2100+В=3400.
Отсюда находим В=3400-2100=1300.
2. Э=900+В=900+1300=2200
17

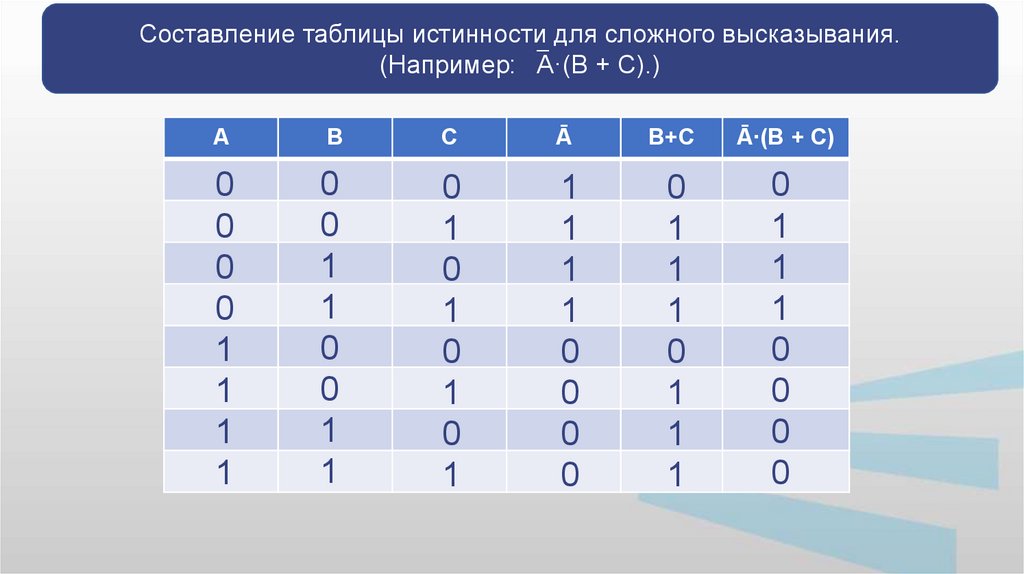
18.

Составление таблицы истинности для сложного высказывания.
(Например: А·(В + С).)
A
B
C
Ā
B+C
Ā·(В + С)
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0

19.

Спасибо за внимание