Лекция 7

1.

Численные методы
оптимизации

2.

Вопросы
• Постановка задачи оптимизации
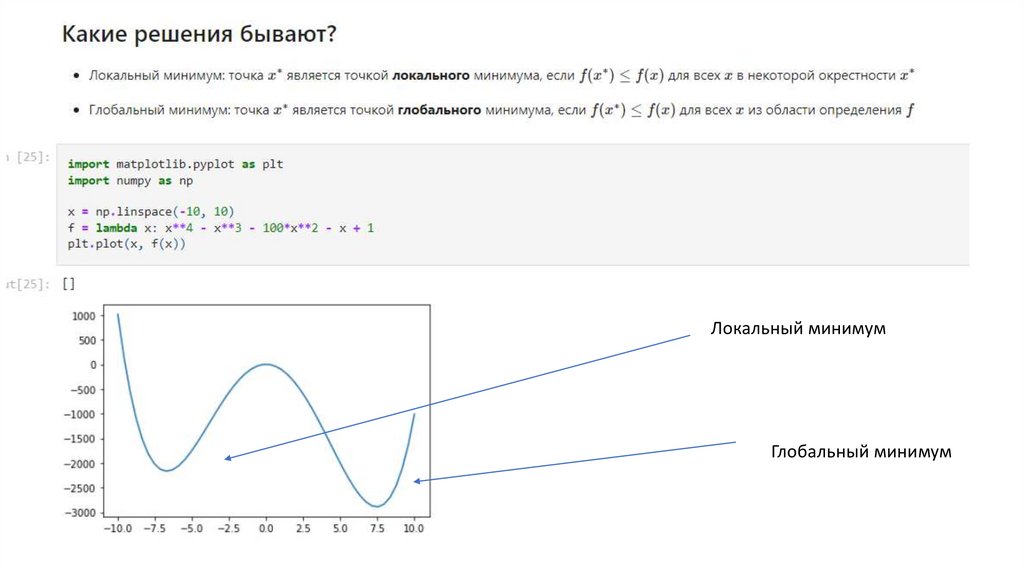
• Локальные и глобальные экстремумы
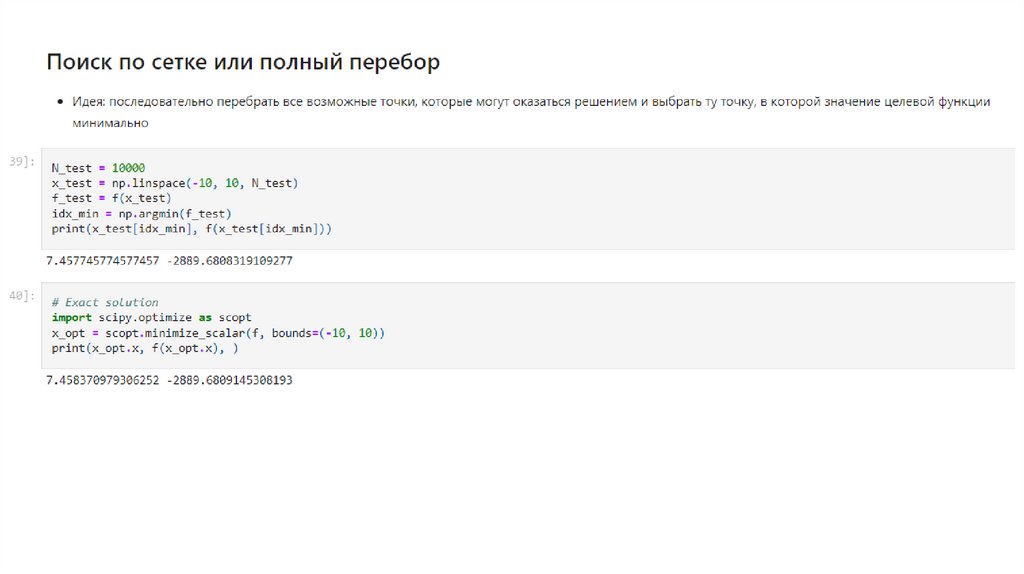
• Поиск по сетке
• Случайный поиск
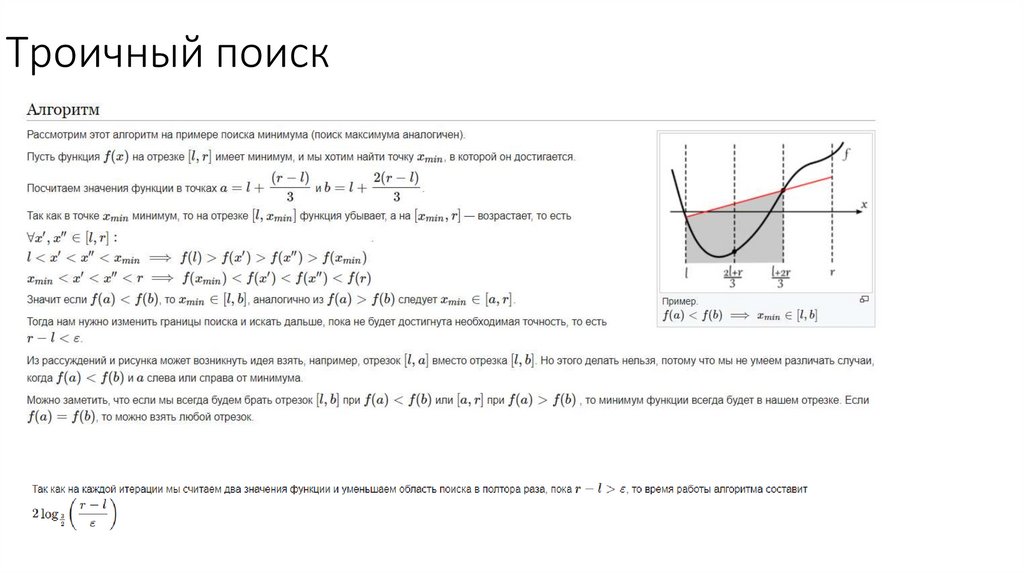
• Троичный поиск
• Метод градиентного спуска: деление шага, наискорейший
спуск
• Метод Ньютона

3.

4.

Локальный минимум
Глобальный минимум

5.

6.

Троичный поиск

7.

8.

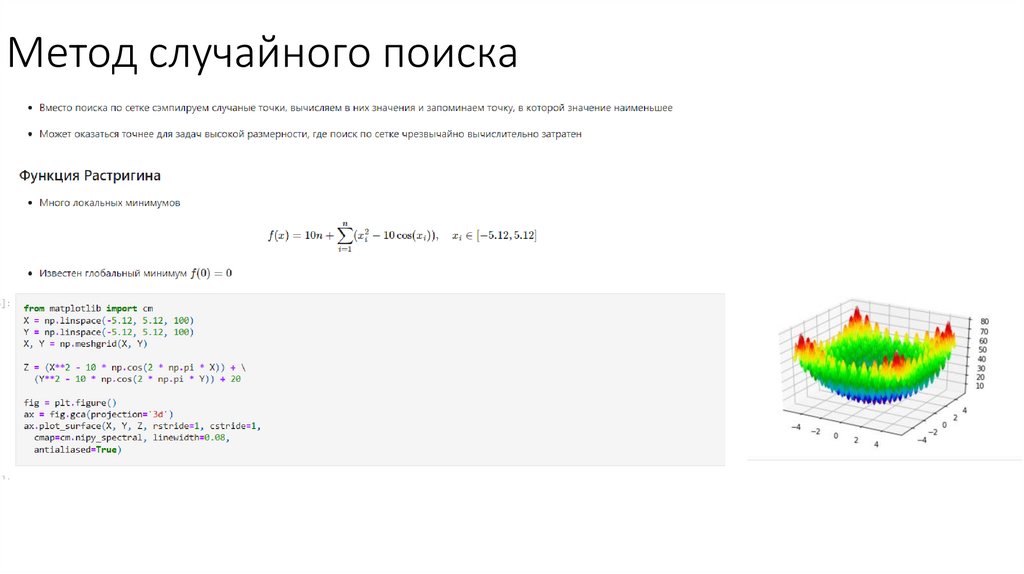
Метод случайного поиска

9.

Метод случайного поиска
• import scipy.optimize as scopt
• scipy.optimize.brute
минимизирует функцию на
заданном диапазоне,
вычисляя функцию на
многомерной сетке, чтобы
найти глобальный минимум
np.random.rand() Create an array of the given shape and populate it with random samples from a uniform
distribution over [0, 1).

10.

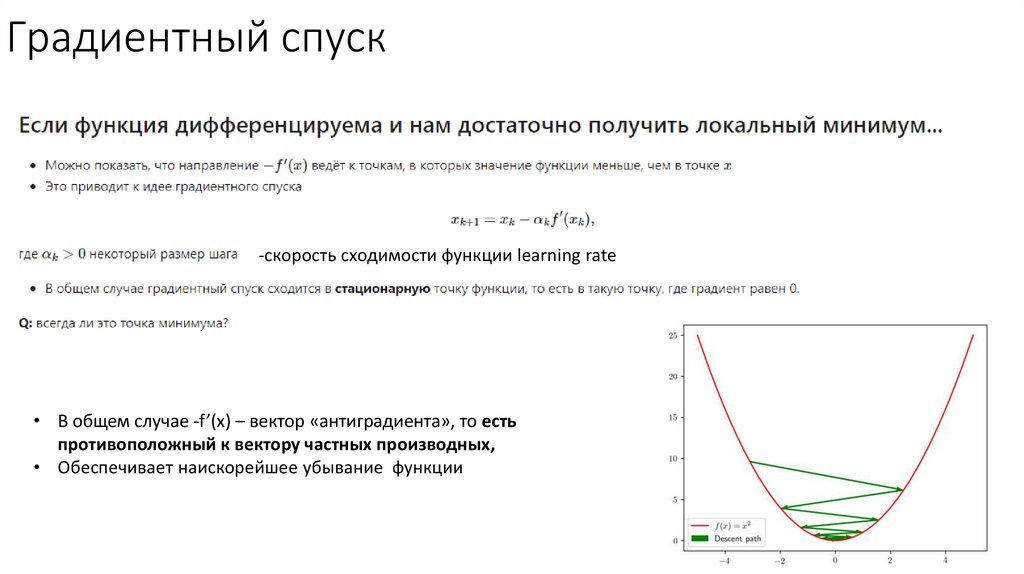
Градиентный спуск
-скорость сходимости функции learning rate
• В общем случае -f’(x) – вектор «антиградиента», то есть
противоположный к вектору частных производных,
• Обеспечивает наискорейшее убывание функции

11.

Градиентный спуск для функции n
переменных
Иногда просто пишут f’(x)

12.

Липшицев градиент

13.

14.

15.

Градиентный спуск для квадратичной выпуклой
функции
A > 0 – положительно определенная матрица, т. е. симметричная , для всех ненулевых x xTAx
>0
положи́ тельно определённая ма́трица — это симметричная матрица, которая во многом
аналогична положительному вещественному числу.

16.

Различные способы выбора шага и условие
останова

17.

2
2
Пример : x1 +x2 -2x1-4x2 -> min
import math
def f(x1, x2):
return pow(x1,2)+pow(x2,2)-2*x1 -4*x2
while (math.sqrt(pow(g1,2)+pow(g2,2)) >= eps):
def gradX(x1, x2):
y1 = x1 - L * g1
return 2*x1-2
y2 = x2 - L * g2
def gradY(x1, x2):
if (f(y1, y2) < fv):
return 2*x2-4
x1 = y1
L=1#
x2 = y2
x1 = 5 #
g1 = gradX(x1, x2)
x2 = 10 #
g2 = gradY(x1, x2)
eps = 0.001 # Точность(Е)
fv = f(x1,x2) #Значение функций двух переменных в
начальной точке(F1)
g1 = gradX(x1,x2)
g2 = gradY(x1,x2)
else:
L=L * 0.5 # Дробление шага
print (x1, x2) #Вывод ответа

18.

Наискорейший спуск

19.

Наискорейший спуск

20.

import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist

21.

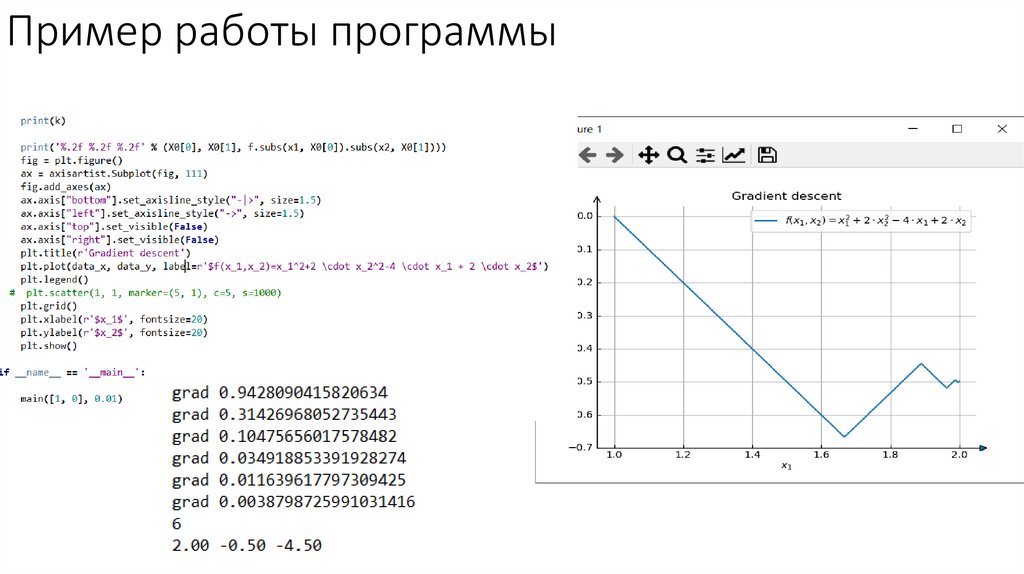
Пример работы программы

22.

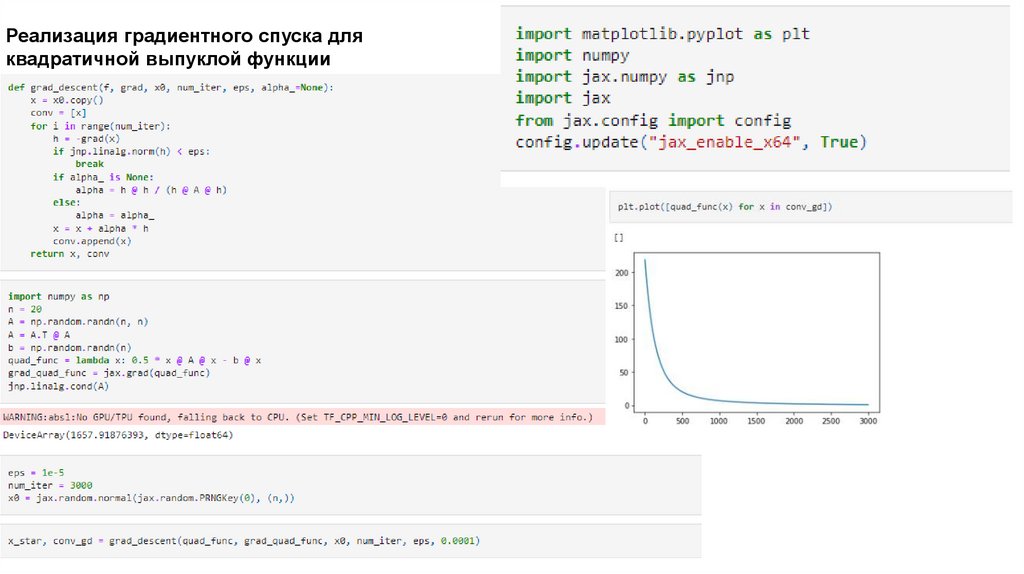
Квадратичная выпуклая функция

23.

Реализация градиентного спуска для
квадратичной выпуклой функции

24.

Оценка скорости г. с.

25.

26.

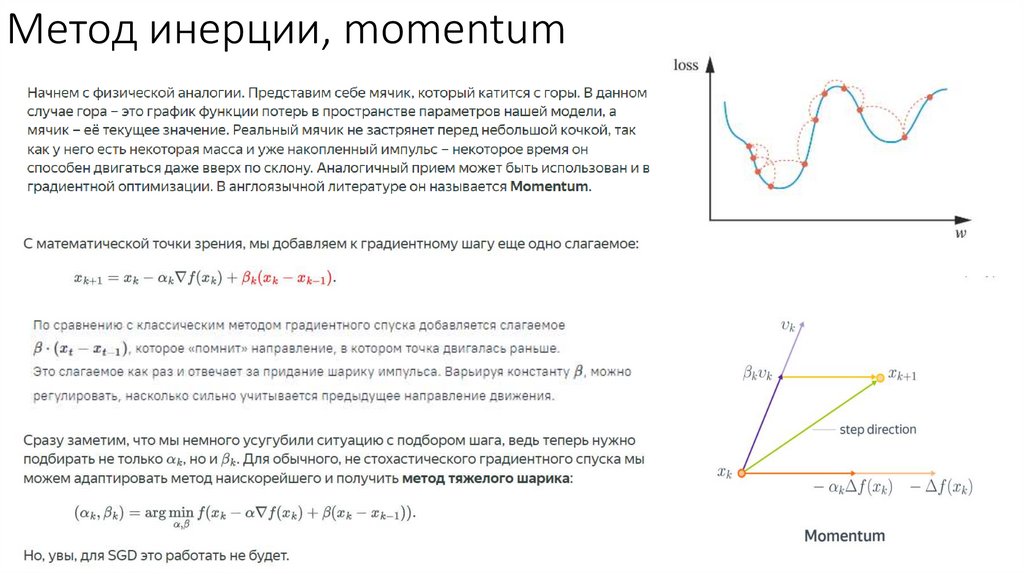
Метод инерции, momentum

27.

28.

Метод инерции, momentum

29.

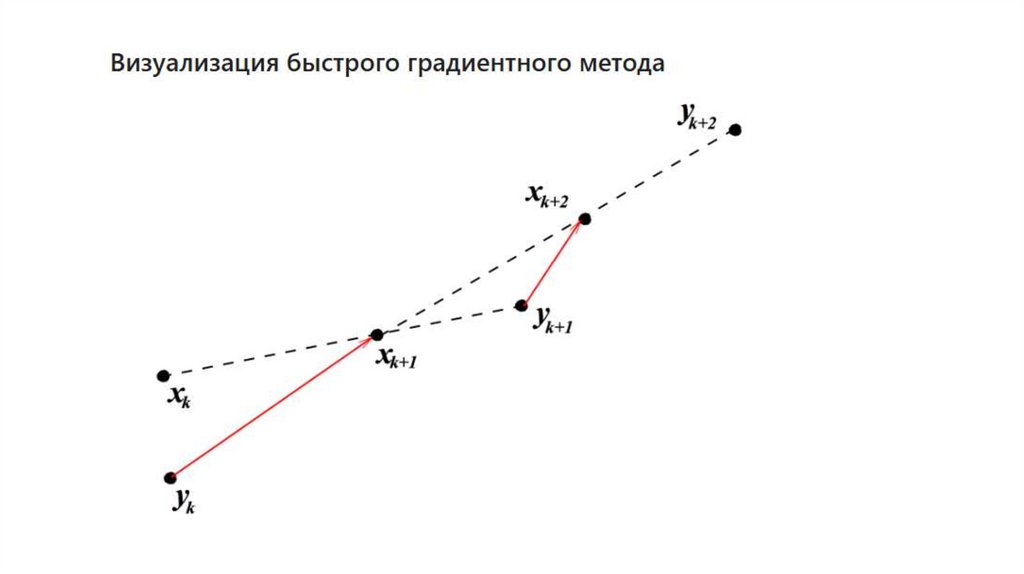
Момент Нестерова

30.

Момент Нестерова
Комментарий: иногда упоминается, что
Nesterov Momentum «заглядывает в
будущее» и исправляет ошибки на данном
шаге оптимизации. Конечно, никто не
заглядывает в будущее в буквальном
смысле.
В работе Нестерова были предложены
конкретные (и довольно магические)
константы для импульса, которые
получаются из некоторой еще более
магической последовательности. Мы
приводить их не будем, поскольку мы в
первую очередь заинтересованы

31.

32.

33.

https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Math/lectures/lecture10/lecture10.ipynb

34.

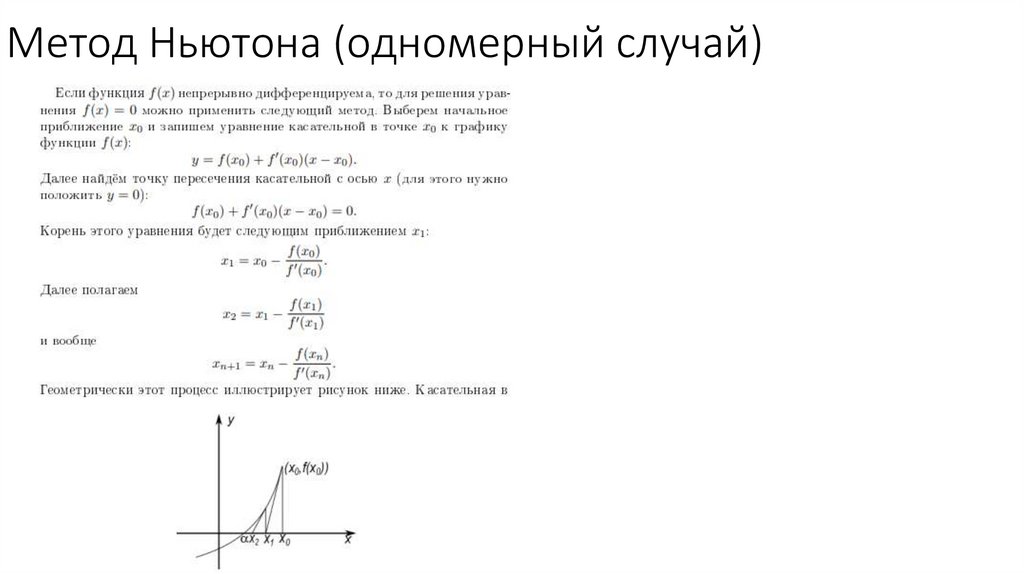
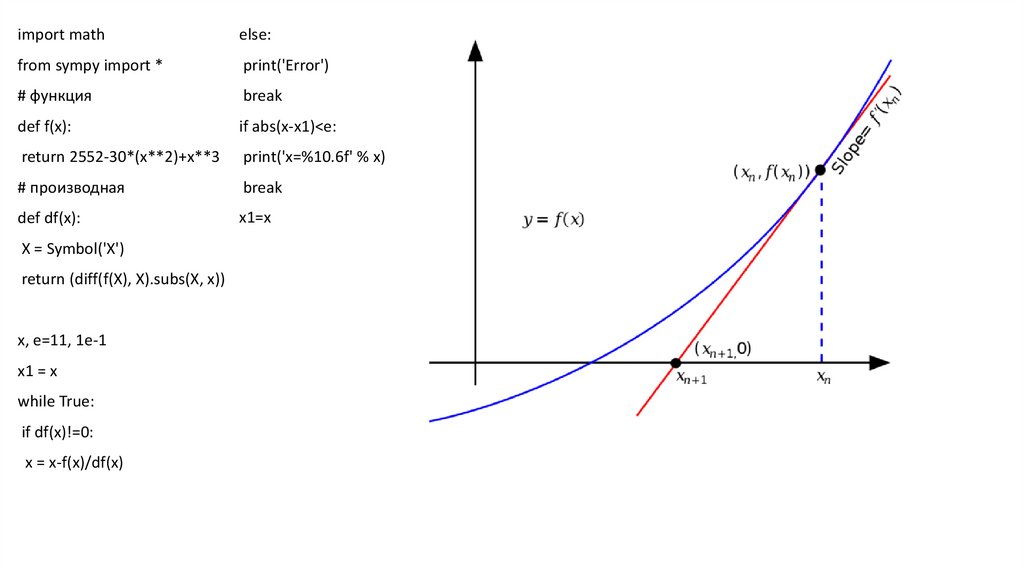
Метод Ньютона (одномерный случай)

35.

Расходимость метода Ньютона: пример

36.

Метод Ньютона (многомерный случай)
Якобиан

37.

Метод Ньютона (многомерный случай)

38.

Метод Ньютона для оптимизации f(x) = 0
Здесь g’(x) – якобиан g(x)

39.

import math
else:
from sympy import *
print('Error')
# функция
break
def f(x):
if abs(x-x1)<e:
return 2552-30*(x**2)+x**3
print('x=%10.6f' % x)
# производная
break
def df(x):
x1=x
X = Symbol('X')
return (diff(f(X), X).subs(X, x))
x, e=11, 1e-1
x1 = x
while True:
if df(x)!=0:
x = x-f(x)/df(x)

40.

Google JAX — фреймворк машинного обучения для преобразования числовых функций.

41.

42.

Оптимизация при помощи метода Ньютона
Случай одного измерения

43.

Оптимизация при помощи метода Ньютона
Рассмотрим задачу оптимизации:
Разложение в ряд Тейлора

44.

Обозначения в методе Ньютона в случае n
переменных
Гессиан
https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Math/lectures/lecture10/lecture10.ipynb
f’(x) – градиент функции –
вектор частных производных

45.

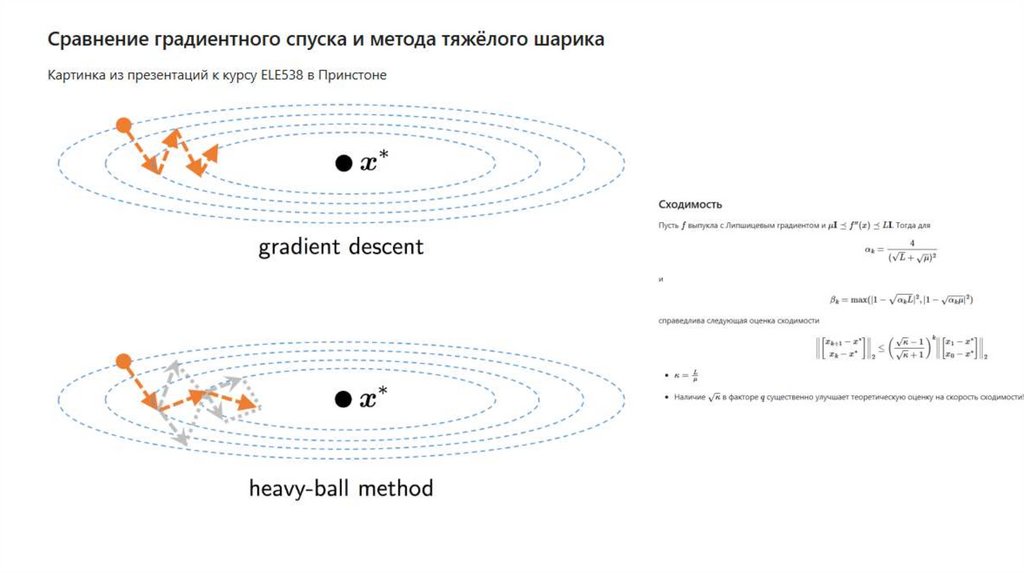
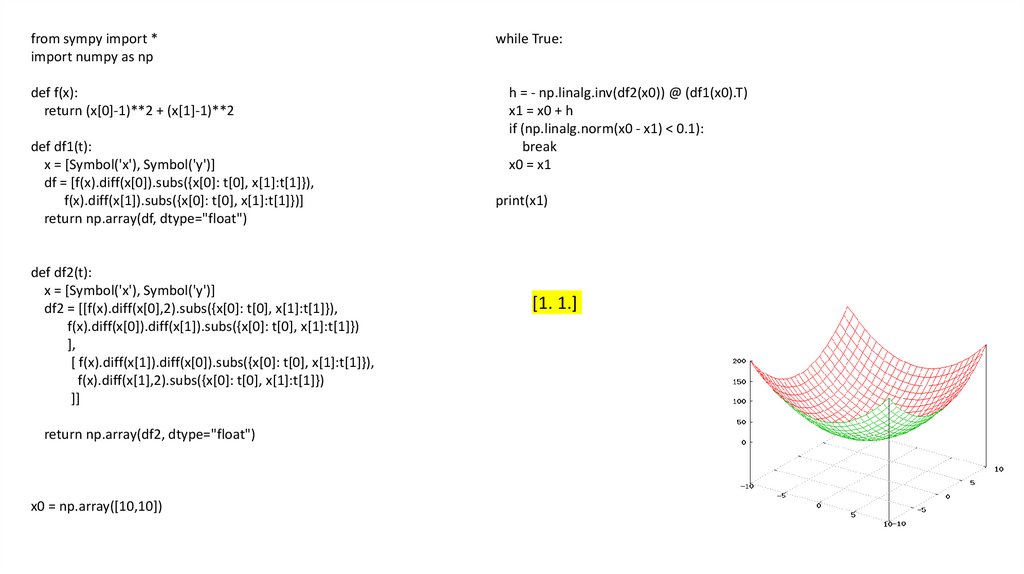
Сравнение метода градиентного спуска и
метода Ньютона

46.

from sympy import *
import numpy as np
def f(x):
return (x[0]-1)**2 + (x[1]-1)**2
def df1(t):
x = [Symbol('x'), Symbol('y')]
df = [f(x).diff(x[0]).subs({x[0]: t[0], x[1]:t[1]}),
f(x).diff(x[1]).subs({x[0]: t[0], x[1]:t[1]})]
return np.array(df, dtype="float")
def df2(t):
x = [Symbol('x'), Symbol('y')]
df2 = [[f(x).diff(x[0],2).subs({x[0]: t[0], x[1]:t[1]}),
f(x).diff(x[0]).diff(x[1]).subs({x[0]: t[0], x[1]:t[1]})
],
[ f(x).diff(x[1]).diff(x[0]).subs({x[0]: t[0], x[1]:t[1]}),
f(x).diff(x[1],2).subs({x[0]: t[0], x[1]:t[1]})
]]
return np.array(df2, dtype="float")
x0 = np.array([10,10])
while True:
h = - np.linalg.inv(df2(x0)) @ (df1(x0).T)
x1 = x0 + h
if (np.linalg.norm(x0 - x1) < 0.1):
break
x0 = x1
print(x1)
[1. 1.]

47.

48.

Обсуждение метода Ньютона
https://academy.yandex.ru/handbook/ml/article/metody-vtorogo-poryadka

49.

50.

Источники
• https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Python/lectures/%D0%9B%D0%B5%D0%BA%D1%86%D0%B8
%D1%8F_8_NumPy.ipynb
• https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Math/lectures/lecture8/lecture8.ipynb
• https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Math/lectures/lecture9/lecture9.ipynb
• https://github.com/MSUcourses/Data-Analysis-withPython/blob/main/Math/lectures/lecture10/lecture10.ipynb
• https://academy.yandex.ru/handbook/ml/article/metody-vtorogo-poryadka
• https://education.yandex.ru/handbook/ml/article/optimizaciya-v-ml
• Т. В. Азарнова, И. Л. Каширина, Г. Д. Чернышова, Методы оптимизации

51.

52.

Проблемы градиентного спуска

53.

Выбор шага
Также для подбора размера шага
может использоваться
деление пополам
на википедии.

54.

Стохастический градиентный спуск
L (x, yi) = LOSS = ОШИБКА на i входном векторе

55.

Стохастический градиентный спуск

56.

Стохастический градиентный спуск
Теперь перейдем к теоретической стороне вопроса. Сходимость
SGD обеспечивается несмещенностью стохастического градиента.
Несмотря на то, что во время итераций копится шум, суммарно он
зачастую оказывается довольно мал.

57.

Метод инерции, momentum

58.

Примеры

59.

Момент Нестерова

60.

Момент Нестерова
Комментарий: иногда упоминается, что
Nesterov Momentum «заглядывает в
будущее» и исправляет ошибки на данном
шаге оптимизации. Конечно, никто не
заглядывает в будущее в буквальном
смысле.
В работе Нестерова были предложены
конкретные (и довольно магические)
константы для импульса, которые
получаются из некоторой еще более
магической последовательности. Мы
приводить их не будем, поскольку мы в
первую очередь заинтересованы

61.

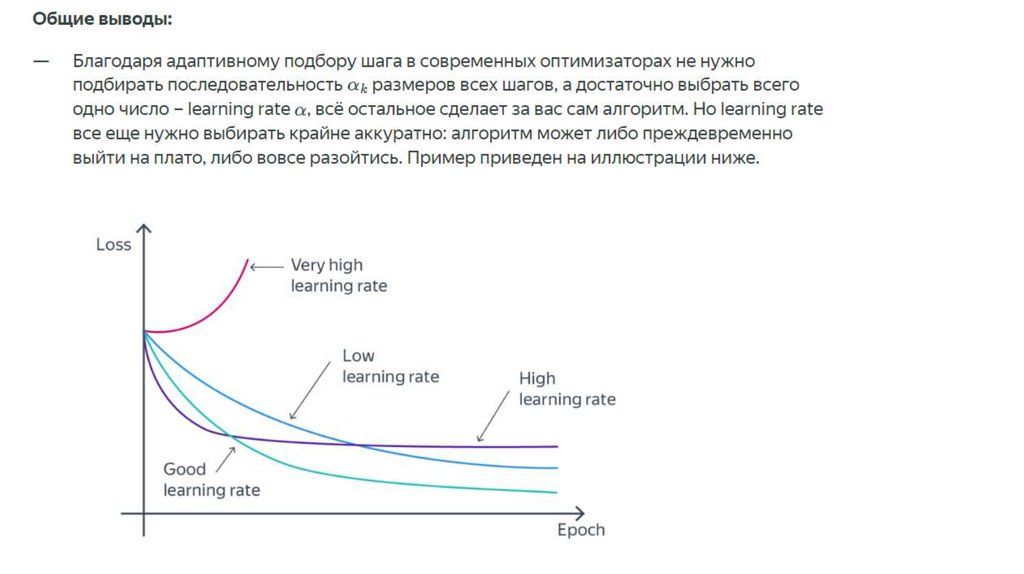
Общие выводы

62.

Адаптивный подбор размера шага

63.

Adagrad

64.

65.

66.

Adam: адаптированный шаг + момент
• Название Adam = ADAptive Momentum
Зачастую, при начале работы с реальными данными
начинают со значения learning rate равного 3e-4.
иногда число 3e-4 называют Karpathy constant).

67.

LARS
• нестандартный оптимизатор для обучения нейронных
сетей, Layer-wise Adaptive Rate Scaling (LARS).
• Он позволяет эффективно использовать большие размеры
батчей, что очень важно при вычислении на нескольких
GPU.
• Основная идея заключена в названии – нужно подбирать
размер шага не один для всей сети или каждого нейрона, а
отдельный для каждого слоя по правилу, похожему на
RMSProp. По сравнению с оригинальным RMSProp подбор
learning rate для каждого слоя дает большую стабильность
обучения.