Лекция 5

1.

Лекция 5.
Статика. Равновесие.

2.

Основные определения
Статика – раздел механики, в котором
изучают условия равновесия тел.
Равновесие
тела
–
это
такое
его
положение, которое сохраняется без
дополнительных воздействий.

3.

Виды равновесия
1. Устойчивое равновесие –
это такое равновесие, при котором
возникает равнодействующая сила,
возвращающая это тело в положение
равновесия.

4.

Виды равновесия
2. Неустойчивое равновесие –
это такое равновесие, при котором
возникает равнодействующая сила,
направленная в противоположную сторону
от положения равновесия.

5.

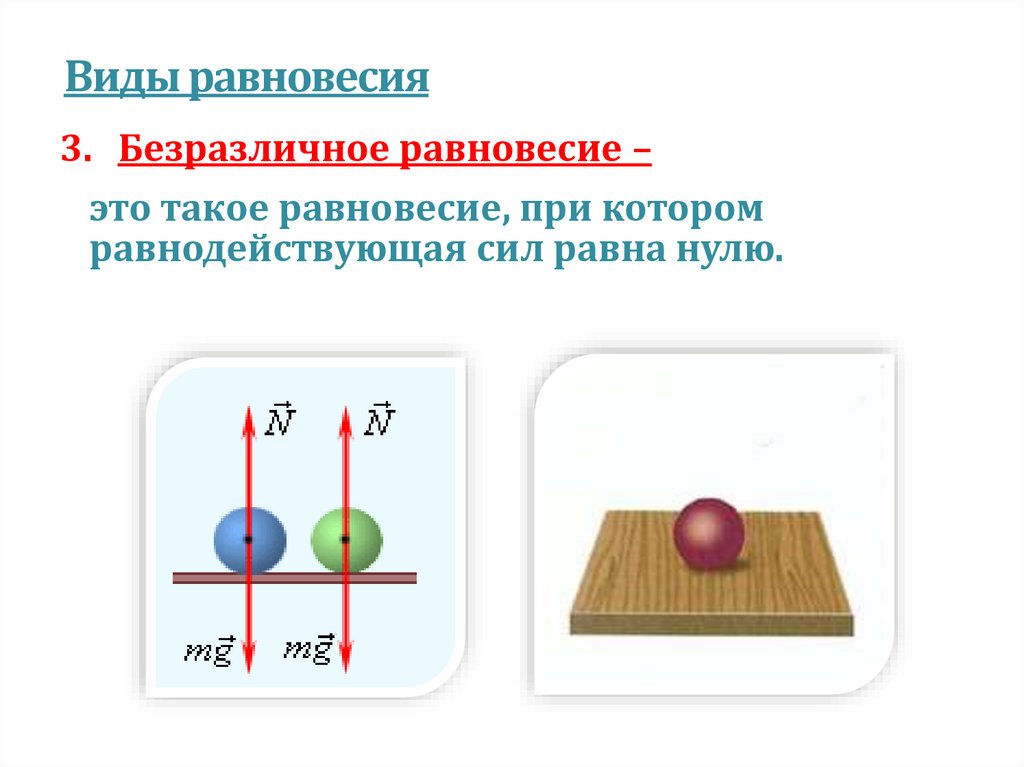
Виды равновесия
3. Безразличное равновесие –
это такое равновесие, при котором
равнодействующая сил равна нулю.

6.

Момент силы
Если
тело
может
вращаться
около
неподвижной оси, то для описания его
движения или равновесия вводится понятие
момента силы.
M – момент силы;
Момент силы – это произведение модуля силы
F на ее плечо d
M= F.d
[М] = Н . м

7.

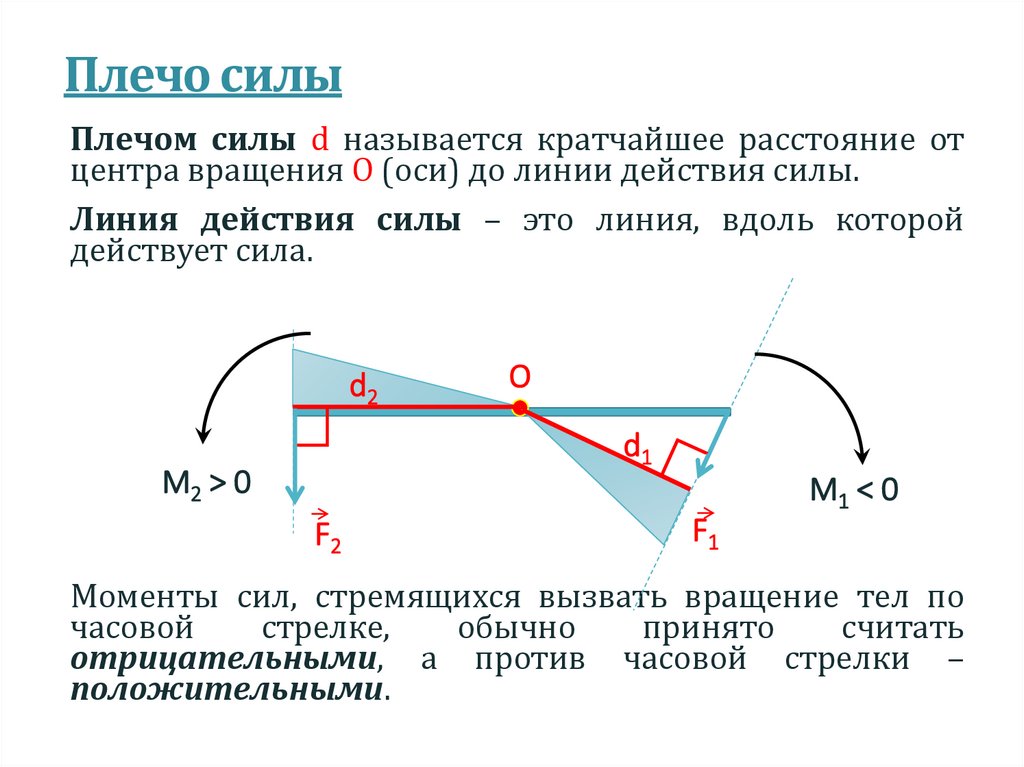
Плечо силы
Плечом силы d называется кратчайшее расстояние от
центра вращения О (оси) до линии действия силы.
Линия действия силы – это линия, вдоль которой
действует сила.
d2
О
d1
M2 > 0
M1 < 0
F2
F1
Моменты сил, стремящихся вызвать вращение тел по
часовой
стрелке,
обычно
принято
считать
отрицательными, а против часовой стрелки –
положительными.

8.

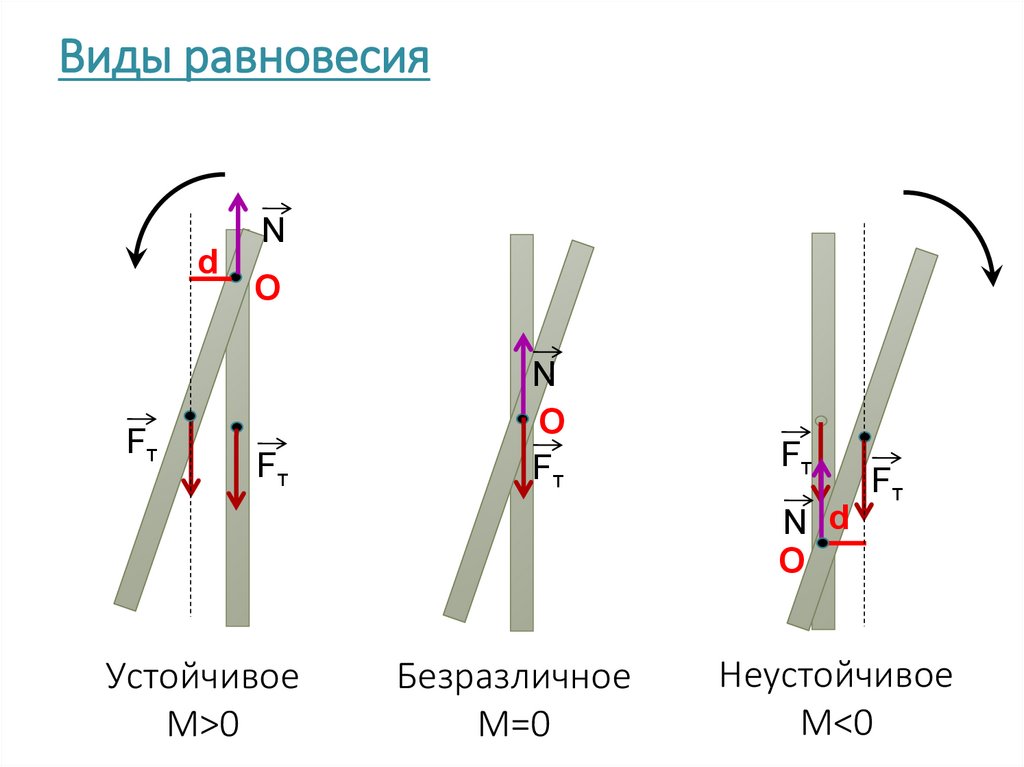
Виды равновесия
d
Fт
N
О
Fт
N
О
Fт
Fт
N d
О
Устойчивое
M>0
Безразличное
M=0
Fт
Неустойчивое
M<0

9.

Условия равновесия тел
1. Твердое тело находится в равновесии, если
геометрическая
сумма
всех
сил,
приложенных к нему, равна нулю.
F1 + F2 +F3+ …=0
2. Твердое тело находится в равновесии, если
алгебраическая сумма моментов всех сил,
действующих на него относительно любой
оси, равна нулю.
М1+М2+М3+…=0

10.

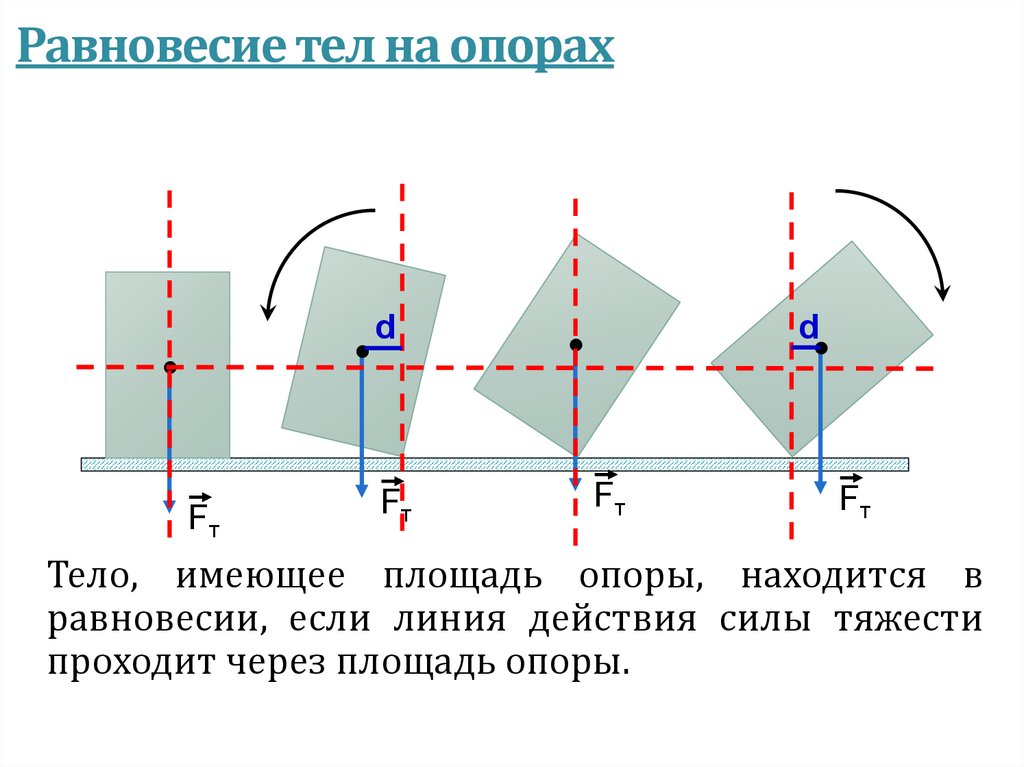
Равновесие тел на опорах
d
d
Fт
Fт
Fт
Fт
Тело, имеющее площадь опоры, находится в
равновесии, если линия действия силы тяжести
проходит через площадь опоры.

11.

Простейшие механизмы
Простые механизмы — это устройства, в которых
работа совершается только за счет механической
энергии.
Простые механизмы (рычаг, наклонная плоскость,
блок и др.) служат для преобразования силы, их
применяют при совершении работы в тех случаях,
когда надо действием одной силы уравновесить
другую силу.

12.

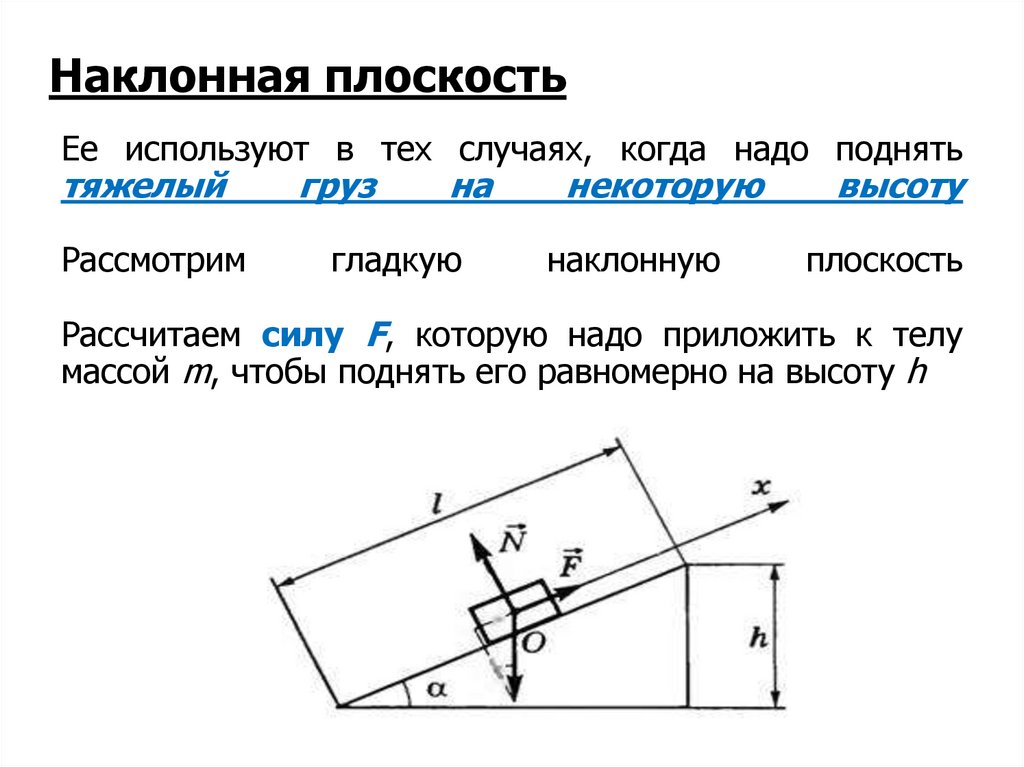
Наклонная плоскость
Ее используют в тех случаях, когда надо поднять
тяжелый
Рассмотрим
груз
на
гладкую
некоторую
наклонную
высоту
плоскость
Рассчитаем силу F, которую надо приложить к телу
массой m, чтобы поднять его равномерно на высоту h

13.

Запишем основное уравнение динамики
F N mg 0
Спроецируем это равенство на ось Ox
F mg sin 0
Отсюда искомая сила
h
mg l
F mg sin mg
l
F
h
т.е для равномерного поднятия груза с помощью
наклонной плоскости необходимо приложить силу, во
столько раз меньшую силы тяжести груза, во сколько раз
длина наклонной плоскости больше ее высоты.

14.

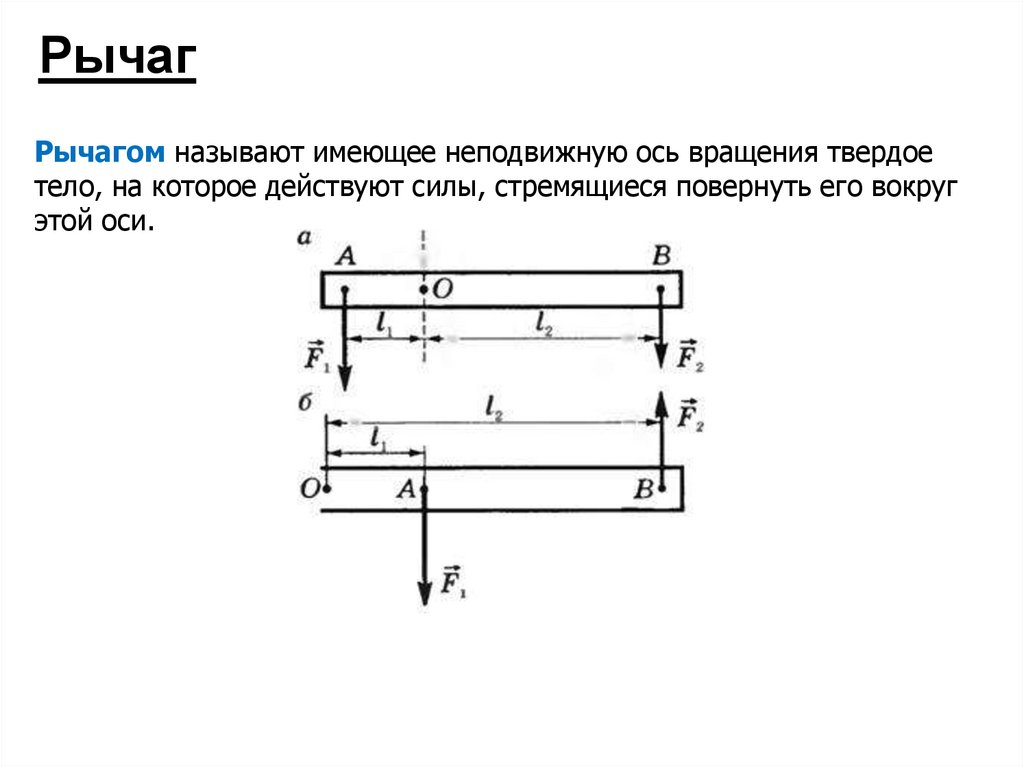
Рычаг
Рычагом называют имеющее неподвижную ось вращения твердое
тело, на которое действуют силы, стремящиеся повернуть его вокруг
этой оси.

15.

условие равновесия рычага
F1 l2
F2 l1
При равновесии рычага под действием двух сил модули
этих сил обратно пропорциональны их плечам.
С помощью рычага можно получить выигрыш в силе, т.е.
меньшей силой можно уравновесить большую силу.

16.

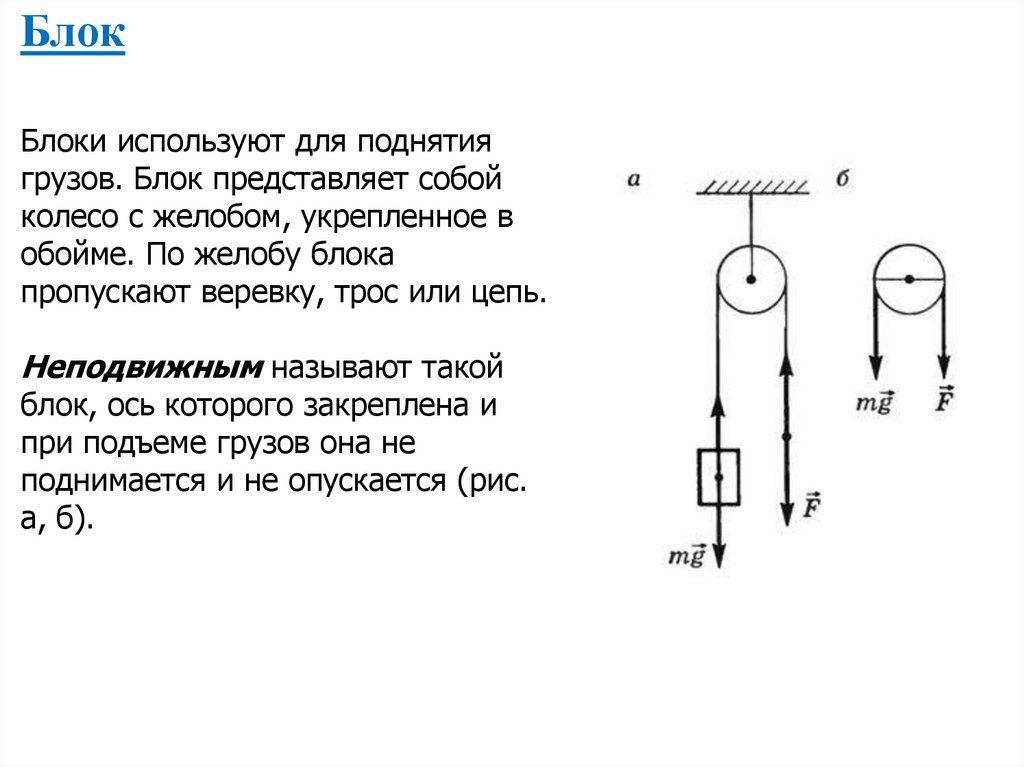
Блок
Блоки используют для поднятия
грузов. Блок представляет собой
колесо с желобом, укрепленное в
обойме. По желобу блока
пропускают веревку, трос или цепь.
Неподвижным называют такой
блок, ось которого закреплена и
при подъеме грузов она не
поднимается и не опускается (рис.
а, б).

17.

Неподвижный блок можно рассматривать
как равноплечий рычаг, у которого плечи
приложенных сил равны радиусу колеса
Следовательно,
из
правила
моментов
mgr = Fr вытекает, что
неподвижный блок выигрыша в силе не
дает (F = mg)
Он позволяет менять направление действия
силы

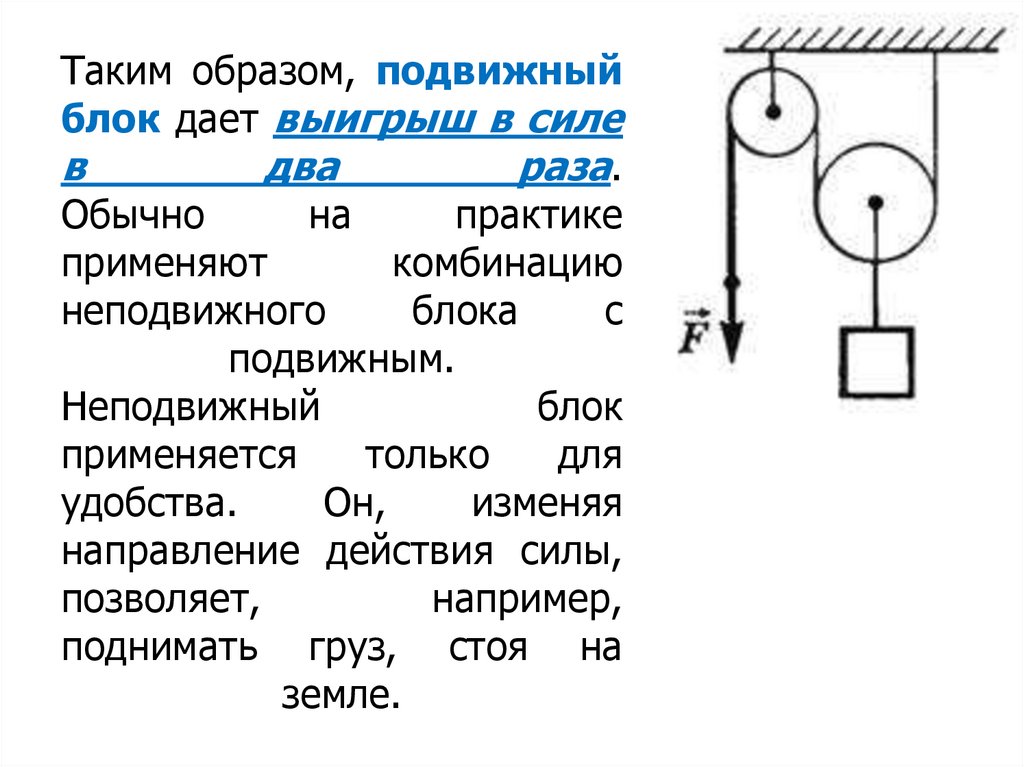
18.

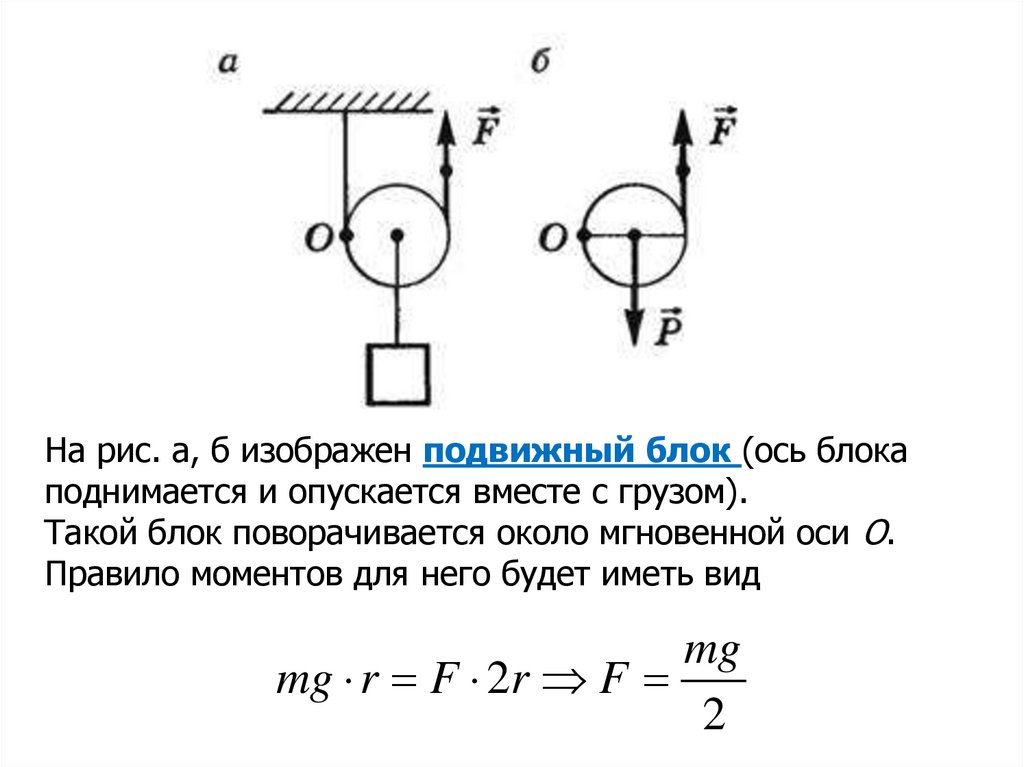
На рис. а, б изображен подвижный блок (ось блока
поднимается и опускается вместе с грузом).
Такой блок поворачивается около мгновенной оси О.
Правило моментов для него будет иметь вид
mg
mg r F 2r F
2

19.

Таким образом, подвижный
блок дает выигрыш в силе
в
два
раза.
Обычно
на
практике
применяют
комбинацию
неподвижного
блока
с
подвижным.
Неподвижный
блок
применяется
только
для
удобства.
Он,
изменяя
направление действия силы,
позволяет,
например,
поднимать груз, стоя на
земле.

20.

Равенство работ при использовании простых
механизмов
Мы видим, что с помощью простых механизмов
можно получить выигрыш в силе. А дают ли
простые механизмы выигрыш в работе?
Рассчитаем работу, которую совершает сила F при
подъеме груза с помощью наклонной плоскости

21.

AF F l
Подставим найденные значения силы
h
F mg
l
и получим
h
AF mg l mgh
l
Таким образом, работа AF равна работе, которую нужно
совершить, чтобы равномерно поднять груз на высоту h,
не используя наклонной плоскости.
Не дает выигрыша в работе и рычаг.

22.

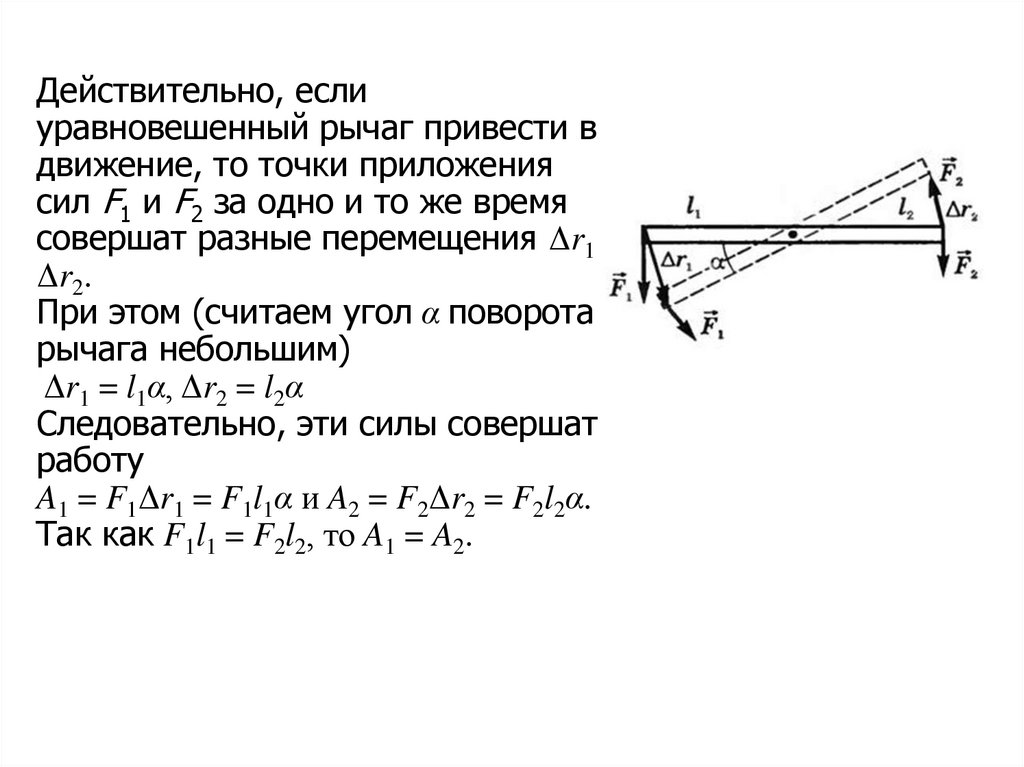
Действительно, если
уравновешенный рычаг привести в
движение, то точки приложения
сил F1 и F2 за одно и то же время
совершат разные перемещения Δr1 и
Δr2.
При этом (считаем угол α поворота
рычага небольшим)
Δr1 = l1α, Δr2 = l2α
Следовательно, эти силы совершат
работу
A1 = F1Δr1 = F1l1α и A2 = F2Δr2 = F2l2α.
Так как F1l1 = F2l2, то A1 = A2.

23.

При использовании неподвижного блока мы видим, что
приложенные силы F и mg равны и пути, пройденные
точками приложения сил при подъеме груза, тоже
одинаковы, а значит, одинаковы и работы.
mg
A2 F 2h
2h mgh
2
Чтобы при помощи подвижного блока поднять груз на
высоту h, необходимо конец веревки, к которому
приложена сила F, переместить на 2h.
Следовательно, A1 = mgh

24.

Таким образом, получая выигрыш в силе в два раза,
проигрывают в два раза в перемещении, следовательно, и
подвижный блок выигрыша в работе не дает.
Еще древние ученые сформулировали правило ("золотое
правило механики"), применяемое ко всем механизмам:
во сколько раз выигрываем в силе, во столько раз
проигрываем в расстоянии.

25.

При рассмотрении простых механизмов мы не
учитываем трение, а также вес самих
механизмов.
В реальных условиях это необходимо
учитывать.
Поэтому
часть
работы
совершается
силой F на перемещение отдельных
частей механизма и против силы
трения.
Работа
же
по
подъему
груза Ap (полезная работа) будет меньше
полной работы А (работы, которую
совершает
сила
F).

26.

Эффективность работы механизма характеризуют
коэффициентом полезного действия (КПД механизма)
Коэффициент полезного действия — физическая
величина, равная отношению полезной работы Ap ко всей
затраченной работе А:
Ap
A
100 0 0

27.

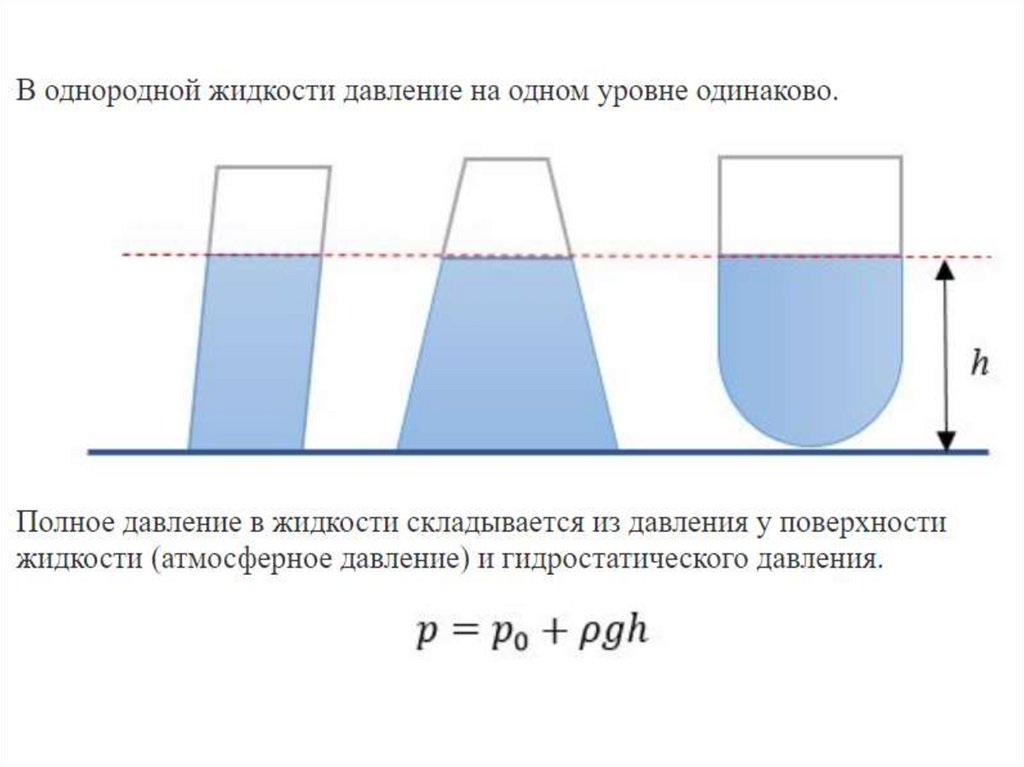
Гидростатика
Гидростатика – раздел механики, изучающий
равновесие жидкостей.
Жидкость
отличается
от
твердого
тела
текучестью,
то
есть
способностью
составляющих жидкость частиц перемещаться
под действием незначительной силы.
Основная задача гидростатики
определение распределения давлений внутри
жидкости, что позволяет определить силы,
действующие
со
стороны
жидкости
на
погруженные в нее тела

28.

Давление – физическая величина, равная
отношению
силы,
действующей
перпендикулярно поверхности, к площади этой
поверхности.
Единица измерения давления – Па (паскаль =
Н/м2).

29.

30.

31.

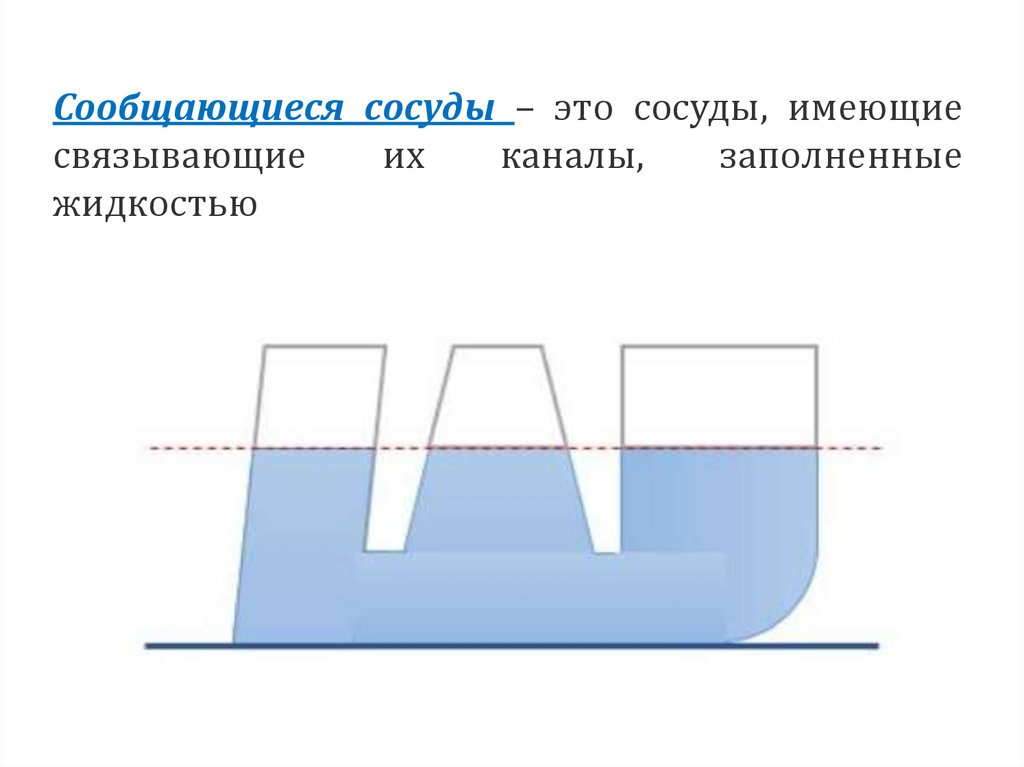
Сообщающиеся сосуды – это сосуды, имеющие
связывающие
их
каналы,
заполненные
жидкостью

32.

Закон сообщающихся сосудов
1. В сообщающихся сосудах, заполненных
однородной жидкостью, давление во всех
точках жидкости, расположенных в одной
горизонтальной плоскости, одинаково и
не зависит от формы сосудов. При этом
поверхности жидкости в сообщающихся
сосудах устанавливаются на одном
уровне.
2. Высоты столбов разнородных жидкостей
обратно пропорциональны плотностям
этих жидкостей:

33.

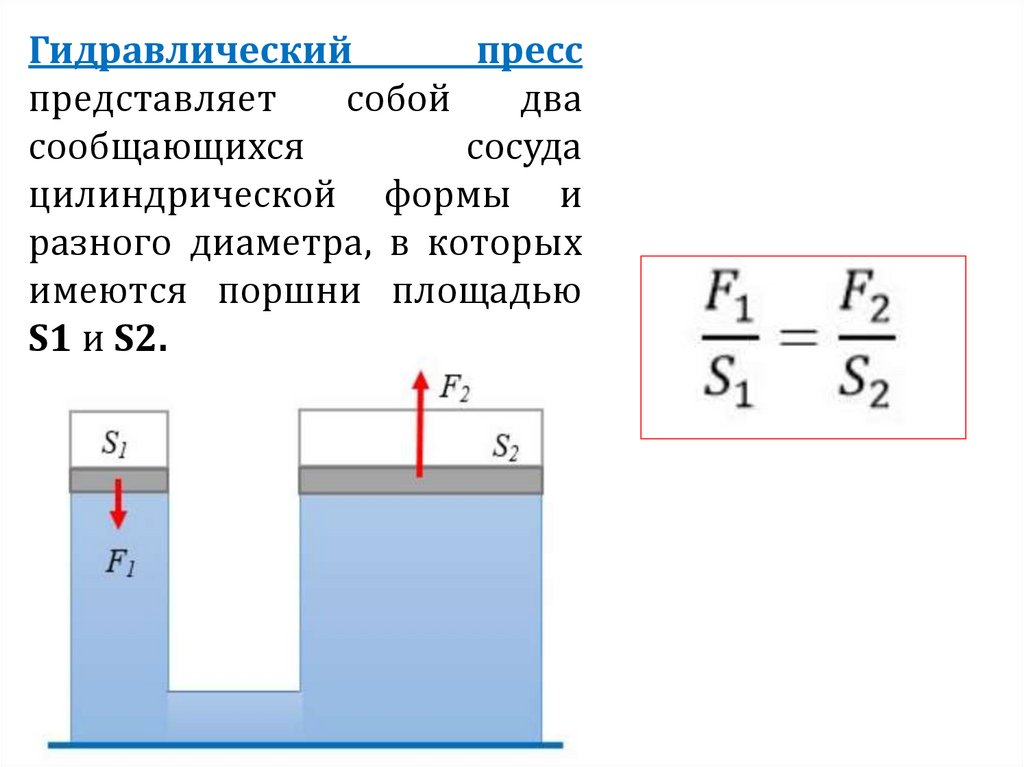
Гидравлический
пресс
представляет
собой
два
сообщающихся
сосуда
цилиндрической формы и
разного диаметра, в которых
имеются поршни площадью
S1 и S2.