Графы

1. Информационные модели на графах

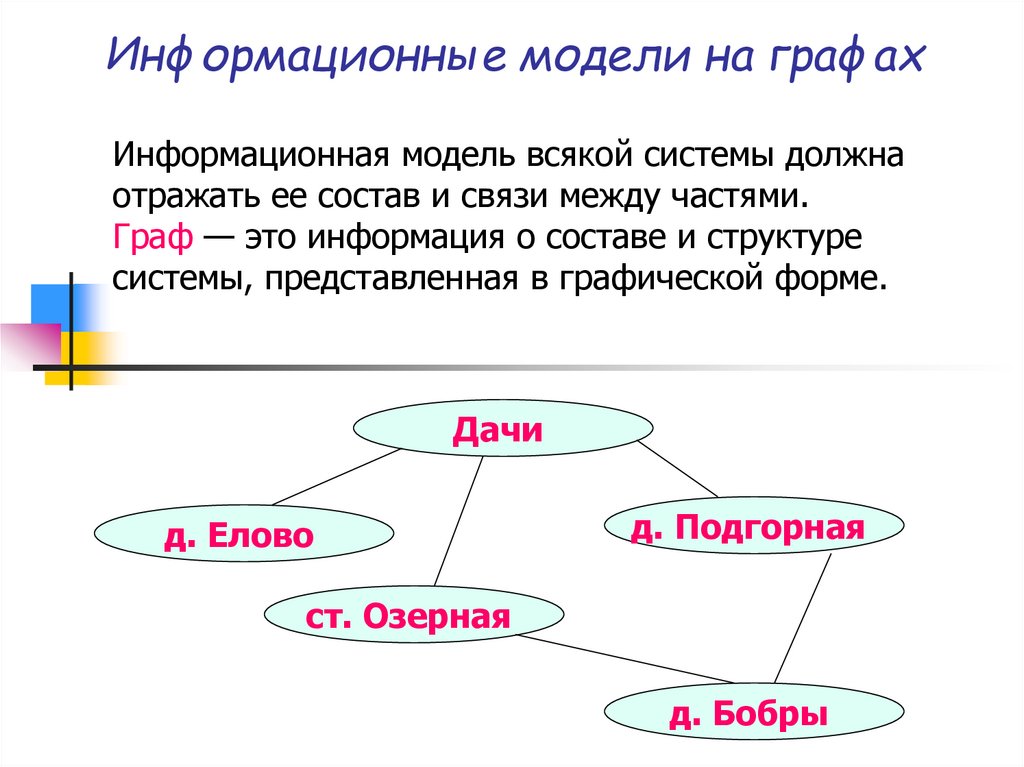
Информационная модель всякой системы должна
отражать ее состав и связи между частями.
Граф — это информация о составе и структуре
системы, представленная в графической форме.
Дачи
д. Елово
д. Подгорная
ст. Озерная
д. Бобры

2. Информационные модели на графах

Структура — это определенный порядок объединения
элементов, составляющих систему.
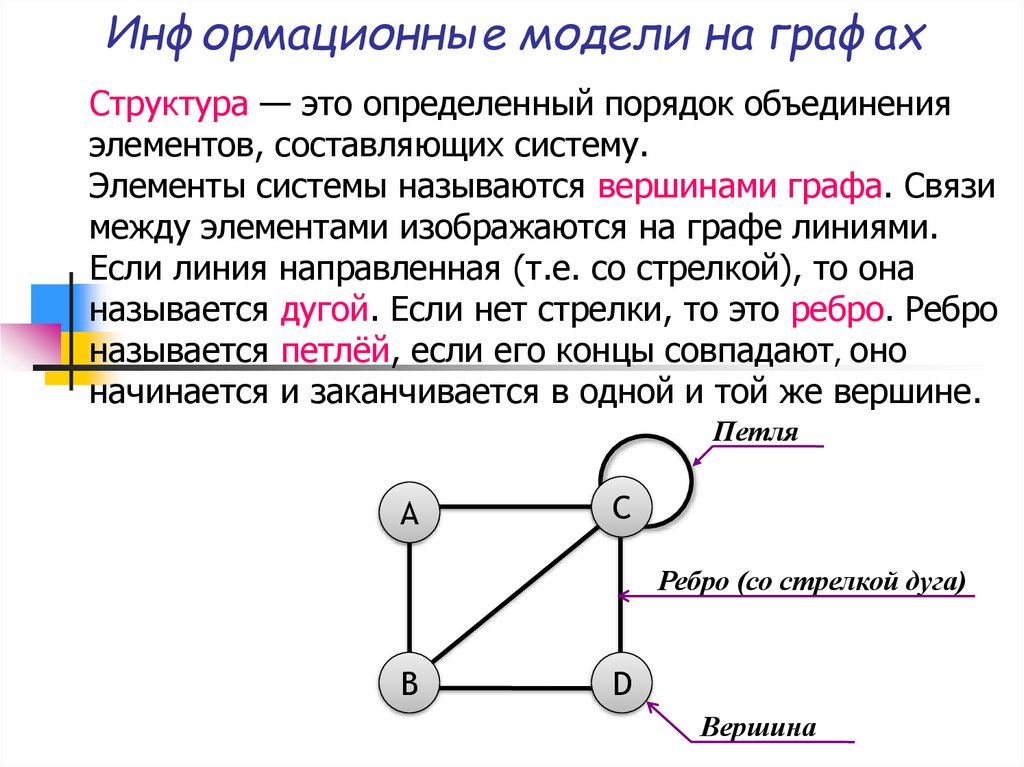
Элементы системы называются вершинами графа. Связи
между элементами изображаются на графе линиями.
Если линия направленная (т.е. со стрелкой), то она
называется дугой. Если нет стрелки, то это ребро. Ребро
называется петлёй, если его концы совпадают, оно
начинается и заканчивается в одной и той же вершине.
Петля
A
C
Ребро (со стрелкой дуга)
B
D
Вершина

3. Информационные модели на графах

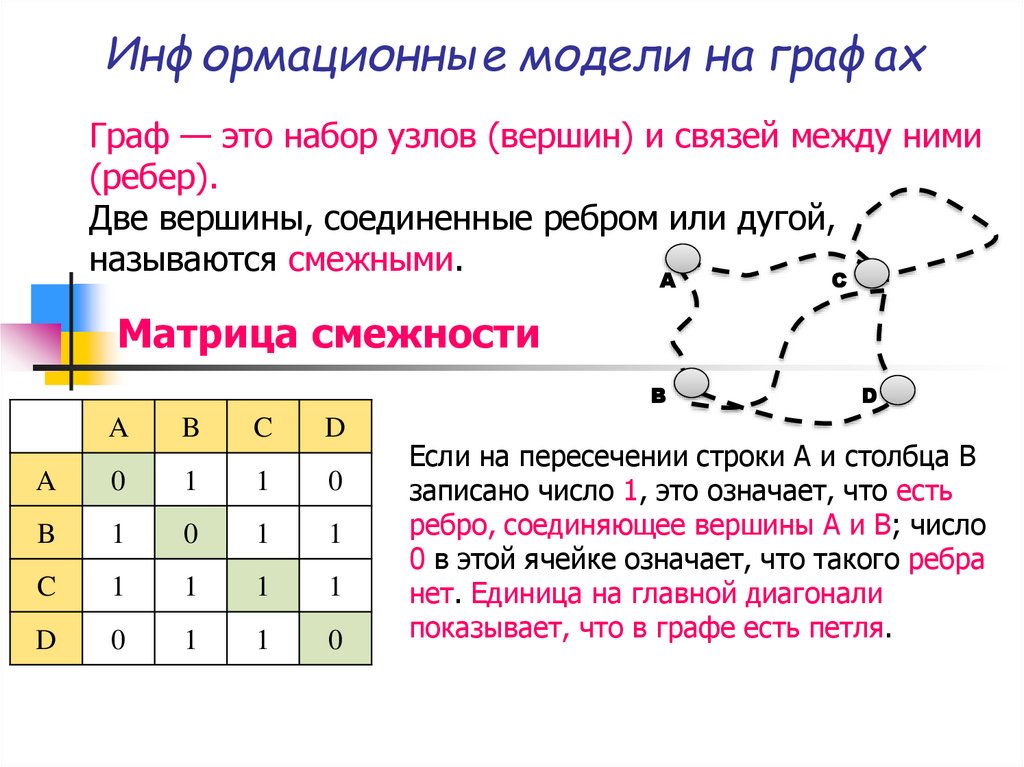
Граф — это набор узлов (вершин) и связей между ними
(ребер).
Две вершины, соединенные ребром или дугой,
называются смежными.
A
С
Матрица смежности
B
A
B
C
D
A
0
1
1
0
B
1
0
1
1
C
1
1
1
1
D
0
1
1
0
D
Если на пересечении строки A и столбца B
записано число 1, это означает, что есть
ребро, соединяющее вершины A и B; число
0 в этой ячейке означает, что такого ребра
нет. Единица на главной диагонали
показывает, что в графе есть петля.

4. Информационные модели на графах

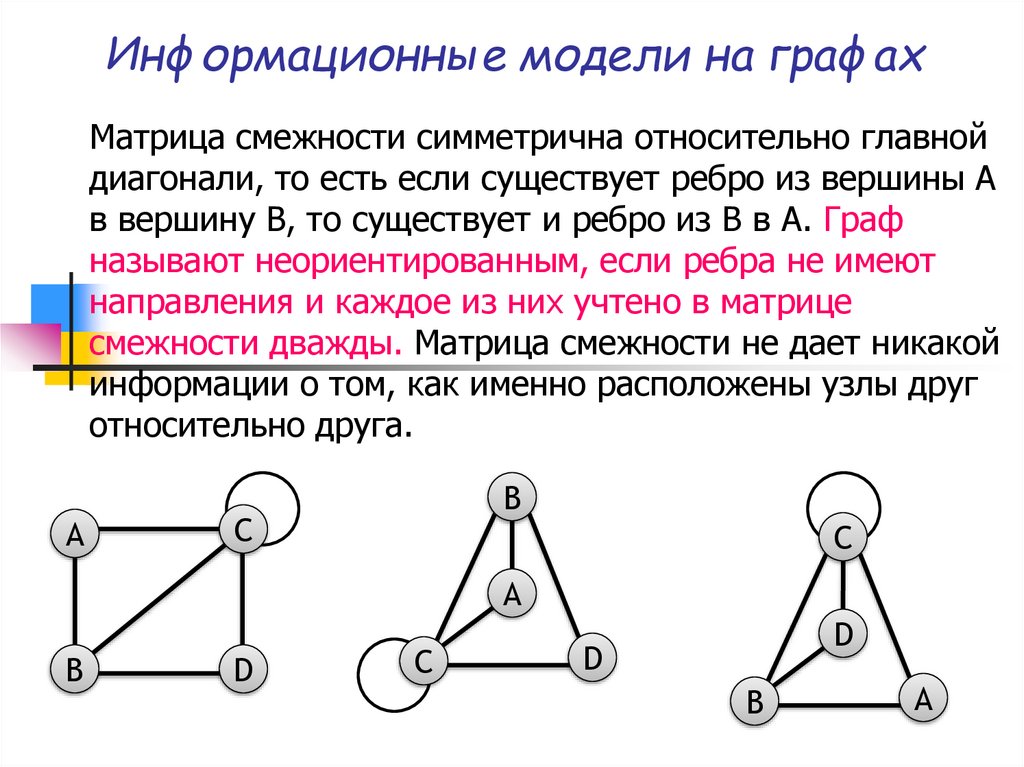
Матрица смежности симметрична относительно главной
диагонали, то есть если существует ребро из вершины A
в вершину B, то существует и ребро из B в A. Граф
называют неориентированным, если ребра не имеют
направления и каждое из них учтено в матрице
смежности дважды. Матрица смежности не дает никакой
информации о том, как именно расположены узлы друг
относительно друга.
A
B
C
C
A
B
D
C
D
D
B
A

5. Информационные модели на графах

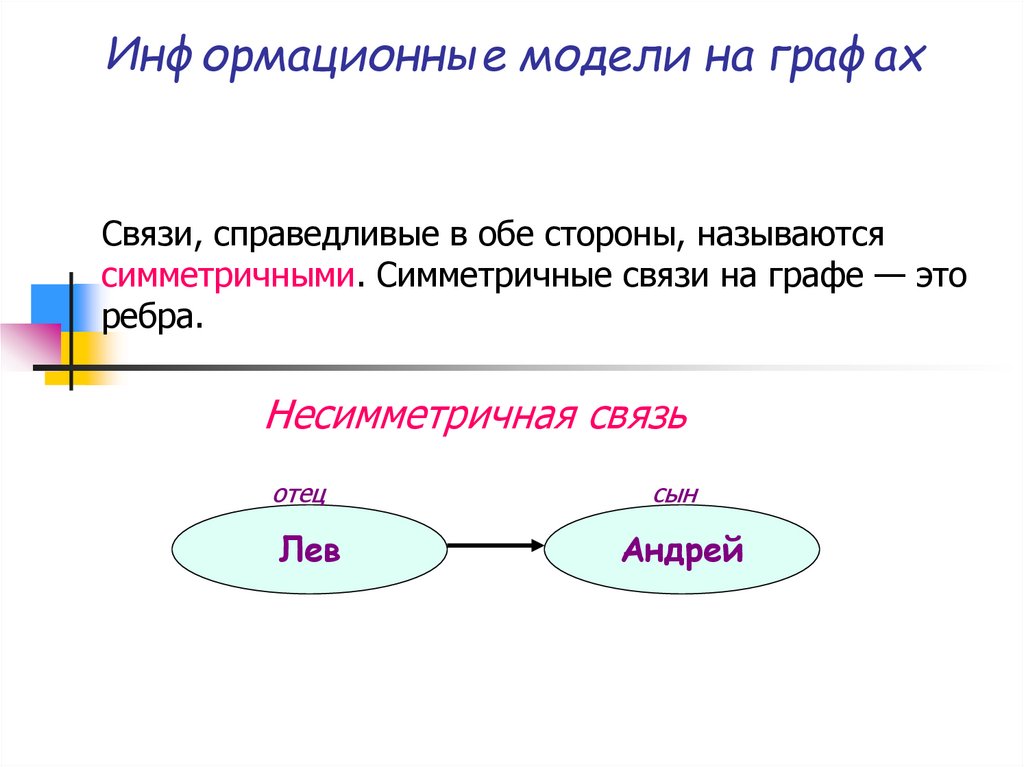
Связи, справедливые в обе стороны, называются
симметричными. Симметричные связи на графе — это
ребра.
Несимметричная связь
отец
сын
Лев
Андрей

6. Информационные модели на графах

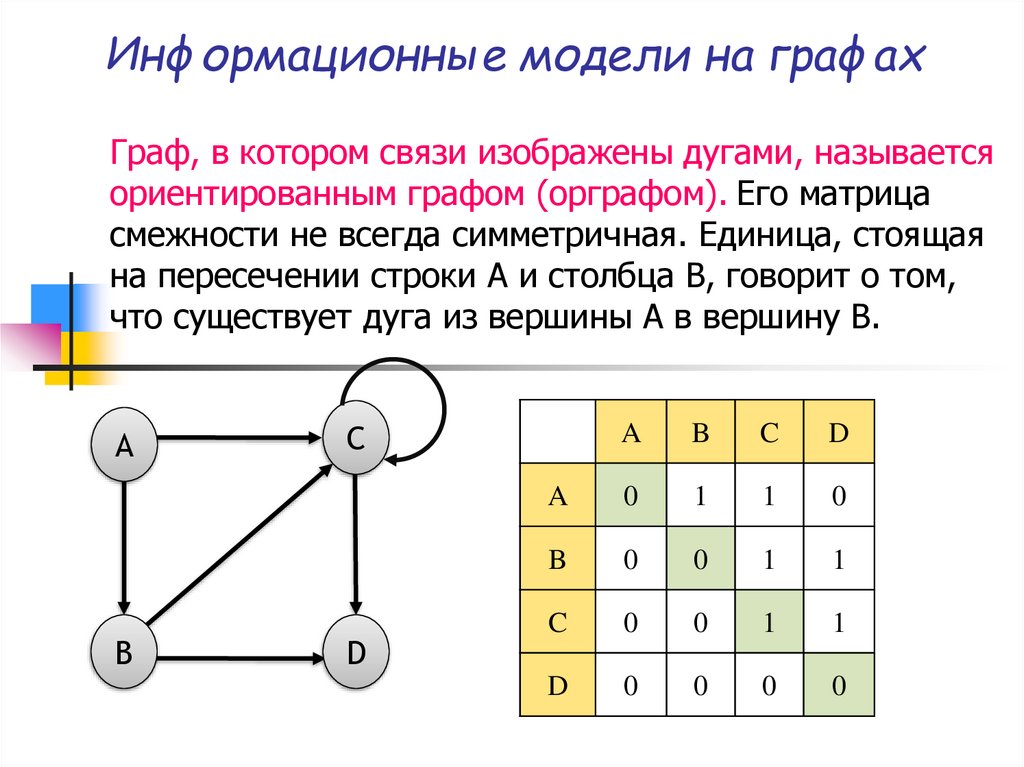
Граф, в котором связи изображены дугами, называется
ориентированным графом (орграфом). Его матрица
смежности не всегда симметричная. Единица, стоящая
на пересечении строки A и столбца B, говорит о том,
что существует дуга из вершины A в вершину B.
A
B
C
D
A
B
C
D
A
0
1
1
0
B
0
0
1
1
C
0
0
1
1
D
0
0
0
0

7. Информационные модели на графах

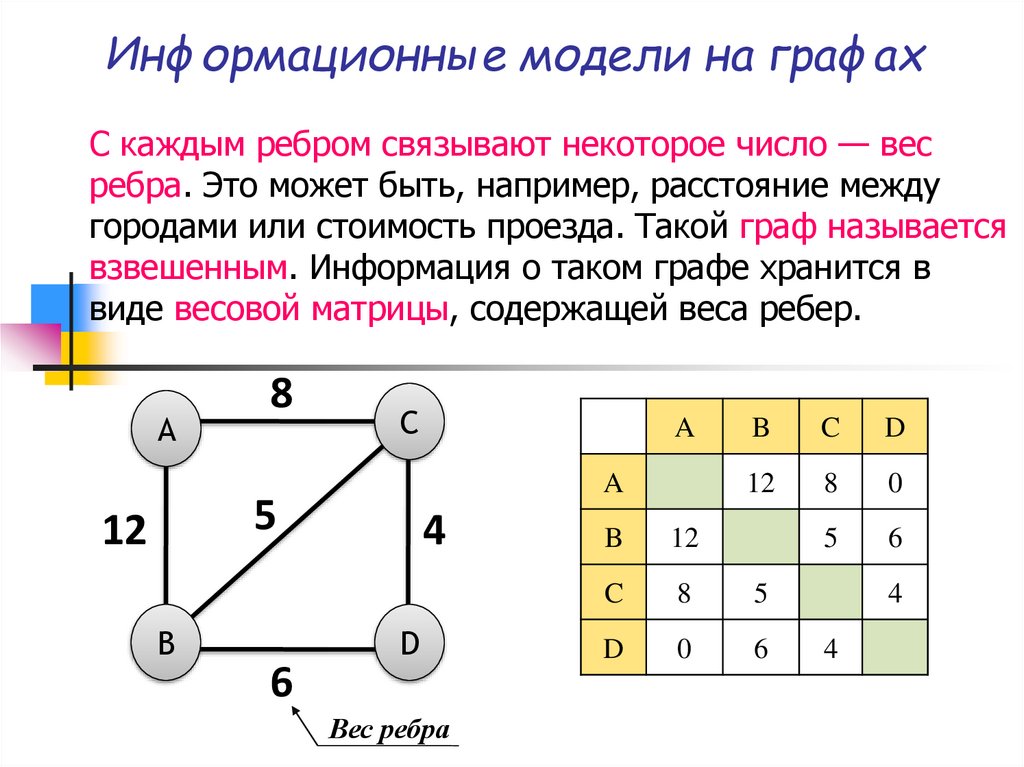
С каждым ребром связывают некоторое число — вес
ребра. Это может быть, например, расстояние между
городами или стоимость проезда. Такой граф называется
взвешенным. Информация о таком графе хранится в
виде весовой матрицы, содержащей веса ребер.
A
8
C
A
5
12
B
A
4
D
6
Вес ребра
B
C
D
12
8
0
5
6
B
12
C
8
5
D
0
6
4
4

8. Информационные модели на графах

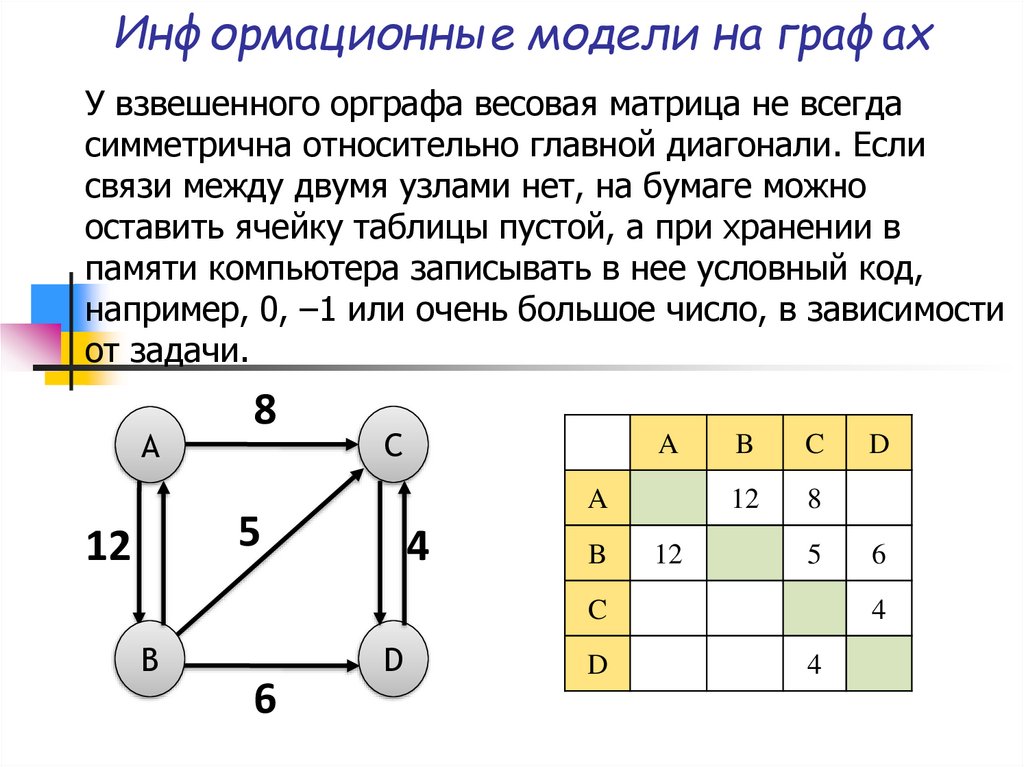
У взвешенного орграфа весовая матрица не всегда
симметрична относительно главной диагонали. Если
связи между двумя узлами нет, на бумаге можно
оставить ячейку таблицы пустой, а при хранении в
памяти компьютера записывать в нее условный код,
например, 0, –1 или очень большое число, в зависимости
от задачи.
A
8
C
A
5
12
A
4
B
12
B
C
12
8
5
C
B
D
6
D
D
6
4
4

9. Информационные модели на графах

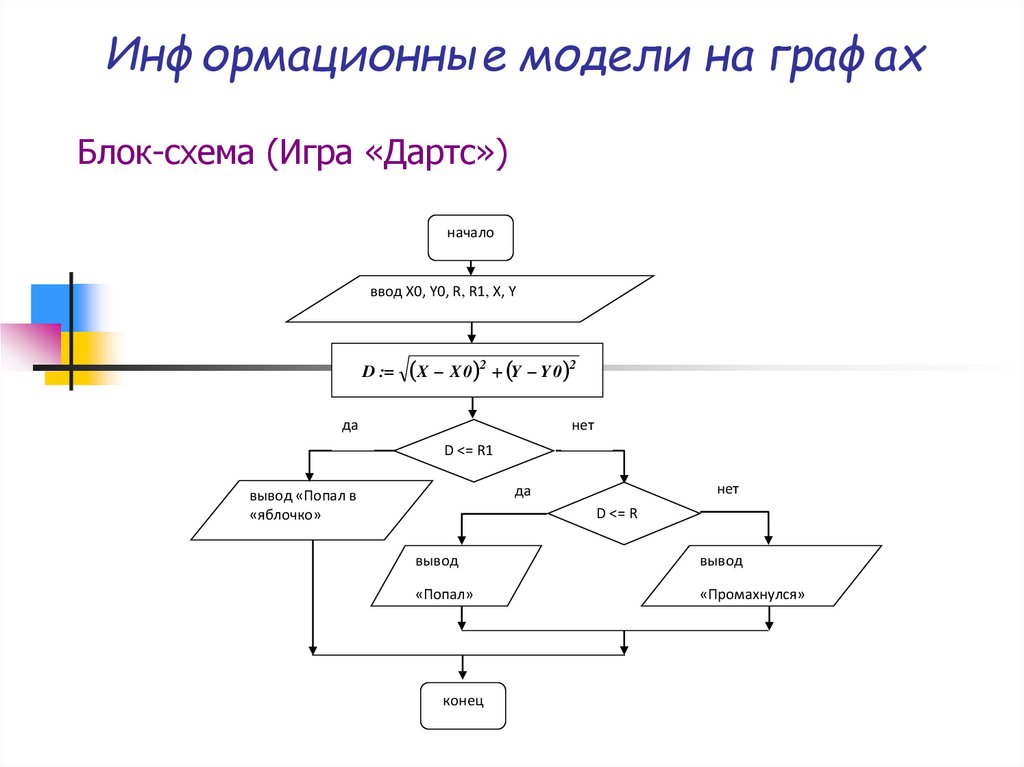
Блок-схема (Игра «Дартс»)
начало
ввод X0, Y0, R, R1, X, Y
D :
X X 0 2 Y Y 0 2
да
нет
D <= R1
нет
да
вывод «Попал в
«яблочко»
D <= R
вывод
вывод
«Попал»
«Промахнулся»
конец

10. Информационные модели на графах

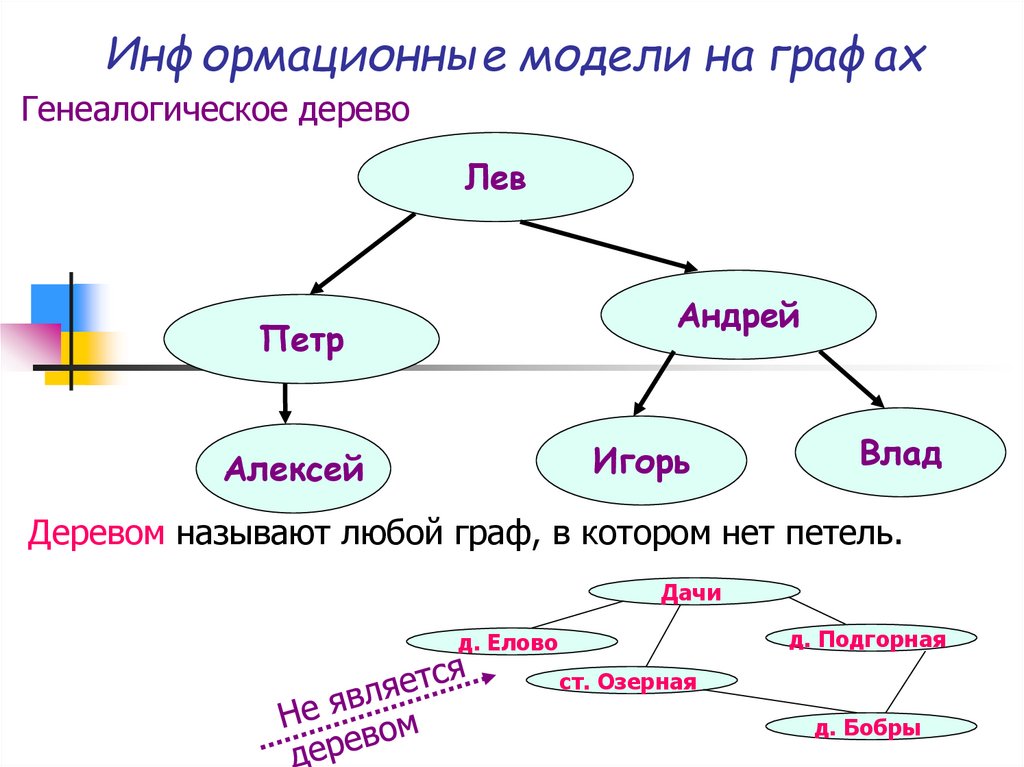
Генеалогическое дерево
Лев
Андрей
Петр
Игорь
Алексей
Влад
Деревом называют любой граф, в котором нет петель.
Дачи
д. Подгорная
д. Елово
ст. Озерная
д. Бобры

11. Информационные модели на графах

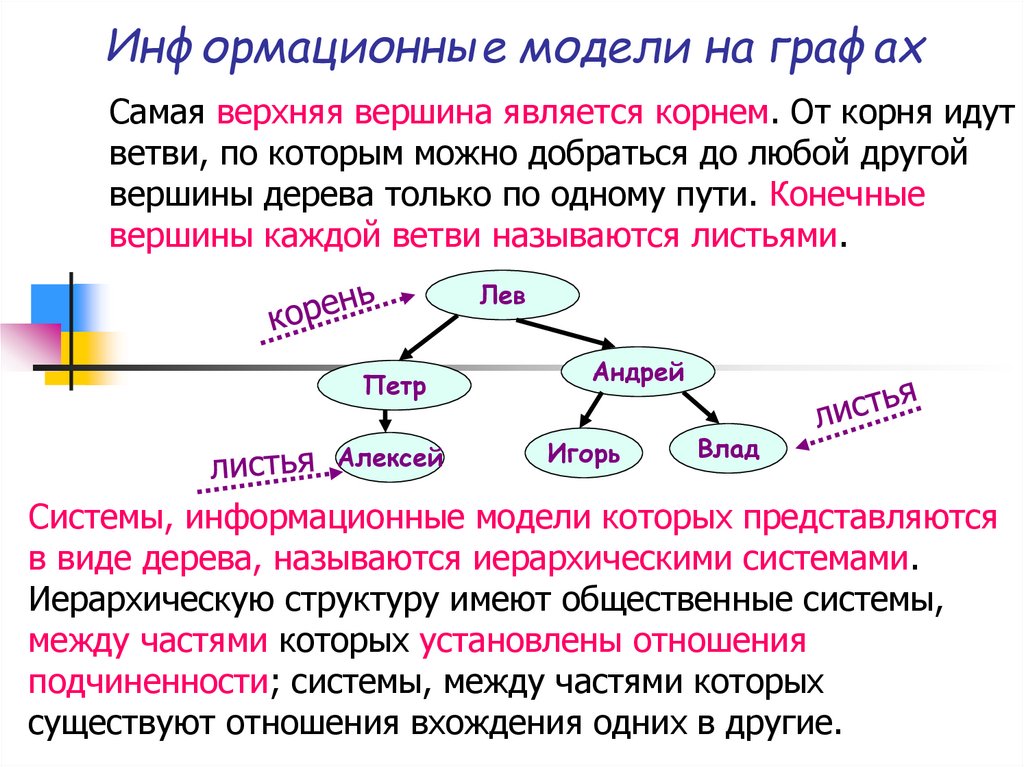
Самая верхняя вершина является корнем. От корня идут
ветви, по которым можно добраться до любой другой
вершины дерева только по одному пути. Конечные
вершины каждой ветви называются листьями.
Лев
Петр
Алексей
Андрей
Игорь
Влад
Системы, информационные модели которых представляются
в виде дерева, называются иерархическими системами.
Иерархическую структуру имеют общественные системы,
между частями которых установлены отношения
подчиненности; системы, между частями которых
существуют отношения вхождения одних в другие.

12. Информационные модели на графах

Свойства иерархической модели
1. Иерархия начинается с верхнего узла. Каждый узел
имеет характеристики (атрибуты), которые описывают
моделируемый объект в данном узле.
2. Чем ниже уровень, тем выше «зависимость» узла.
3. Каждый узел имеет только одну связь с более высоким
уровнем.
4.Каждый узел может иметь несколько связей с
«зависимыми» (более низкими) уровнями.
5. Доступ к любому элементу структуры осуществляется
только через верхний узел по принципу «сверху-вниз».
6. Количество узлов не имеет ограничений.

13. Информационные модели на графах

Планета Земля
Австралия
Африка
Алжир
Европа
Америка
Канбе́рра
США
Франция
Лос-Анджелес
Россия
Россия
Мексика
Россия
Крым
Алжир
Калифорния
Азия
Мехико
Симферополь
Новосибирск
Алтай
Барнаул
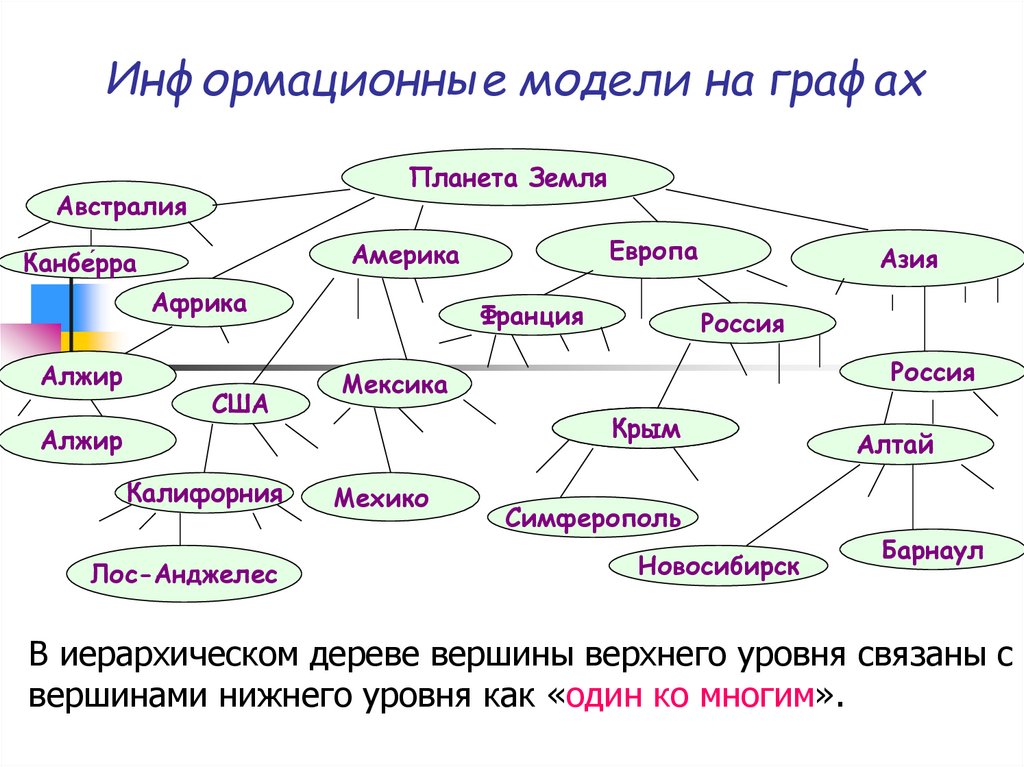
В иерархическом дереве вершины верхнего уровня связаны с
вершинами нижнего уровня как «один ко многим».

14. Информационные модели на графах

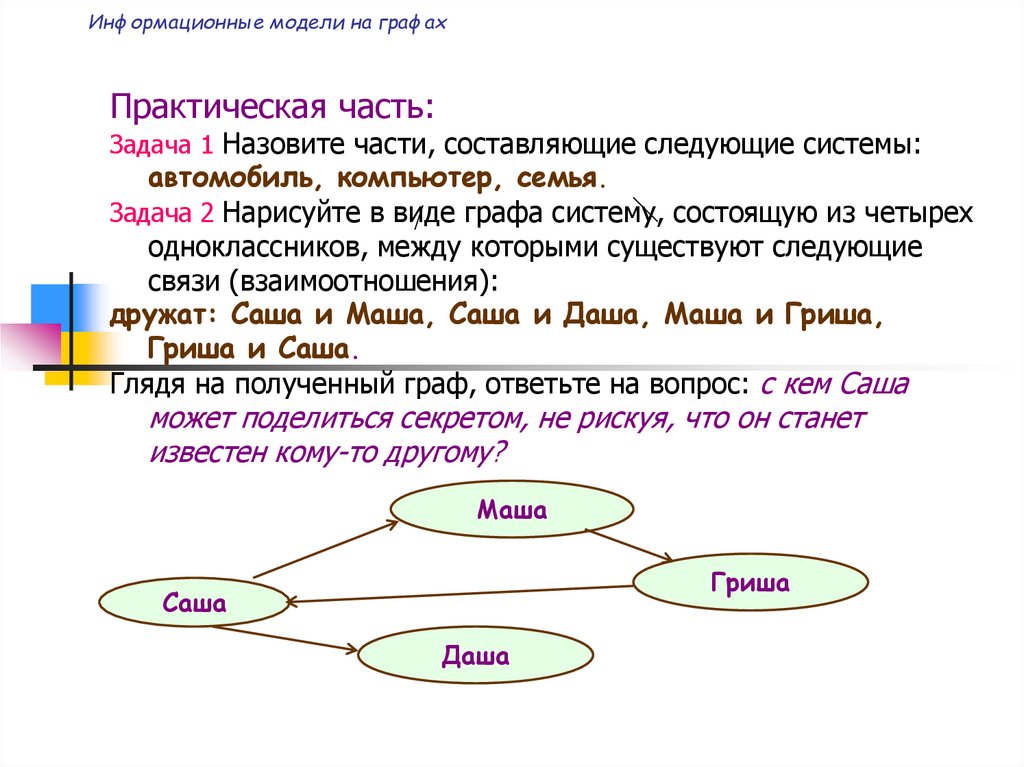
Практическая часть:
Задача 1 Назовите части, составляющие следующие системы:
автомобиль, компьютер, семья.
Задача 2 Нарисуйте в виде графа систему, состоящую из четырех
одноклассников, между которыми существуют следующие
связи (взаимоотношения):
дружат: Саша и Маша, Саша и Даша, Маша и Гриша,
Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша
может поделиться секретом, не рискуя, что он станет
известен кому-то другому?
Маша
Гриша
Саша
Даша

15.

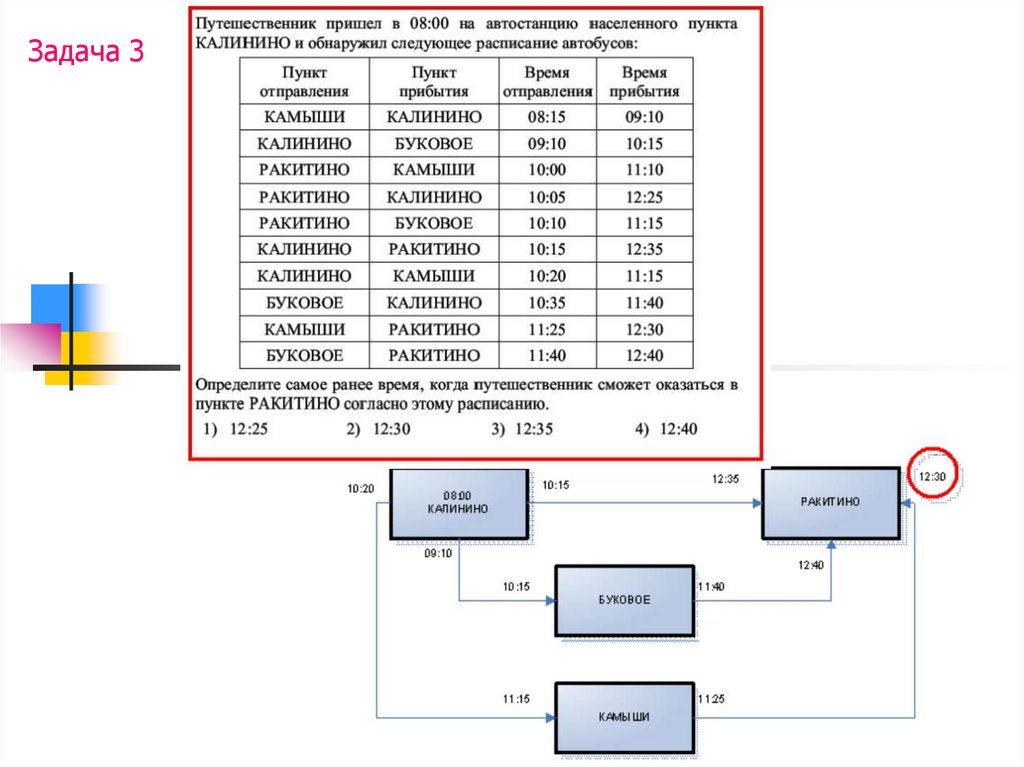
Задача 3

16. Информационные модели на графах

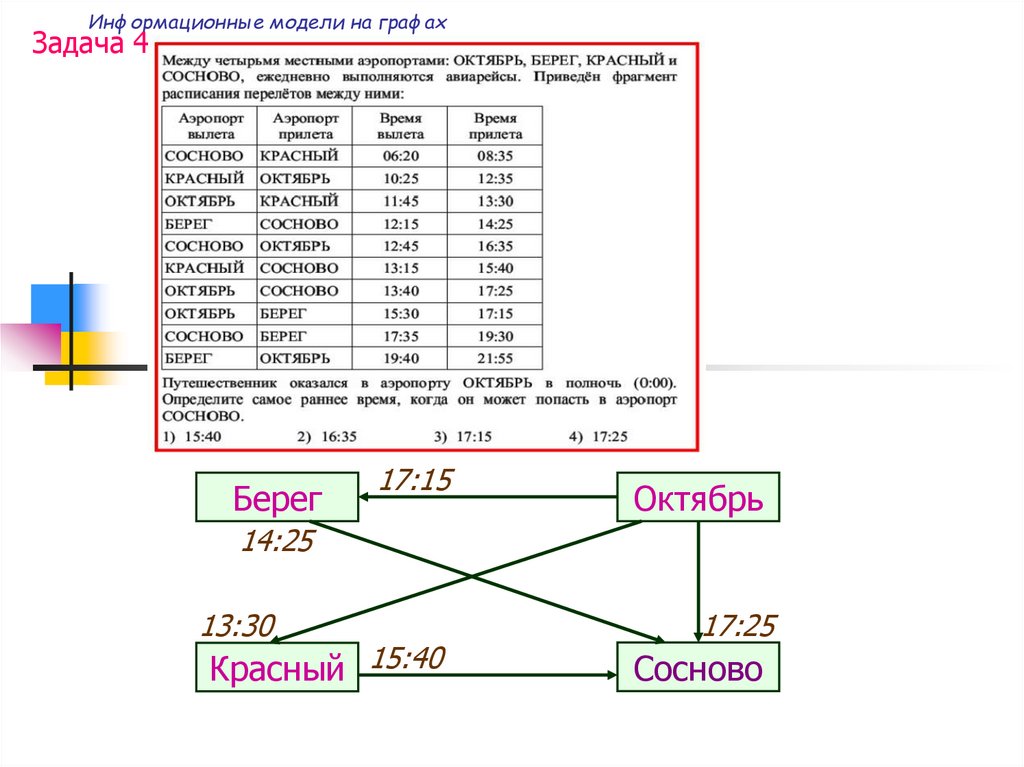
Задача 4
Берег
17:15
Октябрь
14:25
13:30
Красный 15:40
17:25
Сосново

17. Информационные модели на графах

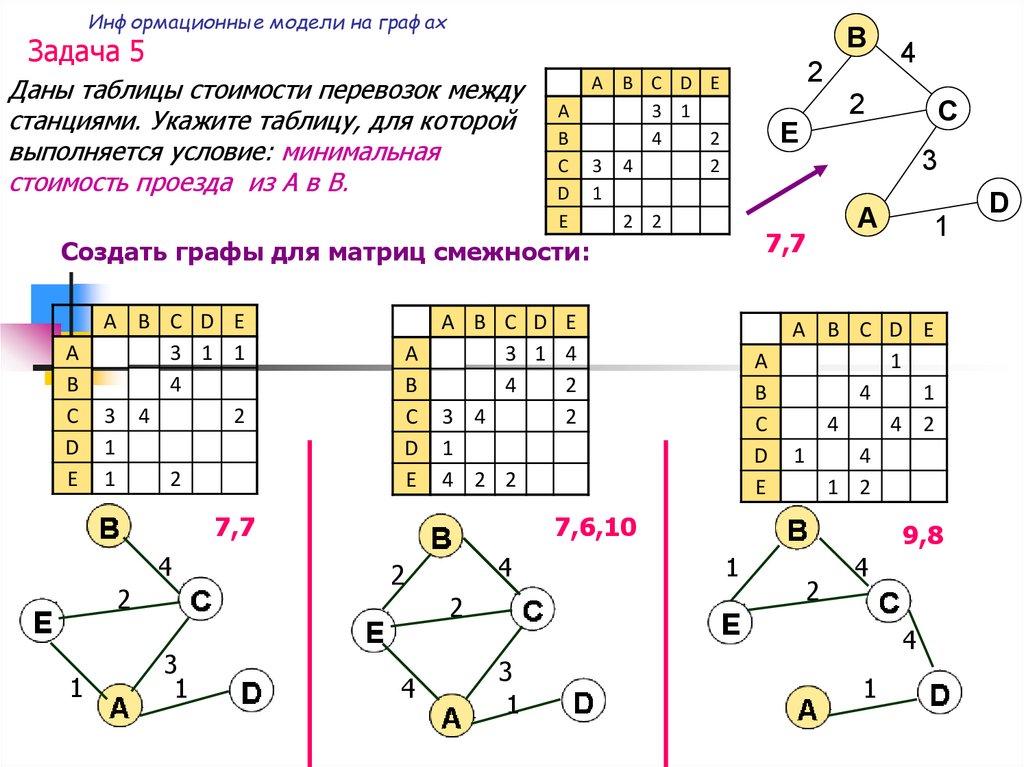
B
Задача 5
Даны таблицы стоимости перевозок между
станциями. Укажите таблицу, для которой
выполняется условие: минимальная
стоимость проезда из А в B.
A
B
C
D
Е
2
A B C D Е
3 1
4
2
3 4
2
1
2 2
2
A
B
C
D
Е
3
7,7
A B C D Е
A
3 1 4
B
4
2
C 3 4
2
D 1
Е 4 2 2
7,7
4
2
1
4
2
3
1
A
B
C
D
Е
A
1
A B C D Е
1
4
1
4
4 2
1
4
1 2
7,6,10
6
2
C
E
Создать графы для матриц смежности:
A B C D Е
3 1 1
4
3 4
2
1
1
2
4
9,8
1
2
4
4
4
3
1
1
D

18.

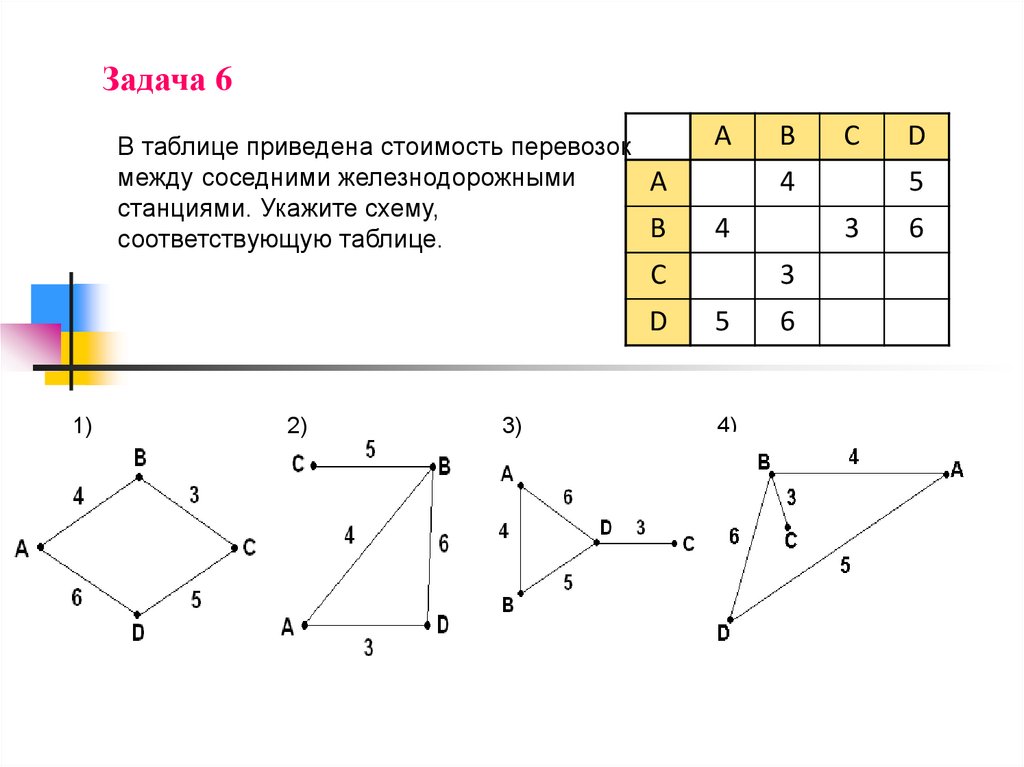
Задача 6
В таблице приведена стоимость перевозок
между соседними железнодорожными
A
станциями. Укажите схему,
B
соответствующую таблице.
A
1)
2)
3)
C
4
4
C
D
B
5
4)
5
3
3
6
D
6

19.

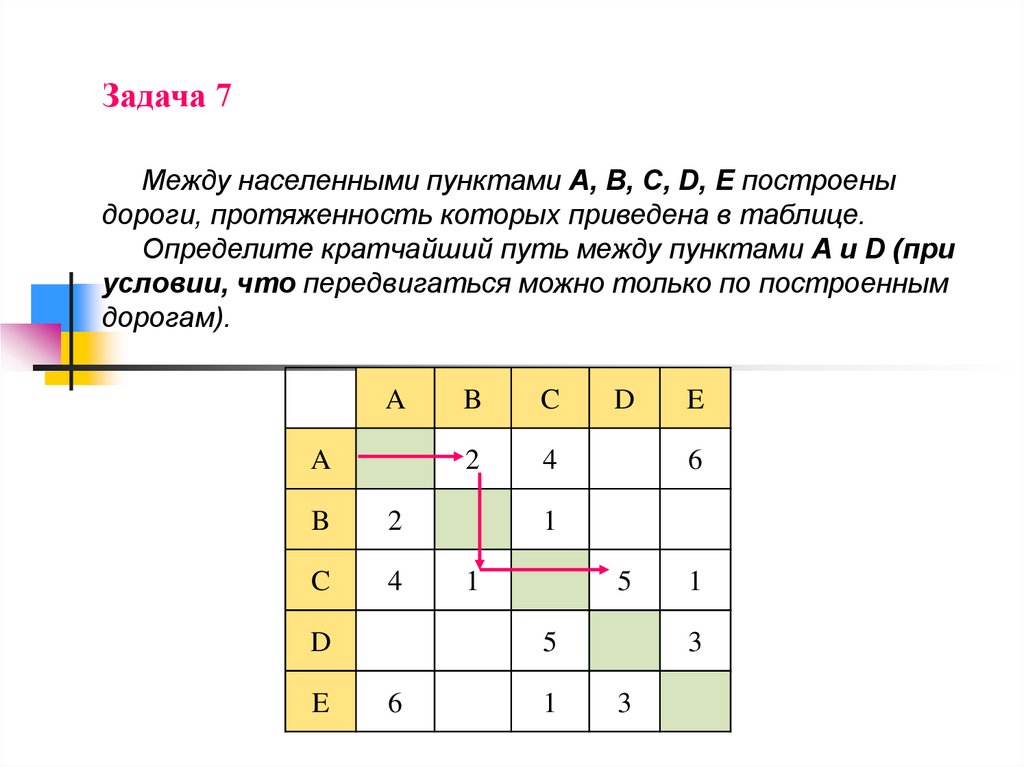
Задача 7
Между населенными пунктами A, B, C, D, E построены
дороги, протяженность которых приведена в таблице.
Определите кратчайший путь между пунктами A и D (при
условии, что передвигаться можно только по построенным
дорогам).
A
A
B
2
C
4
D
E
B
C
2
4
D
6
1
1
5
5
6
E
1
1
3
3

20. Информационные модели на графах

Задача 8