7

1.

Разработка
программных модулей

2.

Практическая работа
https://play.myquiz.ru/

3.

Функции и их аргументы
Функция в python - объект, принимающий аргументы и возвращающий
значение. Обычно функция определяется с помощью инструкции def.
Определим простейшую функцию:
def add(x, y):
return x + y
Инструкция return говорит, что нужно вернуть значение. В нашем
случае функция возвращает сумму x и y.
Теперь мы ее можем вызвать:
>>> add(1, 10)
11
>>> add('abc', 'def')
'abcdef'

4.

Функции и их аргументы
Функция может быть любой сложности и возвращать любые объекты
(списки, кортежи, и даже функции!):
>>> def newfunc(n):
def myfunc(x):
return x + n
return myfunc ...
>>> new = newfunc(100) # new - это функция
>>> new(200) 300

5.

Функции и их аргументы
Функция может и не заканчиваться инструкцией return, при этом
функция вернет значение None:
>>>
>>> def func():
... pass
...
>>> print(func())
None

6.

Аргументы функции
Функция может принимать произвольное количество аргументов или не принимать их
вовсе. Также распространены функции с произвольным числом аргументов, функции с
позиционными и именованными аргументами, обязательными и необязательными.
>>> def func(a, b, c=2): # c - необязательный аргумент
... return a + b + c
>>> func(1, 2) # a = 1, b = 2, c = 2 (по умолчанию)
5
>>> func(1, 2, 3) # a = 1, b = 2, c = 3
6
>>> func(a=1, b=3) # a = 1, b = 3, c = 2
6
>>> func(a=3, c=6) # a = 3, c = 6, b не определен
Traceback (most recent call last):
File "", line 1,
in func(a=3, c=6)
TypeError: func() takes at least 2 arguments (2 given)

7.

Аргументы функции
Функция также может принимать переменное количество позиционных аргументов, тогда
перед именем ставится *:
>>> def func(*args):
return args
>>> func(1, 2, 3, 'abc')
(1, 2, 3, 'abc')
>>> func()
()
>>> func(1)
(1,)
Как видно из примера, args - это кортеж из всех переданных аргументов функции, и с
переменной можно работать также, как и с кортежем.

8.

Аргументы функции
Функция может принимать и произвольное число именованных аргументов,
тогда перед именем ставится **:
>>> def func(**kwargs):
... return kwargs
...
>>> func(a=1, b=2, c=3)
{'a': 1, 'c': 3, 'b': 2}
>>> func()
{}
>>> func(a='python')
{'a': 'python'}
В переменной kwargs у нас хранится словарь, с которым мы, опять-таки, можем
делать все, что нам заблагорассудится.

9.

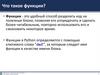
Аргументы и параметры
При создании функции определяются ее параметры. При вызове – мы передаем
аргументы. Данное соглашение о терминологии не является окончательным (среди
разработчиков нет единой договоренности). Не будет большой ошибкой, если вы
перепутаете термины. Тем не менее, лучше следовать официальным рекомендациям.
# Здесь мы определяем параметры
def foo(a, b):
print(a, b)
foo(10, 'K') # Сюда мы передаем аргументы

10.

Аргументы и параметры

11.

Возврат значений с помощью списков
def test():
str1 = "Happy"
str2 = "Coding"
return [str1, str2];
list = test()
print(list)
# ['Happy', 'Coding']

12.

Возврат значений с помощью кортежей
Кортежи — это упорядоченные неизменяемые объекты в Python, которые
обычно используются для хранения коллекций неоднородных данных.
Кортежи напоминают списки, однако их нельзя изменить после того, как они
были объявлены. А еще, как правило, кортежи быстрее в работе, чем списки.
Кортеж можно создать, отделив элементы запятыми: x, y, z или (x, y, z).
На этом примере кортеж используется для хранения данных о сотруднике (имя,
опыт работы в годах и название компании).
Bob = ("Bob", 7, "Google")

13.

Возврат значений с помощью кортежей
А вот пример написания функции для возврата кортежа:
def fun():
str1 = "Happy"
str2 = "Coding"
return str1, str2; # можно также написать (str1, str2)
str1, str2= fun()
print(str1)
print(str2)
# Happy
Coding
Обратите внимание: были опущены круглые скобки в операторе return, поскольку для
возврата кортежа достаточно просто отделить каждый элемент запятой (как показано
выше).
Не забывайте, что кортеж можно создать с помощью запятой вместо круглых скобок.
Круглые скобки требуются только в тех случаях, когда используются пустые кортежи или
вам нужно избежать синтаксической неточности.

14.

Возврат значений с помощью кортежей
Ниже показан пример функции, которая использует для возврата кортежа круглые скобки.
def student(name, class):
return (name, class)
print(student("Brayan", 10))
# ('Brayan', 10)

15.

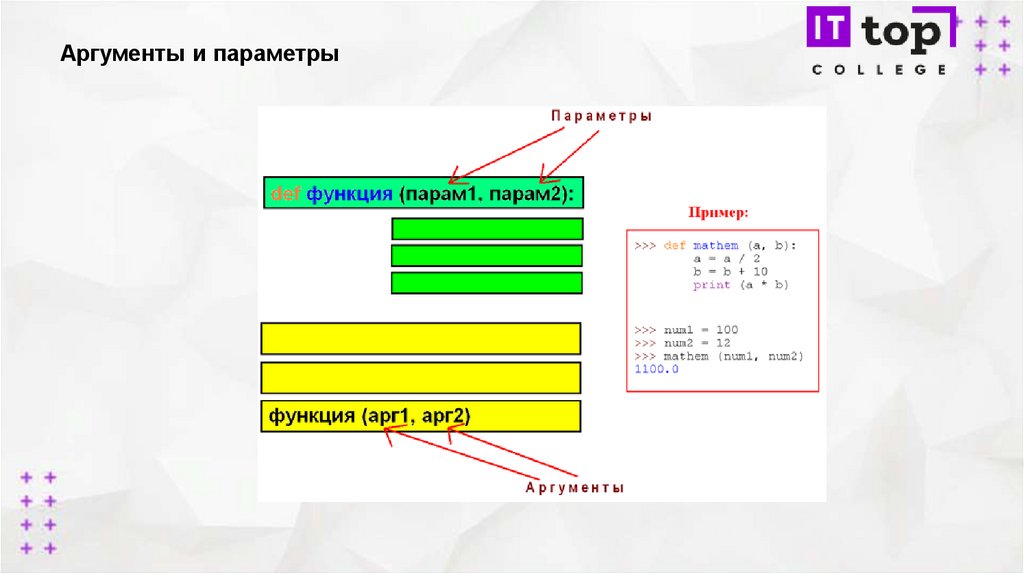
Функции на блок схемах

16.

Рекурсия
Рекурсивная функция – это функция, которая вызывает сама себя, и при
каждом очередном вызове использует данные, созданные во время
предыдущего вызова. В программировании есть ряд задач, которые проще (но
не всегда эффективнее) решаются с помощью рекурсии.

17.

Рекурсия
Рассмотрим приведенный ниже код:
def message():
print('Это рекурсивная функция')
message()
message()
Какова будет работа программы?

18.

Рекурсия
Стек – это структура данных LIFO (last in, first out): информация
последовательно добавляется в «стопку» , каждый новый объект помещается
поверх предыдущего, а извлекаются объекты в обратном порядке, – начиная с
верхнего. Работу стека отлично иллюстрирует добавление данных в список с
помощью append и извлечение информации посредством pop
stack = []
for i in range(1, 11):
stack.append(f'{i}-й элемент')
print(f'+ {i}-й элемент добавлен')
for i in stack:
print(i, end=" ")
print('\n')
for i in range(len(stack)):
print('В стеке: ', end=" ")
for i in stack:

19.

Рекурсия
Стек вызовов, в свою очередь, – это область памяти, в которой выполняются
функции. При каждом вызове функции создается фрейм – фрагмент памяти, – в
котором содержится:
информация о текущем состоянии выполнения функции;
значения всех переменных, которые функция получила для обработки;
локальные данные, созданные во время очередного вызова;
сведения о строке программы, к которой нужно вернуться после выполнения
функции.
Программисту не нужно беспокоиться о работе стека вызовов – созданием
фреймов и управлением стеком занимается интерпретатор. Однако понимание
принципа работы стека вызовов значительно упрощает создание рекурсивных
функций. Неверное же использование рекурсии приводит к переполнению стека
(stack overflow).

20.

Рекурсия
При желании лимит на глубину рекурсии можно увеличить, но сделать его
бесконечным, разумеется, нельзя – даже самый внушительный объем
оперативной памяти в итоге окажется переполненным. Для увеличения
используется модуль:
from sys import getrecursionlimit
setrecursionlimit
Рекурсия в Python имеет ограничение в 1000 слоев.

21.

Рекурсия
Чтобы стек вызовов не переполнялся, в каждой рекурсивной функции всегда
должны быть предусмотрены два случая:
Граничный, при котором функция завершает работу и возвращает данные в
основную программу.
Рекурсивный, при котором функция продолжает вызывать себя.
Вот пример простейшей рекурсивной функции, в которой учтены оба случая:
def greetings(st):
print(st)
if len(st) == 0: # Граничный случай
return
else:
# Рекурсивный случай
greetings(st[:-1])
greetings('Hello, world!')

22.

Рекурсия
Другой пример:
def message(times):
if times > 0:
print('Это рекурсивная функция')
message(times - 1)
message(5)
Во время каждого вызова функции message() в оперативной памяти создается
новый экземпляр переменной times. При первом вызове функции times имеет
значение 5. Когда функция себя вызывает, создается новый экземпляр
переменной times и в него передается значение 4. Этот цикл повторяется до тех
пор, пока в функцию в качестве аргумента не будет передан 0.

23.

Рекурсия
Когда функция достигает своего шестого вызова, значение переменной times
равно 0. В этой точке условное выражение оператора if становится ложным, и
поэтому функция завершает свою работу. Поток управления программы
возвращается из шестого экземпляра функции в точку в пятом экземпляре
непосредственно после вызова рекурсивной функции.
Поскольку после вызова рекурсивной функции больше нет инструкций, пятый
экземпляр функции message() возвращает поток управления программы назад в
четвертый экземпляр функции и т.д.

24.

Рекурсия
Рекурсия никогда не является непременным условием для решения задачи.
Любая задача, которая может быть решена рекурсивно, также может быть
решена на основе цикла.
Рекурсивные алгоритмы обычно менее эффективны, чем итеративные
алгоритмы. Это связано с тем, что процесс вызова функции требует
выполнения компьютером нескольких действий. Эти действия включают
выделение памяти под параметры и локальные переменные и для хранения
адреса местоположения программы. Такие действия, которые иногда
называются накладными расходами, происходят при каждом вызове
функции. Накладные расходы не требуются при использовании цикла.

25.

Рекурсия
Некоторые повторяющиеся задачи легче решаются на основе рекурсии, чем
на основе цикла. Там, где цикл приводит к более быстрому времени
исполнения, программист может быстрее разработать рекурсивный
алгоритм. В целом рекурсивная функция работает следующим образом:
- если в настоящий момент задача может быть решена без рекурсии, то
функция ее решает
- если в настоящий момент задача не может быть решена, то функция ее сводит
к уменьшенной и при этом аналогичной задаче и вызывает саму себя для
решения этой уменьшенной задачи
• Для того чтобы применить такой подход, во-первых, мы идентифицируем по
крайней мере один случай, в котором задача может быть решена без
рекурсии. Он называется базовым случаем. Во-вторых, мы определяем то,
как задача будет решаться рекурсивно во всех остальных случаях. Это
называется рекурсивным случаем. В рекурсивном случае мы все время
должны сводить задачу к уменьшенному варианту исходной задачи. С
каждым рекурсивным вызовом задача уменьшается. В результате будет
достигнут базовый случай, и рекурсия прекратится.

26.

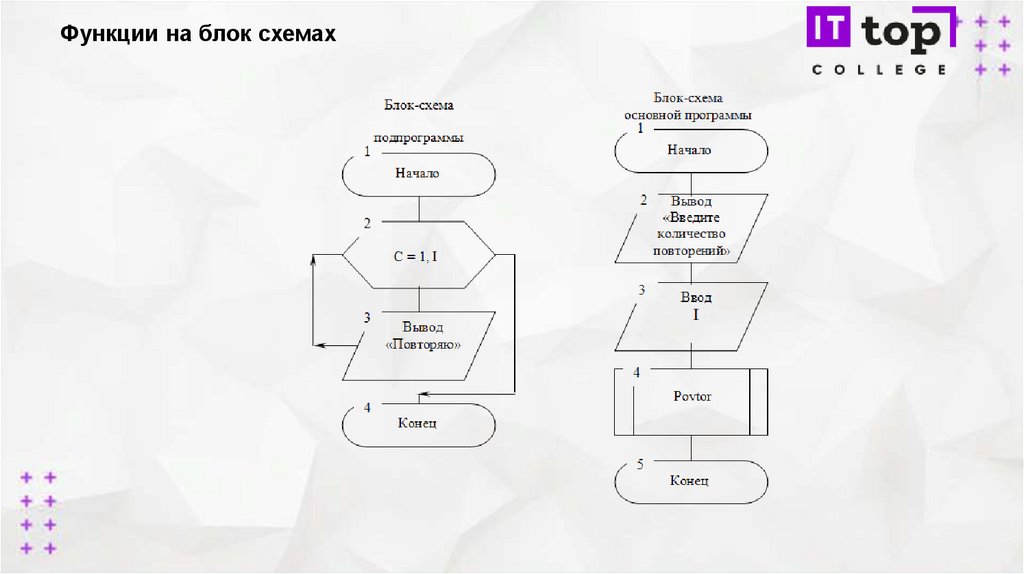
Рекурсия
Хвостовая рекурсия — частный случай рекурсии, при котором любой
рекурсивный вызов является последней операцией перед возвратом из
функции.
def message(times):
if times > 0:
print('Это рекурсивная функция')
message(times - 1)

27.

Самостоятельная работа
Напишите программу на Python для получения суммы цифр у неотрицательных
целых чисел с помощью рекурсии.
Вам поможет различные операции деления, такие как: % (нахождение остатка
от деления) и // (целочисленное деление)

28.

Домашнее задание
Завершить выполнение самостоятельной работы:
Напишите программу на Python для получения суммы неотрицательных целых чисел с
помощью рекурсии.
Вам поможет различные операции деления, такие как: % (нахождение остатка от деления)
и // (целочисленное деление)

29.

ПОДВЕДЕМ ИТОГИ