Похожие презентации:
Некоторые следствия из аксиом стереометрии
1.
02.12.2024Некоторые следствия из
аксиом стереометрии
2.
ПовторениеВ какой аксиоме говорится о том, что
можно провести плоскость?
В аксиоме С₃ - через две
пересекающиеся прямые можно
провести плоскость.
3.
Следствие 1Через прямую и не лежащую
на ней точку проходит
плоскость, и притом только
одна.
4.
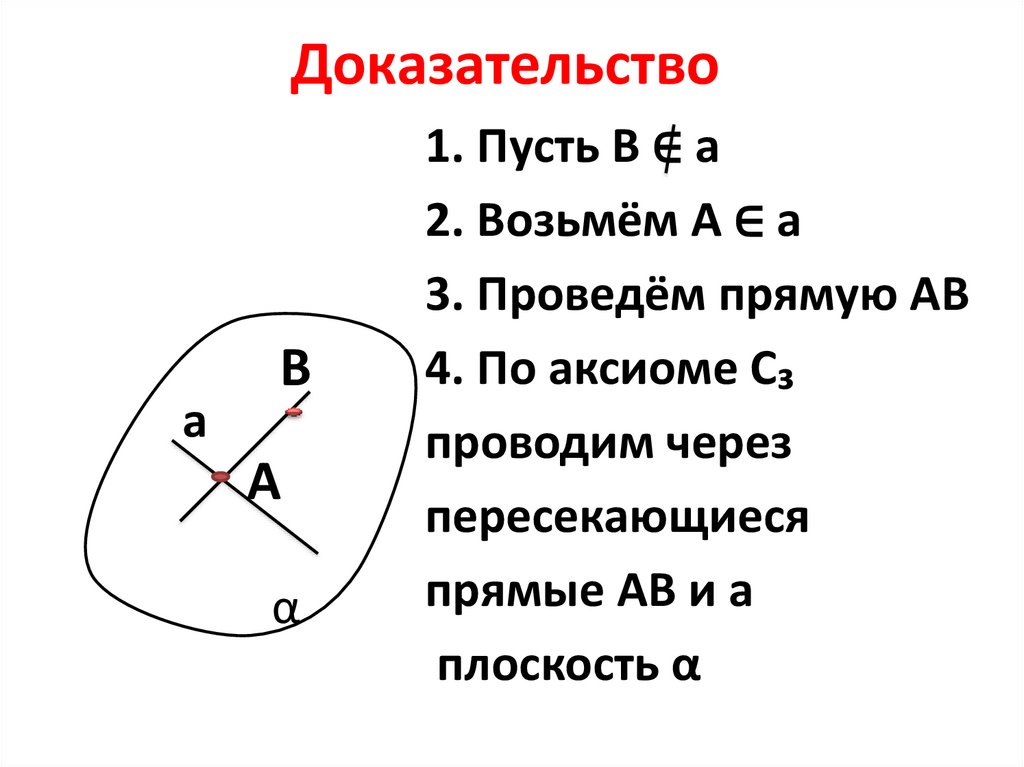
Доказательствоа
В
А
α
1. Пусть В ∈ а
2. Возьмём А ∈ а
3. Проведём прямую АВ
4. По аксиоме С₃
проводим через
пересекающиеся
прямые АВ и а
плоскость α
5.
ВыводЧерез прямую проходит
бесконечное множество плоскостей
6.
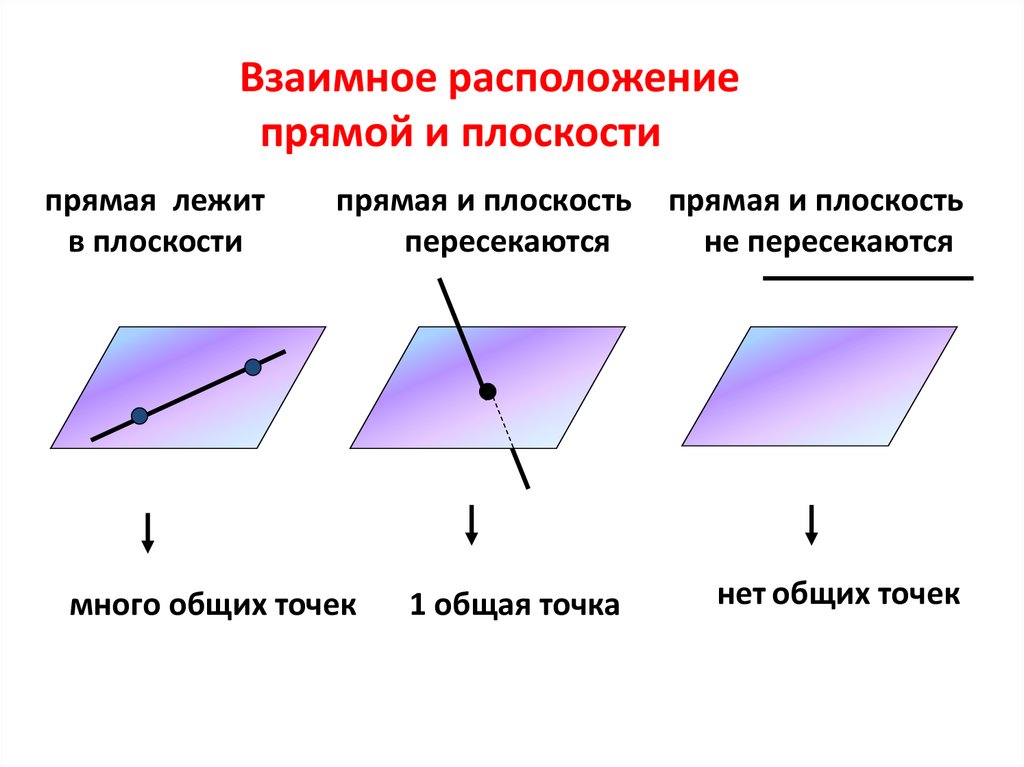
Взаимное расположениепрямой и плоскости
прямая лежит
в плоскости
прямая и плоскость
пересекаются
много общих точек
1 общая точка
прямая и плоскость
не пересекаются
нет общих точек
7.
Следствие 2Если две точки прямой принадлежат
плоскости, то вся прямая
принадлежит этой плоскости
8.
Задача №7Две прямые пересекаются в точке М.
Докажите, что все прямые, не
проходящие через точку М и
пересекающие данные прямые,
лежат в одной плоскости
9.
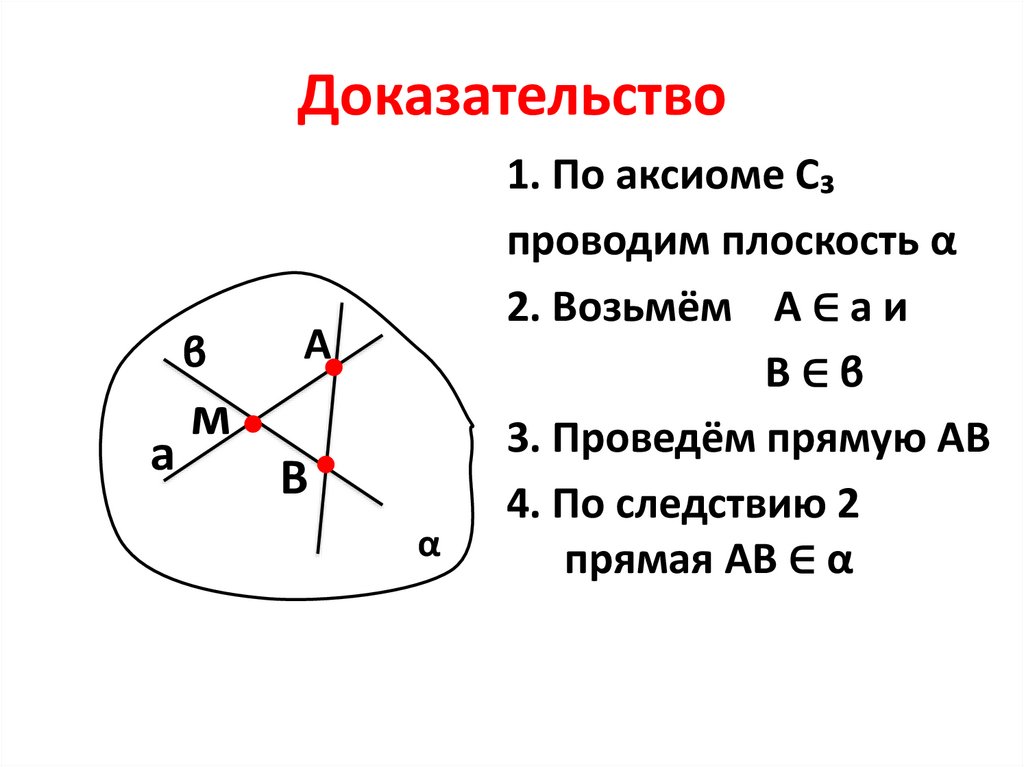
Доказательствоϐ
а
А
м
В
α
1. По аксиоме С₃
проводим плоскость α
2. Возьмём А ∈ а и
В∈ϐ
3. Проведём прямую АВ
4. По следствию 2
прямая АВ ∈ α
10.
Следствие 3Через три точки, не лежащие на
одной прямой , проходит
плоскость,
и притом только одна
11.
Задача 4(а)Точки А,В,С и D не лежат в одной
плоскости.
Могут ли какие – нибудь три
из них лежать на одной
прямой?
12.
Решение:1. Предположим, что 3 из них
лежат на одной прямой.
2. По следствию 1 через прямую и не
лежащую на ней точку проводим
плоскость.
3. Получается 4 точки лежат в одной
плоскости. Это противоречит
условию задачи.
13.
Вставьте пропущенные слова1) Плоскость проходит через три точки, при этом
они ___________
на одной прямой.
2) Если ________ точки прямой принадлежат
плоскости, то и вся прямая принадлежит
плоскости.
3) Через прямую и точку принадлежащую ей
____________________________
4) Две различные плоскости могут иметь только
одну общую _______________










 Математика
Математика








