Презентация 3 Модельный подход_GUM

1.

МОДЕЛЬНЫЙ ПОДХОД К ОЦЕНИВАНИЮ
НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
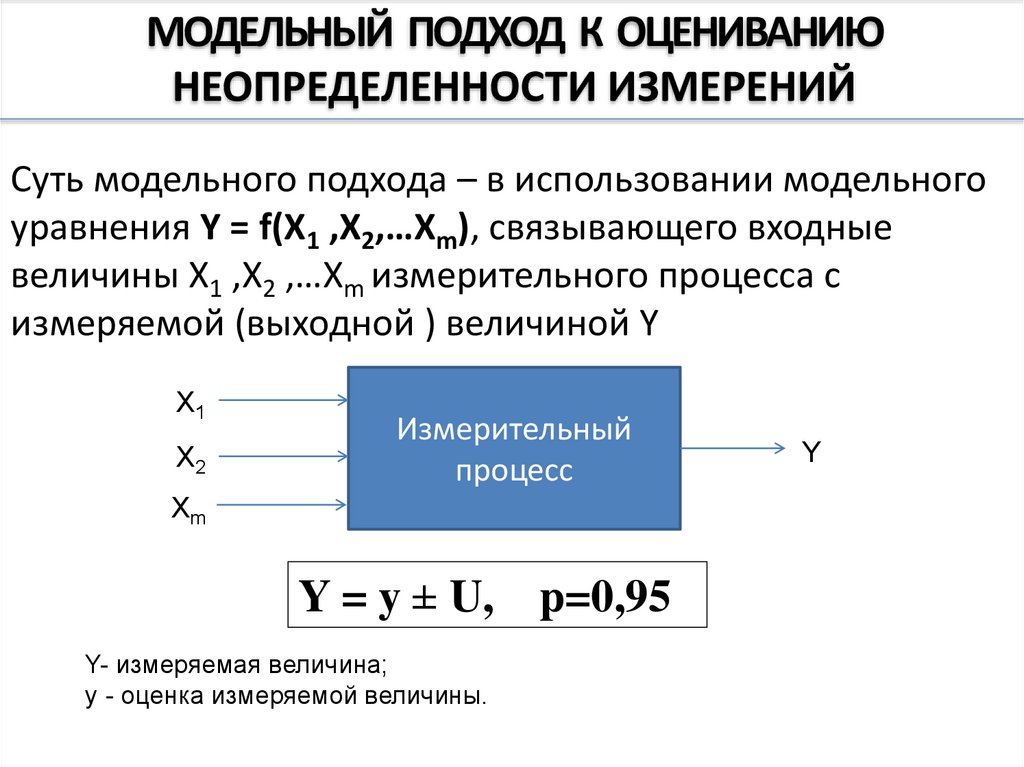
Суть модельного подхода – в использовании модельного
уравнения Y = f(X1 ,X2,…Xm), связывающего входные
величины X1 ,X2 ,…Xm измерительного процесса с
измеряемой (выходной ) величиной Y
X1
X2
Измерительный
процесс
Xm
Y = y ± U, p=0,95
Y- измеряемая величина;
y - оценка измеряемой величины.
Y

2. Примеры модельных уравнений:

Приготовление раствора из навески
По неопределенностям, связанным с входными величинами,
вычисляют неопределенность измеряемой величины.

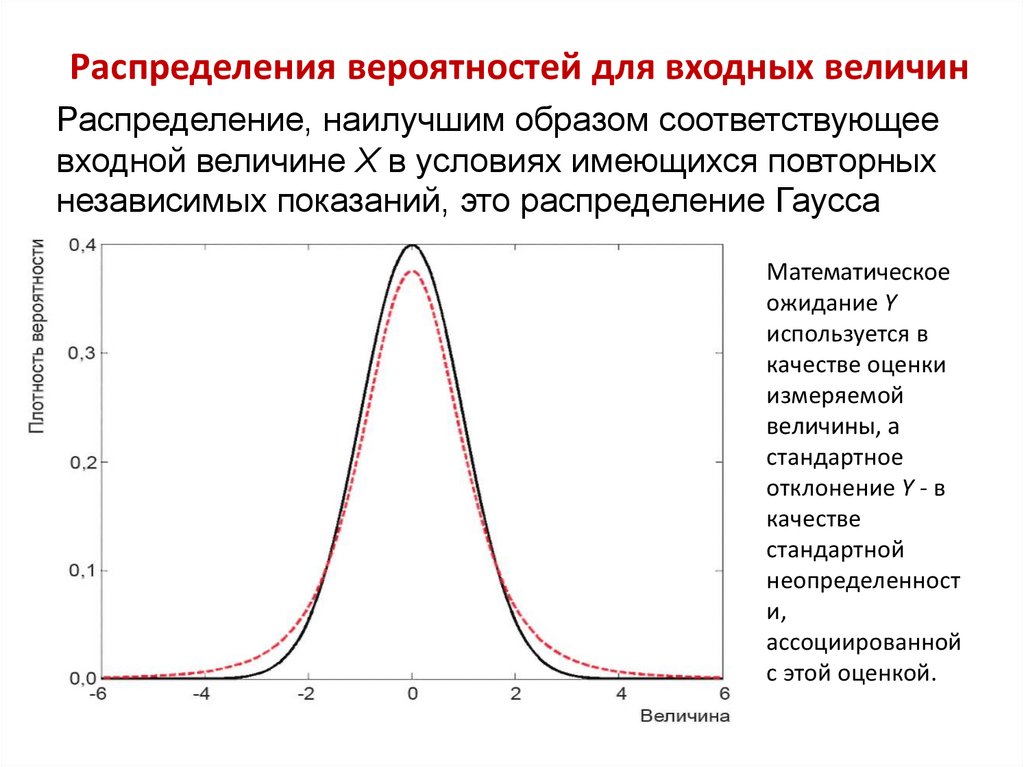
3. Распределения вероятностей для входных величин

Распределение, наилучшим образом соответствующее
входной величине X в условиях имеющихся повторных
независимых показаний, это распределение Гаусса
Математическое
ожидание Y
используется в
качестве оценки
измеряемой
величины, а
стандартное
отклонение Y - в
качестве
стандартной
неопределенност
и,
ассоциированной
с этой оценкой.

4.

Характеристики нормального распределения
Среднее арифметическое, принимаемое за результат измерений
1 n
x xi .
n i 1
Среднее квадратическое отклонение; стандартное отклонение
(СКО): параметр функции распределения измеренных значений или
показаний, характеризующий их рассеивание и равный положительному
корню квадратному из дисперсии этого распределения.

5.

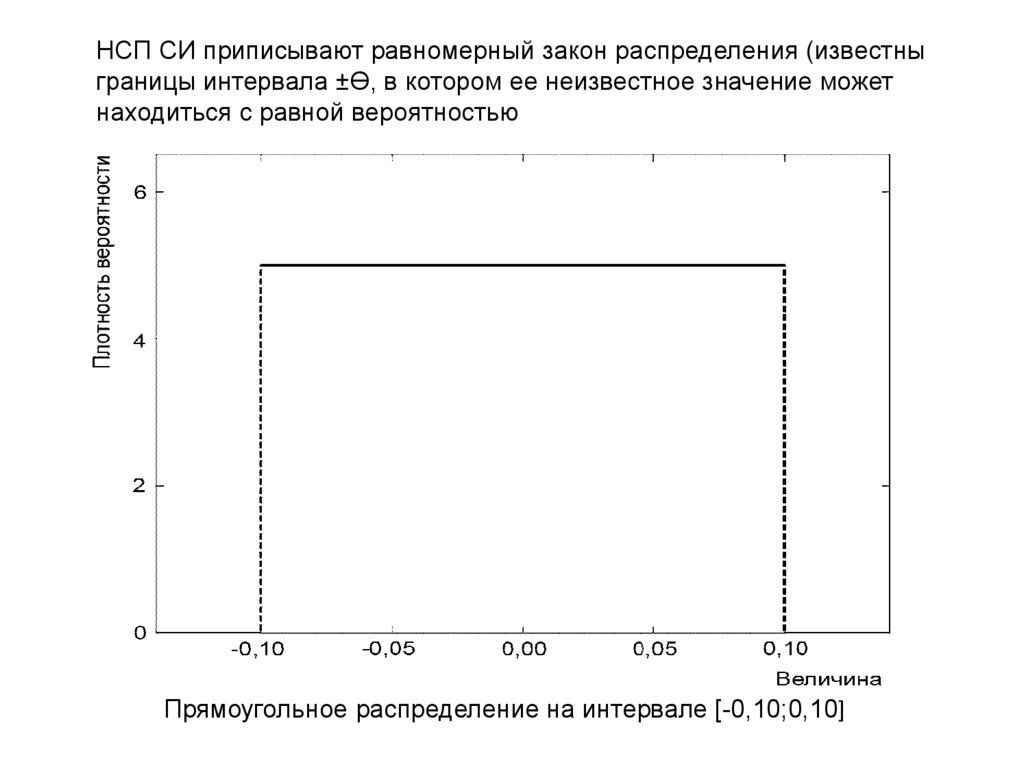
НСП СИ приписывают равномерный закон распределения (известны
границы интервала ±Ɵ, в котором ее неизвестное значение может
находиться с равной вероятностью
Прямоугольное распределение на интервале [-0,10;0,10]

6.

ОСНОВНЫЕ ПОЛОЖЕНИЯ КОНЦЕПЦИИ
НЕОПРЕДЕЛЕННОСТИ
1. Все составляющие неопределенности можно
сгруппировать в две категории в соответствии со
способом их оценивания:
А – составляющие, оцениваемые путем применения
статистических методов (обработкой результатов
многократных измерений);
В составляющие, оцениваемые другим способом
(по характеристикам, взятым из паспорта на прибор,
методик выполнения измерений, из справочников и
т.д.).
! Не являются заменителями слов «случайная» и
«систематическая»

7.

БАЗОВЫЙ АЛГОРИТМ ОЦЕНИВАНИЯ
НЕОПРЕДЕЛЕННОСТИ В ИЗМЕРЕНИЯХ
1. Составление модельного уравнения
Модельное уравнение выражает зависимость между
выходной (измеряемой) величиной Y и входными величинами
X1, X2, …, Xm :
Y f ( X 1 ,..., X m )
2. Оценивание входных величин
Значения входных величин находят путем их измерения с
однократными или многократными наблюдениями или берут
из внешних источников.
При проведении многократных измерений за значение
входной величины принимают среднее арифметическое
результатов ряда отдельных наблюдений:

8.

n
1
x xi .
n i 1
3. Вычисление оценки результата измерения
Оценку выходной величины получают при подстановке в
модельное уравнение оценок входных величин:
y f ( x1 , , x m )
4. Вычисление стандартных неопределенностей входных
величин
4.1. Стандартная неопределенность измерения типа А i-й
входной величины находится по формуле:
ni
u A ( xi )
(x x )
q 1
iq
i
ni (ni 1)
2

9.

4.2. Стандартная неопределенность типа В i-й входной
величины находится в зависимости от априорной информации
о изменчивости входной величины. Если i-я входная величина
является неисключенной систематической погрешностью
(НСП) с границами ±θi, то ее неопределенность вычисляется
по формуле:
uB ( xi ) i i
где αi – коэффициент, соответствующий принимаемому закону
распределения внутри границ НСП.
Для равномерного (или неизвестного) закона распределения:
3;
для нормального закона распределения (для вероятности p=0,95):
α=2;
для треугольного закона распределения:
для закона арксинуса:
2.
3;

10.

5. Определение коэффициентов чувствительности
Коэффициенты чувствительности ci показывают, как оценка
выходной величины y будет изменяется с изменением оценок
входных величин xi . Их находят как частные производные
выходной величины по каждой из входной величин:
f
Y
ci
xi X i x1 , x2 ,..., xm
6. Вычисление вклада неопределенности каждой
входной величины в неопределенность измеряемой
величины
Вклад неопределенности каждой входной величины в
неопределенность
измеряемой величины
(суммарную
стандартную
неопределенность)
определяют
как
произведение коэффициента чувствительности ci на
неопределенность входной величины u(xi): .

11.

ui ( y ) ciu ( xi ).
7. Определение стандартной неопределенности выходной
величины (суммарной стандартной неопределенности)
Осуществляется по формулам, называемым законом
распространения
неопределенности.
При
отсутствии
корреляций между входными величинами стандартная неопределенность выходной величины определяется как
uс ( y )
m
2
2 2
2 2
2 2
u
(
y
)
c
u
(
x
)
c
u
(
x
)
...
c
i
1
1
2
2
m u ( xm )
i 1

12.

8. Вычисление коэффициента охвата
Коэффициент охвата представляет собой множитель, на
который умножают стандартную суммарную оценку
неопределенности
для
получения
расширенной
неопределенности. Его приближенное значение для уровня
доверия
0,95
равно
2.
При наличии вкладов
неопределенности типа А, GUM рекомендует брать в
качестве коэффициента охвата коэффициент Стьюдента
для уровня доверия 0,95 и эффективного числа степеней
свободы νeff, определяемого по формуле ВелчаСаттерсвейта:
u 4 ( y)
eff m
4
u
i ( y) i
i 1

13.

Для прямых многократных измерений (или для косвенных
многократных измерений с одинаковым числом наблюдений n)
эта формула может быть представлена в виде:
uc ( y )
eff (n 1)
u
A
4
9. Вычисление расширенной неопределенности
Расширенную неопределенность U получают путем
умножения неопределенности выходной величины (суммарной
стандартной неопределенности) на коэффициент охвата:
U ( y ) k uc ( y ).
10. Запись полного результата измерения
Полный результат измерения включает в себя оценку
выходной величины и приписанное ей значение расширенной
неопределенности с указанием уровня доверия:
Y y U , p 0,95.

14.

Значение расширенной неопределенности указывается с
числом значащих цифр, не больше двух. Результат измерения,
как и значения входных величин, округляют так, чтобы они
соответствовали своим неопределенностям.
11. Составление бюджета неопределенности
Полученные в процессе реализации базового алгоритма
промежуточные результаты удобно представлять в виде
бюджета неопределенности, который включает в себя список
всех входных величин, их оценок вместе с принадлежащими
им
стандартными
неопределенностями
измерения,
коэффициентами чувствительности и числами степеней
свободы:

15.

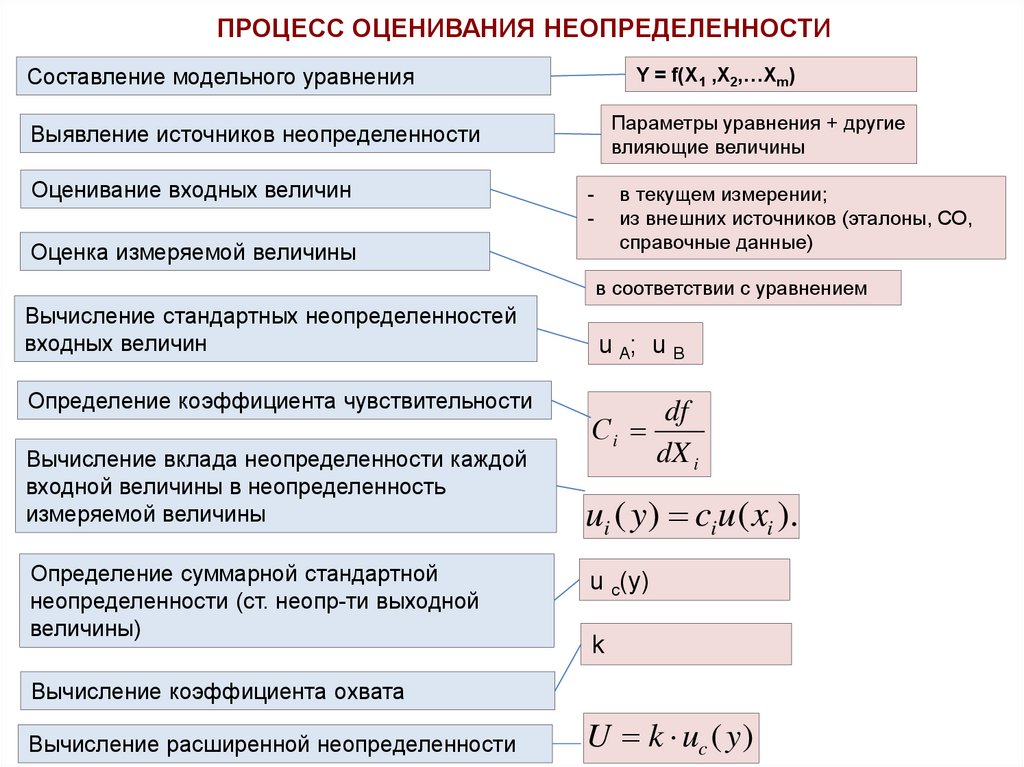
ПРОЦЕСС ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ
Y = f(X1 ,X2,…Xm)
Составление модельного уравнения
Параметры уравнения + другие
влияющие величины
Выявление источников неопределенности
Оценивание входных величин
в текущем измерении;
из внешних источников (эталоны, СО,
справочные данные)
-
Оценка измеряемой величины
в соответствии с уравнением
Вычисление стандартных неопределенностей
входных величин
Определение коэффициента чувствительности
Вычисление вклада неопределенности каждой
входной величины в неопределенность
измеряемой величины
Определение суммарной стандартной
неопределенности (ст. неопр-ти выходной
величины)
u A; u B
df
Сi
dX i
ui ( y ) ciu ( xi ).
u c(y)
k
Вычисление коэффициента охвата
Вычисление расширенной неопределенности
U k uc ( y)

16.

Хотя Руководство дает схему определения
неопределенности, оно не может заменить
критическое размышление, интеллектуальную
честность и профессиональное мастерство. Оценка
неопределенности не является ни рутинной работой,
ни чисто математической; она зависит от детального
знания природы измеряемой величины и измерения.
Поэтому качество и ценность упомянутой
неопределенности результата измерения, в конечном
счете, зависит от понимания, критического анализа и
честности тех, кто участвует в приписывании ее
значения
Руководство по выражению неопределенности измерения
Guide to the Expression of Uncertainty in Measurement
Перевод с англ. под науч. ред. проф. Слаева В.А.
ВНИИМ им. Д.И. Менделеева, С.-Петербург, 1999. - 134 с.

17.

Возможно ли применение модельного подхода для
оценивания
неопределенности
количественных
микробиологических определений?
• применение этого "пошагового" подхода не будет достаточно
удовлетворительным в случае микробиологического анализа пищевых
продуктов, где трудно построить модель, реально всесторонне
охватывающую все этапы измерительного процесса. Из-за возможности
упустить из виду какие-либо значимые источники неопределенности
имеется
высокий
риск
недооценить
истинную
величину
неопределенности. Более того, в микробиологии трудно с достаточной
точностью количественно оценить вклад каждого отдельного шага в
аналитическом процессе, потому что
• аналитом являются живые организмы, физиологический статус которых
может быть весьма разнообразным, и
• аналитическая цель может включать в себя различные виды, штаммы
или различные роды микроорганизмов.
Другими словами, микробиологический анализ не предоставляет
возможности оценить неопределенность результата измерения