Biografiya-Isaaka-Nyutona (2) (1)

1.

Биография Исаака Ньютона
Исаак Ньютон (1643-1727) — английский физик, математик, механик, астроном и алхимик, считается одним из величайших
ученых всех времен. Его работы оказали огромное влияние на науку и философию.
Ньютон открыл закон всемирного тяготения, сформулировал законы движения, заложил основы классической механики.
Он также внес значительный вклад в развитие математического анализа, оптики и астрономии.
Среди его самых известных работ — "Математические начала натуральной философии", где изложены его законы
движения и всемирного тяготения.

2.

Работы Ньютона
1. Математические начала натуральной философии - Фундаментальная работа Ньютона, в которой он изложил свои
законы движения и всемирного тяготения
2. Оптика - В этом труде Ньютон описал свои открытия в области оптики, включая теорию цвета и природу света
3. Исчисление флюксий - Работа Ньютона по математике, внёсшая значительный вклад в развитие дифференциального и
интегрального исчисления
4. Хронология древних царств - Историческое сочинение Ньютона, в котором он реконструировал события древних
цивилизаций
5. Алхимические трактаты - Ньютон также занимался исследованиями в области алхимии, хотя эта сторона его
деятельности была менее известна при жизни

3.

Открытия Ньютона
Законы движения - Ньютоном были сформулированы три основных закона механики, которые стали основой
классической физики.
Закон всемирного тяготения - Ньютон открыл всеобщий закон гравитации, который описывает притяжение между
любыми двумя массивными телами.
Дифференциальное и интегральное исчисление - Ньютон внес значительный вклад в развитие математического
анализа, заложив основы дифференциального и интегрального исчисления.
Открытия в оптике - Ньютон провел фундаментальные исследования в области оптики, включая теорию цвета и
природу света.

4.

Бином Ньютона
Бином Ньютона - это важная математическая формула, которая
описывает расширение степени бинома (a + b)^n. Она имеет широкое
применение в различных областях математики и науки.

5.

История создания
1
Открытие Ньютона
Бином Ньютона был
2
Практическое
применение
впервые описан великим
Ньютон использовал эту
английским ученым
формулу для решения
Исааком Ньютоном в XVII
задач в области
веке.
математического анализа
и теории рядов.
3
Дальнейшее развитие
Бином Ньютона получил дальнейшее изучение и обобщение в
работах других выдающихся математиков.

6.

Формула бинома
Ньютона
1
(a + b)^n
Общий вид формулы бинома Ньютона.
2
n! / (k! * (n-k)!)
Коэффициент, определяющий количество членов с
данной степенью.
3
a^(n-k) * b^k
Составляющие каждого члена в раскрытии бинома.

7.

Свойства бинома Ньютона
Симметрия
Распределительность
Коэффициенты, стоящие при a^k *
Бином Ньютона распределяется по
b^(n-k) и a^(n-k) * b^k, равны.
умножению и возведению в степень.
Вычислительная
эффективность
Формула позволяет быстро и точно
вычислять биномиальные
коэффициенты.

8.

Применение бинома
Ньютона
Математический
анализ
Теория вероятностей
Бином Ньютона широко
вычисления вероятностей в
применяется для разложения
биномиальном
функций в степенные ряды.
распределении.
Комбинаторика
Физика
Биномиальные
В физике бином Ньютона
коэффициенты находят
используется для описания
применение при решении
процессов, связанных с
задач на подсчет сочетаний.
движением, колебаниями и
Формула используется для
распространением волн.

9.

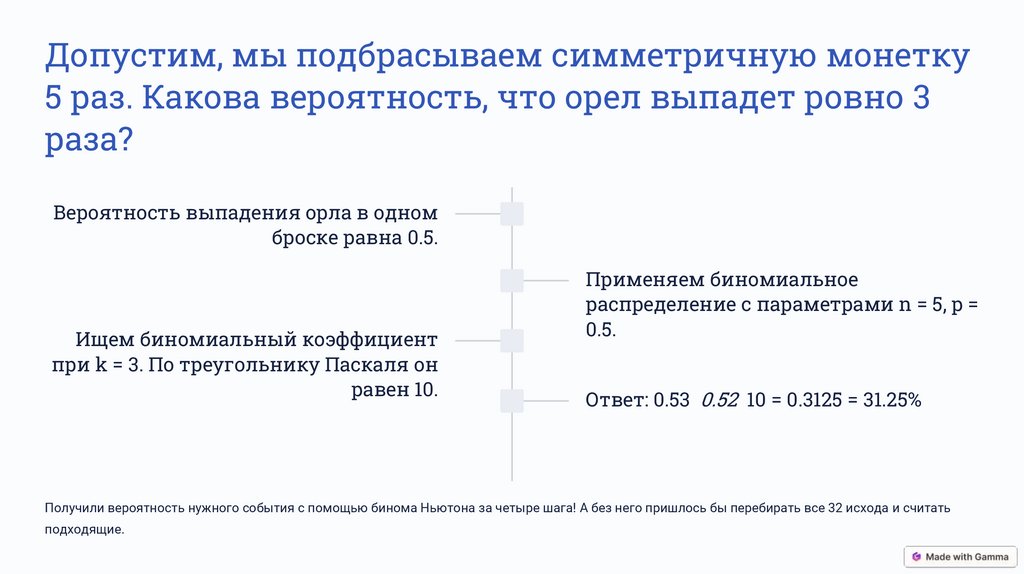
Допустим, мы подбрасываем симметричную монетку
5 раз. Какова вероятность, что орел выпадет ровно 3
раза?
Вероятность выпадения орла в одном
броске равна 0.5.
Ищем биномиальный коэффициент
при k = 3. По треугольнику Паскаля он
равен 10.
Применяем биномиальное
распределение с параметрами n = 5, p =
0.5.
Ответ: 0.53 0.52 10 = 0.3125 = 31.25%
Получили вероятность нужного события с помощью бинома Ньютона за четыре шага! А без него пришлось бы перебирать все 32 исхода и считать
подходящие.

10.

1
Ученик решает тест из 8 вопросов, и вероятность правильного ответа
на каждый вопрос равна 0.7. Какова вероятность того, что он ответит
правильно на 6 вопросов?
2
Игрок бросает шестигранный кубик 4 раза. Какова вероятность того,
что число "4" выпадет ровно 2 раза?

11.

Решение:
1. Определим параметры:
2. • n = 8 (количество вопросов),
3. • k = 6 (количество правильных ответов),
4. • p = 0.7 (вероятность правильного ответа).
2. Находим биномиальный коэффициент:
C(8, 6) = C(8, 2) = 8 / 2(8-2) = 8 × 7 / 2 = 28
1. Подставляем значения в формулу:
P(X = 6) = C(8, 6) ⋅ (0.7)⁶ ⋅ (0.3)²
P(X = 6) = 28 ⋅ (0.7)⁶ ⋅ (0.3)²
P(X = 6) = 28 ⋅ (0.117649) ⋅ (0.09) ≈ 28 ⋅ 0.01058841 ≈ 0.2964
Ответ: Вероятность того, что ученик ответит правильно на 6 вопросов, составляет примерно 0.2964.

12.

Решение:
1.
1. Определим параметры:
2. • n = 4 (количество бросков),
3. • k = 2 (количество выпадений "4"),
4. • p = ⅙ (вероятность выпадения "4").
2. Находим биномиальный коэффициент:
C(4, 2) = 4! / 2!(4-2)! = 4 × 3 / 2 = 6
1. Подставляем значения в формулу:
P(X = 2) = C(4, 2) ⋅ ((1 / 6))² ⋅ ((5 / 6))²
P(X = 2) = 6 ⋅ ((1 / 36)) ⋅ ((25 / 36))
P(X = 2) = 6 ⋅ 25 / 1296 = 150 / 1296 ≈ 0.1157
Ответ: Вероятность того, что число "4" выпадет ровно 2 раза, составляет примерно 0.1157.