KT7

1.

Вставка элемента в
очередь с приоритетом

2.

Теоретическое описание выбранного алгоритма.
Очередь с приоритетом — это структура данных, в которой каждый элемент имеет "приоритет", и
элементы с более высоким приоритетом обрабатываются раньше, чем элементы с более низким
приоритетом. Эта структура может быть реализована с использованием различных подходов,
включая массивы, связанные списки и бинарные деревья.
Один из самых эффективных способов реализации очереди с приоритетом — использование кучи.
Куча — это специализированная бинарная дерево-структура, которая поддерживает следующие
свойства:
Максимальная куча: Родительский элемент всегда больше (или равен) своим дочерним элементам.
Минимальная куча: Родительский элемент всегда меньше (или равен) своим дочерним элементам.

3.

Оценка вычислительной сложности.
Вычислительная сложность алгоритма вставки элемента в
очередь с приоритетом, реализованную с помощью кучи,
составляет O(log n), где n - количество элементов в очереди.
Это связано с тем, что при каждом сравнении приоритетов
можно отбросить половину элементов.

4.

Листинг
import java.util.Arrays;
class PriorityQueue {
private int[] heap;
private int size;
private int capacity;
public PriorityQueue(int capacity) {
this.capacity = capacity;
this.size = 0;
heap = new int[capacity];
}

5.

Листинг
public void insert(int element) {
if (size == capacity) {
throw new RuntimeException("Heap is full");
}
heap[size] = element;
size++;
heapifyUp(size - 1);
}

6.

Листинг
public int extractMin() {
if (size == 0) {
throw new RuntimeException("Heap is empty");
}
int min = heap[0];
heap[0] = heap[size - 1];
size--;
heapifyDown(0);
return min;
}

7.

Листинг
private void heapifyUp(int index) {
while (index > 0 && heap[parent(index)] > heap[index]) {
swap(index, parent(index));
index = parent(index);
}
}

8.

Листинг
private void heapifyDown(int index) {
int smallest = index;
int left = leftChild(index);
int right = rightChild(index);
if (left < size && heap[left] < heap[smallest]) {
smallest = left;
}
if (right < size && heap[right] < heap[smallest]) {
smallest = right;
}
if (smallest != index) {
swap(index, smallest);
heapifyDown(smallest);
}
}

9.

Листинг
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
private int parent(int index) {
return (index - 1) / 2;
}
private int leftChild(int index) {
return 2 * index + 1;
}

10.

Листинг
private int rightChild(int index) {
return 2 * index + 2;
}
public boolean isEmpty() {
return size == 0;
}
public int getSize() {
return size;
}
}

11.

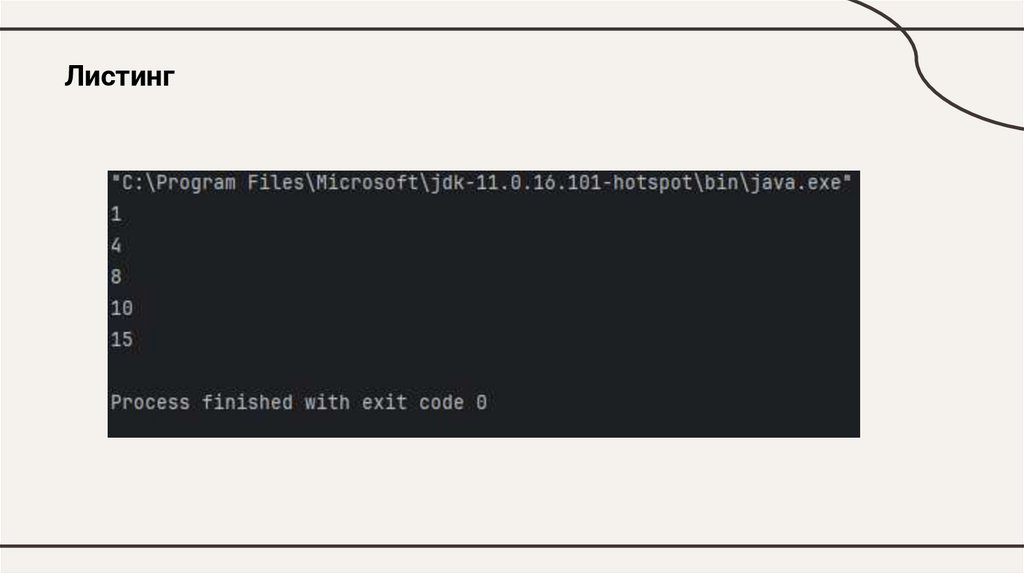
Листинг
class Main {
public static void main(String[] args) {
PriorityQueue pq = new PriorityQueue(100);
pq.insert(10);
pq.insert(4);
pq.insert(15);
pq.insert(1);
pq.insert(8);
while (!pq.isEmpty()) {
System.out.println(pq.extractMin());
}

12.

Листинг

13.

14.

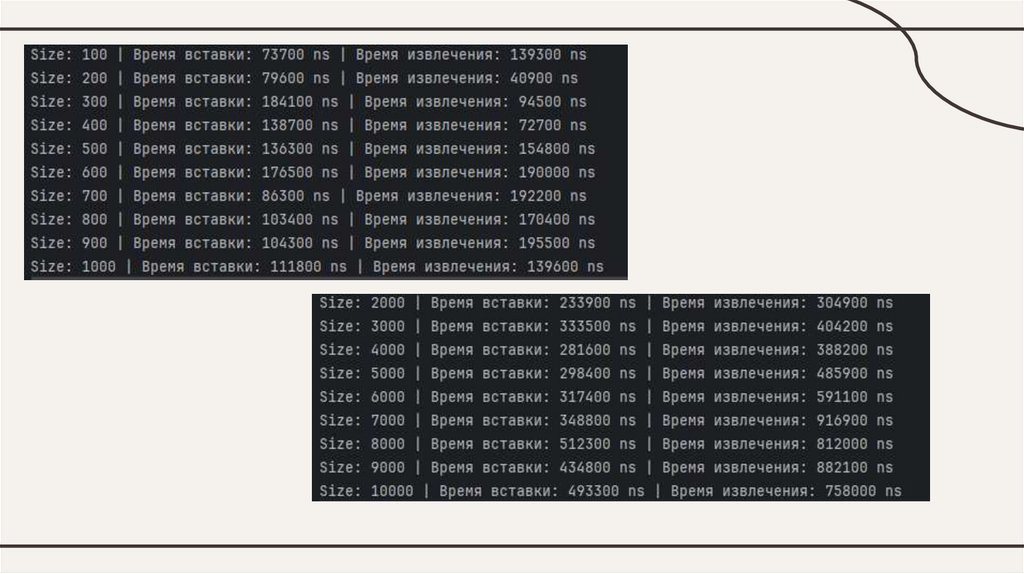
Для небольших наборов данных (менее 1000 элементов) эффективность
приоритетной очереди остается высокой. Время выполнения операций быстро
остается в рамках логарифмической сложности.
С увеличением объема данных, операции вставки и извлечения остаются
эффективными, но объем используемой памяти становится важным, особенно при
использовании других структур данных.
Очереди с приоритетом эффективны для динамического управления данными, где
приоритетный доступ к определенным элементам необходим, например, в
алгоритмах, таких как Дейкстра для поиска пути.