13.11 ВиС_графы

1.

Элементы
теории
графов

2.

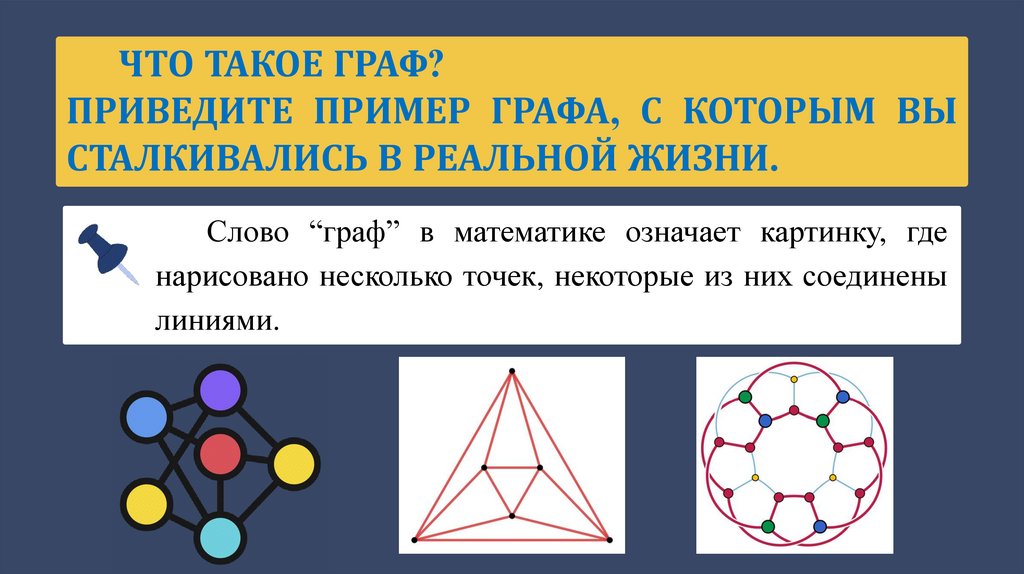
ЧТО ТАКОЕ ГРАФ?
ПРИВЕДИТЕ ПРИМЕР ГРАФА, С КОТОРЫМ ВЫ
СТАЛКИВАЛИСЬ В РЕАЛЬНОЙ ЖИЗНИ.
Слово “граф” в математике означает картинку, где
нарисовано несколько точек, некоторые из них соединены
линиями.

3.

Примеры графов
Схема
метро
Электросхема
Родословная
Схема молекулы

4.

ОПРЕДЕЛЕНИЕ
Графом называется
конечное
множество
точек,
некоторые
из
которых
соединены
линиями.
При
этом
точки
называются
вершинами графа, а
линии — рёбрами.

5.

ОТВЕТЬТЕ НА ВОПРОСЫ:
Чем
ориентированный
неориентированного?
граф
отличается
от
Что называют степенью вершины?
Дайти определение пути в графе. Что такое цепь? Что
такое цикл?
Какой путь называют Эйлеровым?

6.

Степень вершины графа (валентность) - это количество
исходящих из неё рёбер.
Путь в графе - это последовательность вершин, в которой
каждая вершина соединена со следующей ребром.
Цепь (пустой путь)- это путь в графе из одной вершины в
другую, в котором вершины и ребра не повторяются.
Цикл – это замкнутый путь, у которого начало и конец в
одной вершине, а ребра и промежуточные вершины не
повторяются

7.

Эйлеровый путь – это путь, проходящий ровно один раз по
каждому ребру.

8.

РАБОТАЕМ В ТЕТРАДИ
№ 1.
В графе 3 вершины, каждая из которых
имеет степень 2. Сколько у него ребер?
Нарисуйте такой граф.
В графе 4 вершин, каждая из которых
имеет степень 3. Сколько у него ребер?
Нарисуйте такой граф.
В графе 5 вершин, каждая из которых
имеет степень 4. Сколько у него ребер?
Нарисуйте такой граф.

9.

ЗАДАЧА О КРАСКАХ
Почти 100 лет потребовалось на
решение
задачи
о
красках.
Предположим, что на листе бумаги
изображена
контурная
карта.
Нужно раскрасить разные страны,
причем страны с общей границей
нужно красить в разные цвета,
чтобы они не сливались. Сколько
потребуется разных цветов?

10.

ЗАДАЧА О КРАСКАХ
Для решения этой задачи
применили
теорию
графов.
Каждую
страну
обозначали
вершиной. Если у двух стран был
общий
участок
границы,
вершины
графы
соединяли
ребром. Изучая такие графы,
доказали,
что
любую
политическую
карту
можно
раскрасить
всего
четырьмя
красками.
Кеннет Аппель и Вольфганг Хакен
доказали это в 1976 году

11.

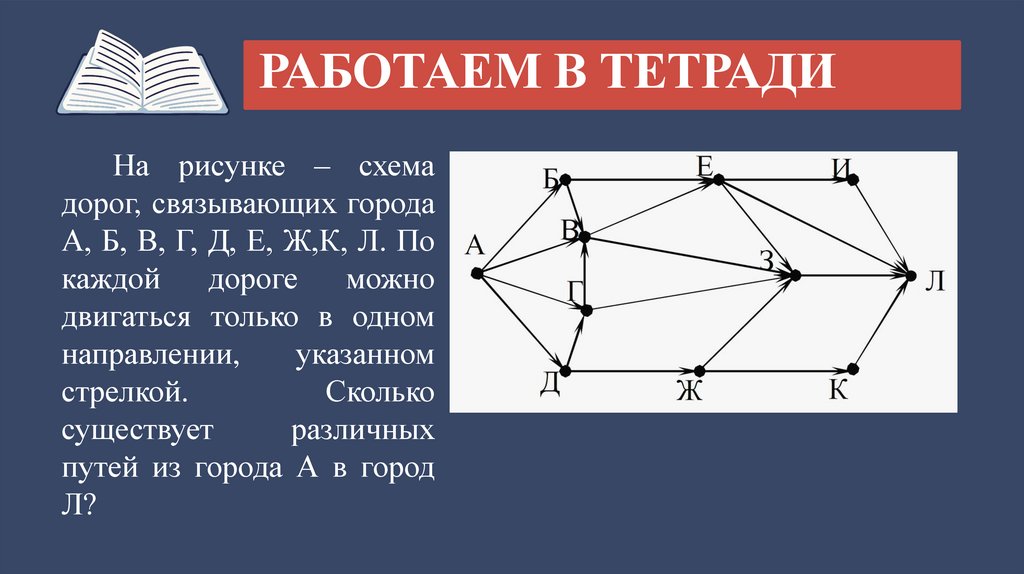
РАБОТАЕМ В ТЕТРАДИ
На рисунке – схема
дорог, связывающих города
А, Б, В, Г, Д, Е, Ж,К, Л. По
каждой
дороге
можно
двигаться только в одном
направлении,
указанном
стрелкой.
Сколько
существует
различных
путей из города А в город
Л?

12.

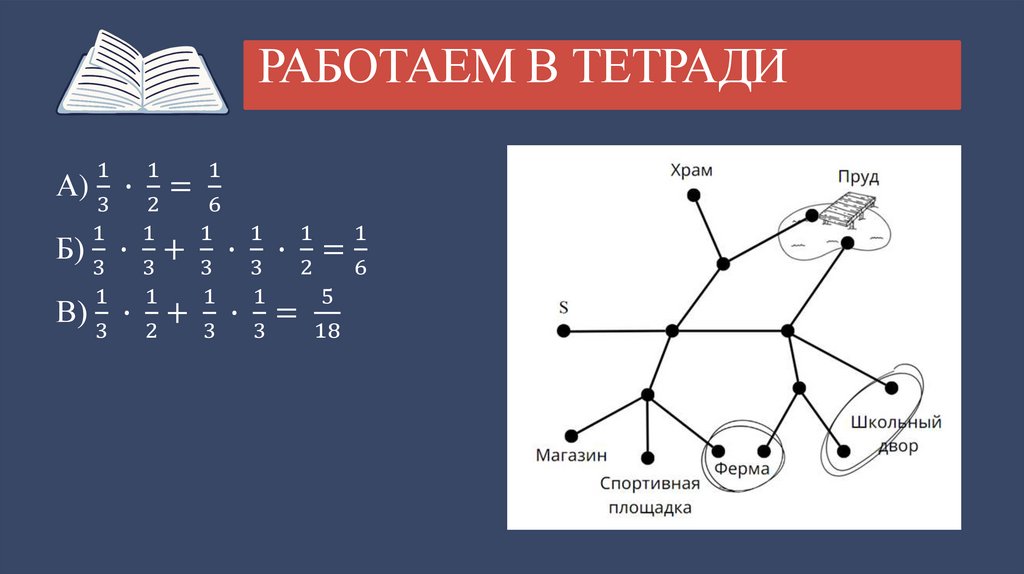
РАБОТАЕМ В ТЕТРАДИ
Иван Викторович гуляет по своему
посёлку. Схема дрожек показана на
рисунке. Он начинает прогулку в точке
S и на каждой развилке с равными
шансами выбирает любую следующую
дорогу (но не возвращается). Найдите
вероятность
того,
что
Иван
Викторович:
а) придёт к храму;
б) придёт к ферме;
в) придёт к пруду.

13.

РАБОТАЕМ В ТЕТРАДИ
1
1
1
А) ∙ =
3
2
6
1
1
1
1
1
1
Б) ∙ + ∙ ∙ =
3
3
3
3
2
6
1
1
1
1
5
В) ∙ + ∙ =
3
2
3
3
18

14.

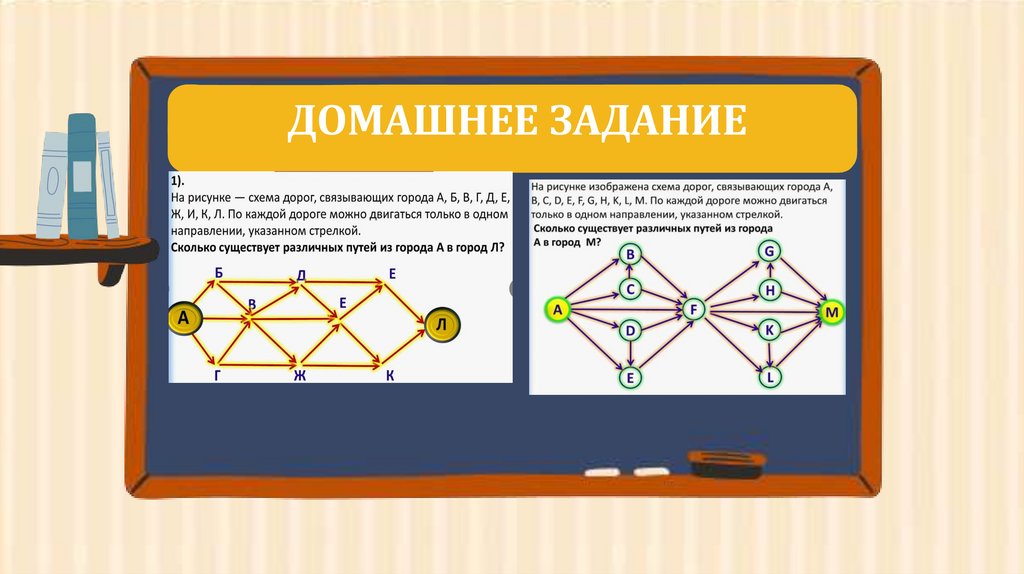
ДОМАШНЕЕ ЗАДАНИЕ

15.

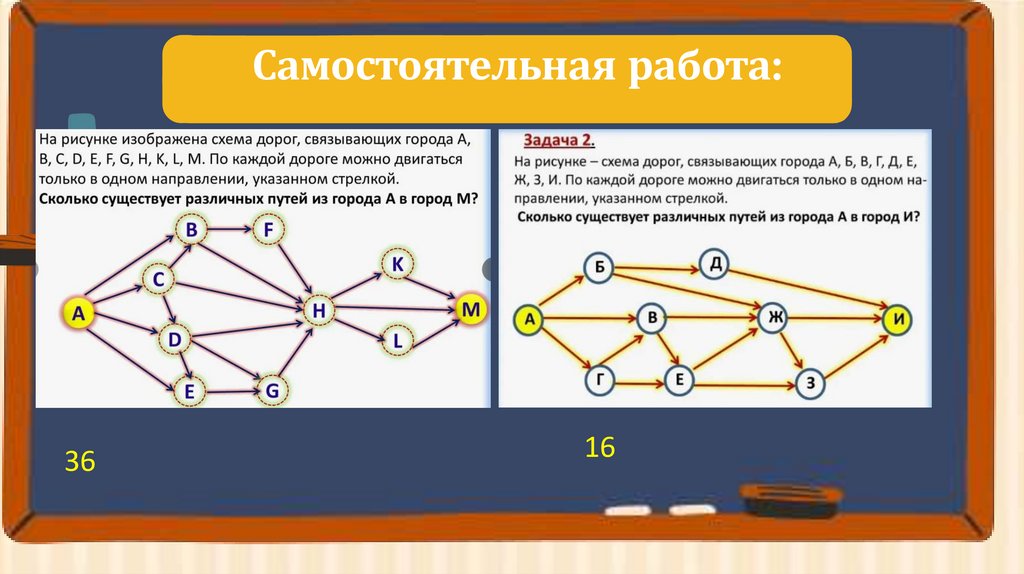
Самостоятельная работа:
36
16