Регрессиялық талдау
1.
РЕГРЕССИЯЛЫҚ ТАЛДАУҚАЗАҚ ҰЛТТЫҚ МЕДИЦИНАЛЫҚ УНИВЕРСИТЕТІНІҢ БИОСТАТИСТИКА
ЖӘНЕ ҒЫЛЫМИ ЗЕРТТЕУ НЕГІЗДЕРІ ҚАЕДРАСЫНЫҢ ДОЦЕНТІ
АХТАЕВА НАЗГУЛ СМАЙЛХАНҚЫЗЫ
2.
РЕГРЕССИЯЛЫҚ ТАЛДАУРЕГРЕССИЯЛЫҚ ТАЛДАУ (REGRESSION ANALYSIS) – БҰЛ БІР ТӘУЕЛДІ АЙНЫМАЛЫ МЕН БІР
НЕМЕСЕ БІРНЕШЕ ТӘУЕЛСІЗ АЙНЫМАЛЫЛАР АРАСЫНДАҒЫ СТАТИСТИКАЛЫҚ ӨЗАРА
БАЙЛАНЫСТЫ ЗЕРТТЕУ ӘДІСІ. РЕГРЕССИЯЛЫҚ ТАЛДАУДА ТӘУЕЛСІЗ АЙНЫМАЛЫНЫ
ПРЕДИКТОР (АҒЫЛ.PREDICTOR - БОЛЖАМШЫ), ТӘУЕЛДІ АЙНЫМАЛЫНЫ «ЖАУАП
АЙНЫМАЛЫ» ДЕП АТАЙДЫ.
«РЕГРЕССИЯ»
ТЕРМИНІН
АЛҒАШ РЕТ БИОМЕТРИЯНЫҢ
НЕГІЗІН САЛУШЫ Ф. ГАЛЬТОН
ЕНГІЗГЕН,
ОНЫҢ
ОЙЫН
ІЗБАСАРЫ
К.
ПИРСОН
ДАМЫТҚАН.
Ф. Гальтон
(1822—1911)
К. Пирсон
(1857—1936)
3.
РЕГРЕССИЯЛЫҚ ТАЛДАУ• РЕГРЕССИЯЛЫҚ ТАЛДАУ – ЖАУАП АЙНЫМАЛЫНЫҢ (ТӘУЕЛДІ) МӘНІН БІР НЕМЕСЕ
БІРНЕШЕ (ТӘУЕЛСІЗ) ПРЕДИКТОРЛЫҚ АЙНЫМАЛЫЛАРДЫҢ БЕЛГІЛІ МӘНДЕРІ БОЙЫНША
АЛДЫН- АЛА АЙТУҒА НЕМЕСЕ БАҒАЛАУҒА МҮМКІНДІК БЕРЕТІН СТАТИСТИКА БӨЛІМІ.
ТӘУЕЛДІ АЙНЫМАЛЫНЫҢ ОРТА МӘНІ МЕН ПРЕДИКТОРЛАРДЫҢ ОРТА МӘНДЕРІ
АРАСЫНДАҒЫ ӨЗАРА БАЙЛАНЫС РЕГРЕССИЯ ТЕҢДЕУІ ТҮРІНДЕ ӨРНЕКТЕЛЕДІ.
• РЕГРЕССИЯ ТЕҢДЕУІ- ТӘУЕЛДІ АЙНЫМАЛЫ МЕН ПРЕДИКТОРЛЫҚ АЙНЫМАЛЫЛАРДЫҢ
БАСТАПҚЫ СТАТИСТИКАЛЫҚ ДЕРЕКТЕРІ НЕГІЗІНДЕ ТАҢДАЛЫНЫП АЛЫНАТЫН
МАТЕМАТИКАЛЫҚ ФУНКЦИЯ. КӨБІНЕСЕ СЫЗЫҚТЫ ФУНКЦИЯ ҚОЛДАНЫЛАДЫ. БҰЛ
ЖАҒДАЙДА РЕГРЕССИЯЛЫҚ ТАЛДАУ СЫЗЫҚТЫ РЕГРЕССИЯЛЫҚ ТАЛДАУ ДЕП АТАЛАДЫ.
4.
РЕГРЕССИЯЛЫҚ ТАЛДАУ• РЕГРЕССИЯЛЫҚ ТАЛДАУ (REGRESSION ANALYSIS) – БҰЛ БІР ТӘУЕЛДІ АЙНЫМАЛЫ МЕН БІР НЕМЕСЕ БІРНЕШЕ
ТӘУЕЛСІЗ АЙНЫМАЛЫЛАР АРАСЫНДАҒЫ СТАТИСТИКАЛЫҚ ӨЗАРА БАЙЛАНЫСТЫ ЗЕРТТЕУ ӘДІСІ. РЕГРЕССИЯЛЫҚ
ТАЛДАУДА ТӘУЕЛСІЗ АЙНЫМАЛЫНЫ ПРЕДИКТОР (АҒЫЛ.PREDICTOR - БОЛЖАМШЫ), ТӘУЕЛДІ АЙНЫМАЛЫНЫ
«ЖАУАП АЙНЫМАЛЫ» ДЕП АТАЙДЫ.
• РЕГРЕССИЯЛЫҚ ТАЛДАУ – ЖАУАП АЙНЫМАЛЫНЫҢ (ТӘУЕЛДІ) МӘНІН БІР НЕМЕСЕ БІРНЕШЕ (ТӘУЕЛСІЗ)
ПРЕДИКТОРЛЫҚ АЙНЫМАЛЫЛАРДЫҢ БЕЛГІЛІ МӘНДЕРІ БОЙЫНША АЛДЫН- АЛА АЙТУҒА НЕМЕСЕ БАҒАЛАУҒА
МҮМКІНДІК БЕРЕТІН СТАТИСТИКА БӨЛІМІ. ТӘУЕЛДІ АЙНЫМАЛЫНЫҢ ОРТА МӘНІ МЕН ПРЕДИКТОРЛАРДЫҢ ОРТА
МӘНДЕРІ АРАСЫНДАҒЫ ӨЗАРА БАЙЛАНЫС РЕГРЕССИЯ ТЕҢДЕУІ ТҮРІНДЕ ӨРНЕКТЕЛЕДІ.
• РЕГРЕССИЯ ТЕҢДЕУІ- ТӘУЕЛДІ АЙНЫМАЛЫ МЕН ПРЕДИКТОРЛЫҚ АЙНЫМАЛЫЛАРДЫҢ БАСТАПҚЫ
СТАТИСТИКАЛЫҚ ДЕРЕКТЕРІ НЕГІЗІНДЕ ТАҢДАЛЫНЫП АЛЫНАТЫН МАТЕМАТИКАЛЫҚ ФУНКЦИЯ. КӨБІНЕСЕ
СЫЗЫҚТЫ ФУНКЦИЯ ҚОЛДАНЫЛАДЫ. БҰЛ ЖАҒДАЙДА РЕГРЕССИЯЛЫҚ ТАЛДАУ СЫЗЫҚТЫ РЕГРЕССИЯЛЫҚ
ТАЛДАУ ДЕП АТАЛАДЫ.
5.
РЕГРЕССИЯЛЫҚ ТАЛДАУДЫҢМАҚСАТЫ МЕН МІНДЕТТЕРІ
РЕГРЕССИЯЛЫҚ ТАЛДАУДЫҢ МАҚСАТЫ- РЕГРЕССИЯ ТЕҢДЕУІ АРҚЫЛЫ ТӘУЕЛДІ АЙНЫМАЛЫНЫҢ КҮТІЛЕТІН
ОРТА МӘНІН АЛДЫН- АЛА БОЛЖАУ.
РЕГРЕССИЯЛЫҚ ТАЛДАУДЫҢ НЕГІЗГІ МІНДЕТТЕРІ ТӨМЕНДЕГІДЕЙ:
• ТӘУЕЛДІЛІКТІҢ ТҮРІ МЕН МОДЕЛІН АНЫҚТАУ;
• РЕГРЕССИЯ ТЕҢДЕУІНІҢ (МОДЕЛЬДІҢ) ПАРАМЕТРЛЕРІН БАҒАЛАУ;
• РЕГРЕССИЯ ТЕҢДЕУІНІҢ МӘНДІЛІГІН ТЕКСЕРУ;
• РЕГРЕССИЯ ТЕҢДЕУІНІҢ КОЭФФИЦИЕНТТЕРІНІҢ МӘНДІЛІГІН ТЕКСЕРУ;
• КОЭФФИЦИЕНТТЕРДІҢ АРАЛЫҚ БАҒАЛАРЫН ТҰРҒЫЗУ;
• МОДЕЛЬДІҢ ПОПУЛЯЦИЯДАҒЫ АҚИҚАТ РЕГРЕССИЯ ТЕҢДЕУІМЕН СӘЙКЕСТІГІН БАҒАЛАУ;
6.
РЕГРЕССИЯЖҰПТАСҚАН
у = f (x)
КӨПТІК
y f x1 , x2 ,..., xn
Регрессиялық талдау келесі кезеңдерден тұрады:
функция түрін анықтаудан;
регрессия коэффициенттерін анықтаудан;
нәтижелі белгінің теориялық мәндерін есептеуден;
регрессия коэффициентінің статистикалық маңыздылығын
тексеруден;
регрессия
теңдеуінің
статистикалық
маңыздылығын
тексеруден.
7.
РЕГРЕССИЯ ТЕҢДЕУІY-тің X –қа регрессиясының теңдеуі деп, X тәуелсіз айнымалысының мәндері мен
Y тәуелді айнымалының шартты орта мәндерінің арасындағы тәуелділікті көрсететін
yx f ( x )
түріндегі теңдеуді айтады. Шартты орта мән деп X-тің нақты бір мәні үшін есептелген
y x арифметикалық орта мәнін айтады.
8.
РЕГРЕССИЯ ТЕҢДЕУЛЕРІБайланысты сипаттау үшін келесі регрессия теңдеулерінің
түрлерін қолданады:
у=a+bx – сызықтық;
y=eax+b – экспоненциалды;
y=a+b/x – гиперболалық;
y=a+b1x+b2x2 – параболалық;
y=abx – көрсеткіштік және т.б.
мұндағы a, b1, b2 - теңдеудің коэффициенттері
(параметрлері); у – нәтижелі белгі; х – факторлық белгі.
9.
Мысалы, салмағы x=60 кг болатын бойларының ұзындықтарыәртүрлі (y1=160, y2=166, y3=164) үш адам кездесуі мүмкін. x=60 үшін
шартты орта мән
160 166 164
y x 60
163,33 болады.
3
Яғни,
кез келген берілген салмақтың мәні үшін әртүрлі бой ұзындықтары кездеседі;
бақыланған бой ұзындықтарының мәні берілген салмақтың мәнінде, салмақ
көрсеткішінің ұлғаюына қарай өседі;
бақыланған салмақтың мәндеріне сәйкес келетін бой ұзындықтарының орта мәндері
нүктелерінің геометриялық орны бойдың (Y) салмақтан (X) регрессиялық тәуелділігі
деп аталады.
10.
СЫЗЫҚТЫ РЕГРЕССИЯ ПАРАМЕТРЛЕРІНЕҢ КІШІ КВАДРАТТАР ӘДІСІ БОЙЫНША
БАҒАЛАУ
РЕГРЕССИЯ ТЕҢДЕУІН ҚҰРУ, ОНЫҢ КОЭФФИЦИЕНТТЕРІН
(ПАРАМЕТРЛЕРІН) БАҒАЛАУҒА АЛЫП КЕЛЕДІ, ОЛ ҮШІН ЕҢ КІШІ
КВАДРАТТАР ӘДІСІ ҚОЛДАНЫЛАДЫ.
2
y y x min БОЛҒАНДА
ЕҢ КІШІ КВАДРАТТАР ӘДІСІ:
ПАРАМЕТРЛЕРДІ БАҒАЛАУҒА МҮМКІНДІК БЕРЕДІ.
ЕҢ КІШІ КВАДРАТТАР ӘДІСІ БОЙЫНША СЫЗЫҚТЫ РЕГРЕССИЯ
У=a+bХ ТЕҢДЕУІНІҢ ПАРАМЕТРЛЕРІН АНЫҚТАУ ФОРМУЛАСЫ:
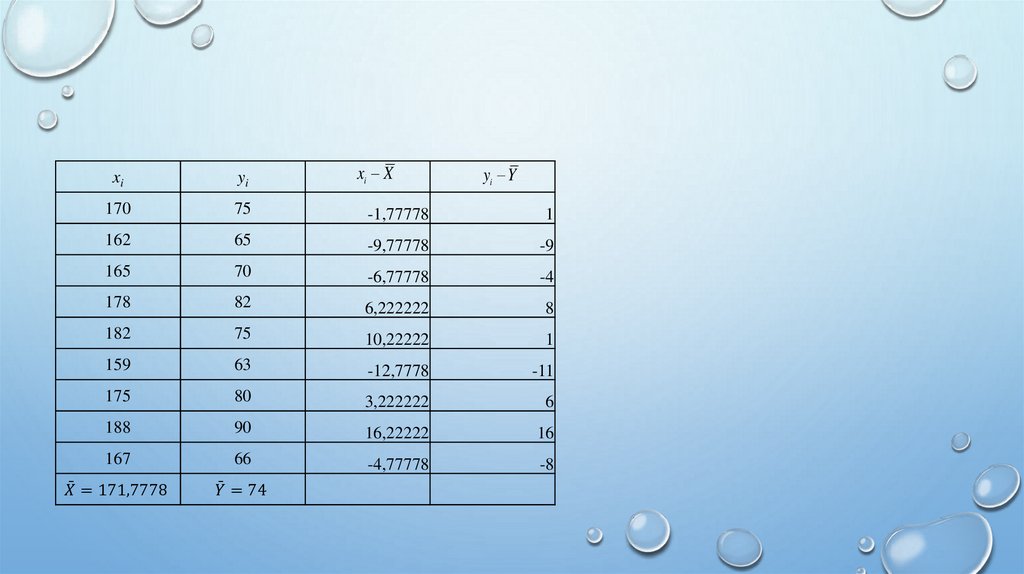
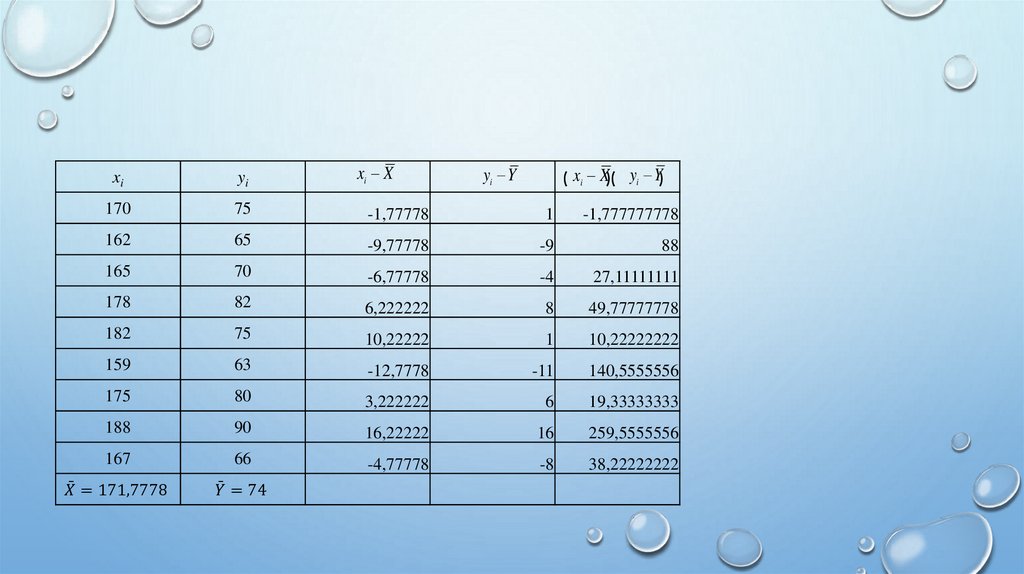
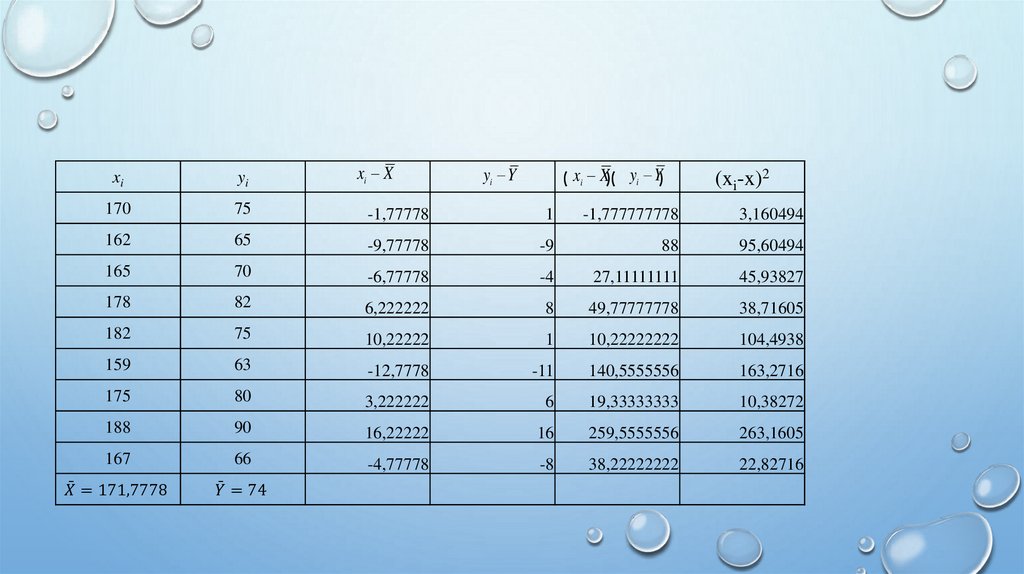
n
x x y y
b i 1 n
i
i
2
x
x
i
i 1
a y bx ,
11.
СЫЗЫҚТЫ РЕГРЕССИЯ ТЕҢДЕУІY=a+bX
МҰНДАҒЫ Y- ТӘУЕЛДІ АЙНЫМАЛЫНЫҢ БОЛЖАНАТЫН МӘНІ, a- БОС МҮШЕ, РЕГРЕССИЯ СЫЗЫҒЫНЫҢ
Y ОСІМЕН ҚИЫЛЫСУ НҮКТЕСІ, b- РЕГРЕССИЯ СЫЗЫҒЫНЫҢ БҰРЫШТЫҚ КОЭФФИЦИЕНТІ, ОНЫ ӘДЕТТЕ
РЕГРЕССИЯ КОЭФФИЦИЕНТІ ДЕП АТАЙДЫ, АЛ X- ПРЕДИКТОРЛЫҚ АЙНЫМАЛЫ, ОНЫҢ КӨМЕГІМЕН Y
МӘНІ БОЛЖАНАДЫ.
12.
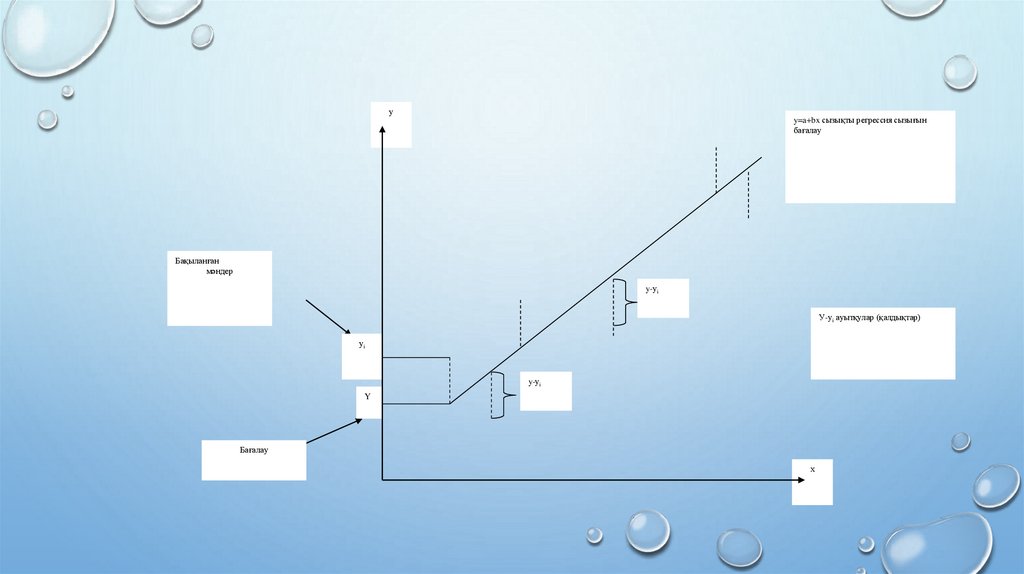
уy=a+bx сызықты регрессия сызығын
бағалау
Бақыланған
мәндер
y-уi
У-уi ауытқулар (қалдықтар)
уi
y-уi
Y
Бағалау
х
13.
РЕГРЕССИЯ ТЕҢДЕУІНІҢ МӘНДІЛІГІН БАҒАЛАУ1) н0: регрессия теңдеуі мәнді емес.
Н1: регрессия теңдеуі мәнді.
2
n
2)














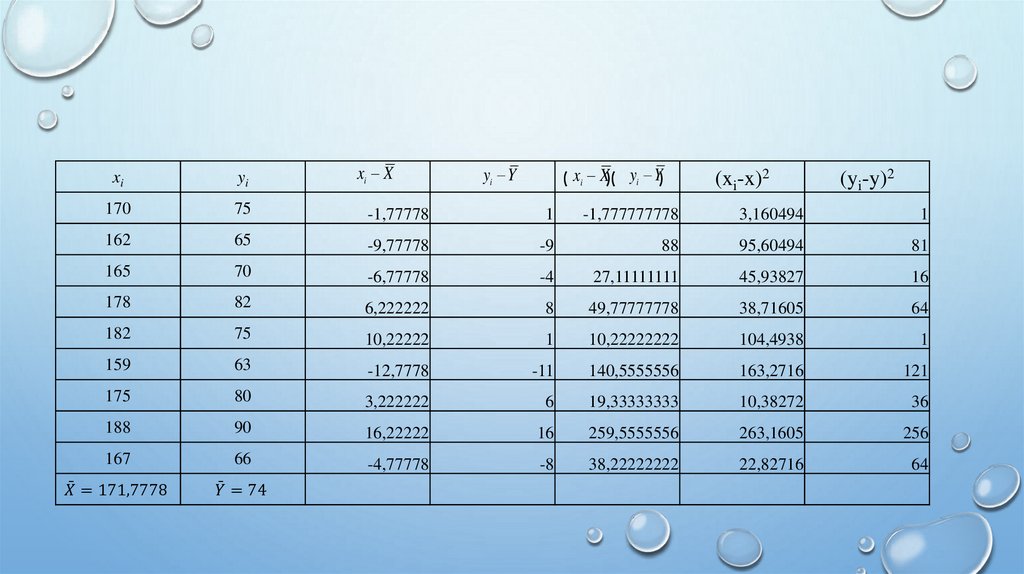
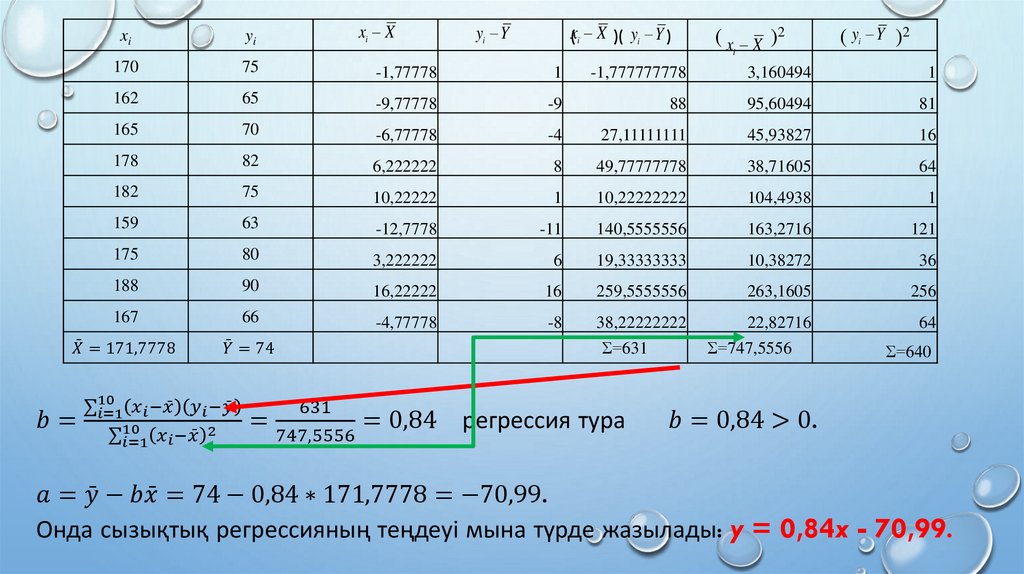

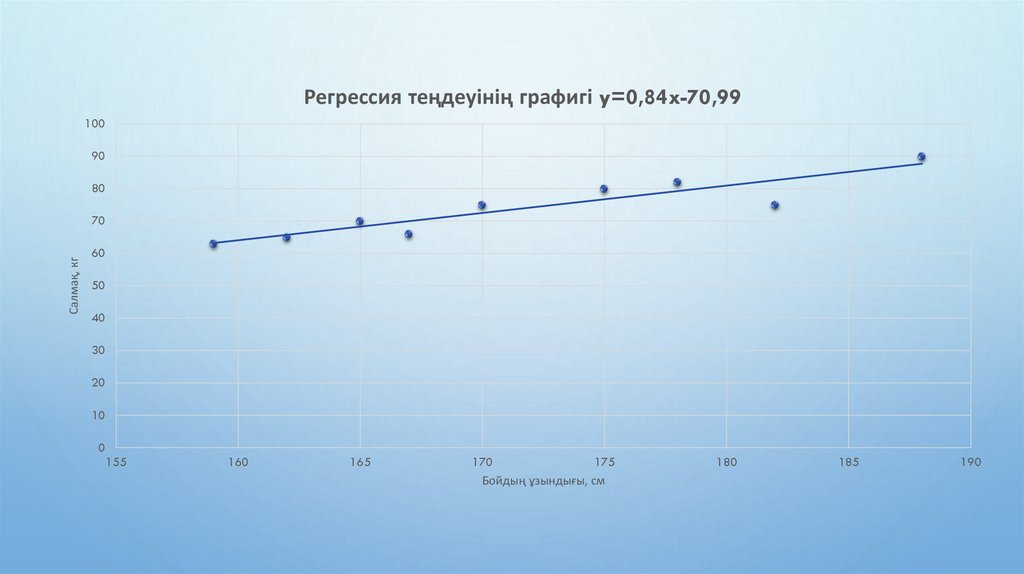
 Образование
Образование