графы 2

1.

Минимальные остовные деревья

2.

Построение минимального
остовного дерева
Generic_MST(G, w){
A=0
while А не является минимальным остовным
деревом
Найти безопасное для А ребро (u, v);
A=AU{(u,v)};
return A ;}

3.

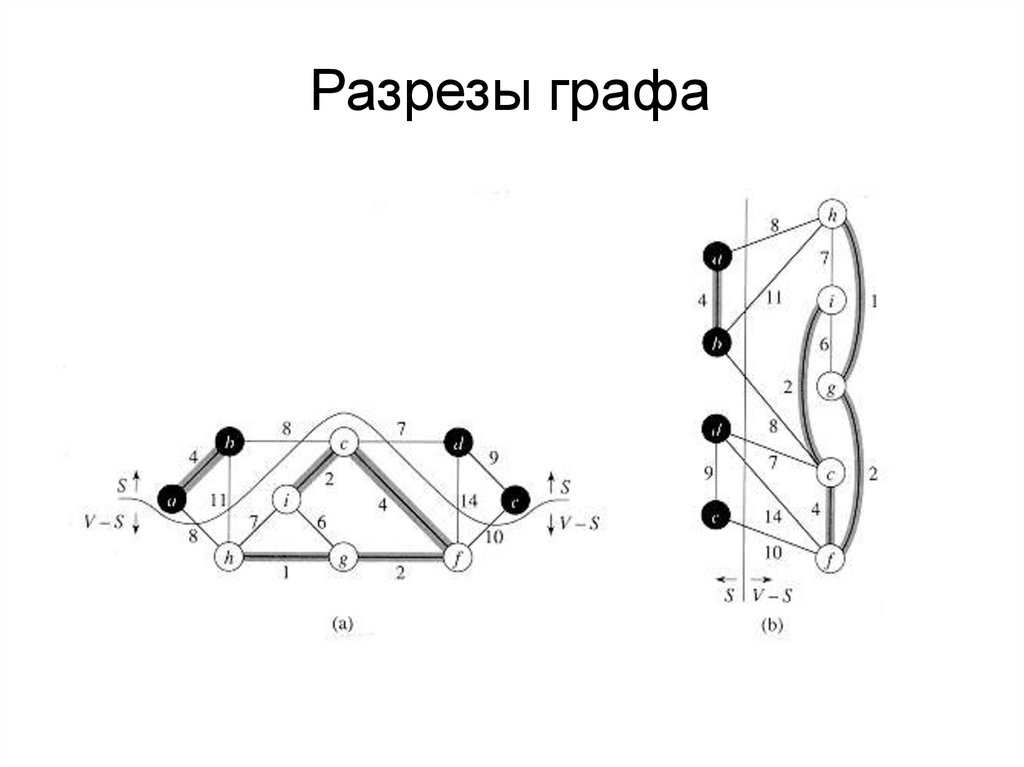
Разрезы графа

4.

Теоремы о легких ребрах
Теорема. Пусть G = (V, Е) — связный неориентированный граф с
действительной весовой функцией w, определенной на Е. Пусть А —
подмножество Е, которое входит в некоторое минимальное остовное
дерево G, (S,V-S) — разрез G, согласованный с А по ребрам, а (u, v) —
легкое ребро, пересекающее разрез (S, V-S). Тогда ребро (u, v) является
безопасным для А.
Следствие. Пусть G = (V, Е) — связный неориентированный граф с
действительной весовой функцией w, определенной на Е. Пусть А —
подмножество Е, которое входит в некоторое минимальное остовное
дерево G, и пусть С ={Vc.Ec) — связный компонент (дерево) в лесу Ga =
(V,А). Если (u, v) — легкое ребро, соединяющее С с некоторым другим
компонентом в Ga, тo ребро (u, v) безопасно для А.

5.

Упражнения(д/з)
1) Покажите, что если ребро (u, v) содержится в
некотором минимальном остовном дереве, то оно
является легким ребром, пересекающим
некоторый разрез графа.
2) Покажите, что если вес любого из ребер графа
положителен, то любое подмножество ребер,
объединяющее все вершины и имеющее
минимальный общий вес, должно быть деревом.
Приведите пример, показывающий, что это не так,
если ребра могут иметь отрицательный вес.

6.

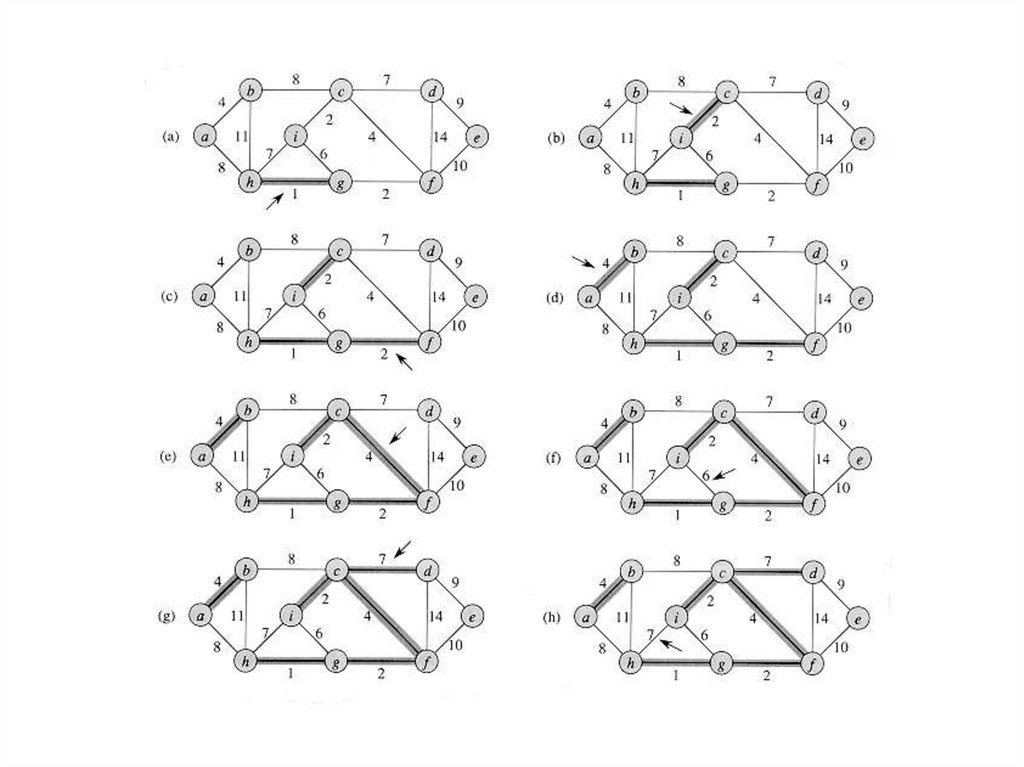
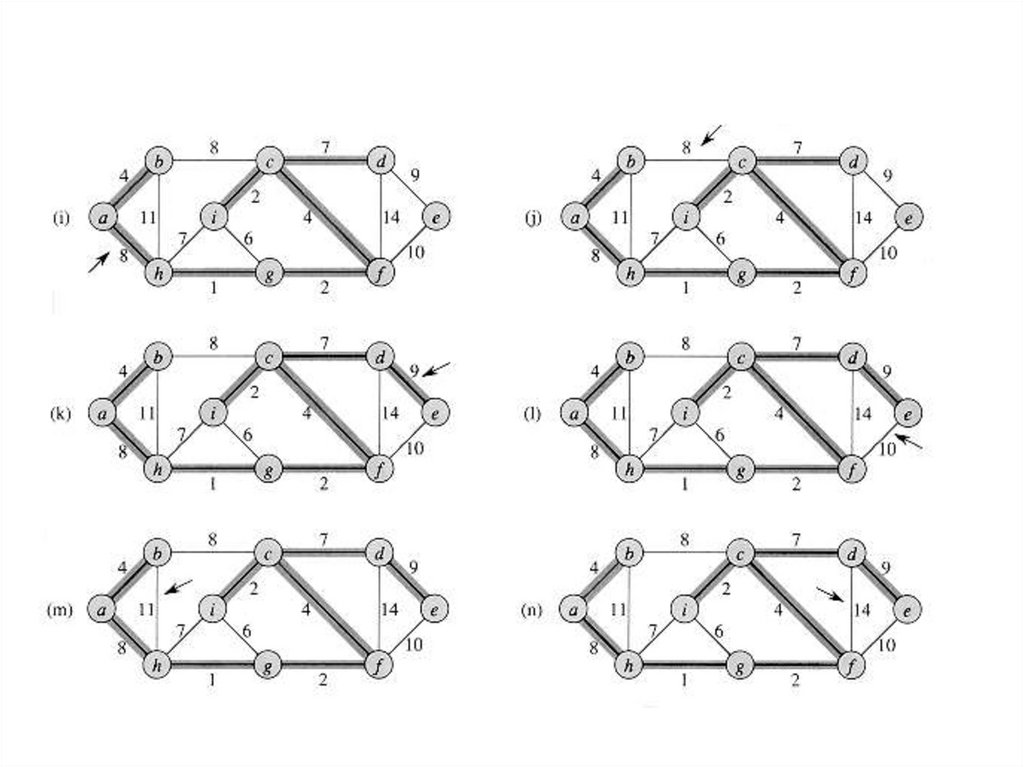
Алгоритм Крускала
MST_Kruskal(G, w){
А=0;
for (каждой вершины v из V[G])
Make_Set(v);
Сортируем ребра из Е в неубывающем порядке их весов w
for ( каждого (u, v) из Е (в порядке возрастания веса)){
if (Find_Set(u) != Find_Set(z))
A = AU{(u,v)}
UNlON(u, v)}
return A ;

7.

8.

9.

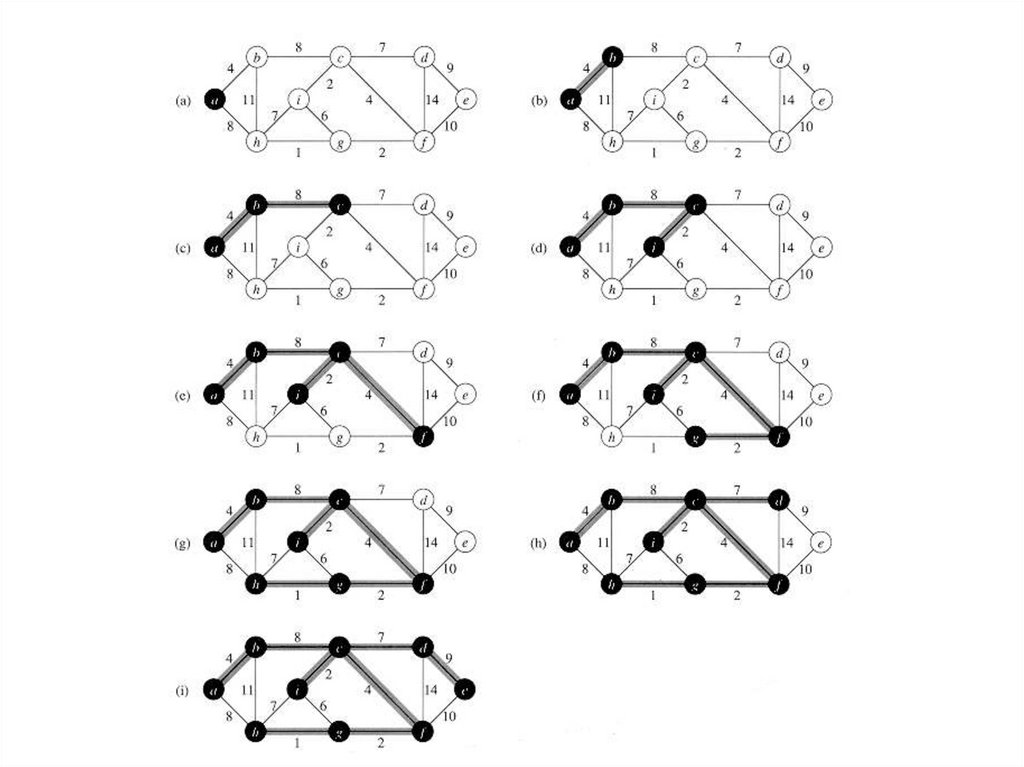
Алгоритм Прима
MST_PRiM(G,w,r){
for( каждой вершины u из V[G]) {
u.key=maxint;
u.p = NIL}
r.key =0;
Q=V[G];
while (not_empty(Q)){
u=Extract_Min(Q);
for (каждой вершины v из Adj[u])
if ((v в Q) и(w(u, v) < v.key)){
v.p=u;
v.key=w(u,v);}}

10.

11.

Упражнения
Предположим, что граф G = (V,E) представлен
при помощи матрицы смежности. Разработайте простую
реализацию алгоритма Прима для
этого случая, время работы которой равно О
(V2).

12.

Варианты
1) Путь в заданный пункт назначения
2) Путь между заданной парой вершин
3) Пути между всеми парами вершин

13.

Оптимальная структра задачи о
кратчайшем пути
Лемма 24.1 (Частичные пути кратчайшего пути
являются кратчайшими путями.)

14.

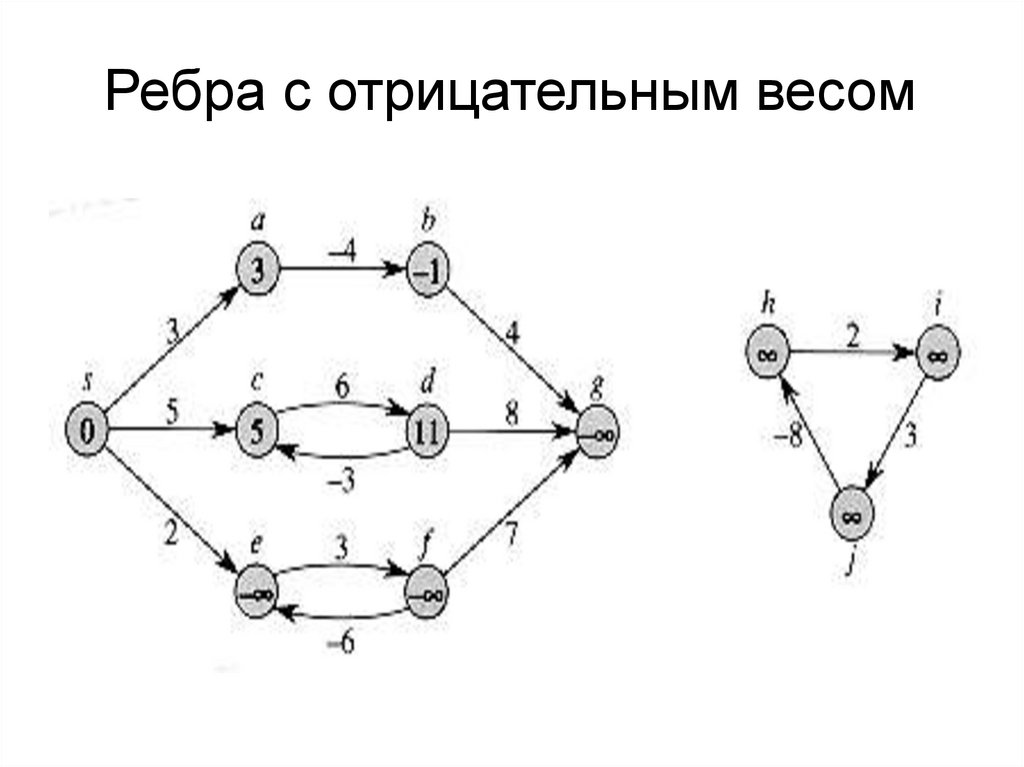
Ребра с отрицательным весом

15.

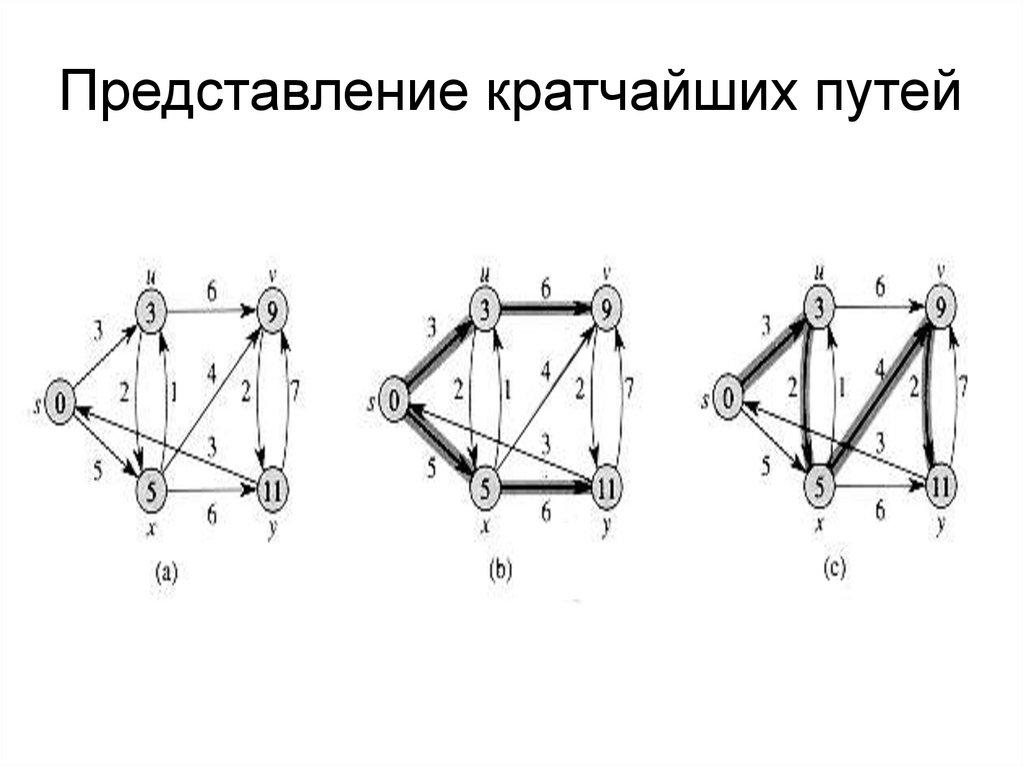
Представление кратчайших путей

16.

Инициализация оценок
кратчайших путей
Initialize_Single_Source(G, s){
for ( каждой вершины v в G.V){
v.d=maxint;
v.p = NULL; }
s.d = 0;}

17.

Инициализация оценок
кратчайших путей
Initialize_Single_Source(G, s){
for ( каждой вершины v в G.V){
v.d=maxint;
v.n = NULL; }
s.d = 0;}

18.

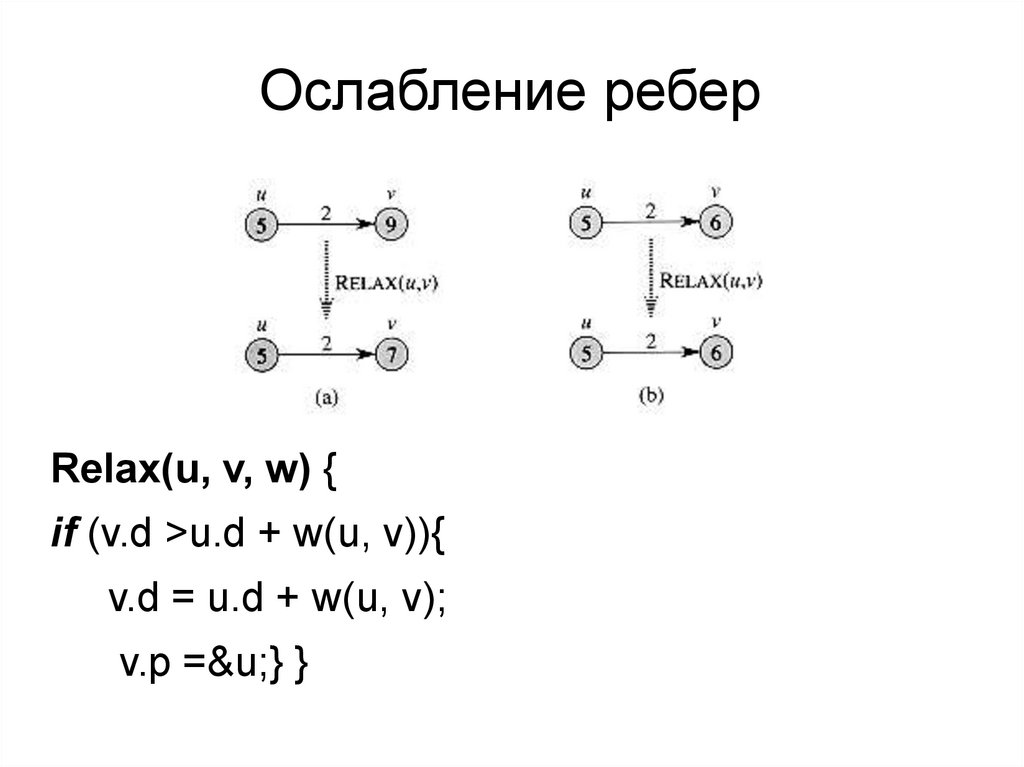
Ослабление ребер
Relax(u, v, w) {
if (v.d >u.d + w(u, v)){
v.d = u.d + w(u, v);
v.p =&u;} }

19.

Свойства кратчайших путей и
ослабления
1)Неравенство треугольника
2)Свойство верхней границы.
3)Свойство отсутствия пути.
4)Свойство сходимости
5)Свойство ослабления пути
6)Свойство подграфа предшествования

20.

Алгоритм Беллмана-Форда
Bellman_Ford(G, w, s){
Initialize_Single_Source(G, 5)
For(i=1;i<n;i++){
for (каждое ребро (u, v) из G.E)
Relax(u, v, w); }
for (каждое ребро (u, v) из G.E)
if (v.d > u.d + w(u, v))
then return false;
return true ;}

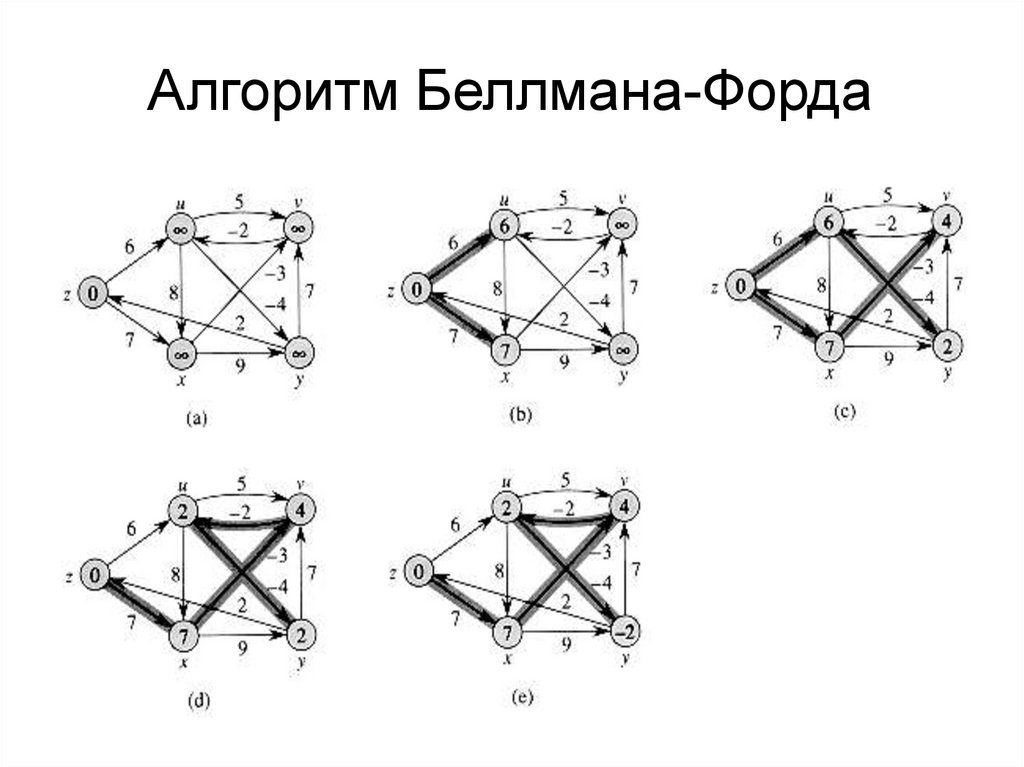
21.

Алгоритм Беллмана-Форда

22.

Корректность алгоритма
Лемма 24.2.
Пусть G = (V, Е) — взвешенный
ориентированный граф с истоком s и весовой
функцией w : Е -> R, который не содержит
циклов с отрицательным весом, достижимых
из вершины s. Тогда по завершении |V|-1
итераций цикла for в строках 2-4 алгоритма
Bellman_Ford, для всех вершин v,
достижимых из вершины s, выполняется
равенство v.d= δ(s, v).

23.

Корректность алгоритма
Следствие 24.3.
Пусть G = (V, E) — взвешенный
ориентированный граф с истоком s и весовой
функцией w : Е -> R. Тогда для каждой
вершины v из V путь из вершины s в вершину
v существует тогда и только тогда, когда после
обработки графа G процедурой Bellman_Ford
выполняется неравенство v.d < maxint.

24.

Теорема 24.4 (Корректность алгоритма БеллманаФорда).
Пусть алгоритм Bellman_Ford обрабатывает
взвешенный ориентированный граф G = (V, E) с
истоком s и весовой функцией w : Е -> R. Если граф
G не содержит циклов с отрицательным весом,
достижимых из вершины s, то этот алгоритм
возвращает значение TRUE, для всех вершин v из
V выполняется равенство v.d= δ(s, v) и подграф
предшествования Gp является деревом
кратчайших путей с корнем в вершине s. Если же
граф G содержит цикл с отрицательным весом,
достижимый из вершины s, то алгоритм возвращает
значение FALSE.

25.

Упражнения
Опишите работу алгоритма BellmanJFord с
ориентированным графом, показанным на
рис., в котором в качестве истока
используется вершина y. В процессе каждого
прохода ослабление ребер должно
выполняться в том же порядке, что и на
рисунке. Составьте список значений, которые
принимают атрибуты d и p после каждого
прохода.

26.

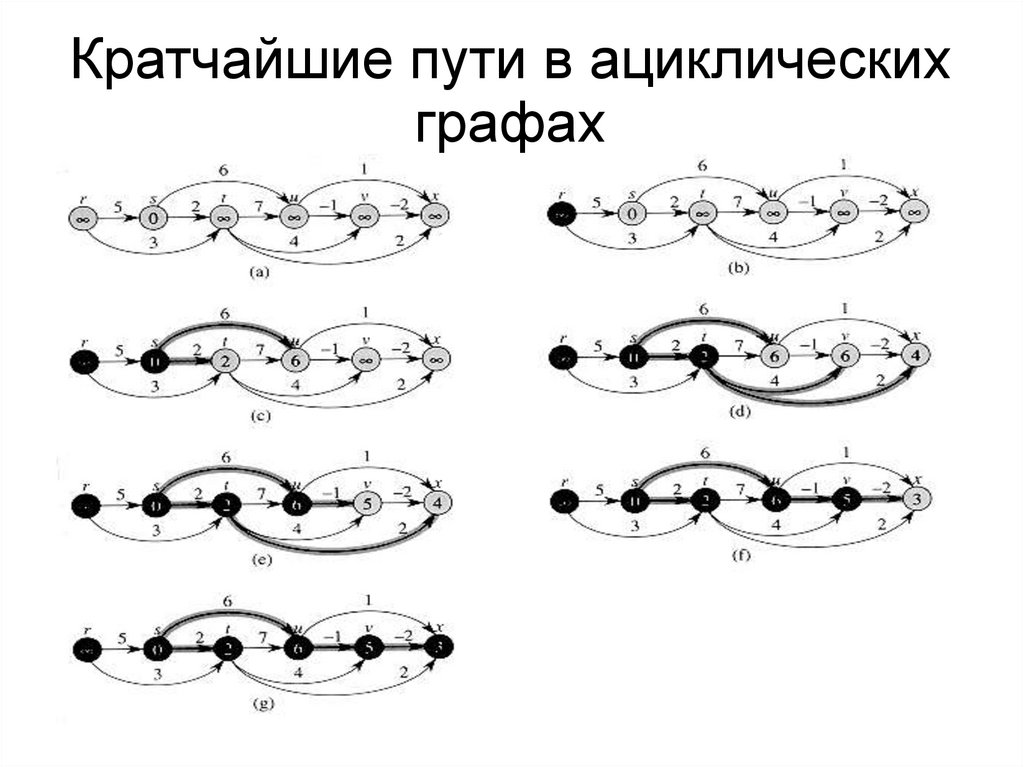
Кратчайшие пути в ациклических
графах
Dag_Shortest_Paths(G, w, s) {
Топологическая сортировка вершин графа G
Initialize_SingleJSource(G, s);
for (для) каждой вершины u в порядке
топологической сортировки {
for каждой вершины v в u.Adj
Relax(u, v, w) ;}}

27.

Кратчайшие пути в ациклических
графах

28.

Корректность алгоритма
Теорема 24.5. Если взвешенный
ориентированный граф G = (V,E) содержит
исток s и не содержит циклов, то по
завершении процедуры Dag_Shortest_Paths
для всех вершин v G V выполняется
равенство d [v] = 6 E, v) и подграф
предшествования Gn представляет собой
дерево кратчайших путей.

29.

Упражнение
Разработайте эффективный алгоритм,
позволяющий определить общее
количество путей, содержащихся в
ориентированном ациклическом графе.
Проанализируйте время работы этого
алгоритма.

30.

Алгоритм Дейкстры
Dijkstra(G, w ){
Initialize Single Source(G,s)
S=0;
Q = G.V;
while Not_Empty(Q) {
u =Extract_Min(Q);
S=S U {u};
for(каждая вершина v из G)
Relax(u, v, w);}
}

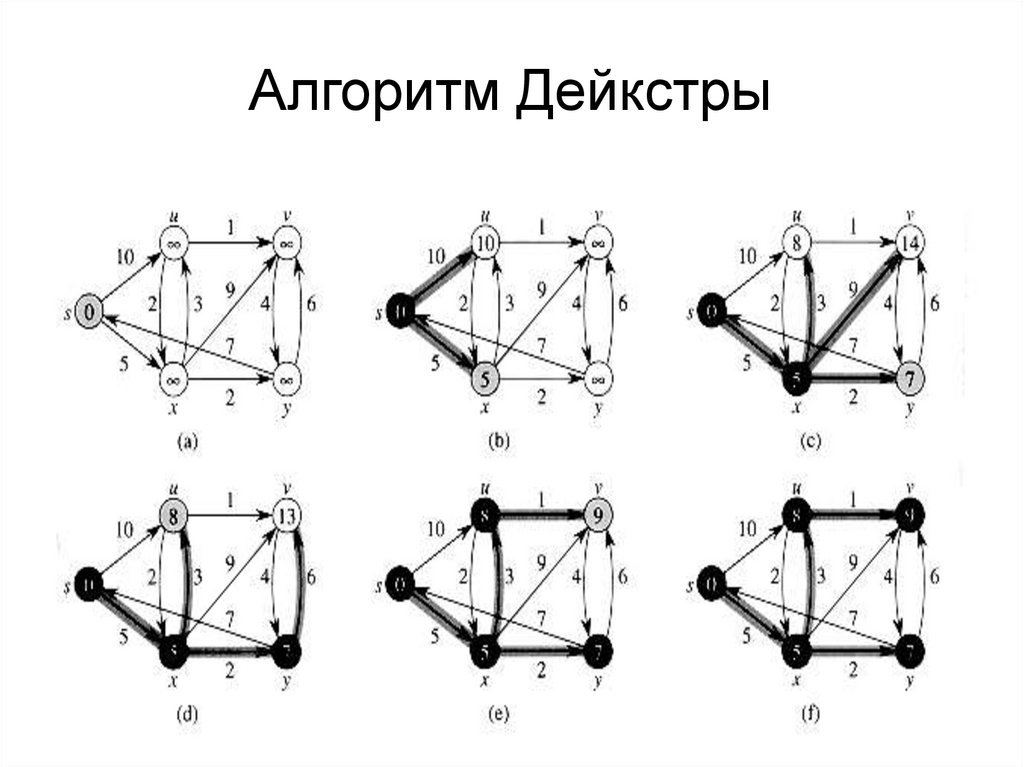
31.

Алгоритм Дейкстры

32.

Корректность алгоритма
Дейкстры
Теорема 24.6 (Корректность алгоритма Дейкстры).
По завершении обработки алгоритмом Дейкстры
взвешенного ориентированного графа G = (V, Е) с
неотрицательной весовой функцией w и истоком s для
всех вершин ие V выполняется равенство u.d=δ(s, u).
В начале каждой итерации цикла while в строках 4-8
для каждой вершины v из S выполняется равенство
v.d= δ(s, v).
Следствие 24.7. Если выполнить алгоритм Дейкстры для
взвешенного ориентированного графа G = (V, Е) с
неотрицательной весовой функцией w и истоком s, то
по завершении работы алгоритма подграф
предшествования Gp является деревом кратчайших
путей с корнем в вершине 5.

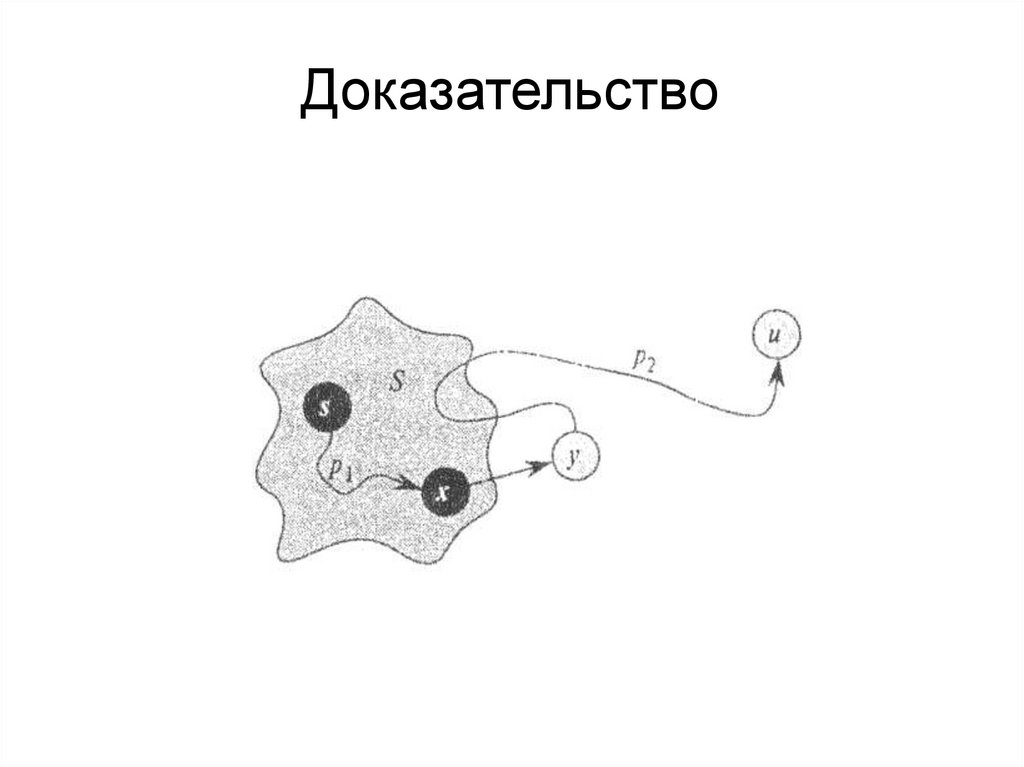
33.

Доказательство

34.

Корректность графа ограничений
Теорема 24.9. Пусть G = (V, Е) — граф
ограничений, соответствующий заданной
системе разностных ограничений Ах ≤B.
Если граф G не содержит циклов с
отрицательным весом, то вектор
х = (δ (vo, v1), δ (vo, v2),..., δ(v0, vn)) является
допустимым решением системы. Если граф
G содержит циклы с отрицательным весом,
то допустимых решений не существует.