metod_grafov

1.

Решение задач ЕГЭ с
помощью графов.
Презентацию подготовили ученицы 7 класса
средней школы № 8 г Аткарска Саратовской
области.
Савинова Дарья и Курапова Анастасия.
Учитель: Юшкова Е.А

2.

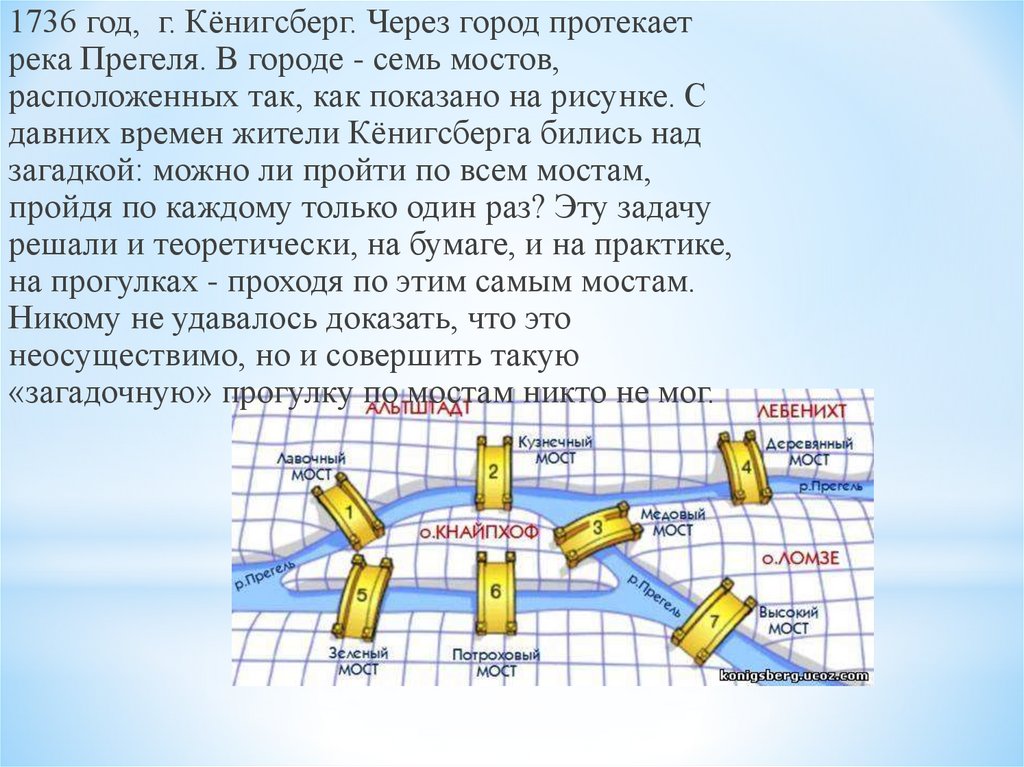
1736 год, г. Кёнигсберг. Через город протекает
река Прегеля. В городе - семь мостов,
расположенных так, как показано на рисунке. С
давних времен жители Кёнигсберга бились над
загадкой: можно ли пройти по всем мостам,
пройдя по каждому только один раз? Эту задачу
решали и теоретически, на бумаге, и на практике,
на прогулках - проходя по этим самым мостам.
Никому не удавалось доказать, что это
неосуществимо, но и совершить такую
«загадочную» прогулку по мостам никто не мог.

3.

Разрешить проблему удалось знаменитому математику
Леонарду Эйлеру. Причем, он решил не только эту
конкретную задачу, но придумал общий метод решения
подобных задач. При решении задачи о Кёнигсбергских
мостах Эйлер поступил следующим образом: он "сжал" сушу
в точки, а мосты "вытянул" в линии. Такую фигуру,
состоящую из точек и линий, связывающих эти точки,
называют ГРАФОМ.

4.

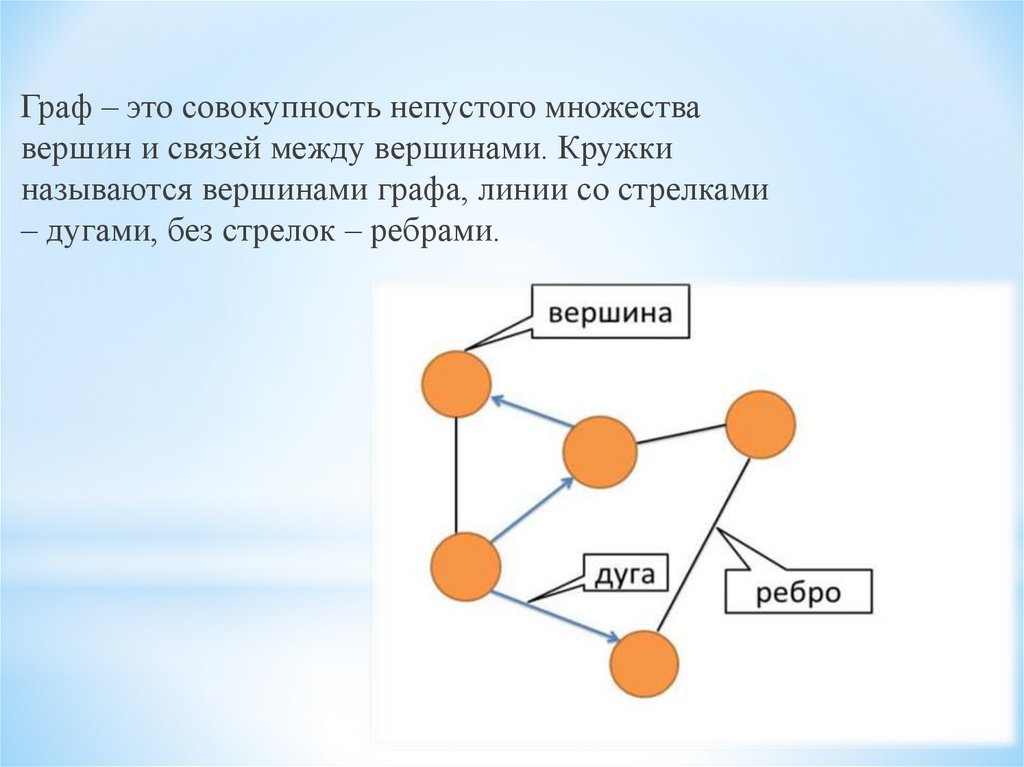
Граф – это совокупность непустого множества
вершин и связей между вершинами. Кружки
называются вершинами графа, линии со стрелками
– дугами, без стрелок – ребрами.

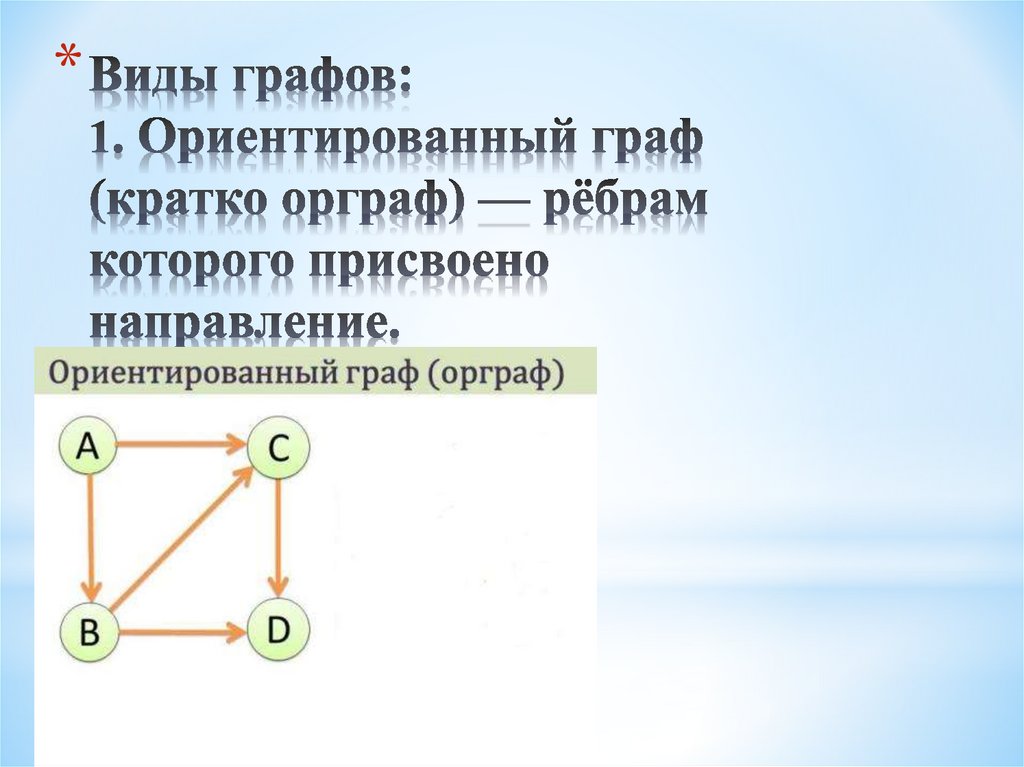
5. Виды графов: 1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.

*

6.

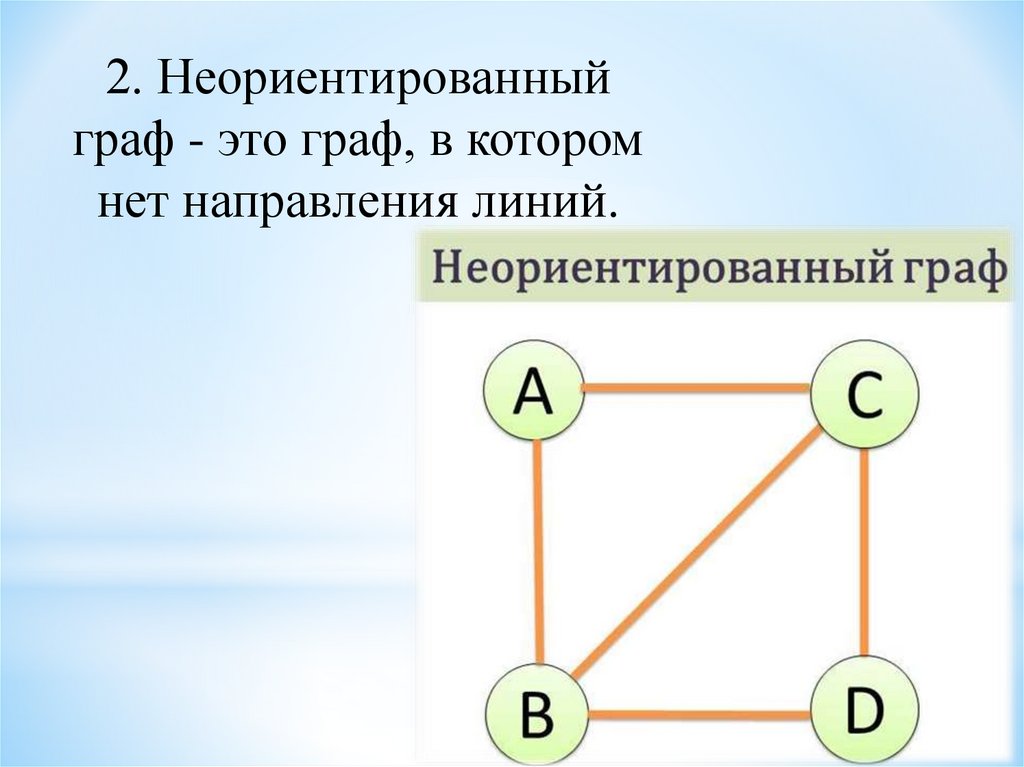
2. Неориентированный
граф - это граф, в котором
нет направления линий.

7.

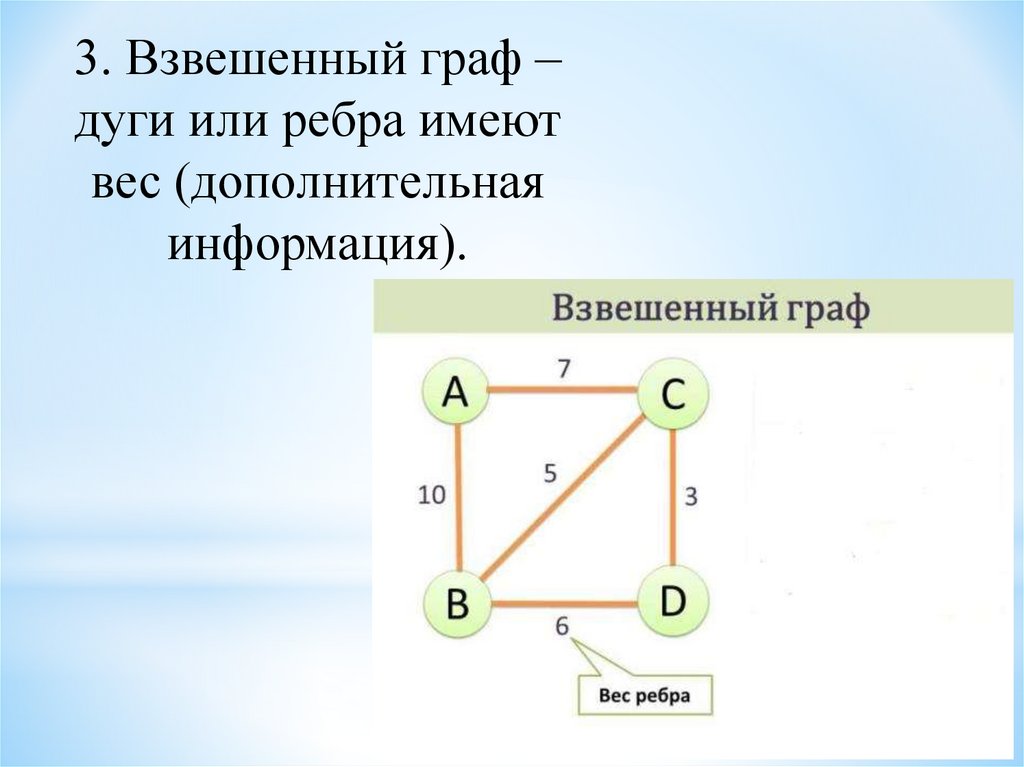
3. Взвешенный граф –
дуги или ребра имеют
вес (дополнительная
информация).

8.

Решение задач с помощью
графов:
Задача 1.
Пятеро ученных, участвовавших в
научной конференции, обменялись
рукопожатиями. Сколько всего было
сделано рукопожатий?
1
5
2
Ответ: 10.
3
4

9. Ответ: 45

Задача 2 (для самостоятельного решения):
В шахматном турнире участвуют 10 шахматистов.
Сколько будут сыграно партий, если каждый
участник турнира сыграл с каждым по одной партии?
Решение:
10 9:2=45
*

10. Ответ: 200

Задача 3 (для самостоятельного решения):
В государстве 100 городов, и из каждого из них
выходит 4 дороги. Сколько всего дорог в государстве?
Решение:
100 4:2=200
*

11.

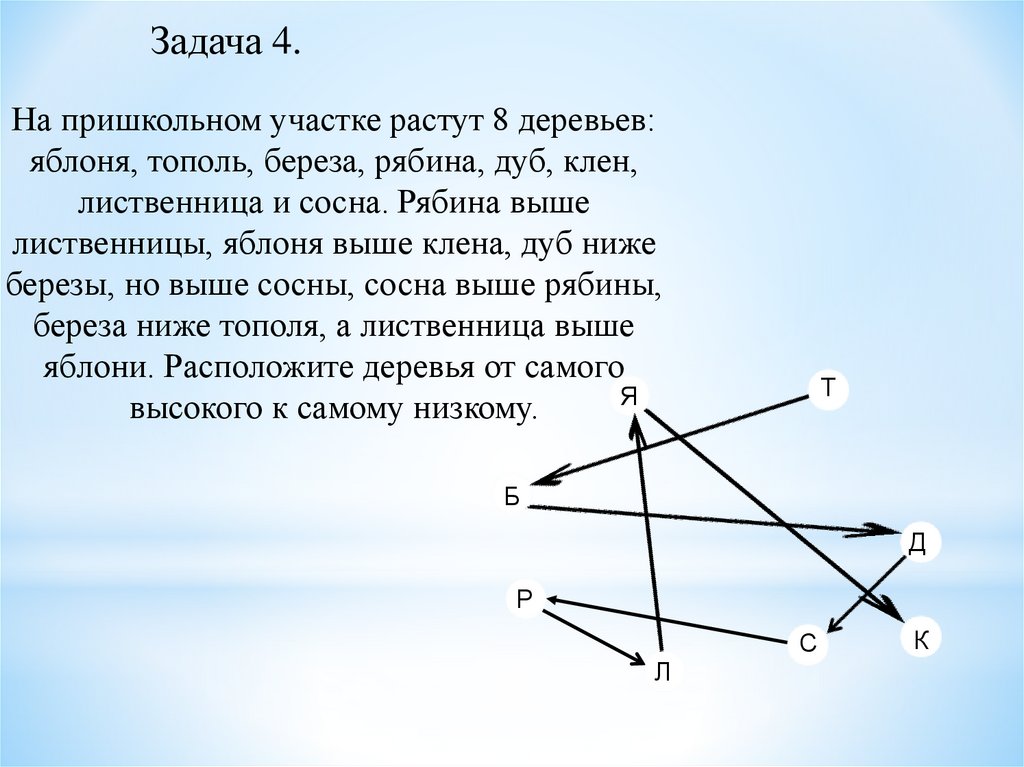
Задача 4.
На пришкольном участке растут 8 деревьев:
яблоня, тополь, береза, рябина, дуб, клен,
лиственница и сосна. Рябина выше
лиственницы, яблоня выше клена, дуб ниже
березы, но выше сосны, сосна выше рябины,
береза ниже тополя, а лиственница выше
яблони. Расположите деревья от самого
Я
высокого к самому низкому.
Т
Б
Д
Р
Л
С
К

12.

Задача 5 (для самостоятельного решения):
Пять наиболее длинных рек России (учитывается
наибольшая длина с притоками) — это Амур, Енисей,
Иртыш, Лена и Обь. При этом Лена длиннее Енисея,
но короче Оби, Амур длиннее и Лены и Иртыша. Выберите утверждения, которые следуют из приведённых данных.
1) Амур — первая или вторая по длине река
2) Енисей — вторая или третья река по длине
3) Лена длиннее Иртыша
4) Амур длиннее Оби
(Образовательный портал по подготовке к экзаменам «Решу ЕГЭ»)
Ответ: 1 утверждение

13.

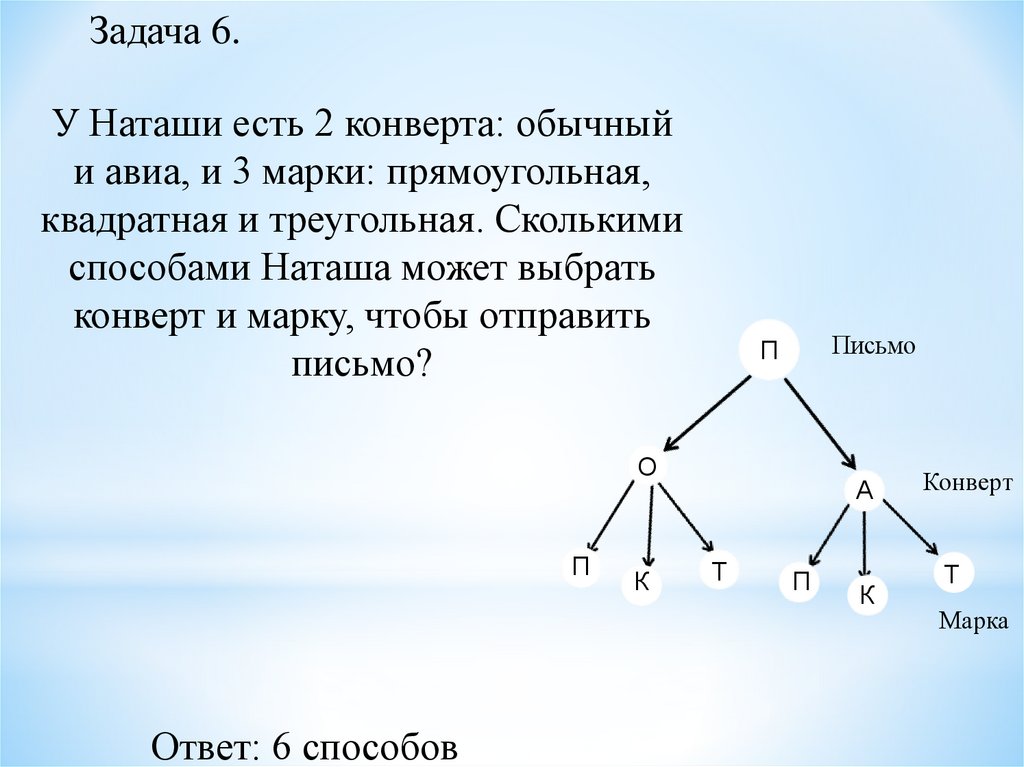
Задача 6.
У Наташи есть 2 конверта: обычный
и авиа, и 3 марки: прямоугольная,
квадратная и треугольная. Сколькими
способами Наташа может выбрать
конверт и марку, чтобы отправить
письмо?
Письмо
П
О
П
Ответ: 6 способов
К
А
Т
П
К
Конверт
Т
Марка

14. Ответ: 60

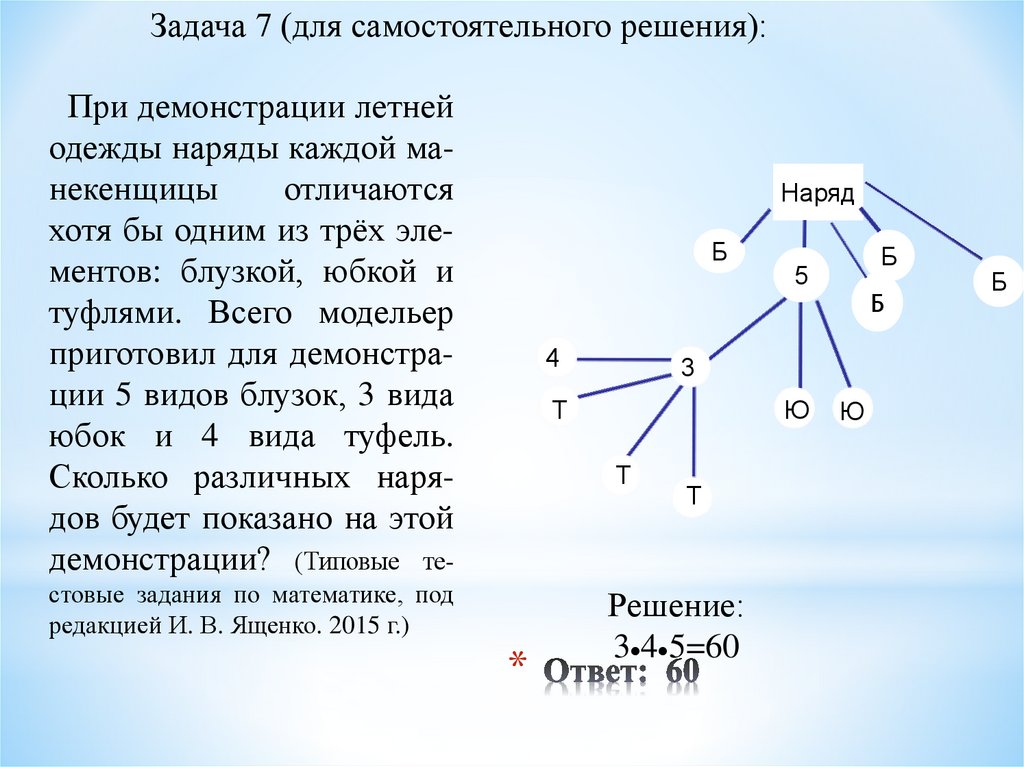
Задача 7 (для самостоятельного решения):
При демонстрации летней
одежды наряды каждой манекенщицы
отличаются
хотя бы одним из трёх элементов: блузкой, юбкой и
туфлями. Всего модельер
приготовил для демонстрации 5 видов блузок, 3 вида
юбок и 4 вида туфель.
Сколько различных нарядов будет показано на этой
демонстрации? (Типовые те-
Наряд
Б
Б
5
4
3
Т
Ю
Т
стовые задания по математике, под
редакцией И. В. Ященко. 2015 г.)
*
Б
Т
Решение:
3 4 5=60
Ю
Б

15. Ответ: 360

Задача 8 (для самостоятельного решения):
В меню ресторана имеется 6 видов салатов, 3 вида
первых блюд, 5 видов вторых блюд и 4 вида десерта.
Сколько вариантов обеда из салата,
первого, второго и десерта могут выбрать посетители
этого ресторана? (Образовательный портал по подготовке к экзаменам
«Решу ЕГЭ»)
Решение:
6 3 5 4=360
*

16.

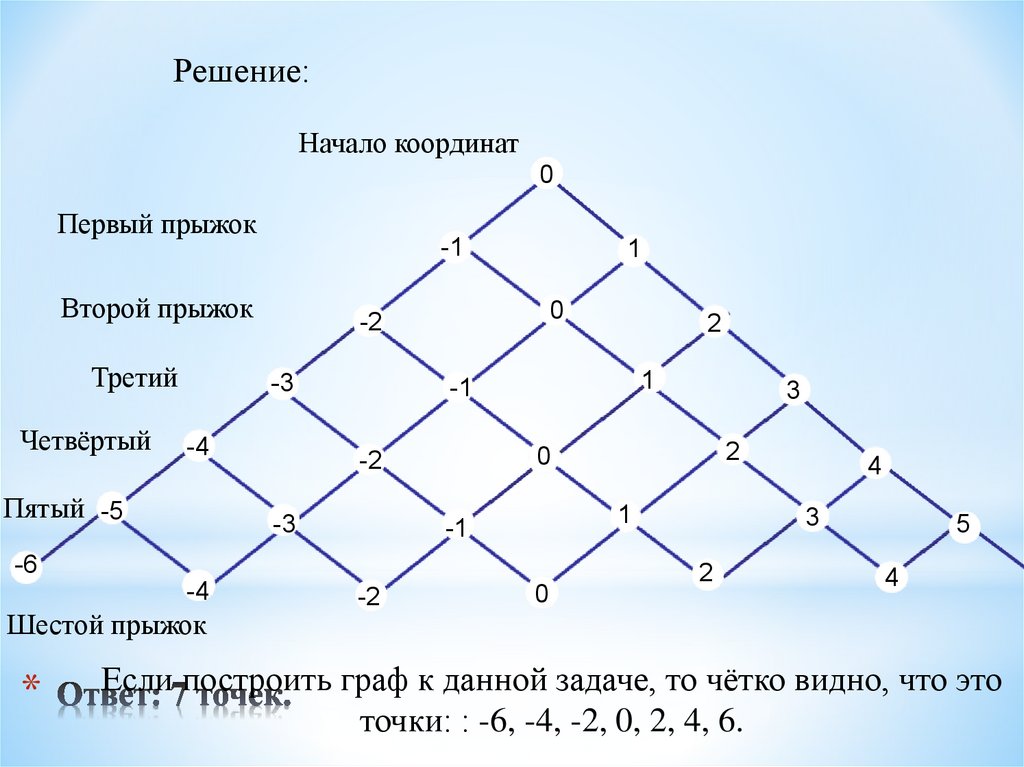
Задача 9 (для самостоятельного решения):
Кузнечик прыгает вдоль координатной прямой в
любом направлении на единичный отрезок за
прыжок. Сколько существует различных точек на
координатной прямой, в которых кузнечик может
оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат? (Образовательный портал по
подготовке к экзаменам «Решу ЕГЭ»)

17. Ответ: 7 точек.

Решение:
Начало координат
0
Первый прыжок
-1
Второй прыжок
Третий
Четвёртый
0
-2
-3
-4
Пятый -5
1
1
-1
-6
Шестой прыжок
*
2
1
-1
-2
3
0
-2
-3
-4
2
0
4
3
2
5
4
Если построить граф к данной задаче, то чётко видно, что это
точки: : -6, -4, -2, 0, 2, 4, 6.

18.

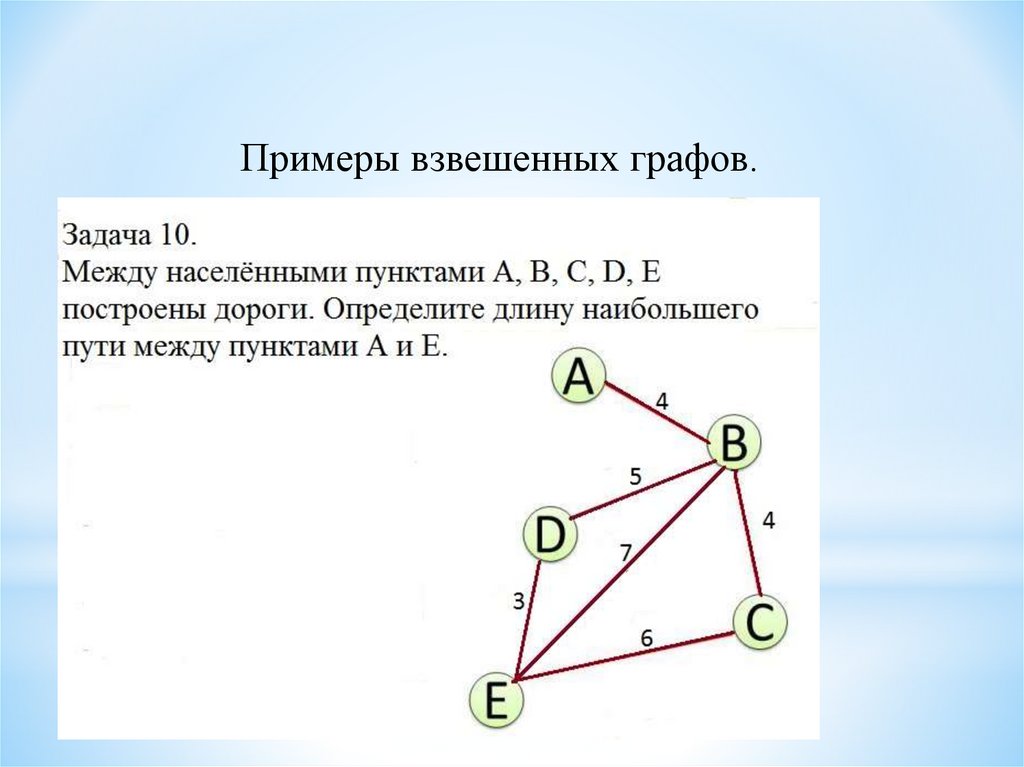
Примеры взвешенных графов.

19.

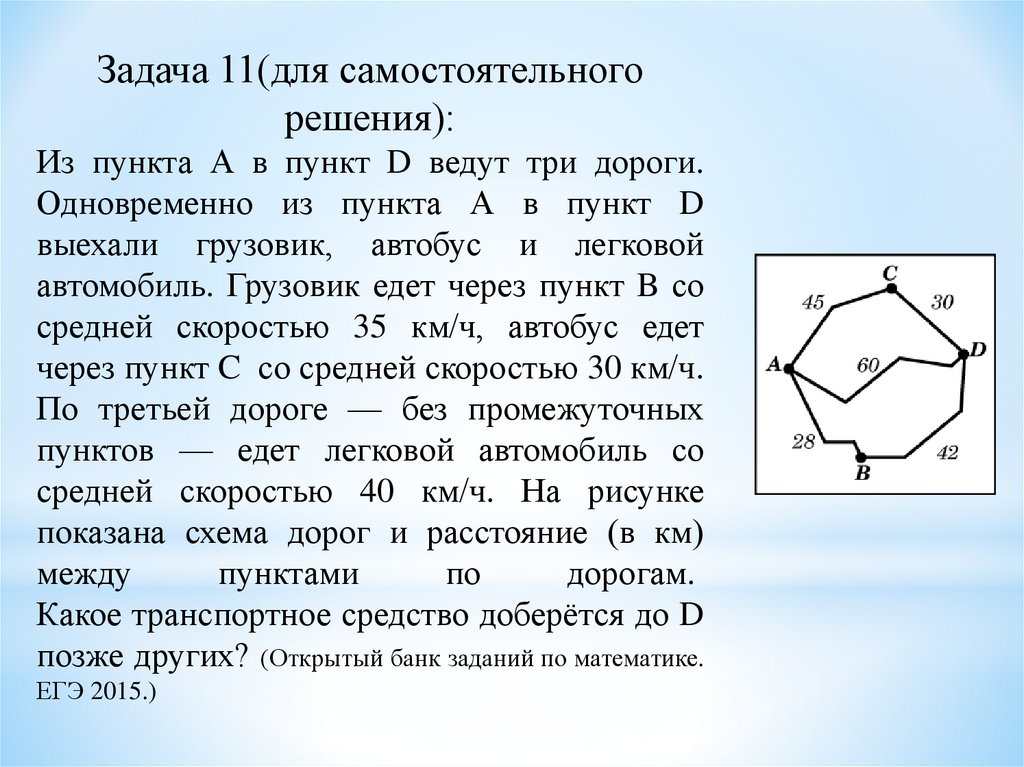
Задача 11(для самостоятельного
решения):
Из пункта А в пункт D ведут три дороги.
Одновременно из пункта А в пункт D
выехали грузовик, автобус и легковой
автомобиль. Грузовик едет через пункт B со
средней скоростью 35 км/ч, автобус едет
через пункт C со средней скоростью 30 км/ч.
По третьей дороге — без промежуточных
пунктов — едет легковой автомобиль со
средней скоростью 40 км/ч. На рисунке
показана схема дорог и расстояние (в км)
между
пунктами
по
дорогам.
Какое транспортное средство доберётся до D
позже других? (Открытый банк заданий по математике.
ЕГЭ 2015.)

20.

Литература:
Березина Л.Ю. Графы и их применение. Пособие для учителей. М.:
Наука, 1980 г.
Мельников О.И. Теория графов в занимательных задачах. М.:
Либроком, 2008 г.
Интернет ресурсы:
Википедия – https://ru.wikipedia.org
Открытый банк заданий по математике – http://mathege.ru
Образовательный портал по подготовке к экзаменам «Решу ЕГЭ» http://math.reshuege.ru
Глобальная школьная лаборатория - https://globallab.org
Учимся решать логические задачи - http://logika.vobrazovanie.ru