лекция Аксонометрические проекции (1)

1.

Аксонометрические проекции

2.

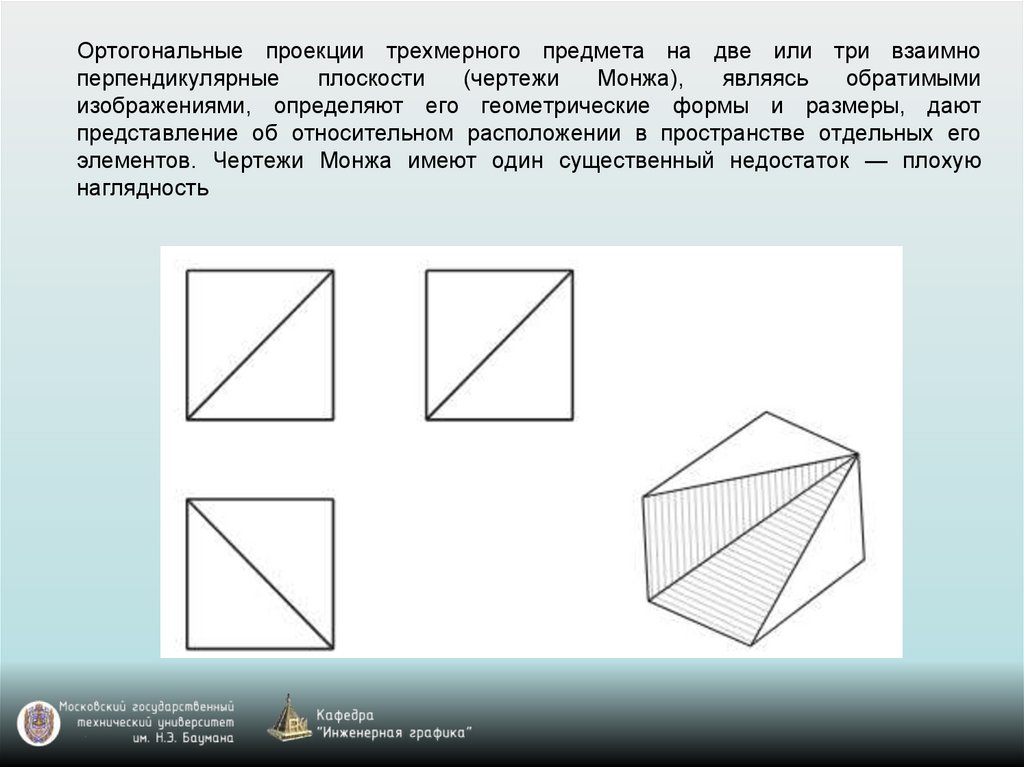
Ортогональные проекции трехмерного предмета на две или три взаимно
перпендикулярные
плоскости
(чертежи
Монжа),
являясь
обратимыми
изображениями, определяют его геометрические формы и размеры, дают
представление об относительном расположении в пространстве отдельных его
элементов. Чертежи Монжа имеют один существенный недостаток — плохую
наглядность

3.

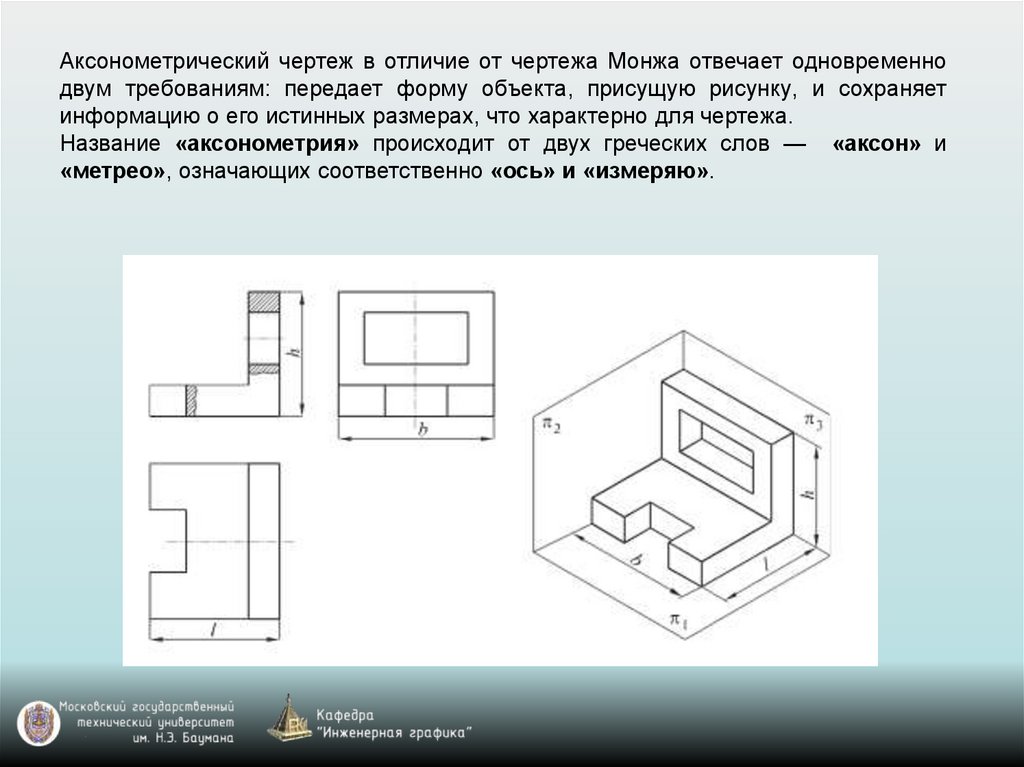
Аксонометрический чертеж в отличие от чертежа Монжа отвечает одновременно
двум требованиям: передает форму объекта, присущую рисунку, и сохраняет
информацию о его истинных размерах, что характерно для чертежа.
Название «аксонометрия» происходит от двух греческих слов — «аксон» и
«метрео», означающих соответственно «ось» и «измеряю».

4.

ГОСТ 2.317-2011 ЕСКД. Аксонометрические проекции
Аксонометрическое изображение (проекция) получается в результате
проецирования геометрического тела, отнесенного к пространственной
(натуральной) системе координат, на плоскость проекций, называемую также
картинной плоскостью или просто картиной.
Наглядность изображения в этом случае достигается тем, что ни одна из осей
координат не проецируется на картинную плоскость в точку.

5.

Основная теорема аксонометрии
(теорема К. Польке 1851г.)
Три отрезка прямых произвольной длины, лежащих в одной плоскости
и выходящих из одной точки под произвольными углами друг к другу,
представляют параллельную проекцию трех равных отрезков,
отложенных на прямоугольных координатных осях от начала.

6.

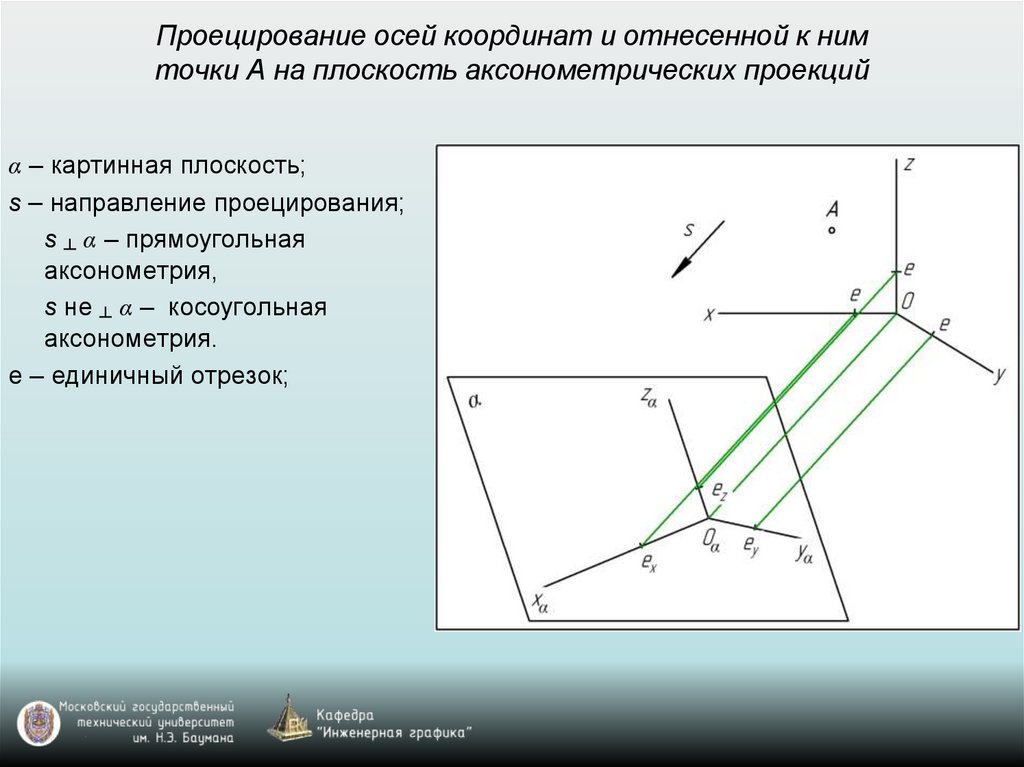
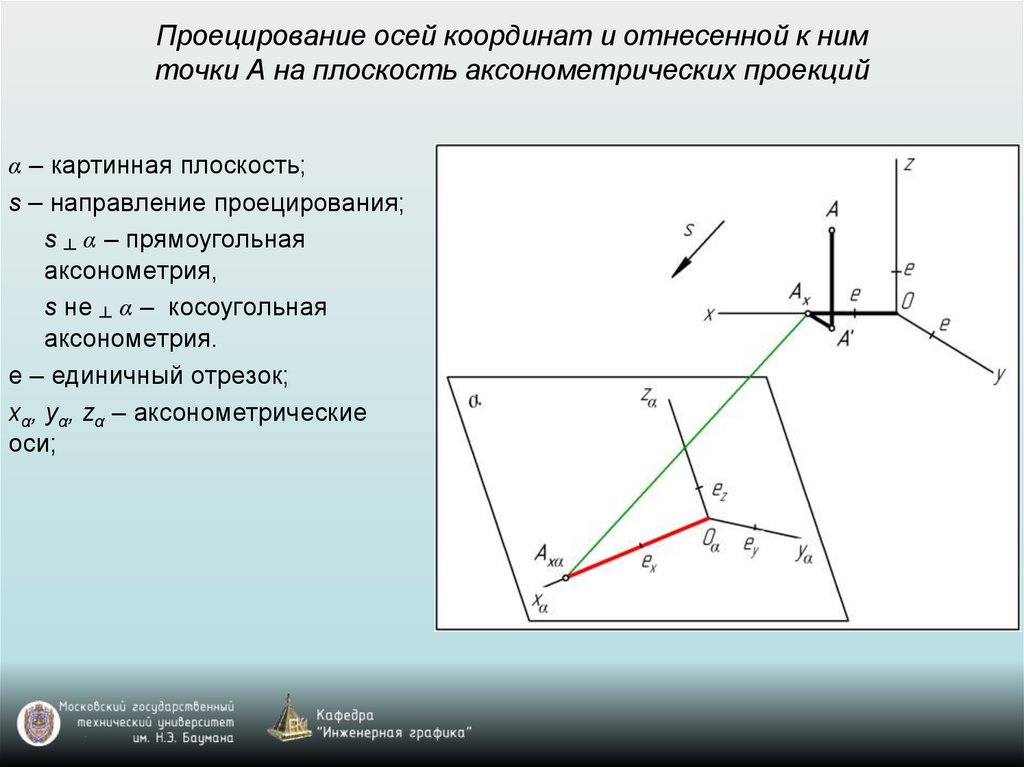
Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;

7.

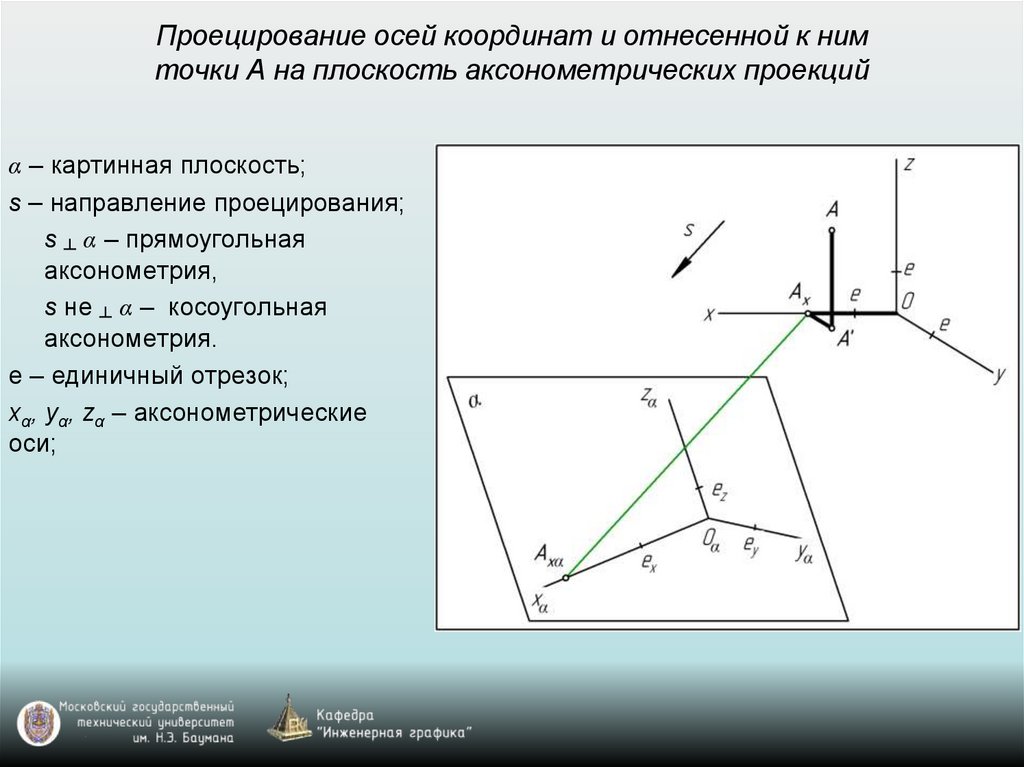
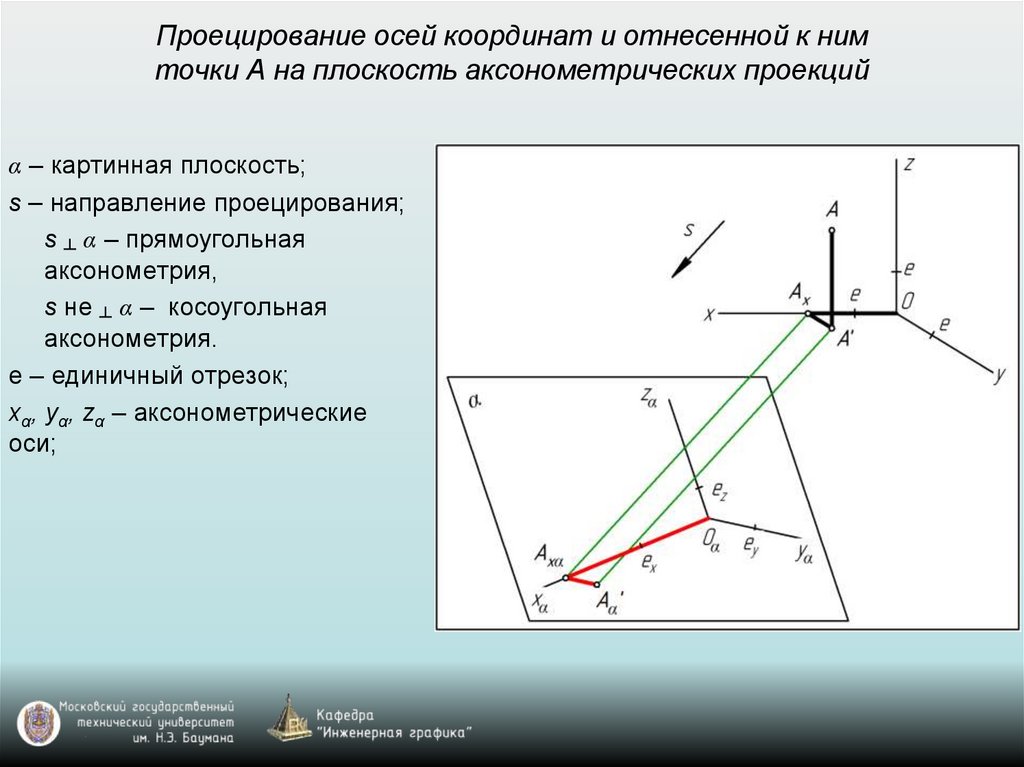
Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;

8.

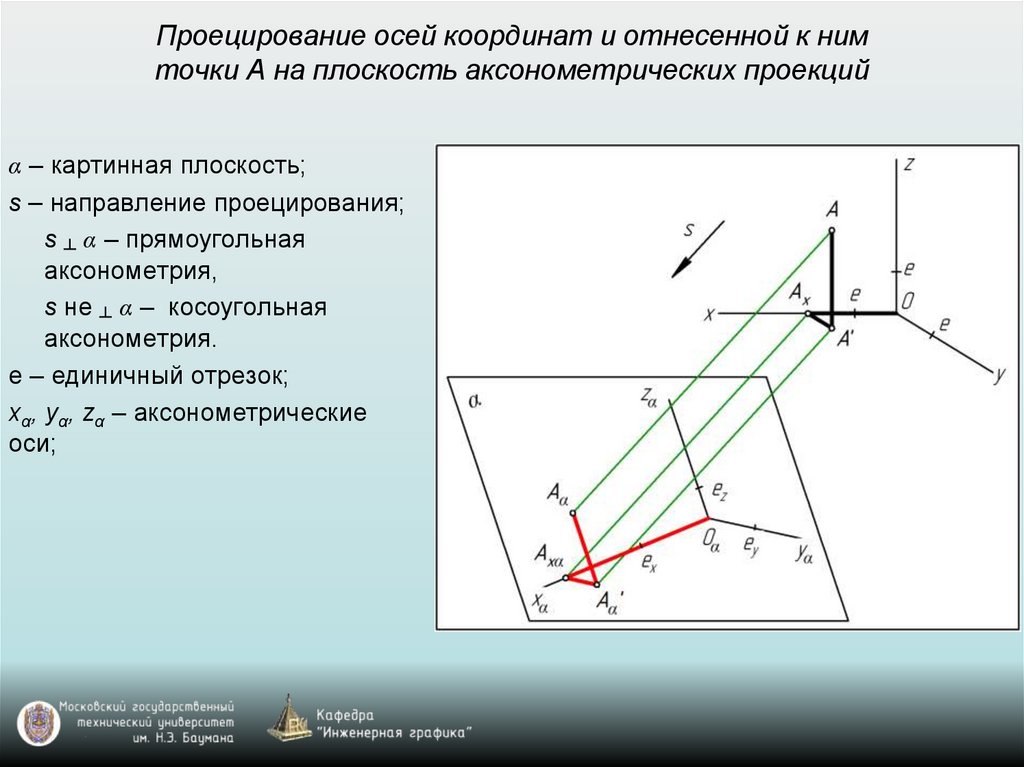
Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

9.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

10.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

11.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

12.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

13.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

14.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

15.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;

16.

Проецирование осей координат и отнесенной к ним
точки А на плоскость аксонометрических проекций
α – картинная плоскость;
s – направление проецирования;
s ┴ α – прямоугольная
аксонометрия,
s не ┴ α – косоугольная
аксонометрия.
е – единичный отрезок;
xα, yα, zα – аксонометрические
оси;
Аα – аксонометрическая проекция
точки A;
Аα' – вторичная проекция точки A.
Оα Аxα Аα′Аα - аксонометрическая
координатная ломаная.

17.

В общем случае еx ≠ еy≠ еz ≠ е
k, m, n - коэффициенты (или показатели) искажения по
аксонометрическим осям.
Виды аксонометрических проекций:
• Триметрическая проекция - все три показателя искажений
между собой не равны.
• Диметрическая проекция - два показателя искажения равны
(например, k = n), а третий отличен от них.
• Изометрическая проекция - все три показателя равны
(k=m=n).

18.

ГОСТ 2.317-2011 устанавливает следующие виды аксонометрических проекций:
1.
2.
3.
4.
5.
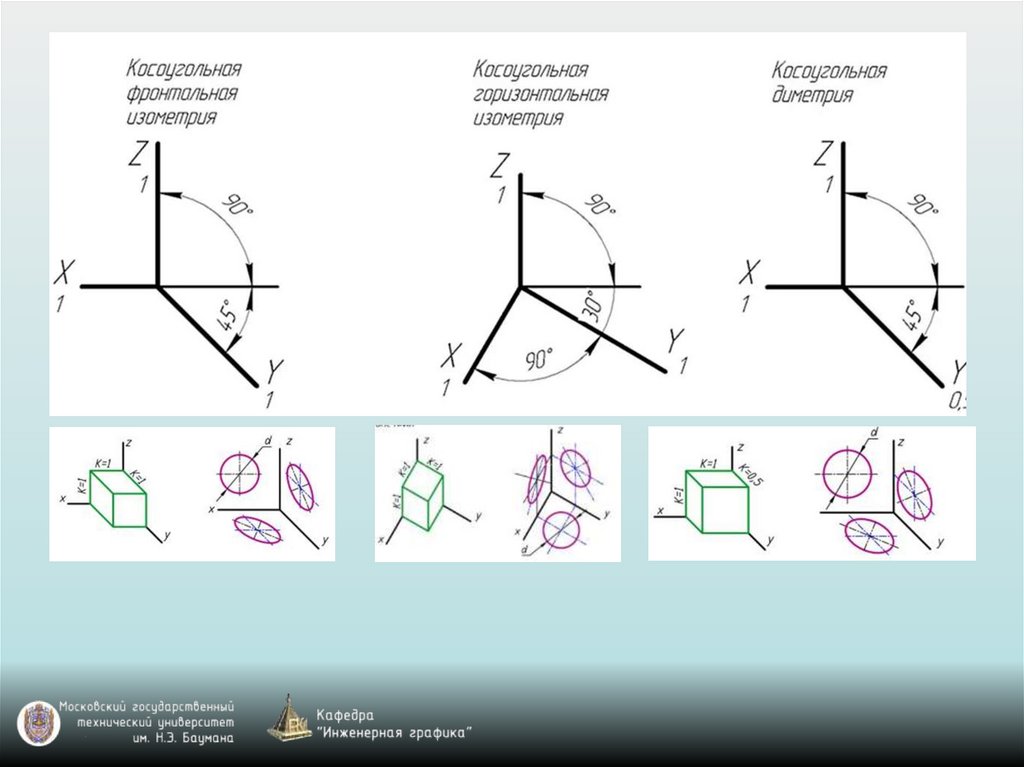
прямоугольная изометрическая проекция;
прямоугольная диметрическая проекция;
косоугольной фронтальная изометрическая проекция;
косоугольной горизонтальная изометрическая проекция;
косоугольной фронтальная диметрическая проекция.

19.

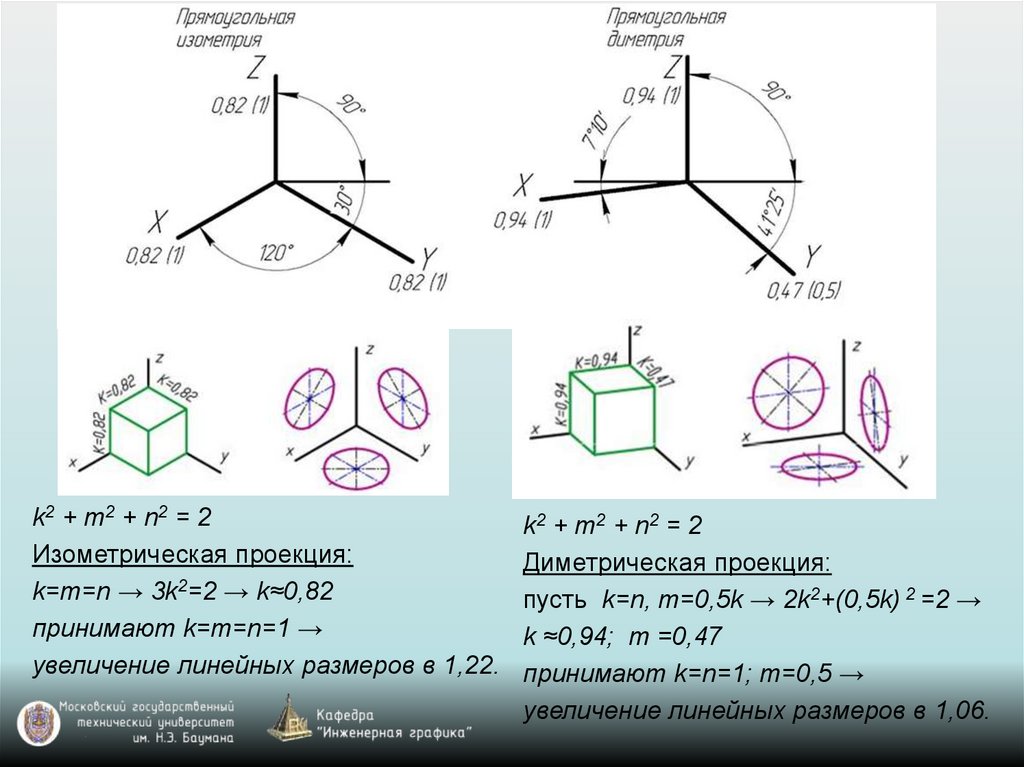
k2 + m2 + n2 = 2
Изометрическая проекция:
k=m=n → 3k2=2 → k≈0,82
принимают k=m=n=1 →
увеличение линейных размеров в 1,22.
k2 + m2 + n2 = 2
Диметрическая проекция:
пусть k=n, m=0,5k → 2k2+(0,5k) 2 =2 →
k ≈0,94; m =0,47
принимают k=n=1; m=0,5 →
увеличение линейных размеров в 1,06.

20.

21.

Построение аксонометрических проекций
окружностей, расположенных в координатных
плоскостях xy, xz, yz или в плоскостях, им
параллельных
В прямоугольной изометрии и диметрии направление
больших осей эллипсов перпендикулярно свободным
аксонометрическим осям, а малые оси эллипсов
совпадают
по
направлению
со
свободными
аксонометрическими осями.

22.

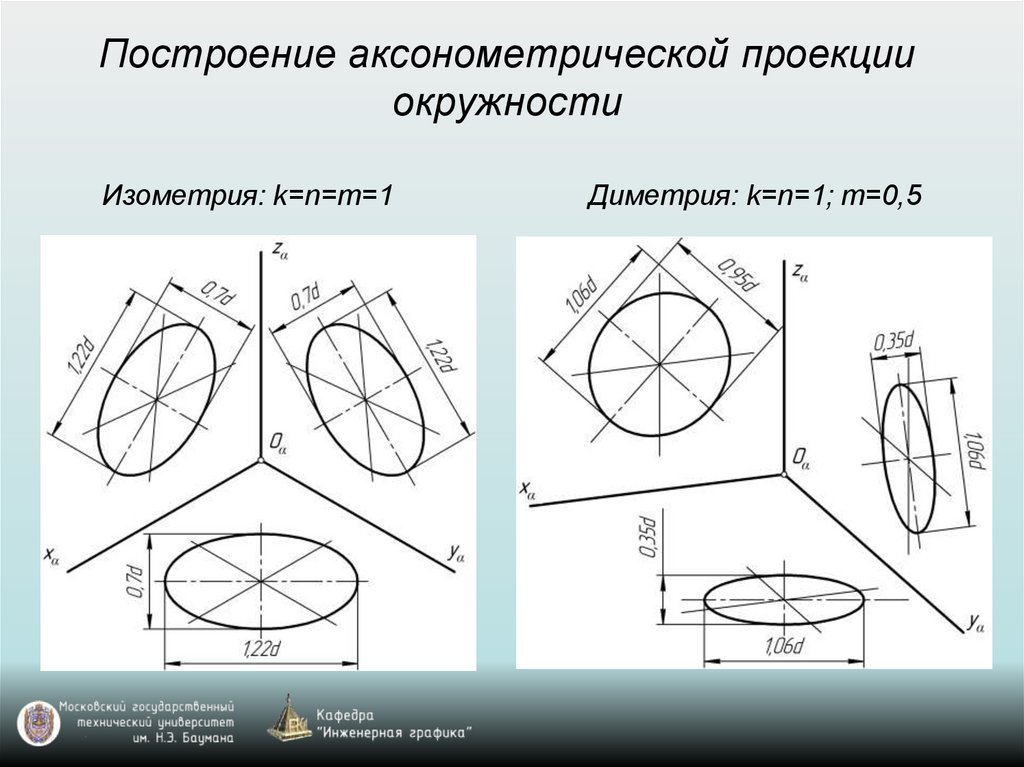
Построение аксонометрической проекции
окружности
Изометрия: k=n=m=1
Диметрия: k=n=1; m=0,5

23.

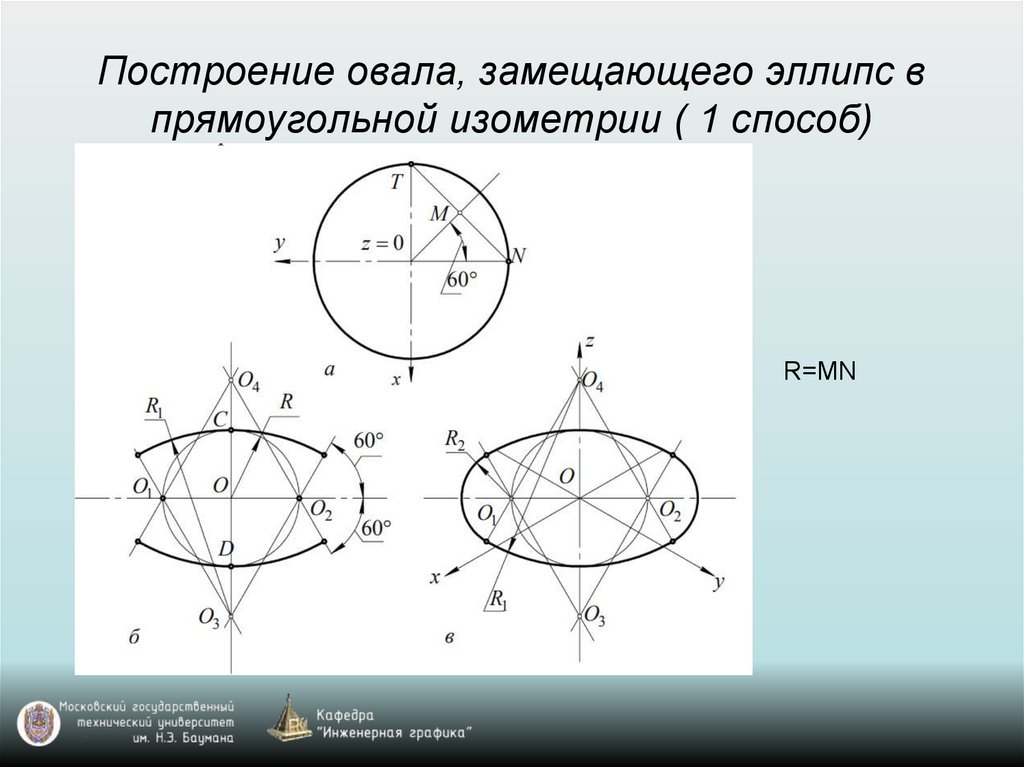
Построение овала, замещающего эллипс в
прямоугольной изометрии ( 1 способ)
R=MN

24.

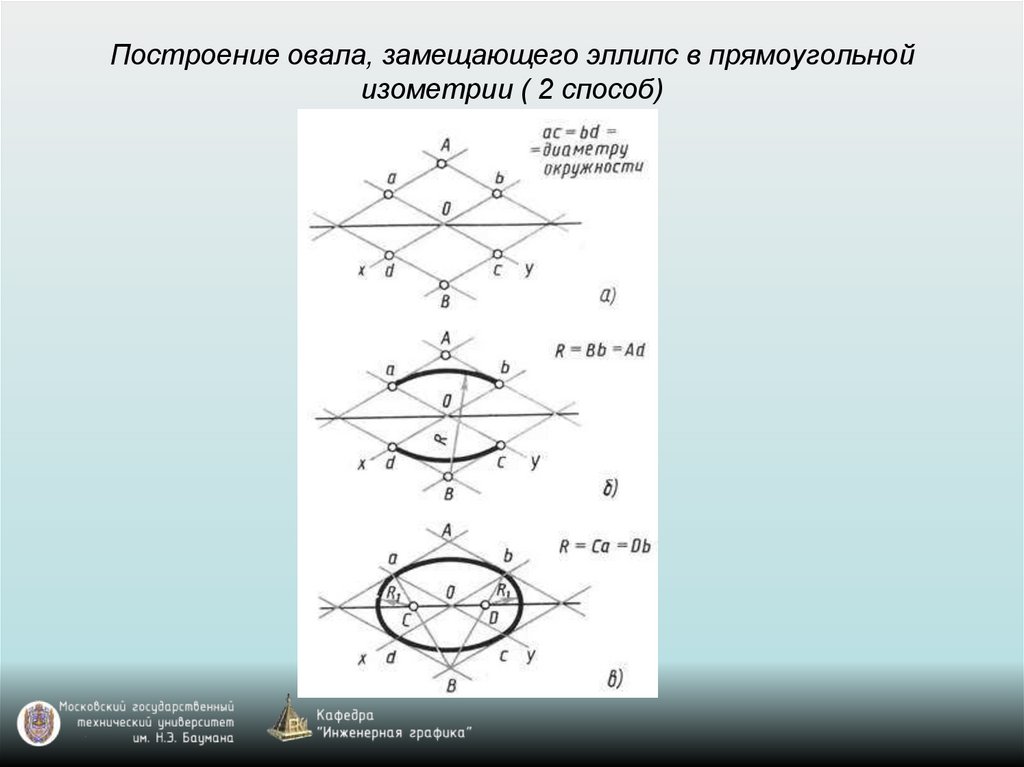
Построение овала, замещающего эллипс в прямоугольной
изометрии ( 2 способ)

25.

Нанесение штриховки сечений в
аксонометрических проекциях
Изометрия

26.

Нанесение штриховки сечений в
аксонометрических проекциях
Диметрия

27.

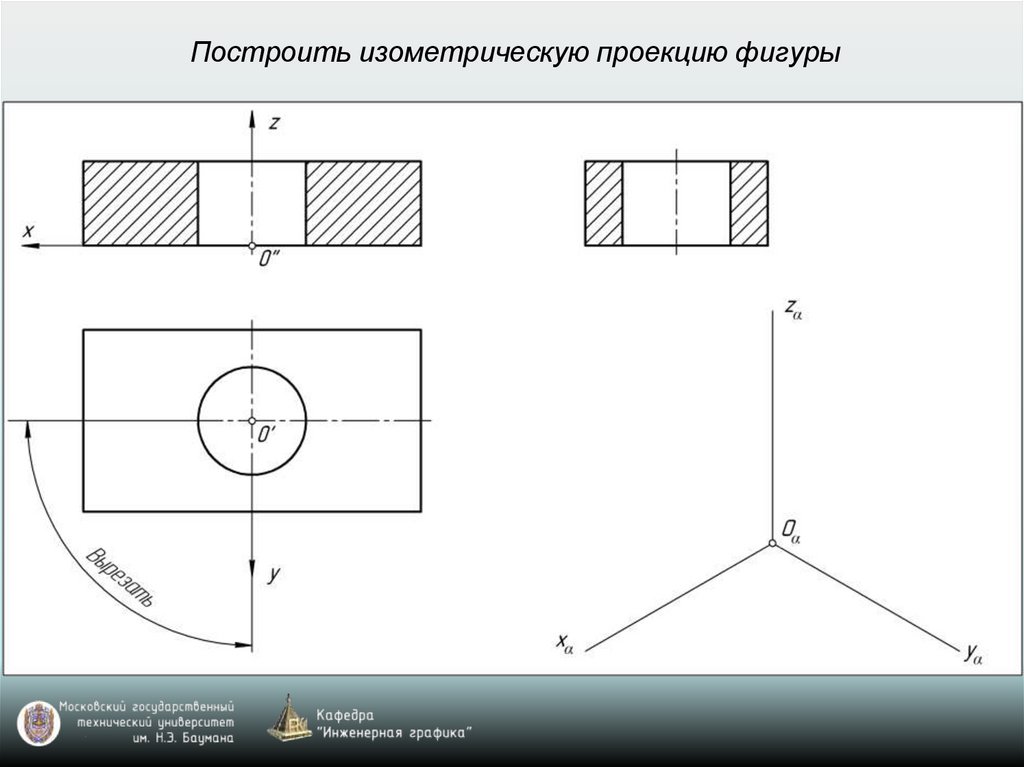
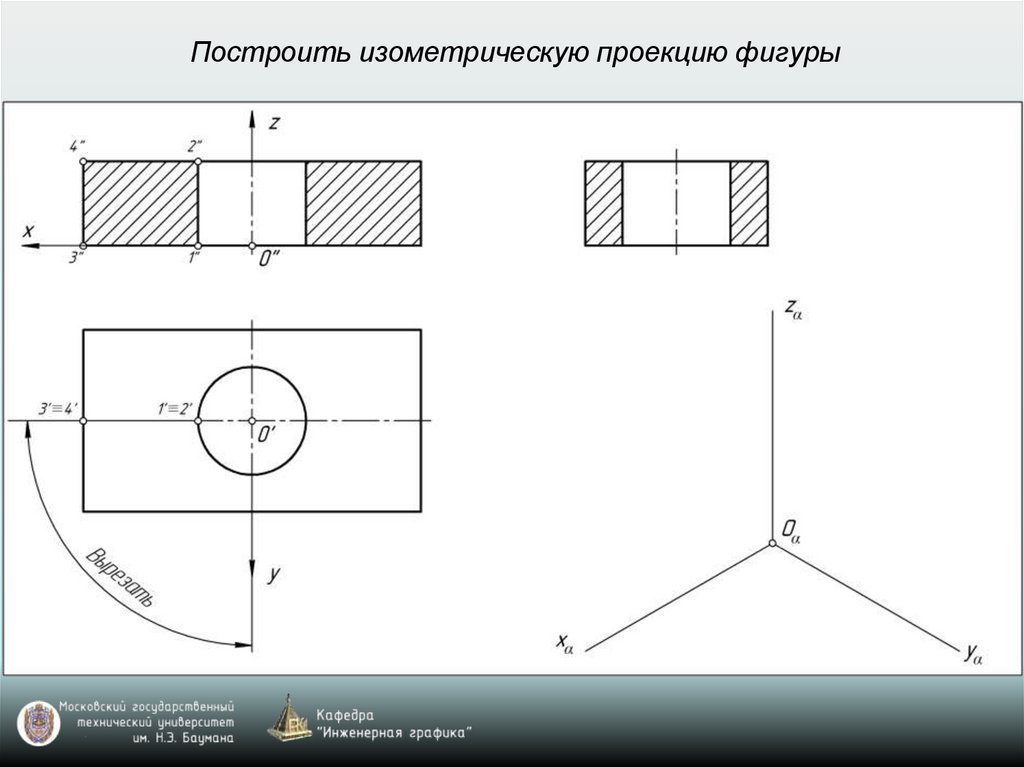
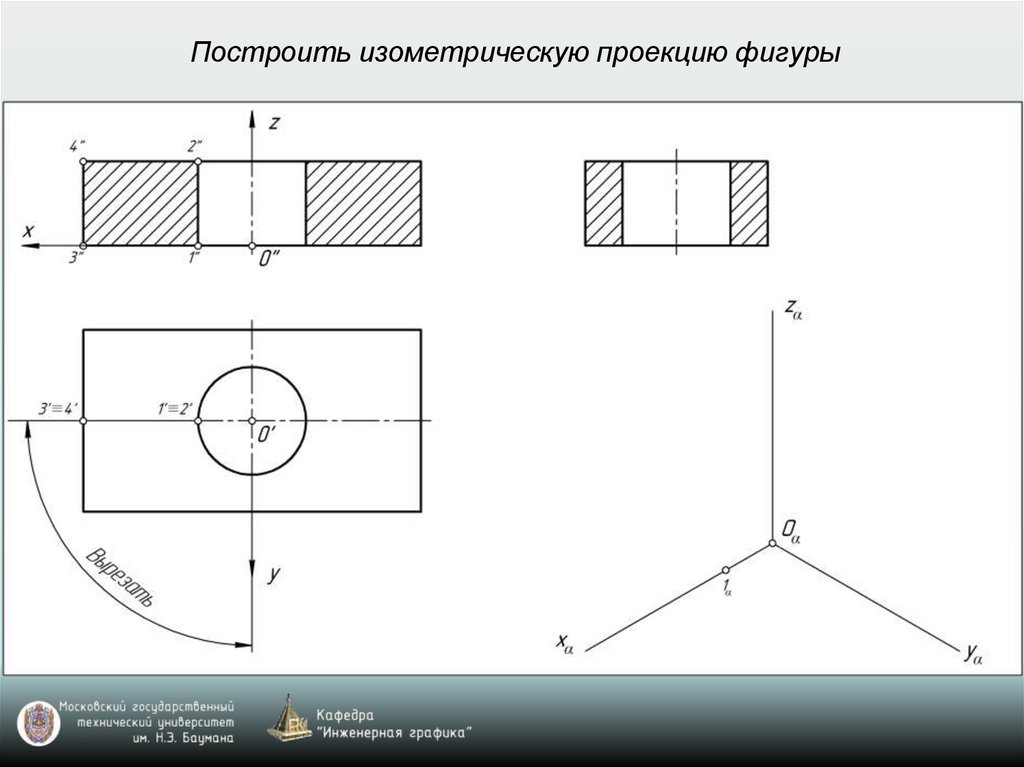
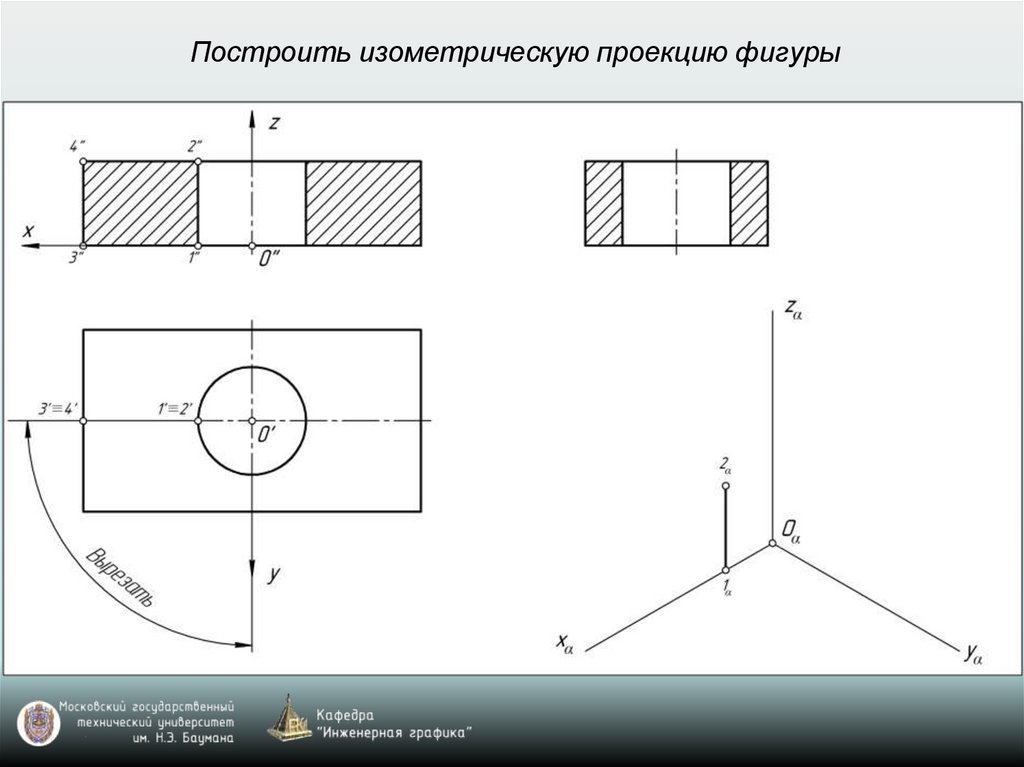
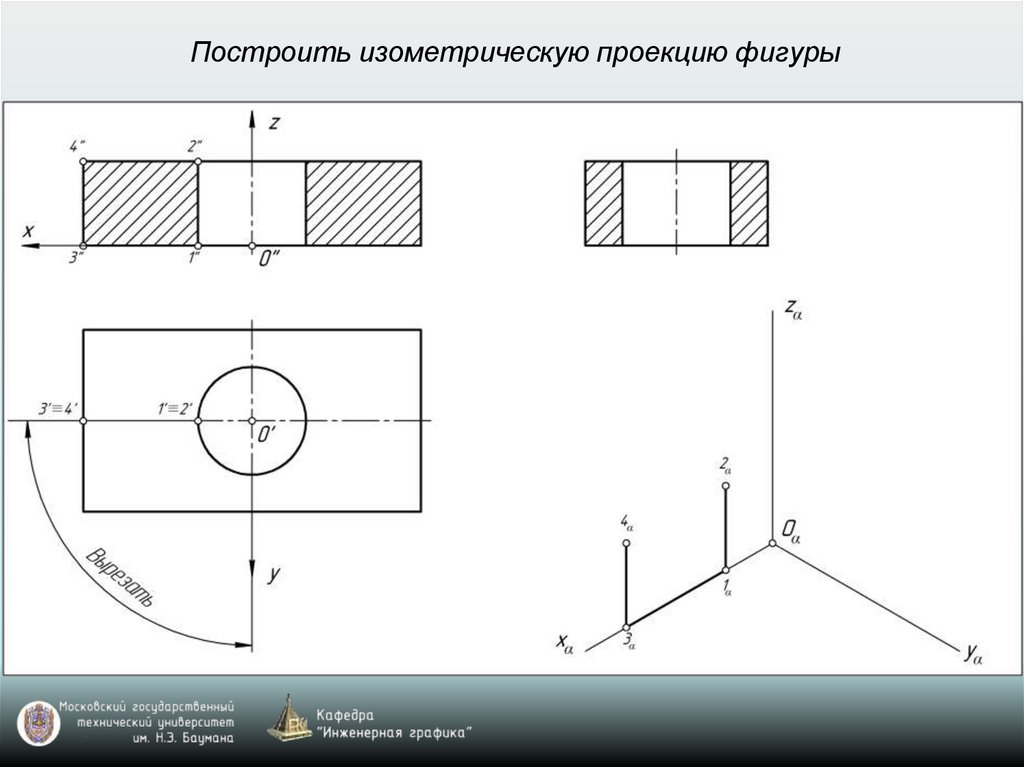
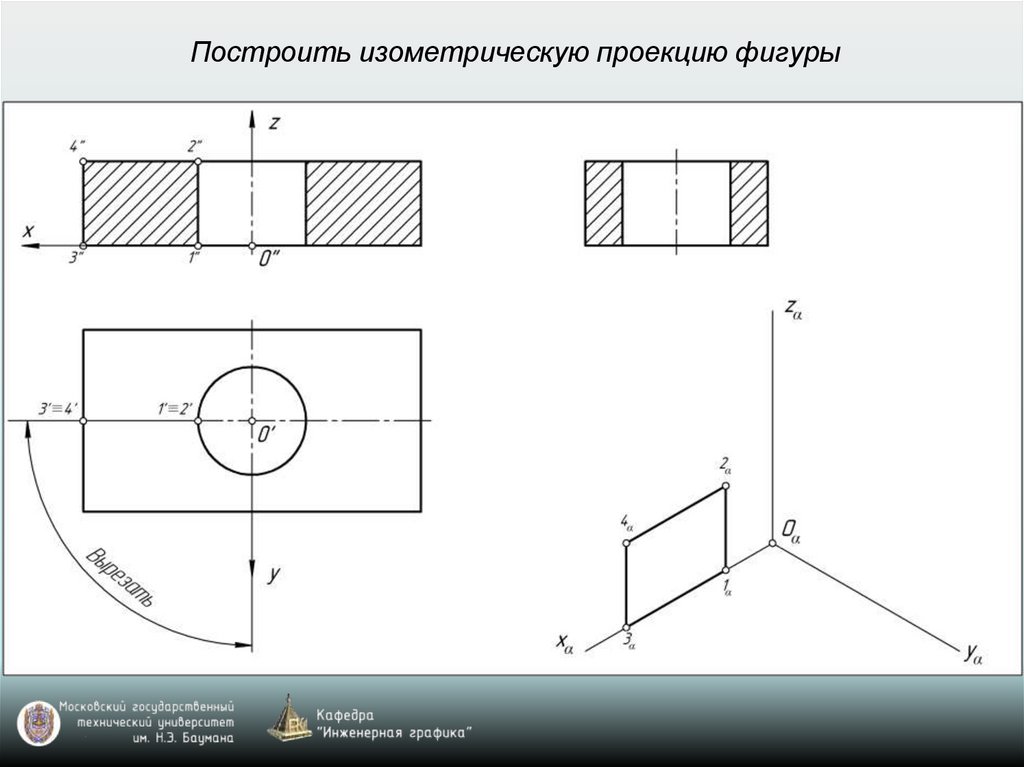
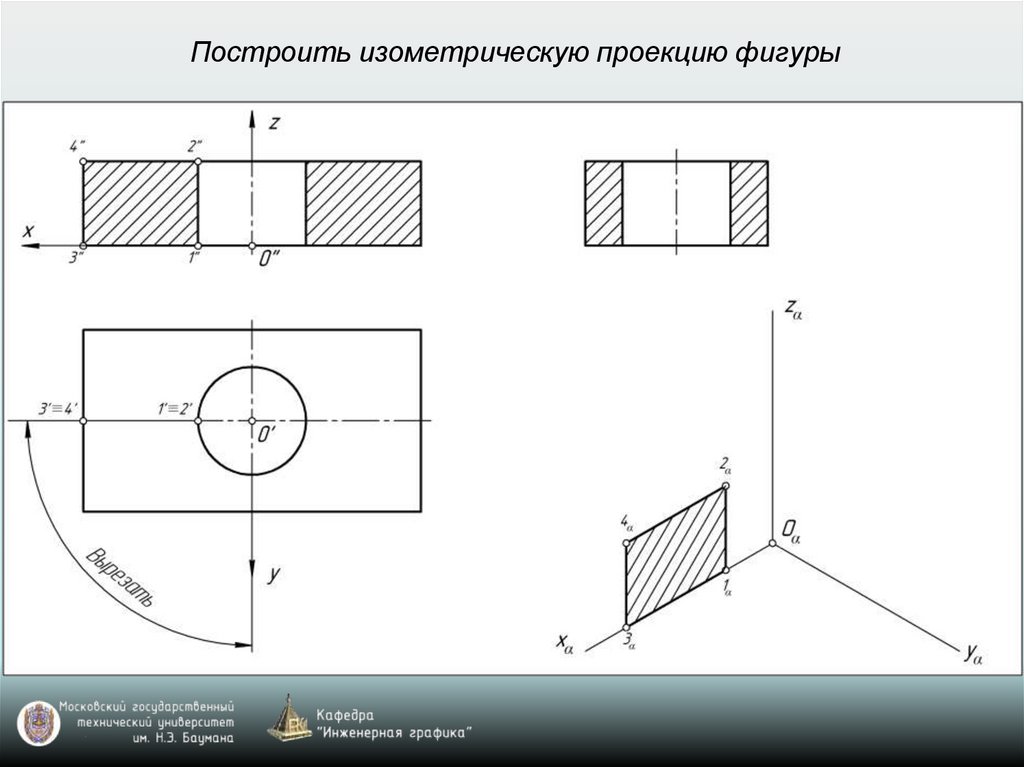
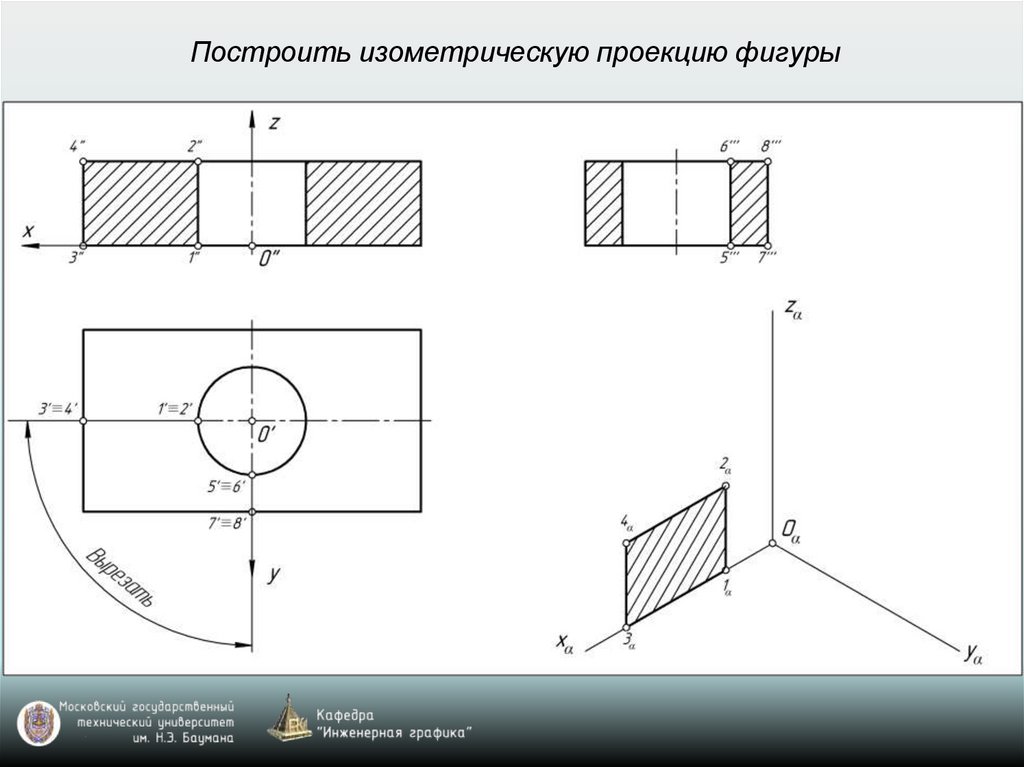
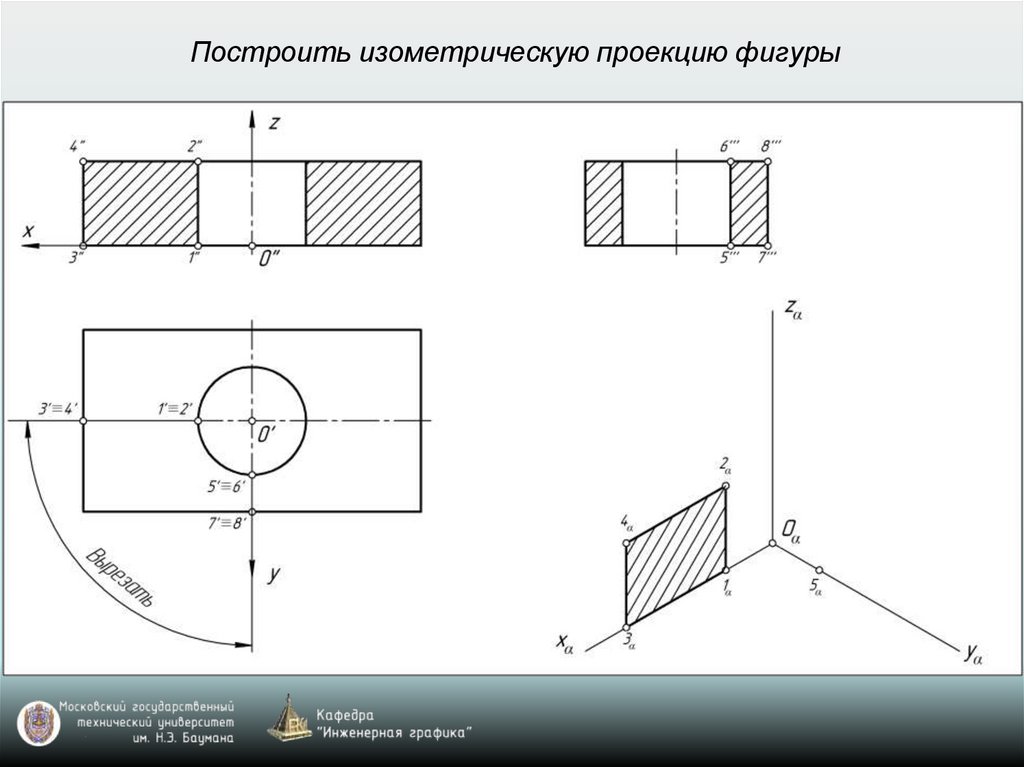
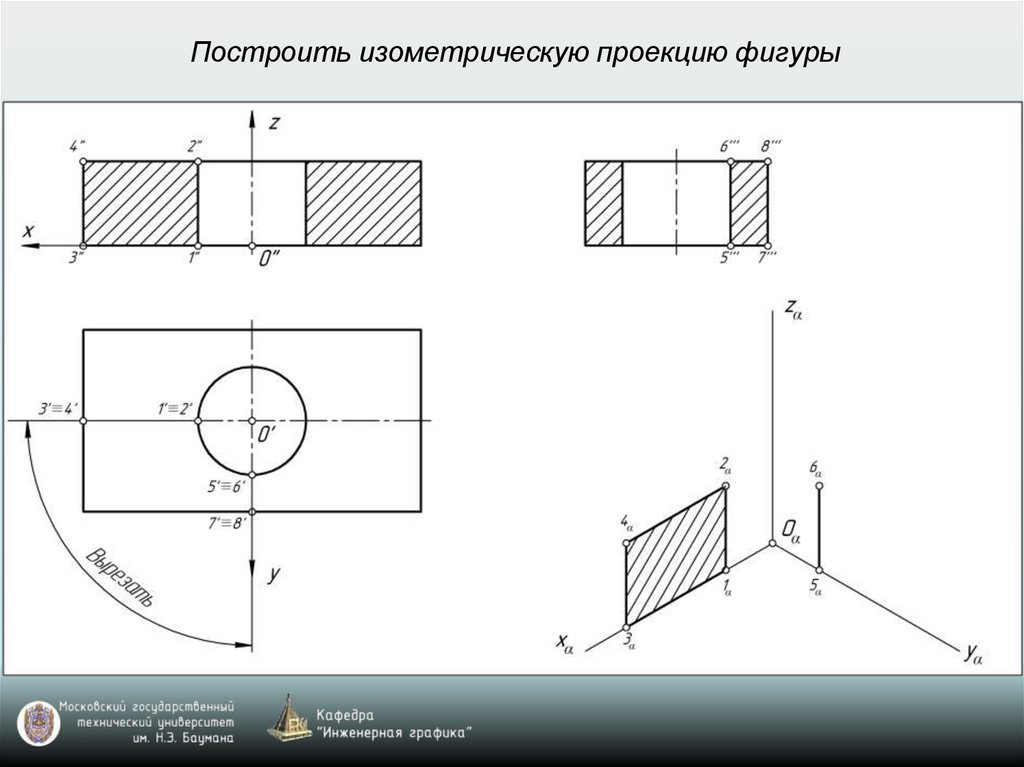
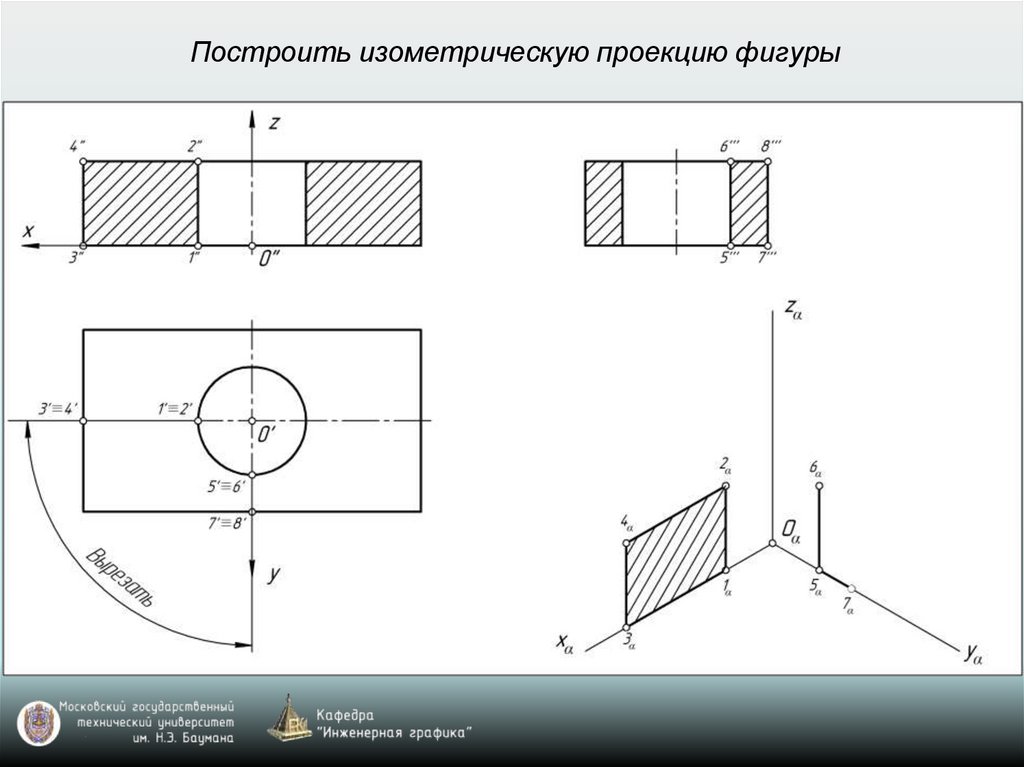
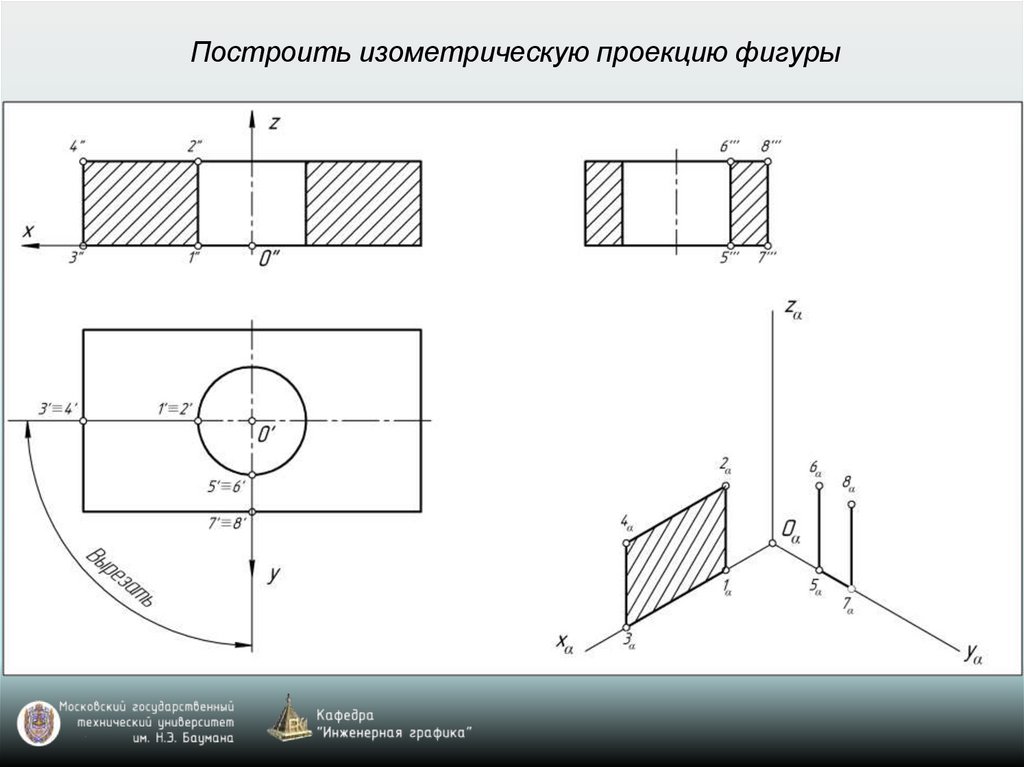
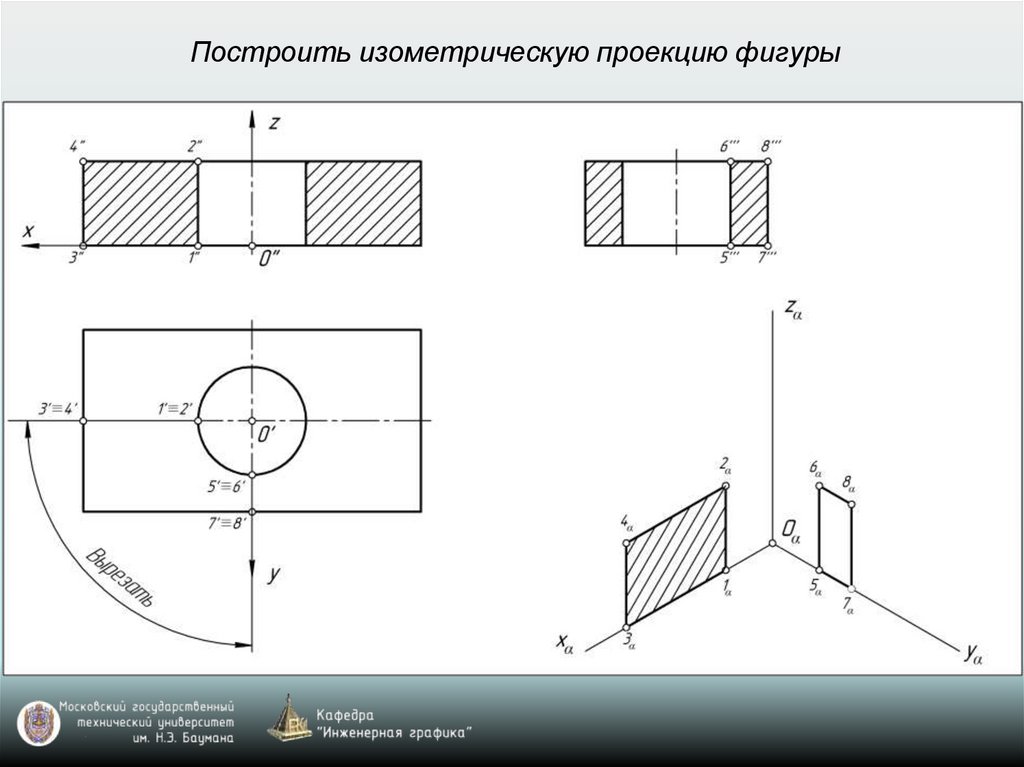
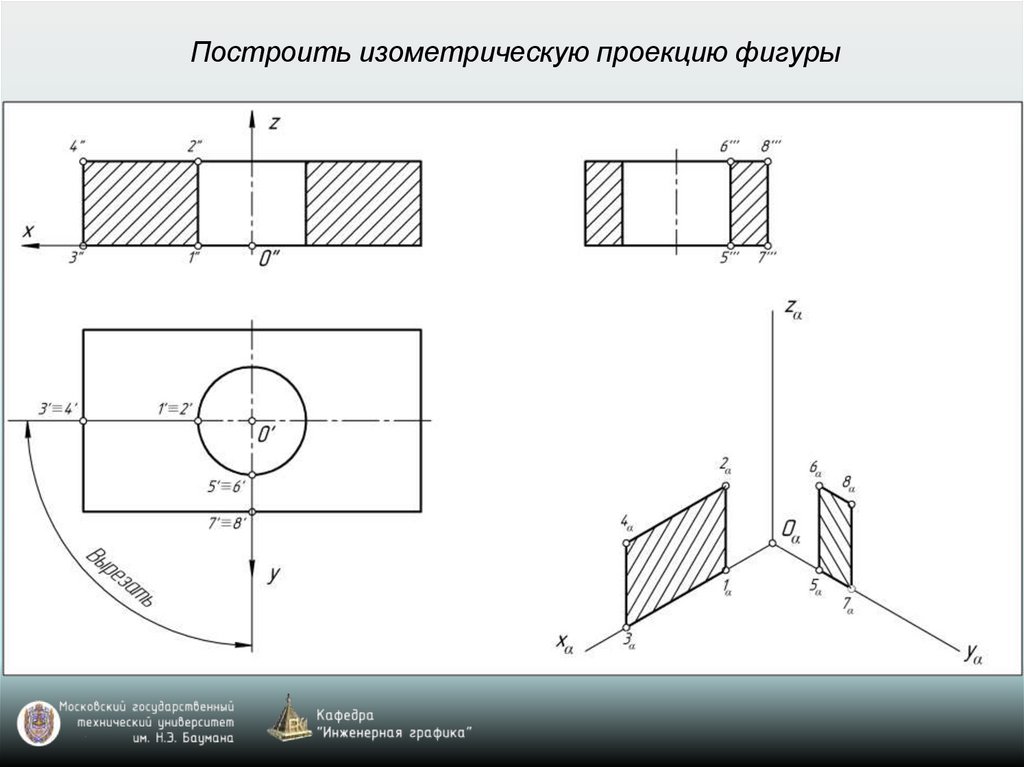
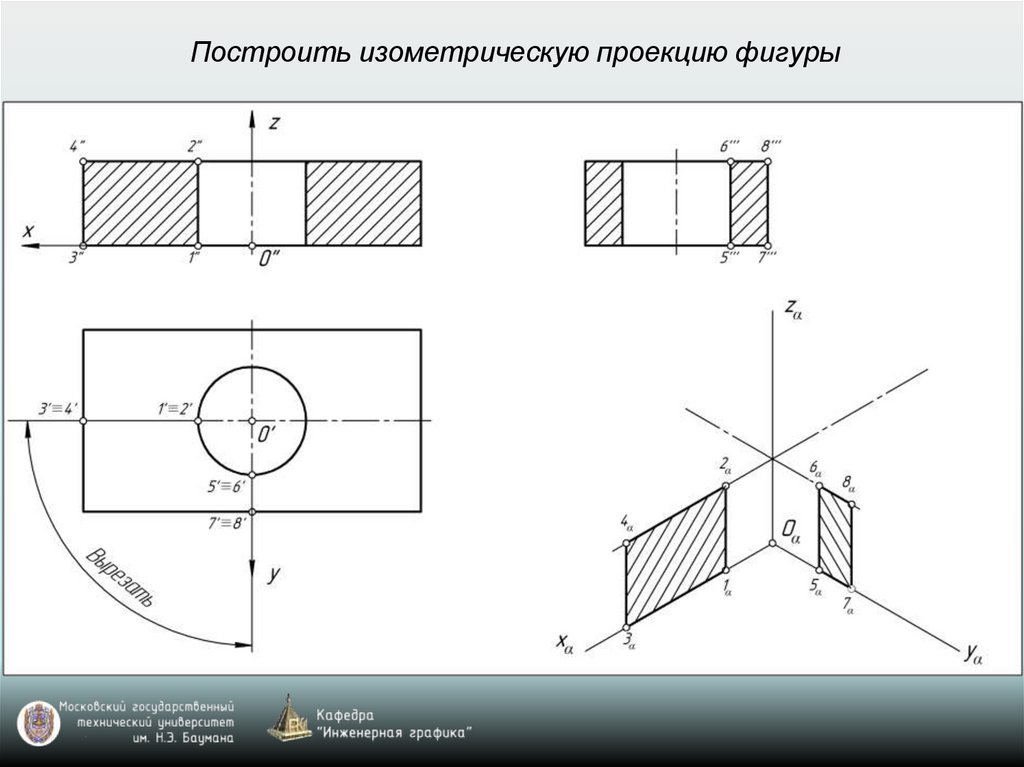
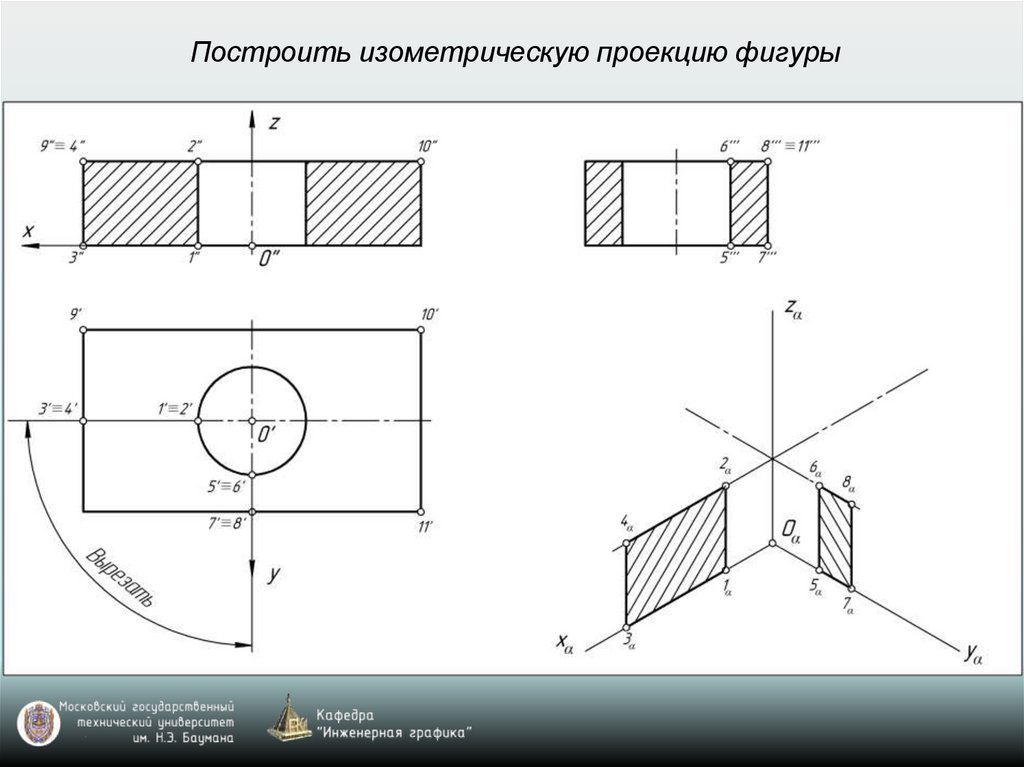
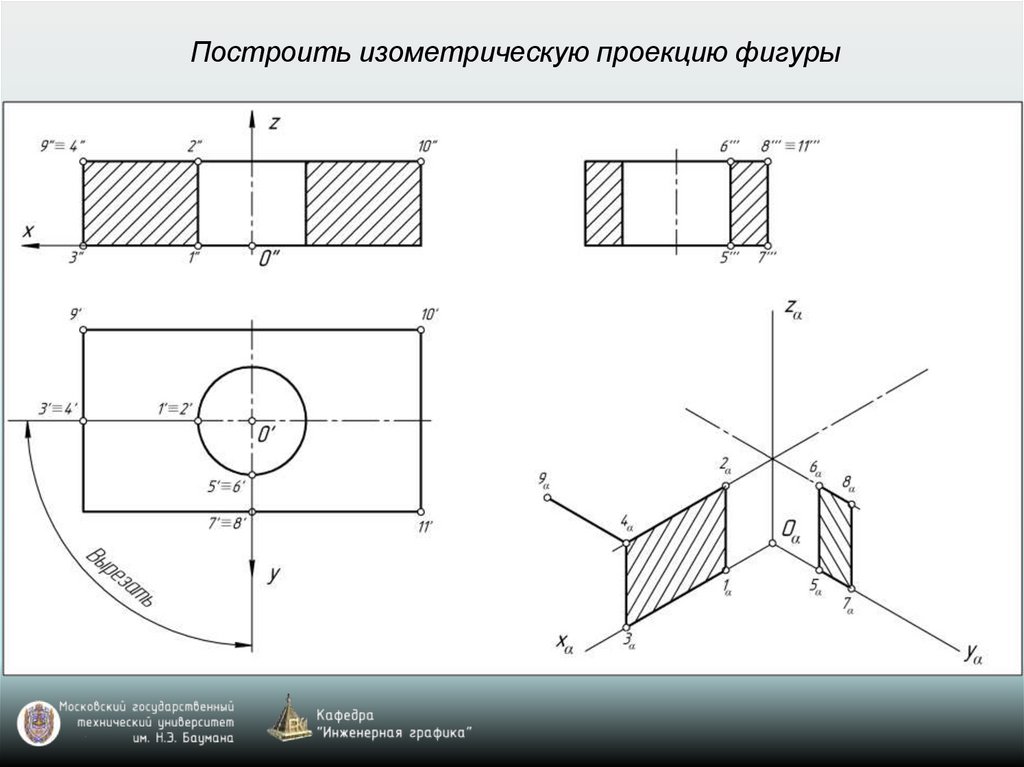
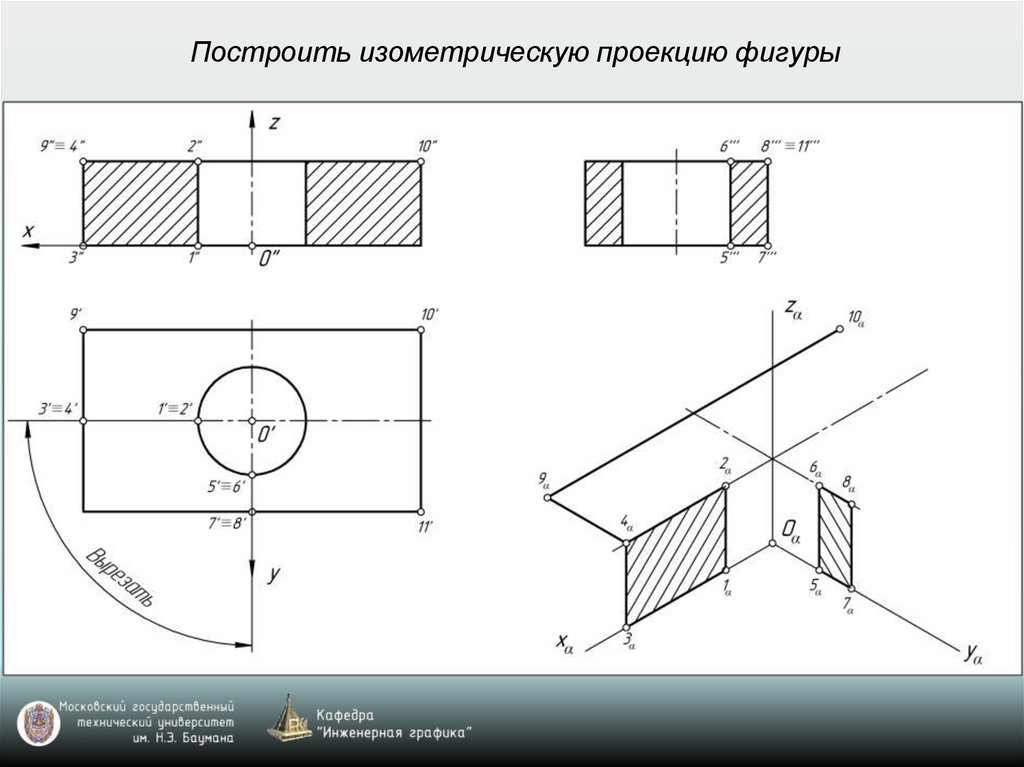
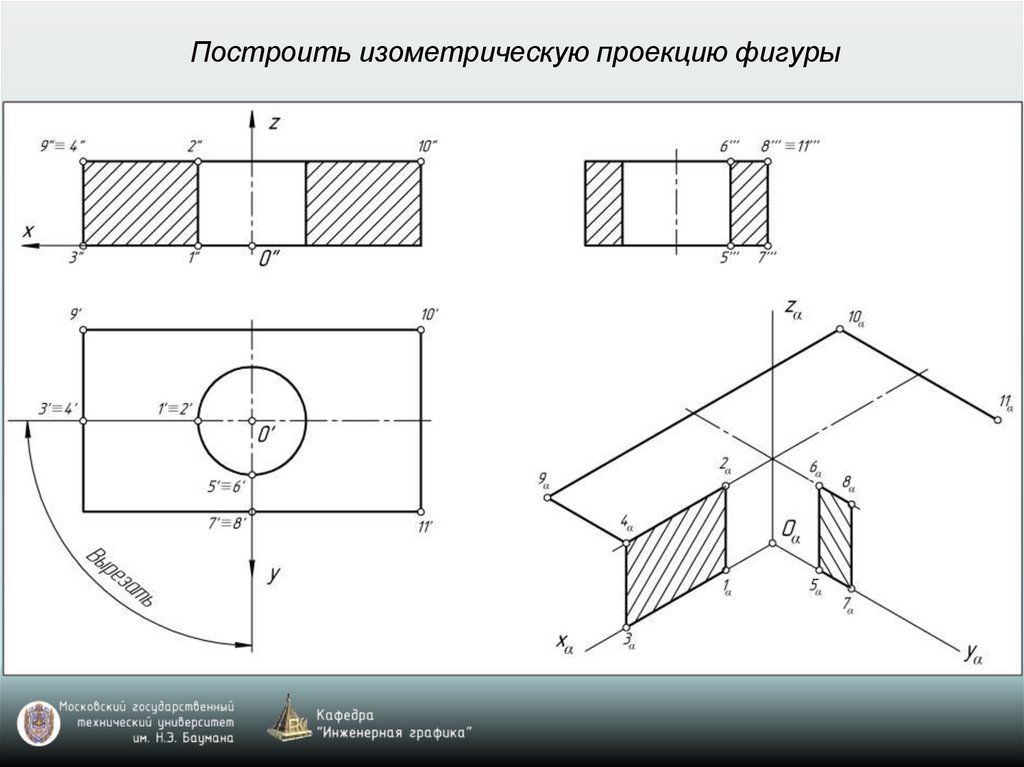
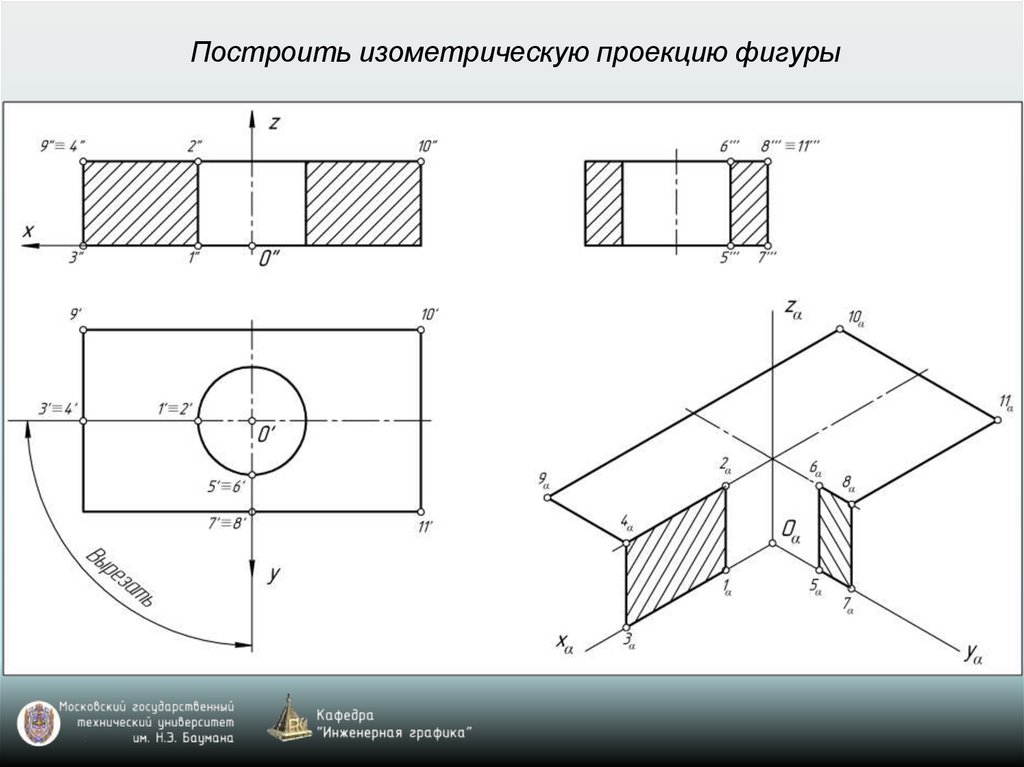
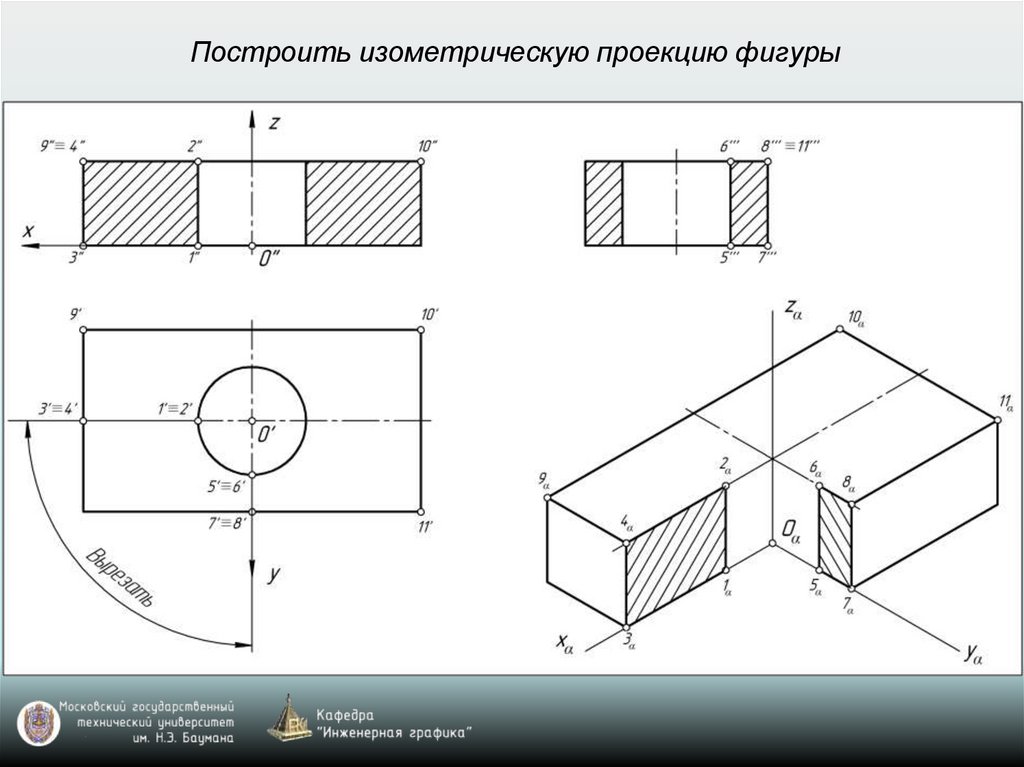
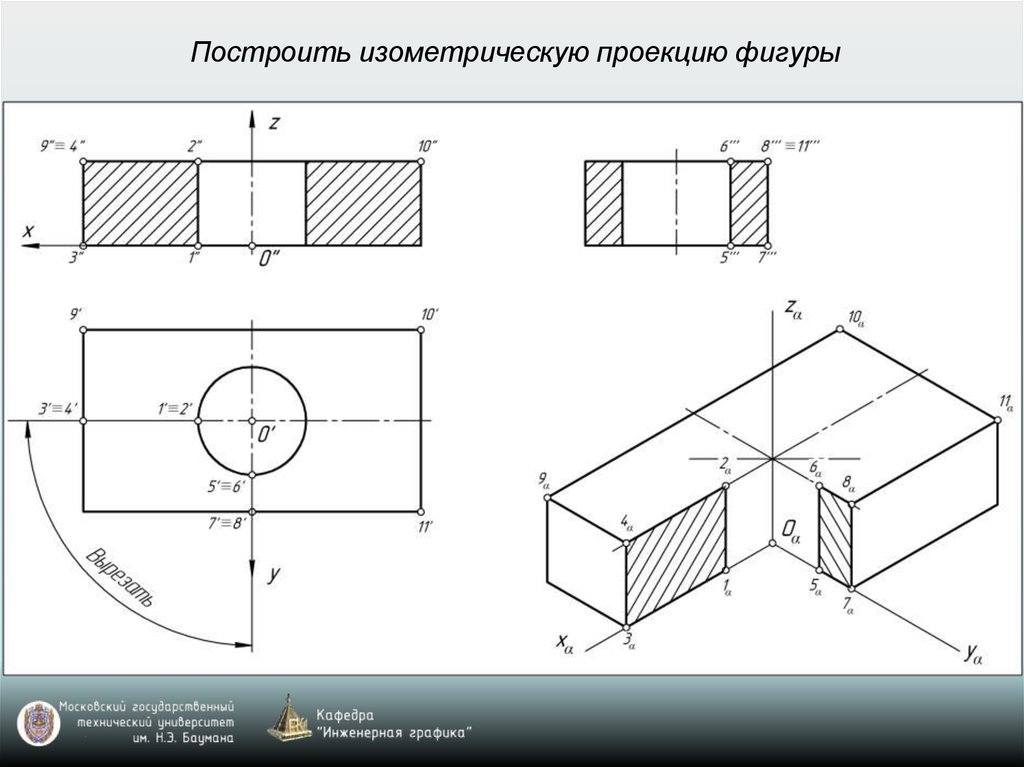
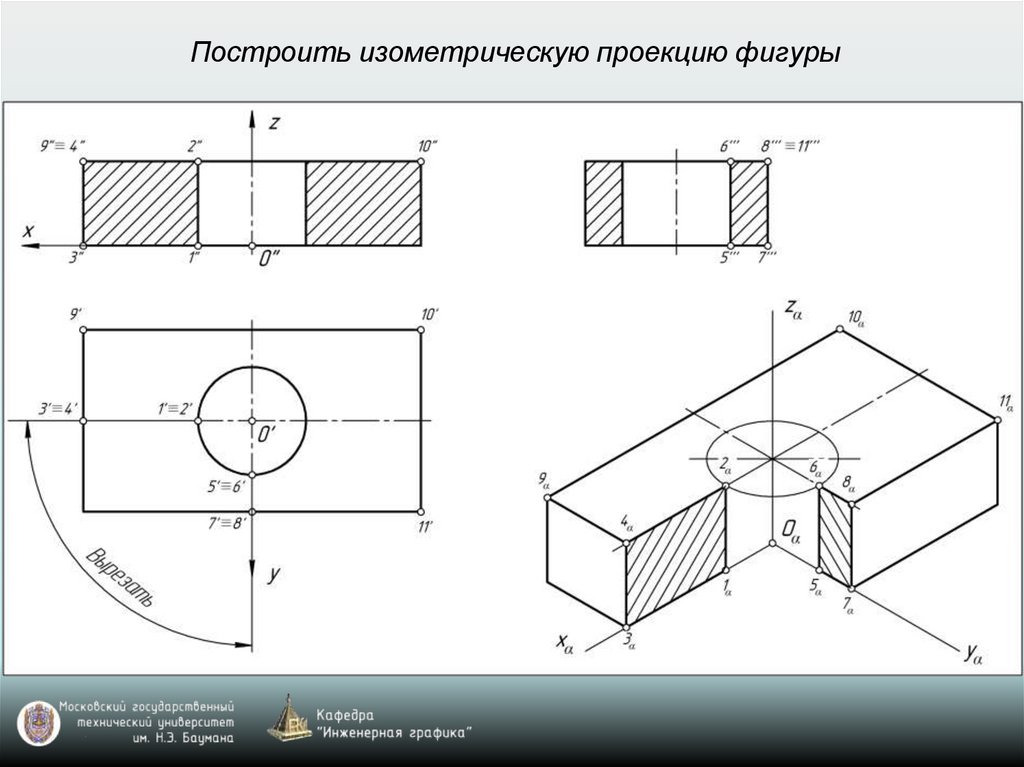
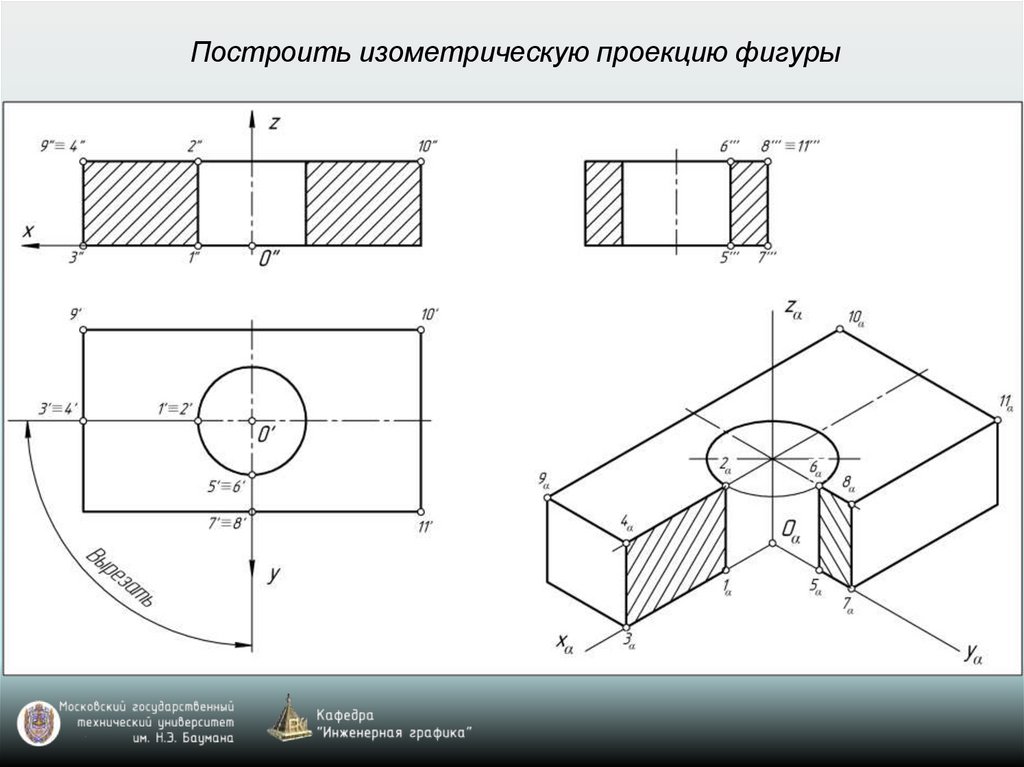
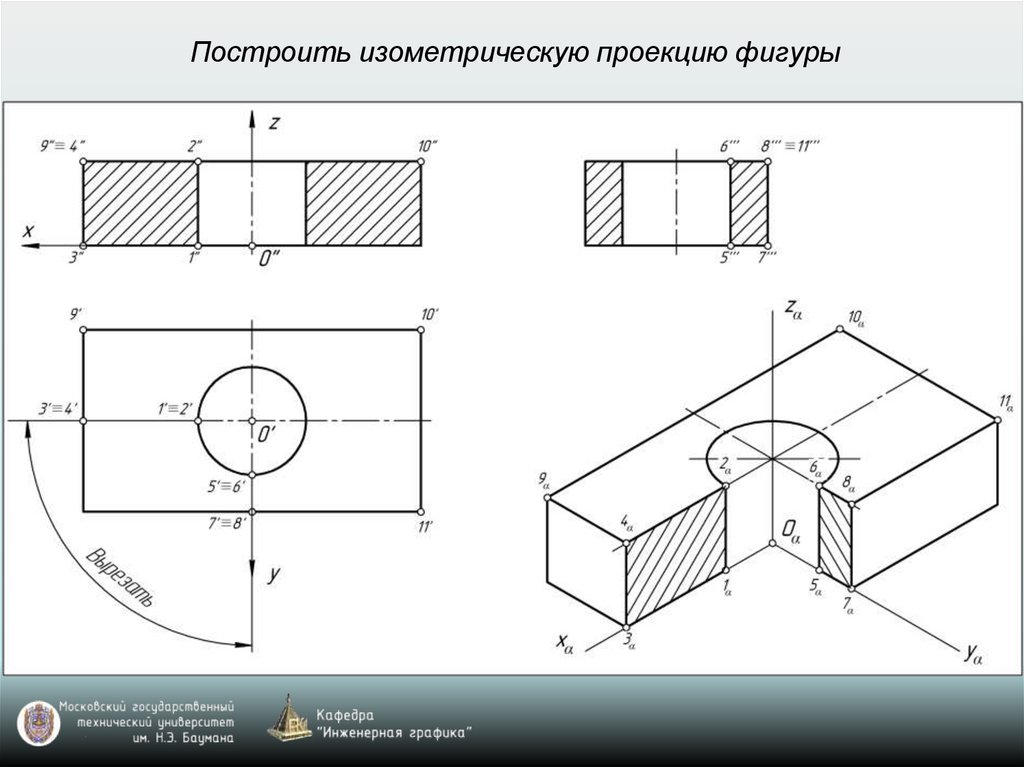
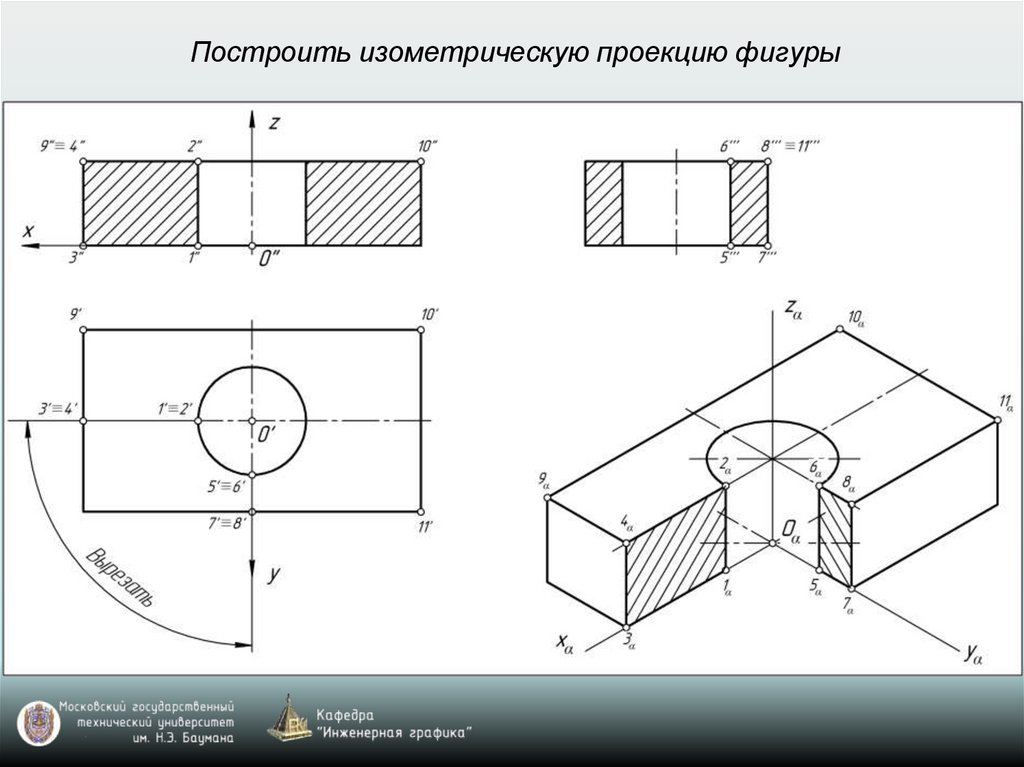
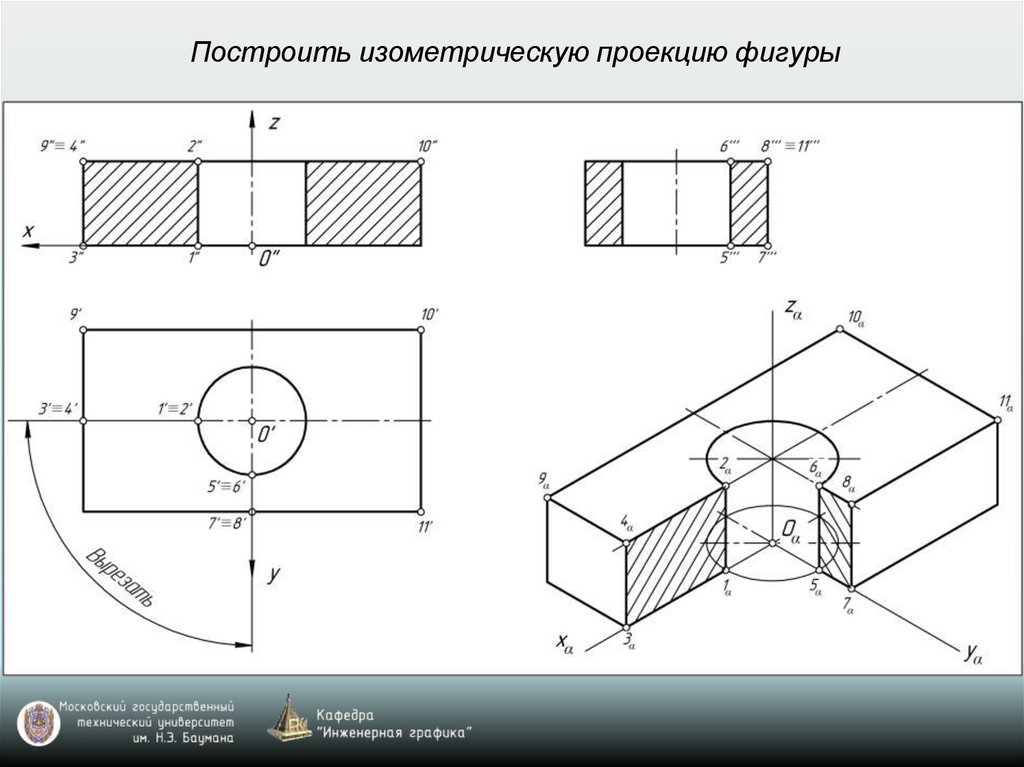
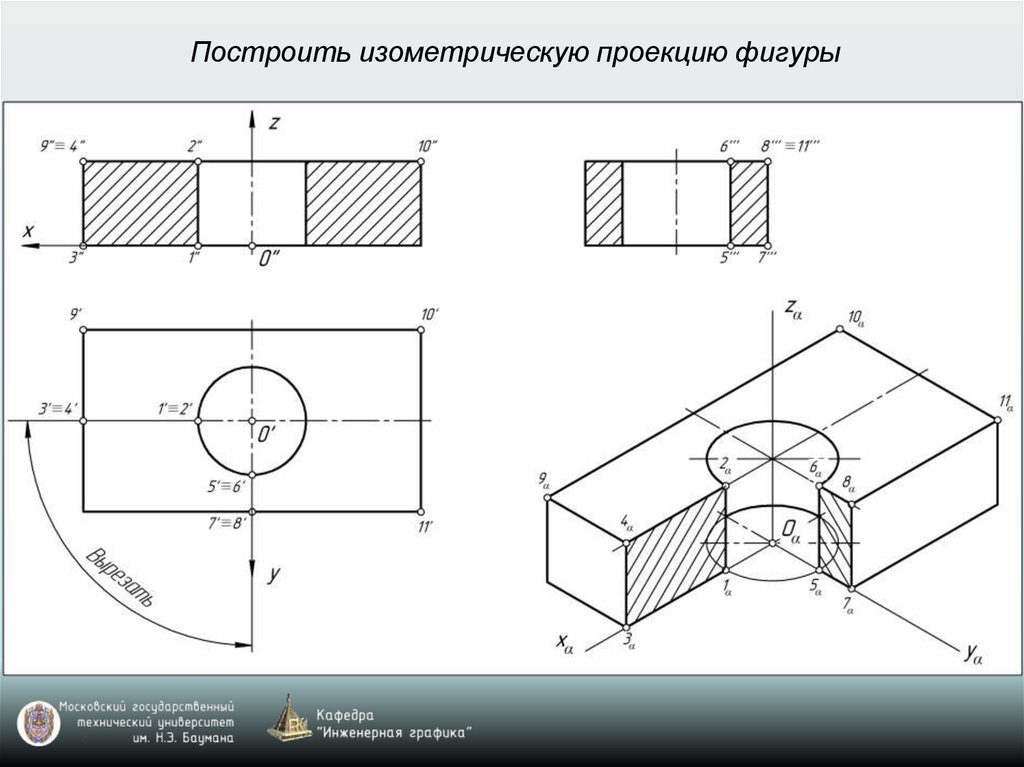
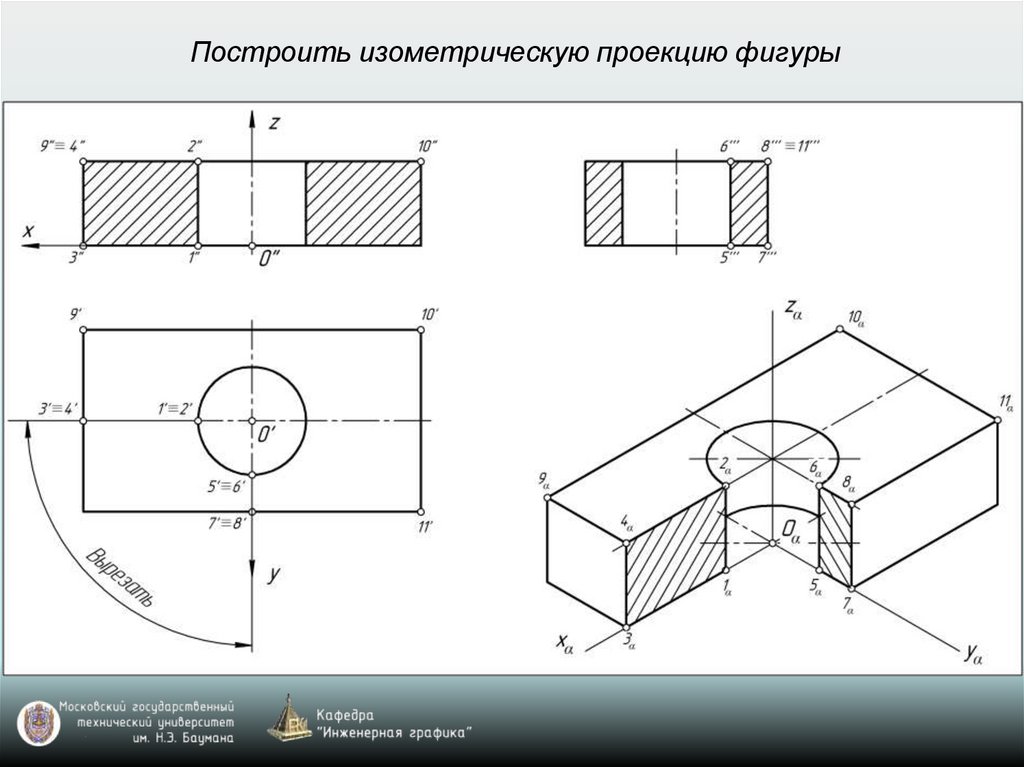
Построить изометрическую проекцию фигуры

28.

Построить изометрическую проекцию фигуры

29.

Построить изометрическую проекцию фигуры

30.

Построить изометрическую проекцию фигуры

31.

Построить изометрическую проекцию фигуры

32.

Построить изометрическую проекцию фигуры

33.

Построить изометрическую проекцию фигуры

34.

Построить изометрическую проекцию фигуры

35.

Построить изометрическую проекцию фигуры

36.

Построить изометрическую проекцию фигуры

37.

Построить изометрическую проекцию фигуры

38.

Построить изометрическую проекцию фигуры

39.

Построить изометрическую проекцию фигуры

40.

Построить изометрическую проекцию фигуры

41.

Построить изометрическую проекцию фигуры

42.

Построить изометрическую проекцию фигуры

43.

Построить изометрическую проекцию фигуры

44.

Построить изометрическую проекцию фигуры

45.

Построить изометрическую проекцию фигуры

46.

Построить изометрическую проекцию фигуры

47.

Построить изометрическую проекцию фигуры

48.

Построить изометрическую проекцию фигуры

49.

Построить изометрическую проекцию фигуры

50.

Построить изометрическую проекцию фигуры

51.

Построить изометрическую проекцию фигуры

52.

Построить изометрическую проекцию фигуры

53.

Построить изометрическую проекцию фигуры

54.

Построить изометрическую проекцию фигуры

55.

Построить изометрическую проекцию фигуры

56.

Построить изометрическую проекцию фигуры

57.

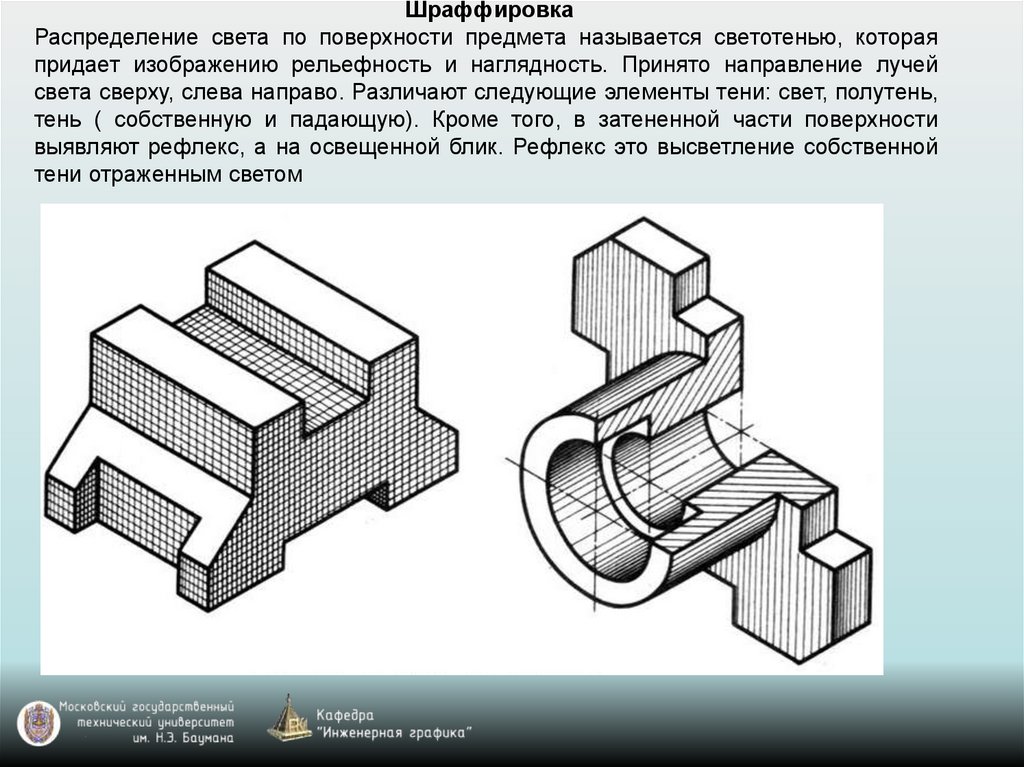
Шраффировка
Распределение света по поверхности предмета называется светотенью, которая
придает изображению рельефность и наглядность. Принято направление лучей
света сверху, слева направо. Различают следующие элементы тени: свет, полутень,
тень ( собственную и падающую). Кроме того, в затененной части поверхности
выявляют рефлекс, а на освещенной блик. Рефлекс это высветление собственной
тени отраженным светом

58.

Собственные
тени
наносят
шраффировкой ( штриховка сеткой).
Линии шраффировки наносят в двух
направлениях
параллельно
тем
аксонометрическим осям, которым
принадлежит ( или параллельна)
данная плоскость, причем следует
знать, что светлые поверхности при
удалении
от
наблюдателя
затемняются,
а
темные
высветляются. Если изображается
поверхность
вращения,
то
два
направления линий шраффировки по
образующей
и
направляющей
поверхности. На рисунке показано
разделение
цилиндрической
поверхности условно на шесть равных
зон: I полутень; I блик ( или свет); I и
IV полутени; V тень; VI рефлекс.
Проекция собственной тени условно
занимает 1/3 видимой поверхности, а
блик 1/6 часть этой поверхности