Похожие презентации:
Числовые алгоритмы
1.
НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТАпо дисциплине
«Основы алгоритмизации и программирования»
на тему:
«Числовые алгоритмы»
Выполнили:
Еремеев Никита
Соловьев Захар
Шевалдина Анастасия
Шиков Артем
Студенты 1 курса группы 1213
18.12.2024
2.
Актуальностьчисловых алгоритмов
3.
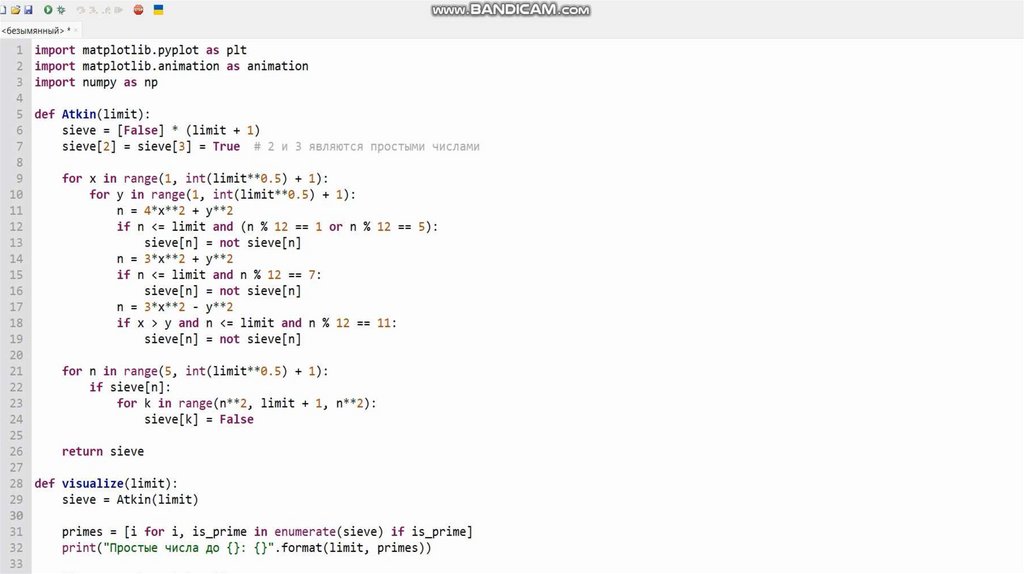
Распределение тем между участниками1.1-1.3, 2.5 – Шиков Артем
(Алгоритм Евклида, RSA, Решето Аткина,
Решето Сундарама);
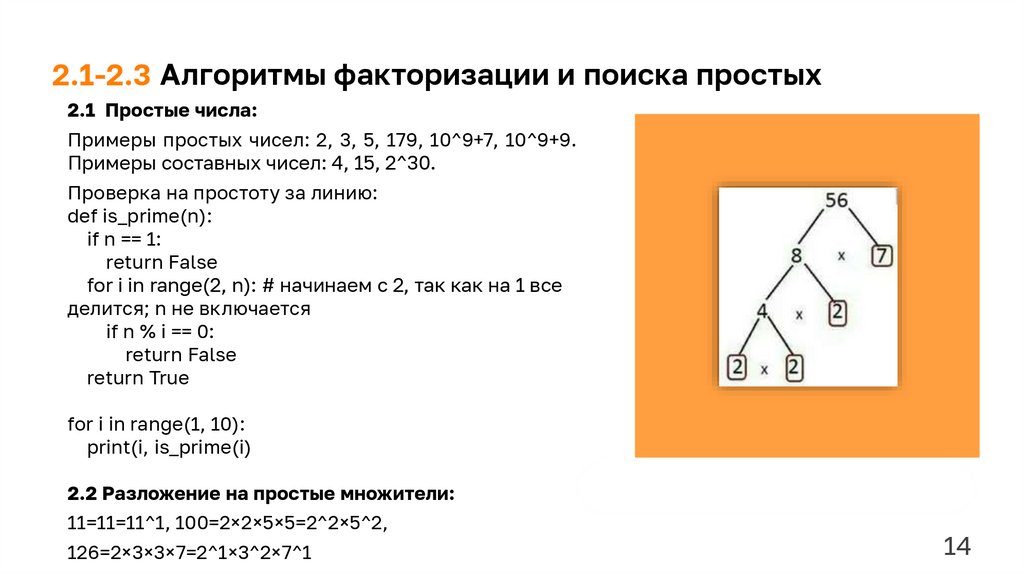
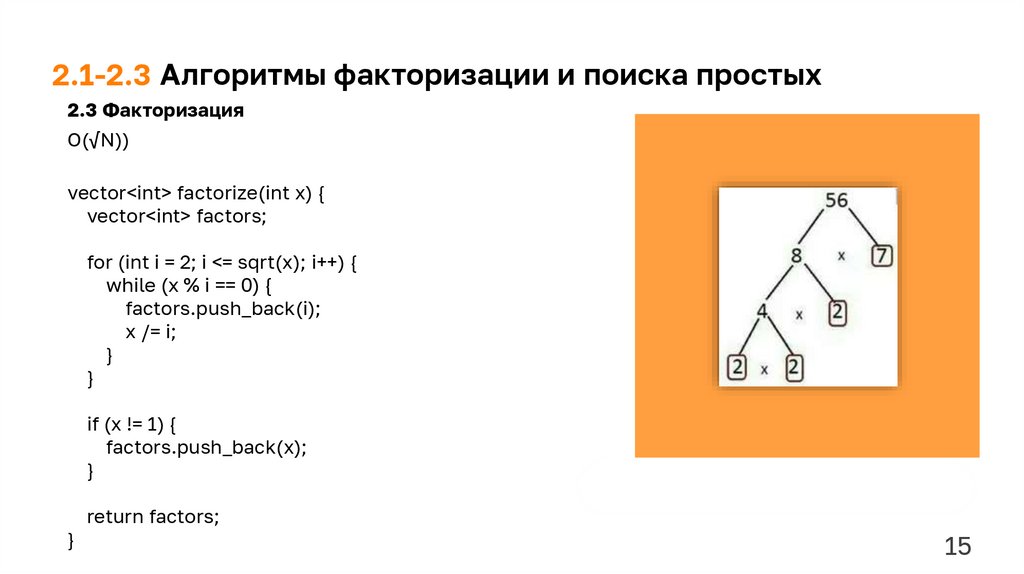
2.1-2.4, 2.6 – Еремеев Никита
(Алгоритмы
простых);
факторизации
и
поиска
3.1-3.6 – Шевалдина Анастасия
(Псевдослучайные числа);
4.1-4.4, 2.7-2.9 – Соловьев Захар
(Методы перемешивания, тест ЛюкаЛемера, числа Ферма, тест Пепина);
3
4.
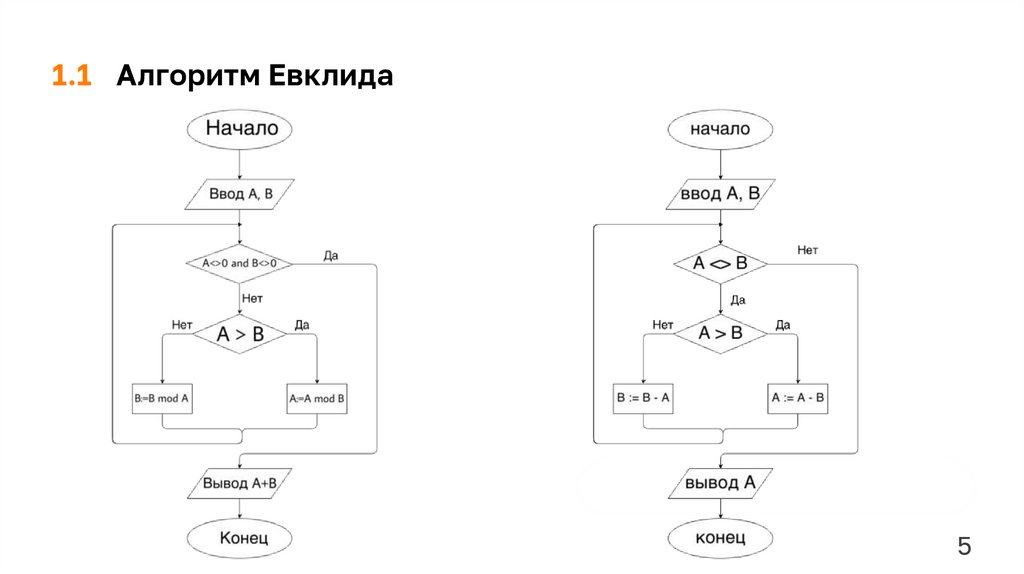
1.1 Алгоритм ЕвклидаДеление
Вычитание
a = input()
a = input()
b = input()
b = input()
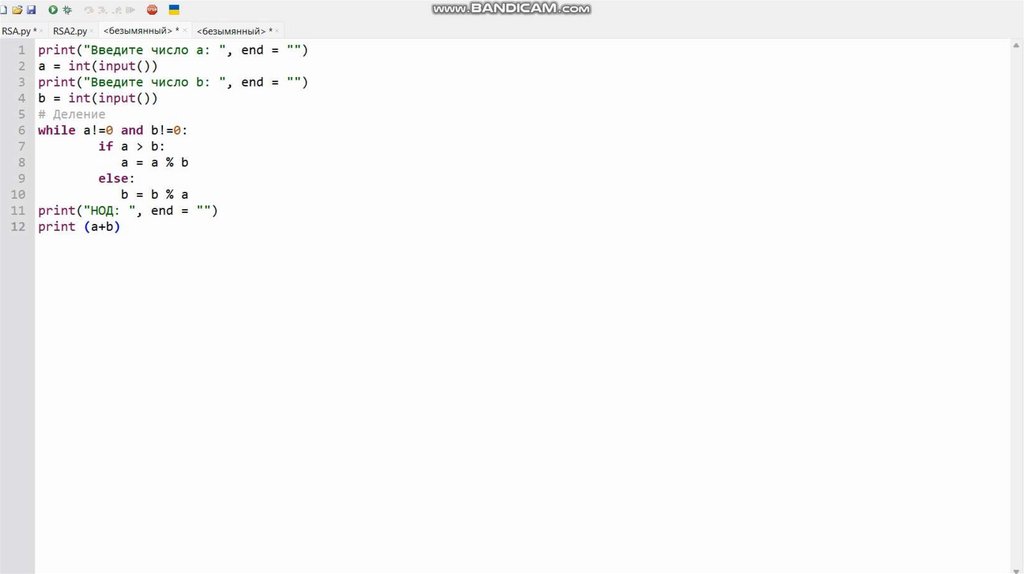
while a!=0 and b!=0:
while a != b:
if a > b:
a=a%b
else:
b=b%a
print (a+b)
if a > b:
a=a–b
else:
b=b–a
print(a)
4
5.
1.1 Алгоритм Евклида5
6.
1.1 Алгоритм Евклида6
7.
13см1 см
23см
7
8.
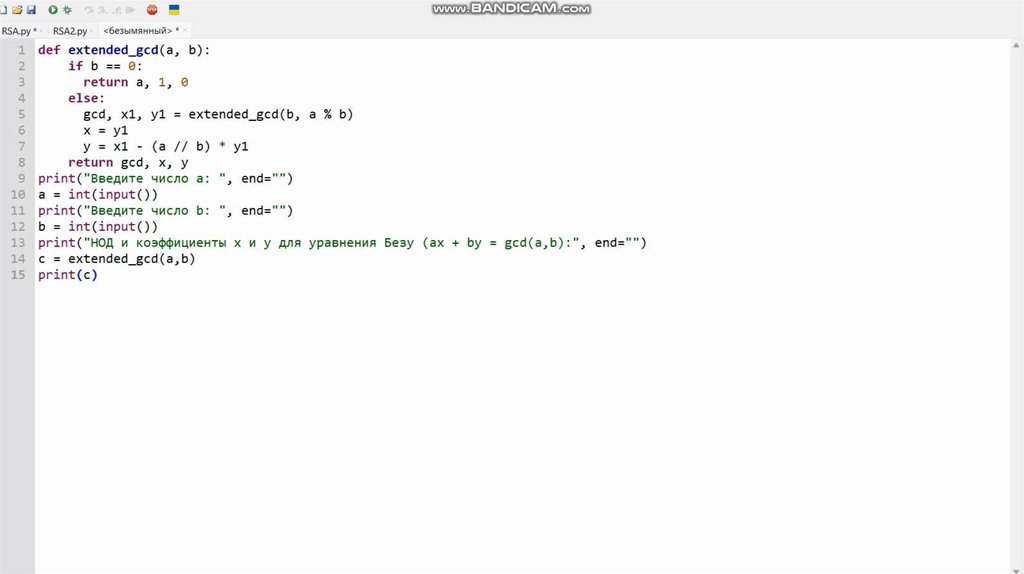
1.2 Расширенный алгоритм ЕвклидаУравнение: a*x + b*y = gcd(a,b)
Алгоритм нахождения:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
else:
gcd, x1, y1 = extended_gcd(b, a % b)
x = y1
y = x1 - (a // b) * y1
return gcd, x, y
8
9.
1.2 Расширенный алгоритм Евклида9
10.
1011.
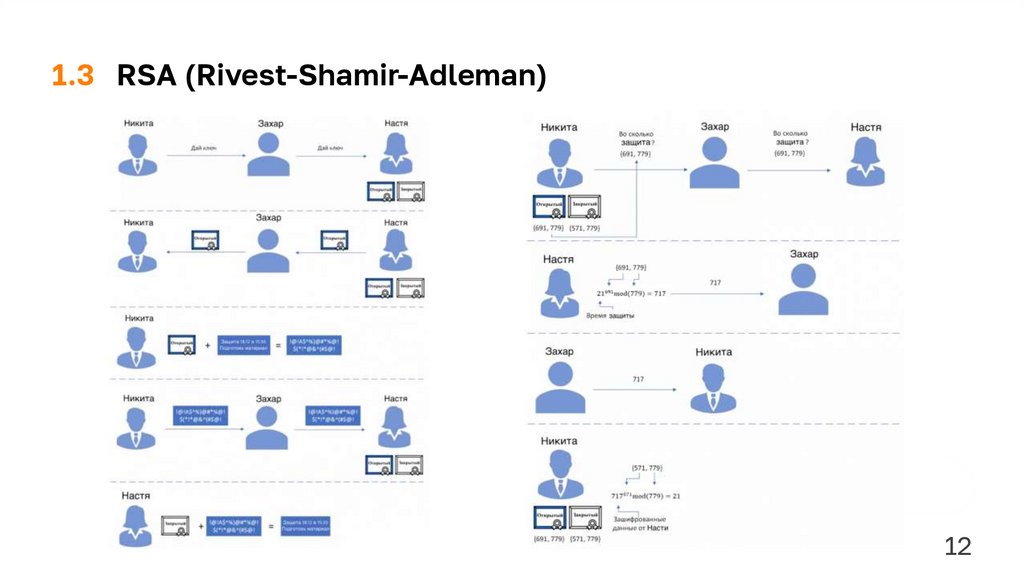
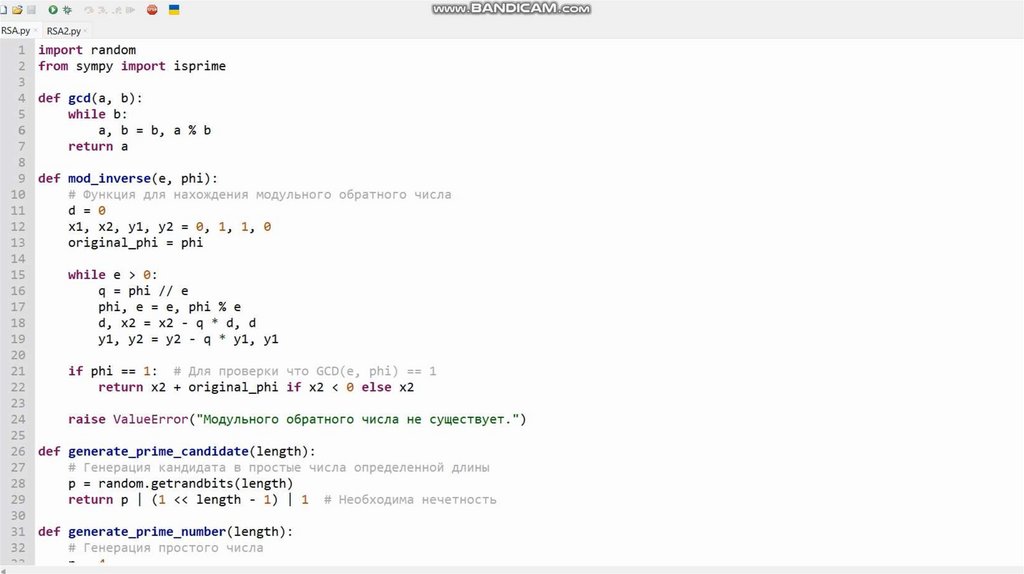
1.3 RSA (Rivest-Shamir-Adleman)1. Генерация ключей:
1) Выбираем два больших простых числа











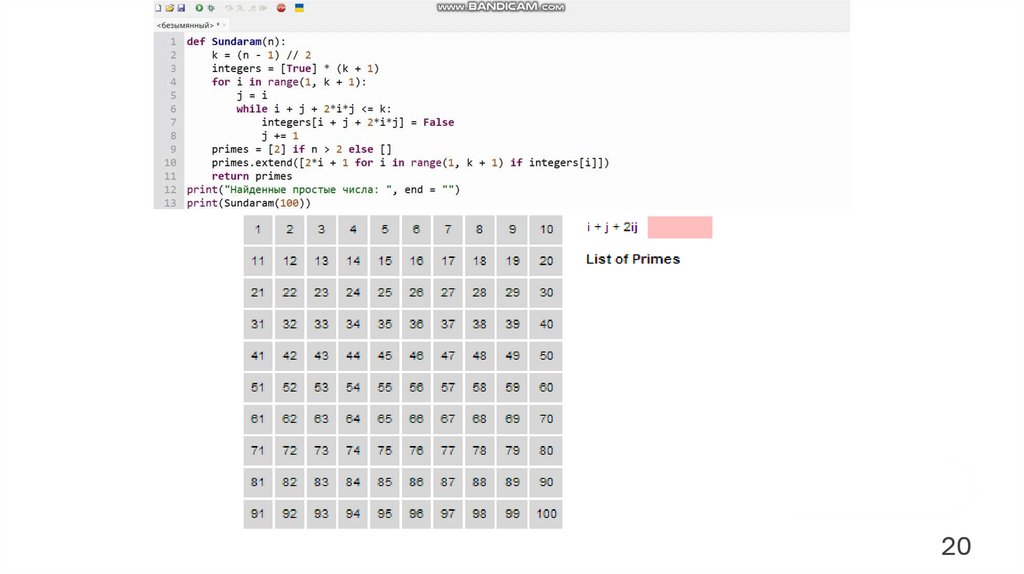









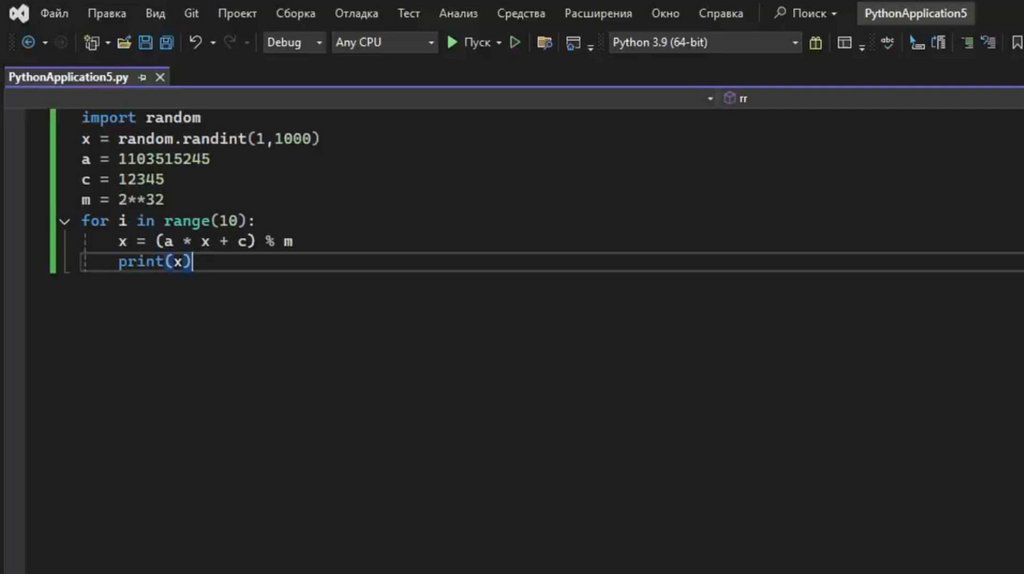








 Программирование
Программирование








