метрология. Погрешности. Виды погрешностей. Нормируемые метрологические характеристики средств измерений

1.

Погрешности.
Погрешности средств измерений.
Нормируемые метрологические
характеристики средств измерений.

2.

Δх = Ем + Еи + Ел
где εм - погрешность методическая; εи - погрешность инструментальная;
εл — погрешность личная.
Инструментальные погрешности измерения - погрешности из-за
несовершенства средств измерений.
Различают основную погрешность СИ - погрешность в условиях,
принятых за нормальные, и дополнительные погрешности, обусловленные отклонением влияющих величин от их нормальных значений.

3.

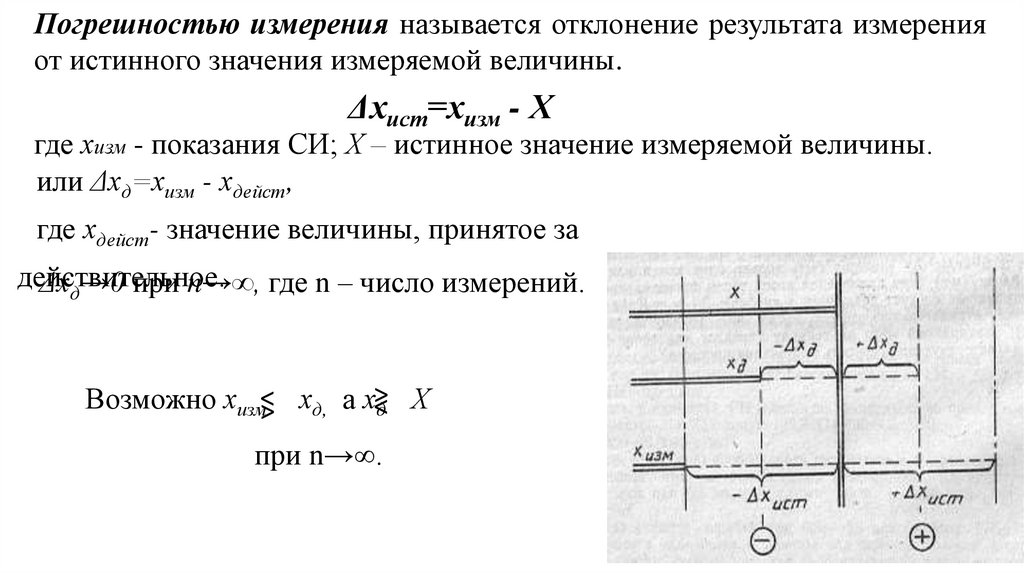
Погрешностью измерения называется отклонение результата измерения
от истинного значения измеряемой величины.
Δхист=хизм - Х
где хизм - показания СИ; Х – истинное значение измеряемой величины.
или Δхд=хизм - хдейст,
где хдейст- значение величины, принятое за
действительное.
Δхд→0 при n→∞, где n – число измерений.
Возможно хизм<> хд, а х><д Х
при n→∞.

4.

Классификация по форме числового выражения
Абсолютная погрешность - это алгебраическая разность между показаниями СИ и действительным значением.
Δх = хизм - Х
• одним числом: Δх = ±а;
• в виде линейной зависимости Δх = ± bх;
• в виде функции Δх =f(х) или графика, таблицы.

5.

Относительная погрешность СИ - это отношение абсолютной
погрешности к измеряемой величине, которое обычно выражают в
процентах:
ε=(Δx/x)*100 %
где Δx - абсолютная погрешность; х - показание СИ.
Приведенная погрешность - это отношение абсолютной погрешности к
некоторому нормирующему значению:
γ=(Δx/xN)*100 %
где хN - нормирующее значение.
Нормирующее значение - это условно принятое значение,
устанавливаемое стандартами на отдельные виды СИ (верхний предел
измерений, диапазон измерений, длина шкалы и т.д.).

6.

Классификация по их свойствам
Систематической называется составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных
измерениях одной и той же величины.
По характеру появления систематические погрешности подразделяют на
постоянные и переменные. Постоянные систематические погрешности
характеризуются тем, что в течение времени измерений их значение и знак
остаются неизменными.
Пример: погрешности гирь, а также погрешности градуировки шкал
измерительных приборов.

7.

Прогрессивными называют погрешности, которые в процессе измерений
постепенно убывают или возрастают. Одной из причин их возникновения
может быть постепенное падение напряжения источника питания
измерительного прибора.
Пример: износ контактирующих деталей средств измерения.
Периодическими называют погрешности, периодически изменяющие
значение и знак.
Пример: СИ с круговой шкалой, стрелка которых при измерении
совершает несколько оборотов (секундомеры, индикаторы часового типа).
Погрешности, изменяющиеся по сложному закону, могут быть выражены
в виде кривой или в виде формулы. Возникают вследствие совместного
действия нескольких систематических погрешностей.

8.

Случайной называется составляющая погрешности измерения, которая
при повторных измерениях одной и той же величины изменяется
случайным образом.
Для оценки случайной погрешности используется математический
аппарат теории вероятностей и математической статистики. Для
уменьшения влияния случайной погрешности на результат измерений
необходимо осуществить многократное измерение одного и того же
значения измеряемой величины с дальнейшей статистической обработкой
полученных результатов.

9.

Грубая погрешность измерения – погрешность измерения,
существенно превышающая ожидаемую при данных условиях.
Результаты измерений, содержащие грубые погрешности в
расчет не берутся. Основными причинами этих погрешностей
являются ошибки экспериментатора, резкое и неожиданное
изменение условий измерения, неисправность прибора и пр.
Для выявления
методы.
погрешности
используют
математические

10.

НОРМИРУЕМЫЕ МЕТРОЛОГИЧЕСКИЕ
ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
Характеристики свойств СИ, оказывающих влияние на результаты
измерений
и
их
точность,
называются
метрологическими
характеристиками СИ.
Метрологические характеристики СИ описывают путем указания
номинальных значений тех или иных характеристик и допустимых
отклонений от них, которые приводятся в нормативно-технической
документации на СИ.
Установление номинальных значений и границ допускаемых отклонений
реальных метрологических характеристик СИ от их значений называется
нормированием метрологических характеристик.

11.

Общим вопросам нормирования метрологических характеристик СИ
посвящен ГОСТ 8.009-84.
Характеристики, предназначенные для определения результата
измерений:
номинальная
статическая
характеристика
преобразования
(градуировочная характеристика) измерительного преобразователя, а
также измерительного прибора с неименованной шкалой;
значение однозначной или значения многозначной меры;
цена деления шкалы измерительного прибора или многозначной меры;
виды и параметры цифрового кода цифровых СИ.

12.

Характеристики погрешностей СИ - характеристики, которые
определяют систематическую и случайную составляющие погрешности.
К нормированным систематическим погрешностям относят значение
систематической составляющей, ее предельные значения и пределы.
К
нормируемым
случайным
погрешностям
относят
среднее
квадратическое значение случайной составляющей погрешности СИ σ[Δ].
Характеристики чувствительности СИ к влияющим величинам
показывают изменения значений метрологических характеристик СИ,
вызванных изменениями влияющих величин в установленных пределах.

13.

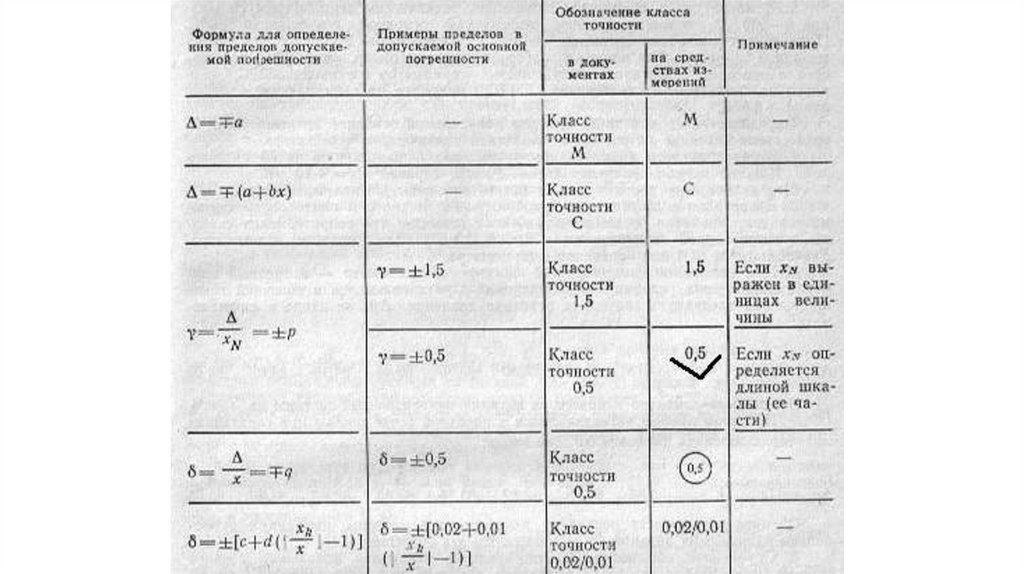
Класс точности СИ - обобщенная характеристика СИ, определяемая
пределами допустимых основных и дополнительных погрешностей, а
также другими свойствами СИ, влияющими на точность, значения
которых устанавливаются в стандартах отдельные СИ.
Метрологические характеристики, определяемые классами точности,
нормируют пределами допускаемых основной и дополнительной
погрешностей, выраженных в форме приведенных, относительных или
абсолютных погрешностей.

14.

Пределы допускаемой абсолютной погрешности устанавливают по формулам:
Δх = ±а
Δх = ±(а+b*x)
где Δх - пределы допускаемых абсолютной погрешности, выраженной в
единицах измеряемой величины на входе (выходе) или условно в делениях
шкалы; х - значение измеряемой величины или число делений,
отсчитанных на шкале; а, b — положительные числа, не зависящие от х.
Пределы допускаемой приведенной основной погрешности (в процентах)
устанавливают по формуле:
γ=(Δx/xn)*100=p
где хn — нормирующие значения, выраженные в тех единицах, что и Δх;
р - отвлеченное положительное число.

15.

Пределы допускаемой
процентах):
относительной
ε=(Δx/x)*100=±q;
основной
погрешности
(в
ε=±[c+d*(|xn/x|-1)],
если класс точности дается в виде дроби, например: 0,02/0,01.
В этих выражениях q - отвлеченное положительное число; хn - больший
(по модулю) из пределов измерений; с, d - положительные числа
соответственно числитель и знаменатель в обозначении класса точности.
Значения р, q, с, d выбирают из ряда [1,0; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0]*10n,
где n = 1, 0, -1, -2 и т.д.