Похожие презентации:
Оптимизация и оптимизационные модели. Линейное программирование. Методы оптимизации
1. Лекция 8_9_10
Оптимизация и оптимизационныемодели.
Линейное программирование.
Методы оптимизации
2.
Оптимизация - поиск наилучшего решения сучётом ограничений.
Для оптимизации ищется целевая функция.
Эта функция конструируется искусственно на
основе уравнений, описывающих объект
оптимизации.
Целевая
функция обычно имеет много
аргументов: φ=f (х1, х2, ..., хn).
3.
Чтобынайти оптимальное значение,
перебирают значение аргументов хi
пошагово до тех пор, пока значение φ
станет удовлетворять условиям оптимума.
Даже для количество аргументов не
более трёх перебор может потребовать
очень много времени.
4.
Поэтомуразработаны десятки методов
оптимизации.
Первый строгий математический метод
предложил в 1840 г. венгерский математик
Коши - МСС - метод скорейшего спуска.
При формулировании задач оптимизации
обычно стараются ее свести к поиску
минимума. МСС относится к классу
градиентных методов.
5.
Градиент- вектор, указывающий на
направление максимального возрастания
функции.
Антиградиент - вектор, указывающий на
направление максимального убывания
функции.
Чтобы повернуть вектор на 180 градусов,
достаточно изменить все знаки
у
градиентов на противоположные.
6.
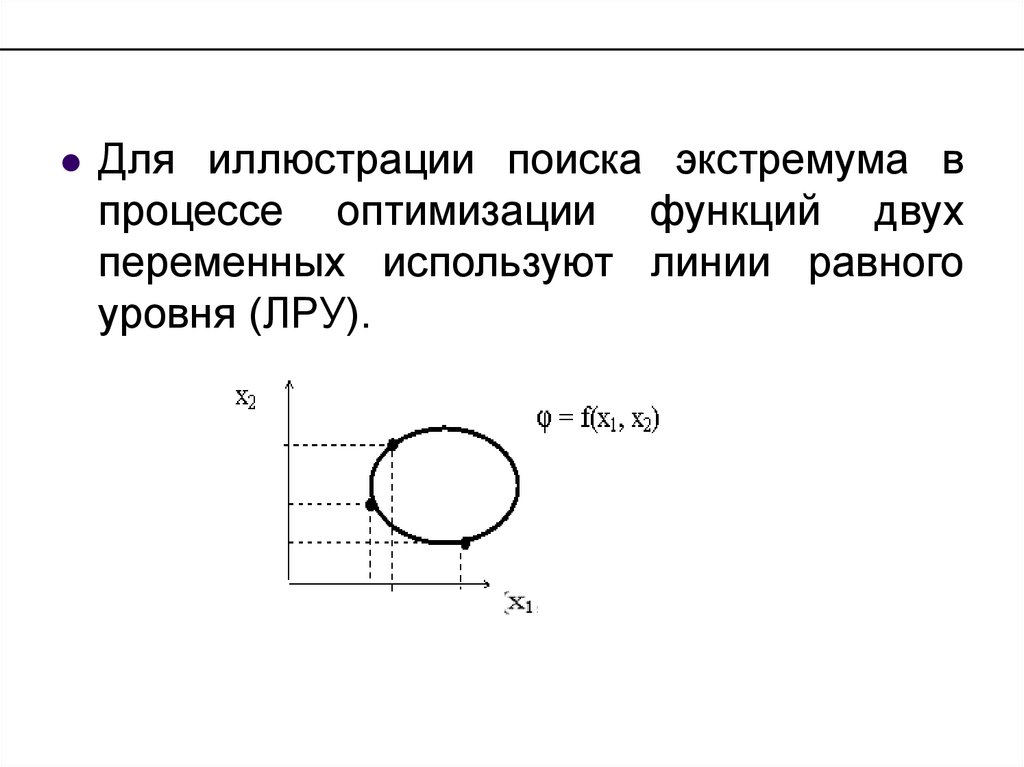
Дляиллюстрации поиска экстремума в
процессе оптимизации функций двух
переменных используют линии равного
уровня (ЛРУ).
7.
Если задаться постоянным значением φ итак подбирать значения хi чтобы значение
φ было равным заданному значению, то
геометрическое место точек φ составит
линию равного уровня.
8.
В зависимости от целевой функции линий равногоуровня могут характеризоваться следующими
географическими понятиями:
Долина - когда соседние линии равного уровня
изменяется очень слабо в широком диапазоне
аргументов.
Возвышенность - когда соседние линии равного
уровня представляют собой замкнутые линии и
значение φ возрастает от внешних линий к
внутренним.
9.
Впадина - когда соседние линии равного уровняпредставляют собой замкнутые линии, и значение φ
убывает от внешних линий к внутренним.
Седловина - локальный минимум, в центре которого
векторы указывают на возрастание функции, но
вскоре направление вектора резко изменяется вверх
или вниз.
10. Порядок поиска оптимума в МСС:
выбирается исходная точка в виде значенийпараметров целевой функции φ=f (х1, х2, ..., хn).
ищется градиент;
движемся в направлении антиградиента с заданным
шагом;
на каждом шаге проверяем выполнение условия
движения, оно такое:
φi < φi-1 ( текущее значение φ должно быть меньше
предыдущего).
если условие движения нарушается, то процесс
останавливается, иначе, движение продолжается;
при
нарушении условий движения уточняется
одномерный минимум и ищется новый градиент.
11.
Условия останова:а) значение φ меньше заданного;
б) разность значений соседних φ меньше
заданной;
в) количество шагов превышает допустимое.
если
после
останова
минимума
не
удовлетворяет требованиям, то либо ищется
другая исходная точка и процесс повторяется,
либо выбирается другой метод оптимизации.
12. Линейное программирование
- раздел математического программирования, в которомрешаются задачи отыскания max (min) линейной функции
L(х) при линейных ограничениях в виде равенств или
неравенств.
Условия существования задачи линейного
программирования:
Условия задачи должны быть выражены количественно,
через линейные соотношения.
Доступность математической формулировки.
Решение
математической
задачи
должно
иметь
экономический смысл.
13. Элементы математических моделей
Вопрос 1. Постановка задачи оптимизацииЭлементы математических моделей
Исходные данные
Детерминированные
Случайные
Искомые
переменные
Непрерывные
Дискретные
Зависимости
Линейные
Нелинейные
Распространенные задачи математического
программирования
ИД
Детерминированные
(постоянные)
Случайные
Переменные
Непрерывные
Зависимости Задачи оптимизации
Линейные
Линейного (ЛП)
Целочисленные
Целочисленного
программирования (ЦЧП)
Непрерывные,
Нелинейные
целочисленные
Нелинейного
программирования (НЛП)
Непрерывные
Стахостического
программирования (СТП)
Линейные
14. Общая задача линейного программирования в общем случае имеет вид:
Вопрос 1. Общая постановка задачи линейного программированияОбщая задача линейного программирования в общем случае имеет вид:
Задача:
необходимо найти такое
решение Х=(х1, х2, … хn),
удовлетворяющее
ограничениям и условию
неотрицательности, при
котором функция примет
определенное значение.
Стандартная задача – определение оптимального значения целевой
функции
(1.1) при выполнении условий (1.2), (1.4).
Каноническая задача - определение максимального значения
целевой функции (1.1) при выполнении условий (1.3), (1.4).
15.
Вопрос 1. Общая постановка задачи линейного программированияСтандартная форма задача:
Первая стандартная форма задача
ЛП – форма задачи ЛП, в которой
целевая функция требует нахождения
максимума, переменные
неотрицательные, а компоненты
произведения матрицы ограничений
и вектора переменных меньше либо
равны соответствующих компонент
вектора ограничений.
Вторая стандартная форма задача
ЛП – форма задачи ЛП, в которой
целевая функция требует нахождения
минимума, переменные
неотрицательные, а компоненты
произведения матрицы ограничений
и вектора переменных больше либо
равны соответствующих компонент
вектора ограничений.
16.
Вопрос 1. Общая постановка задачи линейного программированияКаноническая форма задача:
форма задачи ЛП, в которой целевая функция требует нахождения
минимума, переменные неотрицательные, а компоненты произведения
матрицы ограничений и вектора переменных равны соответствующим
компонентам вектора ограничений.
Во всех этих задачах функцию
называют целевой функцией.
Вектор
называют вектором коэффициентов
линейной формы, вектор - вектором ограничений.
Матрицу
называют матрицей коэффициентов.
17. Любая задача ЛП может быть сведена к канонической, стандартной или общей задаче.
Вопрос 1. Общая постановка задачи линейного программированияЛюбая задача ЛП может быть сведена к
канонической, стандартной или общей задаче.
Если целевая функция в задаче линейного программирования
задана в виде
то умножая её на (- 1), приведем её к виду
1.
2. Смена знака неравенства.
Если ограничение задано в виде
то его можно заменить эквивалентной системой двух неравенств
или такой же системой неравенств со знаками больше либо равно .
18.
Вопрос 1. Общая постановка задачи линейного программирования3. Превращение равенства в систему неравенств.
Если ограничение задано в виде
или такой же системой неравенств со знаками больше либо
равно .
Указанные выше приемы позволяют приводить задачи
линейного программирования к стандартной форме.
19.
Вопрос 1. Общая постановка задачи линейного программирования4. Превращение неравенств в равенства.
Пусть исходная форма задачи линейного программирования имеет вид
20.
Вопрос 1. Общая постановка задачи линейного программирования21.
Вопрос 1. Общая постановка задачи линейного программирования22.
Вопрос 1. Общая постановка задачи линейного программирования5. Ограничения на неотрицательность переменных.
23.
Если в задаче линейного программирования имеется только двепеременные, то ее можно решить графическим методом.
Рассмотрим задачу линейного программирования с двумя
переменными:
Здесь
есть произвольные числа. Задача может быть, как на
нахождение максимума (max), так и на нахождение минимума (min). В
системе ограничений могут присутствовать как знаки >=, так и знаки <=.
24. Графический метод
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Графический метод
Алгоритм решения
1.
Записывают уравнения граничных прямых.
2.
Строят графики граничных прямых на плоскости.
3.
Выделяют область решения неравенств системы.
4.
Строят многоугольник решений.
5.
Строят графики линейной формы.
6.
Определяют экстремальную точку многоугольника.
7.
Вычисляют значение линейной формы в полученной
точке.
25.
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
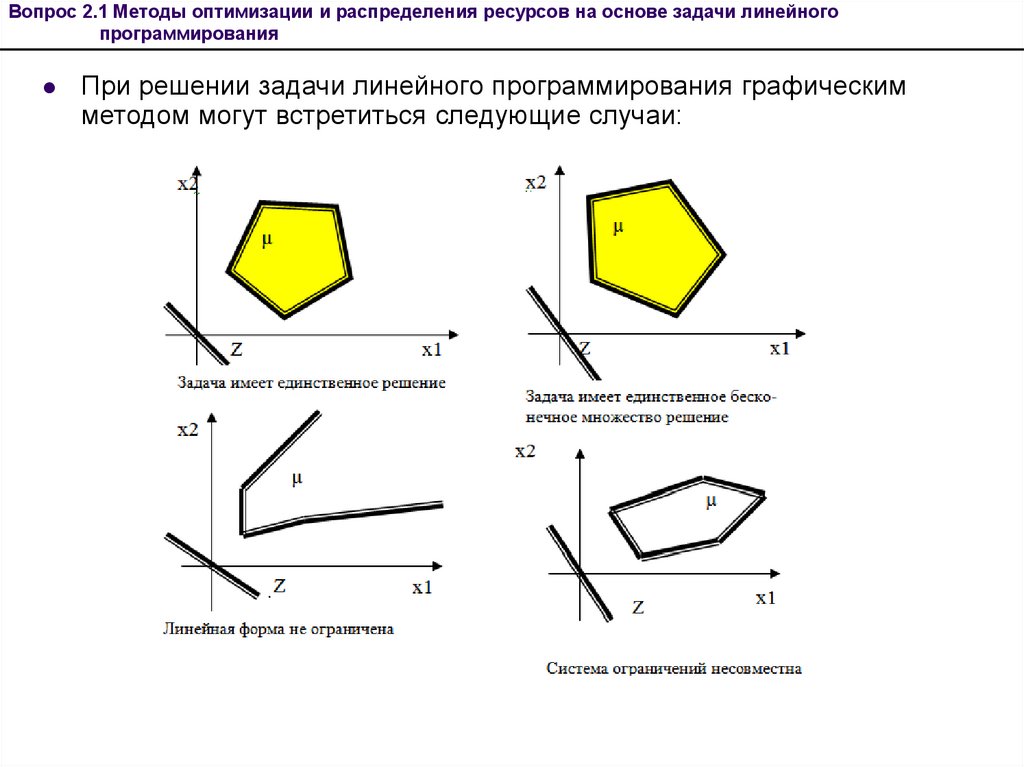
При решении задачи линейного программирования графическим
методом могут встретиться следующие случаи:
26. Графический метод
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Графический метод
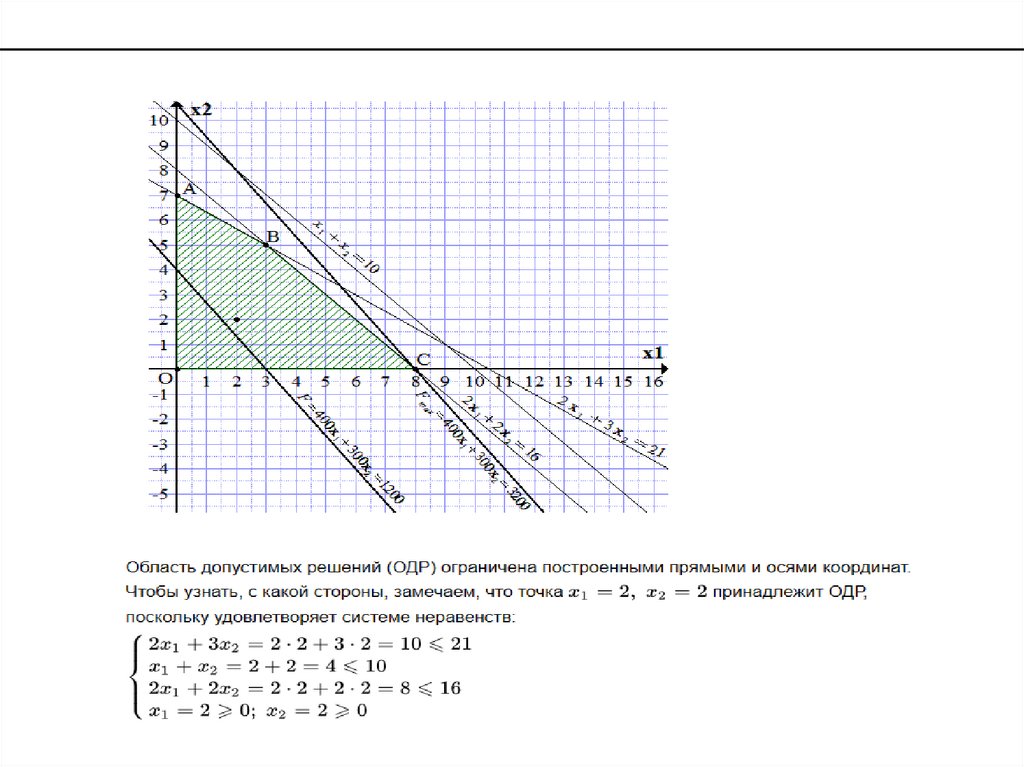
Пример.
Фирма выпускает платья двух моделей А и В. При
этом используется ткань трёх видов. На изготовление
одного платья модели А требуется 2 м ткани первого
вида, 1 м ткани второго вида, 2 м ткани третьего вида.
На изготовление одного платья модели В требуется 3 м
ткани первого вида, 1 м ткани второго вида, 2 м ткани
третьего вида. Запасы ткани первого вида составляют
21 м, второго вида - 10 м, третьего вида - 16 м. Выпуск
одного изделия типа А приносит доход 400 ден. ед.,
одного изделия типа В - 300 ден. ед.
Составить план производства, обеспечивающий
фирме наибольший доход. Задачу решить графическим
методом.
27.
28.
29.
30.
31. Симплексный метод -
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Симплексный метод это итерационный процесс, который начинается с одного
решения и в поисках наилучшего варианта движется по
угловым точкам области возможных решений до тех пор,
пока не достигнет оптимального значения.
Цель симплексного метода
- последовательное улучшение решения.
Элементы симплексного метода
1)
Способ определения какого-либо первоначального
допустимого базисного решения задачи;
2)
Правило перехода к лучшему (точнее, не худшему)
решению;
3)
Критерий проверки оптимальности найденного решения.
32.
Рассмотрим следующую задачу линейногопрограммирования
33.
Далее систему уравнений при помощи симплексныхпреобразований надо привести к единичному базису, т.е. найти
исходное опорное решение .
Для того, чтобы проверить будет ли это решение оптимальным,
надо составить оценочную строку ( Z строку) по следующему
правилу:
где
- искомый элемент Z строки;
- столбец коэффициентов целевой функции при базисных
переменных;
столбец коэффициентов при неизвестном ;
столбец свободных членов;
скалярное произведение указанных столбцов – векторов;
коэффициент целевой функции при неизвестном
34.
1.Для задачи на максимум.
Если в Z строке все элементы положительные Z j 0 , то найдено
оптимальное решение X max X 1 , Z max Z 0 . Если же в Z строке есть хоть
один отрицательный элемент, то найденное решение не оптимально. Есть
возможность его улучшения. Для этого среди отрицательных элементов
Z строки находим минимальный (например, Z p ). Столбец с номером p
становится разрешающим. Разрешающую строку выбираем по
симплексным преобразованиям (для этого в симплексной таблице
заводится последний столбец). В столбце с номером p в качестве
разрешающего элемента берется положительный элемент, если он один.
Если в этом столбце положительных элементов несколько, то берется тот
из них, для которого отношение свободных членов к этим
положительным элементам будет наименьшее. Если в столбце с номером
p вообще нет положительных элементов, то задача не имеет оптимального
решения и Z max . После того, как разрешающий элемент найден,
производим расчеты по методу Гаусса, включая и элементы Z строки.
Получаем новое опорное решение. После этого возвращаемся к началу
пункта 5.
35.
Для задачи на минимум. Если в Z строке все элементы Z j 0 , то найденооптимальное решение X min X 1 , Z min Z 0 . Если же в Z строке есть хоть
один положительный элемент, то найденное решение не оптимально. Для
улучшения решения среди положительных элементов Z строки находим
максимальный (например, Z q ). Столбец с номером q становится
разрешающим. Разрешающую строку ищем по симплексным
преобразованиям (смотреть задачу на максимум.) Если в столбце с номером q
нет положительных элементов, то задача не имеет оптимального решения и
Z min . После того, как разрешающий элемент выбран, выполняем
расчеты по методу Гаусса, включая и элементы Z строки, и получаем
новое опорное решение. Переходим к началу пункта 6. Процесс
продолжается до тех пор, пока не будет найдено оптимальное решение или
мы не убедимся, что его нет.
36.
1. Прежде чем решать задачу симплексным методом, надопроверить,
что
правые
части
системы
ограничений
неотрицательны, т.е.
Если это не так, то в соответствующем
ограничении меняем знак.
2. Далее исходную задачу надо записать в канонической форме,
если она не имеет такой формы записи. Для этого каждое
ограничение неравенство вида надо превратить в равенство
добавлением дополнительной неотрицательной (балансовой)
переменной, а каждое ограничение
неравенство вида
превратить в равенство вычитанием балансовой переменной.
Таким образом, все ограничения в задаче будут уравнения с
неотрицательными правыми частями.
37.
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Симплекс метод
Алгоритм решения
1.
Подготовительный
1)
Этап формализации задачи линейного программирования.
2)
Приведение в каноническую форму.
3)
Формирование первой симплекс таблицы
2.
Решение с помощью симплекс метода
1)
Поиск разрешающего столбца: mах абсолютное значение
элементов последней строки.
2)
Поиск разрешающей строки: min отношение элементов столбца
свободный член и положительных элементов разрешающего
столбца.
3)
Определяется генеральный элемент: на пересечении
разрешающего столбца разрешающей строки.
4)
Применяются формулы пересчета элементов таблицы:
5)
Проверка на оптимальность: (на max) отсутствие отрицательных
элементов в последней строке, (на min) вывод из базиса
искусственных переменных или в F и в Z – нули, или
отрицательные.
3.
Интерпретация результата
38.
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Симплекс метод
Алгоритм решения
1.
Подготовительный
4) Применяются формулы пересчета элементов таблицы:
1)
Этап формализации задачи линейного программирования.
2)
Поделим
разрешающую
строку
Приведение
в каноническую
форму.на генеральный элемент.
Формирование
первой
симплексэлементов
таблицы строк в следующей
3)
Для
заполнения
оставшихся
2.
Решение
с помощью
симплекс
метода воспользоваться
симплексной
таблице
необходимо
1)
Поиск разрешающего столбца: mах абсолютное значение
формулой:
элементов последней строки.
х2)
хij1 - (PC
),
разрешающей
min отношение элементов столбца
ij2 = Поиск
j1 * РГi1/ ГЭстроки:
член и положительных
элементов разрешающего
где хij1свободный
–
соответствующий
элемент
предыдущей
симплексной
столбца.
таблицы;
3)
Определяется генеральный элемент: на пересечении
столбца
разрешающей
строки. строки;
PCj – разрешающего
соответствующий
элемент
разрешающей
4)
Применяются формулы пересчета элементов таблицы:
РГi – соответствующий элемент разрешающего столбца (графы);
5)
Проверка на оптимальность: (на max) отсутствие отрицательных
элементов в последней
(на min) вывод из базиса
ГЭ – генеральный
элементстроке,
таблицы.
искусственных переменных или в F и в Z – нули, или
отрицательные.
3.
Интерпретация результата
39. Симплекс метод
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
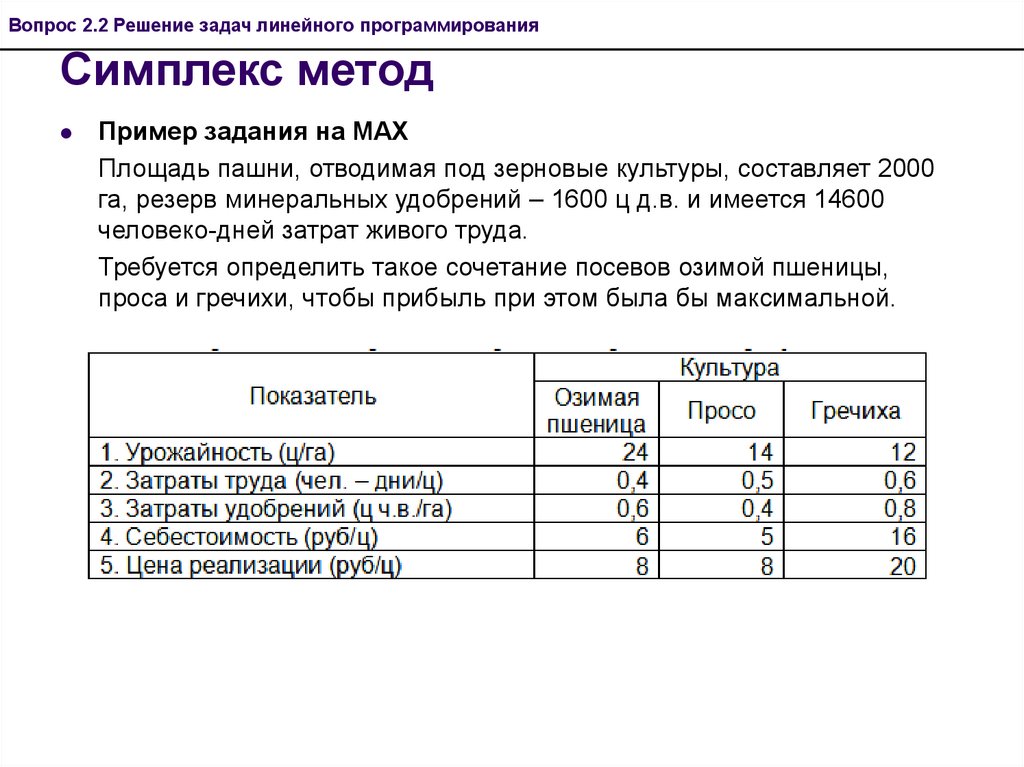
Пример задания на MAX
Площадь пашни, отводимая под зерновые культуры, составляет 2000
га, резерв минеральных удобрений – 1600 ц д.в. и имеется 14600
человеко-дней затрат живого труда.
Требуется определить такое сочетание посевов озимой пшеницы,
проса и гречихи, чтобы прибыль при этом была бы максимальной.
40.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
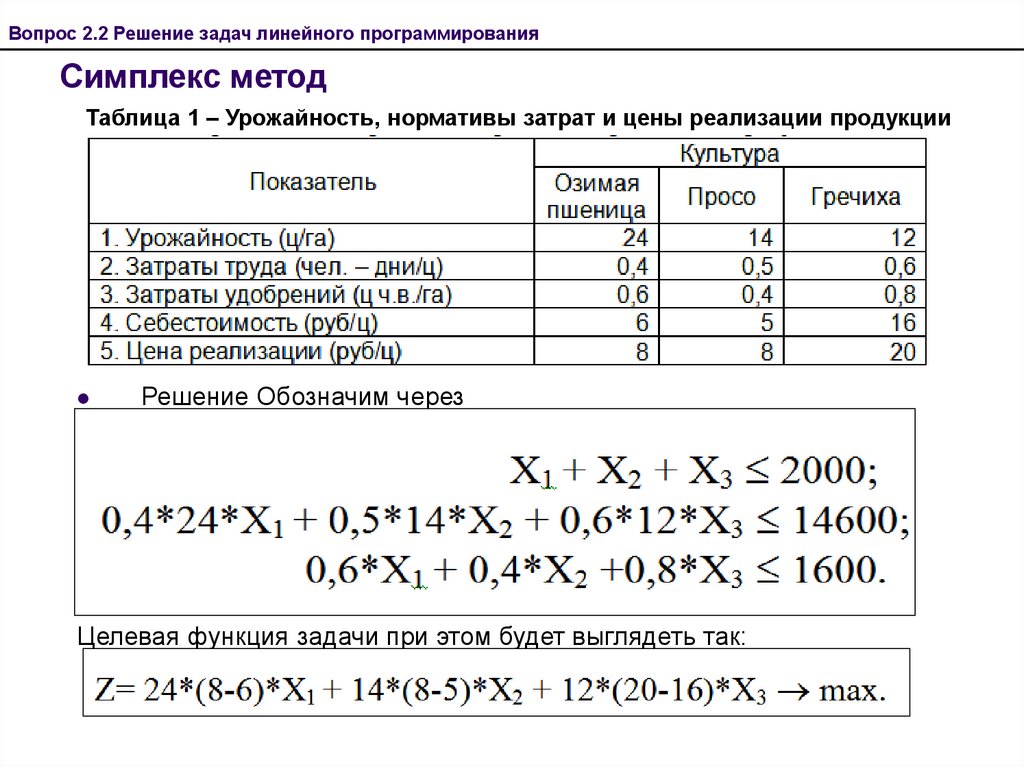
Таблица 1 – Урожайность, нормативы затрат и цены реализации продукции
Решение Обозначим через
Х1 –площадь посева озимой пшеницы (га),
Х2 – площадь посева проса (га),
Х3 – площадь посева гречихи(га).
Тогда получим систему ограничений:
Целевая функция задачи при этом будет выглядеть так:
41.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
После упрощения получим следующую систему неравенств:
Введем дополнительные переменные: Х4, Х5, Х6, преобразующие
неравенства в уравнения. Тогда система (I) без целевой функции
запишется так (II):
42.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
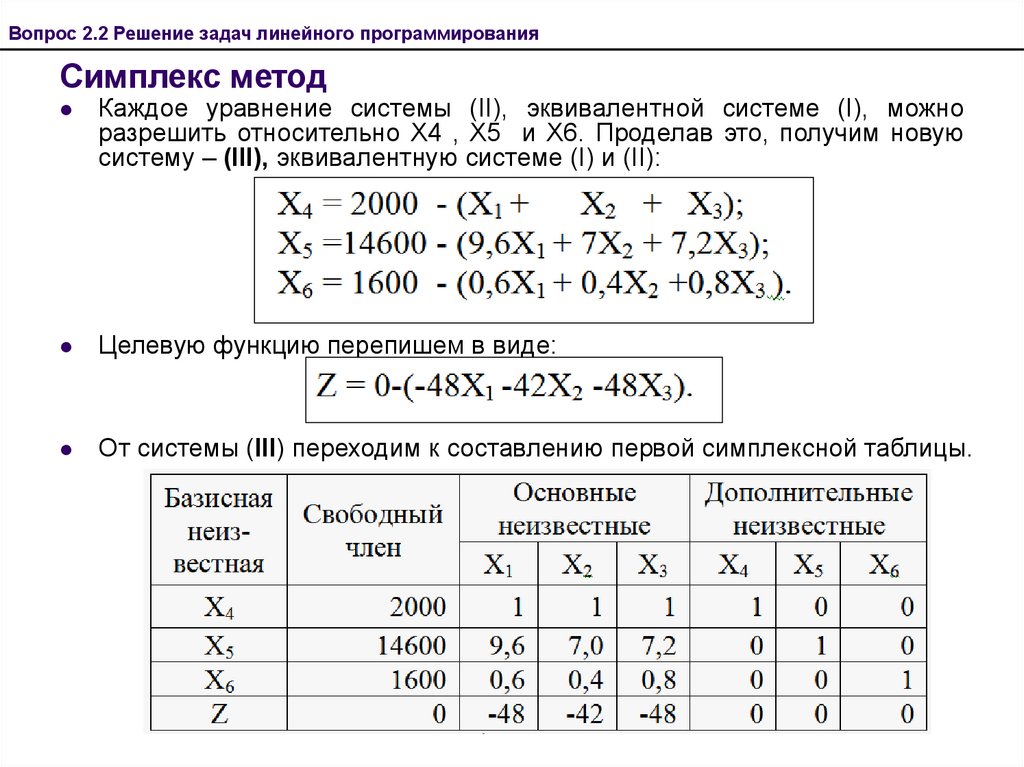
Каждое уравнение системы (II), эквивалентной системе (I), можно
разрешить относительно Х4 , Х5 и Х6. Проделав это, получим новую
систему – (III), эквивалентную системе (I) и (II):
Целевую функцию перепишем в виде:
От системы (III) переходим к составлению первой симплексной таблицы.
43.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
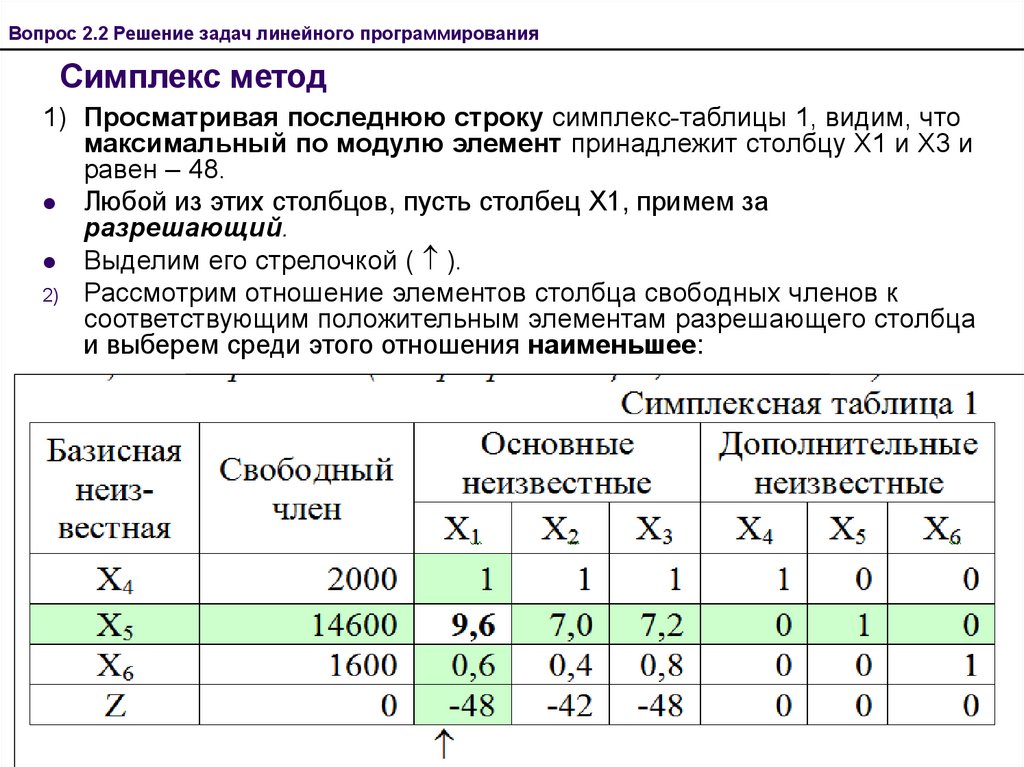
1) Просматривая последнюю строку симплекс-таблицы 1, видим, что
максимальный по модулю элемент принадлежит столбцу Х1 и Х3 и
равен – 48.
Любой из этих столбцов, пусть столбец Х1, примем за
разрешающий.
Выделим его стрелочкой ( ).
2) Рассмотрим отношение элементов столбца свободных членов к
соответствующим положительным элементам разрешающего столбца
и выберем среди этого отношения наименьшее:
Минимальное отношение, равное 1520,8 соответствует строке,
содержащей Х5.
Эта строка будет разрешающей.
Элемент 9,6 – генеральный (или разрешающий, или ключевой).
44.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
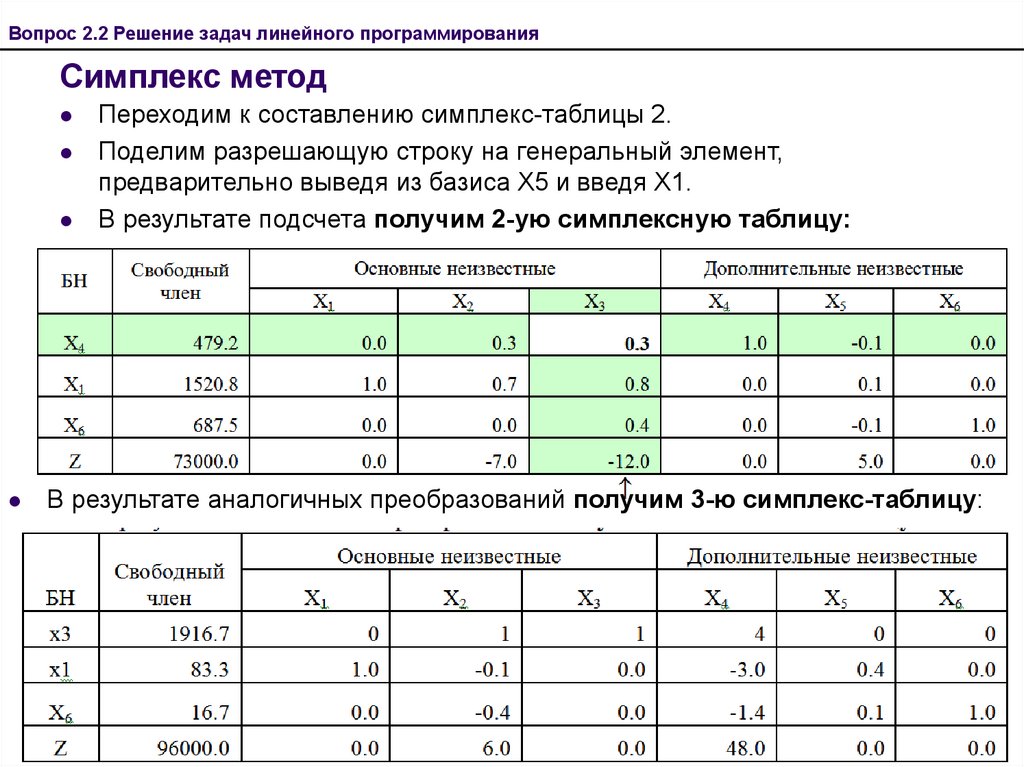
Переходим к составлению симплекс-таблицы 2.
Поделим разрешающую строку на генеральный элемент,
предварительно выведя из базиса Х5 и введя Х1.
В результате подсчета получим 2-ую симплексную таблицу:
В результате аналогичных преобразований получим 3-ю симплекс-таблицу:
45.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
Пример задания на MIN
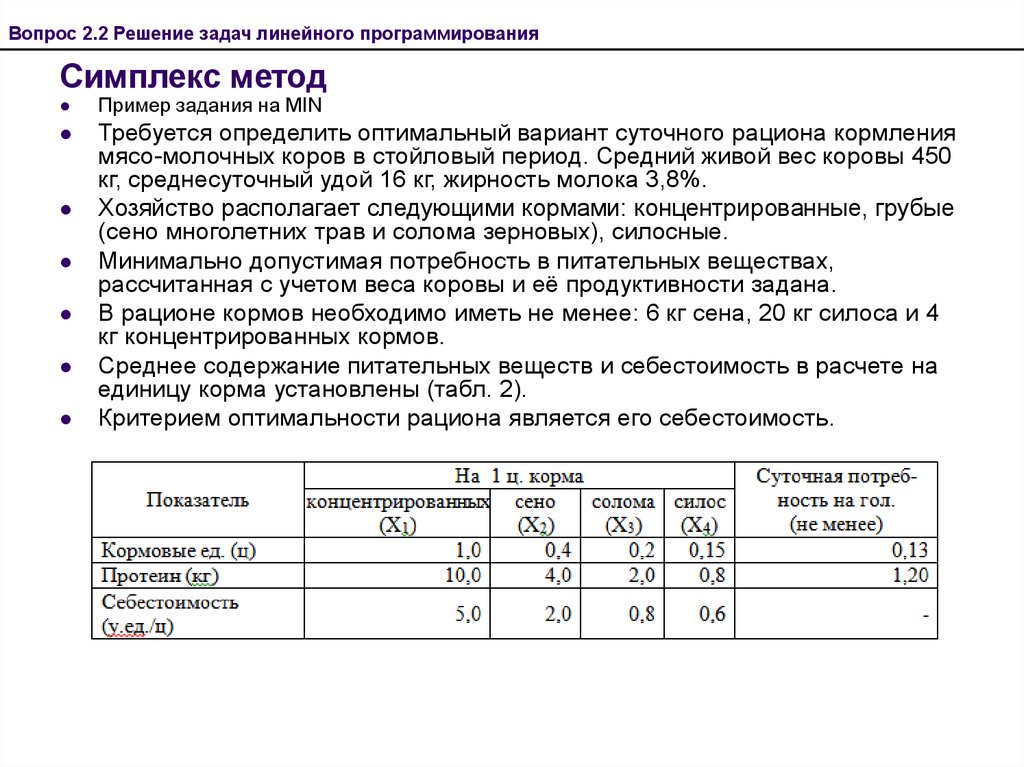
Требуется определить оптимальный вариант суточного рациона кормления
мясо-молочных коров в стойловый период. Средний живой вес коровы 450
кг, среднесуточный удой 16 кг, жирность молока 3,8%.
Хозяйство располагает следующими кормами: концентрированные, грубые
(сено многолетних трав и солома зерновых), силосные.
Минимально допустимая потребность в питательных веществах,
рассчитанная с учетом веса коровы и её продуктивности задана.
В рационе кормов необходимо иметь не менее: 6 кг сена, 20 кг силоса и 4
кг концентрированных кормов.
Среднее содержание питательных веществ и себестоимость в расчете на
единицу корма установлены (табл. 2).
Критерием оптимальности рациона является его себестоимость.
46.
Вопрос 2.2 Решение задач линейного программированияСимплекс метод
Решение. С учетом принятых условных обозначений (см. табл.2)
модель, описывающая минимальную стоимость рациона (Z) запишется
так:
найти Z = 5*Х1 + 2*Х2 + 0,8*Х3 + 0,6 * Х4 MIN
при условии (I):
Х1 + 0,4Х2 + 0,2*Х3 + 0,15 * Х4 0,13;
10*Х1 + 4*Х2 + 2*Х3 + 0,8 * Х4 1,20;
Х1 0,04;
Х2 0,06;
Х4 0,20.
Преобразуя неравенства системы (I) в уравнения путем введения
дополнительных неизвестных Х5, Х6 , Х7 , Х8 и Х9 получим (II):
Х1 + 0,4Х2 + 0,2*Х3 + 0,15 * Х4 - Х5 = 0,13;
10*Х1 + 4*Х2 + 2*Х3 + 0,8 * Х4 - Х6 = 1,20;
Х1 - Х7 = 0,04;
Х2 - Х8 = 0,06;
Х4 – Х9 =0,20;
Z = 5*Х1 + 2*Х2 + 0,8*Х3 + 0,6 * Х4 MIN.
47.
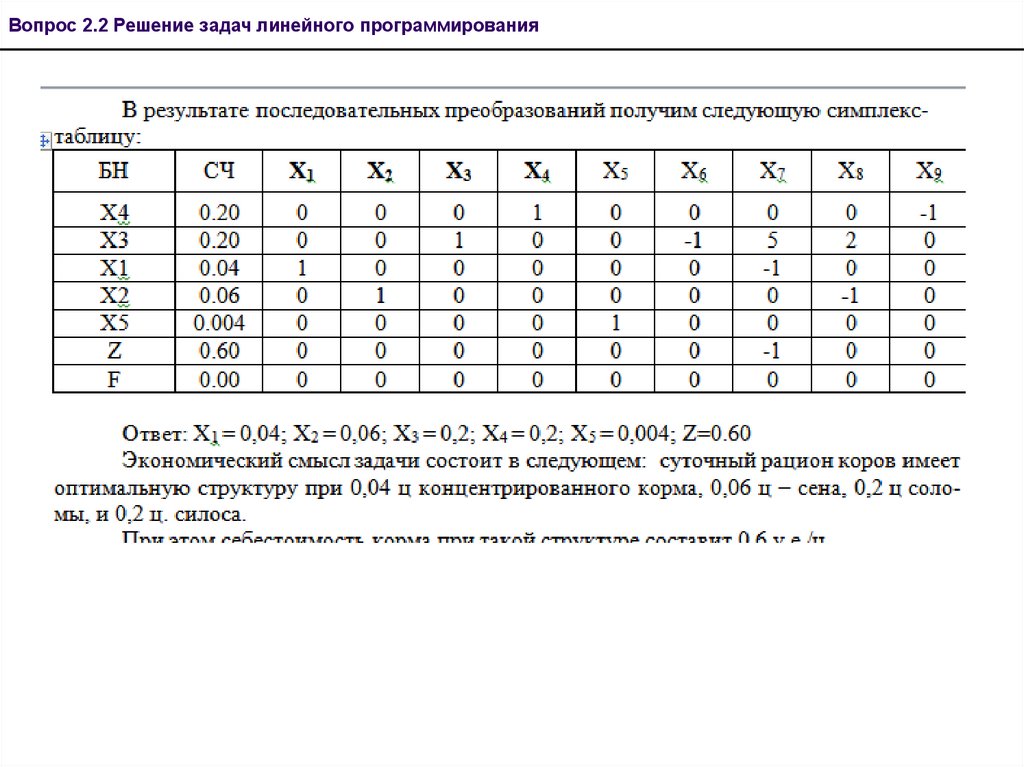
Вопрос 2.2 Решение задач линейного программированияВведем в левую часть каждого уравнения системы (II) по одному
искусственному неизвестному (Уi) и получим тогда (III):
Х1 + 0,4Х2 + 0,2*Х3 + 0,15 * Х4 - Х5 + У1 = 0,13;
10*Х1 + 4*Х2 + 2*Х3 + 0,8 * Х4 - Х6 + У2 = 1,20;
Х1 - Х7 + У3 = 0,04;
Х2 - Х8 + У4 = 0,06;
Х4 – Х9 + У5 =0,20;
Z = 5*Х1 + 2*Х2 + 0,8*Х3 + 0,6 * Х4 MIN.
При этом У1, У2, У3, У4 и У5 должны быть равны нулю.
48.
Вопрос 2.2 Решение задач линейного программированияПосле этого разрешаем уравнения системы (III) относительно
искусственных неизвестных, преобразуем функцию Z до вида:
Z=0-(-5*Х1 - 2*Х2 - 0,8*Х3 - 0,6 * Х4),
а также минимизируем функцию F=( У1 + У2 + У3 + У4 + У5) , заранее
зная, что ее значение должно быть равно нулю (складываем по
столбцам).
Получим новую систему (IV):
У1 = 0,13 – ( Х1 + 0,4Х2 + 0,2*Х3 + 0,15 * Х4 – Х5 );
У2 = 1,20 – (10*Х1 + 4*Х2 + 2*Х3 + 0,8 * Х4 – Х6 );
У3 = 0,04 – ( Х1 – Х7 );
У4 = 0,06 – ( Х2 – Х8 );
У5 = 0,20 – ( Х4 – Х9 );
Z =0
– ( - 5*Х1 - 2*Х2 - 0,8*Х3 - 0,6 * Х4);
F = 1,63 – (12*Х1 + 5,4*Х2 + 2,2*Х3 + 1,95* Х4- Х5 – Х6– Х7– Х8– Х9).
49.
Вопрос 2.2 Решение задач линейного программирования50. Постановка задачи и её математическая модель
Транспортная задачаПостановка задачи и её математическая модель
Некоторый однородный продукт, сосредоточенный у m
поставщиков Аi в количестве ai (i=1,2,…,m) единиц
соответственно, необходимо доставить n потребителям bj
(j=1, 2, …, n) единиц.
Известна стоимость Сij перевозки единиц груза от i-го
поставщика к j-му потребителю.
Необходимо составить план перевозок, позволяющий вывезти
все грузы, полностью удовлетворив потребности, и имеющий
минимальную стоимость.
Решение
Обозначим через хij количество единиц груза, запланированных
к перевозке от i-го поставщика к j-му потребителю.
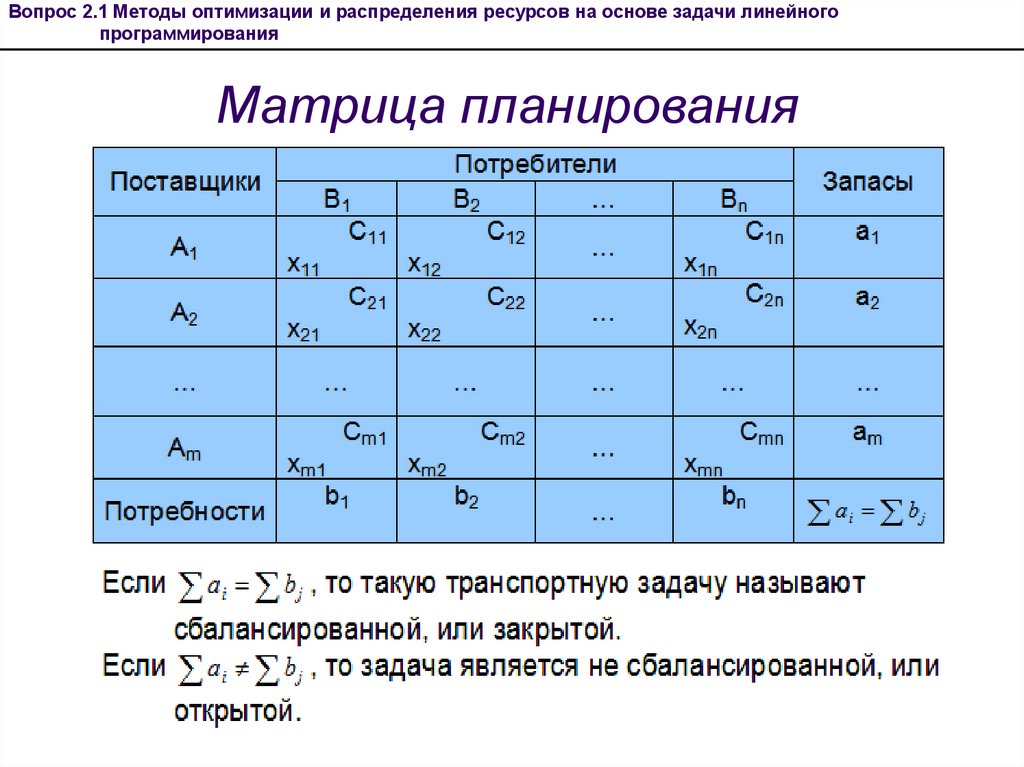
Тогда условие задачи можно записать в виде таблицы – матрицы
планирования.
51. Матрица планирования
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Матрица планирования
52. Алгоритм приведения открытой модели к закрытой
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Алгоритм приведения открытой модели к закрытой
Стоимость (С)перевозки единицы груза полагают равными нулю
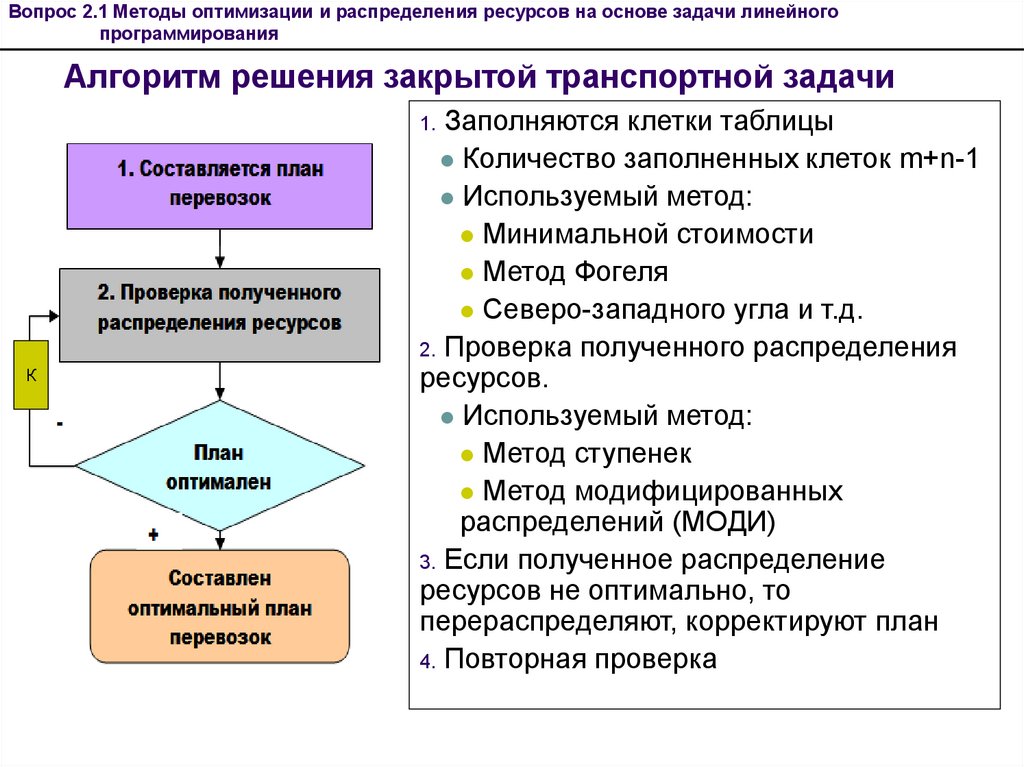
53. Алгоритм решения закрытой транспортной задачи
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Алгоритм решения закрытой транспортной задачи
1. Заполняются клетки таблицы
Количество заполненных клеток m+n-1
Используемый метод:
Минимальной стоимости
Метод Фогеля
Северо-западного угла и т.д.
2. Проверка полученного распределения
К
ресурсов.
Используемый метод:
Метод ступенек
Метод модифицированных
распределений (МОДИ)
3. Если полученное распределение
ресурсов не оптимально, то
перераспределяют, корректируют план
4. Повторная проверка
54. Задачи о назначениях и распределении работ
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Задачи о назначениях и распределении работ
- это частный случай транспортной задачи, в которой
приняты следующие допущения:
Число поставщиков m равно числу потребителей n;
Запасы каждого поставщика ai=1;
Заявки каждого потребителя bi=1;
Каждый поставщик может поставлять грузы только
одному потребителю;
Каждый покупатель может получить грузы только от
одного поставщика.
Методы решения
Методы линейного программирования,
Алгоритм решения транспортной задачи
Венгерский метод
55. Постановка задачи о назначениях и распределении работ
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Постановка задачи о назначениях и распределении работ
Если через Q обозначить ресурсы, а через R – результат их
применения, то при заданных зависимостях результата и
потребных ресурсов от количества выпускаемой продукции
R=f(xj); Q=f(xj) две постановки задачи распределения ресурсов
можно записать следующим образом:
Для первой постановки: F1 =R max; Q<Q3
Для второй постановки: F2 =Q min; R>R3
Значит поставить ее возможно в одном из двух вариантов:
Либо максимизировать производство
Либор минимизировать ресурсы
56. Алгоритм венгерского метода
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Алгоритм венгерского метода
1 этап:
1.
2.
3.
4.
Формализация проблемы в виде транспортной таблицы
В каждой строке таблицы найти наименьший элемент и вычесть
его из всех элементов данной строки
Повторить ту же процедуру для столбцов
Задачей является распределение всех подлежащих назначению
единиц в клетки с нулевой стоимостью. Оптимальное значение
целевой функции в этом случае равно нулю.
57. Алгоритм венгерского метода
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Алгоритм венгерского метода
2 этап:
1. Найти строку, содержащую только одно нулевое значение, в его
клетку помещается один элемент (0 обводится квадратиком).
Если такие строки отсутствуют, допустимо начать с любой строки.
2. Зачеркнуть оставшиеся нулевые значения данного столбца
3. Повторять пп.1-2, пока продолжение указанной процедуры
окажется невозможным
4. Если окажется, что имеется несколько нулей, которым не
соответствуют назначения, и которые остались незачеркнутыми,
необходимо:
5. Найти столбец, содержащий только одно нулевое значение, в его
клетку помещается один элемент.
6. Зачеркнуть оставшиеся нули в данной строке
7. Повторять пп.4-5, пока продолжение указанной процедуры
окажется невозможным
Если выяснится, что таблица содержит неучтенные нули - повторить
пп. 1-6
Если решение является допустимым, оно оптимально. Если нет перейти к этапу 3.
58. Алгоритм венгерского метода
Вопрос 2.1 Методы оптимизации и распределения ресурсов на основе задачи линейногопрограммирования
Алгоритм венгерского метода
3 этап: (Если решение является недопустимым)
1. Провести минимальное количество прямых через столбцы и
строки матрицы таким образом, чтобы они проходили через все
нули, содержащиеся в таблице
2. Найти наименьший из элементов, через которые не проходит ни
одна прямая
3. Вычесть его из всех элементов, через которые не проходят
прямые
4. Прибавить его ко всем элементам, лежащим на пересечении
прямых
5. Элементы, через которые проходит только одна прямая,
оставить неизменными
6. В результате в таблице появится как минимум одно новое
нулевое значение. Вернуться к этапу 2 и повторить решение
заново.
59. Транспортная задача. Метод потенциалов
Вопрос 2.2 Решение задач линейного программированияТранспортная задача. Метод потенциалов
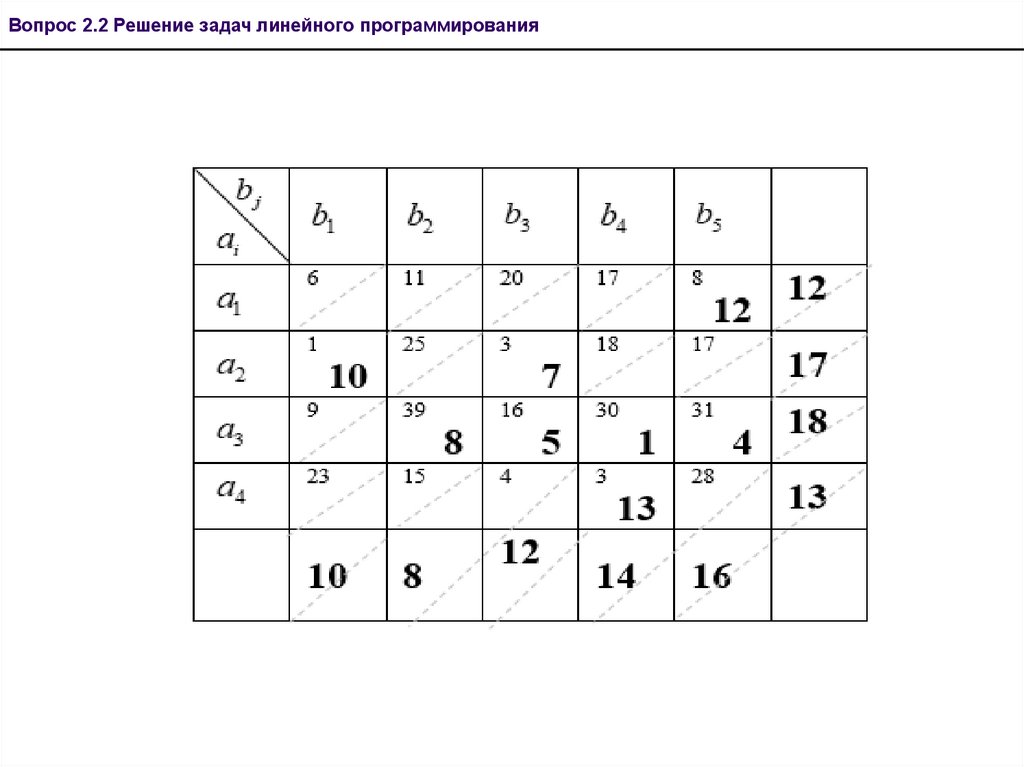
60. Транспортная задача. Метод потенциалов
Вопрос 2.2 Решение задач линейного программированияТранспортная задача. Метод потенциалов
Решение
61.
Вопрос 2.2 Решение задач линейного программирования62.
Вопрос 2.2 Решение задач линейного программирования63.
64.
65.
66.
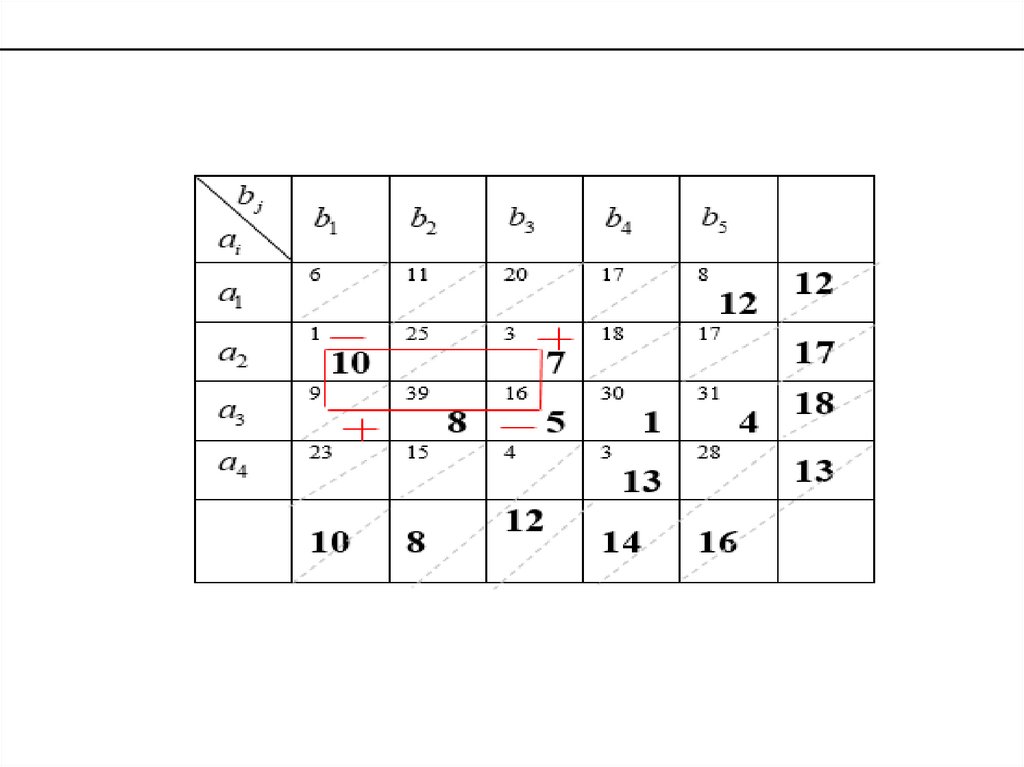
Строим в таблице цикл пересчета относительно клетки (3,1). Он пойдетследующим образом (3,1) (2,1) (2,3) (3,3).
Расставляем знаки «+» и «–» в вершинах цикла, начиная с клетки (3,1). В «–»
клетках ищем минимальный груз min( 10,5) 5 .Этот груз 5 прибавляем к
грузам в «+» клетках и отнимаем от грузов в «–» клетках. Получаем новый
план перевозок:


























































 Математика
Математика








