Машина Алана Тьюринга

1.

Машина Алана Тьюринга
Работу выполнила:
ученица 11 класса
Васильева Ксения

2.

Алан Тьюринг
Алан Мэтисон Тьюринг
(23 июня 1912 — 7 июня 1954)
— английский математик, логик,
криптограф, оказавший существенное
влияние на развитие информатики.

3.

Внешний вид
машины Тьюринга
Внешний вид машины Тьюринга включает бесконечную
ленту, разделённую на ячейки, в каждую из которых может
быть записана только одна буква. Пустая клетка содержит
особый пустой символ, который заполняет все клетки ленты,
кроме тех из них, на которых записаны входные данные.
Управляющее устройство (каретка) располагается над
некоторой ячейкой ленты и воспринимает символ,
записанный в ней. В одном такте работы каретка сдвигается
на одну ячейку (вправо, влево) или остаётся на месте.
Программа для машины Тьюринга записывается в виде
таблицы, где первые столбец и строка содержат буквы
внешнего алфавита и возможные внутренние состояния
автомата (внутренний алфавит). Содержимое таблицы
представляет собой команды для машины Тьюринга.

4.

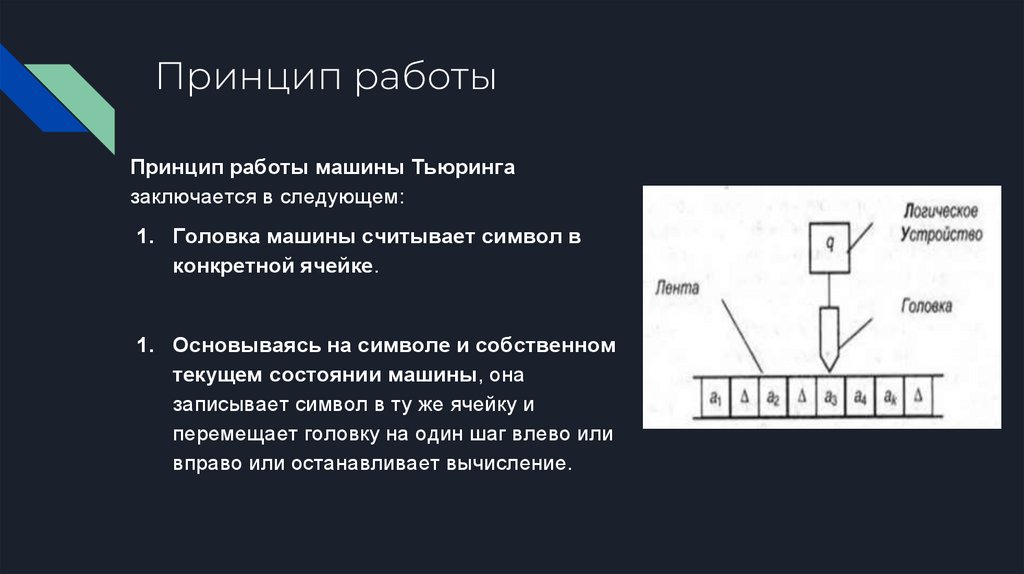
Принцип работы
Принцип работы машины Тьюринга
заключается в следующем:
1. Головка машины считывает символ в
конкретной ячейке.
1. Основываясь на символе и собственном
текущем состоянии машины, она
записывает символ в ту же ячейку и
перемещает головку на один шаг влево или
вправо или останавливает вычисление.

5.

Функции машины
Тьюринга
1. Преобразование входных данных. Согласно формальным правилам
перехода, машина Тьюринга преобразует входные данные с помощью
последовательности элементарных действий.
2. Имитация других исполнителей. С помощью задания правил перехода
на машине Тьюринга можно имитировать всех исполнителей, которые
реализуют процесс пошагового вычисления, в котором каждый шаг
достаточно элементарен.
3. Перечисление рекурсивно перечислимого языка. В контексте теории
формального языка машина Тьюринга способна перечислять произвольное
подмножество допустимых строк алфавита.
4. Обработка неограниченной грамматики. Машина Тьюринга способна
надёжно оценивать логику первого порядка бесконечным числом способов.