Похожие презентации:
Организационные и математические основы ЭЭС
1.
Тема 1 Организационные иматематические основы ЭЭС
1.1 Организационные основы ЭЭС
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
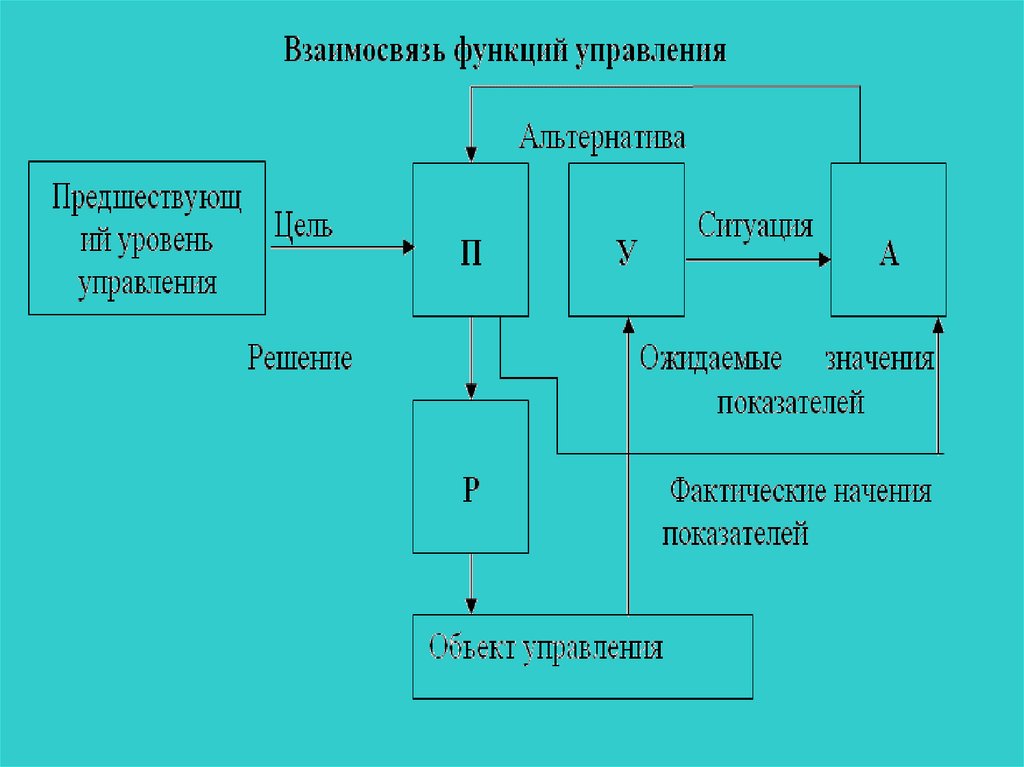
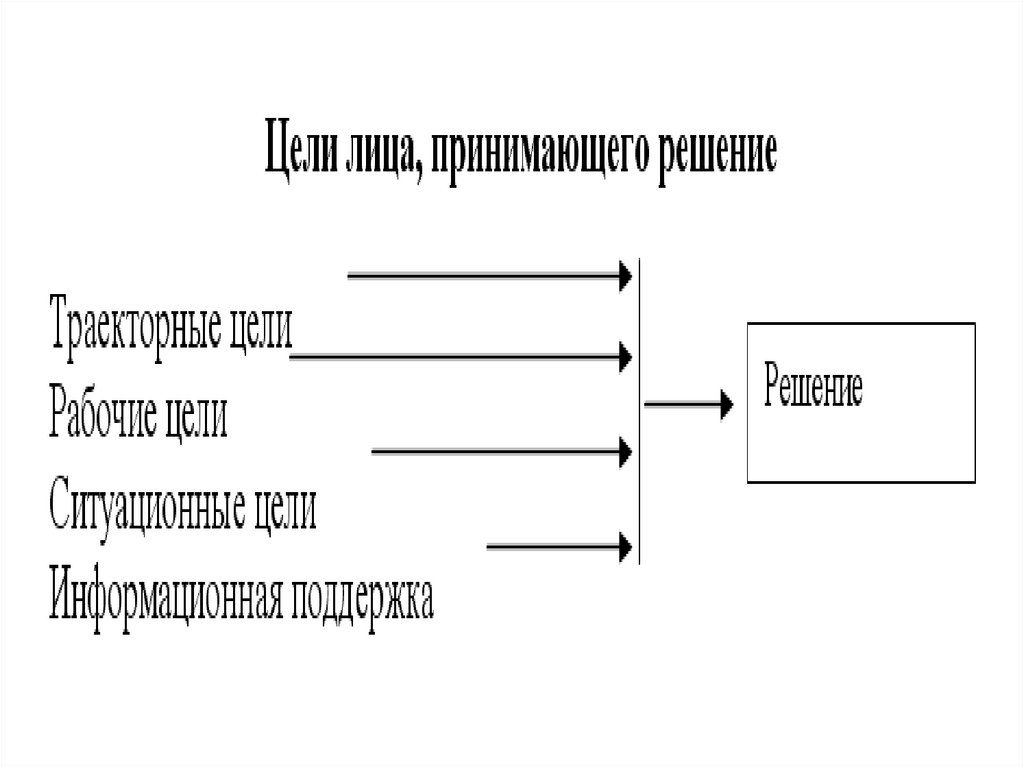
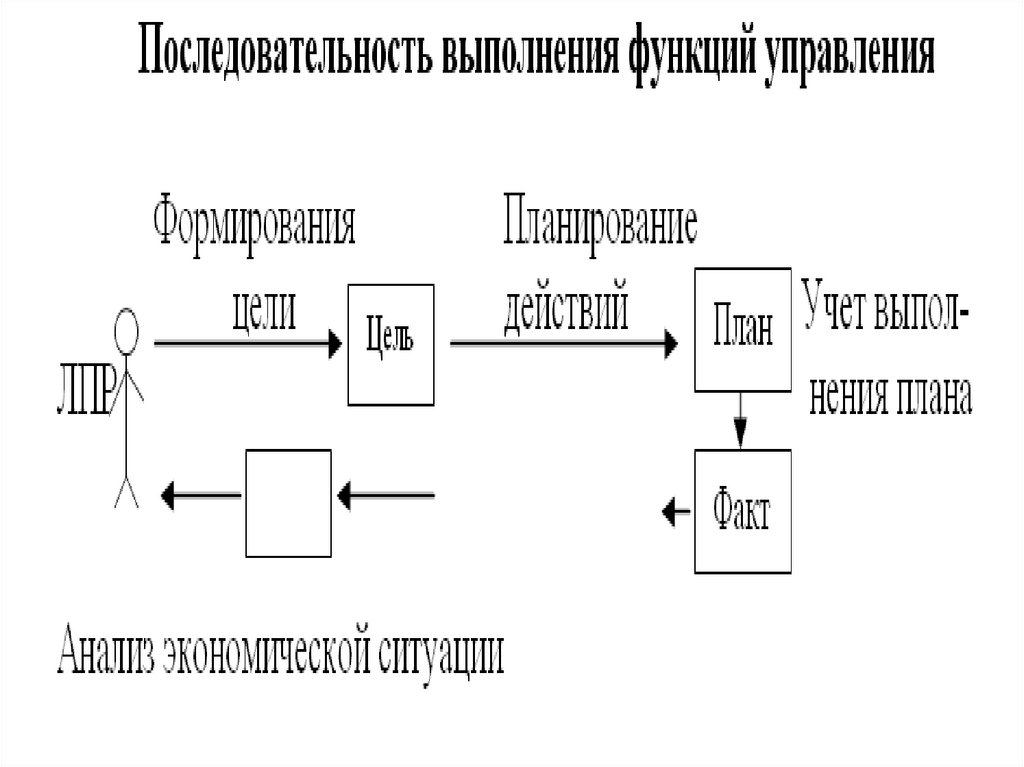
1.2 Математические основы ЭЭСЗначение показателя применяется
пользователем для принятия решения, а
наименование используется проектировщикам
для создания ЭЭС. Все показатели,
характеризующие хозяйственную деятельность
предприятия, связываются в граф, дуги которого
отражают последовательность их расчета.
Практика управления в сфере экономики
доказана, что именно экономический показатель
всесторонне, однозначно, компактно и
формально в состоянии отразить сущность
какого-либо хозяйственного процесса или
явления.
13.
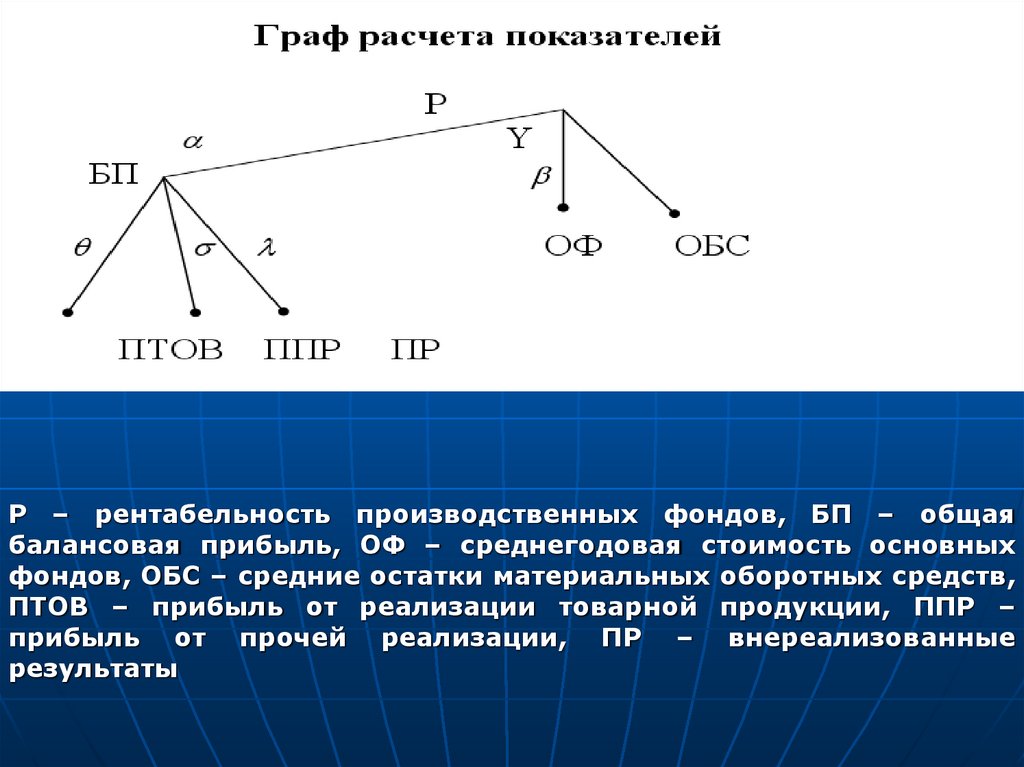
Р – рентабельность производственных фондов, БП – общаябалансовая прибыль, ОФ – среднегодовая стоимость основных
фондов, ОБС – средние остатки материальных оборотных средств,
ПТОВ – прибыль от реализации товарной продукции, ППР –
прибыль от прочей реализации, ПР – внереализованные
результаты
14.
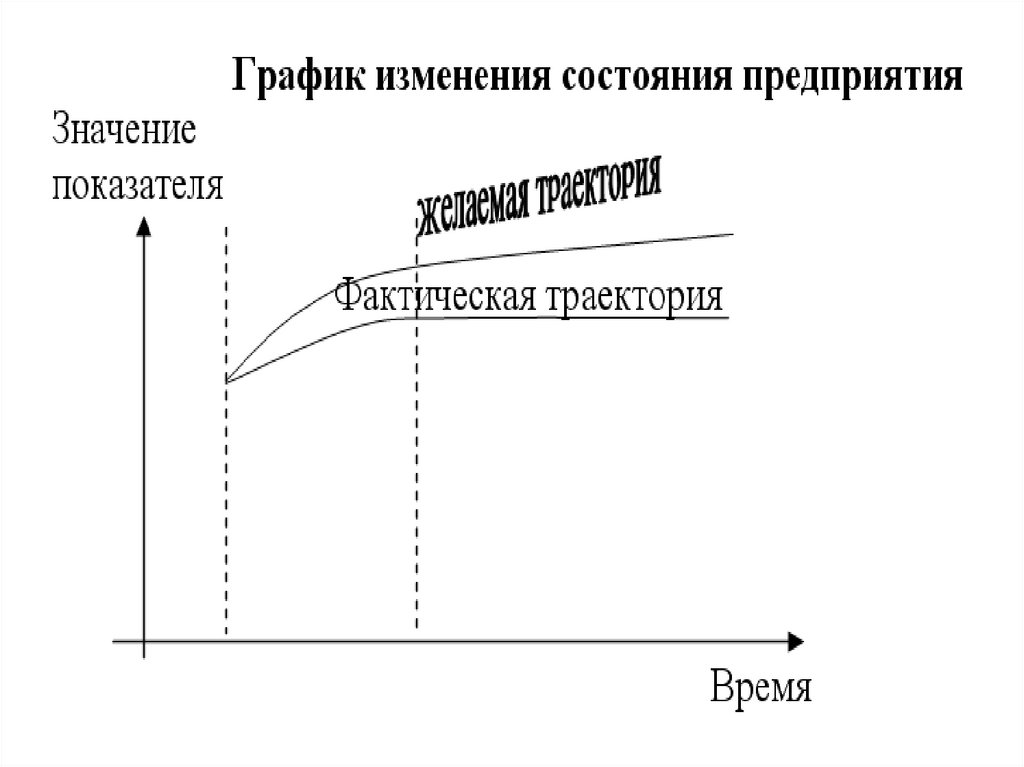
В общем виде задачу достижения целейпредприятия на основании построенного графа
«цель-показатель» можно сформулировать
следующим образом:
желаемое значение главной вершины,
соответствующей главной цели
предприятия
текущие значения показателей,
отражающихся в оставшихся вершинах
графа
направления изменения каждого из
показателей, соответствующих
определенным целям
15.
16.
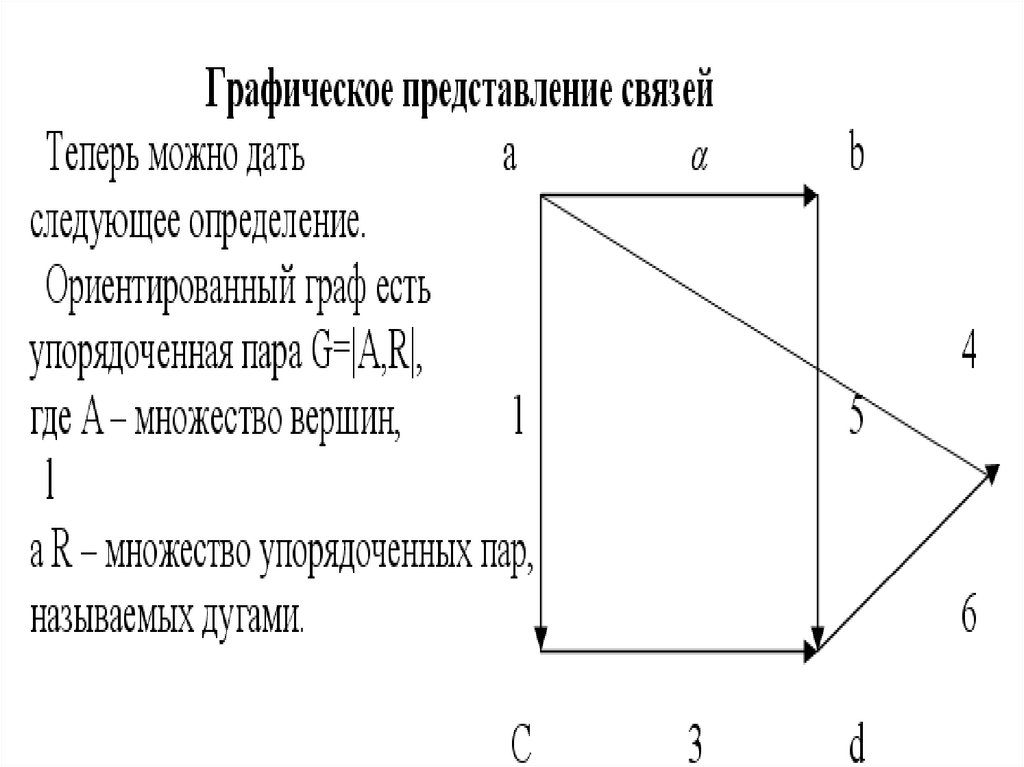
Граф можно задать одним из трех способов.Первый способ состоит в перечислении всех вершин и пар,
соединенных между собой линиями. Например:
A={a,b,c,d,e};
R={(a,b),(a,c),(c,d),(b,a),(a,e),(d,e)}
На рисунке представлено графическое использование матрицы
смежности. Две вершины называются смежными, если они
соединены дугой. Этот факт можно отобразить элементом
матрицы Х следующим образом:
если Размерность матрицы nxn, где n – число вершин. Тогда для
графа изображенного на рисунке, матрица смежности будет
выглядеть так:
a
a
b
c
d
e
b
0
0
0
0
0
c
1
0
0
0
0
d
1
0
0
0
0
0
1
1
0
0
e
1
0
0
1
0
17.
Ещё одним способом представления графа являетсяматрица инциденций. Размерность матрицы nxm, где n–
число вершин, m–число дуг графа. Каждой i-й строке
матрицы инциденций поставлена в соответствии
вершина графа, а каждому j-му столбцу–дуга. Элемент
yij=1, если в вершину заходит дуга uj, равен+1, если из
вершины исходит дуга и j, и равен 0, если дуга uj и
вершина не являются инцидентными. Для графа
представленного на рисунке матрица инциденции
имеет вид:
a 1 1 0 1 0 0
b
0
1
0
0
1
0
Y c
1 0 1 0 0 0
d 0 0
1 0
1 1
e
1 0
1
0 0 0
18.
На основании матрицы смежности можно построитьматрицу достижимости, часто применяемую для
решения задач технической подготовки производства.
Матрица достижимости позволяет установить
множество вершин графа, достижимых из заданной
вершины. Матрица достижимости определяется
следующим образом:
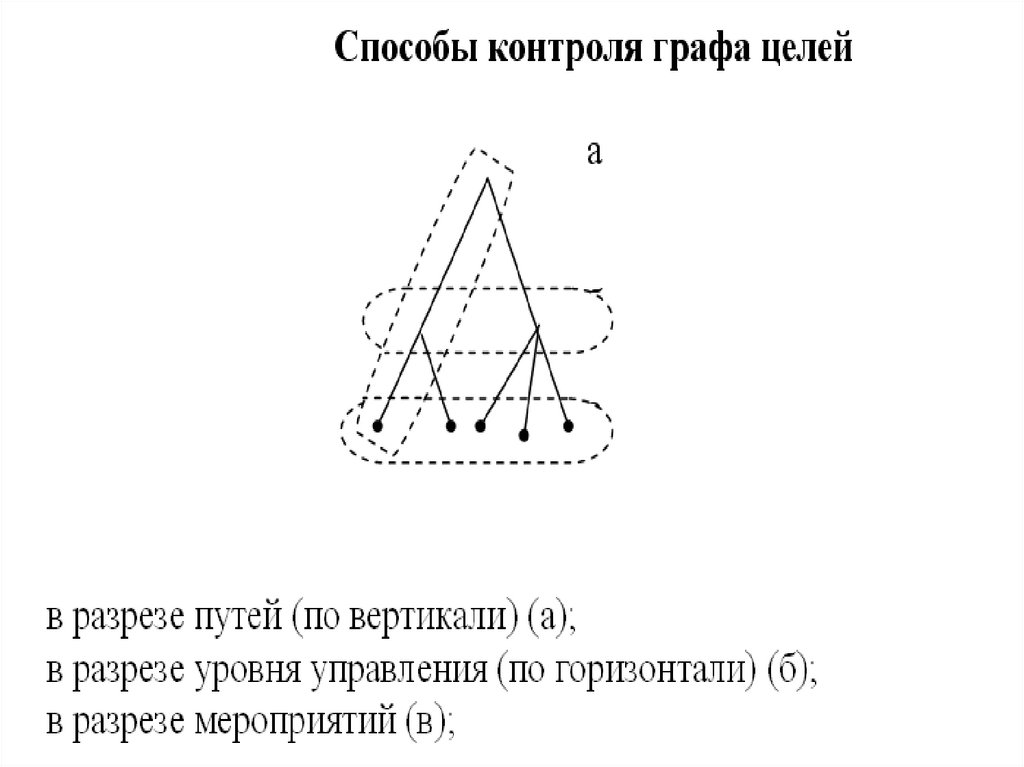
Наиболее распространенный способ задания
количественной характеристики цепи – введение в граф
коэффициентов относительной важности цели. Сумма КОВ
альтернативных путей одного уровня = 1.
19.
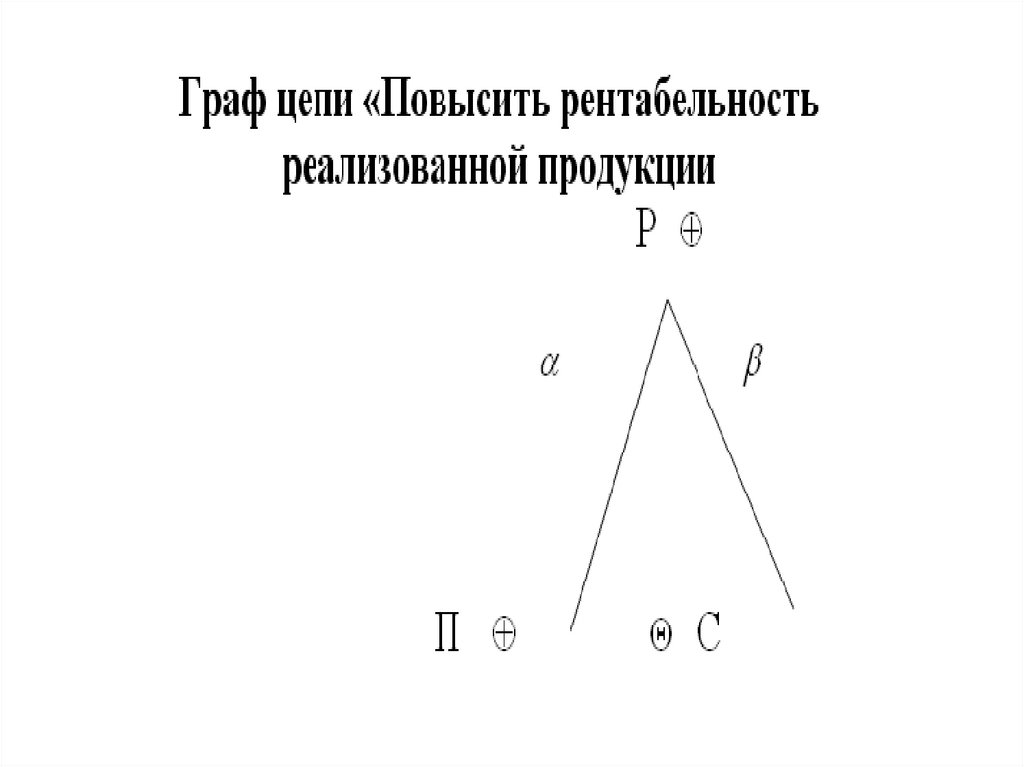
Рентабельность реализованной продукцииП
P
С
П – балансовая прибыль от
реализации продукции,
С – себестоимость
реализованной продукции.
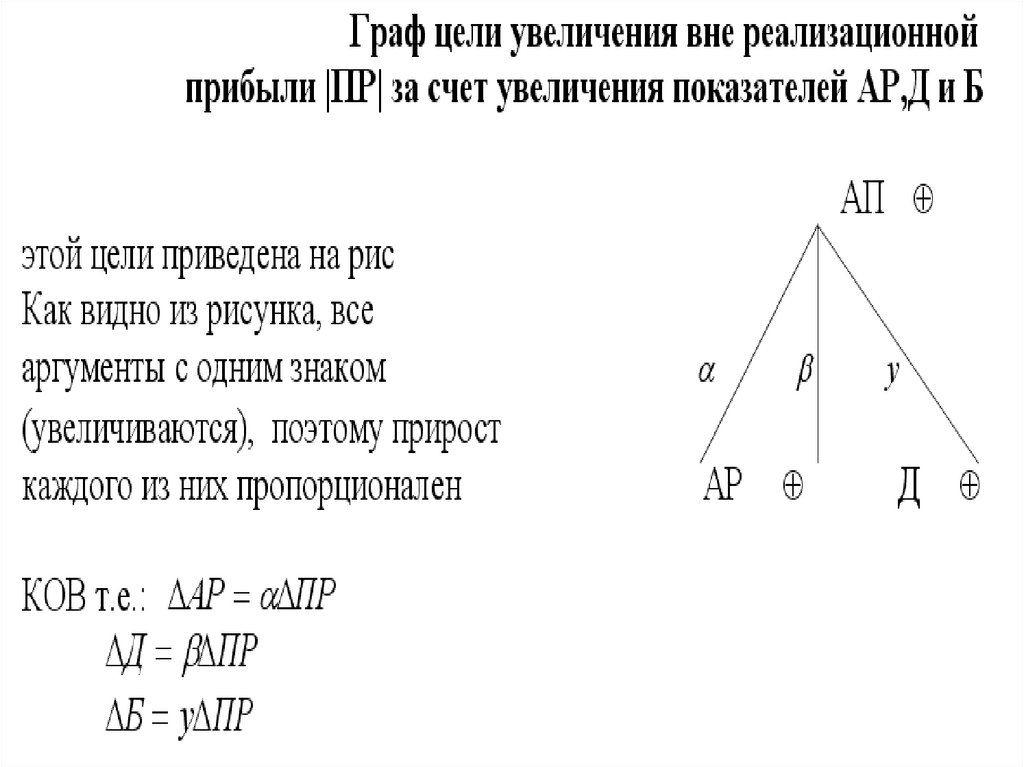
Наличие КОВ позволяет установить в приросте функции
пропорции приростов ее аргументов с помощью следующего
соотношения:
П
,
С
1
Воспользуемся этим соотношением для вывода коэффициентов
прироста аргументов П и С. Исходя из содержания понятия
рентабельности, ее прирост можно представить так
П
П
Р
Р Причем
С
С
П
П К
1П
С
С С
К2
20.
21.
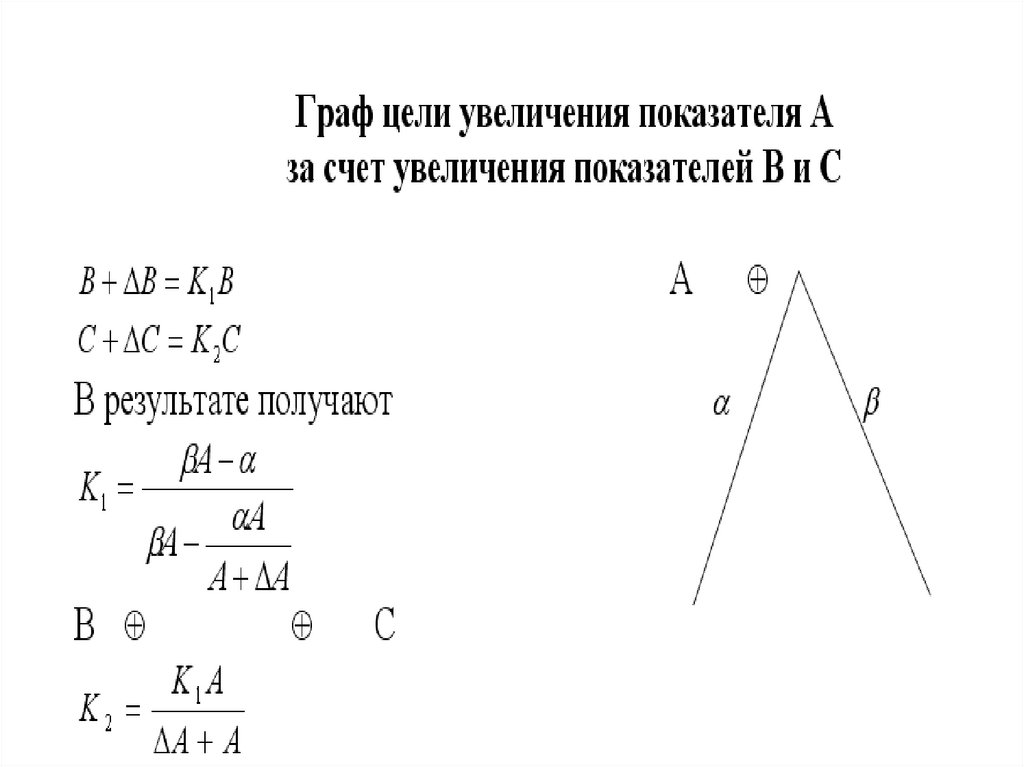
КоэффициентыK1 K 2- это искомые величины, которые
позволяет определить требуемый прирост аргументов.
Рассчитаем их. Очевидно, что:
K1П
Р Р
С
К2
К
К
Р
Р
,
1
2Р
Р
Р
К
К
Р
,
1 2
Р
Р
Р
К
,
2
К
1Р
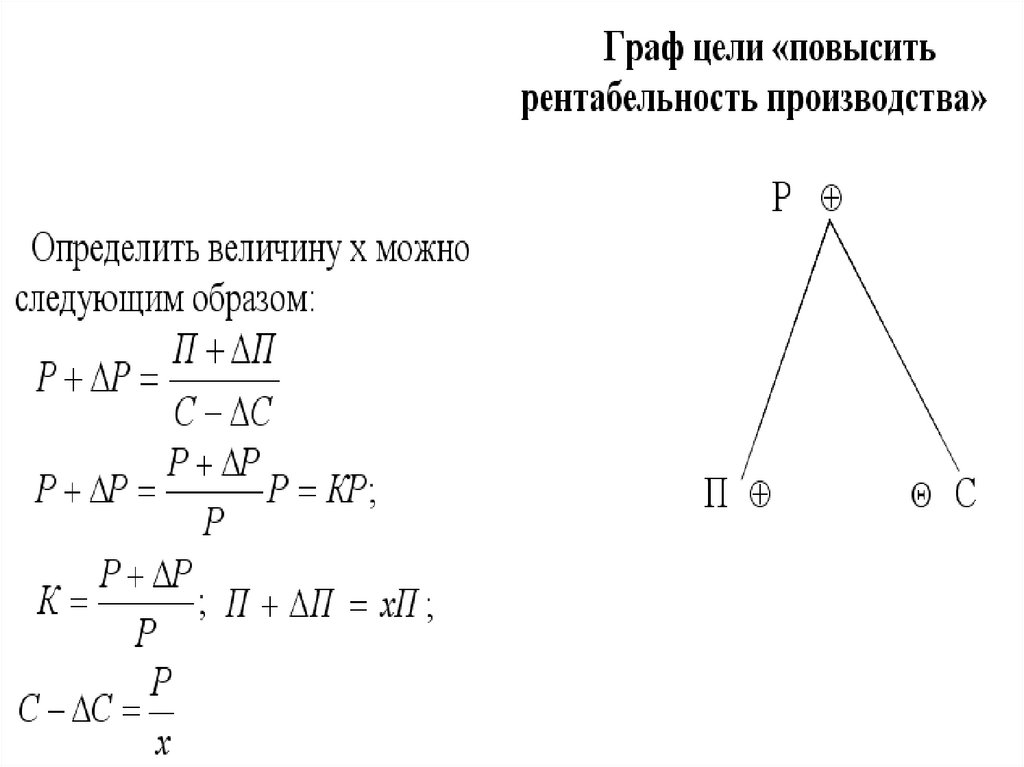
Так как
П
Р
С
Р
то опуская промежуточные преобразования, получим:
P
K
1
P
P
P
P
22.
23.
24.
25.
Вычислениеформулам:
коэффициентов
выполняется
по
K
D
C
(
) yD
K
D
K
B
1
1
4
K
,
K
,
K
1
2
3
C
(P
P
)
A
P
y
P
P
26.
B К Цгде В – выручка;
К – количество товарной продукции;
Ц – цена единицы продукции
Обозначив, как и ранее, приросты аргументов с помощью
соответствующих коэффициентов получили:
K
K K
1K
Ц
Ц K
2Ц
Формулы после выполнения соответствующего вывода имеют
вид:
2
В
В
(
αα
β
КК
(
αα
β
КК
4
ααβ(
Δ
ВВ
К
K
2
1
К
В
2
ВВ
1
Результатирующие показатели могут рассчитываться и на
основании произведения трех исходных показателей,
например, по формуле:
P A B C
Особенностью вывода коэффициентов в данном случае
является решение
27.
28.
Если у проектировщика появилась необходимость в использовании формулы видаP
A B
;
C
то для вывода коэффициентов следует вначале рассматривать числитель как
единое целое, а затем рассчитывать коэффициенты приростов для его
составляющих.
Обозначив через
yD
C
(
)
K
;
1
D
y
P
P
D A B
получили
K1
K
1D
;
K
; K3
2
K4
C
(P
P
)
2
2
2
2
(
B
AB
)
(
B
AB
)
4
В
K
DB
)
1
K
4
2
В
29.
30.
31.
32.
33.
34.
Тема 2. Пролог – использованиелогики предикатов
Хорошие
языки
не
только
строятся
на
основе
математических
понятий, делающих возможными
логические
умозаключения относительно программ, они
еще
поддерживают
небольшое число понятий и правил, которые
могут
комбинироваться
друг с другом.
Никлаус Вирт
35.
2.1 Простейшие программы. Синтаксис и семантика.Программирование в логических языках состоит в описании модели рассматриваемой предметной области. Модель строится в терминах объектов и отношений.
Отношения между объектами могут быть заданы в виде фактов и правил.
Факт - это некоторое утверждение, истинность которого считается доказанной.
Простейшая ПРОЛОГ-программа состоит из одного факта и имеет следующий вид:
А.
что интерпретируется следующим образом:
“утверждение А выполнимо”, “факт А имеет место”, “А истинно”.
Пример: Пусть предметная область может быть описана двумя фактами:
R - сегодня идет дождь;
S - сегодня идет снег.
Программа
R.
означает, что в ПРОЛОГ-систему помещено утверждение “сегодня идет дождь”.
Факт R в программе считается доказанным по определению.
Обращение к ПРОЛОГ-программе организовано с помощью вопросов. Пример
обращения:
?-R.
Интерпретация этого предложения такова:
“выполнимо ли утверждение R ?”, “имеет ли место факт R ?”,
“истинно ли R?”.
36.
В ПРОЛОГе принята следующая концепция: “отсутствие факта означает егонеудачное выполнение”, поэтому, если программа состоит из одного факта “Л.”, а
вопрос задан “?- В.”, то ответом будет “нет” (“неудача”, “ложь”, “No”), если же задан
вопрос “?- А.”, то ответом будет “да” (“удача”, “истина”, “Yes”).
Синтаксически вопрос от факта отличается наличием вначале предложения
конструкции “?- ”. Вопрос и факт обязательно заканчиваются точкой “ . ”.
Утверждение без точки будем называть целью.
Следующий уровень сложности ПРОЛОГ-программы связан c рассмотрением
новой конструкции языка, называемой правилом. Правило имеет следующий вид:
Состоит правило из двух частей, разделенных конструкцией “:- ”, которую можно
читать как “если”. Левая часть правила (“Л”) называется заголовком (головой
предложения) и является атомарной формулой. Правая часть правила называется
телом правила и представляет собой конечное множество целей, возможно пустое,
здесь
- факты либо правила, соединенные в единую конструкцию
символами “ , ”. Таким образом, символ “ , ” означает в теле правила связку “и”
(конъюнкцию ). Интерпретируется правило следующим образом: “утверждение А
выполнимо, если выполнимы все
”, “заключение А имеет место, если
имеют место одновременно B1 и B2 …, и Bn”, “A истинно, если истинны
все
”
Внимание. Правила, также как и факты, и вопросы, обязательно заканчиваются
точкой “.”
37.
Факт можно рассматривать как частный случай правила, когда тело правила пусто(п = 0).
Используя понятие процедуры, ПРОЛОГ-программу, имеющую cледующий вид:
можно прочитать следующим образом. Если при выполнении процедуры А
успешно выполнены процедуры B1 и B2 , то процедура А выполнена успешно. Если
хотя бы одна из процедур B1 или B2 завершилась неуспешно, то выполняется
второе предложение процедуры А, и, соответственно, выполняются процедуры B3
и B4. Если обе эти процедуры закончены успешно, то процедура А успешно
завершена, в противном случае выполнение процедуры А завершается неуспехом.
Таким образом, правила в процедуре связаны связкой “или”
(дизъюнкция).
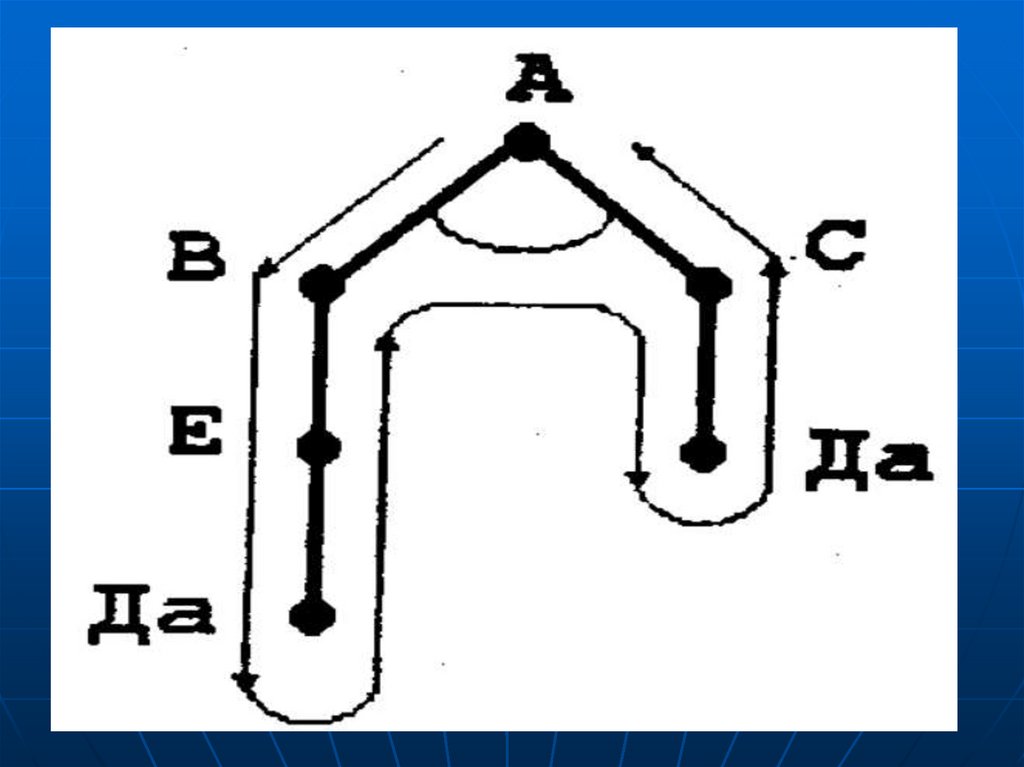
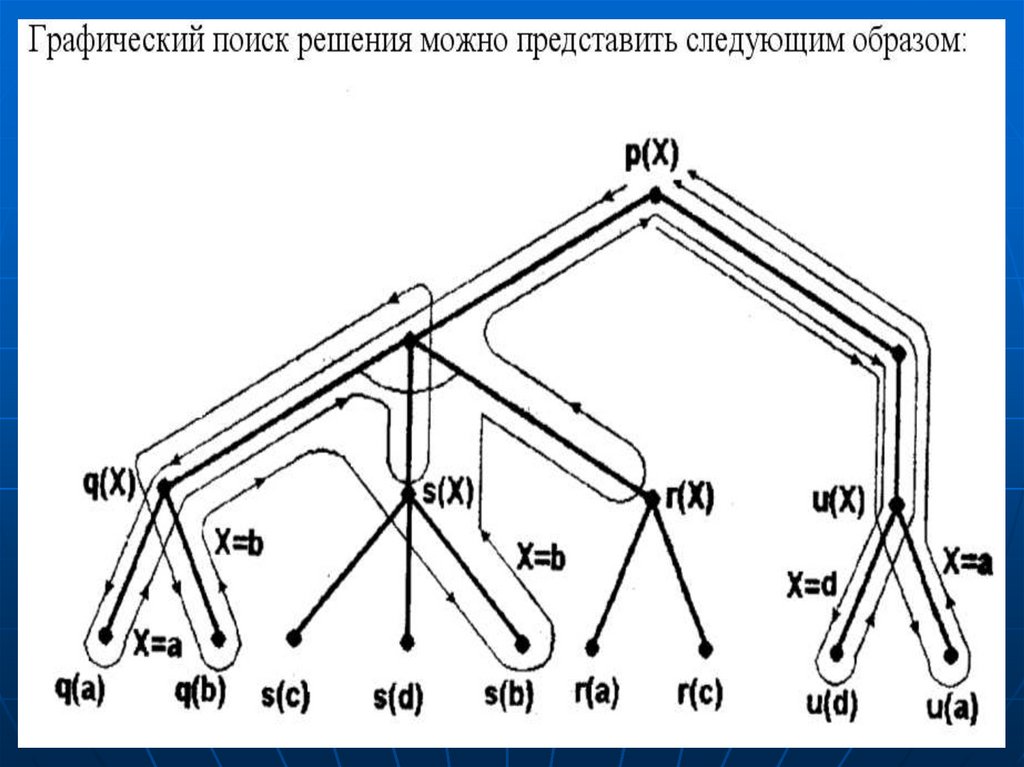
ПРОЛОГ-программа и поиск ответа на вопрос могут быть представлены на дереве
И-ИЛИ. Вершина типа И успешно разрешима, если успешно разрешимы все ее
вершины-потомки. Вершина типа ИЛИ успешно разрешима, если успешно
разрешима хотя бы одна из ее вершин-потомков. Принято отмечать узел И дугой,
охватывающий все относящиеся к нему ветви, узел ИЛИ такой пометки не имеет.
38.
39.
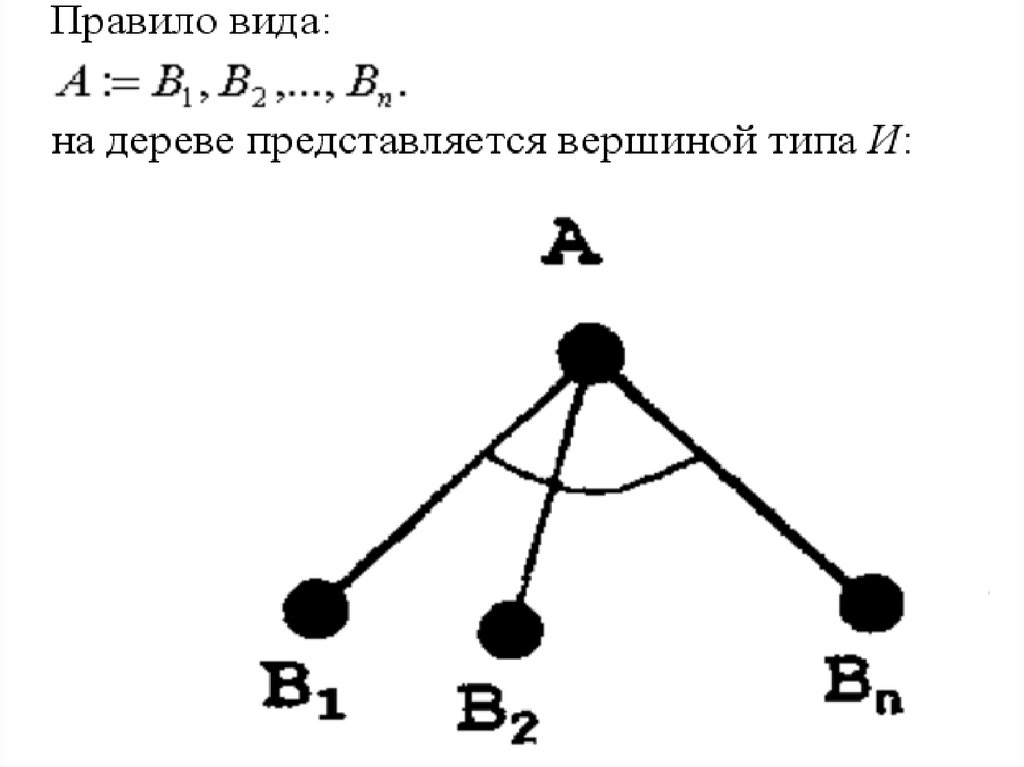
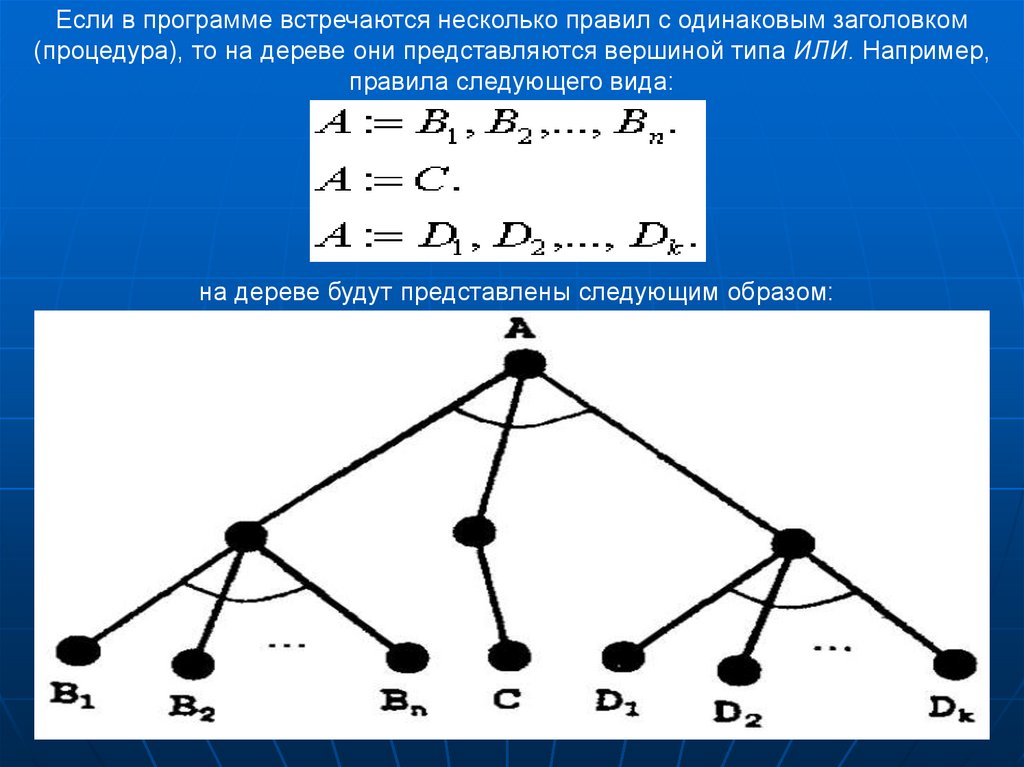
Если в программе встречаются несколько правил с одинаковым заголовком(процедура), то на дереве они представляются вершиной типа ИЛИ. Например,
правила следующего вида:
на дереве будут представлены следующим образом:
40.
41.
42.
Переменная в ПРОЛОГе- это последовательность букв и цифр, начинающаяся спрописной буквы или символа подчеркивания и содержащая только символы букв,
цифр и подчеркивания. Переменная, состоящая из одного символа подчеркивания
— это анонимная переменная, использующаяся в предложении только один раз.
Во многих версиях ПРОЛОГа приняты следующие соглашения: заглавные буквы
обозначают переменные, а строчные буквы, целые или действительные числа, или
любые символы, заключенные в кавычки, обозначают постоянные значения —
константы.
Фундаментальными операциями над переменными является конкретизация и
унификация, с помощью которых выполняются однократное присваивание и
передача параметров.
Константы, переменные, сложные термы в ПРОЛОГе, также как и в логике
предикатов первого порядка, называются термами. Также как и в логике,
фундаментальной операцией над термами является операция унификации.
Два терма унифицируемы в следующих случаях:
• термы абсолютно одинаковы;
• первый терм переменная, второй - любой терм;
• когда у них одни и те же функтор и арность и все их аргументы унифицируемы.
43.
Поиск решенияНеформально поиск решения в логической программе может быть описан
следующим образом. Он начинается с некоторого исходного вопроса и
завершается одним из двух результатов: успешное завершение или отказ. Для
данного вопроса может существовать несколько успешных решений, дающих
различные результаты. Кроме того, может иметь место бесконечный поиск
(зацикливание), с которым не связываются никакие результаты. Поиск решения
проводится с помощью редукции цели. На каждом этапе имеется некоторая
резольвента. Выбирается такая цель в резольвенте и такое предложение в
логической программе, что заголовок предложения унифицируем с целью.
Поиск решения продолжается с новой резольвентой, полученной из старой
заменой выбранной цели на тело выбранного предложения и последующим
применением наиболее общего унификатора заголовка предложения и
выбранной цели. Поиск решения завершается, если резольвента пуста. В этом
случае говорят, что решение найдено программой [Стерлинг-89].
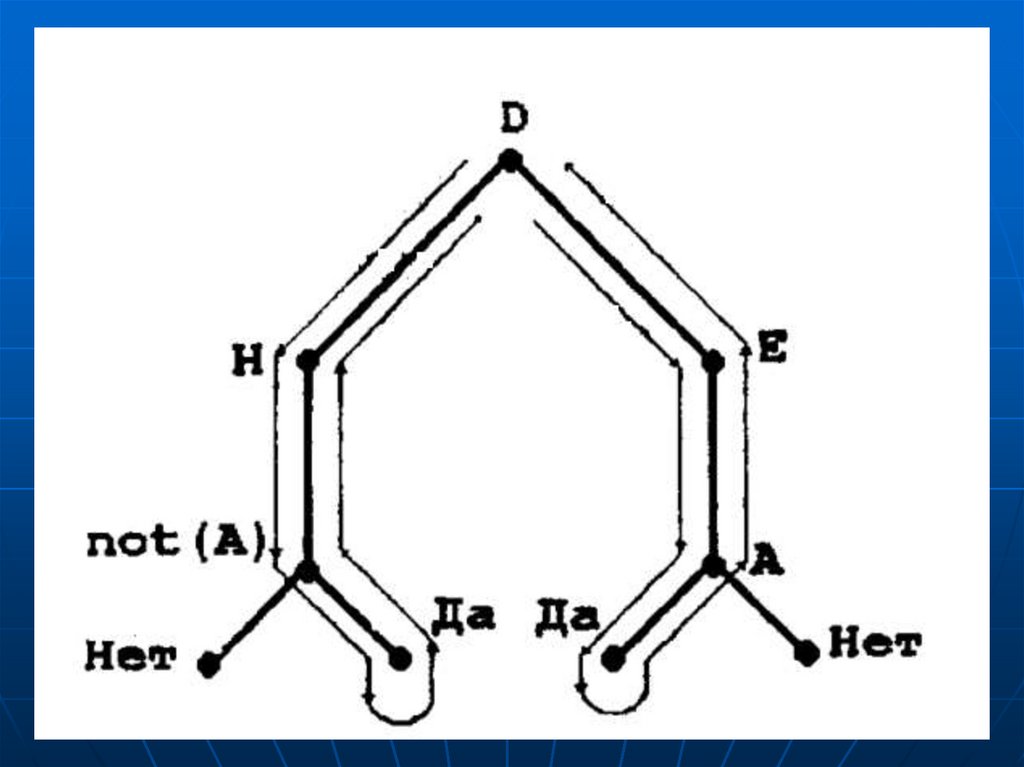
44.
45.
Таким образом, поиск решения в ПРОЛОГ- программе выполняется отисходного вопроса к фактам, т.е. в обратном направлении. Если
предложений, подлежащих унификации, несколько, то производится
унификация с первым из них. Если данное предложение выполнено, то
программа выполняется дальше. Если же данное предложение не
выполнено, то после бекгрекинга выполняются другие предложения,
подлежащие унификации.
46.
Техника программирования. Рекурсия и итерация.Сначала, обратимся к теории рекурсивных функций. Здесь рекурсия - это способ
задания функции путем определения каждого его значения в терминах ранее
определенных значений и, возможно, использования других уже определенных
функций [Катленд 83]. Уточним это определение на примере. Пусть имеются
функции f(x) и g(x, у, z), тогда новую функцию h(x, у) можно определить следующим
образом:
1. h(x,0)--=f(x},
2. h(x, у) = g(x, у, h(x, у)).
В этом определении, на первый взгляд, присутствует порочный круг, в пункте два h
определяется в терминах самой функции h. На самом деле, это вполне корректное
определение, так как, например, для нахождения h(х, 0), сначала, находим h(x, 0),
используя пункт один определения. Затем, зная h(х, 0), используя пункт два,
находим h(x, 1). Аналогично получаем h(x, 2), h(x, 3) и h(x, 4) многократным
применением пункта два определения функции h(x, у). Порочного круга в
определении удается избежать, так как, если определено одно конкретное
значение h(х, у), остальные определяются через полученные ранее.
47.
Теперь обратимся непосредственно к программированию. Один из стандартныхприемов решения сложной задачи состоит в том, чтобы разбить задачу на более
простые подзадачи, решить эти простые задачи, а затем объединить эти
подзадачи для получения общего решения. Когда подход к решению подзадачи
совпадает с подходом к решению задачи в целом, тогда такой процесс называется
рекурсией. Она используется как метод описания программ, выполнению которых
предшествует выполнение их собственных копий. Рекурсия является одним из
основных приемов программирования на ПРОЛОГе.
В предыдущей главе рассматривались правила, описывающие новые отношения в
терминах существующих отношений. Важным расширением множества подобных
правил являются рекурсивные определения, в которых отношения определяются в
терминах этих же отношений. Таким образом, процедуру прямо или косвенно
обращающуюся к себе, называют рекурсивной. Рекурсивное определение должно
обязательно содержать утверждение, прерывающее процесс рекурсивного
обращения. Такое утверждение называют граничным условием.
48.
В общем случае ПРОЛОГ-система находит ответ на поставленный запрос внесколько этапов. На первом этапе (этап разбиения), используя принцип редукции
поставленной задачи, система отвечает на вопрос возможно ли вообще решение
задачи, откладывая вычисление некоторых утверждений на более поздние этапы.
После завершения редукции задачи, система возвращается к ранее отложенным
утверждениям и находит конкретный ответ на поставленную задачу (этап
вычисления).
Главной целью является - показать, как осмысленно конструировать и
разрабатывать добротные программы, то считаю необходимым поговорить и об
эффективности программ. Для создания эффективной программы необходимо
проанализировать особенности решаемой задачи. Так, например, возведение в
степень некоторого числа можно провести, используя только операцию умножения.
Рекурсивно операцию возведения в степень можно определить следующим
образом:
Рекурсивное определение можно сформулировать следующим образом:
возведенное в степень N число Х вычисляется как умноженное N раз само на себя
число X.
expon(N, X, Е):- N > 0, N1 = N-l, expon(N1, X, E1), Е = X * E1.
49.
В приведенной выше программе для получения результата необходимо провести Nумножений. При возведении в степень n числа Х можно воспользоваться
следующими свойствами:
Базирующаяся на этих свойствах ПРОЛОГ-программа возведения числа в степень
будет иметь следующий вид:
quick_expon(0, X, 1).
quick_expon( N, X, Е):- N > 0, 0 = N mod 2,!, N1 = N div 2,
quick_expon(Nl, X, R), Е = R * R.
quick_expon(N, X, Е):- N > 0, N1 = N-l,
quick_expon(Nl, X, El), Е = X * E1
50.
Эффективность программы quick_expon относительно программыexpon проявляется с ростом показателя степени. Например,
вычисление X4096 потребует 4096 умножений в случае использования
программы expon, и только 13 умножений в случае использования
программы quick_expon. Однако при малых показателях степени
предпочтительнее использование программы expon, так как здесь
отсутствуют проверка на четность и деление показателя степени на
два. Второе предложение процедуры содержит встроенный системный
предикат ! (отсечение), присутствует он для того, чтобы третье
предложение процедуры не участвовало в вычислениях, когда
показатель степени является четным числом. Отсечение также
используется для повышения эффективности программ, устраняя
ненужные возвраты и альтернативные пути, которые не приведут к
решению задачи.
51.
Итерация.В ПРОЛОГе отсутствуют конструкции типа for ... do, while ... do, repeat...
until, задающие циклическое выполнение программ. Вместо них
используются рекурсивные конструкции. Рекурсия используется в
ПРОЛОГе и для организации итерационных циклов, которые
характеризуются последовательным приближением к искомому
значению. Главное отличие итерации от рекурсии состоит в том, что
при использовании первой отсутствуют отложенные вычисления, а
значит, нет необходимости в использовании дополнительной памяти
стека. В общем случае объем памяти при рекурсивной реализации
линейно зависит от числа выполненных рекурсивных обращений, в то
время как объем памяти для выполнения итераций ограничен
конкретным значением и не зависит от числа обращений [Стерлинг 89].
В работе [Стерлинг 89] утверждается, что почти все рекурсивные
программы, выполняющие арифметические вычисления, могут быть
представлены в виде итерационных программ.
52.
Представление списка.С математической точки зрения список - это конечная упорядоченная
последовательность элементов. Список в языках программирования - это
бинарная структура или специальный вид сложного терма, состоящий из головы
списка и хвоста списка, где голова - это элемент списка, а хвост - это список.
Элементы списка, в свою очередь, сами могут быть списками. Функтор для
обозначения списка принят следующий:
.(X, L),
однако чаще используется инфиксная форма записи следующего вида:
[X | L],
где X - голова, L - хвост, операция “|” соответствует ЛИСП-функции CONS и
обозначает слияние элемента-головы и элемента-хвоста списка в единый список.
Операцию “|” можно интерпретировать и как операцию разбиения списка на голову
и хвост. Таким образом, список в ПРОЛОГе - это такая структура, в которой
операции включения/исключения производятся только в начале этой структуры.
Для элементов списка справедливо следующее правило: “Первым пришел последним ушел”. На вопрос
?-L=[a | [b, c, d]].
будет дан ответ
L = [а, Ь, с, d].
53.
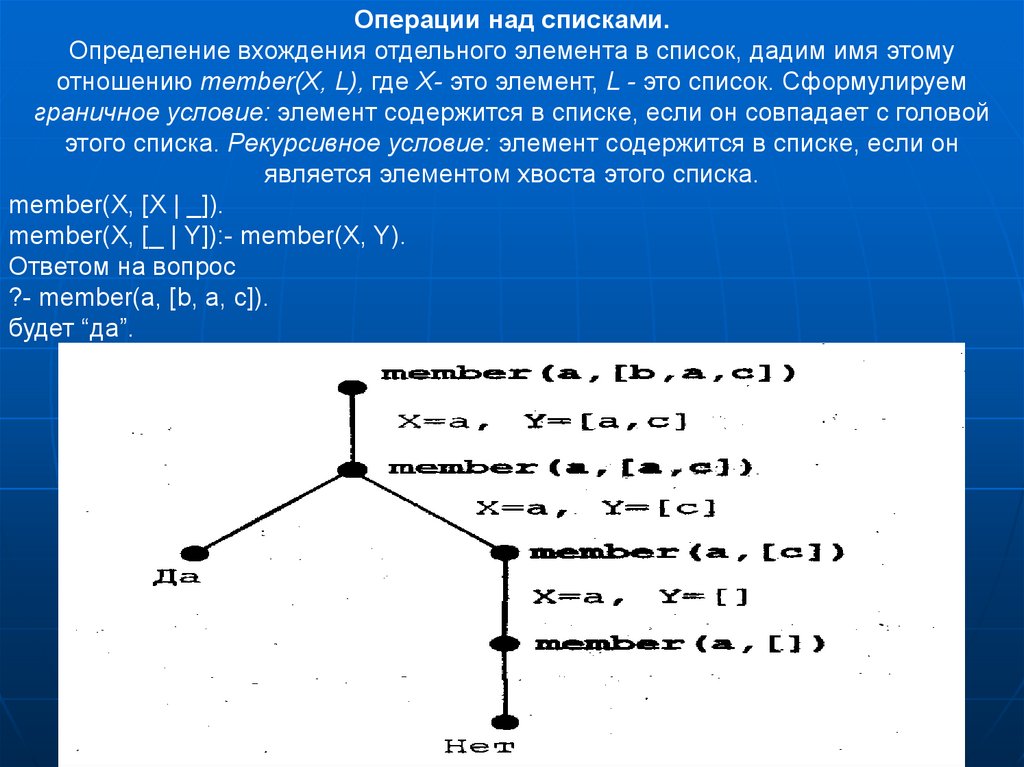
Операции над списками.Определение вхождения отдельного элемента в список, дадим имя этому
отношению member(X, L), где Х- это элемент, L - это список. Сформулируем
граничное условие: элемент содержится в списке, если он совпадает с головой
этого списка. Рекурсивное условие: элемент содержится в списке, если он
является элементом хвоста этого списка.
member(X, [X | _]).
member(X, [_ | Y]):- member(X, Y).
Ответом на вопрос
?- member(a, [b, a, c]).
будет “да”.
54.
Не менее важной операцией над списками является операция соединения двухсписков для получения третьего, имя этому отношению дадим append(L1, L2, L3),
здесь L3 - это конкатенация списков L1 и L2. Граничное условие: результатом
соединения пустого списка со списком L будет список L. Рекурсивное условие:
результатом соединения списка L1 и списка L2 является список L3; соединение
выполняется следующим образом: голова списка L1 добавляется к хвосту списка
L3.
Ниже приведена программа, задающая заданное отношение:
append([], L, L).
append([X | XL], YL, [Х | ZL]):- append(XL, YL, ZL).
Ответом на вопрос
?-append([a, b, c],[1, 2], Z).
будет Z = [а, b, с, 1, 2].
Процесс получения результата условно разбит на два этапа – разбиения и
вычисления. На первом этапе ПРОЛОГ-система ищет принципиальную
возможность выполнить поставленную задачу, формируя при этом
вспомогательные переменные. На втором этапе, используя вспомогательные
переменные, система формирует непосредственно сам результат. Первый
этап на приведенном выше рисунке представлен жирными линиями, второй более тонкими.
55.
Алгоритмы обнаружения закономерностей.Для построения решающего правила распознавания из Фз необходимо было
разработать алгоритмы обнаружения логических закономерностей,
характеризующих эмпирическую таблицу. Эти закономерности могут представлять,
как об атом упоминалось ранее, самостоятельную ценность для специалистов. В
литературе по распознаванию образов известны алгоритмы обнаружения
логических закономерностей для булевых признаков (алгоритм КОРА [31]) и для
признаков, замеренных в шкале наименований [36, 37].
Алгоритм CORAL [58] реализует направленную процедуру поиска
закономерностей, характеризующих образ w (w =1,…,K), и дает локальнооптимальное решение.
Алгоритм TЭМП [55]. С помощью алгоритма CORAL можно не выбрать некоторые
закономерности, так как он реализует направленную процедуру перебора
высказываний, Алгоритм ТЭМП выбирает все аакономерности с точностью до
элементарных высказываний, но требует больше вычислений.
Алгоритмы ТЭМП и КОРА различаются схемой перебора. Согласно классификации
Э. Ханта [62 ], существуют переборы в ширину и глубину. Алгоритм ТЭМП
осуществляет перебор в ширину, .алгоритм КОРА— в глубину. Можно показать, что
трудоемкость рассматриваемого алгоритма значительно ниже, чем трудоемкость
алгоритма КОРА при одинаковых результатах перебора.
56.
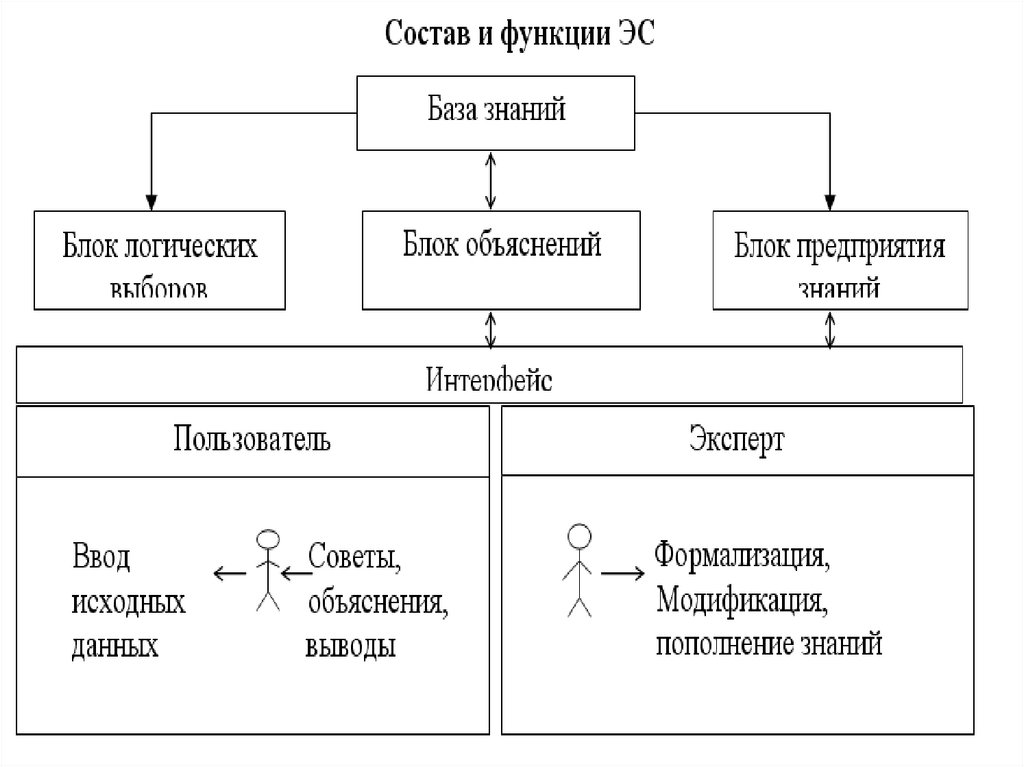
Тема 3 Инженерия знаний.57.
Исходные понятия и теоретические основы инженерии знаний.Одной из наук, развивающих теоретическую базу для
информатики, является
когнитология, которая изучает моделирование мыслительных процессов. Такого
рода процессы основываются на персональных и социальных знаниях.
Социальные знания – это вербализованные (представление в виде текстов) и
таким образом отчужденные от конкретных носителей (людей) персональные
знания.
Представление знаний – это формализация, т.е. моделирование знаний
посредством различных изобразительных средств (графических, формульных)
Одним из универсальных способов представления фактуальных знаний, является
семантическая сеть. В основе лежит ориентированный граф, наглядно
отображающий отношения между объектами любой природы. Универсальность
семантических сетей обеспечивает систематизацию и структурирование знаний о
предметной области. Кроме того, визуализация знаний обеспечивает проверку
правильности графической и формально логической версии исчисления
предикатов.
Имеются два базовых элемента семантических сетей. Первый из них соответствует
объектам, их признакам и значениям, и будет изображаться в виде
прямоугольников, а второй – отношениям.
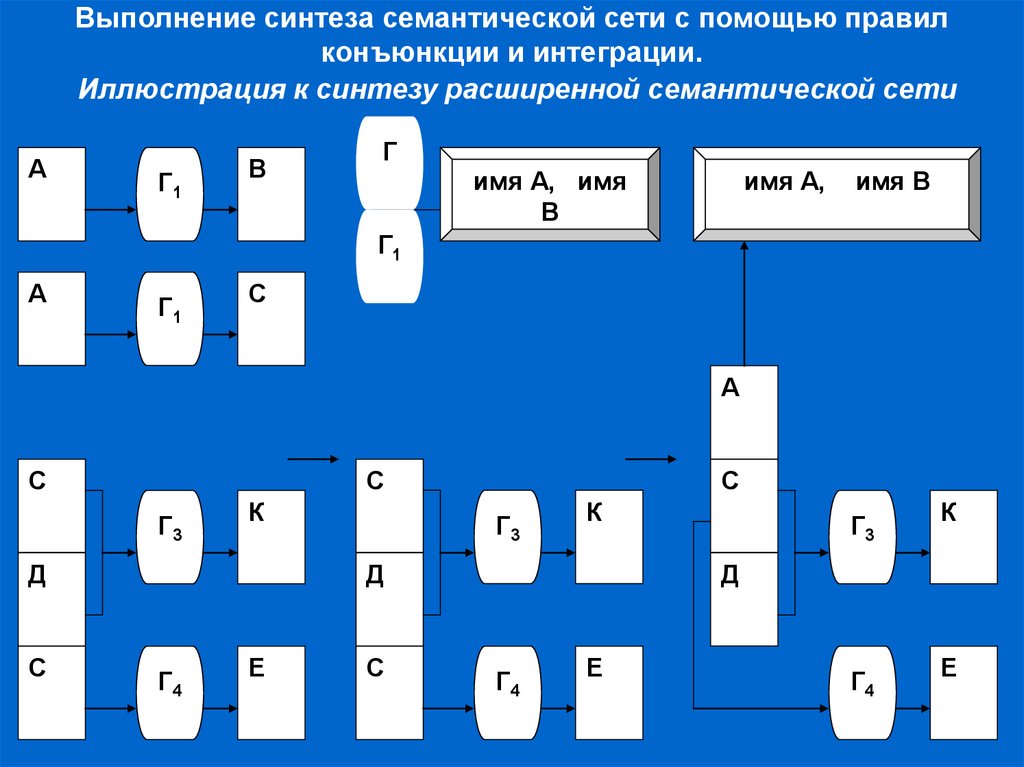
Семантические сети создаются путем синтеза графических представлений знаний
отдельных фрагментов описания предметной области. Синтез происходит по
правилу: если вершина а1 в подграфе g1, идентично вершине а2 в подграфе g2, то
подграф g2 получают удалением а2 и соединением с а1 всех связывающих
вершин, которые были связаны с а2 в подграфе g2 .
58.
Воспроизведение знаний с помощью семантических сетей позволяет явно отразитьтакже и контекстные, т.е. глубинные, знания о предметной области. Это
достигается классификацией понятий и выявлением иерархических зависимостей
между понятиями.
Существует ряд терминов, используемых для отражения процесса получения
знаний: извлечение, приобретение, отчуждение, выявление, форматирование и т.д.
Извлечение
–
без
использования
вычислительной
техники
путем
непосредственного контакта проектировщика и источника знаний (эксперт,
литература, документы.)
Приобретение – с использованием ЭВМ при наличии специального программного
инструментария.
Форматирование – с использованием программ обучения и самообучения
(автоматическое пополнение базы знаний).
Наиболее распространенным пока является извлечение знаний, основывающееся
на коммуникативных и текстологических методах.
Технология проектирования ЭЭС ориентирована на извлечении знаний, причем
этот процесс в основном базируется на текстологических методах. Источниками
знаний служат письменные тексты, представляющие собой описание предметной
области и решаемой задачи, или специалисты в данной предметной области.
Актуальное членение – это приспособление грамматической структуры
предложения к задачам коммуникации. Предложение делится на тему и рему.
59.
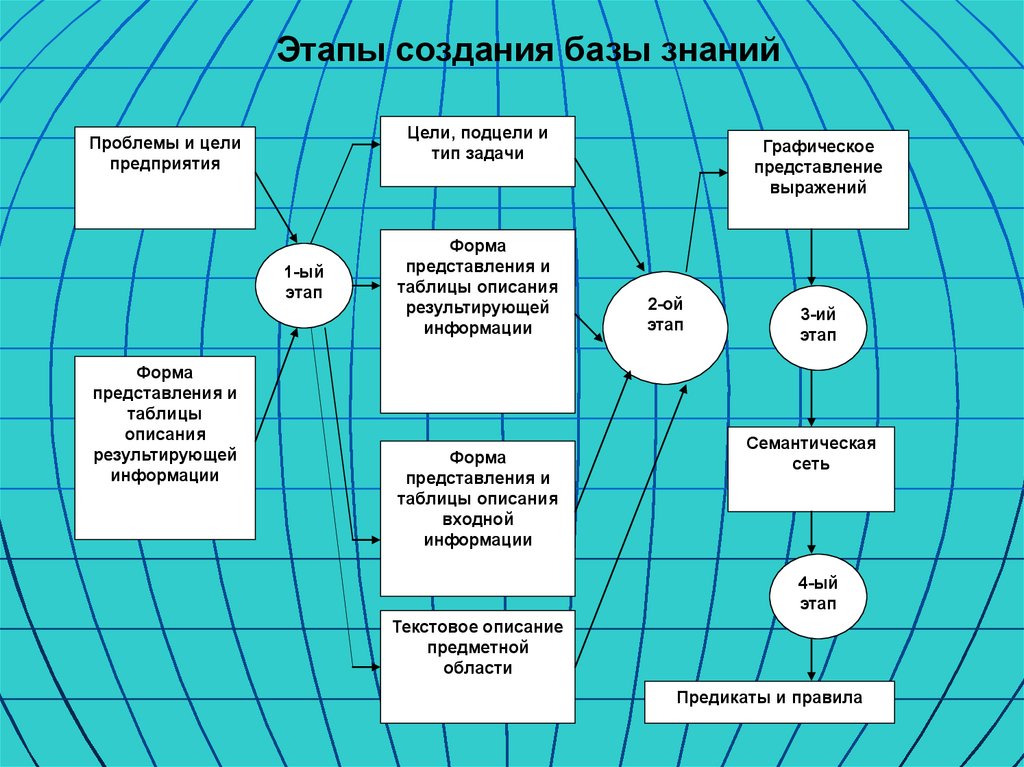
Этапы создания базы знанийЦели, подцели и
тип задачи
Проблемы и цели
предприятия
1-ый
этап
Форма
представления и
таблицы
описания
результирующей
информации
Форма
представления и
таблицы описания
результирующей
информации
Форма
представления и
таблицы описания
входной
информации
Графическое
представление
выражений
2-ой
этап
3-ий
этап
Семантическая
сеть
4-ый
этап
Текстовое описание
предметной
области
Предикаты и правила
60.
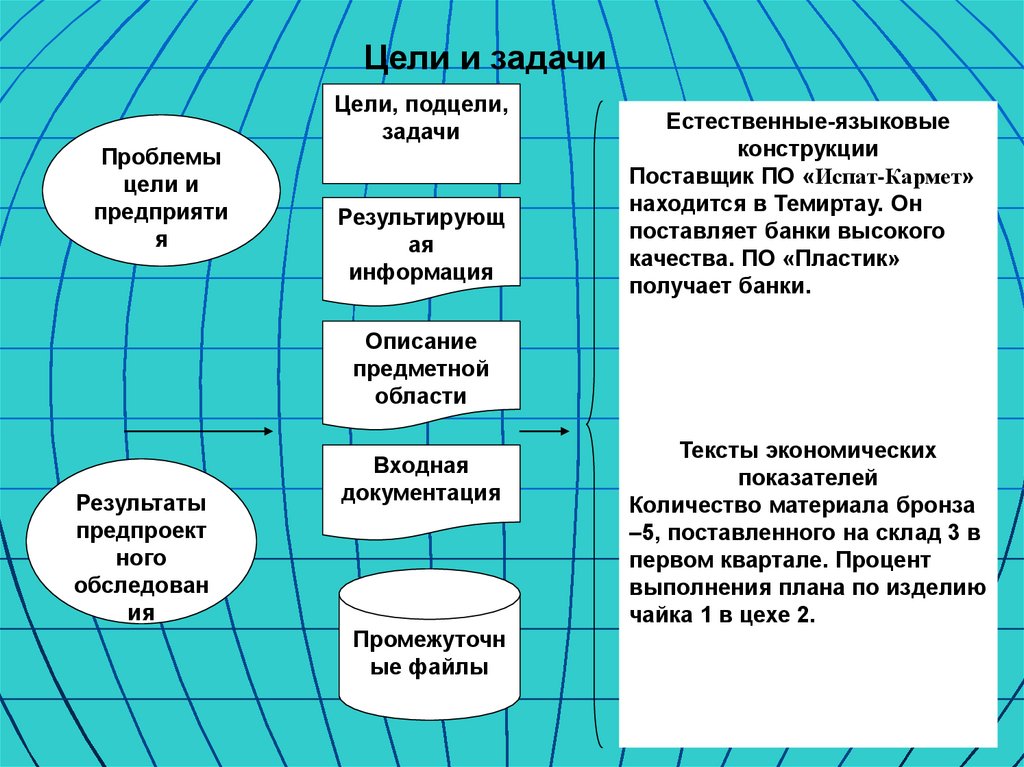
Цели и задачиЦели, подцели,
задачи
Проблемы
цели и
предприяти
я
Результирующ
ая
информация
Естественные-языковые
конструкции
Поставщик ПО «Испат-Кармет»
находится в Темиртау. Он
поставляет банки высокого
качества. ПО «Пластик»
получает банки.
Описание
предметной
области
Результаты
предпроект
ного
обследован
ия
Входная
документация
Промежуточн
ые файлы
Тексты экономических
показателей
Количество материала бронза
–5, поставленного на склад 3 в
первом квартале. Процент
выполнения плана по изделию
чайка 1 в цехе 2.
61.
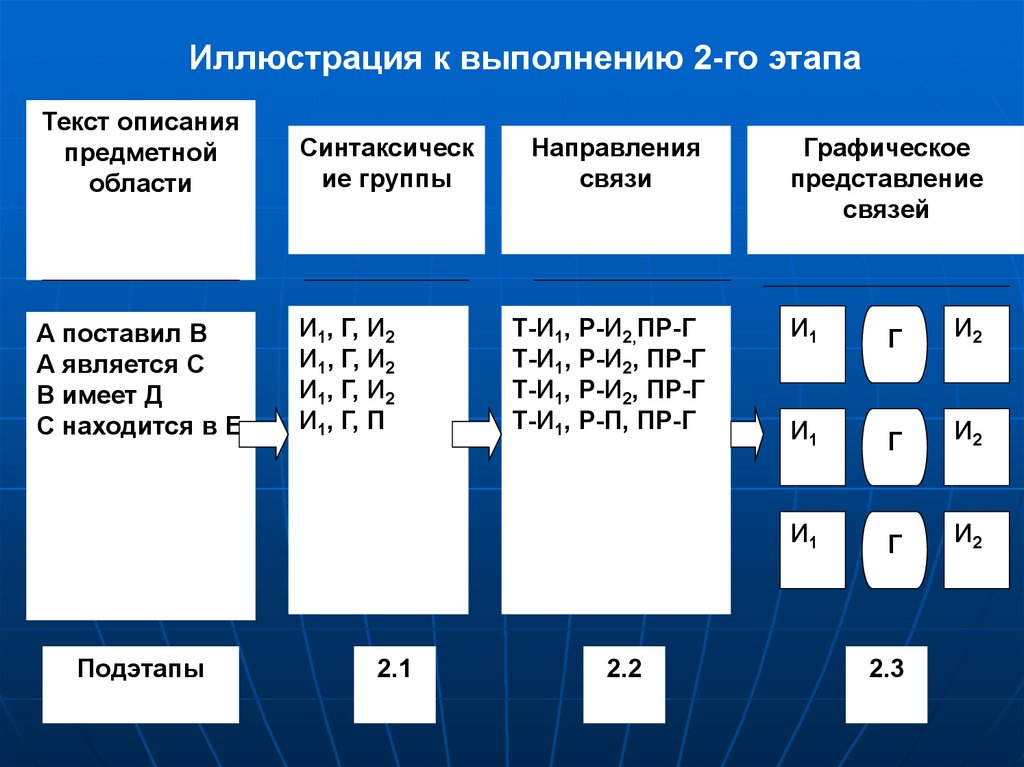
Иллюстрация к выполнению 2-го этапаТекст описания
предметной
области
Синтаксическ
ие группы
А поставил В
А является С
В имеет Д
С находится в Е
И1, Г, И2
И1, Г, И2
И1, Г, И2
И1, Г, П
Подэтапы
2.1
Направления
связи
Т-И1, Р-И2,ПР-Г
Т-И1, Р-И2, ПР-Г
Т-И1, Р-И2, ПР-Г
Т-И1, Р-П, ПР-Г
2.2
Графическое
представление
связей
И1
Г
И2
И1
Г
И2
И1
Г
И2
2.3
62.
Выполнение синтеза семантической сети с помощью правилконъюнкции и интеграции.
Иллюстрация к синтезу расширенной семантической сети
А
Г1
В
Г
имя А, имя
В
имя А,
имя В
Г1
А
Г1
С
А
С
С
Г3
К
Д
С
С
Г3
К
Д
Г4
Е
С
Г3
К
Д
Г4
Е
Г4
Е
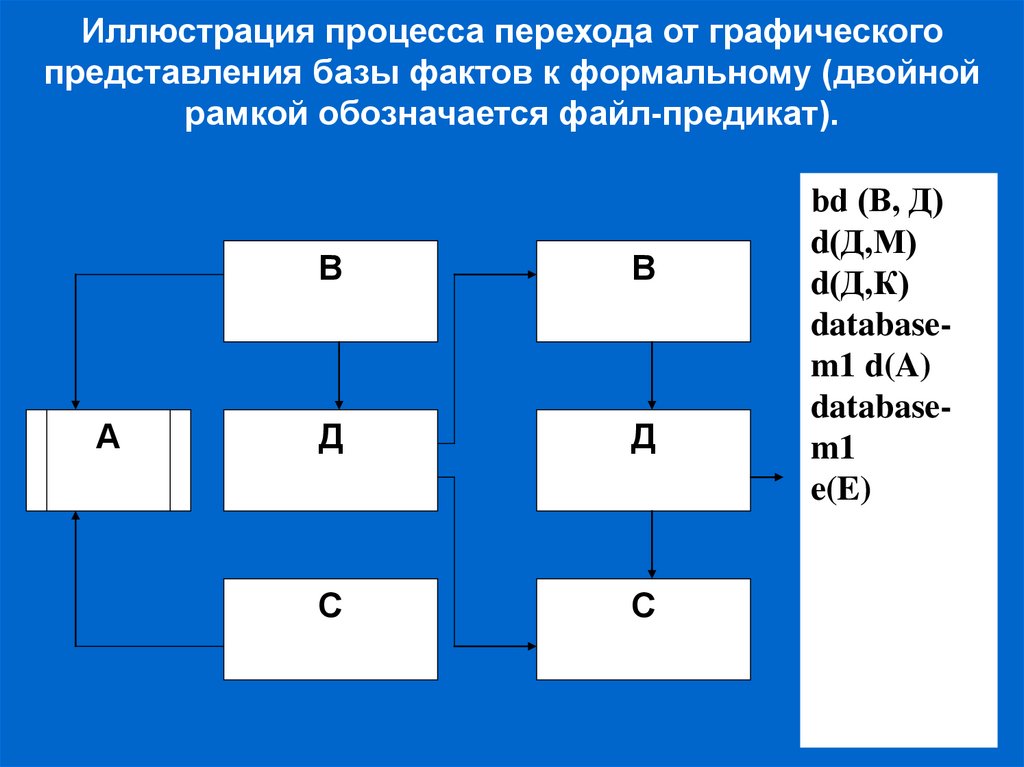
63.
Иллюстрация процесса перехода от графическогопредставления базы фактов к формальному (двойной
рамкой обозначается файл-предикат).
А
В
В
Д
Д
С
С
bd (B, Д)
d(Д,М)
d(Д,К)
databasem1 d(A)
databasem1
e(E)
64.
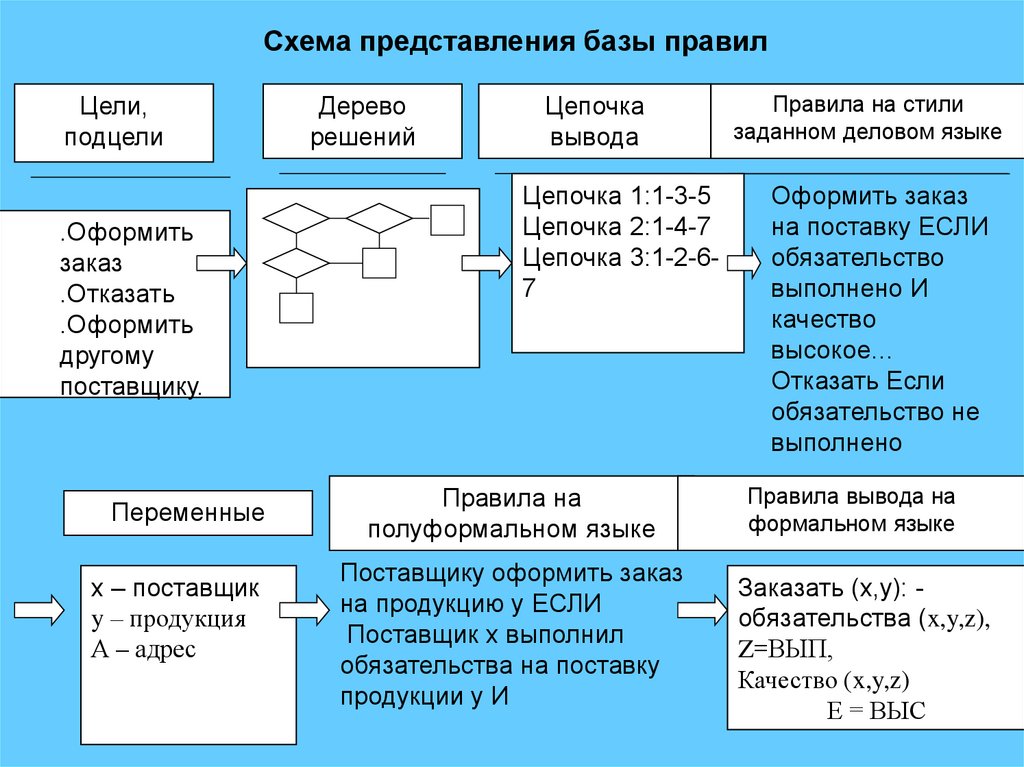
Схема представления базы правилЦели,
подцели
.Оформить
заказ
.Отказать
.Оформить
другому
поставщику.
Переменные
х – поставщик
y – продукция
А – адрес
Дерево
решений
Цепочка
вывода
Цепочка 1:1-3-5
Цепочка 2:1-4-7
Цепочка 3:1-2-67
Правила на
полуформальном языке
Поставщику оформить заказ
на продукцию у ЕСЛИ
Поставщик х выполнил
обязательства на поставку
продукции у И
Правила на стили
заданном деловом языке
Оформить заказ
на поставку ЕСЛИ
обязательство
выполнено И
качество
высокое…
Отказать Если
обязательство не
выполнено
.
Правила
вывода на
.
формальном языке
.
Заказать (x,y): обязательства (x,y,z),
Z=ВЫП,
Качество (x,y,z)
Е = ВЫС
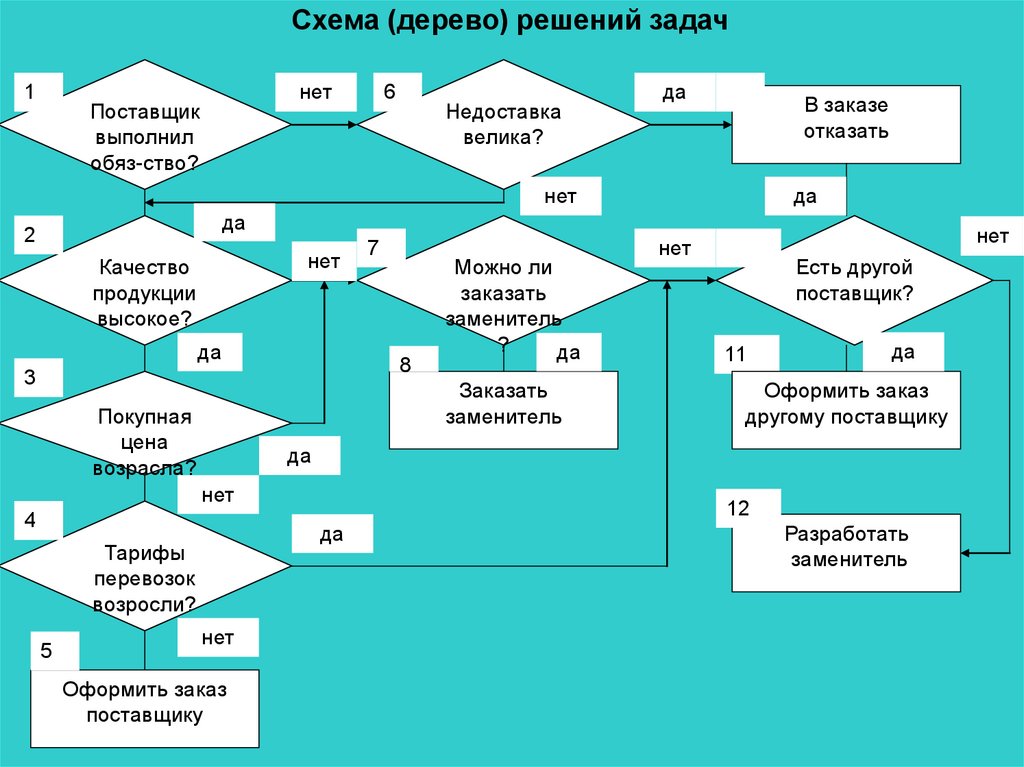
65.
Схема (дерево) решений задач1
нет
Поставщик
выполнил
обяз-ство?
6
Недоставка
велика?
да
9
В заказе
отказать
нет
да
да
2
нет
Качество
продукции
высокое?
да
8
3
Можно ли
заказать
заменитель
?
да
Заказать
заменитель
Покупная
цена
возрасла?
нет
нет
10
Есть другой
поставщик?
11
да
Оформить заказ
другому поставщику
да
нет
4
12
да
Тарифы
перевозок
возросли?
5
7
нет
Оформить заказ
поставщику
Разработать
заменитель
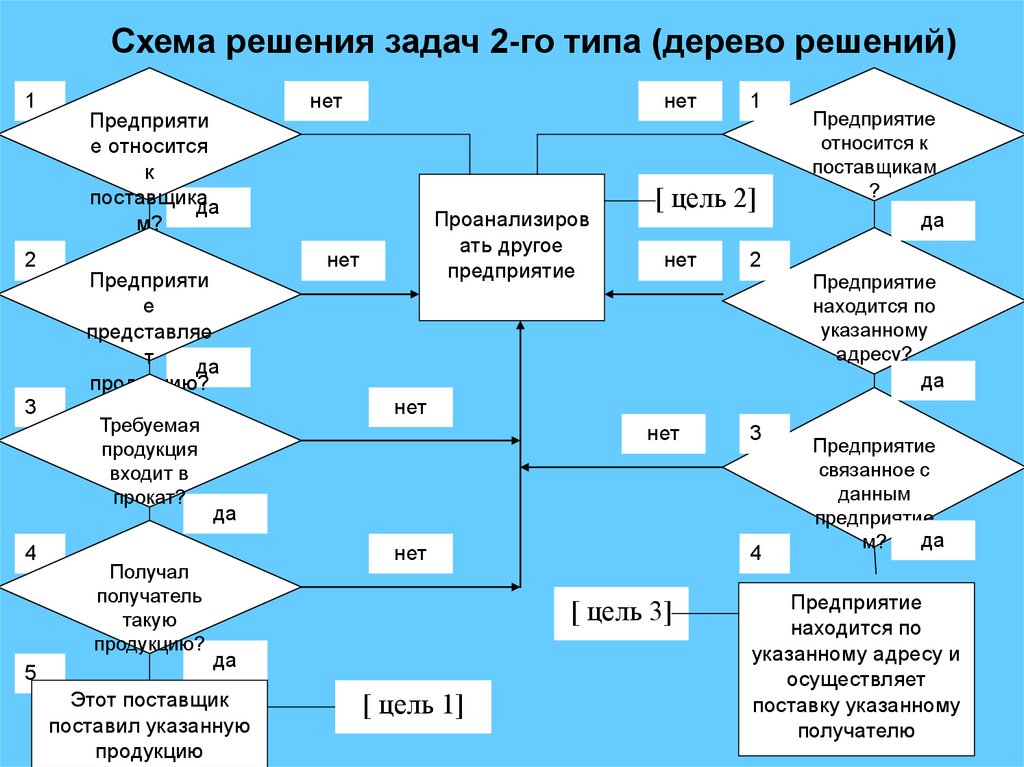
66.
Схема решения задач 2-го типа (дерево решений)1
2
3
4
5
Предприяти
е относится
к
поставщика
да
м?
Предприяти
е
представляе
т
да
продукцию?
Требуемая
продукция
входит в
прокат?
Получал
получатель
такую
продукцию?
нет
нет
Проанализиров
ать другое
предприятие
нет
1
[ цель 2]
нет
2
да
Предприятие
находится по
указанному
адресу?
да
нет
нет
3
да
нет
4
[ цель 3]
да
Этот поставщик
поставил указанную
продукцию
Предприятие
относится к
поставщикам
?
[ цель 1]
Предприятие
связанное с
данным
предприятие
да
м?
Предприятие
находится по
указанному адресу и
осуществляет
поставку указанному
получателю
67.
Тема 4 Статистический подход к ЭС.68.
Формирование матрицыПостроить ЭС – несложно. Прежде всего определим двухмерный массив,
считая его образом прямоугольной матрицы. И обдумав все вопросы, которые
вы хотели бы задать вашей ЭС, поместите в столбцы матрицы все возможные
ответы, затем продумайте все отсутствующие фрагменты исходной
информации, которые возможно потребуется экспертиза для получения
ответов на поставленные вопросы, и отметьте строки матрицы с указанными
фрагментами.
Область запросов – это та область, в которой экспертная система должна быть
экспертом.
Следует различать два типа информации. Постоянная информация – это
программная часть, а переменная информация – данные для конкретной
задачи.
Вероятность совершения события
Вероятности являются удивительно точными характеристиками. Они задаются
числами в диапазоне от 0 до 1. Рассмотрим два крайних случая, когда
вероятности = 0 и 1. Существует различия между случаем, когда вероятность
равна в точности 1, и случаем, когда она равна приблизительно 1, хотя эта
равна настолько, что мы могли бы писать просто 1.
Если вероятность какого-то события равно точно 1, то это событие должно
произойти.
Событие, вероятность наступления которого 0, исключена. Но событие,
вероятность которого близка к нулю, не исключена.
69.
Теорема БайесаТеорема Байеса утверждает, что:
Р(Д:Х)=Р(Х:Д)Р(Д)/(Р(Х:Д)Р(Д)+Р(Х: не Д) Р(не Д)
т.е. Д – событие, означающее Дождь завтра, Х – любая
конкретная комбинация событий, описывающих погоду
сегодня. (Например, Сыро, Ветрено) Тогда вероятность дождя
завтра при условии, что погода сегодня характеризуется
комбинаций Х, равна вероятности наступления события Х
сегодня при условии, что завтра будет дождь, умноженной на
вероятность дождя сегодня, деленной на полную вероятность
наступления событий Х. Докажем это утверждение.
Известно, что Р(Д:Х)=Р(Д:Х)/Р(Х),
поэтому Р(Х:Д)=Р(Х&Д)/Р(Д),
а поскольку Р(Х&Д)=Р(Х:Д)Р(Д)=Р(Д:Х)Р(Х),
то окончательно получаем
Р(Д:Х)=Р(Х:Д)Р(Д)/Р(Х)=Р(Х:Д)Р(Д)/(Р(Х:Д)Р(Д)+Р(Х: не Д) Р(не Д))
70.
Для ответа на один вопрос вам придется найтивероятность дождя завтра при наступлении события Х
сегодня. Для ответа на другой вопрос вам придется
вычислить вероятность наступления события Х при
условии, что завтра пойдет дождь. Вам также нужно
задать вероятность Р(Х, не Д), т.е. вероятность
наступления события Х при условии отсутствия осадков
сегодня. Будет совсем плохо, если все события окажутся
коррелированными друг с другом. Тогда вам придется
задавать
вероятности
для
каждой
возможной
комбинации. Если же они окажутся независимыми, можно
вычислить вероятность Р(Д:Х). Допустим, например, что
под событии Х подразумевается два события Y и Z. В
этом случае
Р(Х:Д)=Р(Y&Z:Д)=Р(Y:Д) Р(Z:Д).
Но Р(Д:Х)= Р(Д:Y&Z) не равно Р(Д:Y)Р(Д:Z).








































 Математика
Математика








