Похожие презентации:
Введение в дисциплину «Математические основы интеллектуальных технологий»
1.
Математические основыинтеллектуальных технологий
Преподаватель –
Тонких Артём Петрович
2.
1. Введение в дисциплину«Математические основы
интеллектуальных технологий»
3.
Теория нечетких множеств:- Новый раздел математики
- Практико-ориентированный характер
Причина популярности:
- Предоставляет аппарат формализации
неопределенностей при моделировании реальных
объектов
Формализация любого объекта (процесса)
начинается с описание на естественном языке.
ТНМ позволяет формализовать понятия:
“высокий уровень инфляции”, “средний уровень
доходов” и т.п.
4.
Т.е.1. ТНМ позволяет проводить математическое
моделирование рассуждений человека.
2. ТНМ является инструментом управления
объектами в условиях неполной и нечеткой
информации.
3. Алгоритмы и технологии ТНМ являются
универсальными.
5.
“Нечеткие множества” (Fuzzy Sets) - Lotfi Askar Zadeh(1965) американский ученый.
“Нечеткая математика”, “Нечеткая логика”,
“Нечеткая геометрия”
Основная идея:
Расширение канторовского понятия множества.
(функция принадлежности)
6.
2. Примеры обычных инечетких множеств
7.
Множество – неопределяемое понятие математики.Георг Кантор (1845-1918) – “… множество – это
многое, мыслимое как единое”
Каждый раздел математики использует свои
множества.
Универсальное множество U – множество,
включающее в себя все объекты рассматриваемой
задачи. U – максимальное множество.
– минимальное множество.
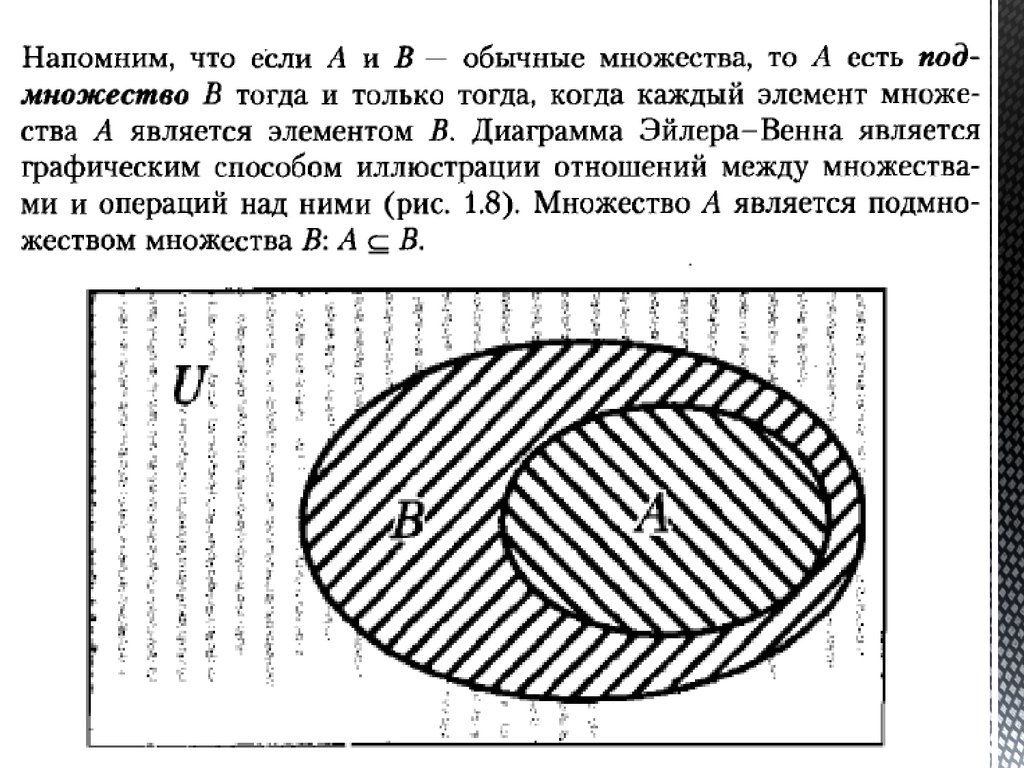
Любое множество является подмножеством U
8.
Множество A называют подмножеством B – есливсе элементы А являются также элементами B.
Задать множество А – определить правило,
позволяющее относительно любого элемента х
однозначно определить x A или x A
Один из способов задания множества - с помощью
характеристической функции
9.
Характеристическая функция множества А –функция A ( x) заданная на универсальном
множестве U и принимающая значение 1 на тех
элементах множества U, которые принадлежат A, и
значение ноль на тех элементах которые не
принадлежат A:
0, если x A
A ( x)
1, если x A
x U
10.
ПримерU 1,2,3,...,10
Необходимо задать множество А – числа меньше 7
Тогда характеристическую функция будет такой:
0, если x 7
A ( x)
1, если x 7
11.
ПримерU 1,2,3,...,10
Множество B – множество чисел немного меньше 7
Описать такое множество с помощью
характеристической функции нельзя.
- “Намного” или “ненамного” 3 меньше 7?
- Включать 1 и 2 в множество B?
Ответы на эти вопросы зависят от:
- Условий, решаемой задачи.
- Эксперта, решающего задачу.
12.
U 1,2,3,4,5,6,7,8,9,10Эксперт относительно каждого элемента U может
высказать мнение, выраженное в виде числа [0; 1] о
принадлежности к множеству B.
B ( x) 1 полная уверенность в принадлежности x к B
B ( x) 0 полная уверенность в непринадлежности
xкB
B ( x) 0,4
B ( x) 0,7
13.
Функция, определяющая степень принадлежностилюбого элемента универсального множества к
нечеткому множеству в виде значения на отрезке
[0; 1] называют функцией принадлежности
функция принадлежности описывает субъективный
взгляд эксперта
Таким образом:
А – четкое множество, заданное характеристической
функцией.
B – нечеткое множество, заданное функцией
принадлежности.
14.
Запись множеств:Значения A ( x ) и B ( x) можно представить в
виде таблицы
Компактная запись конечных множеств:
“+” это не сложение, а объединение
одноэлементных подмножеств U
15.
При компактной записи используется тольконесущее множество (носитель) – те элементы
универсального множества U, у которых степень
принадлежности >0
Общая форма записи декретного нечеткого
множества имеет вид:
n
A A (ui ) / ui (ui U )
i 1
16.
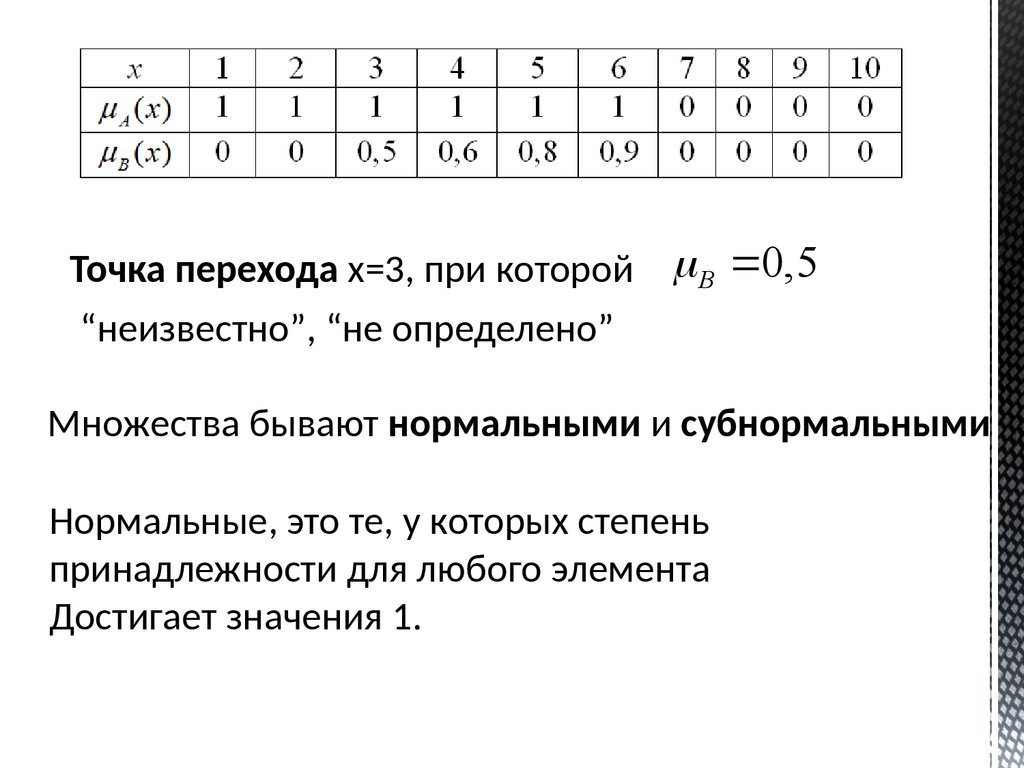
Точка перехода x=3, при которой B 0,5“неизвестно”, “не определено”
Множества бывают нормальными и субнормальными
Нормальные, это те, у которых степень
принадлежности для любого элемента
Достигает значения 1.
17.
Субнормальные множества можно нормировать путемлинейного преобразования значений степени
принадлежности μ
18.
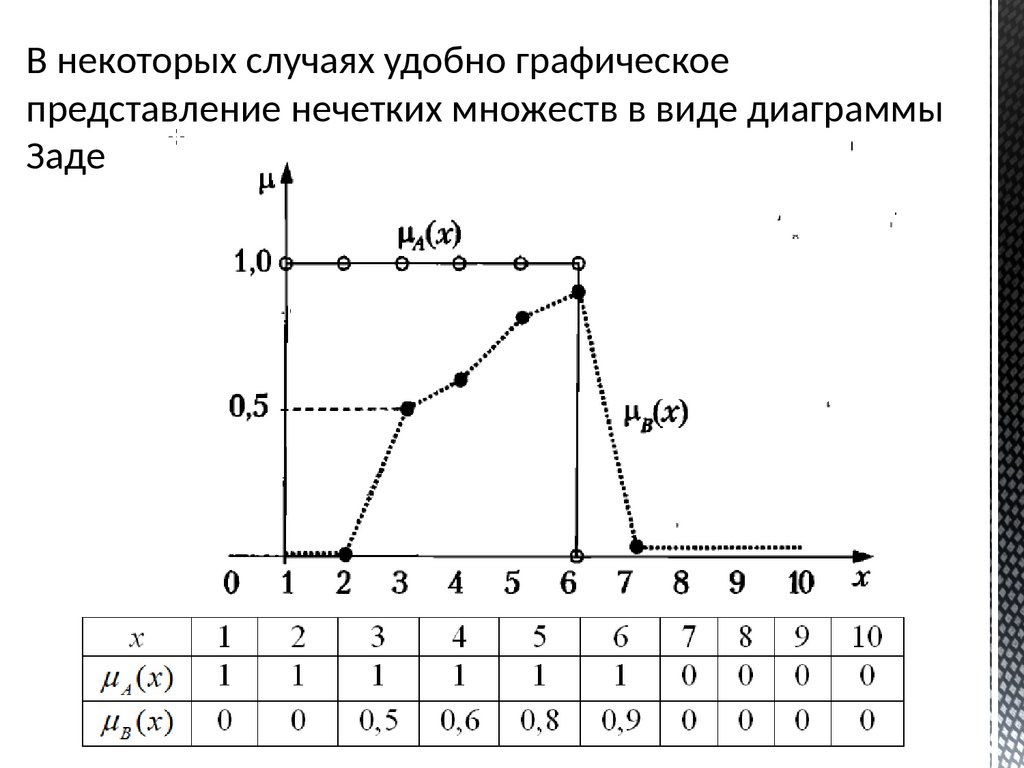
В некоторых случаях удобно графическоепредставление нечетких множеств в виде диаграммы
Заде
19.
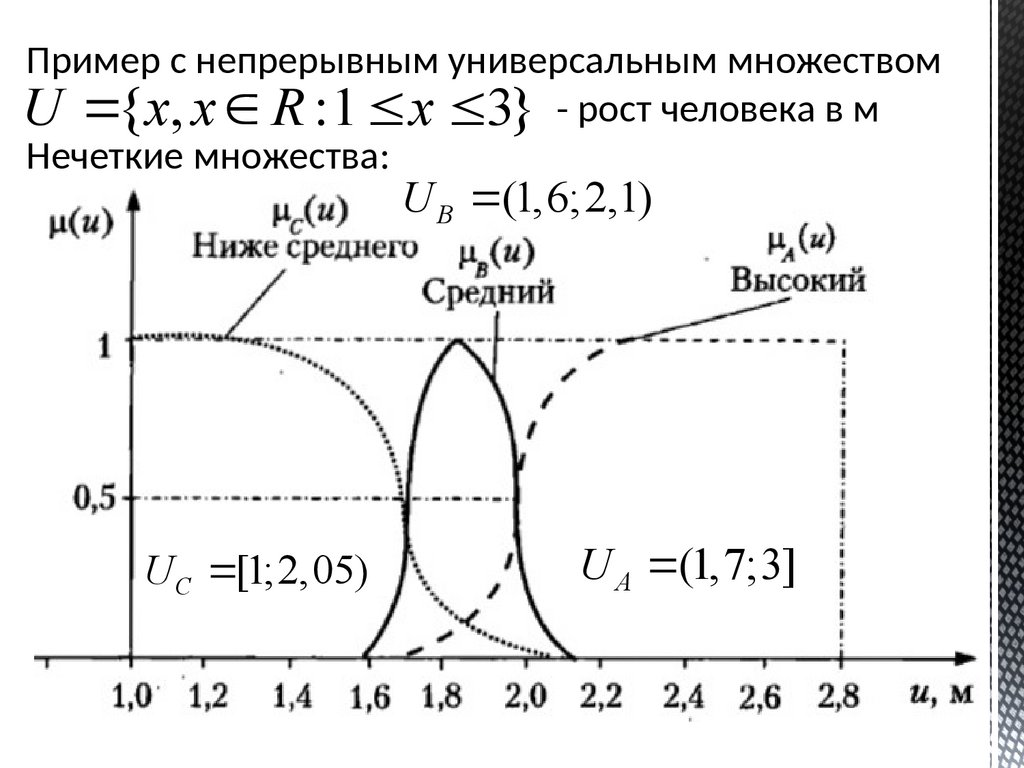
Пример с непрерывным универсальным множествомU {x, x R :1 x 3} - рост человека в м
Нечеткие множества:
U B (1,6;2,1)
U C [1;2,05)
U A (1,7;3]
20.
U A (1,7;3]U B (1,6;2,1)
U C [1;2,05)
Это не интегрирование, а объединение элементов
несущего множества с непрерывным носителем
Запись для дискретного и непрерывного носителя
разная, но читаются оба знака, как “сумма по
множеству U”
21.
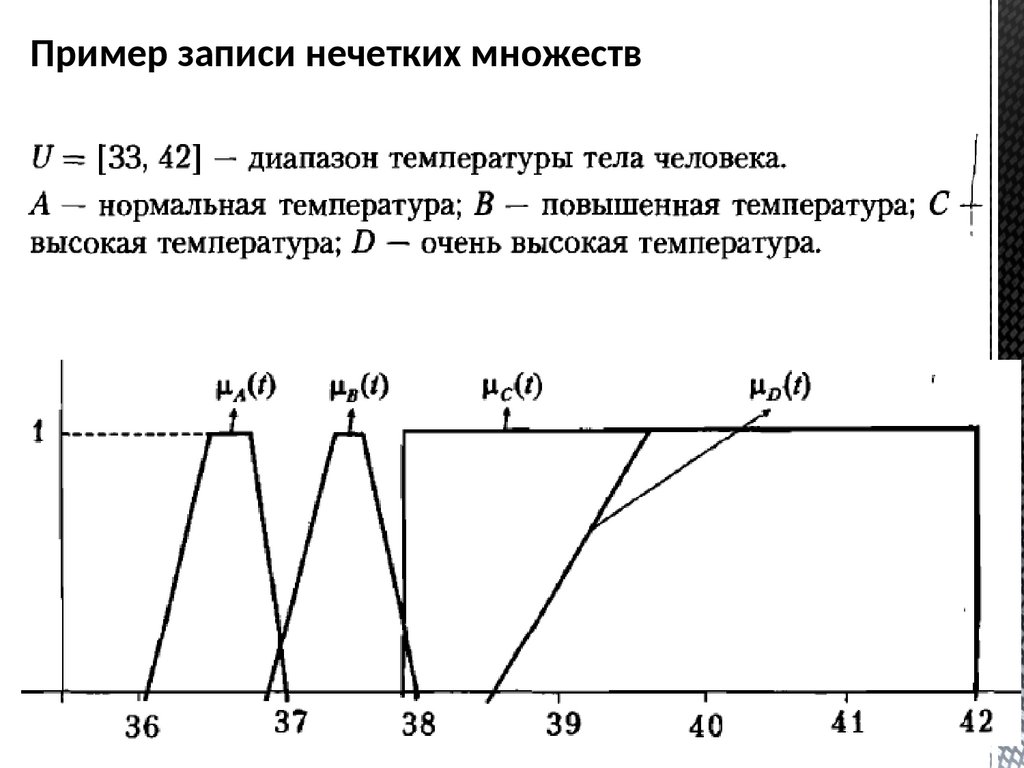
Пример записи нечетких множеств22.
23.
24.
Пример записи нечетких множеств №2Игра – в кости. Подбрасываются 2 кости, необходимо
угадать количество выпавших очков.
Игрок М делает следующие ставки: 2, 3, 4 – 50 коп.,
5,6,7 – 10 руб., 8,9,10 – 20 руб., 11,12 – 10 руб.
Сформируем неч. множ. А – ожидаемое количество
очков
U 1,2,3,...,10
25.
Табличная запись:Запись - поэлементная сумма по множеству U:
Запись - сумма по множеству U:
26.
27.
28.
3. Множества α-уровня29.
Множества α-уровня нечеткого множества – обычноемножества заданного через μA, состоящие из всех
элементов универсального множества U, для которых
выполняется неравенство μA≥α.
Применяются, например, при расчете нечеткого
вывода в нечетких системах управления, а
также при выполнении операций над
нечеткими множествами.
30.
Пример №1:{0,1; 0,2; 0,5; 0,9}
Множества α-уровня:
31.
Нечеткое множество для α=0,1:Нечеткие множества остальных уровней:
32.
Объединим:Получаем:
- знак логической суммы, операция
нахождения супремума
33.
Результат объединения:А вот исходное множество:
Результат:
Различия:
34.
Пример №2:А – числа примерно равные 5.
Множество значений α.
35.
36.
Объединим нечеткие множества α-уровня:Результат:
37.
Сравним результаты примеров №1 и 2:В первом случаеВо втором случаеПричина различия:
В первом случае множество α включает в
себя не все уникальные значения
степеней принадлежности множества А.
Во втором случае множество α включает
все уникальные значения.
38.
Форма записи разложения множества Ана множества α-уровня.
Запись на не сущем множестве:
Общая форма записи:
“·” – это не умножить, а присвоить степень
принадлежности
39.
Разложением дискретного нечеткогомножества по множествам уровня –
называется его представление в виде
равенства:
Читается, как “сумма множеств αуровня”
40.
Пример №3:Пусть функция принадлежности нечеткого
множества A имеет следующий вид
Выполним разложение нечеткого
множества по множествам уровня.
41.
42.
43.
Разложением непрерывного нечеткогомножества по множествам уровня –
называется его представление в виде
равенства:
44.
Пример №4:Пусть функция принадлежности нечеткого
множества A имеет следующий вид
Требуется выполнить приближенное
разложение нечеткого множества
45.
1. Разобьем отрезок [0; 1] на равные части2. Получим набор дискретных значений
3. Тогда приближенное разложение для
непрерывного множества A примет
“дискретный” вид
46.
4. Методы построенияфункции принадлежности
47.
Основная проблема теории нечеткихмножеств:
“Основной
трудностью,
мешающей
интенсивному
применению
теории
нечетких множеств при решении
практических задач, является то, что
функция принадлежности должна быть
задана
вне
самой
теории
и
следовательно ее адекватность не может
быть
проверена
непосредственно
средствами теории…
48.
… В каждом известном методепостроения функции принадлежности
формулируются свои требования и
обоснования к выбору именно такого
построения”
Ronald Robert Yager,
Director of the Machine Intelligence Institute and
Professor of Information Systems at Iona College.
49.
Результат:Наряду с нечеткими множествами
разрабатываются и применяются другие
методы работы с неполной, неточной,
нечеткой информацией:
- Робастные методы
- Вероятностные методы
- Интервальные методы
50.
2метода
задания
принадлежности:
функций
1. Прямой метод:
Задание
функции
принадлежности
экспертом для каждого значения
универсального множества. Не требуется
точное задание функции, достаточно
фиксации ее вида и характерных
значений
51.
2. Косвенный метод:Применяется, когда у объекта есть
измеримые свойства.
Примеры:
- функция принадлежности
должна
отражать
близость
к
заранее
выделенному эталону;
- объекты множества
U являются
точками
в
параметрическом
пространстве;
- при попарном сравнении объектов.
52.
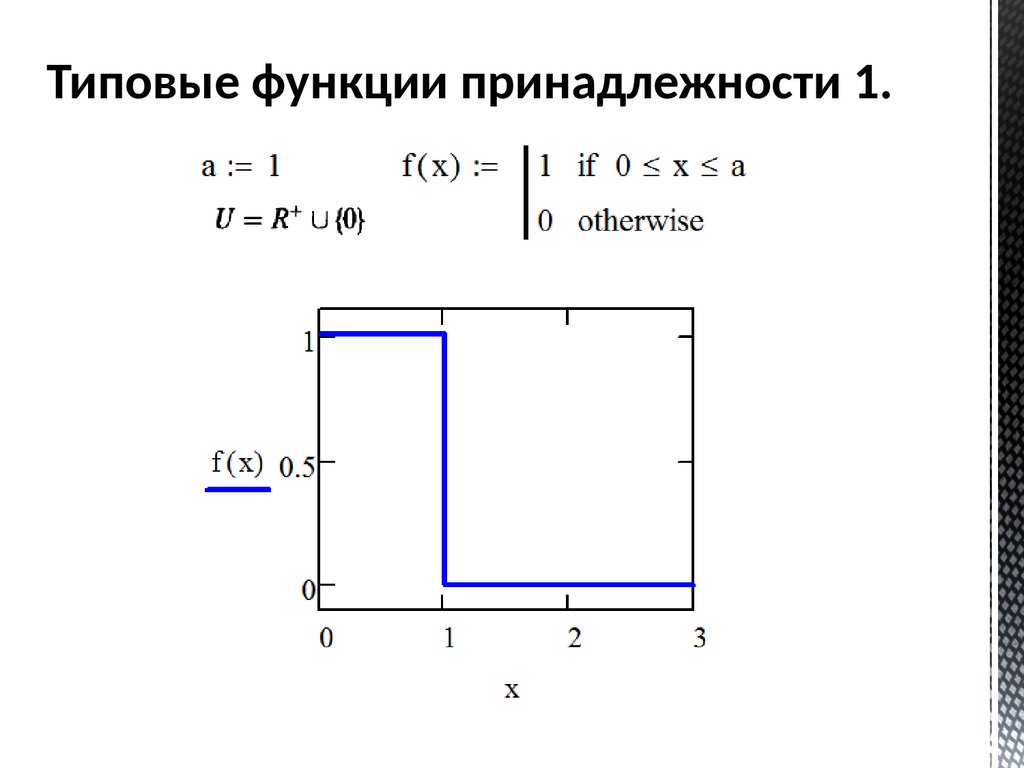
Типовые функции принадлежности 1.53.
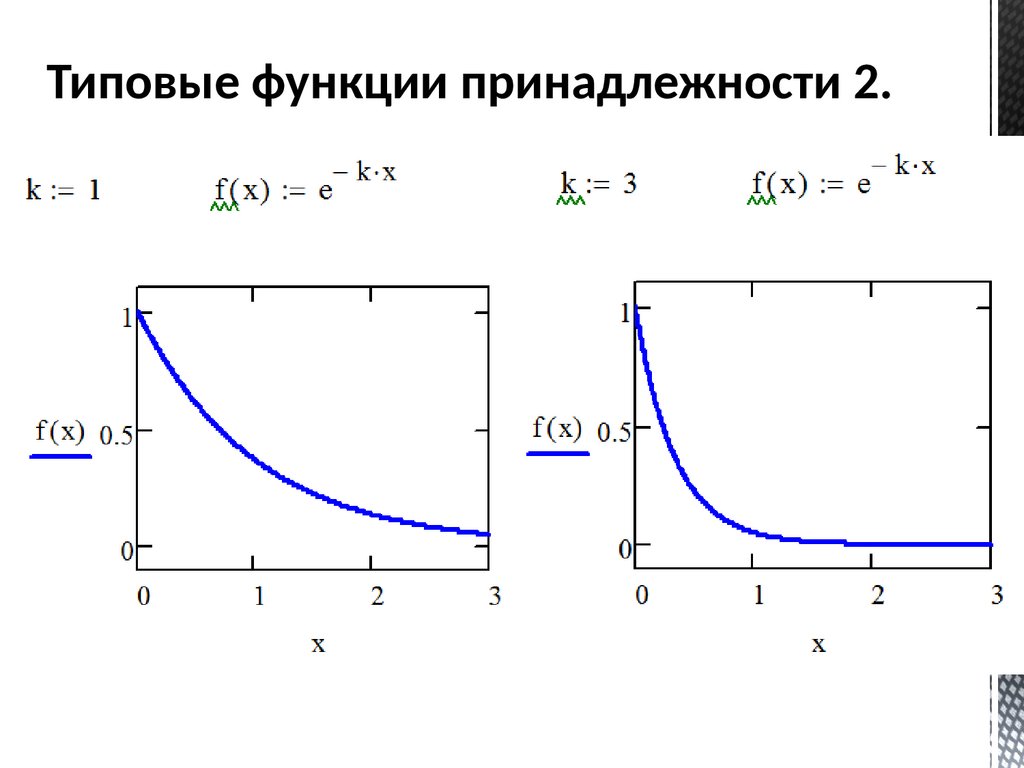
Типовые функции принадлежности 2.54.
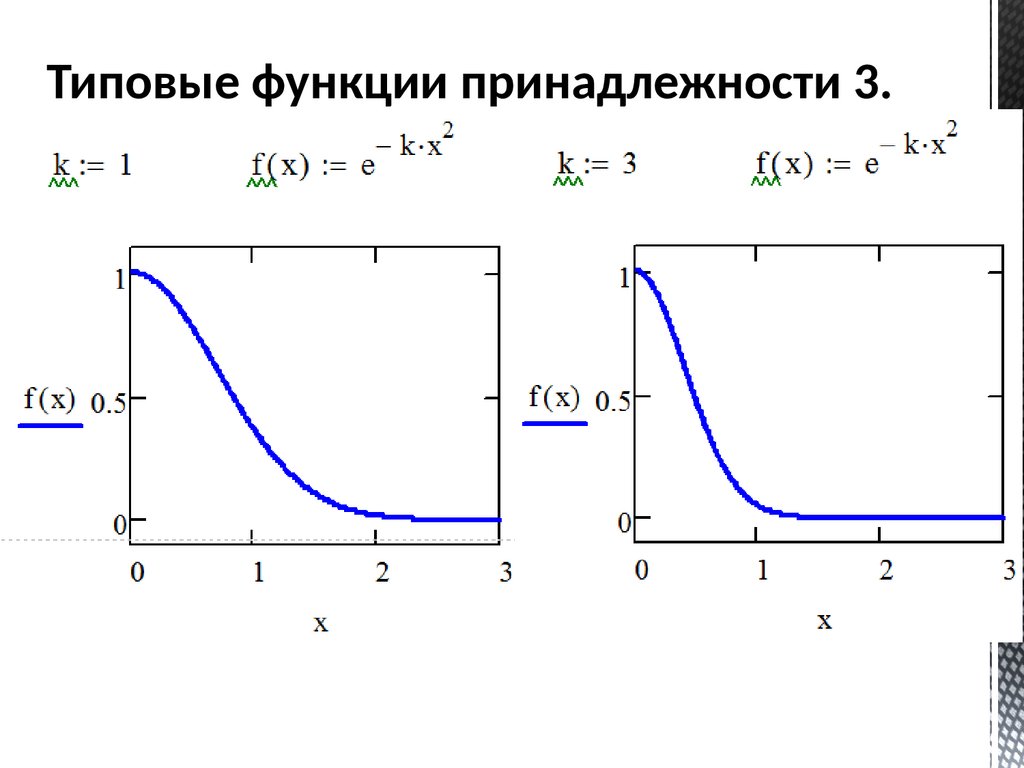
Типовые функции принадлежности 3.55.
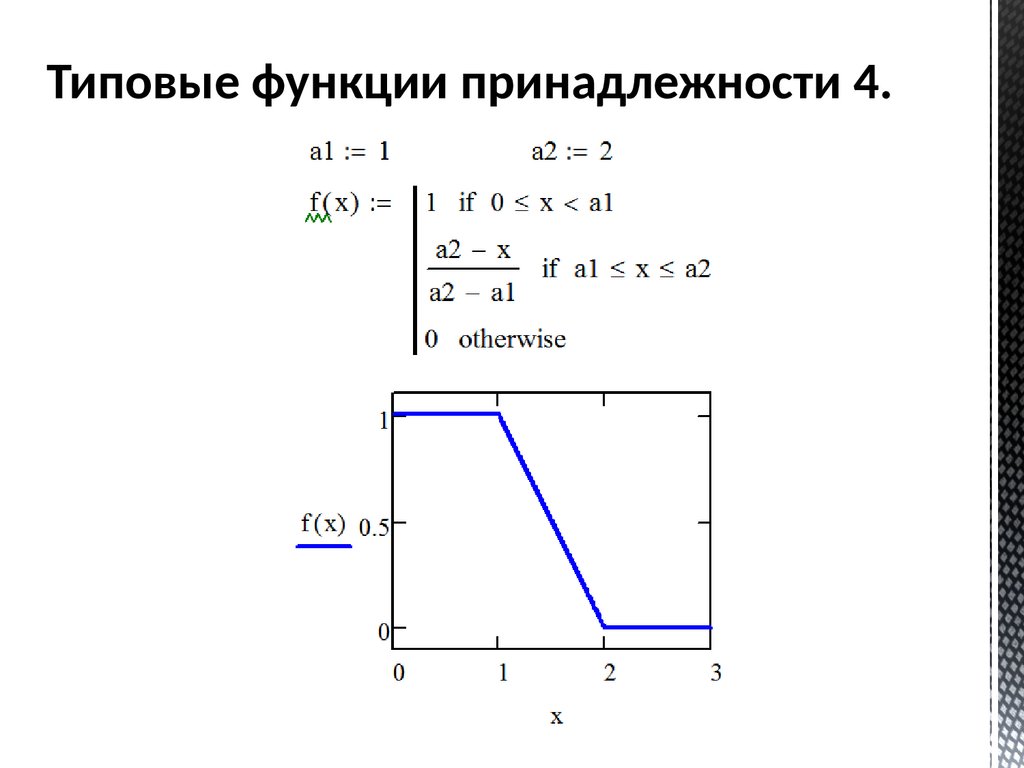
Типовые функции принадлежности 4.56.
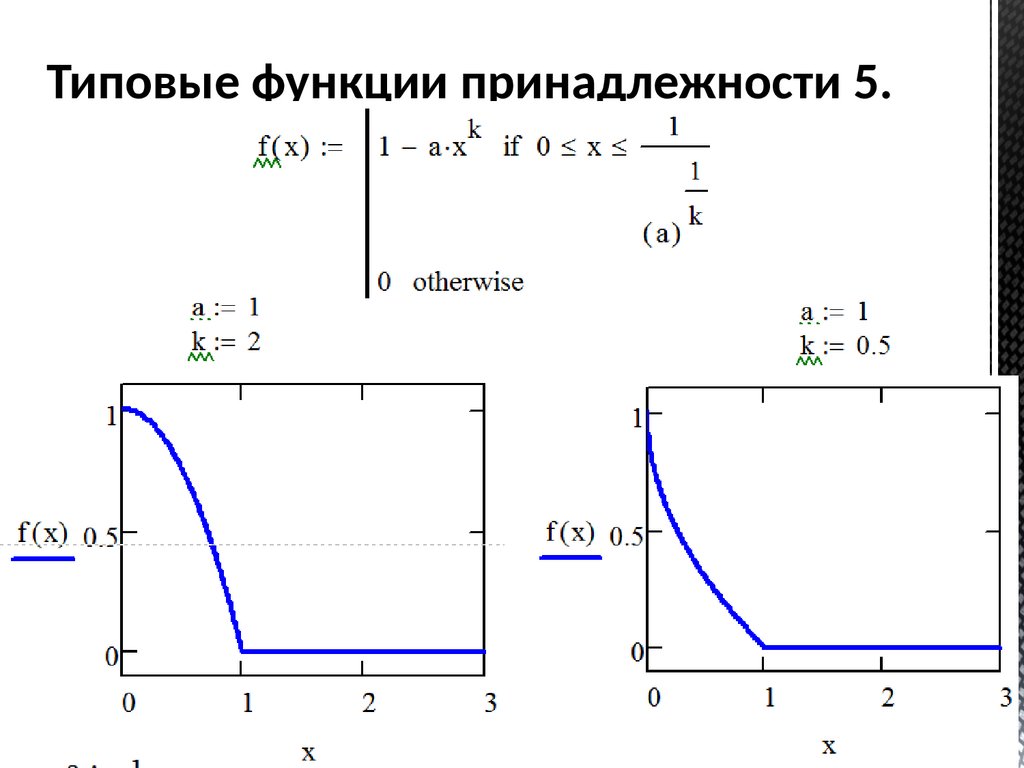
Типовые функции принадлежности 5.57.
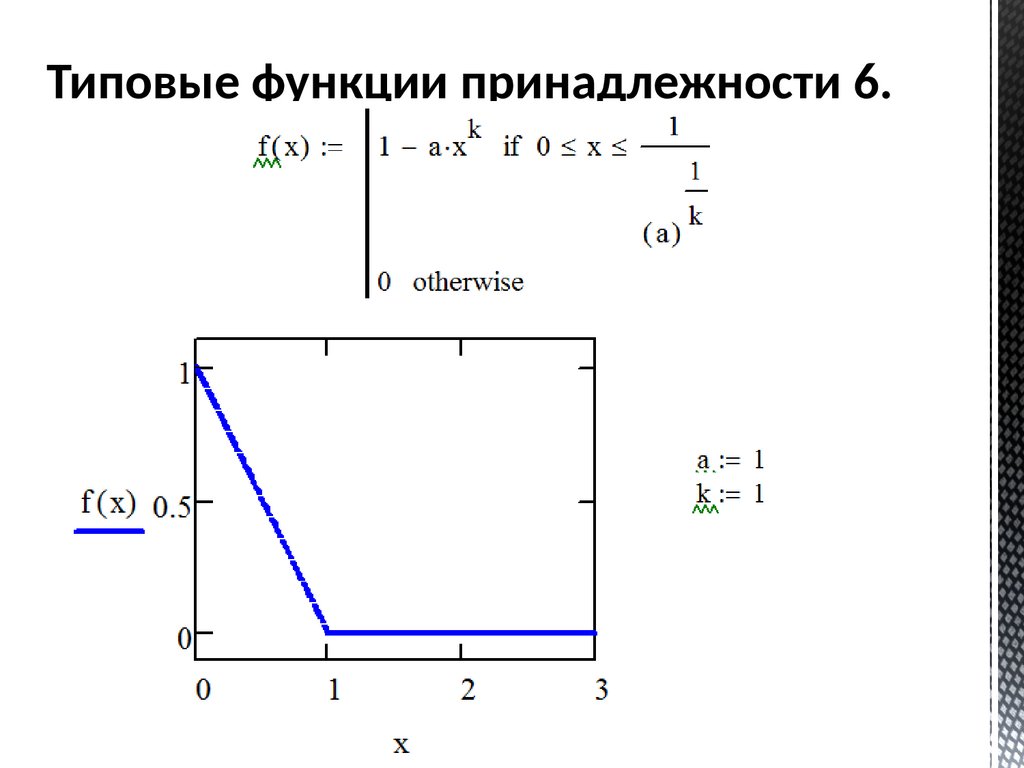
Типовые функции принадлежности 6.58.
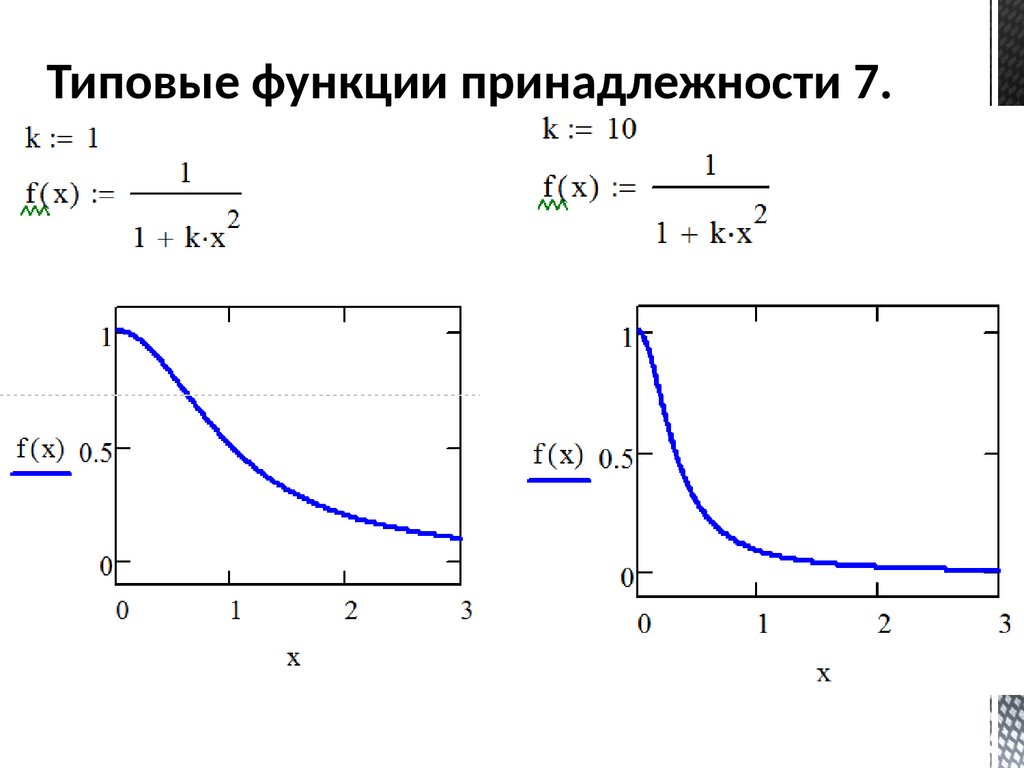
Типовые функции принадлежности 7.59.
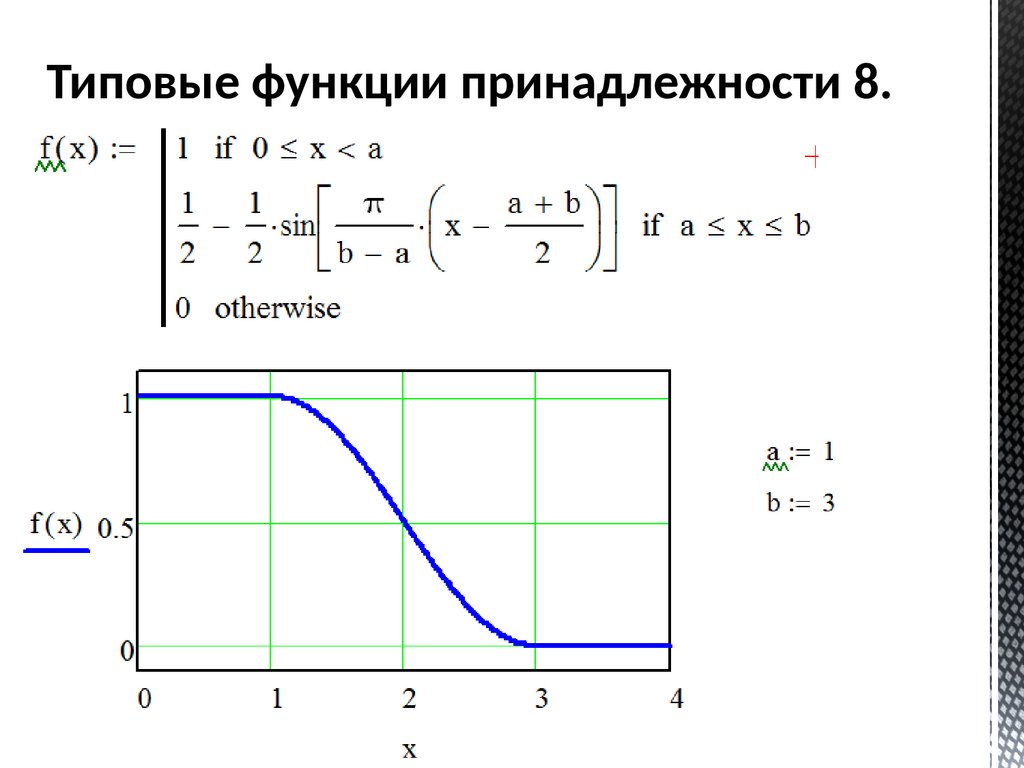
Типовые функции принадлежности 8.60.
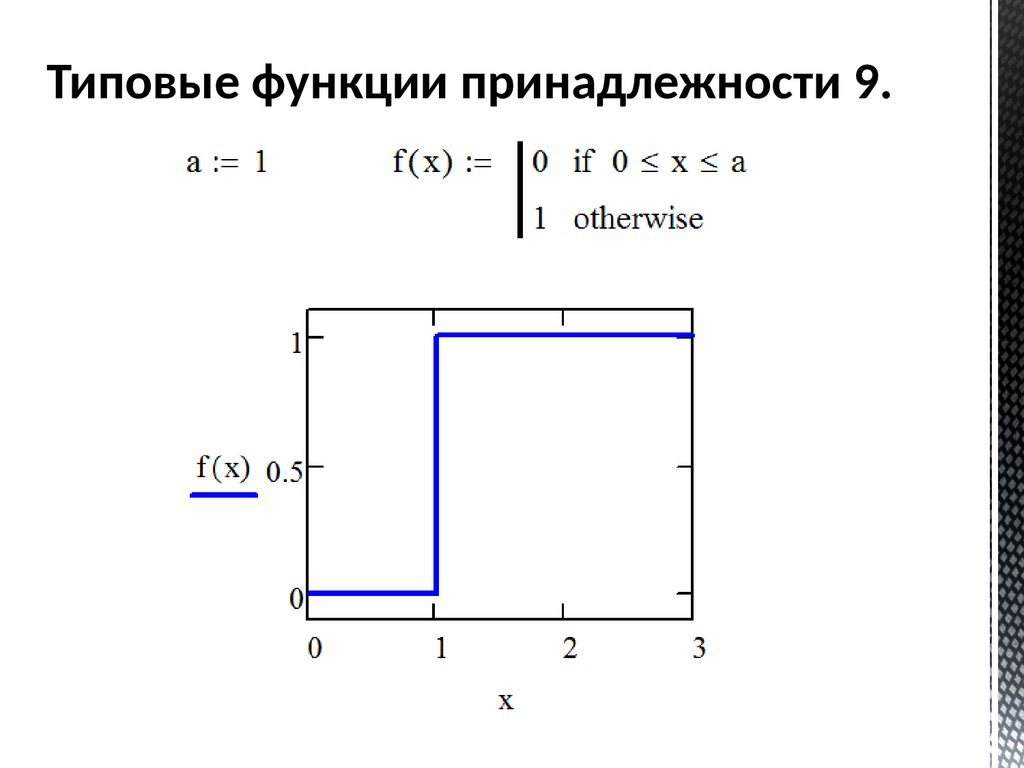
Типовые функции принадлежности 9.61.
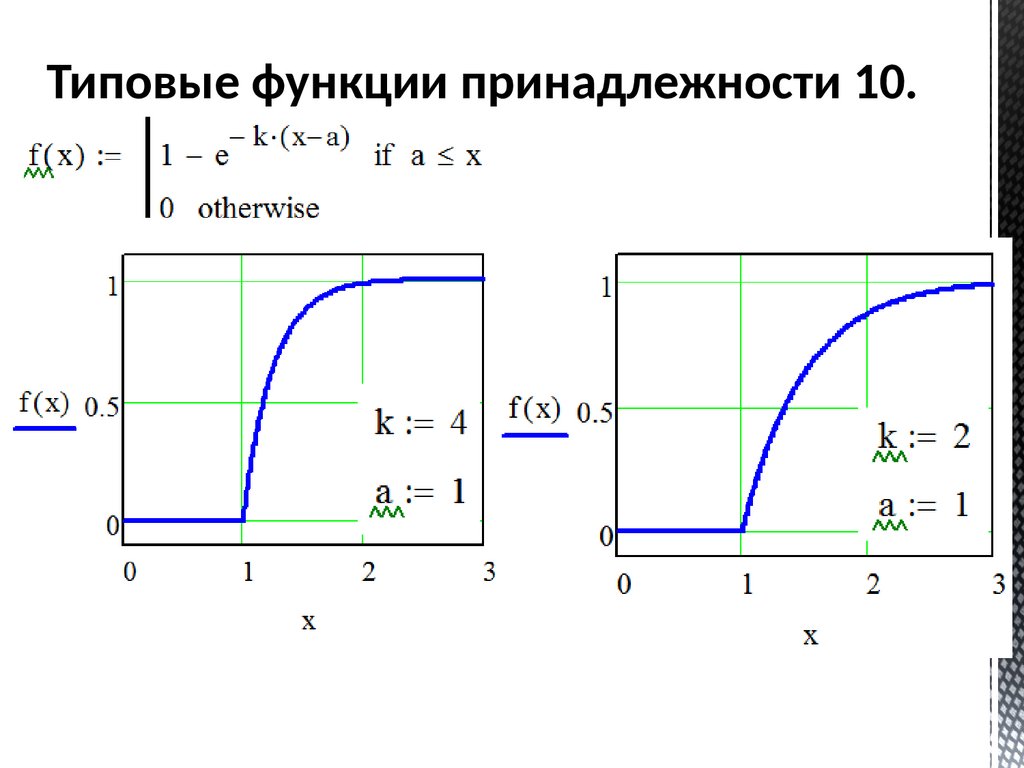
Типовые функции принадлежности 10.62.
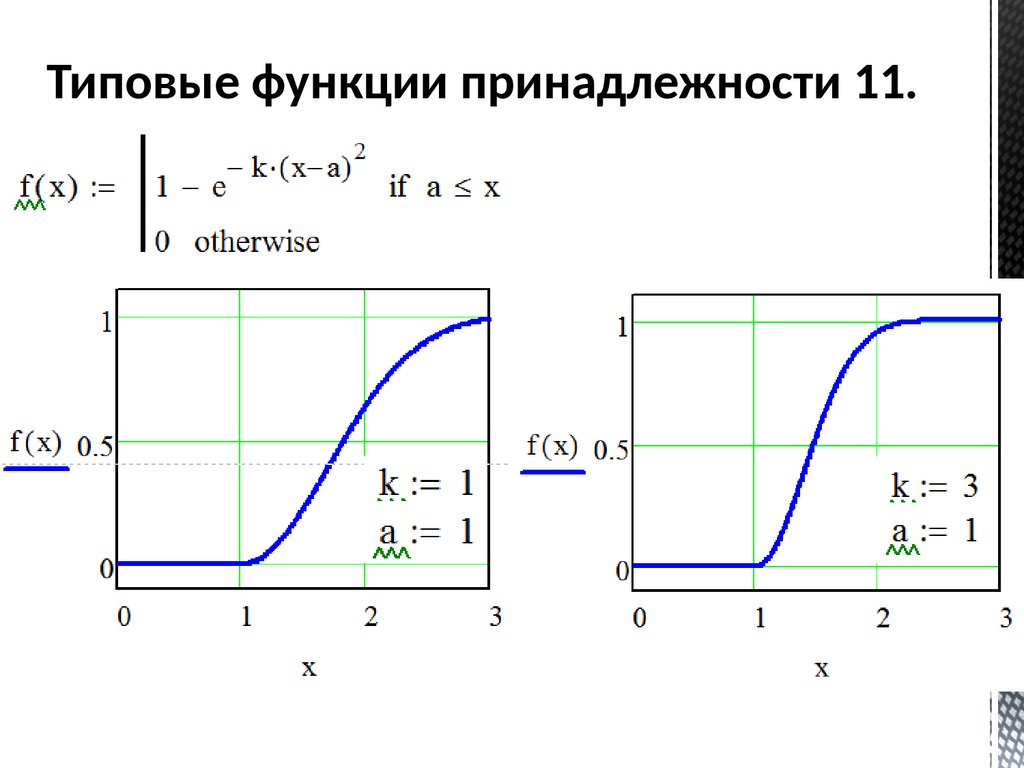
Типовые функции принадлежности 11.63.
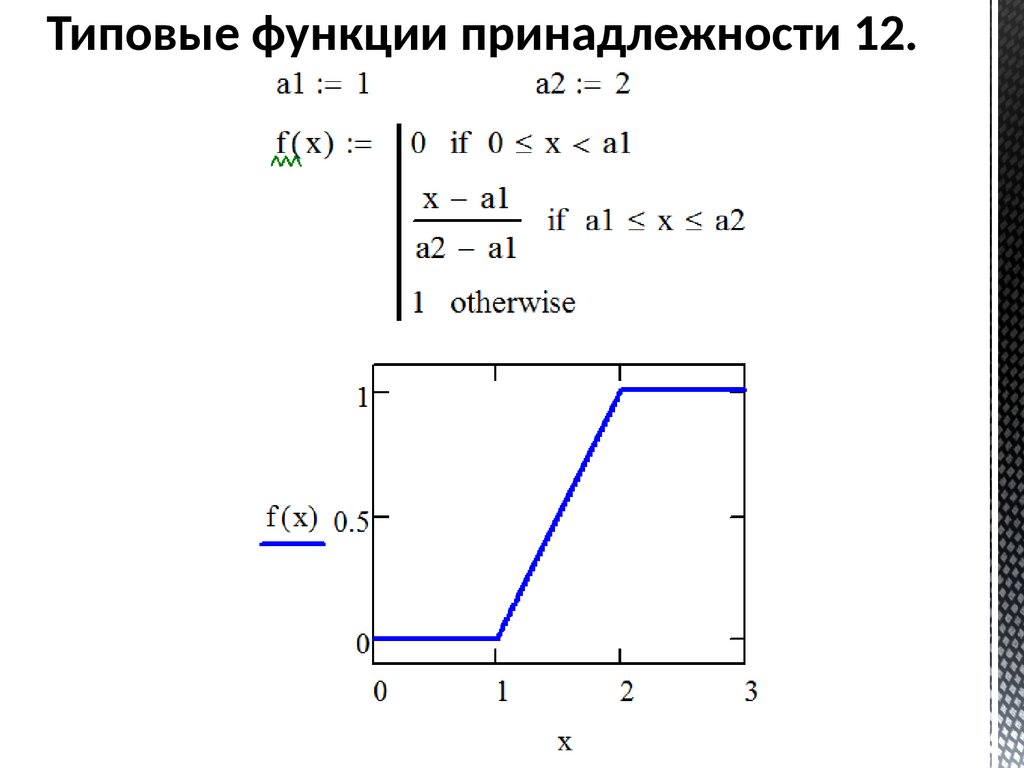
Типовые функции принадлежности 12.64.
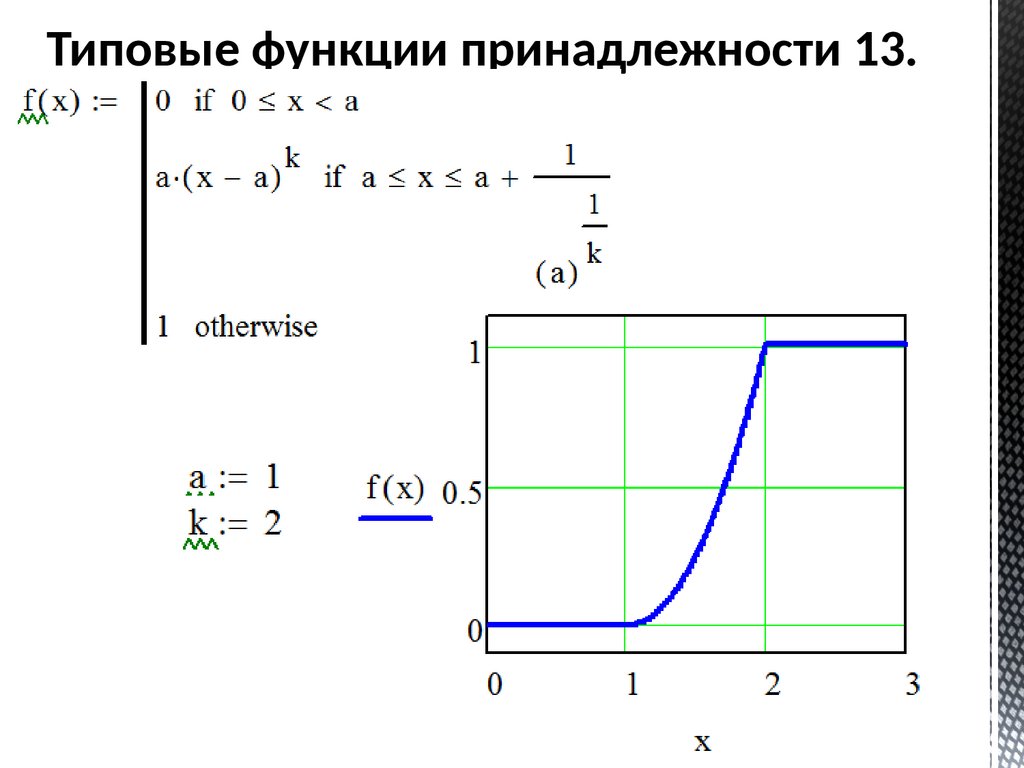
Типовые функции принадлежности 13.65.
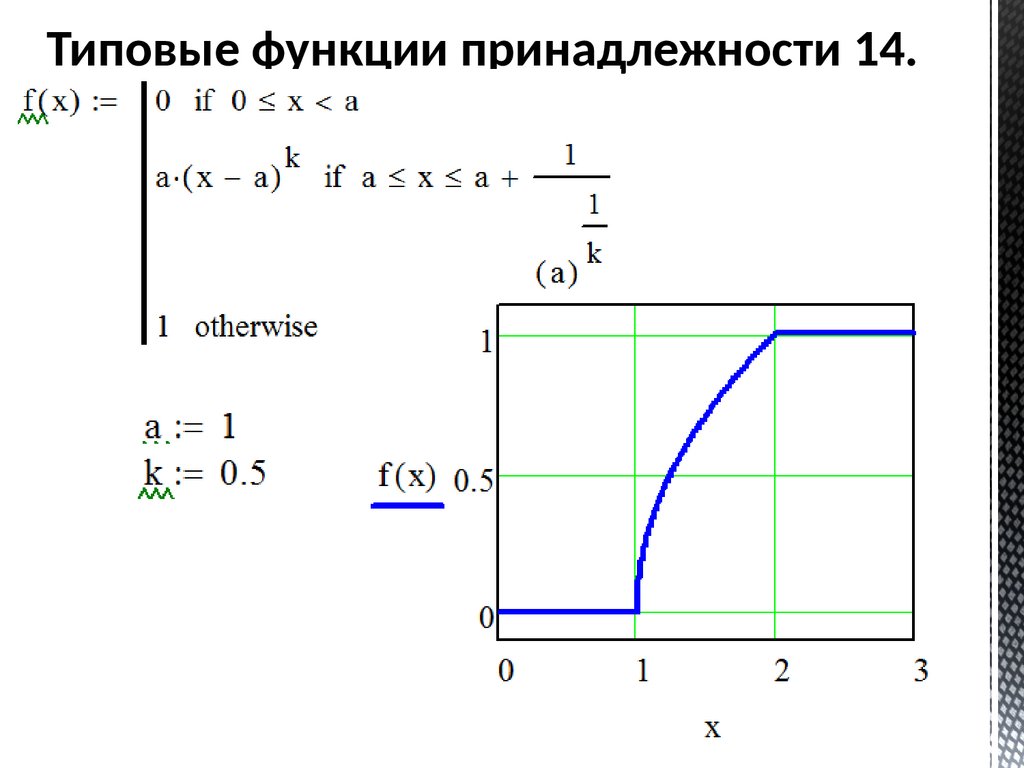
Типовые функции принадлежности 14.66.
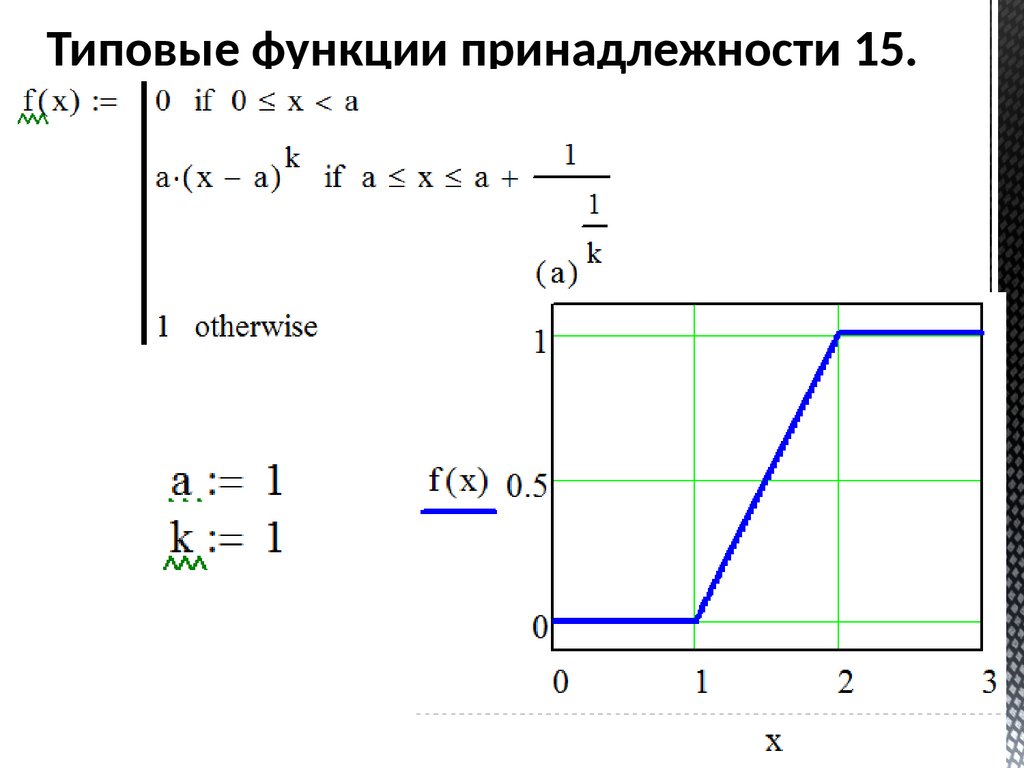
Типовые функции принадлежности 15.67.
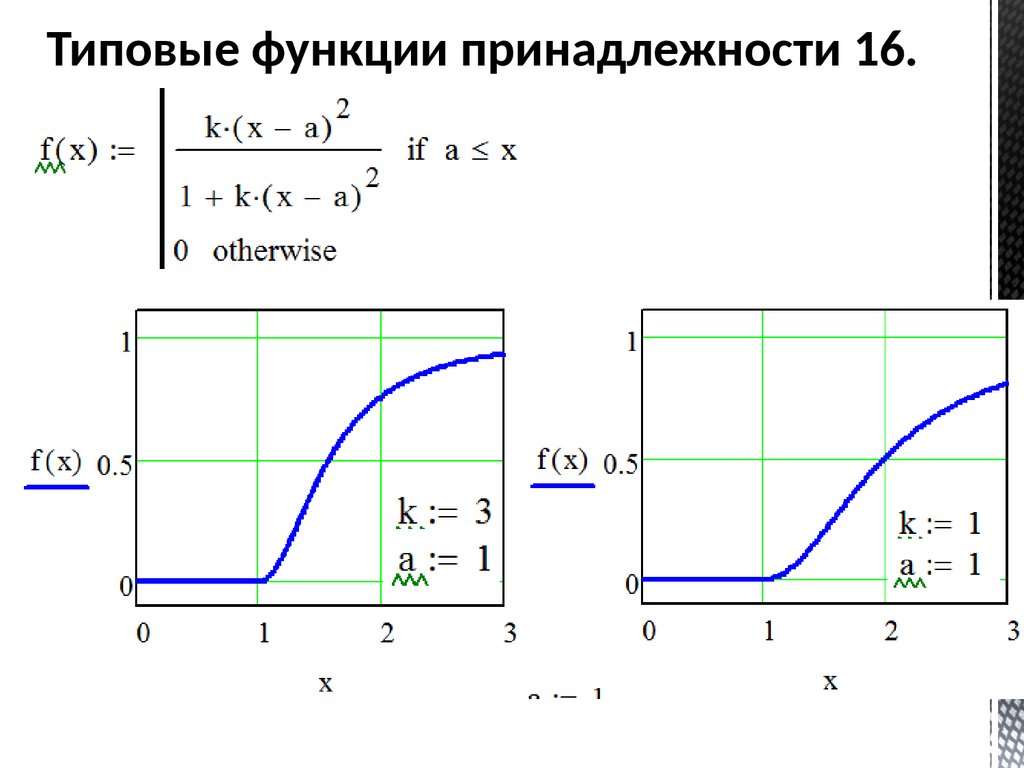
Типовые функции принадлежности 16.68.
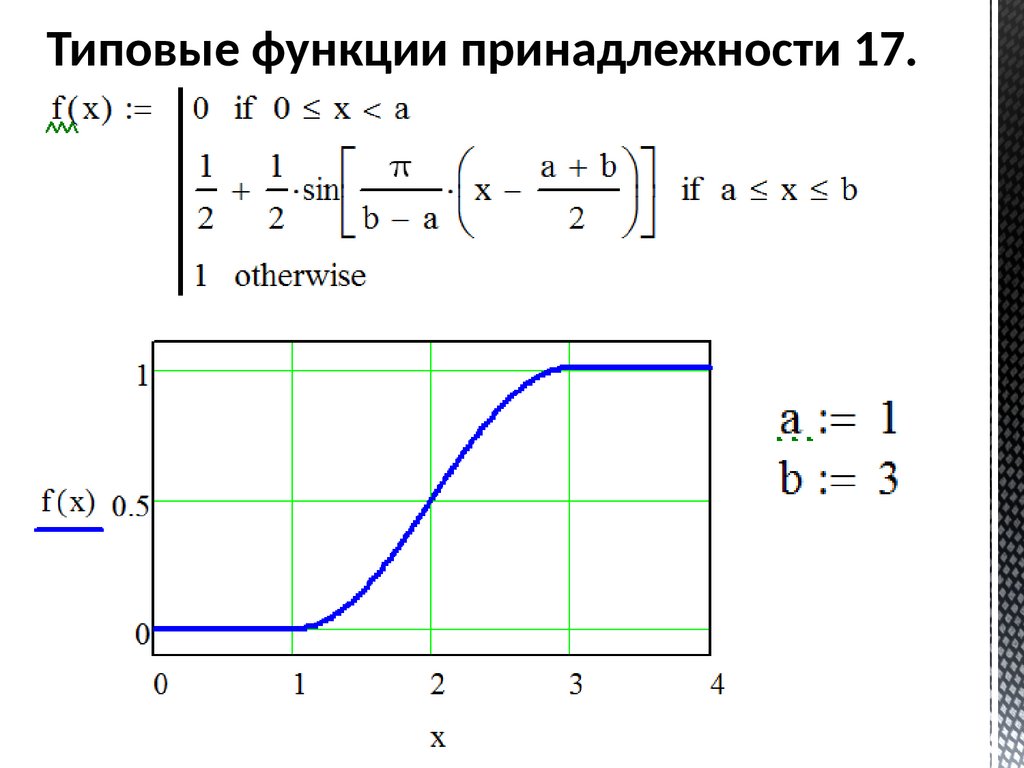
Типовые функции принадлежности 17.69.
5. Меры нечеткости70.
Идея оценки нечеткости1. “самое нечеткое” множество
(μ(ui)=0,5)
2. “самое нечеткое” множество
(μ(ui)=0 или 1)
Основная идея:
Определять нечеткость множеств в
зависимости от близости значений
μ(ui) к 0 или 1.
71.
Мера нечеткостиМера – это значит, что на выходе
должно быть нечеткое число, в
зависимости от степени нечеткости
72.
Аксиомы меры нечеткости73.
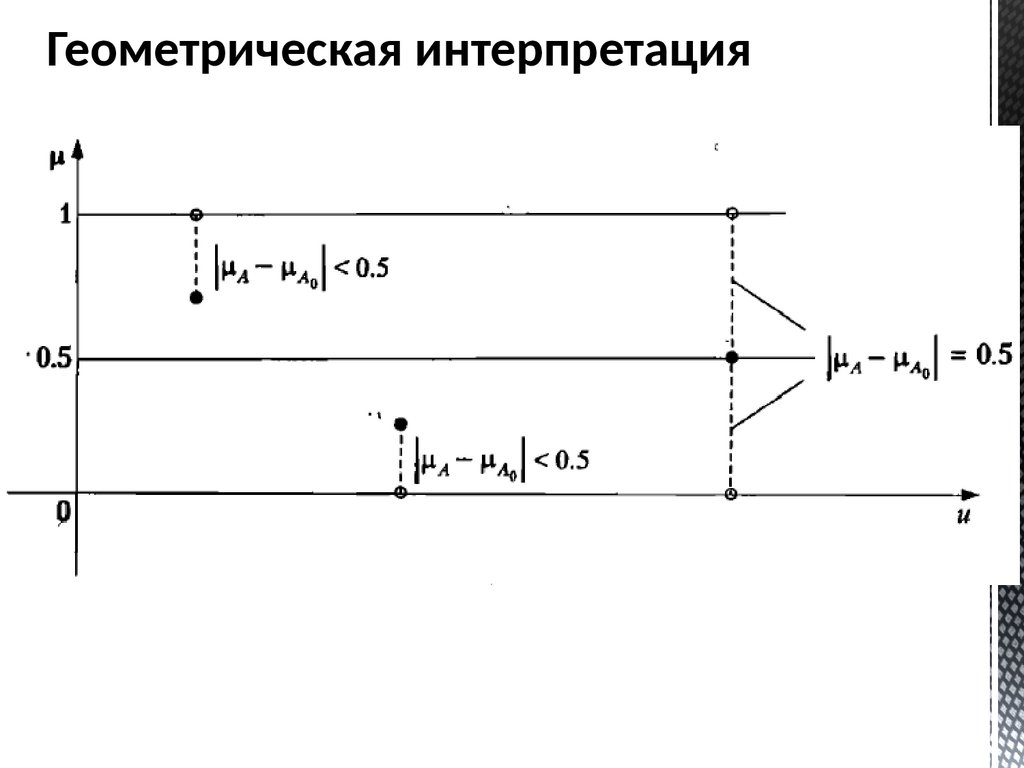
Мера нечеткости обычно рассчитываетна основе расстояния от нечеткого
множества А до ближайшего к нему
обычного множества A0
74.
Геометрическая интерпретация75.
Наложение метрики76.
Виды метрик77.
Виды метрик78.
Самое нечеткое множество должно быть С (IIаксиома меры нечеткости):
(?!)
79.
Причина противоречия – “сравнение того, что нельзясравнивать”
Решение (2 пути):
1) Дополнить носитель множества С элементами 4 и
5 (значения μ=0)
2) Модифицировать выбранную меру нечеткости.
80.
Модификация алгоритма :- Нормировка метрики так, чтобы для любого
множества мера нечеткости не превышала 1.
Нормированное расстояние называется индексом
нечеткости.
81.
Индексом нечеткости.Линейное расстояние.
Евклидово расстояние.
Линейное расстояние.
Евклидово расстояние.
82.
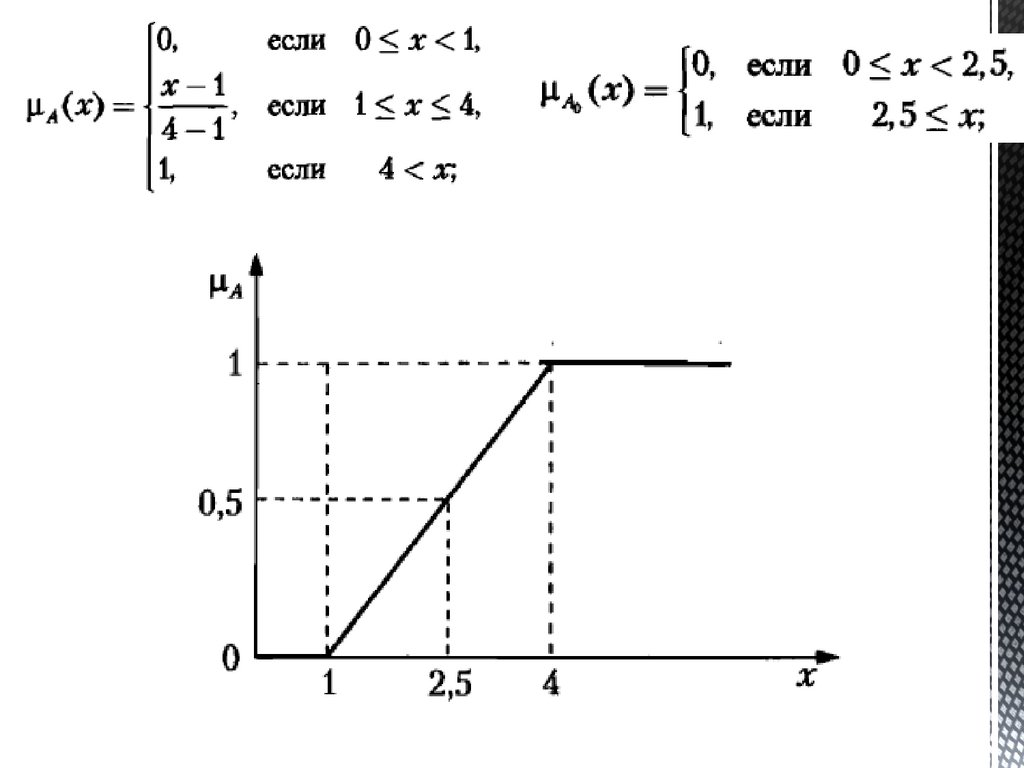
Вернемся к тому примеру:Индексом нечеткости.
83.
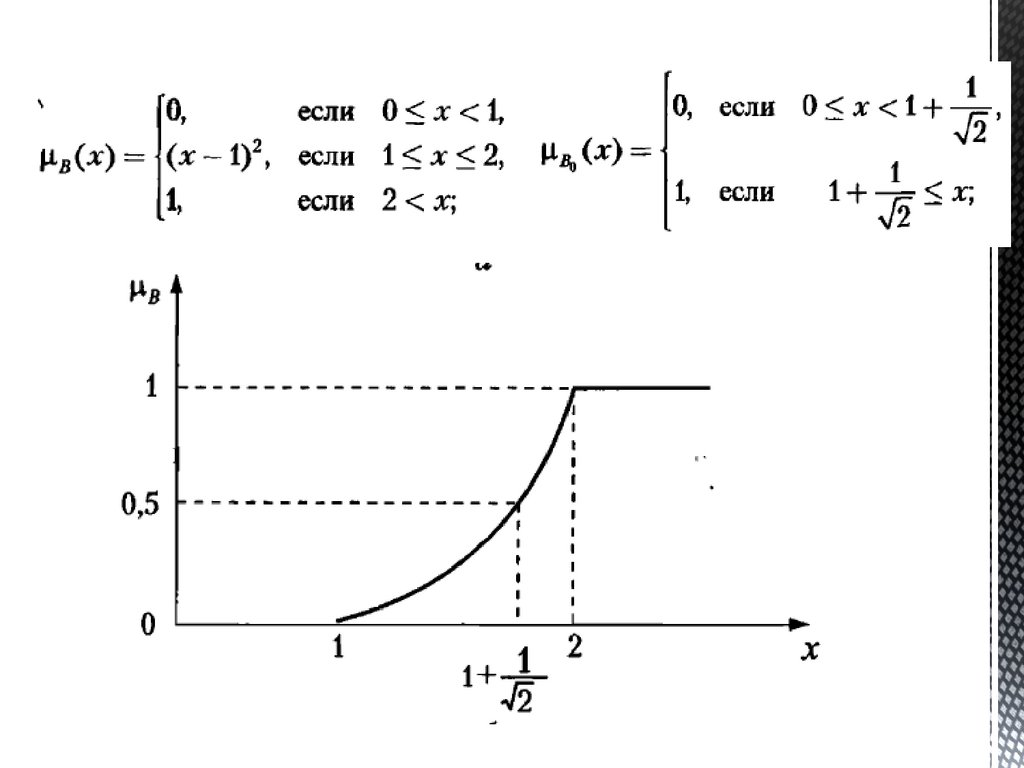
Еще один пример84.
85.
86.
87.
88.
Операции концентрирования и растяжения89.
Операции над нечеткимимножествами
90.
91.
92.
93.
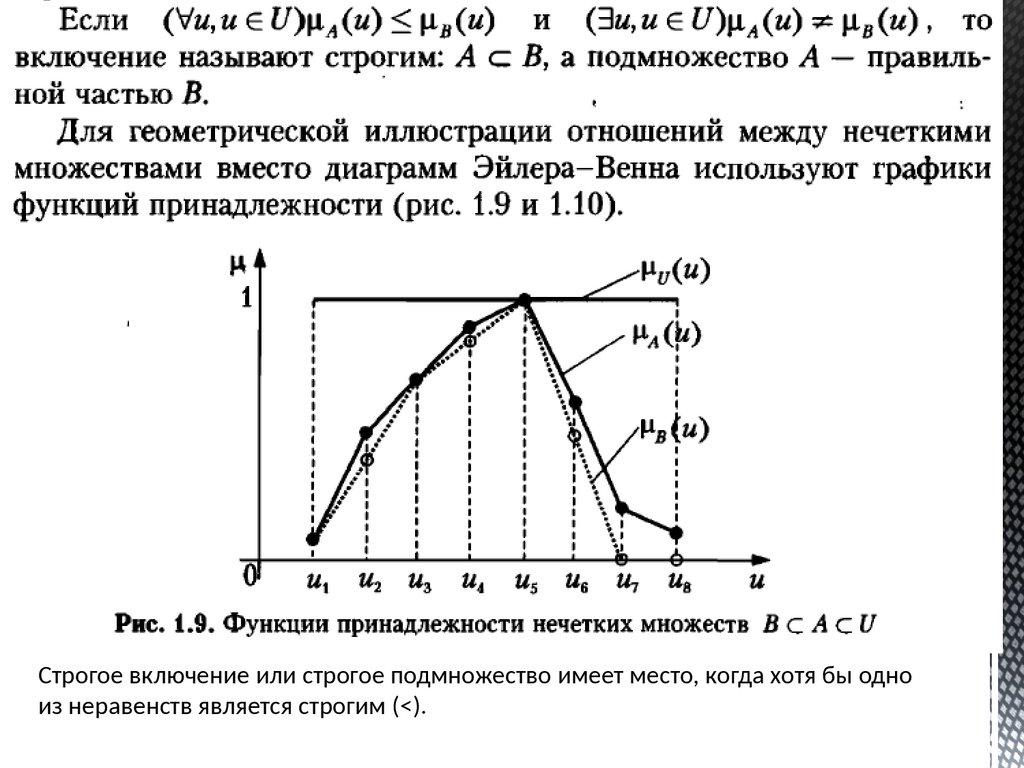
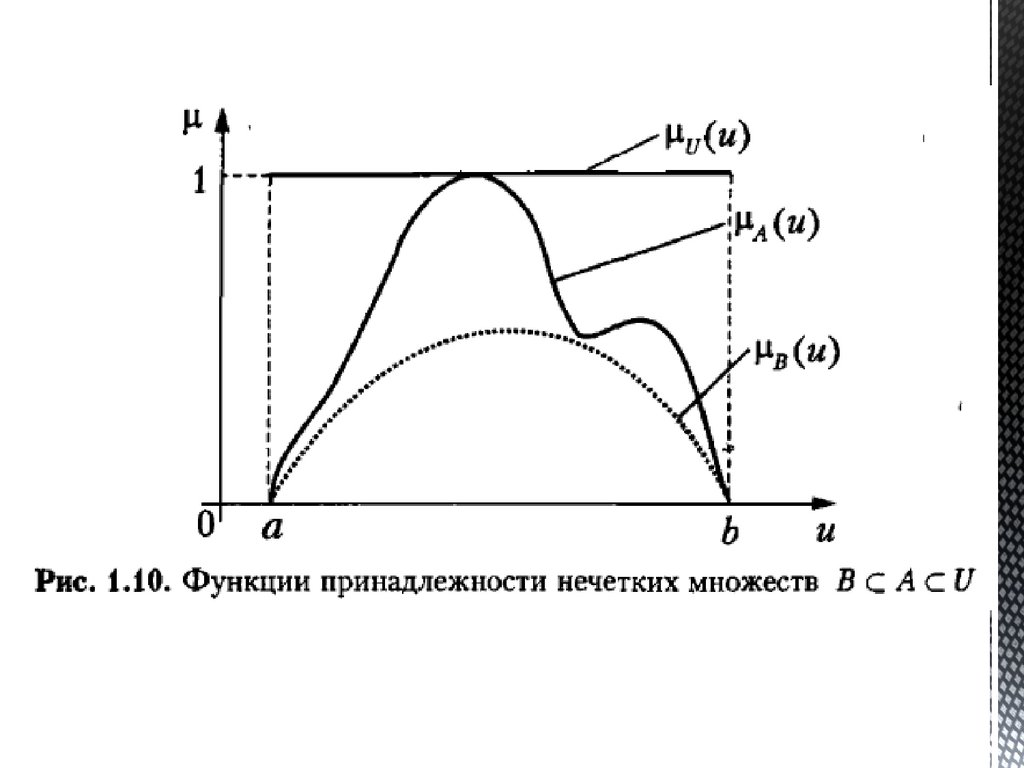
Строгое включение или строгое подмножество имеет место, когда хотя бы одноиз неравенств является строгим (<).
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
6. Синтез нечетких систем112.
Традиционный подход к постановкеи решению задач управления и
регулирования основывается на
предположениях, что модель
объекта управления (ОУ) известна
На практике – математические
модели ОУ очень сложные….
113.
Система управления/диагностики:1. Объект управления
2. Управляемый сигналы (на
которые можно оказывать
воздействие)
3. Измеряемые сигналы
4. Воздействия внешней среды
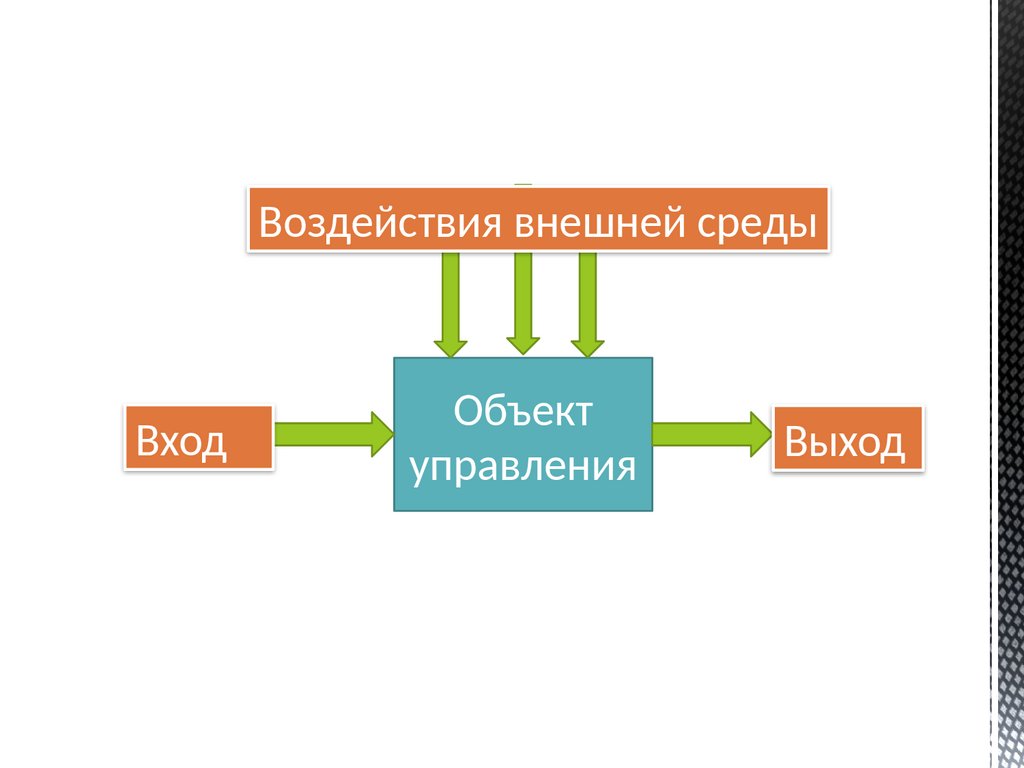
114.
Воздействия внешней средыВход
Объект
управления
Выход
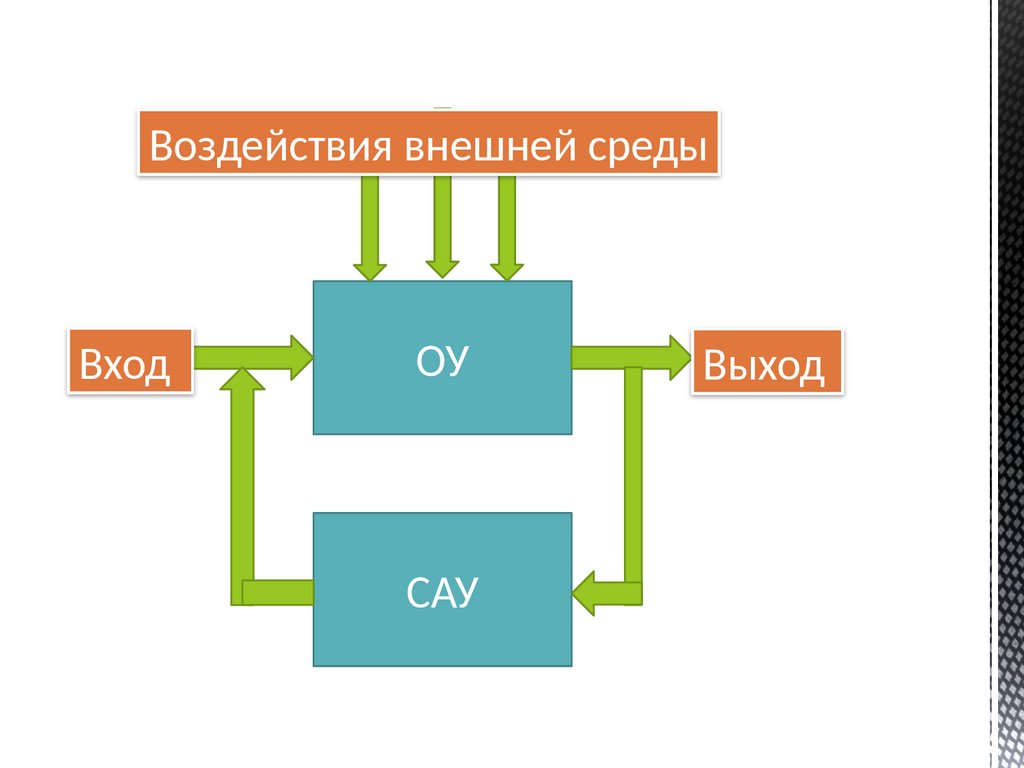
115.
Воздействия внешней средыВход
ОУ
САУ
Выход
116.
Для того чтобы произвести синтезнечеткой системы надо знать 1-4.
И как зависят управляемый сигнал от
измеряемых в виде правил
ЕСЛИ …. И … И …. , ТО
117.
Для того, чтобы сформулировать правилавида
ЕСЛИ …. И … И …. , ТО
Необходимо определить все возможные
состояния для каждого измеряемого
параметра.
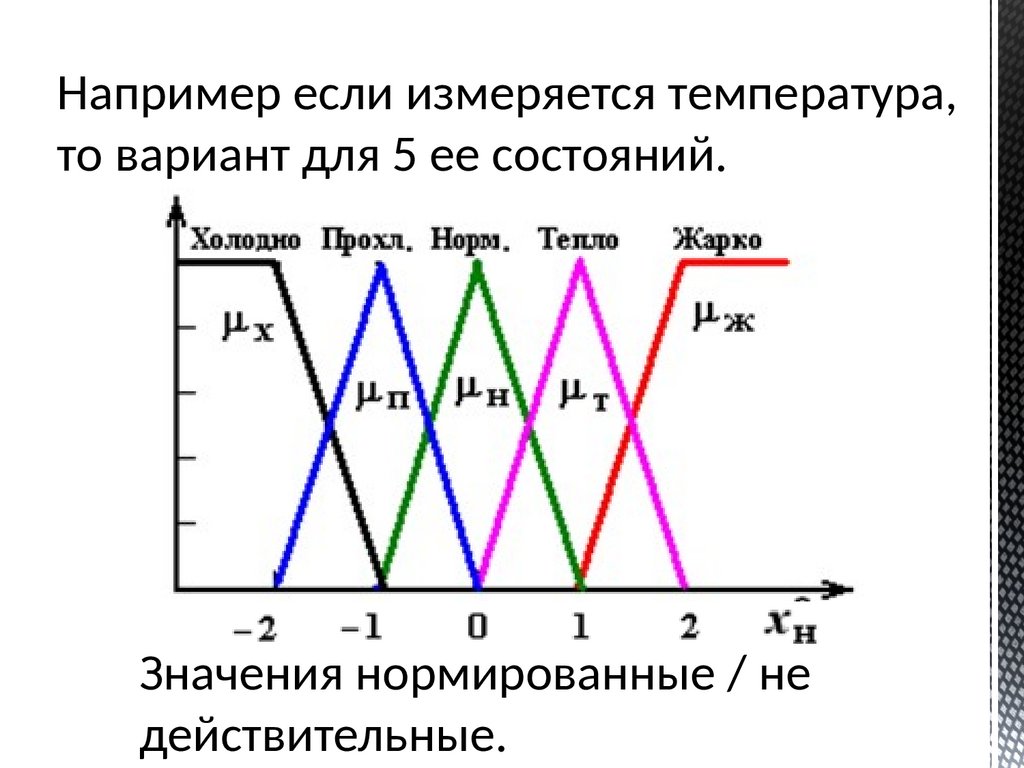
118.
Например если измеряется температура,то вариант для 5 ее состояний.
Значения нормированные / не
действительные.
119.
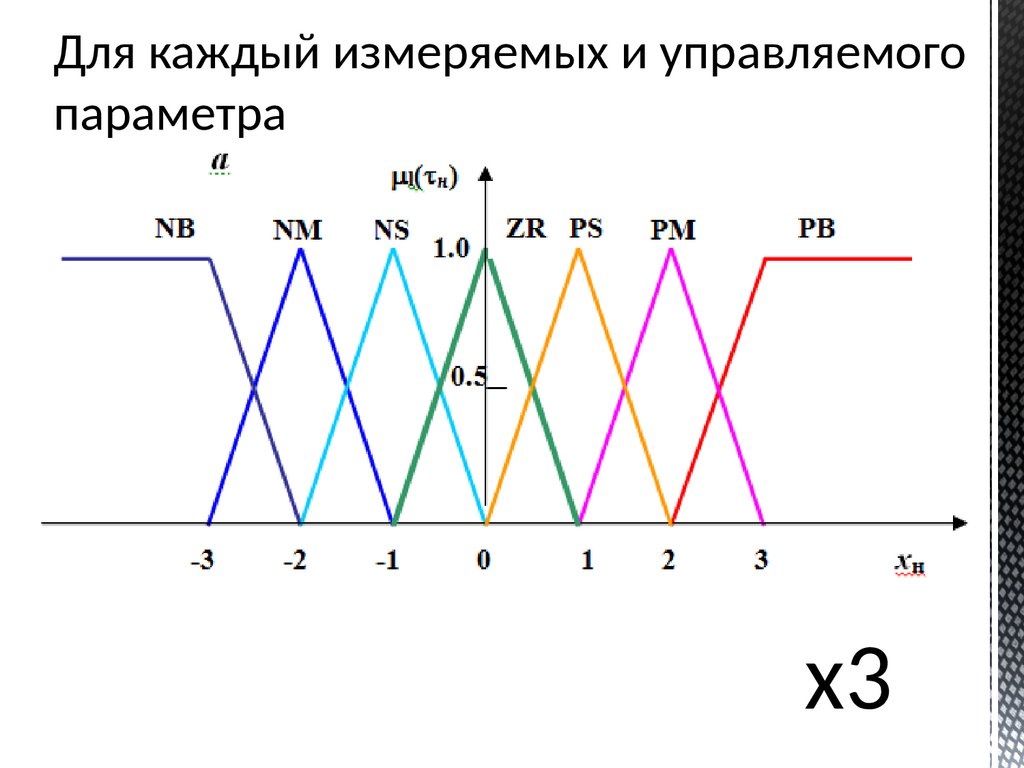
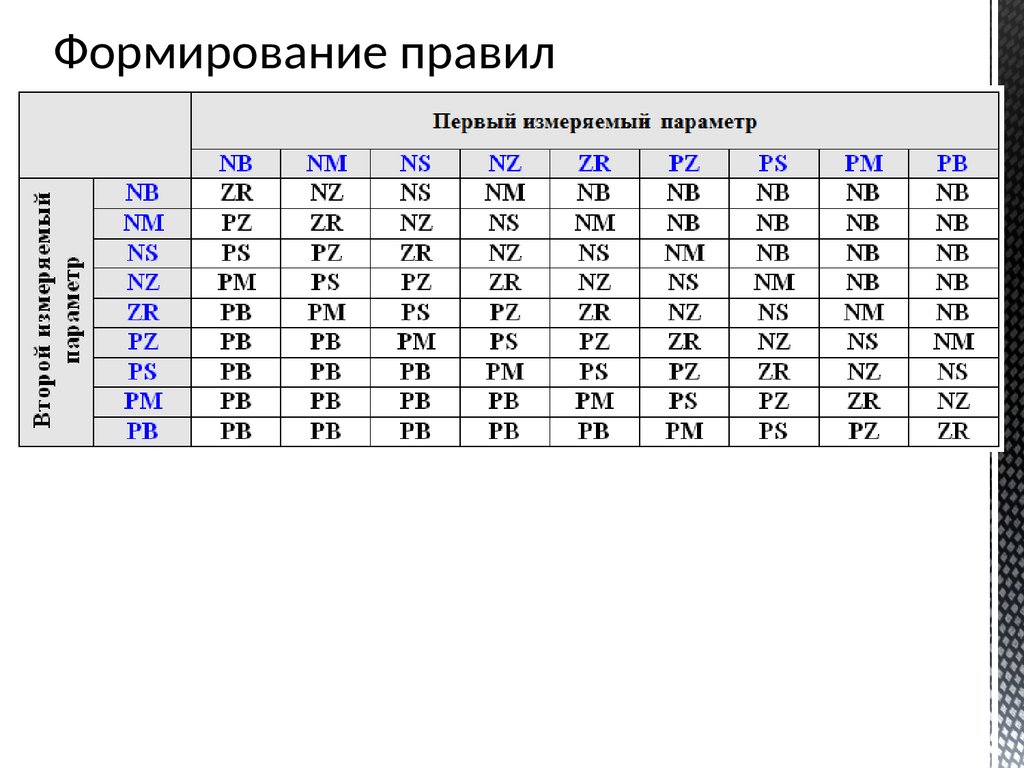
Варианты возможных состояний:negative big (NB),
negative medium (NM),
negative small (NS),
zero (ZR),
positive small (PS),
positive medium (PM),
positive big (PВ)
Количество состояний может быть:
3, 5, 7, 9
120.
Для каждый измеряемых и управляемогопараметра
x3
121.
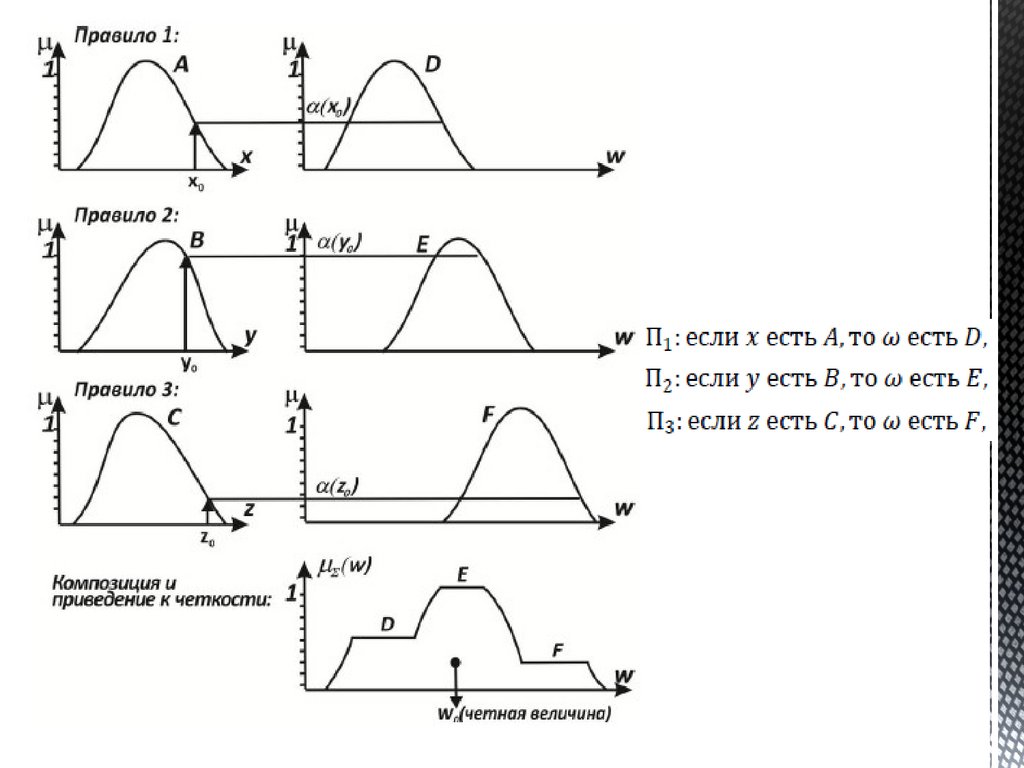
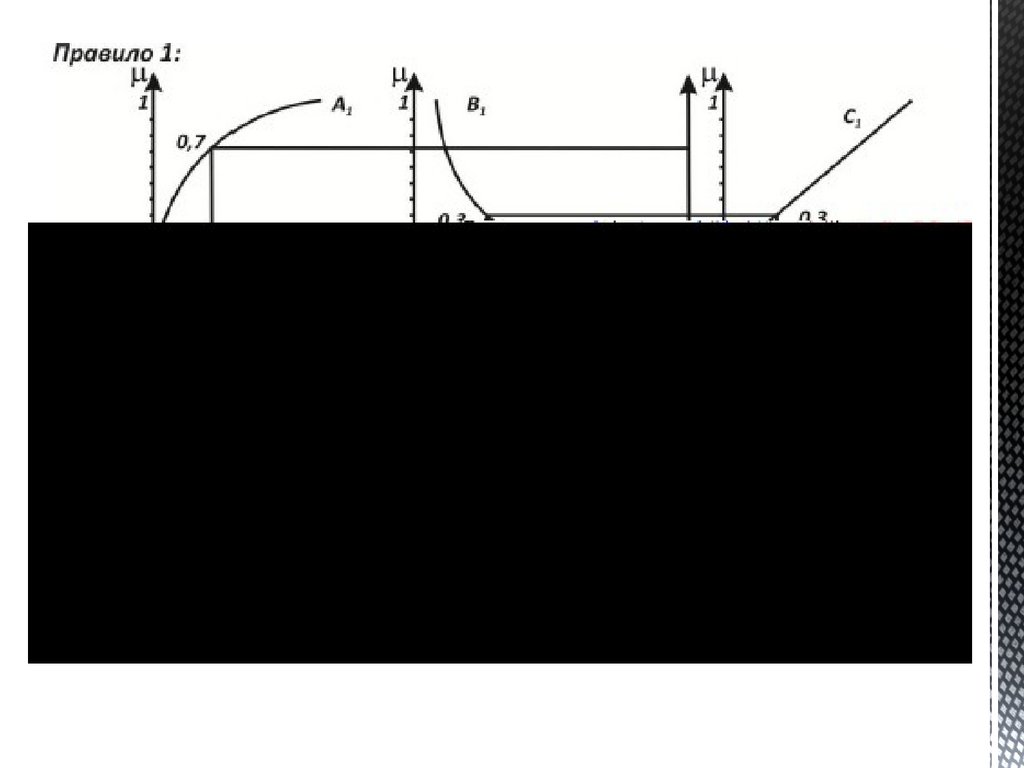
Формирование правил122.
1. Фаззификация2. Расчет нечеткого выхода по базе
нечетких правил
3. Дефаззификация
Эти три оператора зависит от выбранного
алгоритма (Larsen, Mamdani, )
123.
7. Нечеткие илингвистические
переменные
124.
Понятие нечеткой и лингвистическойпеременных используется при
описании объектов и явлений с
помощью нечетких множеств.
125.
Нечеткая переменная характеризуетсятройкой (α, X, А),где
α — наименование переменной;
X — универсальное множество (область
определения α);
А — нечеткое множество на X, описывающее
ограничения (т.е. μA(x))на значения нечеткой
переменной α.
126.
Лингвистическойпеременной (ЛП)называется набор (β, Т, X, G, М), где
β — наименование лингвистической
переменной;
Т — множество ее значений (терммножество), представляющих собой
наименования нечетких переменных,
областью определения каждой из которых
является множество X.
Множество Т называется базовым терммножеством лингвистической
переменной;
127.
G — синтаксическая процедура, позволяющаяоперировать элементами терм-множества T, в
частности, генерировать новые термы
(значения). Множество T∪G(T), где G(T) —
множество сгенерированных термов,
называется расширенным терм-множеством
лингвистической переменной;
М — семантическая процедура, позволяющая
превратить каждое новое значение
лингвистической переменной, образуемое про
цедурой G, в нечеткую переменную, т.е.
сформировать соответствующее нечеткое
множество.
128.
Общепринятые упрощения1) символ β используют как для названия
самой переменной, так и для всех ее
значений;
2) пользуются одним и тем же символом
для обозначения нечеткого множества и
его названия, например терм «Молодой»,
являющийся значением лингвистической
переменной β = «возраст», одновременно
есть и нечеткое множество М(«Молодой»).
129.
Пример. Пусть эксперт определяеттолщину выпускаемого изделия с
помощью понятий «Малая толщина»,
«Средняя толщина» и «Большая толщина»,
при этом минимальная толщина равна 10
мм, а максимальная – 80 мм.
Формализация такого описания может
быть проведена с помощью следующей
лингвистической переменной (β, Т, X, G, М)
130.
β — толщина изделия;Т — {«Малая толщина», «Средняя толщина»,
«Большая толщина»};
X — [10, 80];
G — процедура образования новых термов с
помощью связок «и», «или» и модификаторов
типа «очень», «не», «слегка» и т.п. Например:
«Малая или средняя толщина», «Очень малая
толщина» и т.д.;
131.
М — процедура задания на X = [10, 80]нечетких подмножеств А1 = «Малая
толщина», А2= «Средняя толщина», A3 =
«Большая толщина», а также нечетких
множеств для термов из G(Т)в
соответствии с правилами трансляции
нечетких связок и модификаторов «и»,
«или», «не», «очень», «слегка» и других
операций над нечеткими множествами
вида: А⋂В, A∪В, ̅A,CONА = A2, DILА = А0,5и
т. п.
132.
Наряду с рассмотренными вышебазовыми значениями лингвистической
переменной «Толщина» (Т = {«Малая
толщина», «Средняя толщина», «Большая
толщина»}) возможны значения, завися
щие от области определения X. В данном
случае значения лингвистической
переменной «Толщина изделия» могут
быть определены как «около 20 мм»,
«около 50 мм», «около 70 мм», т.е. в виде
нечетких чисел.
133.
Терм-множество и расширенное терммножество в условиях примера можнохарактеризовать функциями
принадлежности, приведенными на
рисунке на следующих слайдах
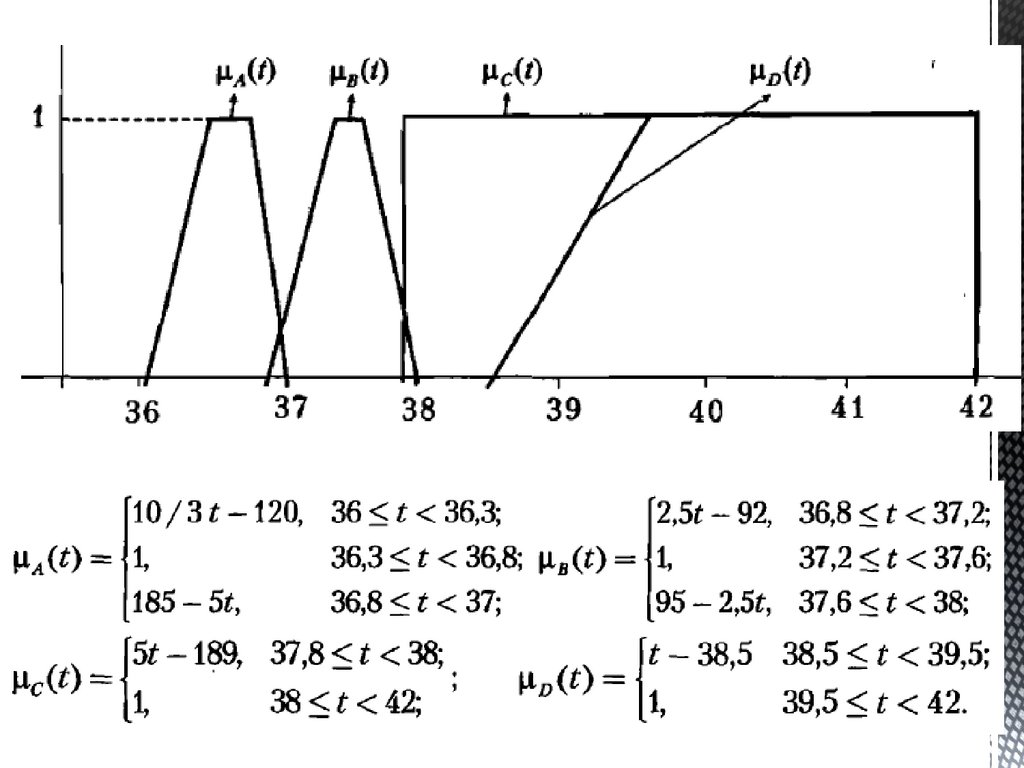
134.
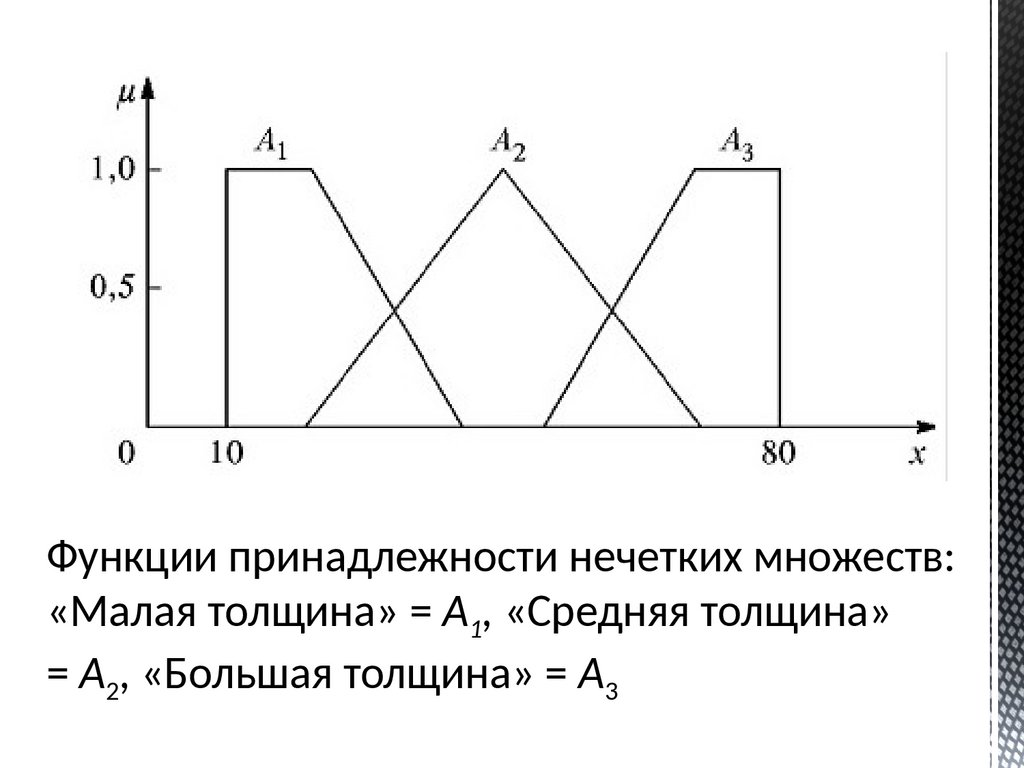
Функции принадлежности нечетких множеств:«Малая толщина» = А1, «Средняя толщина»
= А2, «Большая толщина» = А3
135.
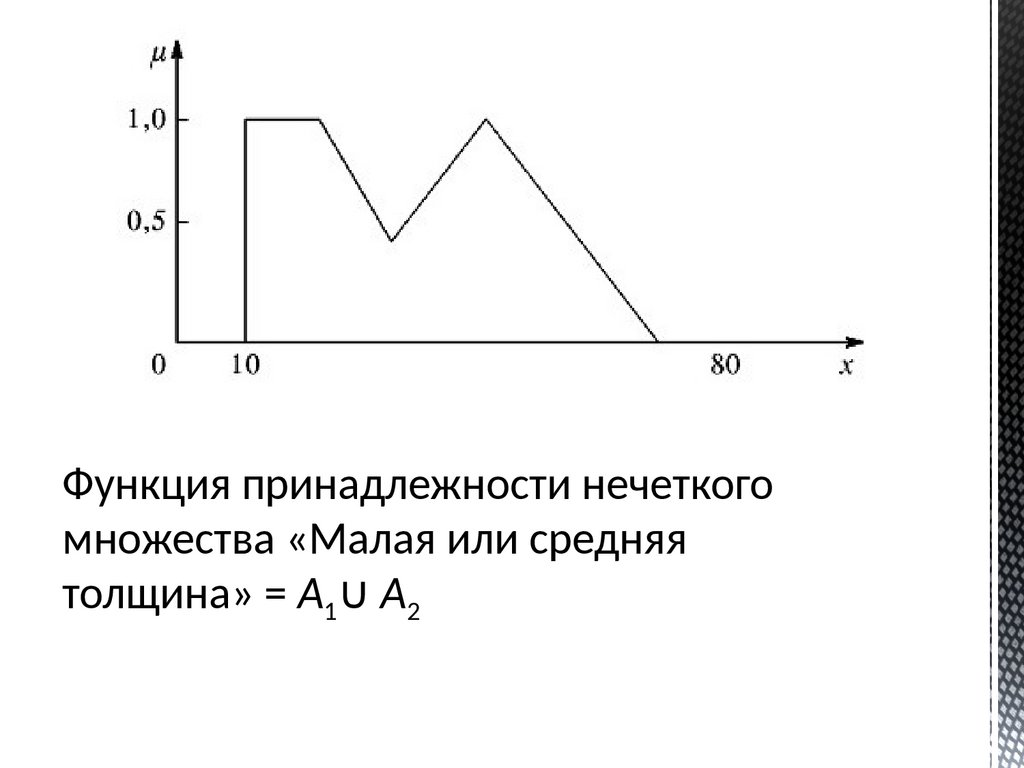
Функция принадлежности нечеткогомножества «Малая или средняя
толщина» = A1∪ А2
136.
1. Фаззификация2. Расчет нечеткого выхода по базе
нечетких правил
3. Дефаззификация
Эти три оператора зависит от выбранного
алгоритма (Larsen, Mamdani, )
Go to слайд 151
137.
Операции над нечеткими числами.Расширенные бинарные арифметические
операции (сложение, умножение и др.) для
нечетких чисел определяются через
соответствующие операции для четких
чисел с использованием принципа
обобщения следующим образом.


























































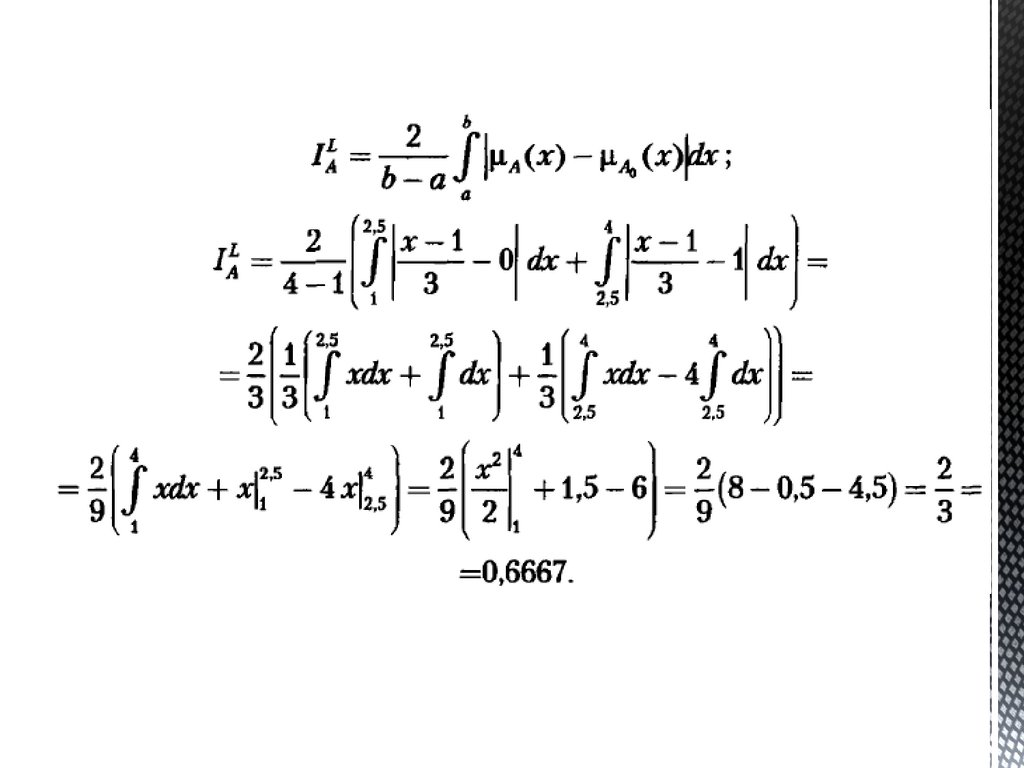



















































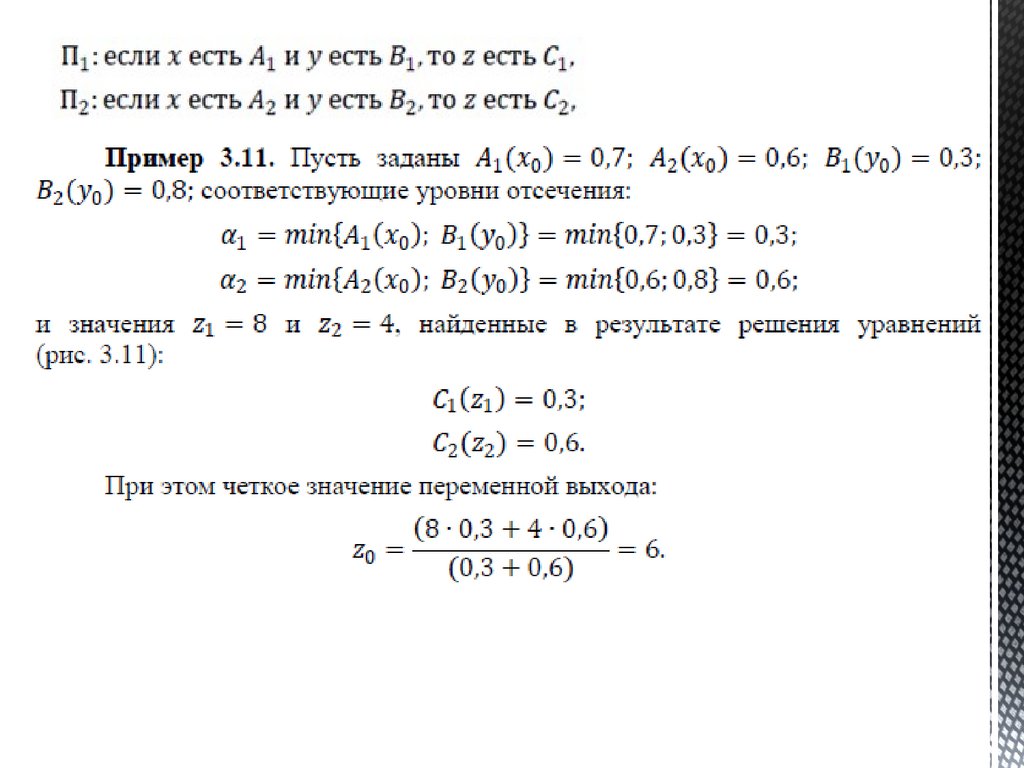


 Математика
Математика








