Похожие презентации:
Тема 2 Симметричные криптосистемы Часть 2 Шифрование методами замены
1. Симметричные криптосистемы
1Тема 2
Симметричные
криптосистемы
Часть 2
Шифрование методами
замены
2.
Содержание1. Шифры простой замены
2. Многоалфавитные шифры замены
2
3.
31. Шифры простой замены
4.
Одноалфавитная подстановкаВ шифре простой замены каждый символ исходного текста
заменяется символами того же алфавита одинаково на
всем протяжении текста.
Шифры простой замены называют также шифрами
одноалфавитной (моноалфавитной) подстановки.
В общем случае, преобразование открытого текста в
шифрах замены задается с помощью различных таблиц,
которые носят название таблиц замены.
4
5.
Полибианский квадратОдним из первых шифров простой замены считается так
называемый полибианский квадрат.
За два века до нашей эры греческий полководец и
историк Полибий изобрел для целей шифрования
квадратную таблицу размером 5 5, заполненную
буквами алфавита в случайном порядке.
При шифровании в этом полибианском квадрате
находили очередную букву открытого текста и
записывали в шифротекст букву, расположенную ниже
ее в том же столбце.
Если буква текста оказывалась в нижней строке
таблицы, то для шифротекста брали самую верхнюю
букву из того же столбца.
5
6.
Полибианский квадратИдею квадрата Полибия проиллюстрируем таблицей с
русскими буквами.
Число букв в русском алфавите отличается от числа букв в
греческом алфавите, поэтому и размер таблицы выбран
иным:
не квадрат 5 5, а прямоугольник 4 8.
Зашифруем фразу: КРИПТОГРАФИЯ:
23 31 21 28 33 27 14 31 11 35 11 35 21 48.
В данном примере видно, что в шифрограмме
первым указывается номер строки,
а вторым – номер столбца.
6
7.
Полибианский квадрат7
Концепция полибианского квадрата оказалась плодотворной
и нашла применение в криптосистемах последующего
времени.
8.
Подстановка Цезаря8
Подстановка Цезаря является самым простым вариантом
подстановки.
Этот шифр реализует следующее преобразование открытого
текста:
каждая буква открытого текста заменяется третьей
после неё буквой в алфавите, который считается
написанным по кругу,
т.е. после буквы «я» следует буква «а».
Цезарь заменял букву третьей после неё буквой,
но можно заменять и какой-нибудь другой.
Главное, чтобы тот, кому посылается сообщение, знал
эту величину сдвига.
Класс шифров, работающих по указанному принципу, и к
которым относится шифр Цезаря, называется шифрами
замены.
9.
Подстановка ЦезаряПодмножество Cm ={Ck : 0 ≤ k < m}, содержащее m
подстановок:
Ck: j (j+k) (mod m), 0 ≤ k < m,
называется подстановкой Цезаря.
Т.к. умножение коммутативно, то
C kCj =Cj Ck =Ck+j.
Обозначим через:
C0 идентичную подстановку,
т.е. не осуществляющую замены букв алфавита,
Ck-1 =Cm-k , где 0 ≤ k < m, обратную к Ck подстановку.
Семейство подстановок Цезаря названо по имени римского императора
Гая Юлия Цезаря, который поручал Марку Туллию Цицерону
составлять послания с использованием 50-буквенного алфавита и
подстановки C3.
9
10.
Подстановка Цезаря10
Подстановка определяется по таблице замещения,
содержащей пары соответствующих букв “исходный текст
– шифрованный текст”.
Для C3 подстановки приведены ниже.
Стрелка ( ) означает, что буква исходного текста (слева)
шифруется при помощи C3 в букву шифрованного текста.
А г
Б д
В е
Г ж
Д з
Е и
Ж й
З к
И л
Й м
К н
Л о
М п
Н р
О с
П т
Р у
С ф
Т х
У ц
Ф ч
Х ш
Ц щ
Ч ъ
Ш ы
Щ ь
Ъ э
Ы ю
Ь я
Э _ (пробел)
Ю а
Я б
_ (пробел) в
11.
Подстановка Цезаря11
Системой Цезаря называется моноалфавитная
подстановка, преобразующая n-грамму исходного текста
(x0, x1, .., xn-1) в n-грамму шифрованного текста (y0, y1, ..,
y n-1 ) в соответствии с правилом:
yi =Ck (xi ), 0 ≤ i < n.
12.
Подстановка ЦезаряПример.
Таблица замещения для латинского алфавита показана ниже.
Тогда известное послание Цезаря
VENI VIDI VICI
(в переводе на русский означает "Пришел, увидел, победил")
выглядело бы в зашифрованном виде так:
YHQL YLGL YLFL.
A D
B E
C F
D G
E H
F I
G J
H K
I L
J M
K N
L O
M P
N Q
O R
P S
Q T
R U
S V
T W
U X
V Y
W Z
X A
Y B
Z C
12
13.
Подстановка ЦезаряДостоинством системы шифрования Цезаря является
простота шифрования и расшифровывания.
13
14.
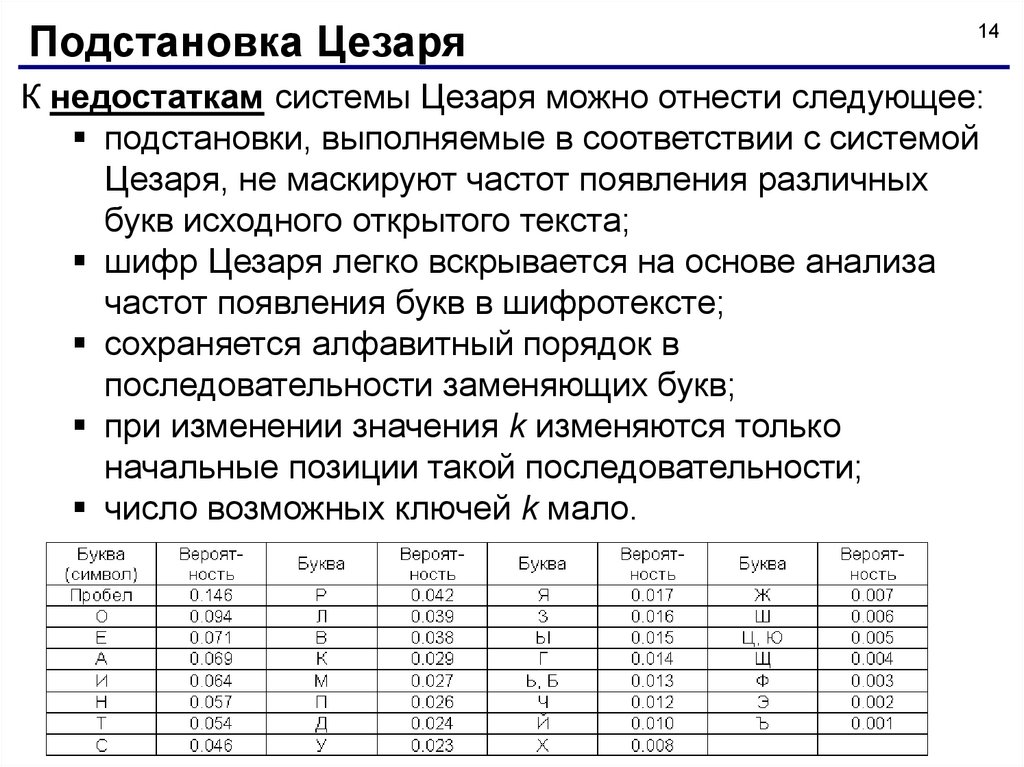
Подстановка Цезаря14
К недостаткам системы Цезаря можно отнести следующее:
подстановки, выполняемые в соответствии с системой
Цезаря, не маскируют частот появления различных
букв исходного открытого текста;
шифр Цезаря легко вскрывается на основе анализа
частот появления букв в шифротексте;
сохраняется алфавитный порядок в
последовательности заменяющих букв;
при изменении значения k изменяются только
начальные позиции такой последовательности;
число возможных ключей k мало.
15.
Подстановка Цезаря15
Криптоаналитическая атака против системы
одноалфавитной замены начинается с подсчета частот
появления символов:
определяется число появлений каждой буквы в
шифротексте;
затем полученное распределение частот букв в
шифротексте сравнивается с распределением частот
букв в алфавите исходных сообщений,
например, в русском языке;
буква с наивысшей частотой появления в шифротексте
заменяется на букву с наивысшей частотой появления
в русском языке и т.д.
Вероятность успешного вскрытия системы шифрования
повышается с увеличением длины шифротекста.
16.
Подстановка ЦезаряВместе с тем идеи, заложенные в системе шифрования
Цезаря, оказались весьма плодотворными, о чем
свидетельствуют многочисленные модификации.
16
17.
Шифр Цезаря с ключевым словом17
Модификацией этого шифра является система
шифрования Цезаря с ключевым словом. Эта система
также является одноалфавитной.
Особенностью ее является использование ключевого
слова для смещения и изменения порядка символов в
алфавите подстановки.
Ключевое слово записывается под буквами алфавита,
начиная с буквы, числовой код которой совпадает с
выбранным числом k.
Необходимо, чтобы все буквы ключевого слова были
различны (иначе повторяющиеся буквы исключить).
Буквы алфавита подстановки, не вошедшие в
ключевое слово, записываются после ключевого слова
в алфавитном порядке.
Получается подстановка для каждой буквы
произвольного сообщения.
18.
Шифр Цезаря с ключевым словомПример.
Выберем ключевое слово «информация» и k =3. Тогда правило
подстановки будет следующим:
буквы исходного текста:
абвгдеёжзийклмнопрстуфхцчшщьыъэюя
буквы шифртекста:
эюинформацябвгдеёжзйклпстухчшщьыъ
Преимуществом системы Цезаря с ключевым словом
является то, что
количество возможных ключевых слов практически
неисчерпаемо.
18
19.
Аффинная система подстановок Цезаря19
В системе шифрования Цезаря использовались только
аддитивные свойства множества чисел.
Однако символы можно также умножать по модулю m.
Применяя одновременно операции сложения и умножения
по модулю m над буквами алфавита, можно получить
систему подстановок, которую называют аффинной
системой подстановок Цезаря.
В аффинной системе подстановок Цезаря буква,
соответствующая числу t, заменяется на букву,
соответствующую числовому значению (at+b) по модулю
m.
Следует заметить, что данное преобразование
является взаимно однозначным отображением тогда и
только тогда, когда НОД (a, m) наибольший общий
делитель чисел a и m равен единице,
т.e. если a и m взаимно простые числа.
20.
Аффинная система подстановок Цезаря20
Пример.
Пусть m = 26, a = 3, b = 5.
Тогда, очевидно, НОД (3,26) = 1, и мы получаем следующее
соответствие между числовыми кодами букв:
t
(3t+5)
mod m
0
5
1
8
2 3 4 5 6
11 14 17 20 23
7
0
8
3
9
6
10 11 12 13 14 15
9 12 15 18 21 24
t
16 17 18 19 20 21 22 23 24 25
(3t+5) 1 4 7 10 13 16 19 22 25 2
mod m
Преобразуя числа в буквы английского языка, получаем следующее
соответствие для букв открытого текста и шифротекста:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
F I L O R U X A D G J M P S V Y B E H K N Q T W Z C
Тогда исходное сообщение HOPE преобразуется в шифротекст
AVYR.
21.
Аффинная система подстановок ЦезаряДостоинством аффинной системы является
удобное управление ключами –
ключи шифрования и дешифрования
представляются в компактной форме в виде пары
чисел (a, b).
Недостатки аффинной системы аналогичны недостаткам
системы шифрования Цезаря.
Аффинная система использовалась на практике несколько
веков назад, а сегодня ее применение ограничивается
большей частью иллюстрациями основных
криптологических положений.
21
22.
Шифр Плейфера22
23.
Шифр ПлейфераШифр Плейфера использует
матрицу 5х5 для латинского алфавита,
для русского алфавита необходимо увеличить размер
матрицы до 6х6),
содержащую ключевое слово или фразу.
23
24.
Шифр Плейфера24
Для создания ключевой матрицы и использования шифра
достаточно запомнить ключевое слово и четыре простых
правила.
В первую очередь нужно заполнить пустые ячейки
матрицы
буквами ключевого слова, не записывая
повторяющиеся символы,
потом заполнить оставшиеся ячейки матрицы
символами алфавита, не встречающимися в ключевом
слове, по порядку
в английских текстах обычно опускается символ "Q", чтобы
уменьшить алфавит,
в других версиях "I" и "J" объединяются в одну ячейку.
Ключевое слово может быть записано
в верхней строке матрицы слева направо,
либо по спирали из левого верхнего угла к центру.
Ключевое слово, дополненное алфавитом составляет
25.
Шифр ПлейфераДалее алгоритм шифрования состоит в следующем.
Открытый текст разбивается на блоки по два символа в
каждом. Такой блок называют биграммой. Если в
последнем блоке оказался один символ, то он
либо отбрасывается (если это возможно),
либо добавляется один символ, который не влияет на
содержание открытого текста.
Пусть символы ab являются некоторой биграммой
открытого текста.
25
26.
Шифр Плейфера26
Определяются координаты символа a и символа b в
таблице.
Пусть координаты символа а будут числа (i, j),
а координаты символа b – (t, q).
В этом случае если:
i≠t и j≠q (буквы биграммы находятся в разных строках и
разных столбцах таблицы), то
символ a биграммы переходит в символ таблицы с
координатами (i, q),
а символ b – в символ с координатами (t, j);
27.
Шифр Плейфера27
i=t и j≠q (буквы биграммы находятся в одной строке, но
разных столбцах таблицы), то
символ a биграммы переходит в символ таблицы с
координатами (i, j+1),
а символ b – в символ с координатами (t,q+1).
Если j=m или q=m, то координаты новых символов
соответственно будут равны (i, 1) или (t, 1);
28.
Шифр Плейфераi≠t и j=q (буквы биграммы находятся в разных строках,
но одном столбце таблицы), то
символ a биграммы переходит в символ таблицы с
координатами (i+1, j),
а символ b – в символ с координатами (t+1,q).
Если i=n или t=n, то координаты новых символов
соответственно будут равны (1, j) или (1, q).
Две одинаковые буквы с координатами (i, j)
преобразуются в две одинаковые буквы с
координатами (i+1, j);
28
29.
Шифр Плейфера29
Расшифровка текста происходит точно так же.
Преобразованный текст разбивается на блоки по два
символа.
Затем по координатам зашифрованных символов в той же
последовательности определяются символы открытого
текста.
30.
Шифр Плейфера. Пример30
Используем ключ «Playfair example», тогда матрица примет
вид:
P
L
A
Y
F
I
R
E
X
M
B
C
D
G
H
J
T
K
U
N
V
O
W
S
Z
Зашифруем сообщение «Hide the gold in the tree stump».
31.
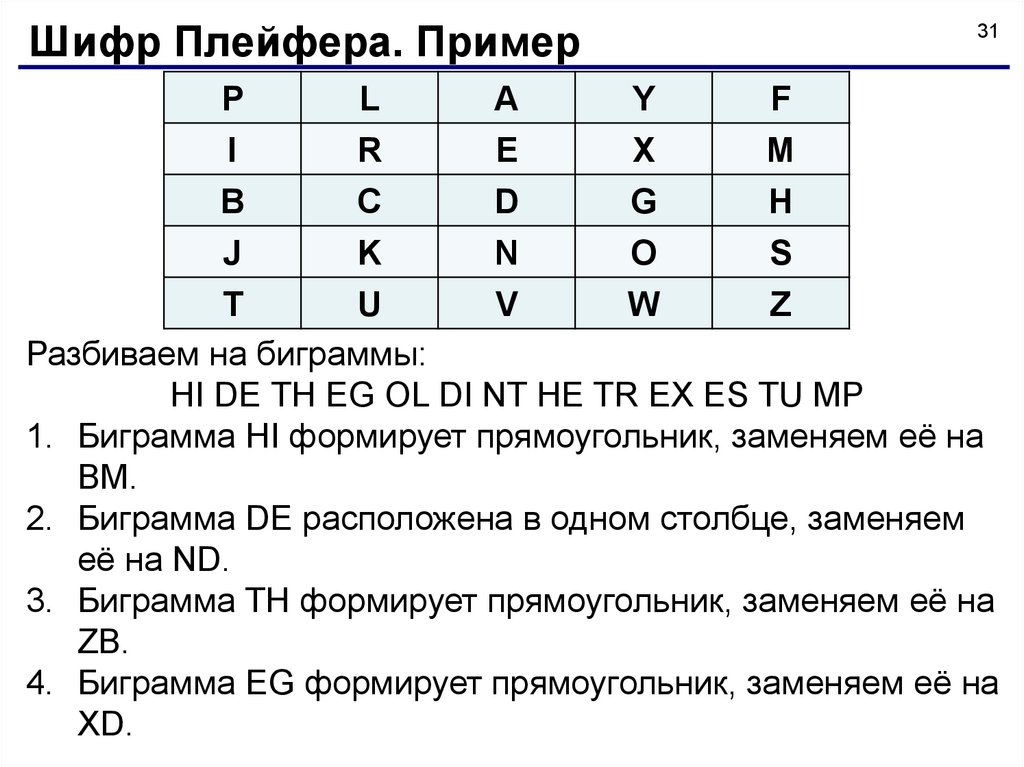
Шифр Плейфера. ПримерP
I
B
L
R
C
A
E
D
31
Y
X
G
F
M
H
J
K
N
O
S
T
U
V
W
Z
Разбиваем на биграммы:
HI DE TH EG OL DI NT HE TR EX ES TU MP
1. Биграмма HI формирует прямоугольник, заменяем её на
BM.
2. Биграмма DE расположена в одном столбце, заменяем
её на ND.
3. Биграмма TH формирует прямоугольник, заменяем её на
ZB.
4. Биграмма EG формирует прямоугольник, заменяем её на
XD.
32.
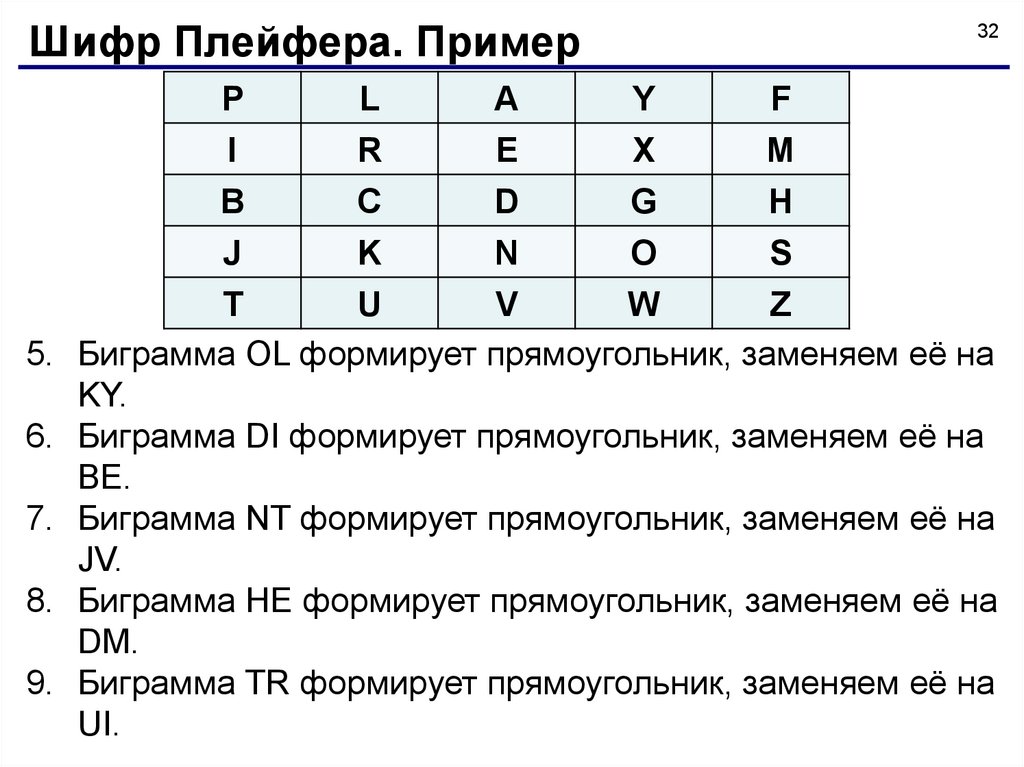
Шифр Плейфера. ПримерP
I
B
L
R
C
A
E
D
32
Y
X
G
F
M
H
J
K
N
O
S
T
U
V
W
Z
5. Биграмма OL формирует прямоугольник, заменяем её на
KY.
6. Биграмма DI формирует прямоугольник, заменяем её на
BE.
7. Биграмма NT формирует прямоугольник, заменяем её на
JV.
8. Биграмма HE формирует прямоугольник, заменяем её на
DM.
9. Биграмма TR формирует прямоугольник, заменяем её на
UI.
33.
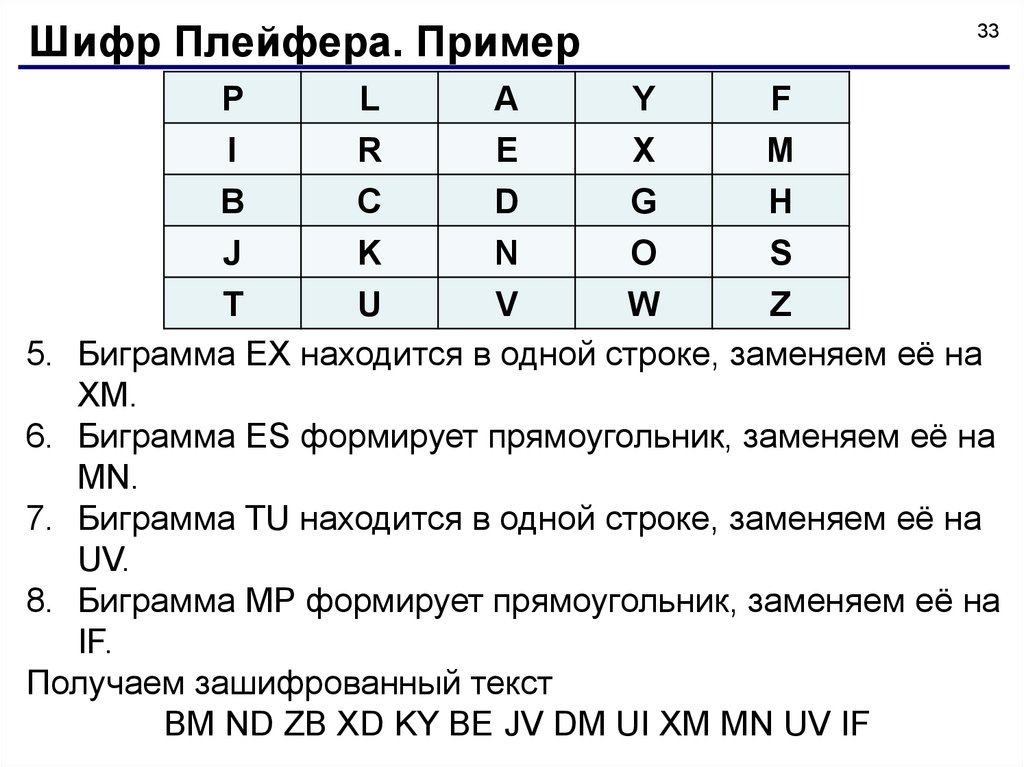
Шифр Плейфера. ПримерP
I
B
L
R
C
A
E
D
33
Y
X
G
F
M
H
J
K
N
O
S
T
U
V
W
Z
5. Биграмма EX находится в одной строке, заменяем её на
XM.
6. Биграмма ES формирует прямоугольник, заменяем её на
MN.
7. Биграмма TU находится в одной строке, заменяем её на
UV.
8. Биграмма MP формирует прямоугольник, заменяем её на
IF.
Получаем зашифрованный текст
BM ND ZB XD KY BE JV DM UI XM MN UV IF
34.
Шифры Хилла34
Шифр Хилла – полиграммный шифр подстановки (элементы
исходного открытого текста заменяются зашифрованным
текстом в соответствии с некоторым правилом), в котором
буквы открытого текста заменяются группами с помощью
линейной алгебры.
Для латинского алфавита каждой букве сопоставляется
число, например,
A – 0, B – 1, C – 2, …, Z – 25.
В общем случае соответствия “буква – число” можно выбрать
произвольно.
35.
Шифры Хилла35
Открытый текст представляет собой n-мерный вектор. Ключ
– квадратная матрица размера n x n.
Для получения шифротекста ключ умножается на открытый
текст по модулю выбранной числовой схемы,
в случае латинского алфавита – 26.
36.
Шифры ХиллаПусть
"p1p2p3" – открытый текст,
ключ – матрица размера 3 x 3
и шифротекст – вектор размерности – 3, "c1c2c3"
соответственно.
В матричном виде эта система описывается так:
Или в качестве системы уравнений:
Из уравнений видно, что каждый символ открытого текста
участвует в шифровании шифротекста. Именно поэтому
шифр Хилла принадлежит к категории блочных шифров.
36
37.
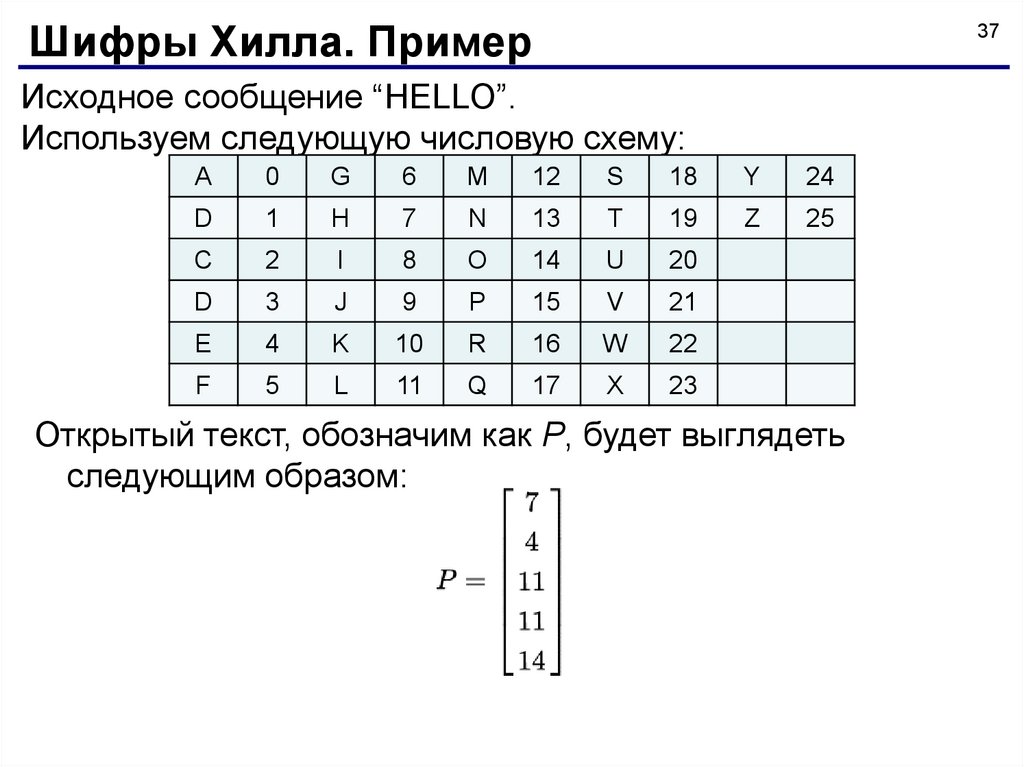
Шифры Хилла. Пример37
Исходное сообщение “HELLO”.
Используем следующую числовую схему:
A
0
G
6
M
12
S
18
Y
24
D
1
H
7
N
13
T
19
Z
25
C
2
I
8
O
14
U
20
D
3
J
9
P
15
V
21
E
4
K
10
R
16
W
22
F
5
L
11
Q
17
X
23
Открытый текст, обозначим как P, будет выглядеть
следующим образом:
38.
Шифры Хилла. ПримерВыберем ключ – матрицу размером 5 x 5 (mod 26):
Это соответствует ключевому слову
GYBCHNQKNBURPVOSCXPHJELQV
38
39.
Шифры Хилла. ПримерТогда шифротекст C может быть получен, как K x P.
Получим зашифрованное сообщение C:
JGUAU
39
40.
Шифры Хилла40
Чтобы получатель смог расшифровать сообщение,
переданное отправителем, ключ – матрица должна иметь
обратную матрицу. Такое возможно, если
детерминант матрицы не равен нулю
и не имеет общих делителей с основанием модуля.
Именно это условие позволяет упростить задачу. Можно
выбрать в качестве основания модуля простое число,
путем добавления в числовую схему новых элементов,
например, знаков препинания.
Таким образом детерминант любой матрицы не будет иметь
общих делителей с основанием такого модуля.
41.
Шифры Хилла. ПримерДетерминант ключ – матрицы K, приведенной выше:
det(K) = –413965 – не равен 0.
Делители детерминанта = 413965:
5, 82, 793, 413965.
Делители основания модуля = 26:
2, 13, 26.
Следовательно, данная ключ – матрица имеет обратную
матрицу K–1 (mod 26).
41
42.
Шифры Хилла. ПримерБерем зашифрованный раннее текст C = “JGUAU” и
расшифруем его:
После расшифровывания получили “HELLO”.
42
43.
Криптостойкость шифра Хилла43
Атаковать грубой силой шифр Хилла сложно.
Если размерность матрицы – ключа n x n, то всего существует
26n2 таких матриц.
Но не каждая матрица обратима, поэтому область несколько
сужается. Количество обратимых матриц можно рассчитать с
помощью китайской теоремы об остатках. Например, количество
обратимых матриц по модулю 26 равно:
|K| = 26n2(1 – 1/2)(1 – 1/22)…(1 – 1/2n) (1 – 1/13)(1 – 1/132)…(1 – 1/13n)
В результате эффективное пространство ключей составляет около
4.64n2 – 1.7.
Для ключа размера 5x5 этот параметр будет равен 114 битам, что
делает вариант полного перебора неприменимым.
44.
Криптостойкость шифра Хилла44
Так же шифр Хилла не поддается частотному анализу, так
как каждый символ открытого текста принимает участие в
шифровании.
Однако, можно провести анализ частоты слов размера n, в связи с
этим не стоит применять шифр Хилла на данных имеющих такое
строение.
45.
Криптостойкость шифра Хилла45
Шифр Хилла очень уязвим для атаки по открытому тексту,
так как в нем используются линейные операции.
Если взломщик знает m пар
“открытое сообщение”/ “зашифрованное сообщение”,
то он может вычислить ключ.
Предположим, что взломщик перехватила 3 пары “открытое
сообщение”/ “зашифрованное сообщение”:
46.
Криптостойкость шифра Хилла46
Если составить матрицы P и C из этих пар, то можно найти
ключ K.
Если матрица P не будет являться обратимой, то
необходимо задействовать другие m наборов пар
“открытое сообщение”/ “зашифрованное сообщение”.
В данном случае матрица P обратима.
Взломщик может прочитать любое сообщение!!!
47.
472. Многоалфавитные шифры
замены
48.
Шифры сложной замены48
Шифры сложной замены называют многоалфавитными,
так как для шифрования каждого символа исходного
сообщения применяют свой шифр простой замены.
Многоалфавитная подстановка последовательно и
циклически меняет используемые алфавиты.
Многоалфавитная подстановка определяется ключом
=( 1, 2, ...), содержащим не менее двух различных
подстановок.
49.
Шифры сложной замены49
При r-алфавитной подстановке
символ х0 исходного сообщения заменяется символом
из алфавита В0,
символ х1 – символом из алфавита B1
и так далее,
символ хr-1 заменяется символом из алфавита Br-1,
символ хr заменяется символом снова из алфавита В0
и т.д.
Пример многоалфавитной подстановки (r=4):
Входной символ
х0 х1 х2 х3 х4 х5 х6 х7 х8 х9
Алфавит подстановки B0 B1 B2 B3 B0 B1 B2 B3 B0 B1
50.
Шифры сложной замены50
Эффект использования многоалфавитной
подстановки заключается в том, что обеспечивается
маскировка естественной статистики исходного языка,
т.к. конкретный символ из исходного алфавита Х может
быть преобразован в несколько различных символов
шифровальных алфавитов В.
Степень обеспечиваемой защиты теоретически
пропорциональна длине периода r в
последовательности используемых алфавитов В.
51.
Диск Альберти51
Многоалфавитные шифры замены предложил и ввел в
практику криптографии Леон Батист Альберти, который
также был известным архитектором и теоретиком
искусства.
Его книга "Трактат о шифре", написанная в 1566 г.,
представляла собой первый в Европе научный труд по
криптологии. Криптологи всего мира почитают
Альберти основоположником криптологии.
Он же впервые выдвинул идею повторного
шифрования, которая в виде идеи многократного
шифрования лежит в основе всех современных
шифров с секретным ключом.
Кроме шифра многоалфавитной замены Альберти
также подробно описал устройства для его
реализации.
52.
Диск Альберти52
Диск Альберти представляет собой систему из внешнего
неподвижного и внутреннего подвижного дисков, на
которые нанесены символы алфавита и цифры.
На внешнем диске символы расположены в
алфавитном порядке,
на внутреннем – в произвольном.
Ключом шифрования являются порядок букв на
внутреннем диске и начальное положение внутреннего
диска относительно внешнего.
После шифрования слова внутренний диск сдвигался
на один шаг.
Количество алфавитов r в нем
равно числу символов на диске.
53.
Шифр Гронсфельда53
Шифр сложной замены, называемый шифром
Гронсфельда, представляет собой модификацию шифра
Цезаря числовым ключом.
Для этого под буквами исходного сообщения
записывают цифры числового ключа.
Если ключ короче сообщения, то его запись
циклически повторяют.
Шифротекст получают аналогично, как в шифре
Цезаря, но отсчитывают по алфавиту не третью букву
(как это делается в шифре Цезаря), а выбирают ту
букву, которая смещена по алфавиту на
соответствующую цифру ключа.
54.
Шифр ГронсфельдаПример.
Применим в качестве ключа группу из четырех начальных цифр
числа е (основания натуральных логарифмов), а именно 2718.
Получим для исходного сообщения
ВОСТОЧНЫЙ ЭКСПРЕСС
следующий шифротекст:
Сообщение В О С Т О Ч Н Ы Й Э К С П Р Е С С
Ключ
2 7 1 8 2 7 1 8 2
7 1 8 2 7 1 8 2
Шифртекст Д Х Т Ь Р Ю О Г Л
Д Л Щ С Ч ЖЩ У
Чтобы зашифровать первую букву сообщения В, используя первую
цифру ключа 2 , нужно отсчитать вторую по порядку букву от В,
получается первая буква шифротекста Д.
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч ШЩ Ь Ъ Ы Э Ю Я
54
55.
Шифр ГронсфельдаСледует отметить, что шифр Гронсфельда вскрывается
относительно легко, если учесть,
что в числовом ключе каждая цифра имеет только
десять значений,
а значит, имеется лишь десять вариантов прочтения
каждой буквы шифротекста.
С другой стороны, шифр Гронсфельда допускает
дальнейшие модификации, улучшающие его стойкость, в
частности двойное шифрование разными числовыми
ключами.
Этот шифр представляет собой по существу частный
случай системы шифрования Вижинера.
55
56.
Система шифрования ВижинераСистема Вижинера впервые была опубликована в 1586г. и
является одной из старейших и наиболее известных
многоалфавитных систем.
Свое название она получила по имени французского
дипломата XVI века Блеза Вижинера, который
развивал и совершенствовал криптографические
системы.
Она подобна такой системе шифрования Цезаря, у
которой ключ подстановки меняется от буквы к букве.
56
57.
Система шифрования Вижинера57
Автор шифра предложил для шифрования таблицу, которую
называют таблицей (или квадратом) Вижинера.
Её размер равен длине алфавита.
Верхняя (нулевая) строка заполняется символами
алфавита, левый столбец – цифрами.
Сама таблица заполняется по следующему правилу.
Первая строка имеет цифровой ключ «0» и
заполняется всеми символами по алфавиту,
вторая имеет цифровой ключ «1» и заполняется
теми же символами, сдвинутыми влево на один
символ по кругу,
и далее, k-я имеет цифровой ключ «k-1» и
заполняется теми же символами, сдвинутыми влево
на (k-1) символ по кругу.
58.
Система шифрования ВижинераТаблица Вижинера
для русского
алфавита
Ключ
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я
а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я
б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а
в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б
г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в
д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г
е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д
ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е
з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж
и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з
й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и
к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й
л м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к
м н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л
н о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м
о п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н
п р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о
р с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п
с т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р
т у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с
у ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т
ф х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у
х ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф
ц ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х
ч шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц
шщ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч
щ ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч ш
ь ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ
ы ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь
ъ э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч ш щ ь ы
э ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч ш щ ь ы ъ
ю я а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э
я а б в г д е ж з и й к л м н о п р с т у ф х ц ч шщ ь ы ъ э ю
58
59.
Система шифрования ВижинераТаблица Вижинера
для английского
алфавита
Ключ a b c d e f g h i j k l m n o p q r s t u v w x y z
0
a b c d e f g h i j k l mn o p q r s t u v w x y z
1
b c d e f g h i j k l mn o p q r s t u v w x y z a
2
c d e f g h i j k l mn o p q r s t u v w x y z a b
3
d e f g h i j k l mn o p q r s t u v w x y z a b c
4
e f g h i j k l mn o p q r s t u v w x y z a b c d
5
f g h I j k l mn o p q r s t u v w x y z a b c d e
6
g h i j k l mn o p q r s t u v w x y z a b c d e f
7
h i j k l mn o p q r s t u v w x y z a b c d e f g
8
i j k l mn o p q r s t u v w x y z a b c d e f g h
9
j k l mn o p q r s t u v w x y z a b c d e f g h i
10
k l mn o p q r s t u v w x y z a b c d e f g h i j
11
l mn o p q r s t u v w x y z a b c d e f g h i j k
12 m n o p q r s t u v w x y z a b c d e f g h i j k l
13
n o p q r s t u v w x y z a b c d e f g h i j k l m
14
o p q r s t u v w x y z a b c d e f g h i j k l mn
15
p q r s t u v w x y z a b c d e f g h i j k l mn o
16
q r s t u v w x y z a b c d e f g h i j k l mn o p
17
r s t u v w x y z a b c d e f g h i j k l mn o p q
18
s t u v w x y z a b c d e f g h i j k l mn o p q r
19
t u v w x y z a b c d e f g h i j k l mn o p q r s
20
u v w x y z a b c d e f g h i j k l mn o p q r s t
21
v w x y z a b c d e f g h i j k l mn o p q r s t u
22 w x y z a b c d e f g h i j k l m n o p q r s t u v
23
x y z a b c d e f g h i j k l mn o p q r s t u v w
24
y z a b c d e f g h i j k l mn o p q r s t u v w x
25
z a b c d e f g h i j k l mn o p q r s t u v w x y
59
60.
Система шифрования ВижинераПри шифровании верхняя строка подчеркнутых
символов, используется для поиска очередной буквы
открытого текста.
Крайний левый столбец используется для поиска
соответствующего этой букве элемента ключа.
Очередная буква шифротекста находится на
пересечении столбца, определяемого шифруемой
буквой, и строки, определяемой числовым значением
ключа.
Лучше, если ключевая последовательность
выбирается как набор случайных чисел.
Чтобы ключ легче было запомнить, используют слово или
фразу, а затем заменяют буквы в ней их номерами в
алфавите.
Если ключ оказался короче сообщения, то его
циклически повторяют.
60
61.
Система шифрования ВижинераПример 1.
Пусть выбрано ключевое слово АМБРОЗИЯ.
Необходимо зашифровать сообщение ПРИЛЕТАЮ СЕДЬМОГО.
Выпишем исходное сообщение в строку и запишем под ним
ключевое слово с повторением.
В третью строку выпишем шифротекст.
Сообщение
Ключ
Шифротекст
ПРИ Л ЕТ А Ю С Е Д Ь МО Г О
АМБ Р ОЗ И Я АМ Б Р О З И Я
ПЪЙ ЫУЩИ Э С С Е К Ь Х Л Н
61
62.
Система шифрования Вижинера62
Пример 2.
Пусть, например, требуется зашифровать сообщение:
ГРУЗИТЕ АПЕЛЬСИНЫ БОЧКАМИ ТЧК БРАТЬЯ КАРАМАЗОВЫ ТЧК
Ключ – ВЕНТИЛЬ.
Так как в исходном тексте есть пробелы, подлежащие шифрованию, то
используем измененную таблицу Вижинера (см. след. слайд).
Запишем строку исходного текста с расположенной под ней строкой с
циклически повторяемым ключом:
ГРУЗИТЕ АПЕЛЬСИНЫ БОЧКАМИ ТЧК БРАТЬЯ КАРАМАЗОВЫ ТЧК
ВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕ
63.
Система шифрования Вижинера63
64.
Система шифрования Вижинера64
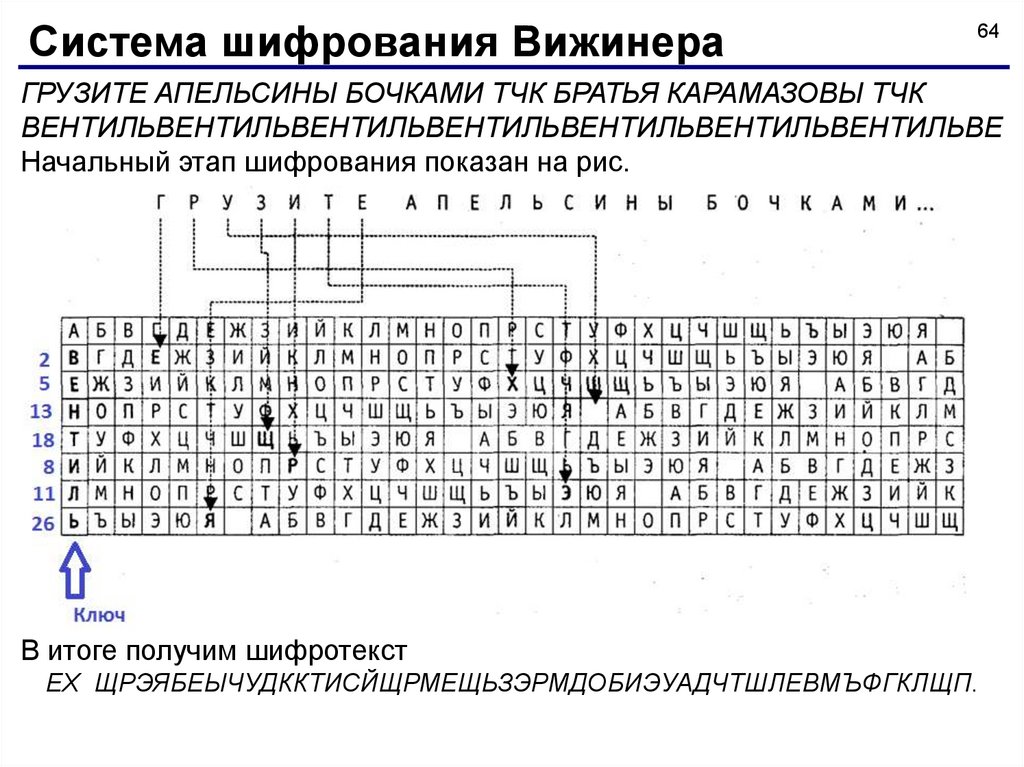
ГРУЗИТЕ АПЕЛЬСИНЫ БОЧКАМИ ТЧК БРАТЬЯ КАРАМАЗОВЫ ТЧК
ВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕ
Начальный этап шифрования показан на рис.
В итоге получим шифротекст
ЕХ ЩРЭЯБЕЫЧУДККТИСЙЩРМЕЩЬЗЭРМДОБИЭУАДЧТШЛЕВМЪФГКЛЩП.
65.
Система шифрования ВижинераРасшифрование осуществляется следующим образом.
Под буквами шифротекста последовательно
записываются буквы ключа;
в строке таблицы, соответствующей очередной букве
ключа, происходит поиск соответствующей буквы
шифротекста.
Находящаяся над ней в первой строке таблицы буква
является соответствующей буквой исходного текста.
65
66.
Система шифрования ВижинераШифры Вижинера с коротким периодическим ключом
используются и в наши дни в системах шифрования, от
которых не требуется высокая криптостойкость.
Для увеличения надежности шифра можно рекомендовать
его использование после предварительной
псевдослучайной перестановки букв в каждой строке
таблицы. Возможны и другие модификации метода.
С развитием математики необходимость в таблицах
шифрования отпала.
Если заменить буквы на числа, то операции
шифрования и дешифрования легко выражаются
простыми математическими формулами.
Так, в шифре Вижинера используются операции
циклического, или модульного сложения.
66
67.
Одноразовые системы67
Пусть {Ki : 0 ≤ i < n} – независимые случайные переменные с
одинаковым распределением вероятностей,
принимающие значения на множестве Zm.
Тогда вероятность выбора в качестве ключа любого из
значений Ki равна Pкл =(1/m).
Система одноразового использования преобразует
исходный текст:
X = (X0, X1, ..., Xn-1)
в шифрованный текст
Y = (Y0, Y1, ..., Y n-1)
при помощи подстановки
Yi = Cki (Xi ) = (Ki +Xi ) (mod m), где i=0 ... n-1.
Для такой системы подстановки используют также термин
“одноразовая лента” и “одноразовый блокнот”.
68.
Одноразовые системыВ классическом понимании одноразовый блокнот является
большой неповторяющейся последовательностью
символов ключа,
распределенных случайным образом,
написанных на кусочках бумаги
и приклеенных к листу блокнота.
Он был изобретен в 1917 году. Первоначально это была одноразовая
лента для телетайпов. Отправитель использовал каждый символ
ключа блокнота для шифрования только одного символа открытого
текста.
68
69.
Одноразовые системы69
Шифрование представляет собой сложение по модулю 26
(для английского алфавита) символа открытого текста и
символа ключа из одноразового блокнота.
Каждый символ ключа используется только единожды и
для единственного сообщения.
Отправитель шифрует сообщения и уничтожает
использованные страницы блокнота или использованную
часть ленты.
Получатель, в свою очередь, используя точно такой же
блокнот, дешифрирует каждый символ шифротекста.
Расшифровав сообщение, получатель уничтожает
соответствующие страницы блокнота или часть ленты.
Для нового сообщения используются новые символы
ключа.
70.
Одноразовые системы70
Пример.
Если сообщением является:
MONEY
а ключевая последовательность в блокноте:
LETUS
то шифротекст будет выглядеть как:
XSGYQ
M + L mod 26 = (12 + 11) mod 26 = 23 = X;
O + E mod 26 = (14 + 4) mod 26 = 18 = S;
N + T mod 26 = (13 + 19) mod 26 = 6 = G;
E + U mod 26 = (4 + 20) mod 26 = 24 = Y;
Y + S mod 26 = (24 + 18) mod 26 = 16 = Q.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
71.
Одноразовые системыТаким образом, одноразовая система шифрует исходный
открытый текст
X = (X0, X1, ..., Xn-1)
в шифротекст
Y = (Y0, Y1, ..., Y n-1)
посредством подстановки Цезаря
Yi = (Ki +Xi ) (mod m), 0 i < n,
где Ki – i -й элемент случайной ключевой
последовательности.
Процедура расшифровывания описывается
соотношением:
Xi = (Yi - Ki) mod m,
где Ki – i-й элемент той же самой случайной ключевой
последовательности.
71
72.
Одноразовые системы72
Пример.
Расшифруем шифротекст
XSGYQ
ключом
LETUS
Получим отрытое сообщение
MONEY
X – L mod 26 = (23 – 11) mod 26 = 12 = M;
S – E mod 26 = (18 – 4) mod 26 = 14 = O;
G – T mod 26 = (6 – 19) mod 26 = (26 + 6 – 19) mod 26 = 13 = N;
Y – U mod 26 = (24 – 20) mod 26 = 4 = E;
Q – S mod 26 = (16 – 18) mod 26 = (26 + 16 – 18) mod 26 = 24 = Y.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
73.
Одноразовые системы73
В предположении, что злоумышленник не сможет получить
доступ к одноразовому блокноту, использованному для
шифрования сообщения, эта схема совершенно
безопасна.
Данное шифрованное сообщение на вид соответствует
любому открытому сообщению того же размера.
Т.к. все ключевые последовательности совершенно
одинаковы (помните, символы ключа генерируемся
случайным образом), у противника отсутствует
информация, позволяющая подвергнув шифротекст
криптоанализу.
Случайная ключевая последовательность, сложенная с
неслучайным открытым текстом, даст совершенно
случайный шифротекст, и никакие вычислительные
мощности не смогут это изменить.
74.
Одноразовые системы74
Необходимо напомнить, что символы ключа должны
генерироваться случайным образом.
Любые попытки вскрыть такую схему сталкиваются со
способом, которым создастся последовательность
символов ключа.
Использование генераторов псевдослучайных чисел не
считается, у них всегда неслучайные свойства.
Если вы используете действительно случайный
источник – это намного труднее, чем кажется на первый
взгляд – это совершенно безопасно.
75.
Одноразовые системы75
Другой важный момент:
ключевую последовательность никогда нельзя
использовать второй раз!!!!
Системы одноразового использования теоретически
не расшифруемы,
т.к. не содержат достаточной информации для
восстановления текста.
Даже если вы используете блокнот размером в
несколько гигабайт,
то если криптоаналитик получит несколько текстов с
перекрывающимися ключами,
он сможет восстановить открытый текст.
76.
Одноразовые системы76
Одноразовые блокноты используются и сегодня, главным
образом для сверхсекретных каналов связи с низкой
пропускной способностью.
По слухам «горячая линия» между США и бывшим СССР
шифровалась с помощью одноразового блокнота.
Многие сообщения шпионов зашифрованы с использованием
одноразовых блокнотов.
Эти сообщения нераскрыты сегодня и навсегда останутся
нераскрытыми.
На этот факт не повлияет время работы
суперкомпьютеров над этой проблемой.
77.
Одноразовые системы77
Почему же эти системы неприменимы для обеспечения
секретности при обработке информации?
Ответ простой – они непрактичны,
т.к. требуют независимого выбора значения ключа для
каждой буквы исходного текста.
78.
Двойной квадрат (Уитстона)78
Для двойного квадрата формируются две таблицы размером
N = n ×m.
Здесь n – число строк, m – число столбцов. Число N должно
совпадать с числом символов в алфавите.
Символы алфавита в таблицах располагаются случайным
образом. Лучше, если порядок символов в таблицах не
совпадает с алфавитом.
Размеры таблиц и расположение символов в них являются
ключом данной криптографической системы.
Одну таблицу принято называть левой – пусть ей будет
соответствовать номер 1, другую правой – пусть ее номер
будет равен 2.
Далее алгоритм шифрования состоит в следующем.
79.
Двойной квадрат79
Открытый текст разбивают на блоки по два символа в
каждом. Такой блок называют биграммой. Если в
последнем блоке оказался один символ, то он
либо отбрасывается (если это возможно),
либо добавляется один символ, который не влияет на содержание
открытого текста.
Пусть символы ab являются некоторой биграммой
открытого текста.
Первый символ биграммы a располагают в первой
таблице.
Пусть пара чисел (i, j) являются координатами этого символа в
первой таблице.
Второй символ биграммы b располагают во второй
таблице.
Пусть пара чисел (t, q) являются координатами этого символа в
первой таблице.
80.
Двойной квадрат80
В этом случае если:
i≠t (номера строк букв биграмм не совпадают, а номера
столбцов, в которых находятся буквы биграмм,
произвольный), то
символ a биграммы переходит в символ второй
таблицы с координатами (i, q),
а символ b – в символ первой таблицы с
координатами (t, j);
i=t и j ≠q (буквы биграммы находятся в строках с
одинаковыми номерами, но с разными номерами
столбцов таблиц), то
символ a биграммы переходит в символ второй
таблицы с координатами (i, j),
а символ b – в символ первой таблицы с
координатами (t, q).
81.
Двойной квадратi= t и j=q (буквы биграммы находятся в строках и
столбцах с одинаковыми номерами), то
символы a и b биграммы переставляются.
Расшифровка текста происходит по тем же правилам с той
лишь разницей, что
первая буква биграммы шифрованного текста
располагается в правой (во второй) таблице,
а вторая буква биграммы располагается в первой
(левой) таблице.
81
82.
Двойной квадрат82
Криптографическая система двойной квадрат весьма
устойчивый к взлому.
Его просто реализовать в виде программы на компьютере. В
этом случае в символы алфавита можно включить все
символы клавиатуры.
Шифрование методом "двойного квадрата" дает весьма
устойчивый к вскрытию и простой в применении шифр.
Взламывание шифртекста "двойного квадрата" требует
больших усилий,
при этом длина сообщения должна быть не менее
тридцати строк.
83.
Двойной квадрат. Пример83
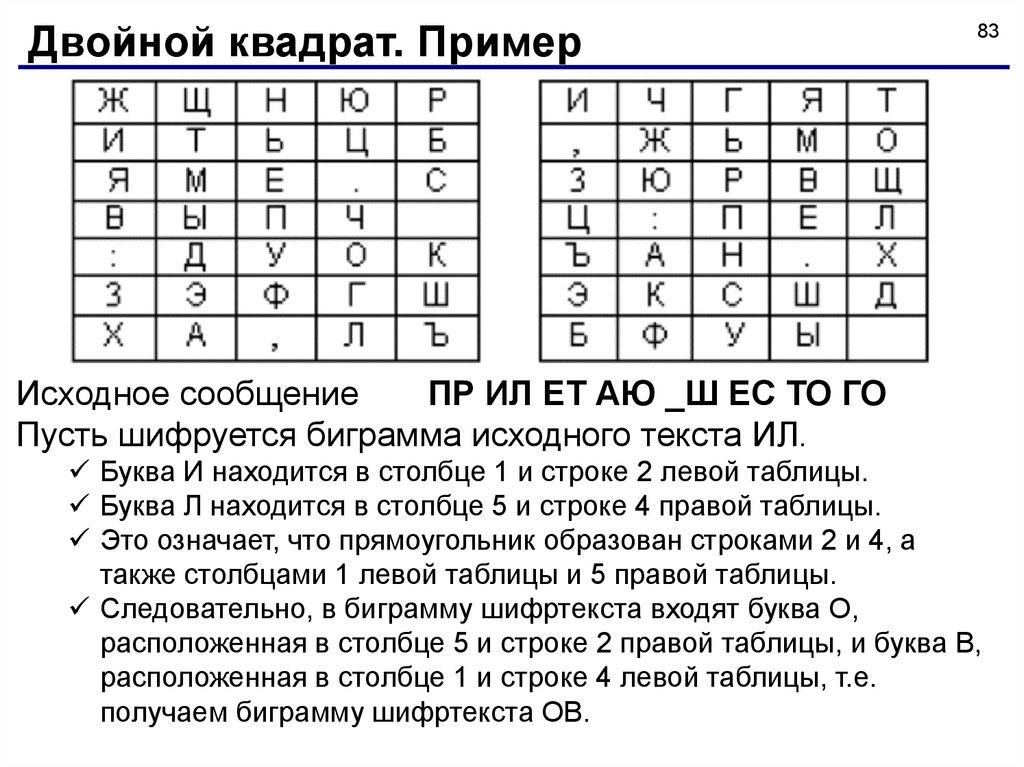
Исходное сообщение
ПР ИЛ ЕТ АЮ _Ш ЕС ТО ГО
Пусть шифруется биграмма исходного текста ИЛ.
Буква И находится в столбце 1 и строке 2 левой таблицы.
Буква Л находится в столбце 5 и строке 4 правой таблицы.
Это означает, что прямоугольник образован строками 2 и 4, а
также столбцами 1 левой таблицы и 5 правой таблицы.
Следовательно, в биграмму шифртекста входят буква О,
расположенная в столбце 5 и строке 2 правой таблицы, и буква В,
расположенная в столбце 1 и строке 4 левой таблицы, т.е.
получаем биграмму шифртекста ОВ.
84.
Двойной квадрат. Пример84
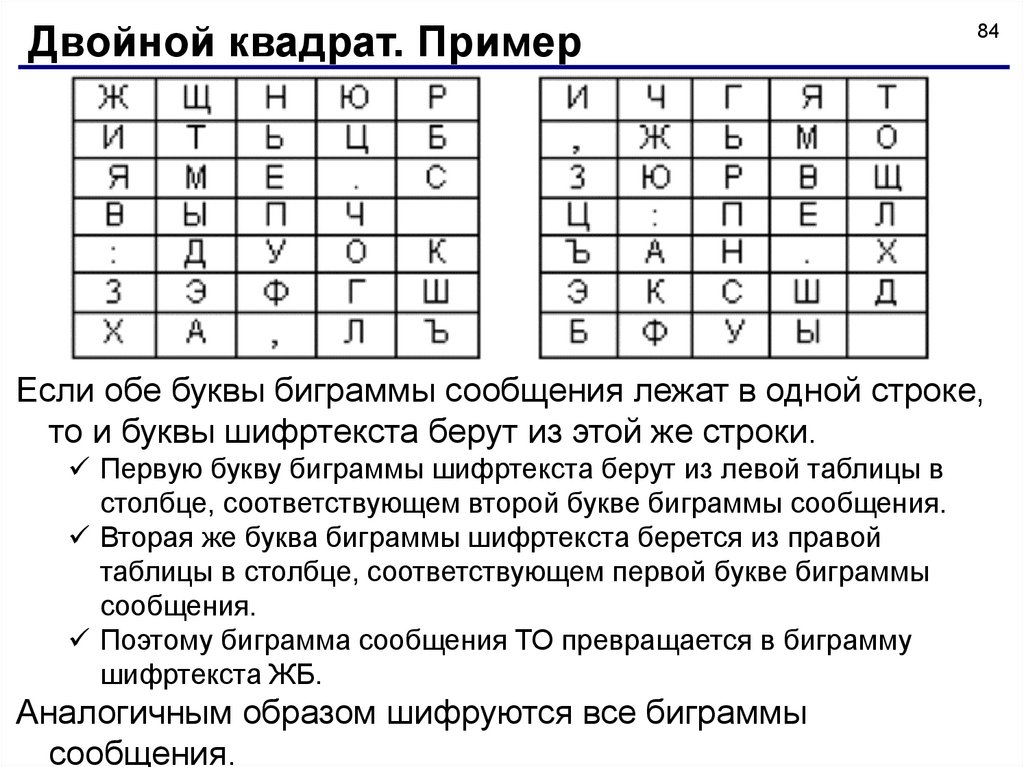
Если обе буквы биграммы сообщения лежат в одной строке,
то и буквы шифртекста берут из этой же строки.
Первую букву биграммы шифртекста берут из левой таблицы в
столбце, соответствующем второй букве биграммы сообщения.
Вторая же буква биграммы шифртекста берется из правой
таблицы в столбце, соответствующем первой букве биграммы
сообщения.
Поэтому биграмма сообщения ТО превращается в биграмму
шифртекста ЖБ.
Аналогичным образом шифруются все биграммы
сообщения.












































































 Информатика
Информатика








