Лекция 7 (Сбалансированные деревья)

1. Сбалансированные деревья

1

2. Идеально сбалансированное дерево

Двоичное дерево считается идеально
сбалансированным, если для каждой его
вершины количество вершин в левом и
правом поддеревьях различается не более
чем на 1
2

3. АВЛ-деревья

Дерево является сбалансированным тогда и
только тогда, когда для каждого его узла
высота его двух поддеревьев различается
не более чем на 1
АВЛ-деревья, Г. М. Адельсон-Вельский, Е.
М. Ландис , 1962 г.
3

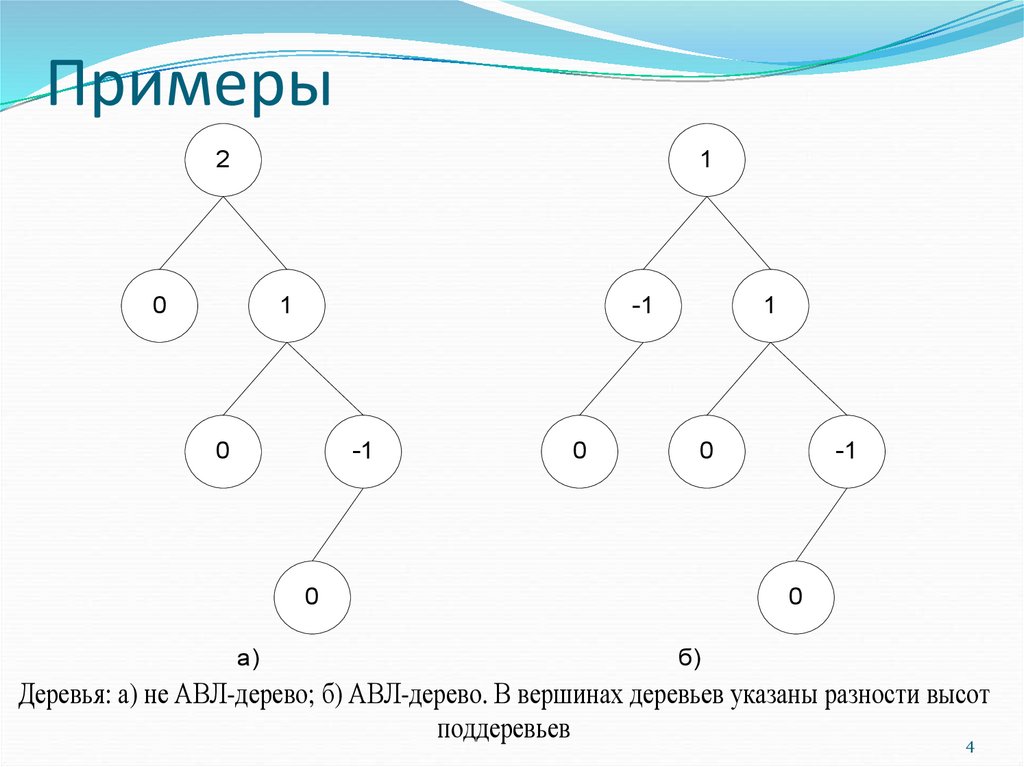
4. Примеры

2
1
0
1
-1
0
-1
0
1
0
0
а)
-1
0
б)
Деревья: а) не АВЛ-дерево; б) АВЛ-дерево. В вершинах деревьев указаны разности высот
поддеревьев
4

5. Описание типа данных

struct node
{
int data;
int height;
node* left;
node* right;
};
typedef node* AVLtree;
AVLtree root = NULL;
5

6. Высота дерева

int height(AVLtree p)
{
return (p!=NULL) ? p->height : 0;
}
6

7. Вычисление высоты поддерева

void fix_height(AVLtree p)
{
int hl = height(p->left);
int hr = height(p->right);
p->height = (hl > hr ? hl : hr) + 1;
}
7

8. Определение разности высот правого и левого поддеревьев

int balance_right_left(AVLtree p)
{
return height(p->right) - height(p->left);
}
8

9.

9

10. Добавление вершины в АВЛ-дерево

Пусть r – корень с левым и правым поддеревом.
Предположим, что в L мы включаем новый
элемент, и это вызывает увеличение его высоты на
единицу. Возможны три случая после включения:
1. HL=HR HL>HR на единицу – критерий
сбалансированности не нарушается
2. HL<HR HL=HR– критерий
сбалансированности не нарушается
3. HL>HR на единицу –> дерево нужно
перестроить
r
L R
10

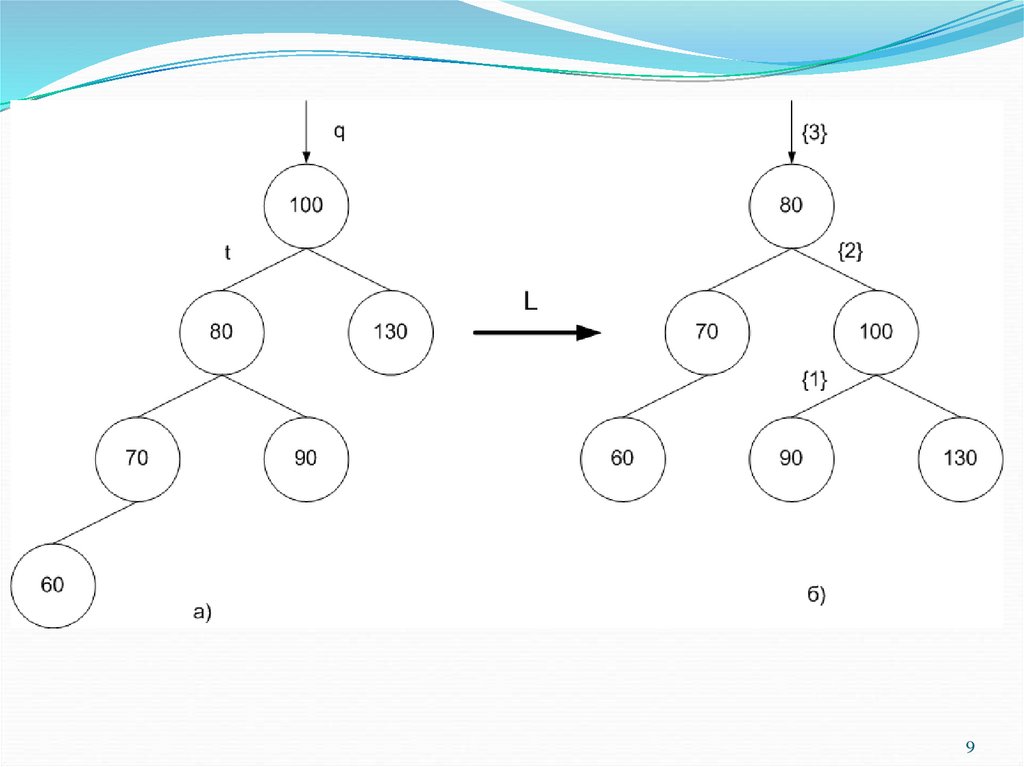
11. Балансировка АВЛ-дерева

существует две принципиально различные
возможности (другие – симметричные)
11

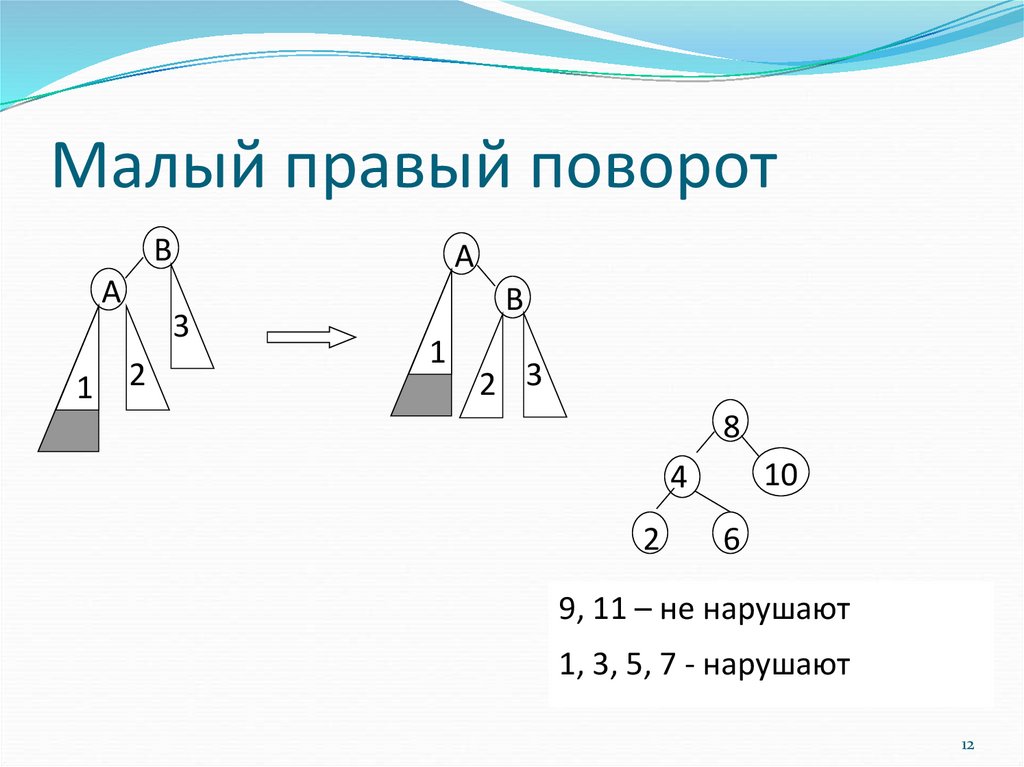
12. Малый правый поворот

B
A
A
3
1
2
B
1
2 3
8
10
4
2
6
9, 11 – не нарушают
1, 3, 5, 7 - нарушают
12

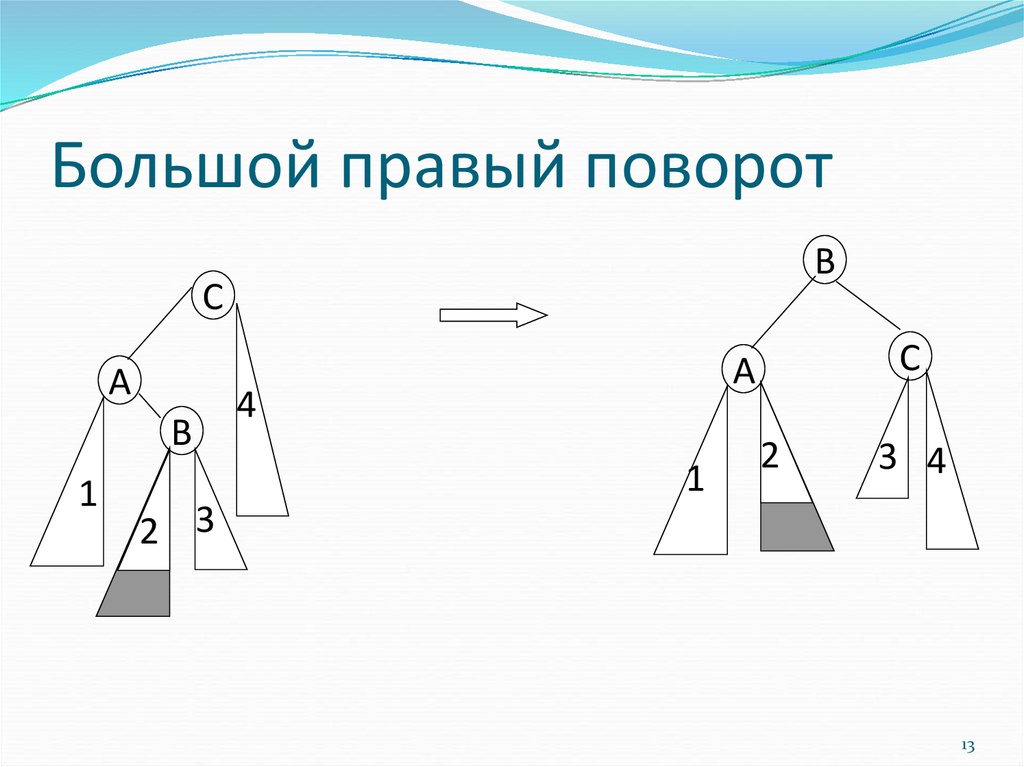
13. Большой правый поворот

B
С
A
B
1
С
A
4
1
2
3 4
2 3
13

14. Пример

Составить АВЛ-дерево с вершинами:
4
5
7
6
1
3
2
14

15. Правый поворот вокруг p

AVLtree rotate_right(AVLtree p)
{
AVLtree q = p->left;
p->left = q->right;
q->right = p;
fix_height(p);
fix_height(q);
return q;
}
15

16. Левый поворот вокруг p

AVLtree rotate_left(AVLtree q)
{
AVLtree p = q->right;
q->right = p->left;
p->left = q;
fix_height(q);
fix_height(p);
return p;
}
16

17. Балансировка узла p

AVLtree balance(AVLtree p) {
fix_height(p);
if (balance_right_left(p) == 2){
if (balance_right_left(p->right) < 0)
p->right = rotate_right(p->right);
return rotate_left(p);}
if (balance_right_left(p) == -2){
if (balance_right_left(p->left) > 0)
p->left = rotate_left(p->left);
return rotate_right(p);}
return p; // балансировка не нужна
}
17

18. Вставка элемента k в дерево p

AVLtree insert(AVLtree p, int k) {
if (p == NULL) {
AVLtree t = new node();
t->data = k;
t->left = t->right = NULL;
t->height = 1;
return t; }
if (k < p->data) p->left = insert(p->left, k);
else
p->right = insert(p->right, k);
return balance(p);
}
18

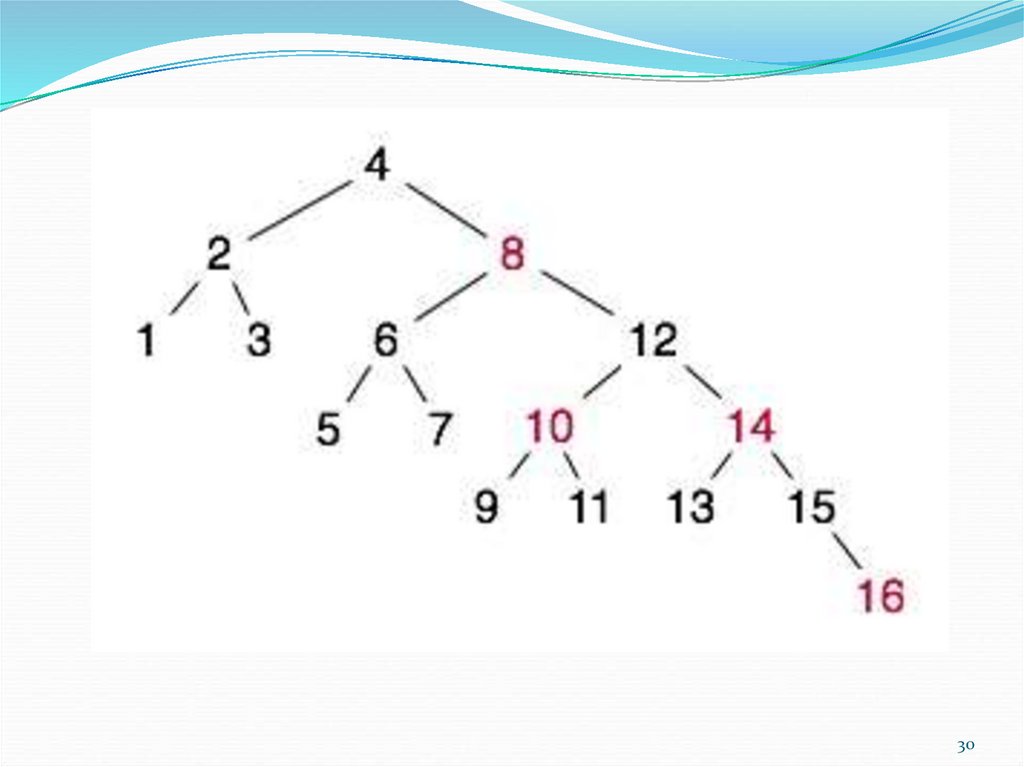
19. Пример

8, 6, 10, 5, 7, 9, 13, 3, 1
19

20. 2-3 деревья

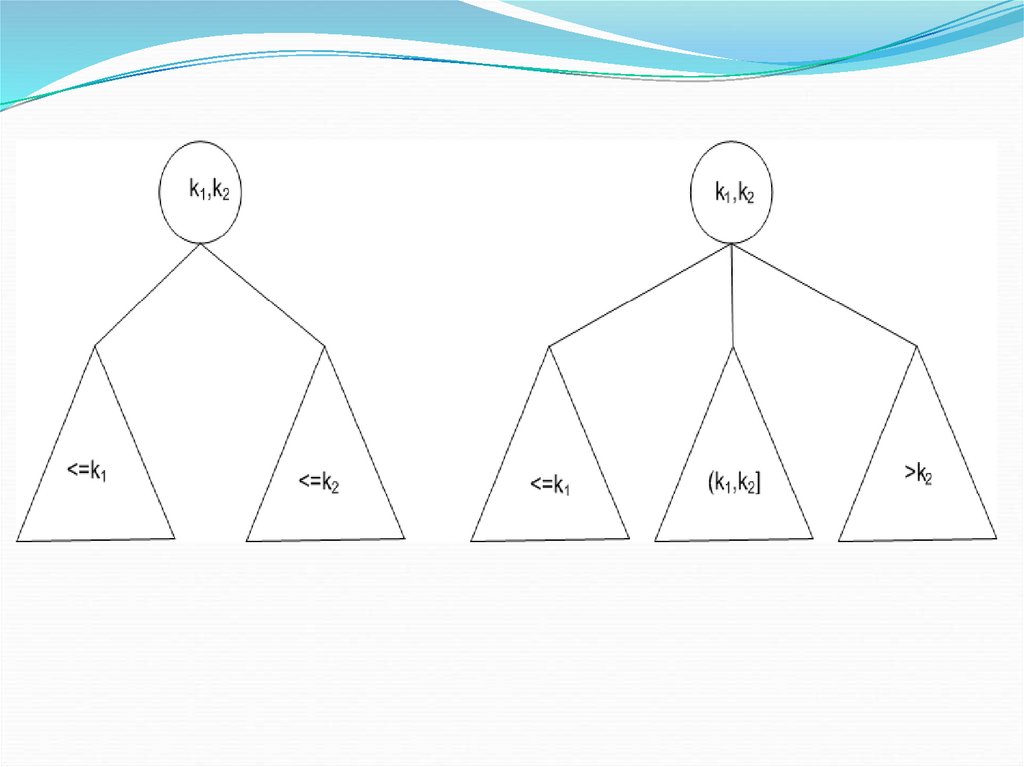
2–3 деревом называется дерево, в котором каждая
вершина, не являющаяся листом, имеет двух или трех
сыновей, а длины всех путей из корня в листья
одинаковы.
2–3 дерево – это сбалансированное дерево. Все его
листья находятся на одной высоте – длина пути от корня
дерева до любого листа одинакова (высота h).
Вершины в 2–3 дереве двух видов: имеющие двух
сыновей и имеющие трех сыновей. В вершине дерева
хранятся два ключа – k1 и k2.
20

21.

22. 2-3 деревья

22

23. Описание структуры данных

struct *node
{
bool leaf; {True - лист; False – внутренняя
вершина}
int key1; int key2; {key1 - максимальное значение
ключа в левой ветви дерева; key2 – максимальное
значение в средней ветви дерева; для листа значение
в key1}
node *left,*mid,*right; {Указатели на левую,
среднюю и правую ветви дерева}
}
*node root; {Корень дерева}
23

24.

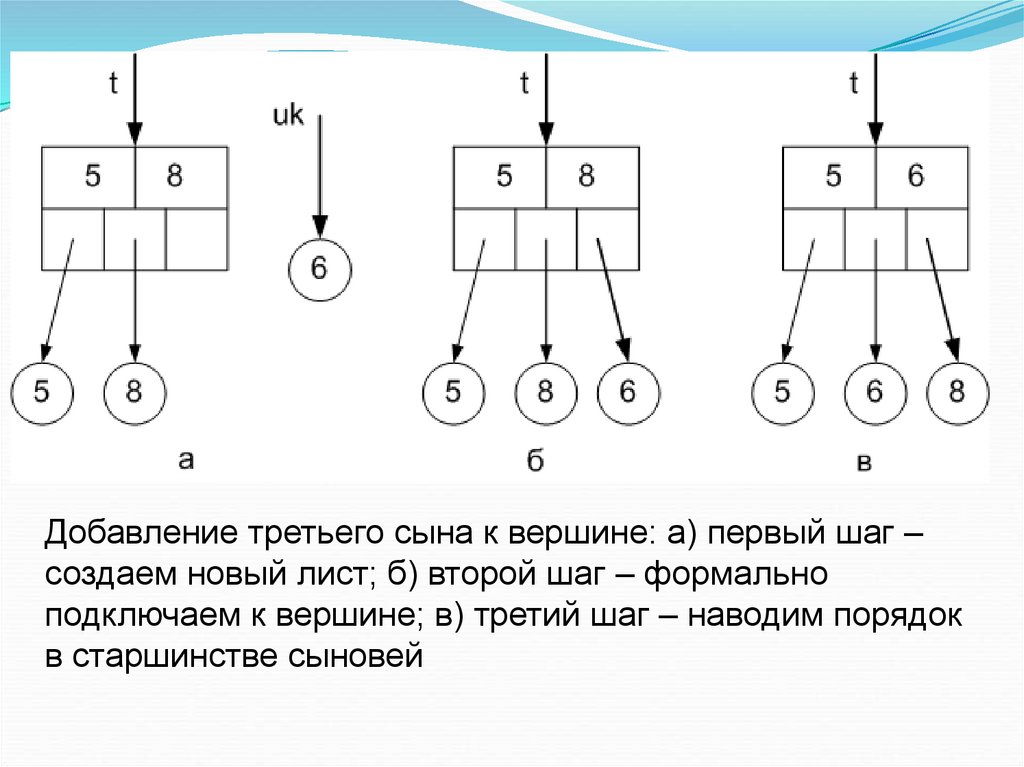
Добавление третьего сына к вершине: а) первый шаг –
создаем новый лист; б) второй шаг – формально
подключаем к вершине; в) третий шаг – наводим порядок
в старшинстве сыновей

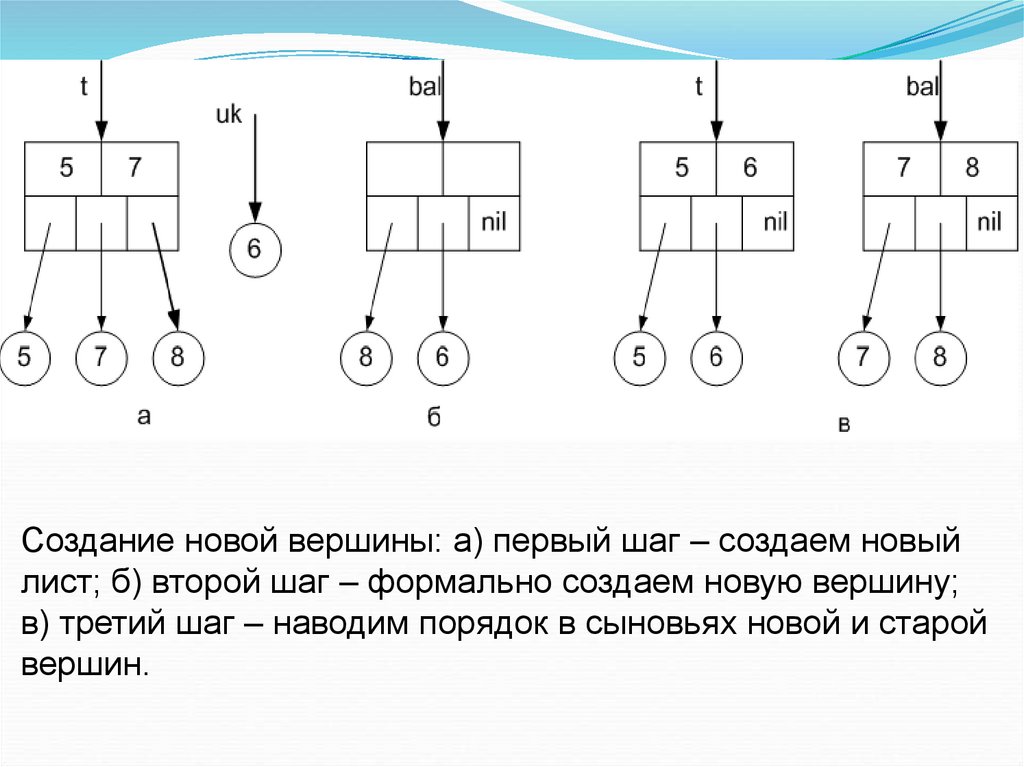
25.

Создание новой вершины: а) первый шаг – создаем новый
лист; б) второй шаг – формально создаем новую вершину;
в) третий шаг – наводим порядок в сыновьях новой и старой
вершин.

26. Красно-черные деревья

Рудольф Байер, 1978
Название появилось в статье
Л. Гимпаса и Р. Седжвика, 1978
Являются одними из наиболее активно используемых
на практике самобалансирующихся деревьев поиска,
на них основаны:
контейнеры set и map в большинстве реализаций
библиотеки STL языка C++
класс TreeMap языка Java
многие другие реализации ассоциативного массива в
26
различных библиотеках

27. Временная сложность

Расход памяти O(n)
Поиск, вставка, удаление O(log n)
27

28. Красно-черные деревья

Двоичное дерево поиска называется красно-черным
деревом, если оно имеет следующие свойства:
каждая вершина либо красная, либо черная
каждый лист – черный
если вершина красная, оба ее сына черные
все пути, идущие вниз от корня к листьям, содержат
одинаковое количество черных вершин
28

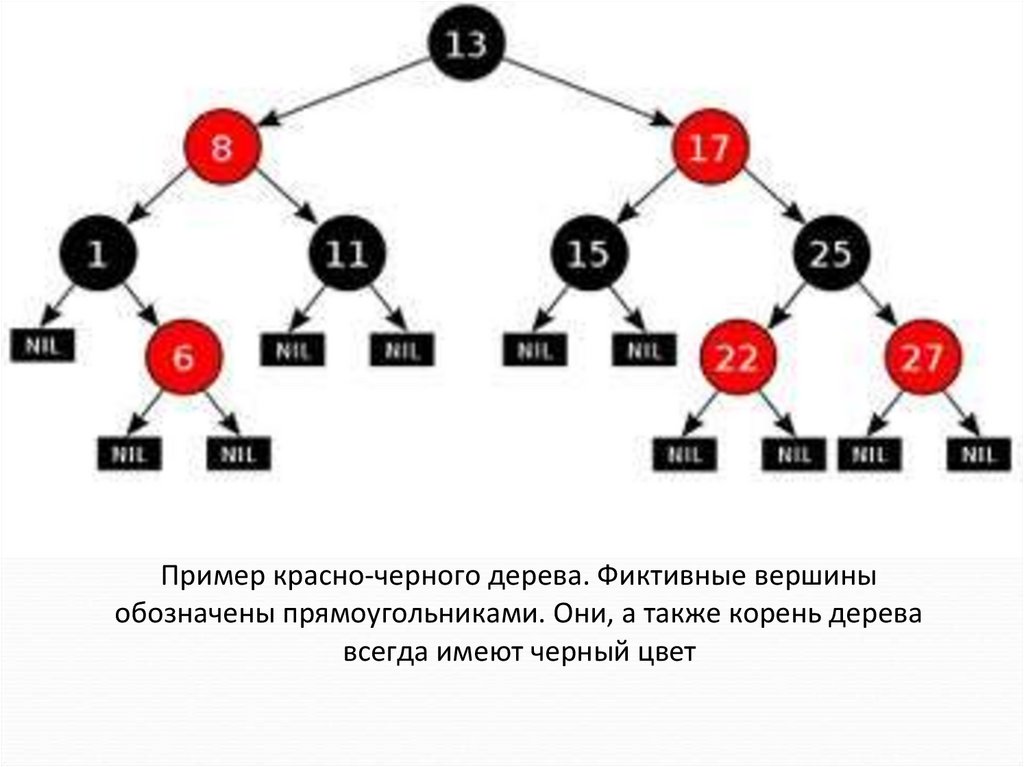
29.

Пример красно-черного дерева. Фиктивные вершины
обозначены прямоугольниками. Они, а также корень дерева
всегда имеют черный цвет

30.

30

31. Утверждение

Красно-черное дерево с n внутренними вершинами
имеет высоту не больше 2log2(n+1)
Поддерево с корнем a содержит, по крайней мере,
2bh(a) – 1 внутренних вершин (bh – число черных
вершин от a до листа
31

32.

32

33. Описание типов данных

typedef enum { BLACK, RED } nodeColor;
typedef struct Node_
{
Node_ *left;
// left child
Node_ *right;
// right child
Node_ *parent;
// parent
nodeColor color;
// node color (BLACK, RED)
int data;
// data stored in node
} Node;
33

34. Описание типов данных

Node nil = { NULL, NULL, NULL, BLACK, NULL };
Node* NIL = &nil;
Node *root = NIL;
Указатель на фиктивную вершину, который заменяет все
листы дерева
34

35.

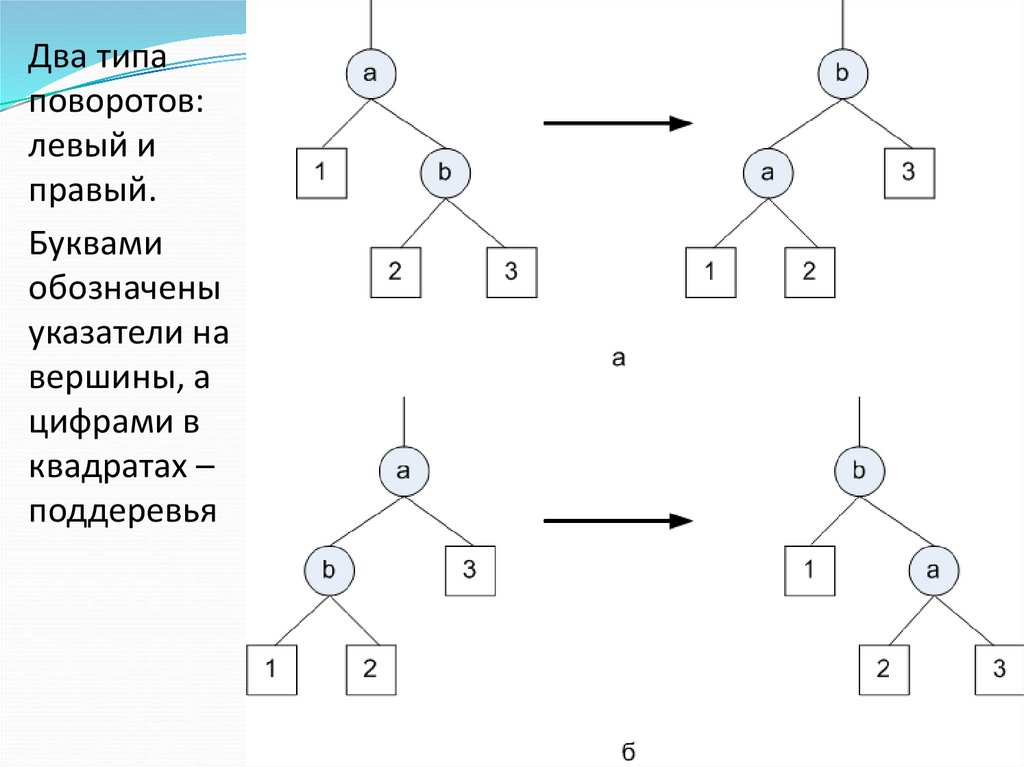
Два типа
поворотов:
левый и
правый.
Буквами
обозначены
указатели на
вершины, а
цифрами в
квадратах –
поддеревья

36. Вставка элемента

Каждый элемент вставляется вместо листа, поэтому
для выбора места вставки идём от корня до тех пор,
пока указатель на следующего сына не станет nil (то
есть этот сын – лист). Вставляем вместо него новый
элемент с nil-потомками и красным цветом. Теперь
проверяем балансировку. Если отец нового элемента
черный, то никакое из свойств дерева не нарушено.
Если же он красный, то нарушается свойство 3, для
исправления достаточно рассмотреть два случая:…
36

37.

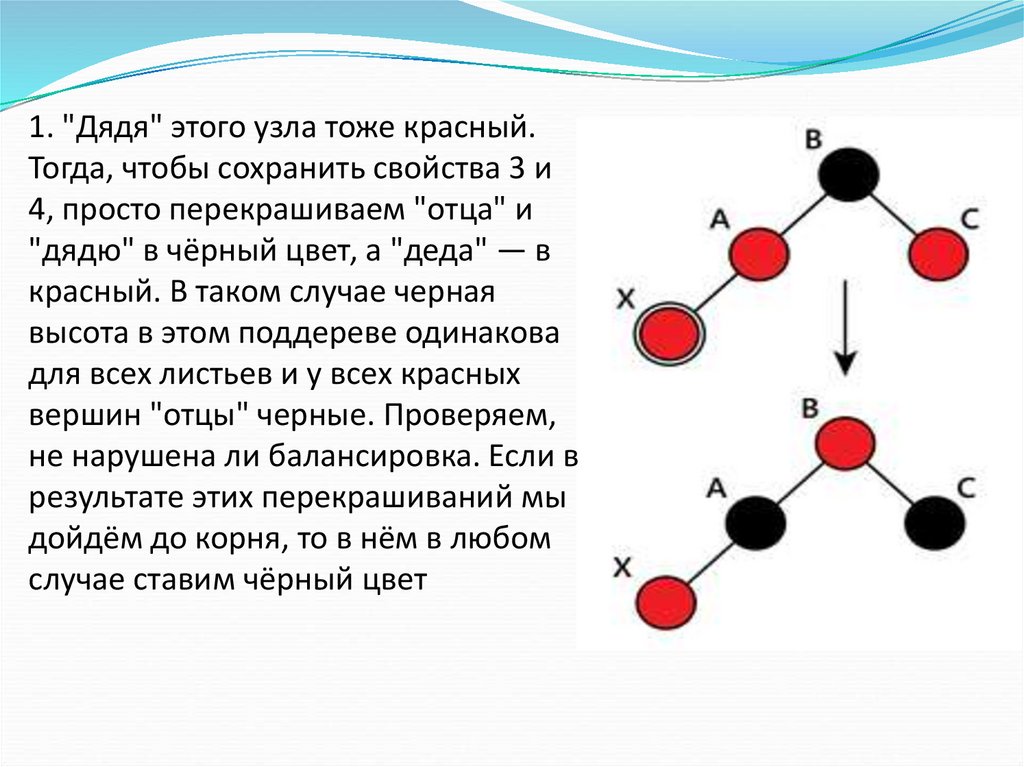
1. "Дядя" этого узла тоже красный.
Тогда, чтобы сохранить свойства 3 и
4, просто перекрашиваем "отца" и
"дядю" в чёрный цвет, а "деда" — в
красный. В таком случае черная
высота в этом поддереве одинакова
для всех листьев и у всех красных
вершин "отцы" черные. Проверяем,
не нарушена ли балансировка. Если в
результате этих перекрашиваний мы
дойдём до корня, то в нём в любом
случае ставим чёрный цвет

38.

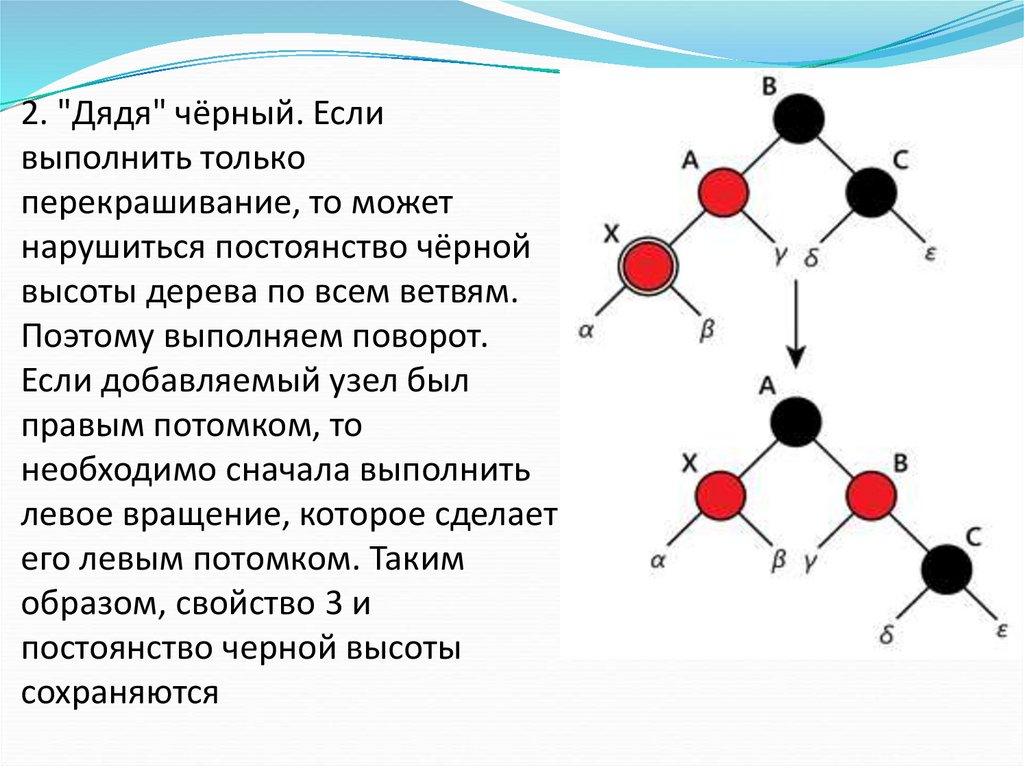
2. "Дядя" чёрный. Если
выполнить только
перекрашивание, то может
нарушиться постоянство чёрной
высоты дерева по всем ветвям.
Поэтому выполняем поворот.
Если добавляемый узел был
правым потомком, то
необходимо сначала выполнить
левое вращение, которое сделает
его левым потомком. Таким
образом, свойство 3 и
постоянство черной высоты
сохраняются

39. Пример

10
80
85
90
15
40
70
5
20
55
60
30
50
65
https://youtu.be/vDHFF4wjWYU
39

40. Удаление вершины

При удалении вершины могут возникнуть три случая в
зависимости от количества её детей:
У вершины нет детей, указатель на неё у родителя изменяем
на NIL
Только один ребёнок, делаем у родителя ссылку на него
вместо этой вершины
Имеются оба ребёнка, находим вершину со следующим
значением ключа. У такой вершины нет левого ребёнка.
Вершина находится в правом поддереве исходной вершины
и она самая левая в нем. Переходим в правое поддерево, и
идем вниз в левое до тех пор, пока у вершины есть левый
ребенок. Удаляем уже эту вершину описанным во втором
пункте способом, скопировав её ключ в изначальную
вершину
40

41. Удаление вершины

Балансировка дерева? При удалении красной
вершины свойства дерева не нарушаются.
Восстановление балансировки потребуется только при
удалении чёрной
41

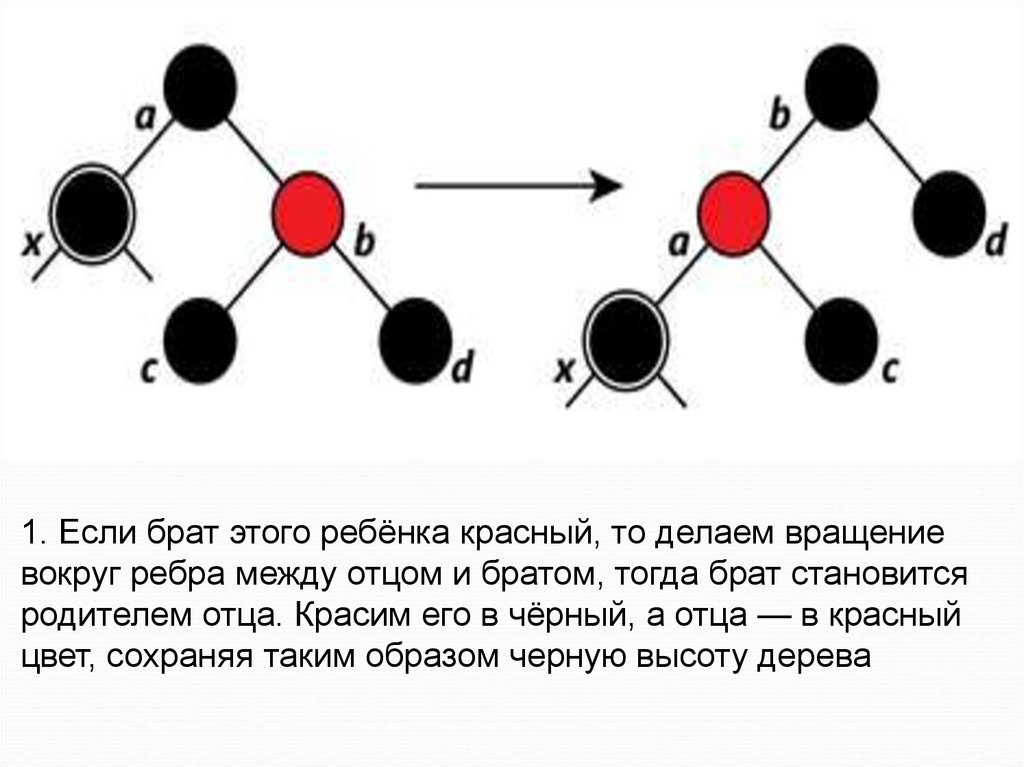
42.

1. Если брат этого ребёнка красный, то делаем вращение
вокруг ребра между отцом и братом, тогда брат становится
родителем отца. Красим его в чёрный, а отца — в красный
цвет, сохраняя таким образом черную высоту дерева

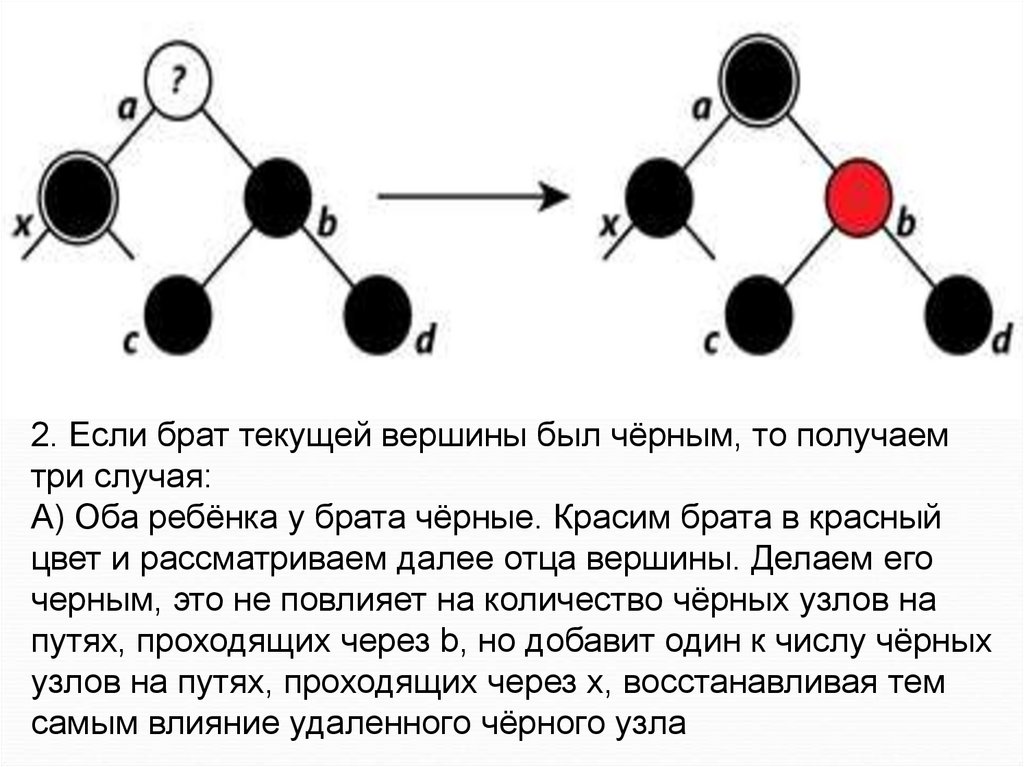
43.

2. Если брат текущей вершины был чёрным, то получаем
три случая:
А) Оба ребёнка у брата чёрные. Красим брата в красный
цвет и рассматриваем далее отца вершины. Делаем его
черным, это не повлияет на количество чёрных узлов на
путях, проходящих через b, но добавит один к числу чёрных
узлов на путях, проходящих через x, восстанавливая тем
самым влияние удаленного чёрного узла

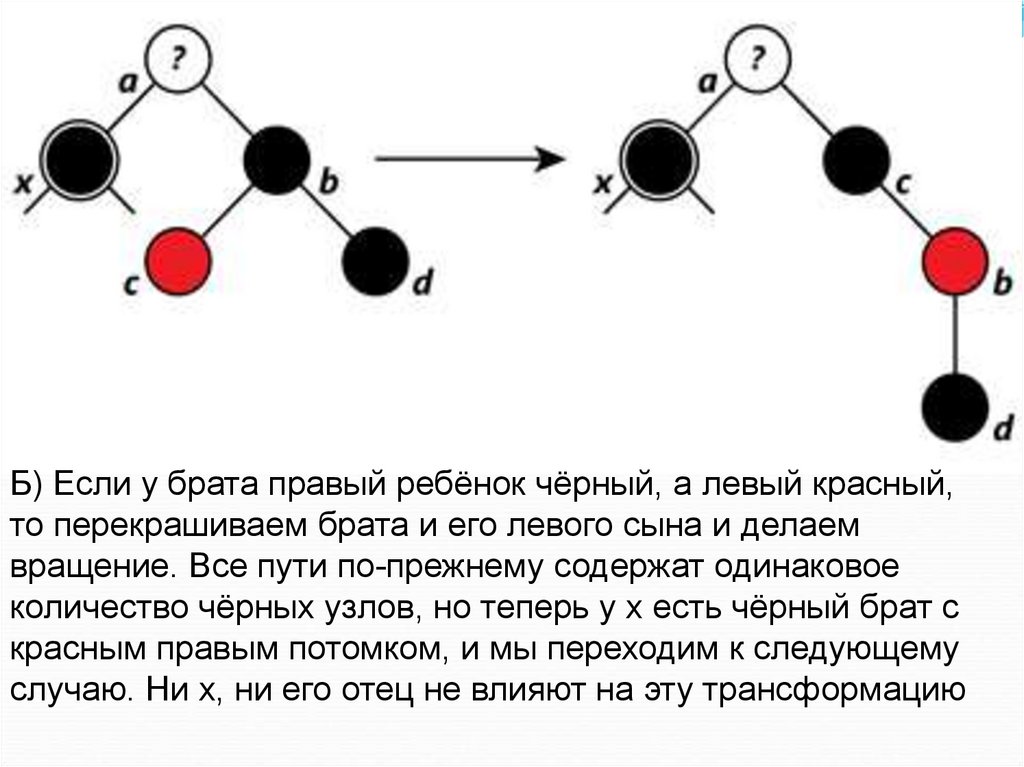
44.

Б) Если у брата правый ребёнок чёрный, а левый красный,
то перекрашиваем брата и его левого сына и делаем
вращение. Все пути по-прежнему содержат одинаковое
количество чёрных узлов, но теперь у x есть чёрный брат с
красным правым потомком, и мы переходим к следующему
случаю. Ни x, ни его отец не влияют на эту трансформацию

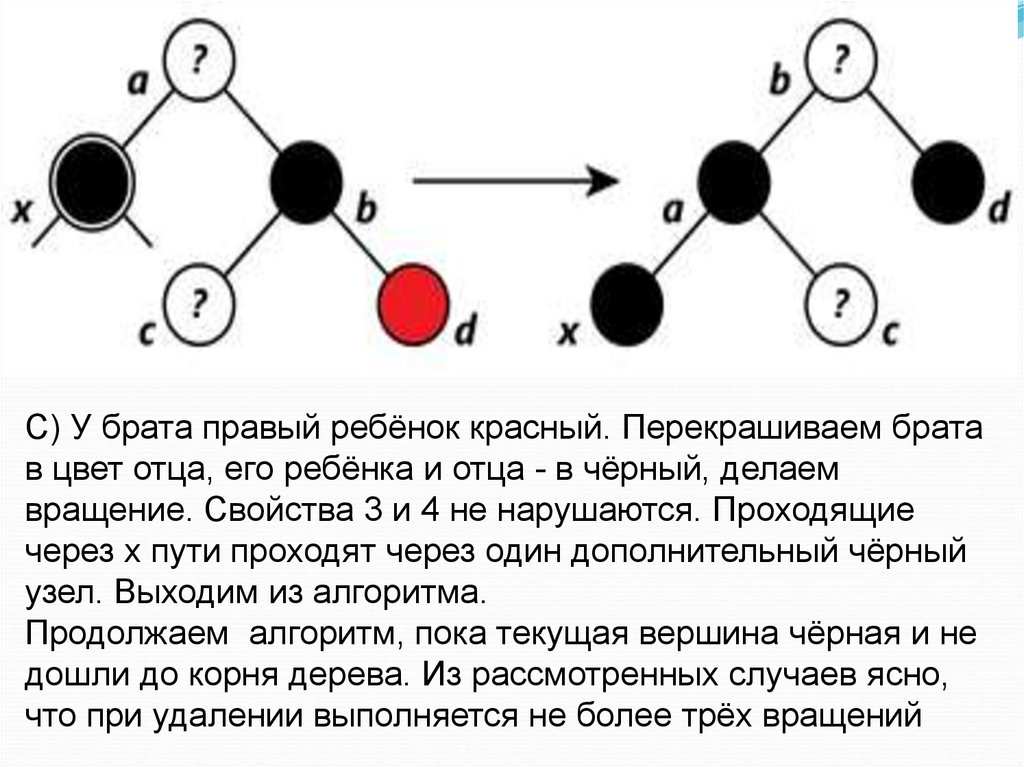
45.

C) У брата правый ребёнок красный. Перекрашиваем брата
в цвет отца, его ребёнка и отца - в чёрный, делаем
вращение. Свойства 3 и 4 не нарушаются. Проходящие
через x пути проходят через один дополнительный чёрный
узел. Выходим из алгоритма.
Продолжаем алгоритм, пока текущая вершина чёрная и не
дошли до корня дерева. Из рассмотренных случаев ясно,
что при удалении выполняется не более трёх вращений

46. Ссылки

http://mech.math.msu.su/~vvb/2course/Borisenko/le
cTree.html
http://algolist.ru/ds/rbtree.php
https://youtu.be/vDHFF4wjWYU
http://videolectures.net/mit6046jf05_demaine_lec10/
https://intellect.icu/krasno-chernoe-derevo-derevopoiska-4612
https://kubokovac.eu/gnarley-trees/
46