Принцип действия лазера

1.

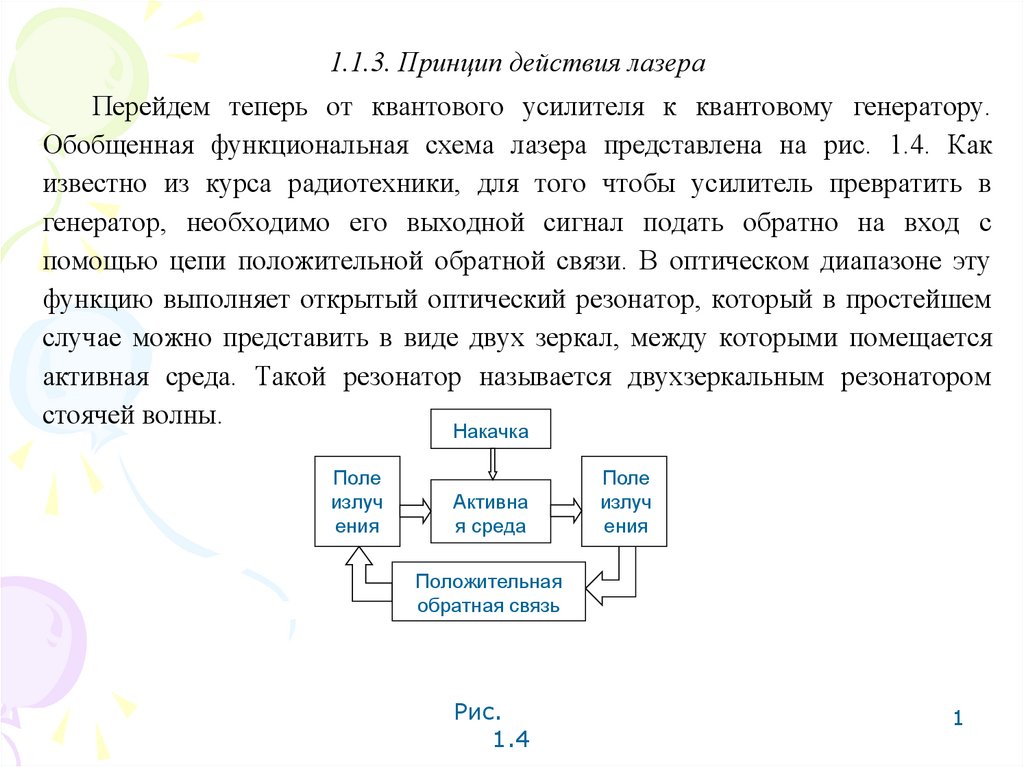
1.1.3. Принцип действия лазера
Перейдем теперь от квантового усилителя к квантовому генератору.
Обобщенная функциональная схема лазера представлена на рис. 1.4. Как
известно из курса радиотехники, для того чтобы усилитель превратить в
генератор, необходимо его выходной сигнал подать обратно на вход с
помощью цепи положительной обратной связи. В оптическом диапазоне эту
функцию выполняет открытый оптический резонатор, который в простейшем
случае можно представить в виде двух зеркал, между которыми помещается
активная среда. Такой резонатор называется двухзеркальным резонатором
стоячей волны.
Накачка
Поле
излуч
ения
Активна
я среда
Поле
излуч
ения
Положительная
обратная связь
Рис.
1.4
1

2.

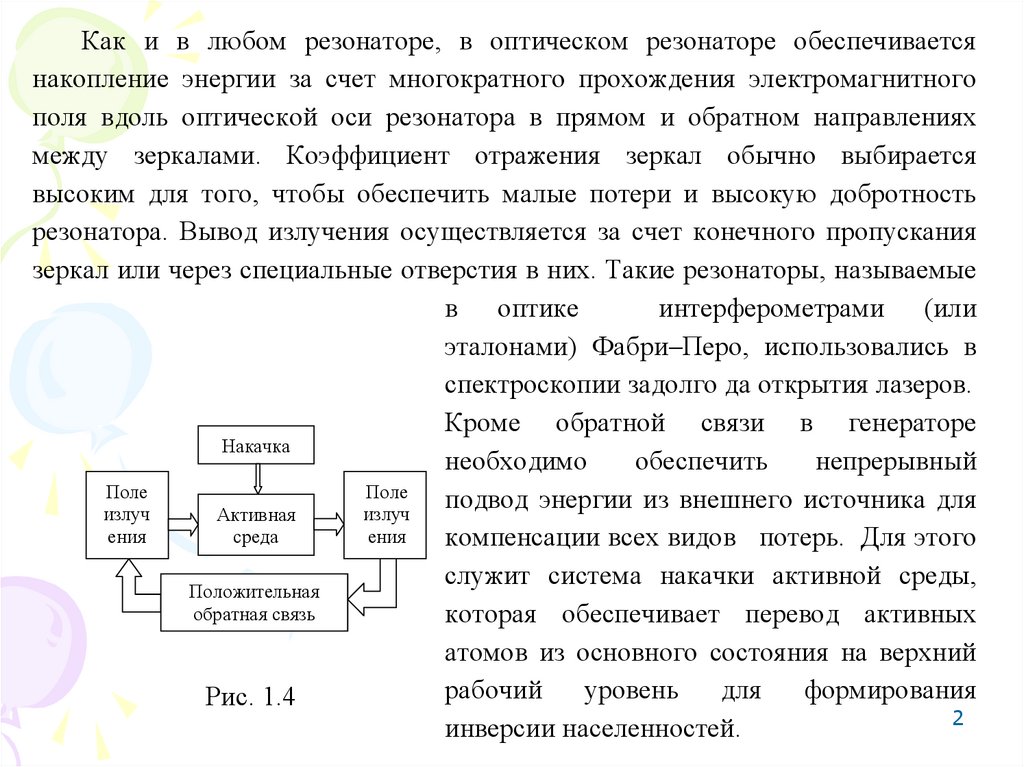
Как и в любом резонаторе, в оптическом резонаторе обеспечивается
накопление энергии за счет многократного прохождения электромагнитного
поля вдоль оптической оси резонатора в прямом и обратном направлениях
между зеркалами. Коэффициент отражения зеркал обычно выбирается
высоким для того, чтобы обеспечить малые потери и высокую добротность
резонатора. Вывод излучения осуществляется за счет конечного пропускания
зеркал или через специальные отверстия в них. Такие резонаторы, называемые
в оптике
интерферометрами (или
эталонами) Фабри–Перо, использовались в
спектроскопии задолго да открытия лазеров.
Кроме обратной связи в генераторе
Накачка
необходимо
обеспечить
непрерывный
Поле
Поле
подвод энергии из внешнего источника для
излуч
излуч
Активная
ения
среда
ения
компенсации всех видов потерь. Для этого
служит система накачки активной среды,
Положительная
обратная связь
которая обеспечивает перевод активных
атомов из основного состояния на верхний
рабочий
уровень
для
формирования
Рис. 1.4
2
инверсии населенностей.

3.

З1
З2
F0
l
L
F(z)
F0
z
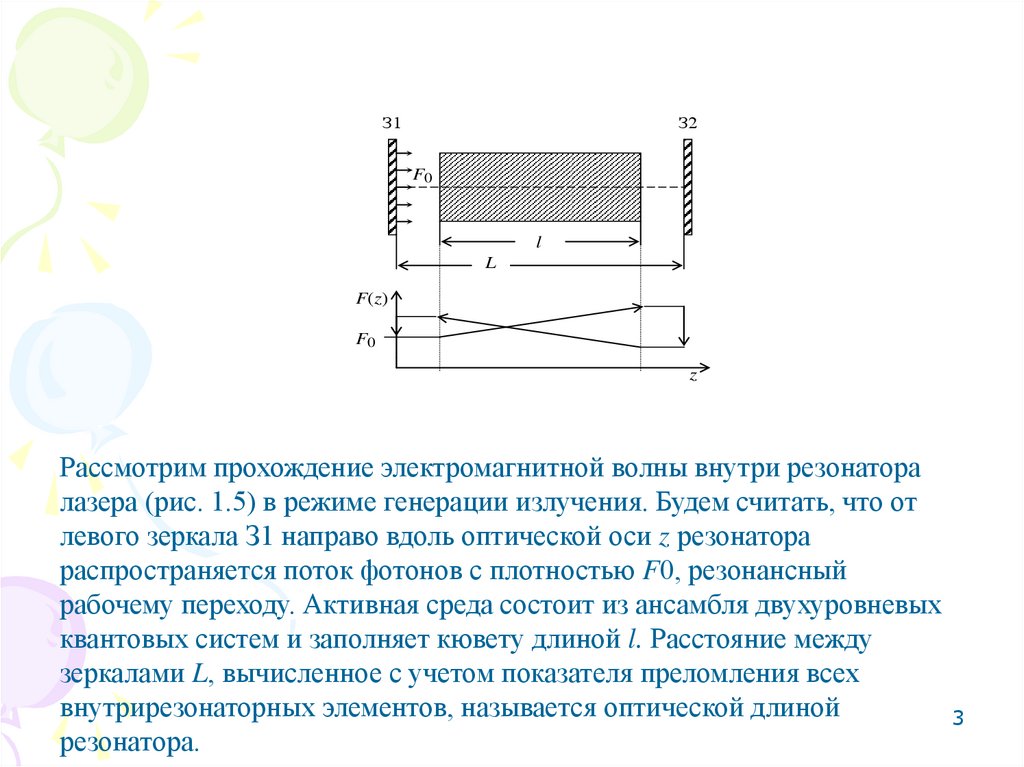
Рассмотрим прохождение электромагнитной волны внутри резонатора
лазера (рис. 1.5) в режиме генерации излучения. Будем считать, что от
левого зеркала З1 направо вдоль оптической оси z резонатора
распространяется поток фотонов с плотностью F0, резонансный
рабочему переходу. Активная среда состоит из ансамбля двухуровневых
квантовых систем и заполняет кювету длиной l. Расстояние между
зеркалами L, вычисленное с учетом показателя преломления всех
внутрирезонаторных элементов, называется оптической длиной
3
резонатора.

4.

При прохождении активной среды световой поток усиливается до значения
F0 exp gl , затем за счет того, что зеркало З2 имеет пропускание
T2
( T2 1 r2 ), часть энергии потока выходит из резонатора и световой поток
уменьшается в r2 раз, где r2 – энергетический коэффициент отражения зеркала.
Далее поток распространяется в обратную сторону и после отражения от
зеркала З1 приобретет значение
F0 1 d 2 exp gl r1 exp gl r2 F0 1 d 2 1 T1 1 T2 exp 2 gl.
С помощью величины d здесь вводятся все остальные виды потерь в
резонаторе (дифракционные, потери на поглощение и отражение в элементах,
находящихся внутри резонатора, и др.) в расчете на проход луча в резонаторе в
одну сторону. Изменение потока света при распространении внутри
резонатора показано на графике, приведенном также на рис. 1.5.
4

5.

В
стационарном
режиме
генерации
излучения
характеристики
электромагнитного поля в любой точке внутри резонатора должны оставаться
неизменными. Поэтому при проходе излучения от зеркала З1 до зеркала З2 и
обратно к зеркалу З1 должны выполняться следующие условия
самосогласования поля:
1. Амплитуда электромагнитной волны при полном обходе резонатора
должна быть равна первоначальной.
2. Фаза волны после полного обхода резонатора должна изменяться на
величину, кратную 2 .
3. Состояние поляризации после обхода резонатора также должно
воспроизводиться.
5

6.

Применим первое условие самосогласования. Для этого полученное
значение плотности потока фотонов приравняем к исходной величине F0 :
F0 1 d 2 1 T1 1 T2 exp 2 gl F0 .
Сократим F0 и учтем, что в большинстве лазеров, в частности в газовых
лазерах, усиление и потери достаточно малы: 2 d , T1 , T2 , 2 gl 1 . Тогда,
разложив это выражение в ряд с точностью до членов первого порядка
малости, получим
2 gl 2 d T1 T2 0 .
Введем средние потери на один проход излучения вдоль резонатора:
T T
d 1 2 , и условие (1.21) приводится к простому виду
2
G ,
означающему, что в режиме генерации всегда выполняется условие равенства
полного усиления активной среды полным потерям в резонаторе, отнесенным
к одному проходу излучения в резонаторе.
6

7.

Расчет проделан для случая достаточно малого электромагнитного поля, когда,
усиление активной среды G N 2 N 1 l , но результат полностью
справедлив и для случая, когда среда насыщается; при этом полное усиление
определяется предыдущим выражением. В случае, когда потери в резонаторе
большие, величина потерь на один проход излучения составляет
d ln 1 T1 ln 1 T2 / 2 .
7

8.

Применим второе условие самосогласования поля и будем рассматривать
электромагнитное поле внутри резонатора в приближении так называемого
продольного типа колебаний, когда поле описывается суперпозицией двух
плоских бегущих электромагнитных волн, каждую из которых можно описать
2
E
z
sin
t
z . Из него следует, что изменению фазы на 2π
выражением
соответствует пройденное расстояние, равное длине волны q . Запишем
полное изменение фазы в виде q2 , q>>1 – целое число, которое мы
будем называть индексом продольного типа колебаний. При полном обходе
резонатора свет проходит расстояние 2 L q q . Таким образом, условие
самосогласования поля приводит к тому, что в резонаторе могут существовать
только электромагнитные волны с длиной волны q 2 L q и частотой
колебаний
q
c
c
q
q
2L .
8

9.

Разность частот двух соседних типов колебаний q можно найти из этого
выражения при изменении q на единицу:
q q 1 q c 2 L .
При выполнении этих условий поле в резонаторе образует стоячую
электромагнитную волну (рис. 1.6). Зеркала резонатора обладают высокой
электропроводностью на оптических частотах, поэтому, с точки зрения
минимума энергии системы, стоячая волна всегда занимает такое положение
при котором узлы привязаны к зеркалам (рис. 1.6). В описываемом
приближении спектр колебаний оптического резонатора (рис. 1.7) является
эквидистантным. Третье условие самосогласования позволяет найти
собственные состояния поляризации оптического резонатора.
c/2L
νq
Рис. 1.6
νq+1
Рис. 1.7
ν
9

10.

1.1.4. Энергетические соотношения в резонаторе
Рассмотрим энергетические характеристики излучения лазера с точки
зрения фотонного представления электромагнитного поля. Пусть, как
изображено на рис. 1.5, внутри резонатора лазера распространяется поток
фотонов с сечением пучка S и плотностью F. Будем считать усиление и потери
малыми, так что f const. Рассчитаем полное число фотонов в резонаторе.
Время прохода фотонов через резонатор определяется как t пр L c . Полное
число фотонов, распространяющихся вправо от зеркала З1, составляет Ft пр S , и
такое же количество фотонов распространяется влево от зеркала З2. Таким
2 LS
n
F.
образом, полное число фотонов n внутри резонатора удваивается:
c
Этот результат позволяет по энергии одного фотона E ф рассчитать
полную энергию, запасенную в резонаторе: E c nEф
2 LS
F .
c
10

11.

Энергия, уходящая за время t пр через зеркало З1 с пропусканием T1, определяется как
E З 1 T1
LS
F . Для нахождения мощности излучения через зеркало необходимо это
c
значение поделить на t пр : P1 T1S F . Аналогично
определяется мощность
излучения через зеркало З2: P2 T2 S F
и мощность, рассеивающаяся внутри
резонатора (для двух встречных потоков фотонов): Pd 2 d S F . После этого уже
можно вычислить полную мощность
P P1 P2 Pd ,
отдаваемую
активной
P (T1 T2 2 d ) S F 2 S F . Эта мощность соответствует
средой:
полной мощности потерь резонатора.
Введем добротность резонатора так, как она вводится в радиотехнике: угловая
частота колебаний, умноженная на отношение запасенной энергии к мощности потерь:
E
L
Q c
.
P
c
С ростом частоты колебаний и длины резонатора добротность растет. Обычные
8
значения этой величины в оптическом диапазоне составляют порядка 10 7 -10 .
11

12.

Рассмотрим динамику потерь энергии в резонаторе. Если приток энергии
c
dE
Pdt
E
dt .
извне отсутствует, за время dt потери энергии составят
c
c
L
Решение этого уравнения при начальном условии E c 0 E c0 дает
зависимость энергии, запасенной в резонаторе, от времени:
c
E c t E c0 exp t E c0 exp t c .
L
Величина
c L c
называется средним временем жизни фотона в резонаторе.
12

13.

Она связана с шириной полосы резонатора
c c 1 ,
неопределенностей
вытекающим из
преобразования Фурье. Значение величины
соотношением
основных свойств
c
c
L
можно получить и из другого известного определения добротности
c c 1
резонатора: Q c . Форма спектральной линии резонатора является
лоренцевской, что соответствует закону экспоненциальному изменения
энергии (предыдущий слайд). Спектры такого типа будут обсуждаться далее.
13

14.

1.1.5. Режимы работы лазера
Проведем анализ режимов работы лазера методом скоростных уравнений.
Для этого рассмотрим следующую простейшую модель квантового усилителя
и квантового генератора. Предположим, что активная среда состоит из N
одинаковых квантовых систем, которые имеют только два энергетических
уровня с населенностями N1 и. В активной среде каким-либо образом создана
инверсия населенностей, т N 2 ак что разность населенностей уровней
N N 2 N1 0 , т. е. состояние среды неравновесно. Через активную среду
проходит резонансный поток фотонов плотностью F с энергией каждого
фотона, равной разности энергий уровней квантовой системы E 2 E1 . По
истечении некоторого промежутка времени за счет вынужденного и
спонтанного излучений населенности уровней сравняются, и затем такая
система перейдет в равновесное состояние без инверсии населенностей N < 0.
14

15.

Стационарное состояние усиления или генерации электромагнитного поля
возможно только при непрерывном подводе к системе энергии от внешнего
источника. Для этого введем в модель резервуар, состоящий из
невозбужденных квантовых систем с энергиями E 0 , значительно меньшими
по сравнению с E 2 и E1 , и населенностью N 0 (это могут быть, например,
квантовые системы в основном состоянии). Резервуар является источником
квантовых систем, поступающих на верхний уровень с энергией E 2 .
Возбуждение этих квантовых систем осуществляется за счет постороннего
источника энергии.
15

16.

16

17.

На рис. 1.8 представлена схема уровней рассматриваемой системы, где также
указаны вероятности всех процессов, протекающих в ансамбле квантовых
систем. Скорость поступления квантовых систем на верхний уровень равна
N 0 , где – скоростная константа возбуждения. Одновременно
осуществляется “тушение” нижнего уровня двухуровневой квантовой системы
со скоростной константой таким образом, чтобы сумма населенностей
верхнего и нижнего уровней оставалась постоянной: N1 N 2 N .
E2
N2
F+A21
E1
F
N1
N0
E0 = 0
Рис. 1.8
17

18.

Рассмотрим баланс квантовых систем на верхнем уровне. В данной схеме
имеют место приход систем в единицу времени за счет возбуждения N 0 и за
счет поглощения излучения FN 1 и уход систем за счет спонтанного
излучения A21 N 2 N 2 2 и за счет индуцированного излучения FN 2 , где
2 – время жизни верхнего уровня по отношению к спонтанному излучению
на нижний уровень (см. выше). В результате получаем следующую систему
скоростных уравнений
dN 2 dt FN1 FN 2 N 0 N 2 / 2 ,
N1 N 2 N .
18

19.

Введем в расчет разность населенностей уровней N N 2 N1 через
N 2 N N 2 и рассмотрим стационарное состояние активной среды
dN 2 dt 0 . В этом случае система (1.29) сводится к следующему уравнению:
F N N 0 N N / 2 / 2 0. Его решением является
N 2 2 N 0 N 1 2 2 F 1.
Из этого выражения видно, что при увеличении плотности потока фотонов F и
интенсивности I = h F происходит насыщение (уменьшение) инверсии
населенностей. Введем параметр насыщения Is = h / 2 2 (см. выше) и
рассмотрим режимы работы лазера при изменении скорости возбуждения λ.
Потери в резонаторе будем считать постоянными и равными .
19

20.

1. Режим работы “ниже порога генерации”, при котором интенсивность
излучения I F 0 . При этом значение плотности инверсии
N 0 2 2 N 0 N
мало, и выполняется условие G0 g 0 l N 0 l . Усиление G 0
является ненасыщенным, в резонаторе присутствует только спонтанное
излучение.
20

21.

2. Режим работы “у порога генерации”, соответствующий началу генерации.
При этом интенсивность излучения по-прежнему равна нулю, и выполняется
условие равенства “ненасыщенного” коэффициента усиления потерям G0 .
Величина
N t l
называется пороговым значением инверсии населенностей. Этому режиму
N / l
соответствует значение скорости возбуждения t
2 2 N 0 .
21

22.

3. Режим работы лазера “выше порога генерации”, соответствующий
увеличению скорости и возбуждения до значения t . При этом вместе с λ
вырастет ненасыщенное значение инверсии и ненасыщенный коэффициент
усиления
Он характеризуется конечным значением
G0 N 0 l.
интенсивности излучения и насыщенным значением инверсии населенностей:
N N 0 1 F / Fs 1 N 0 1 I / I s 1.
В этом режиме всегда выполняется условие G = , что означает, что
инверсия населенностей равна пороговому значению N N t и остается
постоянной. Из этого уравнения мы может определить стационарное значение
интенсивности светового потока внутри резонатора I I s N 0 / N t 1 .
22

23.

Отношение ненасыщенного усиления к потерям, равное отношению
ненасыщенного значения инверсии к ее значению у порога генерации:
G0 N 0 / N t ,
называется относительным возбуждением и является основным параметром,
определяющим режим генерации лазера. Введем величину поперечного
сечения луча внутри резонатора S и определим мощность светового потока
внутри резонатора Pin = SI. Исходя из этого значения, получаем мощность
выходного излучения лазера через зеркало с коэффициентом пропускания T
P = Pin T TSI s 1 .
Аналогично можно проанализировать и случай уменьшения потерь в
резонаторе, начиная со значения G0 . Генерация здесь начинается при
достижении значения потерь G0 N 0 l . С дальнейшим уменьшением
потерь пороговая инверсия населенностей падает, как N t l , а
относительное возбуждение растет, как χ = G0/ . При этом выходная
мощность по-прежнему определяется тем же выражением, а величина G0
определяется в зависимости от степени насыщения.
23