Паросочетания в двудольных графах. Лекция 8

1. Паросочетания в двудольных графах

Лекция 8

2. Паросочетание

• Паросочетанием в графе G называется
множество попарно несмежных ребер.

3. Задача «Максимальное Паросочетание»

• Дан граф G.
• Найти паросочетание в G
максимальной мощности.

4. Совершенное паросочетание

Определение 8.1.
• Пусть G ― граф и M ― паросочетание в G.
Будем говорить, что вершина v покрыта M,
если v e для некоторого e M .
• M называется совершенным паросочетанием,
если все вершины покрыты M.

5. Биразбиение

• Биразбиением графа G называется
разбиение множества вершин на два
подмножества, V(G)=A⋃B, такое что
подграфы индуцированные на A и B
― оба пустые.
• Граф называется двудольным, если он
имеет биразбиение.

6. Паросочетание в двудольном графе

• Для графа G, пусть (G) обозначает
мощность максимального паросочетания,
а (G) ― мощность минимального
вершинного покрытия в G.
Теорема 8.2 (König [1931])
Если G ― двудольный, то (G) = (G).

7. Доказательство

• G' = (V(G)⋃{s,t}, E(G)⋃{{s,a}: a A}⋃ {{b,t}: b B})
• (G) – максимальное число вершинно-непересекающихся
s-t-путей.
• (G) – минимальное число вершин удаление которых
разделяет вершины s и t.

8. Вторая Теорема Менгера

Theorem 7.2 (Menger [1927] )
Пусть G ― граф (ориентированный или
неориентированный), пусть s и t две несмежные
вершины и k N. Тогда существует k вершиннонепересекающихся s-t-путей, тогда и только
тогда, когда после удаления любых k – 1 вершин
(отличных от s и t) t остается достижима из s.

9. Доказательство

• G' = (V(G)⋃{s,t}, E(G)⋃{{s,a}: a A}⋃ {{b,t}: b B})
• (G) – максимальное число
вершинно-непересекающихся s-t-путей.
• (G) – минимальное число вершин удаление
которых разделяет вершины s и t.
• 2-я теорема Менгера (G) = (G).

10. Теорема Холла

Теорема 8.3 (Hall [1935] )
Пусть G ― двудольный граф с биразбиением
V(G) = A⋃B. Тогда G имеет паросочетание,
покрывающее A, тогда и только тогда, когда
| (X)| ≥ |X| для всех X A.
( (X) – множество вершин соседних с X.)

11. Доказательство (достаточность)

• Пусть G не имеет паросочетание,
покрывающее A ( (G) < |A|).
• Теорема 8.2 (G) < |A|.
• Рассмотрим A' A и B' B, такие что A' ⋃ B'
покрывают все ребра и | A' ⋃ B' | < | A |.
• Тогда (A /A' ) B'.
• | (A /A' ) | ≤ |B'| < | A | – | A' | = |A /A' |, что
противоречит условию теоремы.

12. Теорема о бракосочетаниях

Теорема 8.4 (Frobenius [1917] )
Пусть G ― двудольный граф с
биразбиением V(G) = A⋃B. Тогда G
имеет совершенное паросочетание,
тогда и только тогда, когда |A| = |B| и
| (X)| ≥ |X| для всех X A.

13. Паросочетание в двудольном графе

Теорема 8.5
Задача «Максимальное Паросочетание» в
двудольном графе G может быть решена за
время O(nm), где n = |V(G)| и m = |E(G)|.

14. Справка

• Используя идею о кратчайшем
увеличивающем пути можно получить
алгоритм с трудоемкостью O(n0.5(m + n))
(Hopcroft & Karp 1973).

15. M- увеличивающий путь

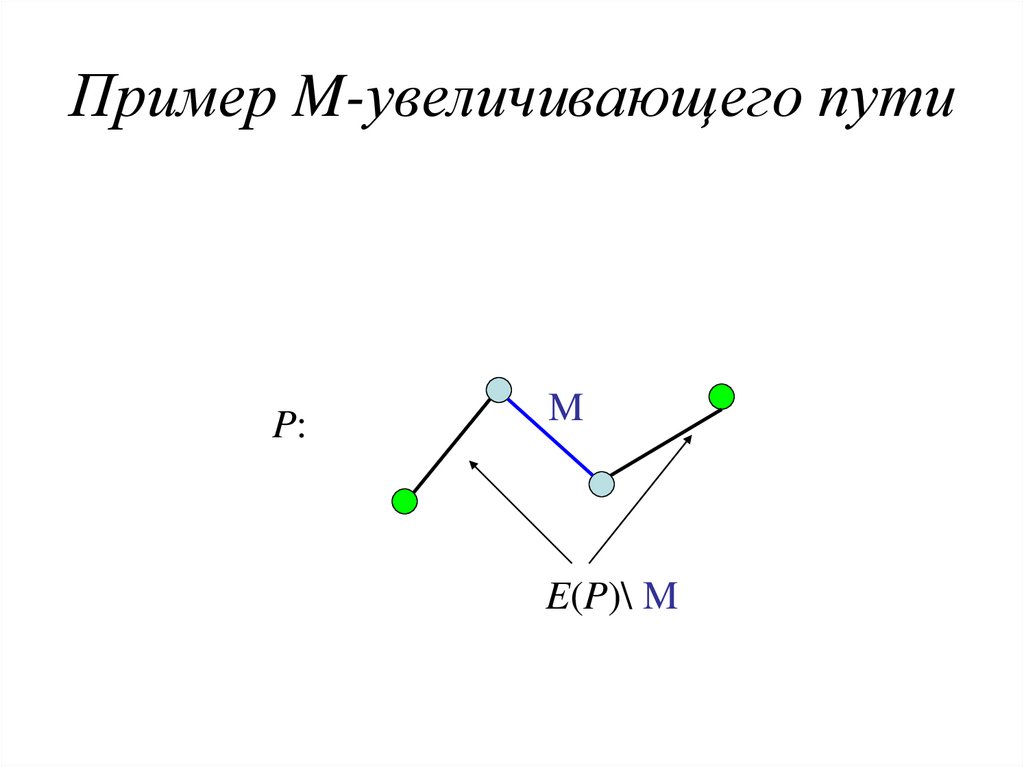
• Определение 8.6
Пусть G ― граф, и M ― паросочетание в G.
Путь P называется M-чередующимся путем,
если E(P) \ M является паросочетанием.
Чередующийся путь называется
M-увеличивающим, если его граничные
точки не покрываются M, то есть
| E(P) \ M | > | E(P) ∩ M |.

16. Пример M-увеличивающего пути

P:
M
E(P)\ M

17. Паросочетание и увеличивающий путь

Theorem 8.7 (Berge [1957] )
Пусть G ― граф, и M ― паросочетание в G.
Тогда M является максимальным тогда и
только тогда, когда не существует
M-увеличивающего пути.

18. Доказательство

• Если M-увеличивающий путь P существует,
то симметрическая разность M∆E(P) будет
паросочетанием большей мощности.
• Если существует паросочетание | M '| > | M |,
то M∆M ' является вершиннонепересекающимся объединением путей и
циклов, один из которых является
увелличивающим.

19. Алгебраический подход

• Пусть G простой граф и пусть G' орграф,
полученный из G произвольной
ориентацией ребер.
• Для произвольного вектора x определим
матрицу Татта.

20. Матрица Татта

x xe e E G
TG x t
x
vw v , w V G
x v , w
x
tvw : x v , w
0
if v, w E G
if w, v E G
иначе

21. Паросочетание и матрица Татта

Теорема 8.8 (Tutte [1947] )
Граф G имеет совершенное паросочетание
тогда и только тогда, когда det TG(x) ≠ 0.

22. Доказательство

• V(G) = {v1,…,vn}
• Пусть Sn множество всех перестановок {1,…, n}.
n
det TG x sgn tvxi v i
S n
i 1
x
S n S n : tvi v i 0
i 1
n
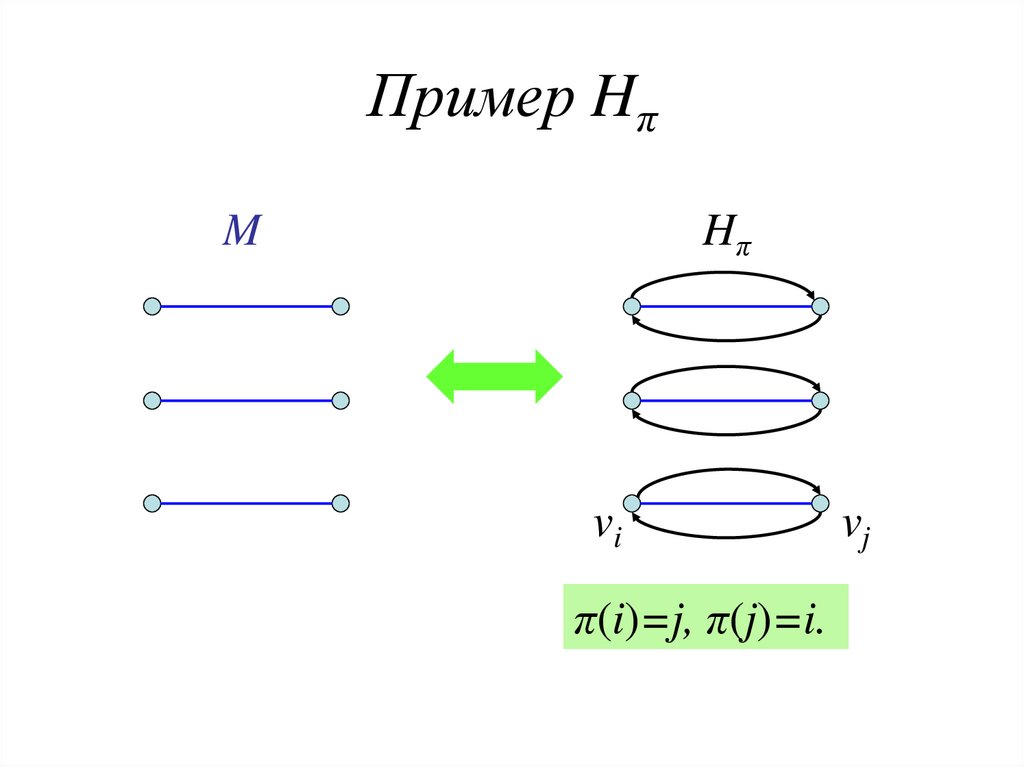
• Каждая перестановка π S'n соответствует орграфу
Hπ = ( V(G),{(vi,vπ(i)): i = 1,…, n}), где ровно одна дуга
входит в каждую вершину и ровно одна дуга выходит
из нее. (Hπ Ğ').

23. Пример Hπ

M
Hπ
vi
π(i)=j, π(j)=i.
vj

24. Доказательство

• Если существует перестановка π S'n такая
что Hπ состоит только из четных циклов, то
в G есть совершенное паросочетание.
• Пусть это не так. То есть для каждой π S'n
существует нечетный цикл.
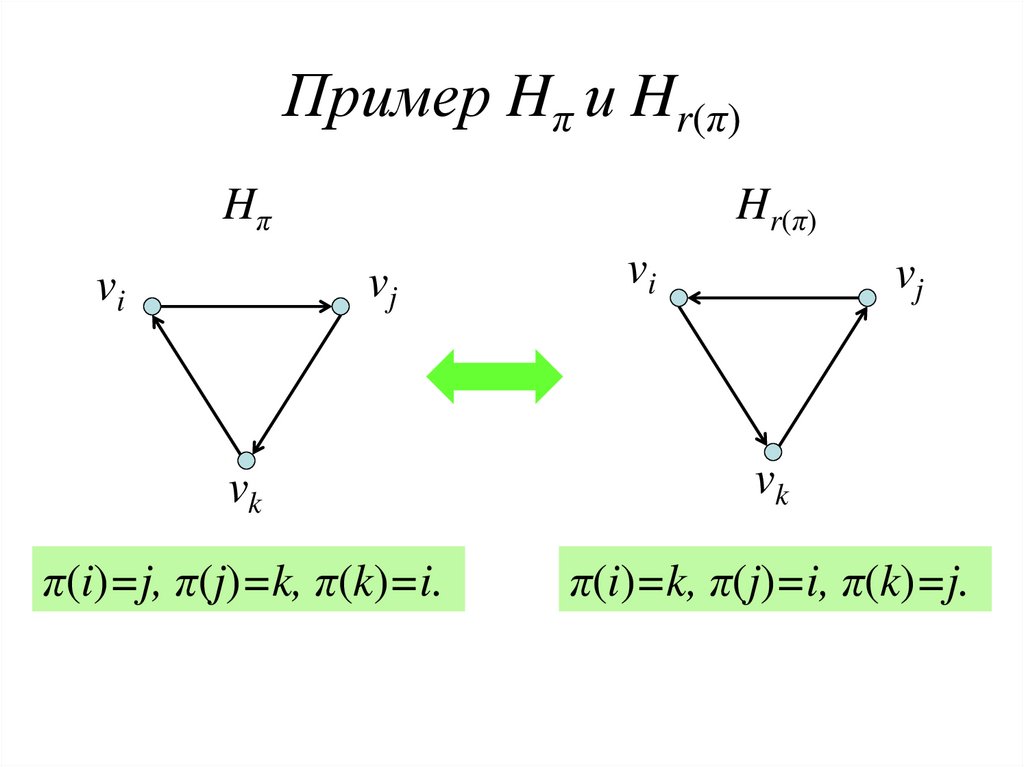
• Тогда r(π) S'n такая, что Hr(π) получается
из Hπ обратной ориентацией дуг в первом
нечетном цикле (r(r(π)) = π).

25. Пример Hπ и Hr(π)

Hπ
Hr(π)
vj
vi
vi
vj
vk
vk
π(i)=j, π(j)=k, π(k)=i.
π(i)=k, π(j)=i, π(k)=j.

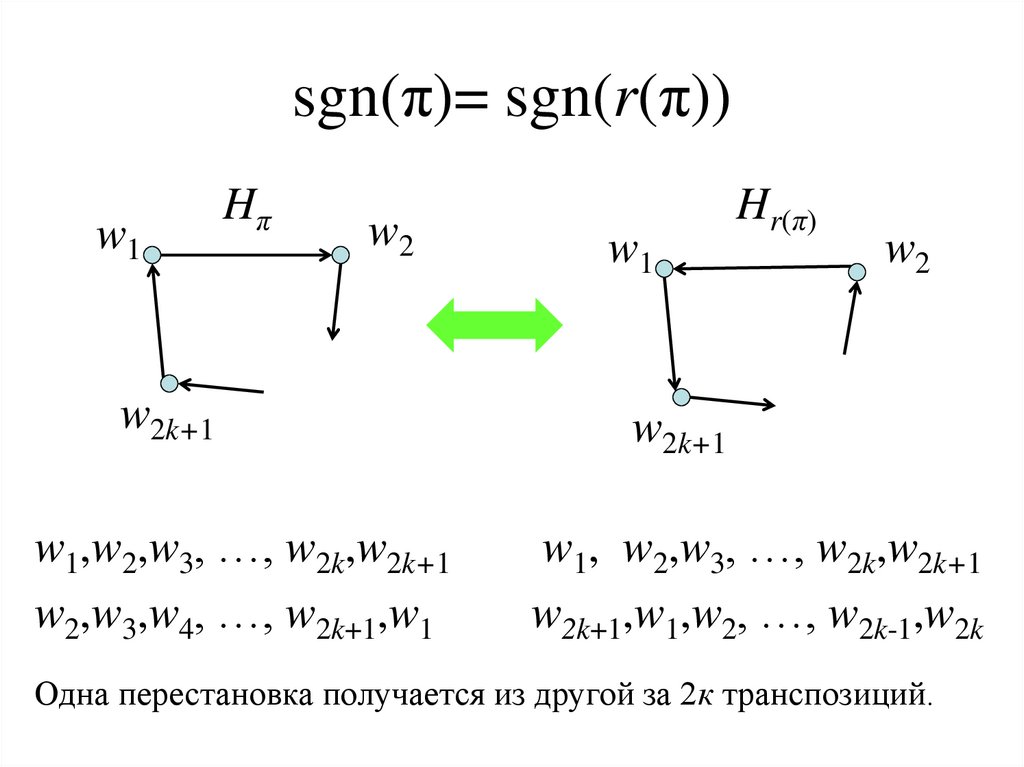
26. sgn(π)= sgn(r(π))

w1
Hπ
w2
w2k+1
w1,w2,w3, …, w2k,w2k+1
w2,w3,w4, …, w2k+1,w1
w1
Hr(π)
w2
w2k+1
w1, w2,w3, …, w2k,w2k+1
w2k+1,w1,w2, …, w2k-1,w2k
Одна перестановка получается из другой за 2к транспозиций.

27. Доказательство

n
n
i 1
i 1
x
t
viv i tvivr i
• Следовательно, два соответствующих этим перестановкам
слагаемые в сумме
n
det TG x sgn tvxi v i
S n
взаимно сокращаются.
i 1
• Так как это выполняется для всех пар π и r(π), то det TG(x)≡0.

28. Вероятностный Алгоритм

Следствие 8.9 (Lovász [1979] )
Пусть x = (xe)e E(G) ― случайный
вектор, каждая координата которого
равномерно распределена в [0,1].
Тогда с вероятностью 1 ранг TG(x) в
точности равен 2 (G).

29. Упражнение 8.1

• Пусть G произвольный граф, M1 и M2 два
максимальных паросочетания в нем.
Доказать, что | M1 | ≤ | M2 |.

30. Упражнение 8.2

• Доказать, что k-регулярный двудольный
граф имеет k попарно не пересекающихся
совершенных паросочетаний.