Алгоритмы и структуры данных

1.

Алгоритмы и Структуры Данных
Жукова Алена Михайловна

2.

УСОВЕРШЕНСТВОВАННЫЕ МЕТОДЫ
РАЗРАБОТКИ И АНАЛИЗА

3.

Динамическое программирование

4.

Пример 1. Расписание работы
конвейера
Два конвейера, на каждом n этапов сборки:
a[1][j], a[2][j] — время каждого этапа сборки.
t[1][j], t[2][j] — время перемещения с конвейера
на конвейер.
e[1], e[2] - время загрузки на конвейер.
t[1],t[2] — время выгрузки.
Как быстрее всего собрать автомобиль?

5.

1. Структура самой быстрой
сборки
Пусть самый быстрый путь проходит через
S[1][j]. Тогда если этот путь проходит через
S[1][j-1], то это самый быстрый из таких
путей.
(Еще 4 подобных утверждения)

6.

2. Рекурсивное решение
Fin= min(f[1][n]+x[1],f[2][n]+x[2])
f[1][1]=e[1]+a[1][1]
f[2][1]=e[2]+a[1][1]
f[1][j]= min(f[1][j-1]+a[1][j],f[2][j-1]+t[2][j-1]+a[1][j])
f[2][j]= min(f[2][j-1]+a[2][j],f[1][j-1]+t[1][j-1]+a[2][j])

7.

3.Вычисление минимальных
промежутков
времени
Fastest_way(a,t,e,x,n){
f1[1]=e[1]+a[1][1];
f2[1]=e[2]+a[2][1];
for(j=2,j<=n,j++){
if (f[1][j]+a[1][j]<f[2][j-1]+t[2][j-1]+a[1][j]) {
f[1][j]=f[1][j-1]+a[1][j];
l[1][j]=1;}
else { f[1][j]=f[2][j-1]+t[2][j-1]a[1][j];
l[1][j]=2;}
if (f[2][j]+a[2][j]<f[1][j-1]+t[1][j-1]+a[2][j]) {
f[2][j]=f[2][j-1]+a[2][j];
l[2][j]=2;}
else { f2[j]=f1[j-1]+t[1][j-1]a[2][j];
l[2][j]=1;}
if (f[1][n]+x[1]<=f[2][n]+x[2]){fin=f1[n]+x[1]; line=1;}
else {fin=f2[n]+x[2]; line=2;}
}}

8.

4. Построение самого быстрого
пути
Print_Stations(l,n){
i=l;
Printf(''Конвейер %n рабочее место %n'&i,&n);
for(j=n,j>=2, j—){
i=l[i][j];
Printf(''Конвейер %n рабочее место %n''&i,&n);}
}

9.

Упражнения
1)Модифицируйте процедуру Print_Stations,
чтобы она выводила данные в порядке
возрастания номеров рабочих мест.

10.

Пример 2.Перемножение цепочки
матриц
Как лучше всего расставить
скобки:(A1(A2(A3A4))) ,
(A1((A2A3)A4)) ,
((A1A2)(A3A4)) ,
((A1(A2A3))A4) ,
(((A1A2)A3)A4) ?

11.

Перемножение двух матриц
Matrix_Multiply(A,B){
If (A.columns!=B.rows) error «Несовместимые
размеры»;
Else { for(i=1,i<=A.rows,i++)
for(j=1, j<=B.columns,j++) {C[i][j]=0;
for(k=1,k<=A.columns)C[i][j]=C[i][j]+A[i][k]*B[i][k];}
Return C;
}

12.

1. Структура оптимальной
расстановки скобок
2. Рекурсивное решение
m[i][j]=
0, если i=j
min{m[i][k]+m[k+1][j]+pi-1pkpj по всем i≤k≤j}, если
i≠j

13.

3. Вычисление оптимальной
стоимости
Matrix_Chain_Order(p){
n=p.length-1;
for(i=1,i<=n,i++) m[i][i]=0;
for(l=2,l<=n,l++){
for(i=1,i<=n-l+1,i++){
j=i+l-1;
m[i][j]=maxint;
for(k=i,k<=j-1){
q=m[i][k]+m[k+1][j]+p[i-1]p[k]p[j];}
if(q<m[i][j]){m[i][j]=q;
s[i][j]=k;}
Return m,s}

14.

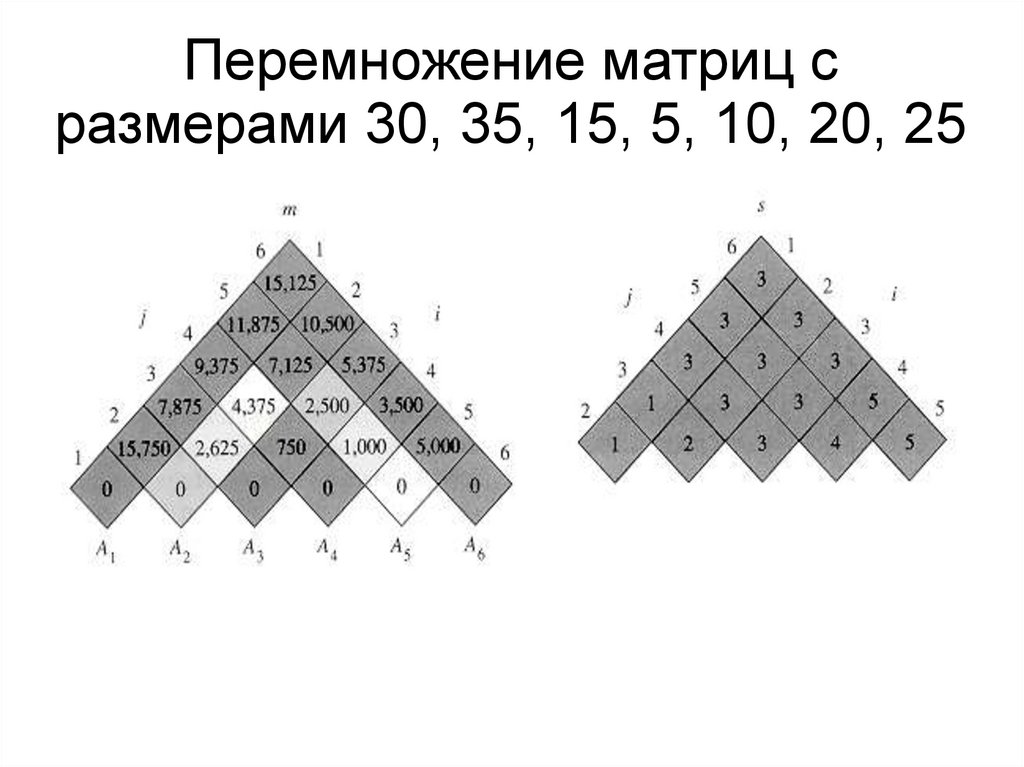
Перемножение матриц с
размерами 30, 35, 15, 5, 10, 20, 25

15.

4. Конструирование
оптимального решения
Print_Optimal_Parents(s,i,j){
If(i=j) printf('A%n',&i);
Else {printf('(');
Print_Optimal_Parents(s,i,s[i,j]);
Print_Optimal_Parents(s,s[i,j]+1,j);
printf(')'); }
}

16.

Упражнения
1) Определите оптимальный способ
расстановки скобок в ряде матриц с
размерами (5,10,3,12,5,50,6)
2)Покажите, что в полной расстановке скобок
используется ровно n-1 пар скобок

17.

Элементы динамического
программирования.

18.

Элементы динамического
программирования.

19.

1) Оптимальная подструктура
(выбор+решение подзадач)
Пример: поиск самого короткого и самого
длинного пути между двумя вершинами во
взвешенном графе.

20.

2) Перекрытие вспомогательных
задач.
Recursive_Matrix_Chain(p,i,j){
if(i=j) return 0;
m[i][j]=maxint;
for(k=i;k<=j-1;k++){
q=Recursive_Matrix_Chain(p,i,j)+Recursive_Ma
trix_Chain(p,i,j)+pi-1pkpj;
If q<m[i][j] m[i][j]=q;
Return m[i][j];
}}

21.

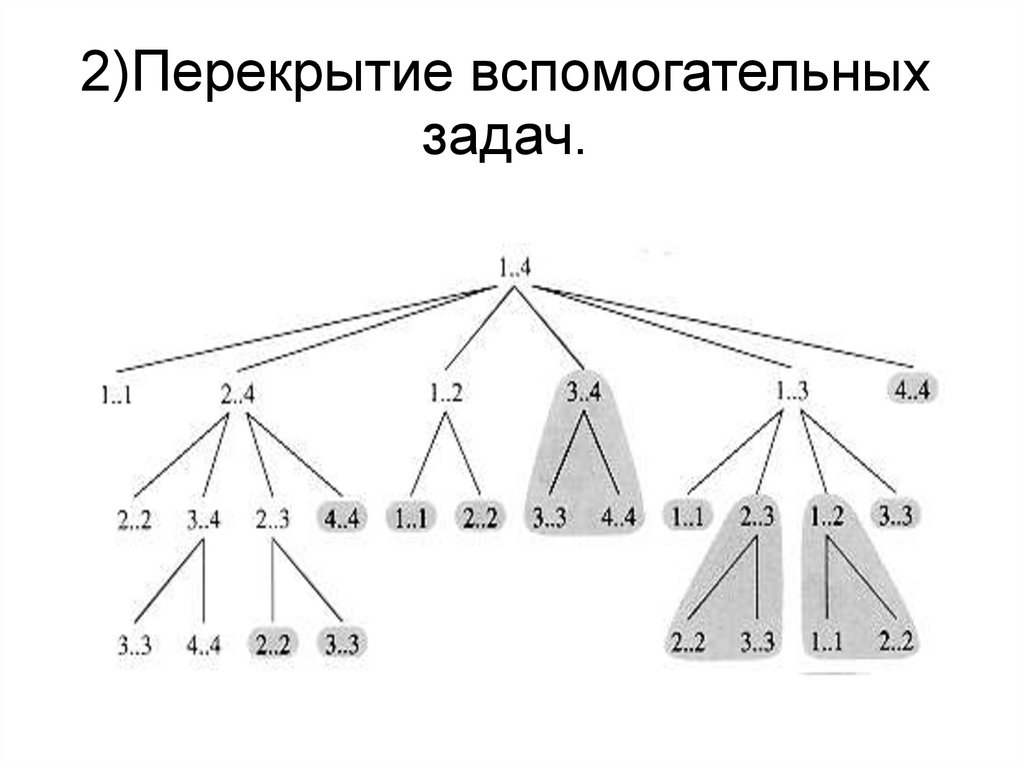
2)Перекрытие вспомогательных
задач.

22.

3)Запоминание
Memoized_Matrix_Chain(p){
n=p.length-1;
for(i=1;i<=n;i++)m[i][j]=maxint;
Return Lookup_Chain(p,1,n)}

23.

3)Запоминание.
Lookup_Chain(p,i,j){
if (m[i][j]<maxint) return m[i][j]
if(i=j) m[i][j]=0
else{ for(k=i;k<j-1;k++){
q=Lookup_Chain(p,i,k)
+Lookup_Chain(p,k+1,j)+pi-1pkpj;
if q<m[i][j] m[i][j]=q;
}}}

24.

Упражнения
1) Нарисуйте рекурсивное дерево для
процедуры Merge_sort, работающей с
массивом из 16 элементов. Будет ли тут
полезным использование запоминания?
2) Опишите, как перекрывающиеся
вспомогательные процедуры возникают при
работе конвейера.

25.

Самая длинная общая
последовательность
S1= (A B C B D A B)
S2= (B D C A B A)
Ответ - (B C B A)

26.

1. Характеристика максимальной
общей подпоследовательности
Теорема. Пусть имеются последовательности
X=<x1,x2,...,xm> и Y=<y1,y2,...,yn>, а
Z=<z1,z2,...,zk> - их самая длинная общая
подпоследовательность. Тогда
1) Если xm=yn, то zk=xm=yn и Zk-1 - LCS
последовательностей Xm-1 и Yn-1
2) Если xm≠yn, то zk≠xm следует Z - LCS
последовательностей Xm-1 и Y
3) Если xm≠yn, то из zk≠yn следует Z - LCS
последовательностей X и Yn-1

27.

2. Рекурсивное решение.
c[i][j]=
0, если i=0 или j=0
c[i-1][j-1]+1, если i,j>0 и xi=yi
max(c[i][j-1], c[i-1][j]) если i,j>0 и xi≠yi

28.

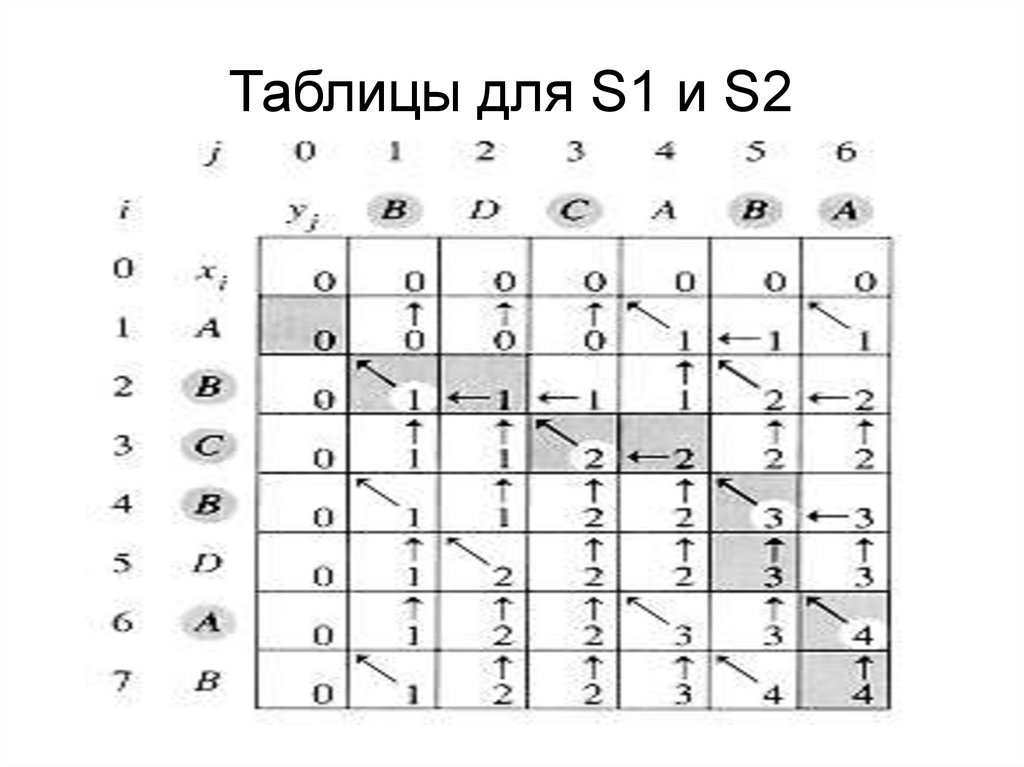
Таблицы для S1 и S2

29.

3. Длина максимальной общей
последовательности
LCS_Length(X,Y){
m=X.length;
n=Y.length;
for(i=1;i<=m;i++) c[i][0]=0;
for(j=0;i<=n;j++) c[0][j]=0;
for(i=1;i<=m;i++)for(j=0;i<=n;j++){
if (x[i]=y[i]){c[i][j]=c[i-1][j-1]+1;
b[i][j]='\'
else if(c[i-1][j-1]>=c[i][j-1]){
c[i][j]=c[i-1][j];
b[i][j]='|';}
else{c[i][j]=c[i][j-1];
b[i][j]='-';} }}
Return c,b}

30.

4. Построение максимальной
подпоследовательности.
Print_LCS(b,X,i,j){
If((i=0) or (j=0)) return
If (b[i][j]='\'){Print_LCS(b,X,i-1,j-1);
Printf(xi);}
Else if(b[i][j]='|') Print_LCS(b,X,i-1,j)
Else Print_LCS(b,X,i,j-1);
}

31.

Упражнения
Определите самую длинную общую
подпоследовательность
последовательностей (1,0,0,1,0,1,0,1) и
(0,1,0,1,1,0,1,1,0).
1) Приведите алгоритм, предназначенный для
вычисления самой длинной неубывающей
подпоследовательности данной
последовательности из n чисел за время
О(n2)

32.

Оптимальные бинарные деревья
поиска

33.

Построение оптимального БДП
OPTIMAL_BST(p, q, n, root) {
for(i=1, n<n+2,n++){e[i,i-1]=q[i-1];
w[i,i-1]=q[i-1];
for(l=1,l<n+1,i++){
for(i=1,i<n-l+2,i++){
e[ij]=maxint;
w[ij]=w[i][j-1]+p[j]+q[j];
for(r=i,r<j+1,r++){
t=e[i][r-1]+e[r+1,j]+w[i][j];
if (t<e[i][j]) then {e[ij]=t;
root[ij]=r;}
return e
}}}}}

34.

Жадные алгоритмы

35.

Задача о выборе процессов
i
1
2
3
4
5
6
7
8
9
10
11
si
1
3
0
5
3
5
6
8
8
2
12
fi
4
5
6
7
8
9
10
11
12
13
14
Sij={ak in S: fi≤sk<fk≤sj} подмножество процессов
и задача по нахождению совместимых
процессов из этого множества.

36.

Преобразование динамического
решения в жадное
Теорема. Рассмотрим непустую задачу Sij и
пусть am -процесс, который оканчивается
раньше других:
fm=min(fk: ak Sij)
В этом случае справедливы утверждения:
1. Процесс am используется в некотором
подмножестве максимального размера,
состоящим из взаимно совместимых
процессов задачи Sij
2. В результате выбора am образуется лишь
подзадача Smj

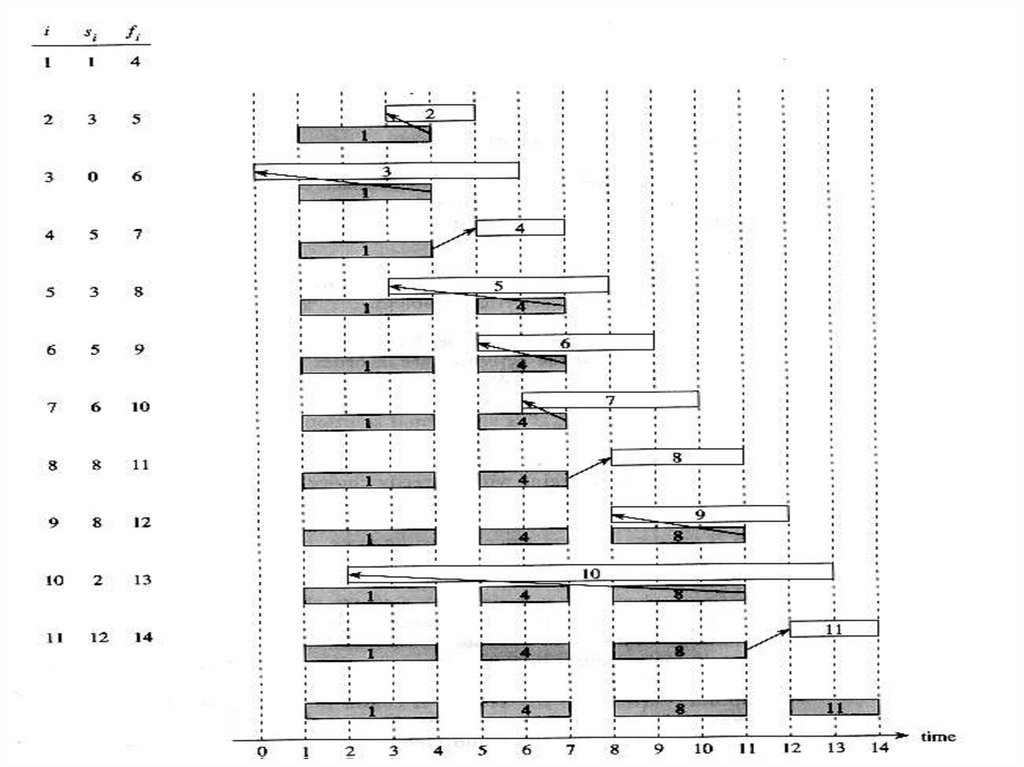
37.

38.

Рекурсивный жадный алгоритм
Recursive_Activity_Selector(s,f,i,n){
m=i+1;
While((m<=n) and (s[m]<f[i])) m=m+1;
if(m<=n)
return {a[m]}URecursive_Activity_Selector(s,f,m,n);
return 0;}

39.

Итерационный жадный алгоритм
Greedy_Activity_Selector(S,F){
n=s.length;
A={a[1]};
i=1;
for(m=2;m<=n;m++){
if(s[m]>=f[i]) {
A=AU{a[m]};
i=m;}
return A;
}

40.

Упражнение
Как можно решить задачу, используя моменты
НАЧАЛА процессов? Разработайте алгоритм.

41.

Элементы жадной стратегии.
Процесс разработки.
1. Привести задачу оптимизации к виду, когда
после сделанного выбора остается решить
только одну подзадачу;
2. Доказать, что всегда существует
оптимальное решение задачи, которое
можно получить путем жадного выбора, так
что такой выбор всегда допустим;
3. Показать, что после жадного выбора
остается подзадача, которая после
объединения с жадным выбором дает
оптимальное решение исходной задачи

42.

Элементы жадной стратегии.
Свойства жадного выбора.
1. Свойство жадного выбора: глобальное
оптимальное решение можно получить,
делая локальный жадный выбор
2. Оптимальная подструктура: появляется,
если в оптимальном решении задачи
содержатся оптимальные решения подзадач.

43.

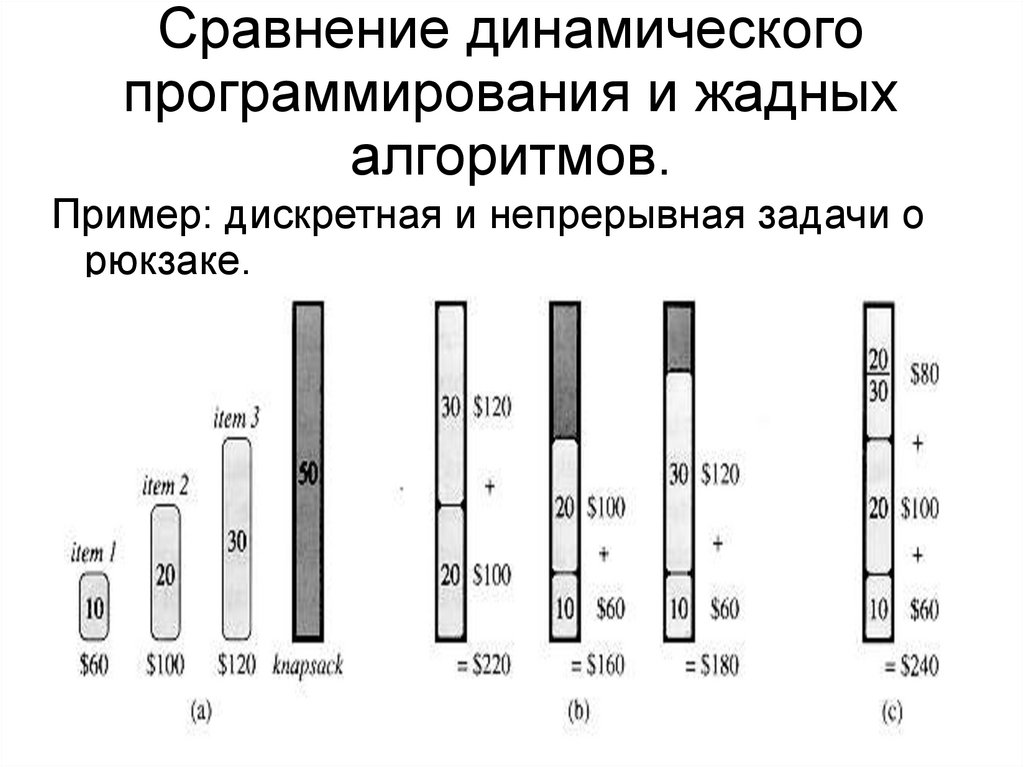
Сравнение динамического
программирования и жадных
алгоритмов.
Пример: дискретная и непрерывная задачи о
рюкзаке.

44.

Упражнение
1.Предположим, что в дискретной задаче о
рюкзаке порядок сортировки по увеличению
веса совпадает с порядком сортировки по
уменьшению стоимости. Сформулируйте
эффективный алгоритм для поиска
оптимального решения этой разновидности
задачи о рюкзаке и обоснуйте его
корректность.
2.Приведите решение дискретной задачи о
рюкзаке с помощью динамического
программирования.

45.

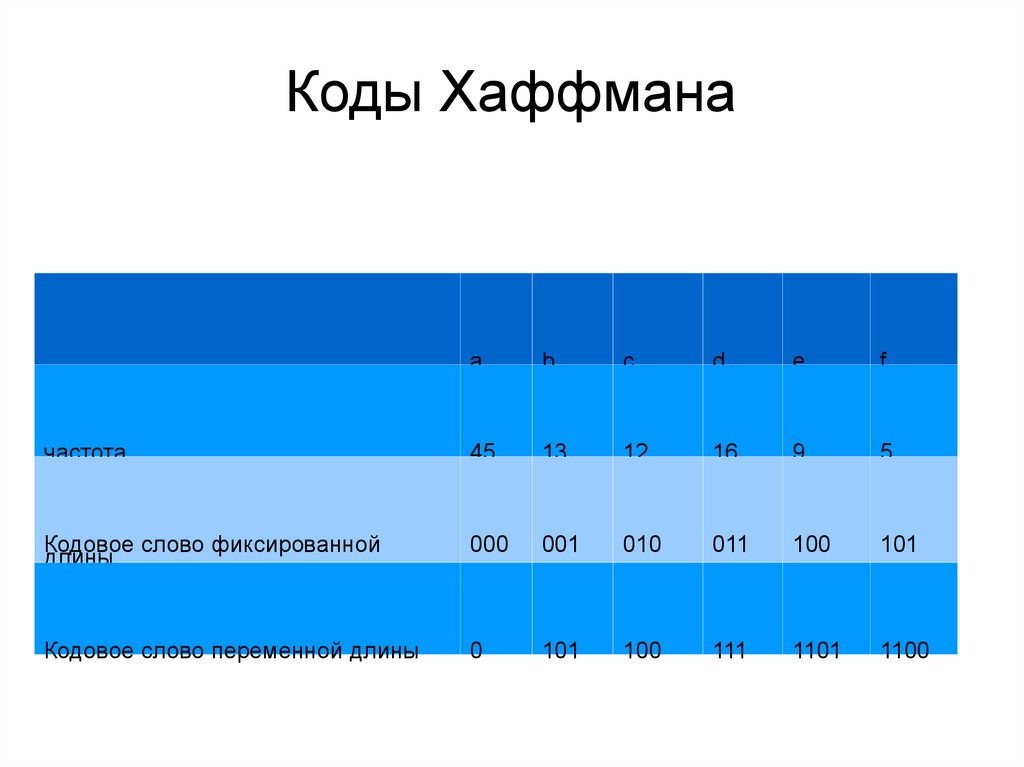
Коды Хаффмана
a
b
c
d
e
f
частота
45
13
12
16
9
5
Кодовое слово фиксированной
длины
000
001
010
011
100
101
Кодовое слово переменной длины
0
101
100
111
1101
1100

46.

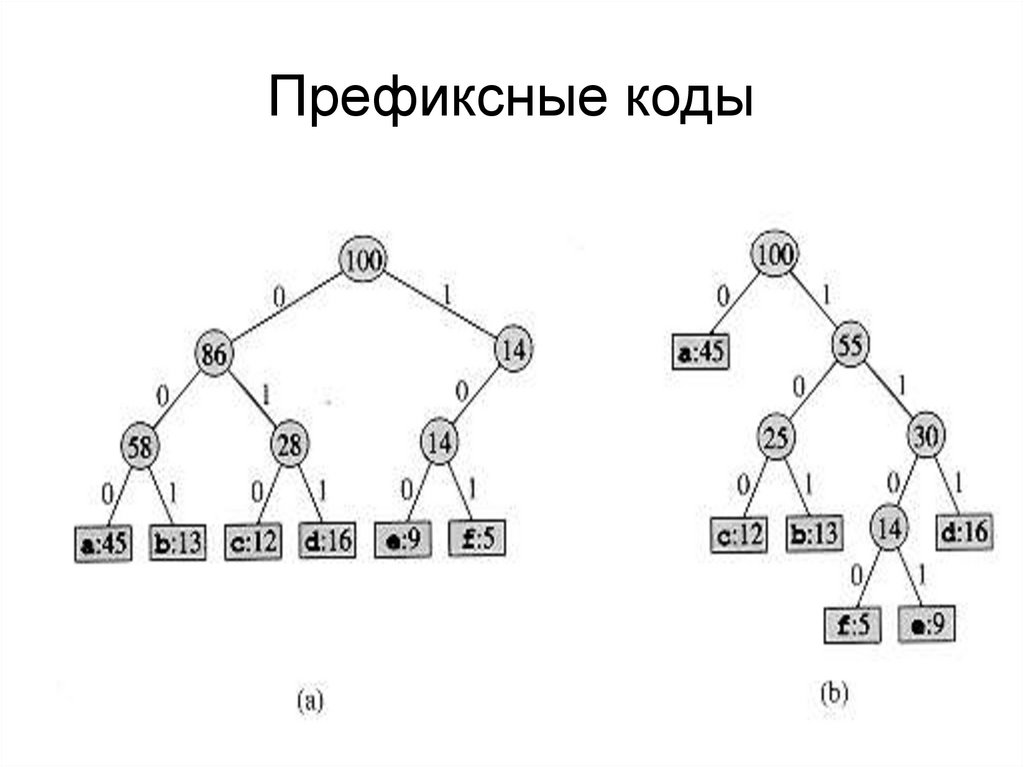
Префиксные коды

47.

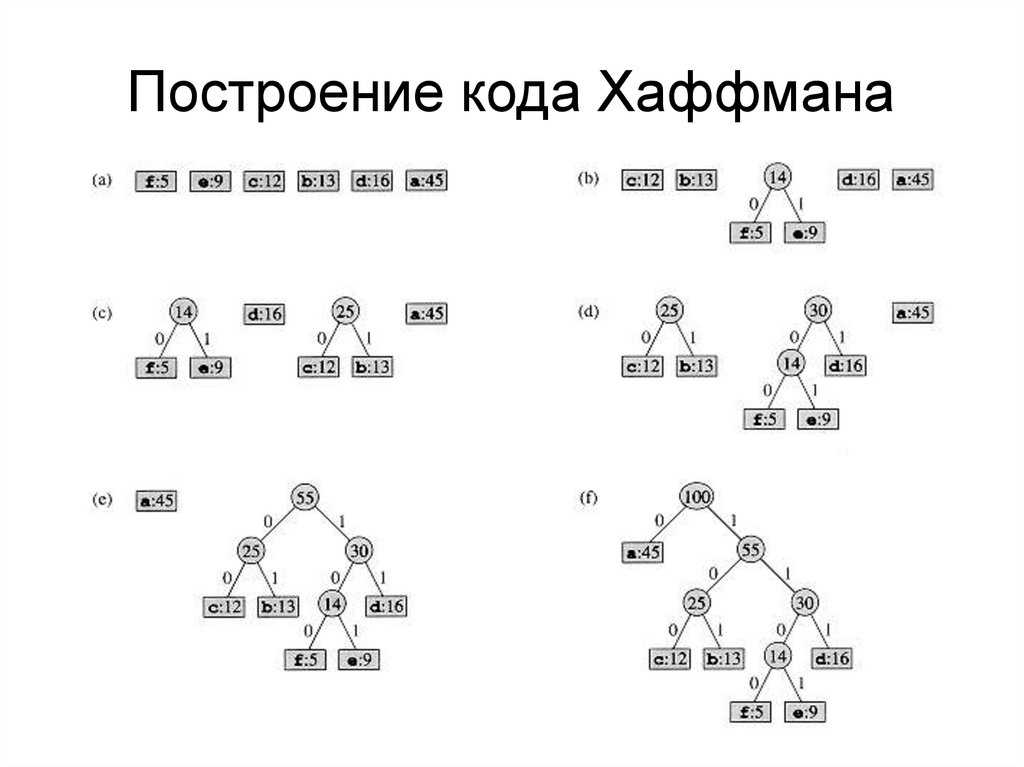
Построение кода Хаффмана

48.

Построение кода Хаффмана
Huffman(C){
n=|C|;
Q=C;
for(i=1;i<+n-1;i++){выделить память для узла z
x=Extract_Min(Q);
y=Extract_Min(Q)
z.left=&x;
z.right=&y;
z.f=x.f+y.f;
insert (Q,z)}
Return Extract_Min(Q);
}

49.

Корректность алгоритма
Хаффмана
Лемма. Пусть C — алфавит, каждый символ c которого
встречается с частотой f(c). Пусть x и y — два символа
алфавита C с самыми низкими частотами. Тогда для
алфавита C существует оптимальный префиксный код,
слова которого для символов x и y имеют одинаковую
длину и отличаются лишь последним битом.

50.

Корректность алгоритма
Хаффмана - 2
Лемма. Пусть C — алфавит, каждый символ c которого
встречается с частотой f(c). Пусть x и y — два символа
алфавита C с самыми низкими частотами. Пусть
алфавит C', получен из C заменой символов x и y на
один символ z с частотой f(z)=f(x)+f(y). Тогда из любого
дерева оптимального префиксного кода для C' можно
получить оптимальное дерево для C путем замены
листа z на внутренний узел с потомками x и y.
Теорема. Процедура Huffman дает оптимальный
префиксный код