Похожие презентации:
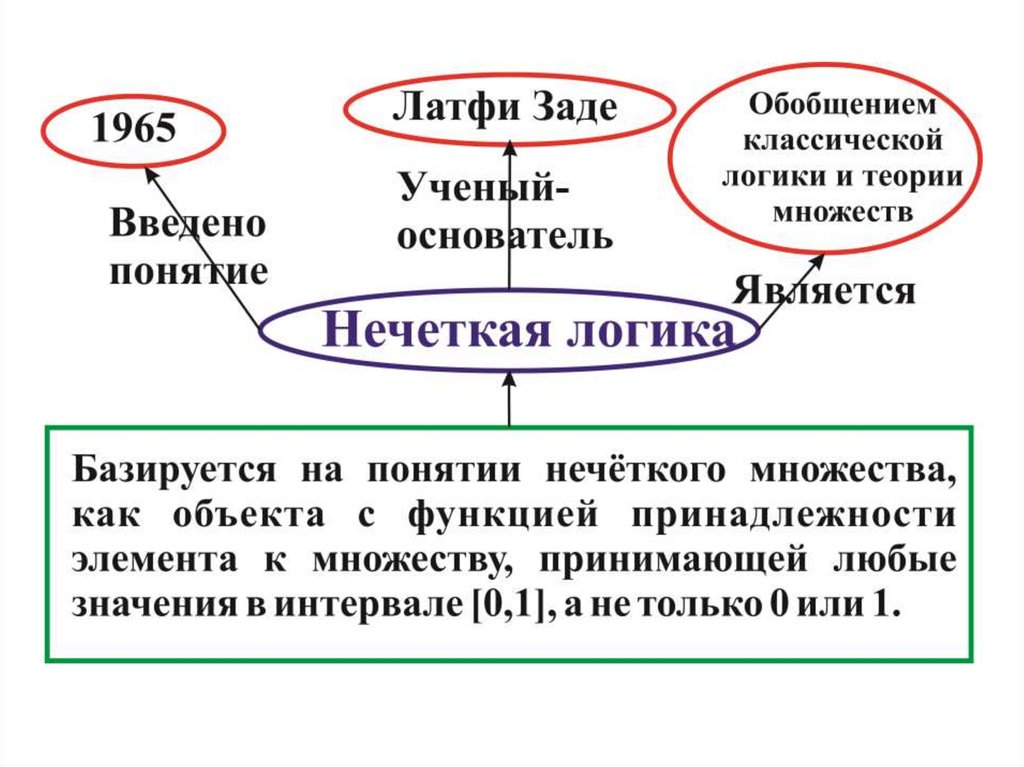
Нечеткая логика
1. Нечеткая логика
2.
3.
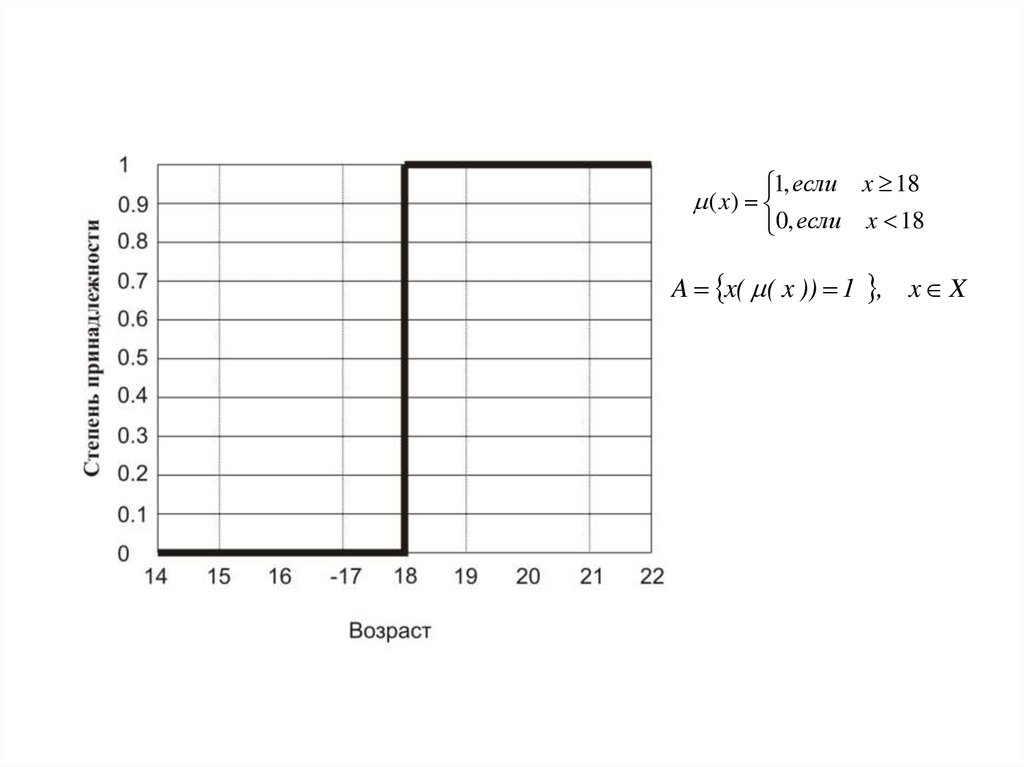
1, если x 180, если x 18
( x)
A x( ( x )) 1 , x X
4.
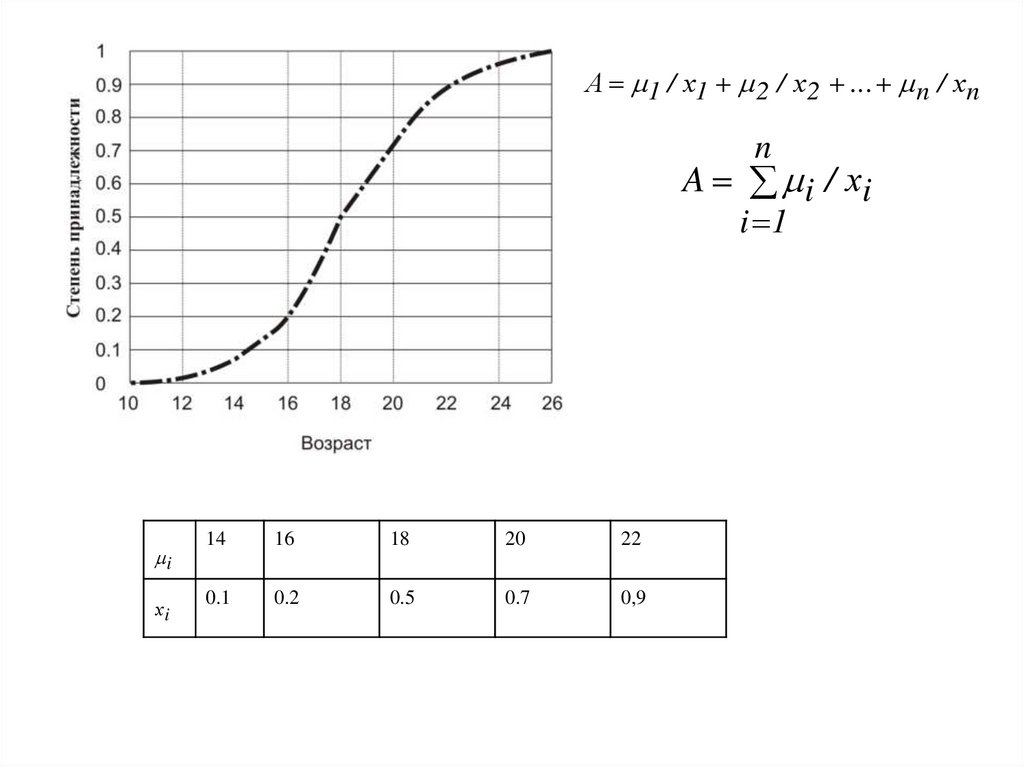
А 1 / х1 2 / х2 ... n / хnn
A i / хi
i 1
i
хi
14
16
18
20
22
0.1
0.2
0.5
0.7
0,9
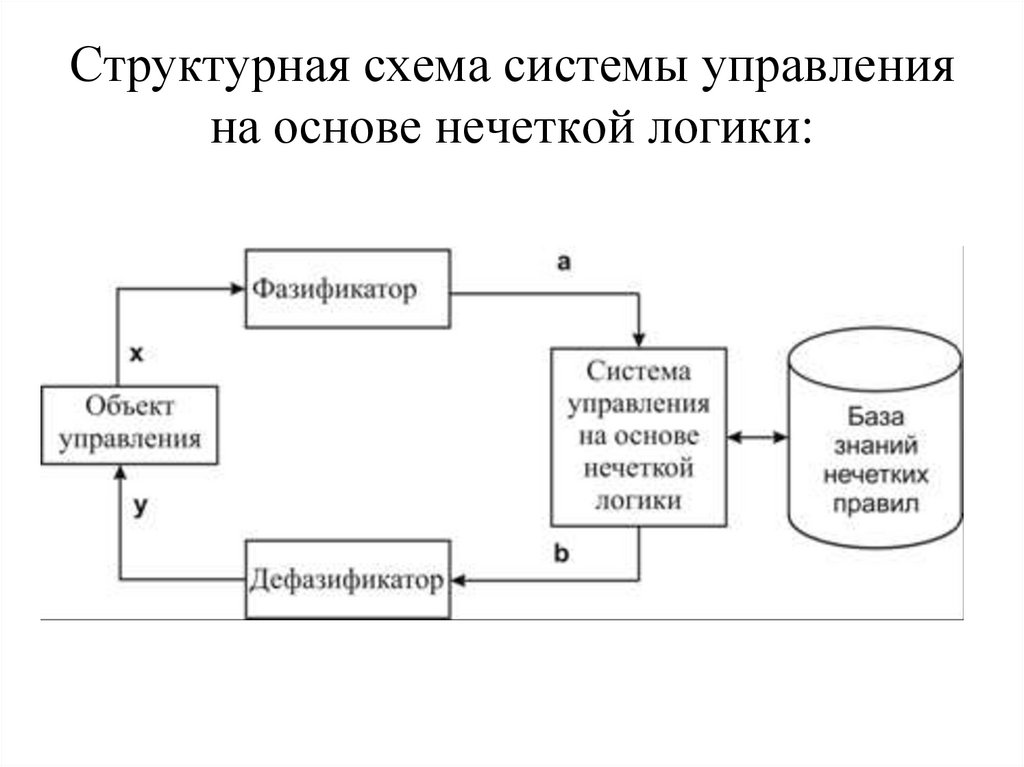
5. Структурная схема системы управления на основе нечеткой логики:
6.
В качестве примера рассмотрим системукондиционирования воздуха в помещении.
Объект управления имеет:
Три четких выходных параметра х
- Температура в помещении (Tпом);
- Температура на улице (Тул);
- Влажность (Вл);
Два четких входных параметров y:
- Скорость вращения вентилятора (V);
- Температура охладителя/нагревателя (Tнаг);
7.
Процесс фазификации и дефазификации строится наоснове понятий лингвистической переменной, которой
называются пять объектов: <A, T(x), U, G, M>,
где: А – имя переменной;
T(x) – некоторое множество значений
лингвистической переменной x, каждое из которых
является нечеткой переменной на множестве X;
G –синтаксическое правило для образования имен
новых значений x;
M – семантическая процедура, позволяющая
преобразовать новое имя, образованное процедурой G,
в нечеткую переменную T(x);
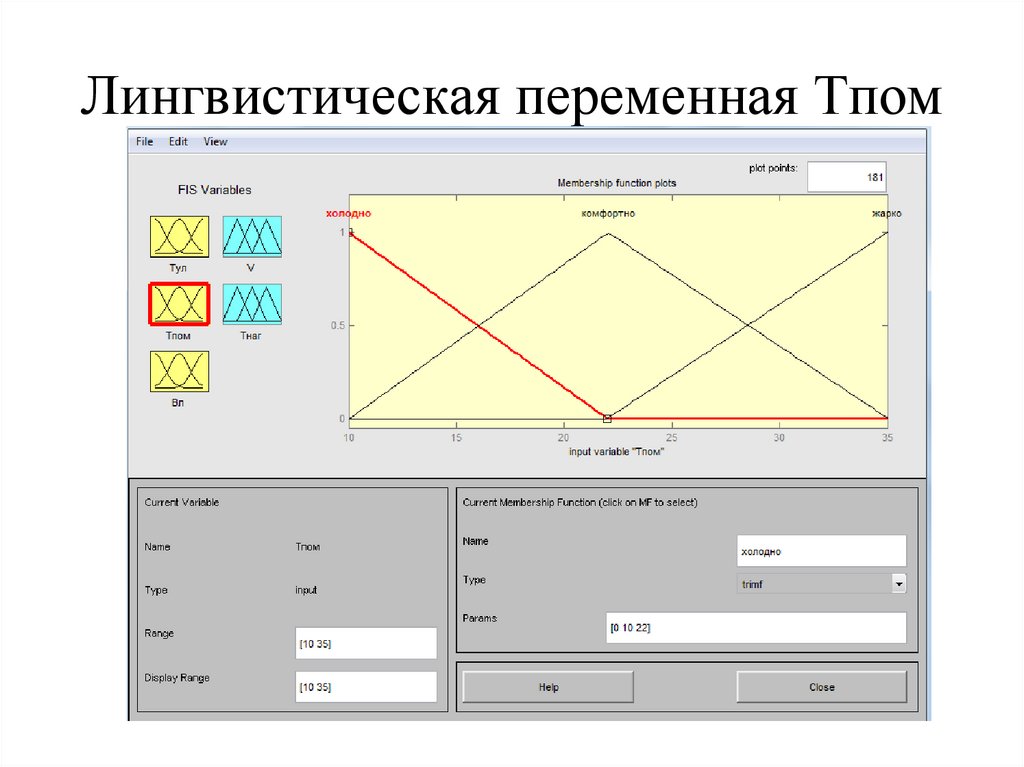
8. Лингвистическая переменная Тпом
9.
Связь между базовым и нечетким значениемобъектной переменной выражается количественно с
помощью
функции
принадлежности
(ФП),
обозначаемой греческой буквой μ.
Функция μ(x, T) отображает базовое значение x и
нечеткое значение T в интервале [0; 1]. По
определению: 0<μ(x, T)<1 для x и T.
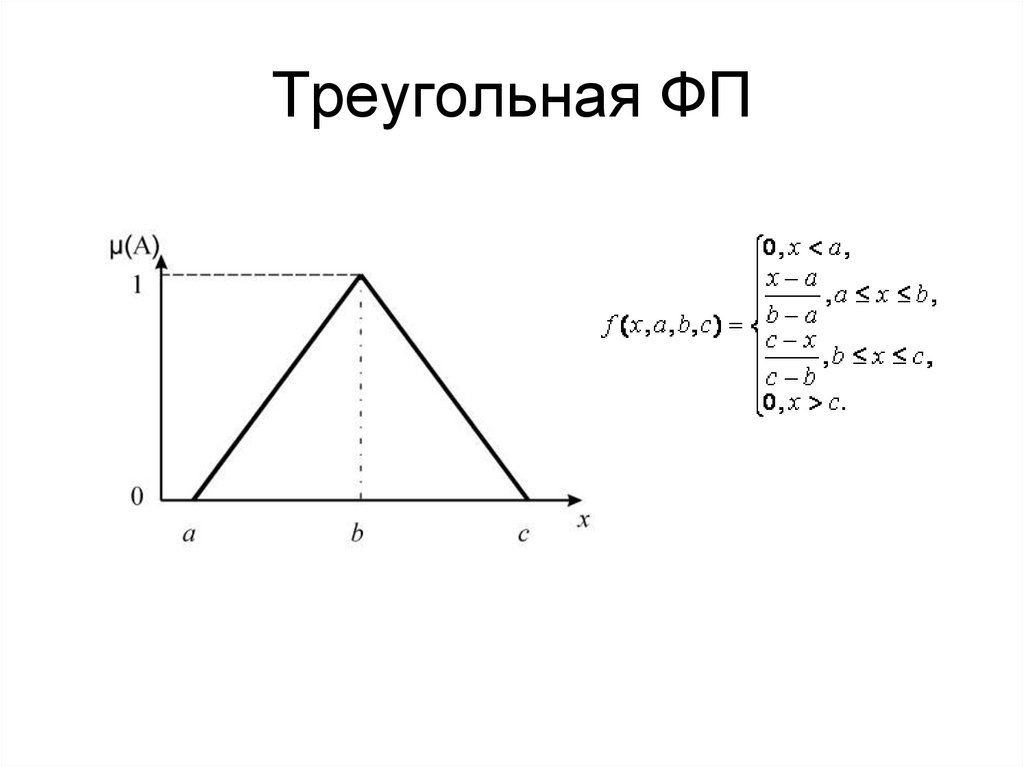
10. Треугольная ФП
11. Трапециевидная ФП
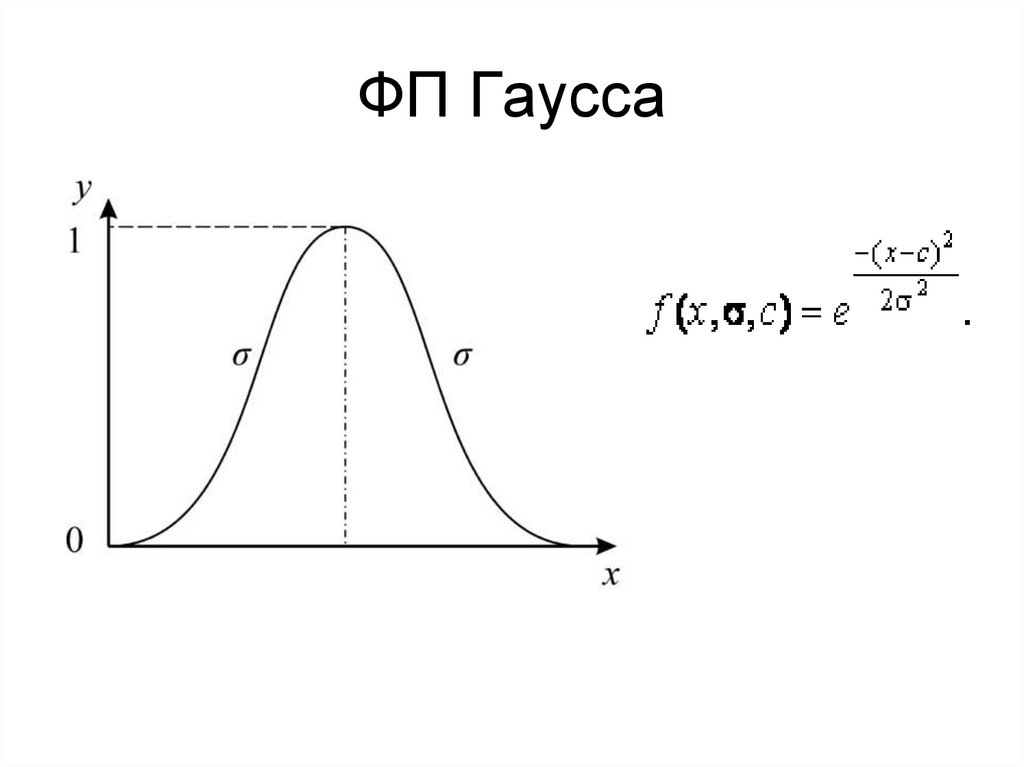
12. ФП Гаусса
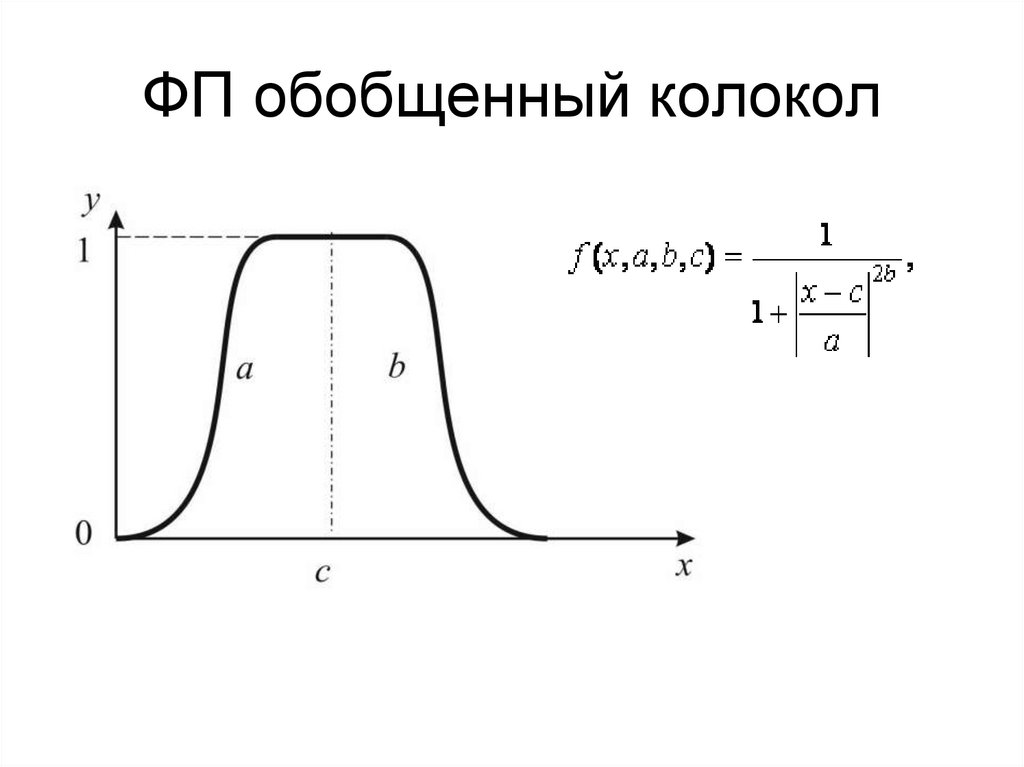
13. ФП обобщенный колокол
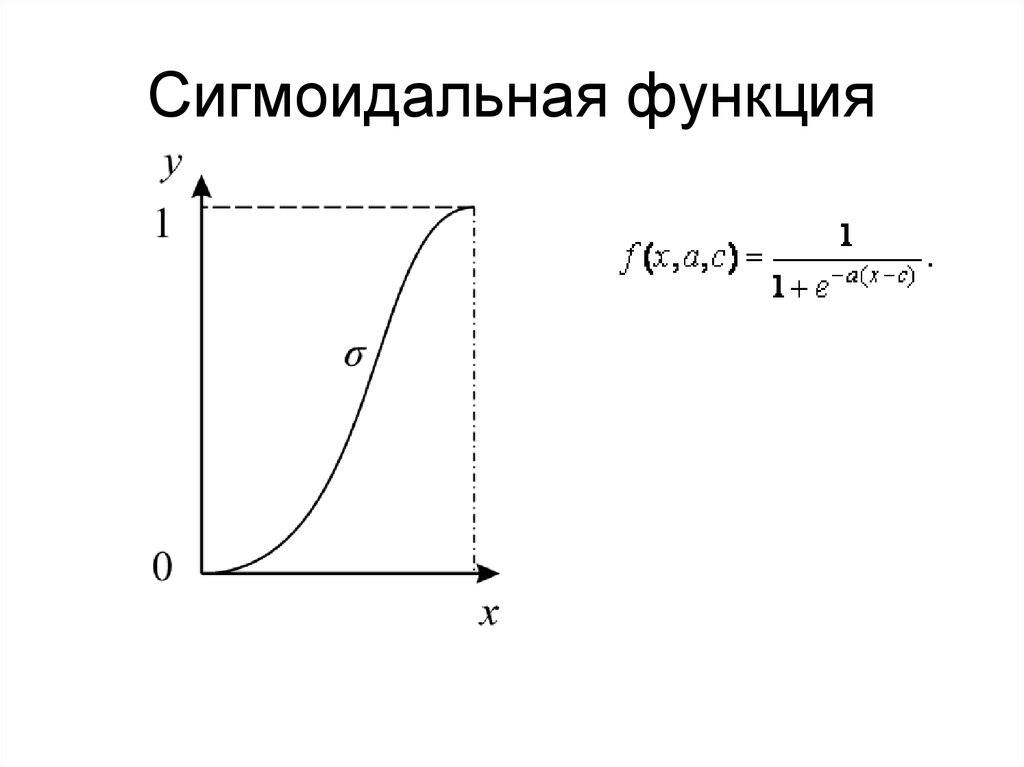
14. Сигмоидальная функция
15. Лингвистическая переменная Вл
1, х 050 x
f (низкая ,0, 50)
, 0 x 50
50
0, x 50
0, х 0
x
, 0 x 50
50
f (средняя,50,100)
100 x
,5 0 x 100
50
0, х 100
0, х 50
x 50
f (высокая,50,100)
,5 0 x 100
50
1, x 100
16. Эквивалентность.
R1 R2A( x ) B ( x )
x X
17. Включение
A( x ) B ( x )x X
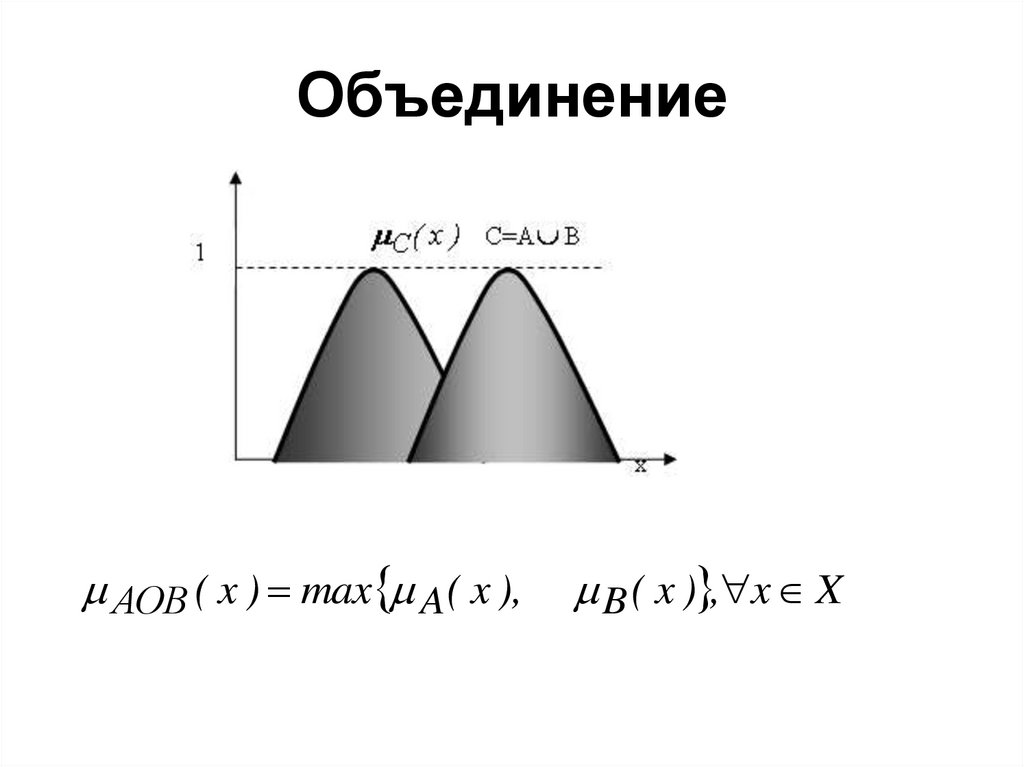
18. Объединение
АОВ ( x ) max A ( x ),B ( x ) , x X
19. Пересечение
АОВ ( x ) min A ( x ),B ( x ) , x X
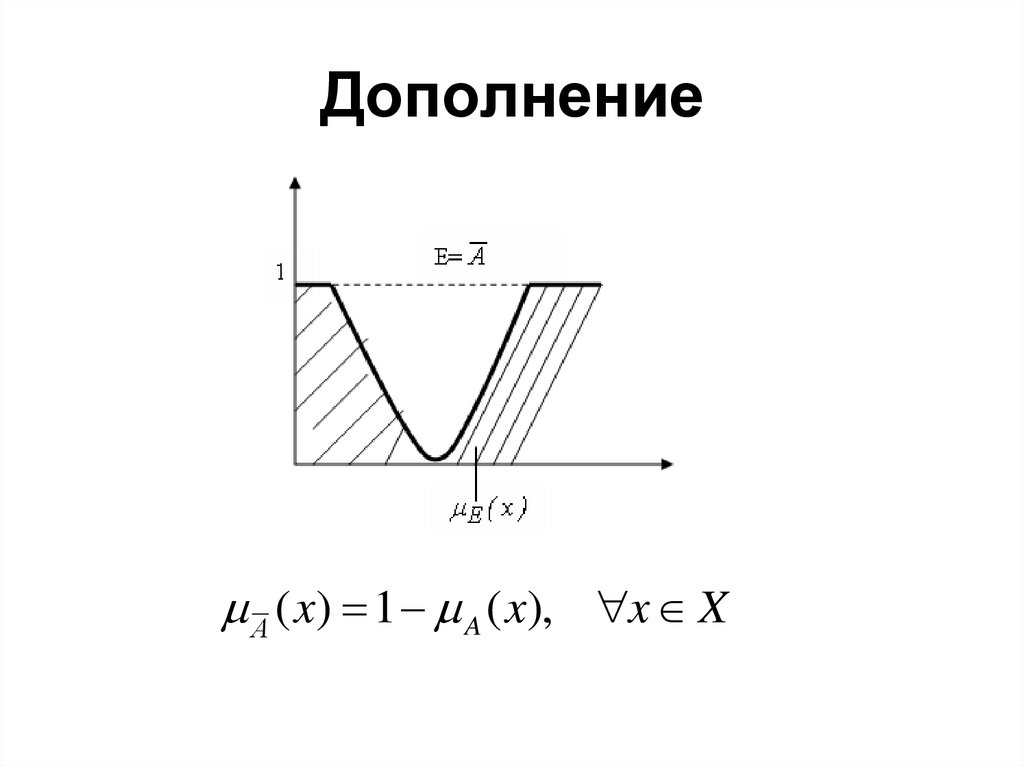
20. Дополнение
А ( x) 1 A ( x), x X21. Алгебраическое произведение
AB ( x) A ( x) B ( x), x X22. Алгебраическая сумма A
A B ( x) A ( x) B ( x) A ( x) B ( x), x X23. Операция концентрация
CON ( A) A2
CON ( x) A ( x), x X
2
A
24. Операция растяжение
DIL ( A) A0.5
DIL ( A) A ( x) , x X
25.
База знаний состоит из правил следующеговида:
Если a1 И a2 И … И aN ТО b1 И b2 И …И bm
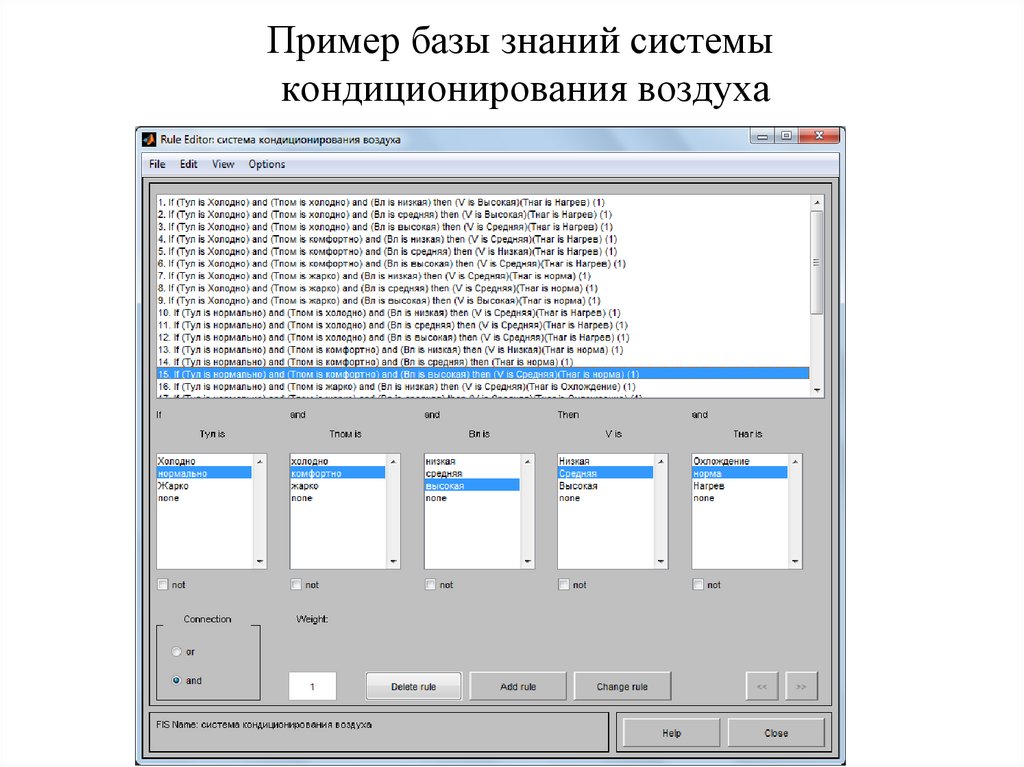
26. Пример базы знаний системы кондиционирования воздуха
27. Дефазификация
Предназначена для перевода нечеткогоуправляющего значения в четкое на
основе нечеткого вывода.
На практике применяется три основных
типа нечетких выводов:
- Дискретный вывод;
- Алгоритм Суджено;
- Алгоритм Мамдани.
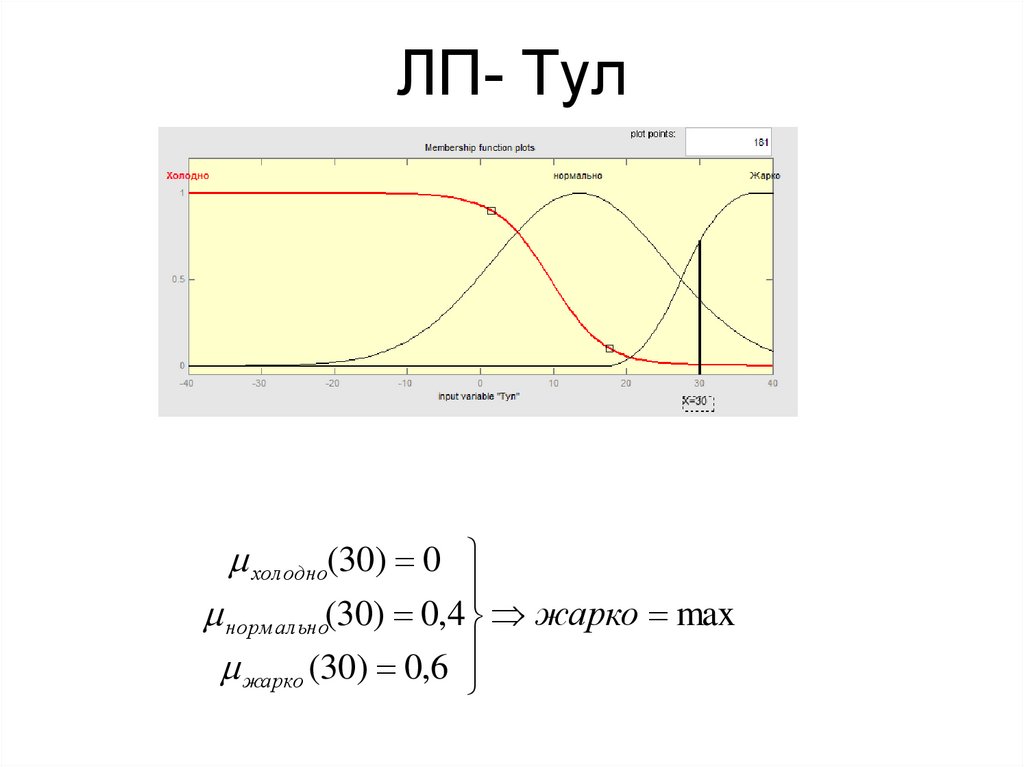
28. ЛП- Тул
хол одно(30) 0норм ал ьно(30) 0,4 жарко max
жарко (30) 0,6
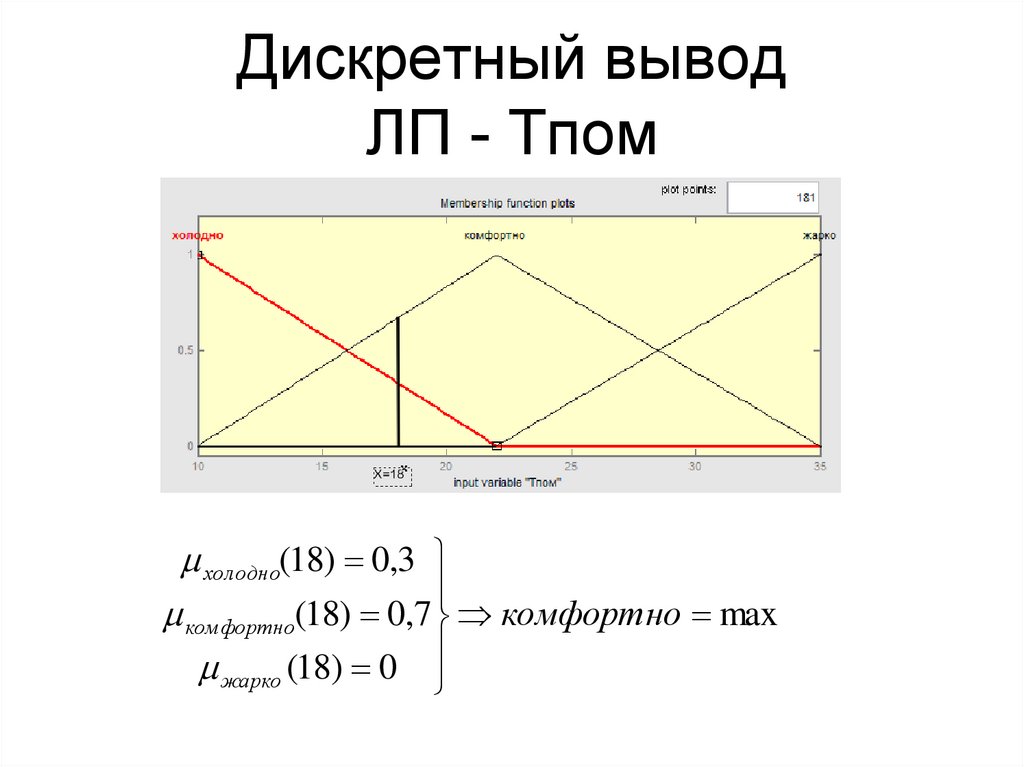
29. Дискретный вывод ЛП - Тпом
хол одно(18) 0,3ком фортно(18) 0,7 комфортно max
жарко (18) 0
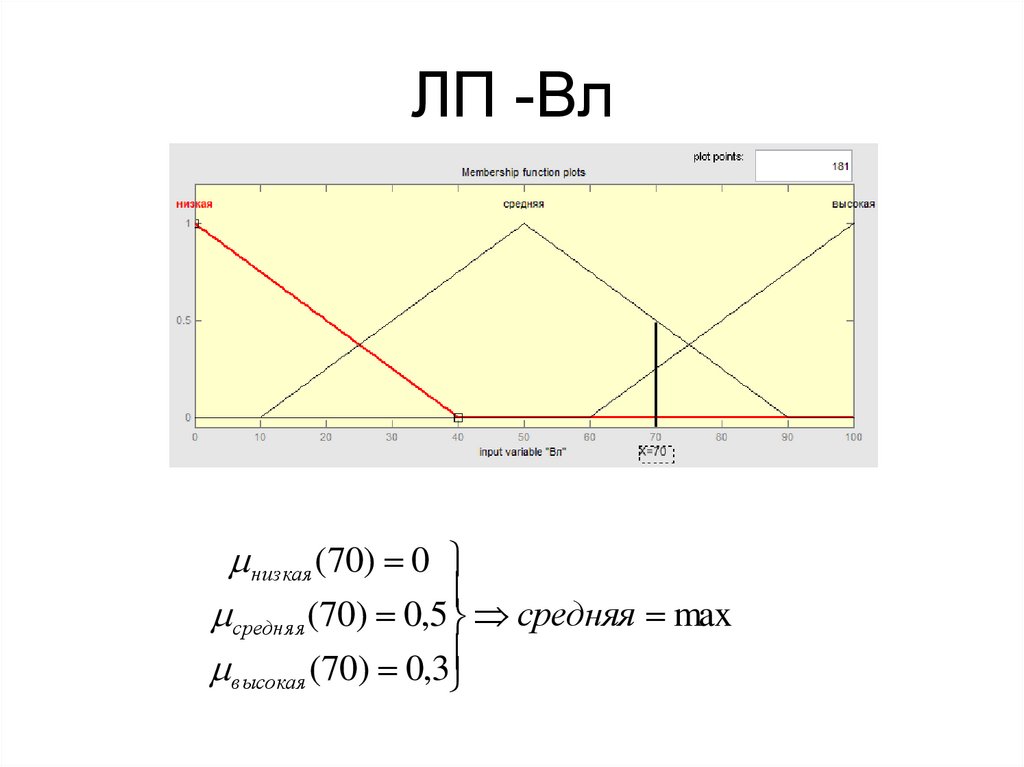
30. ЛП -Вл
низкая (70) 0средняя (70) 0,5 средняя max
высокая (70) 0,3
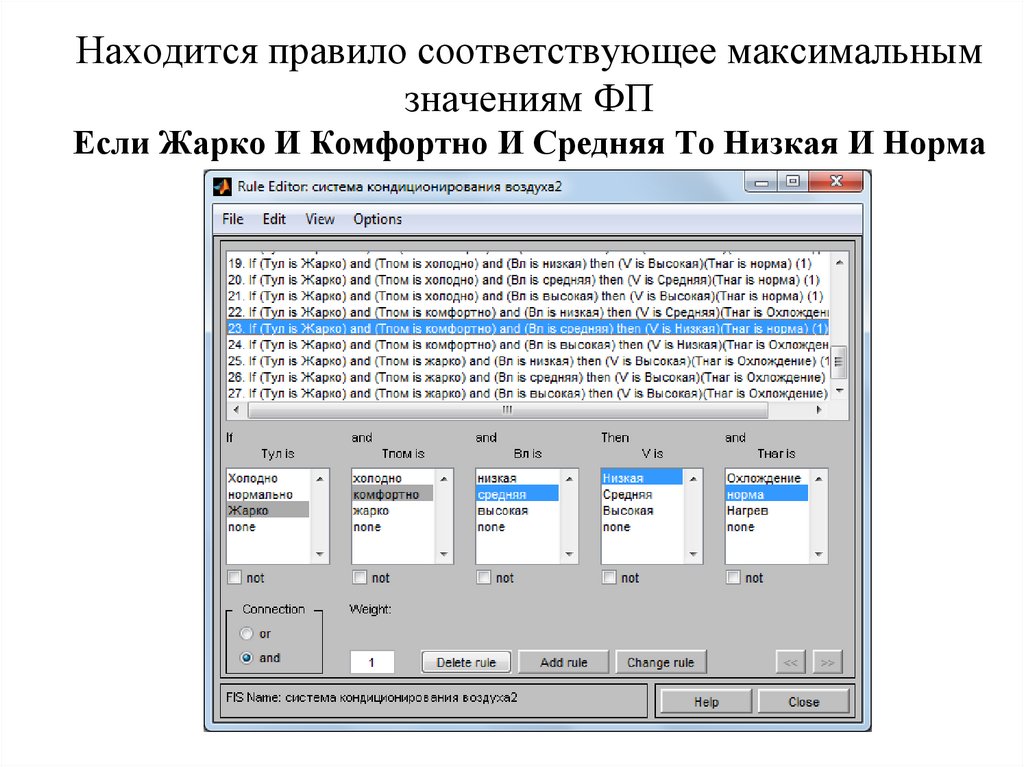
31. Находится правило соответствующее максимальным значениям ФП Если Жарко И Комфортно И Средняя То Низкая И Норма
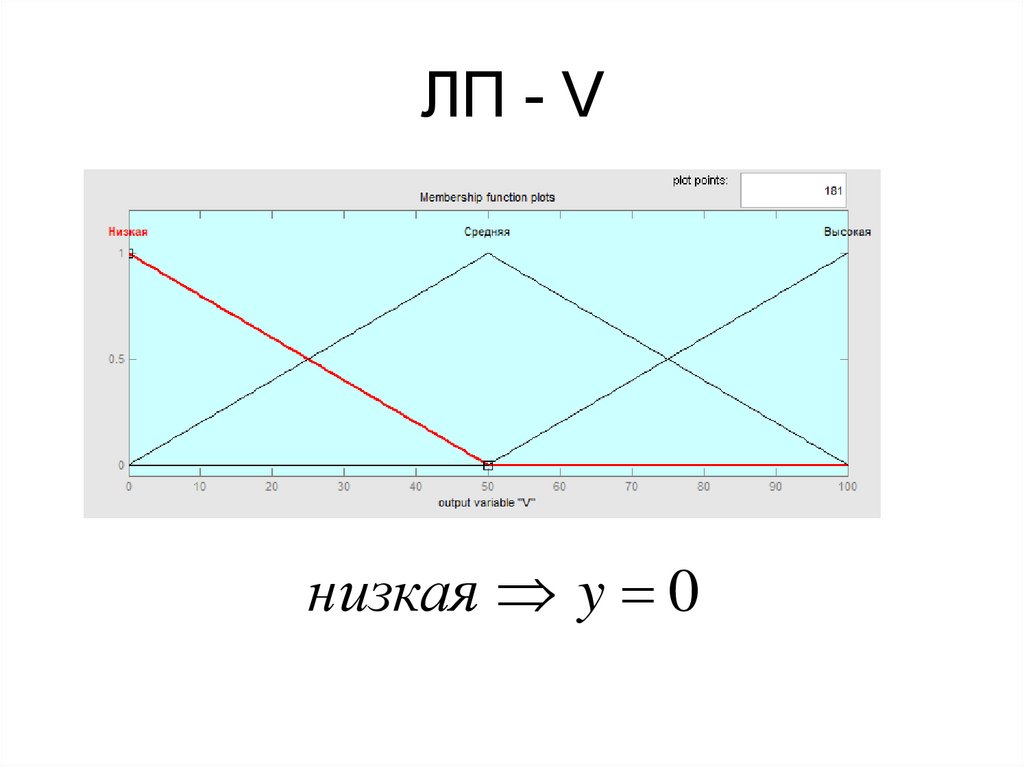
32. ЛП - V
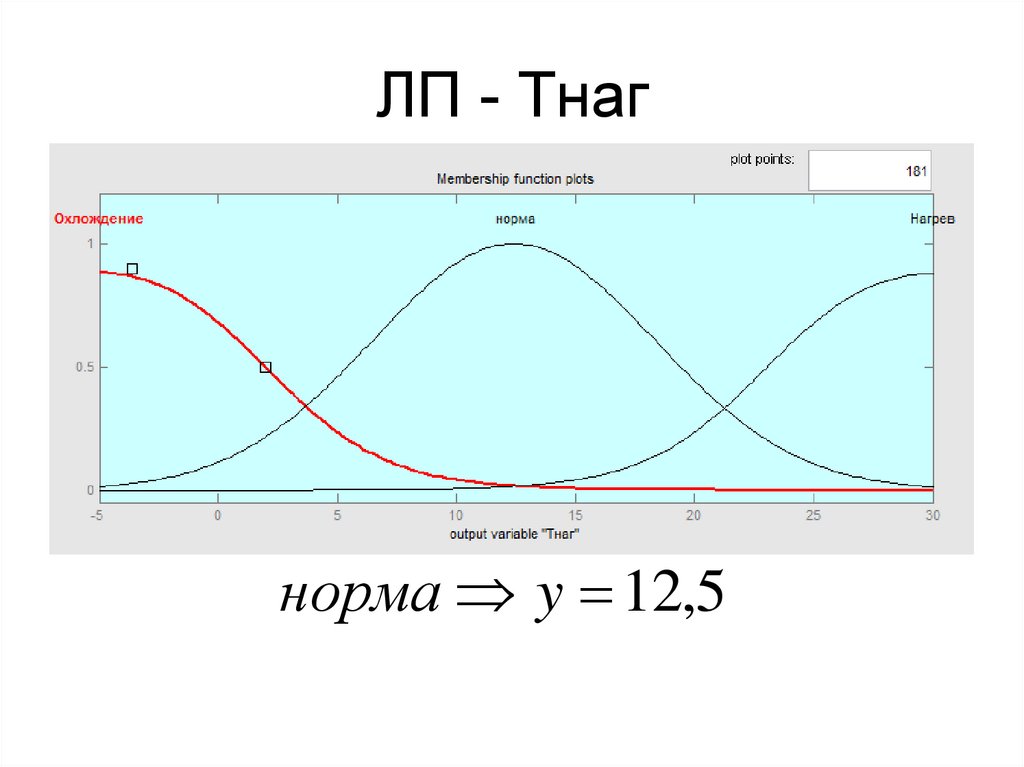
низкая y 033. ЛП - Тнаг
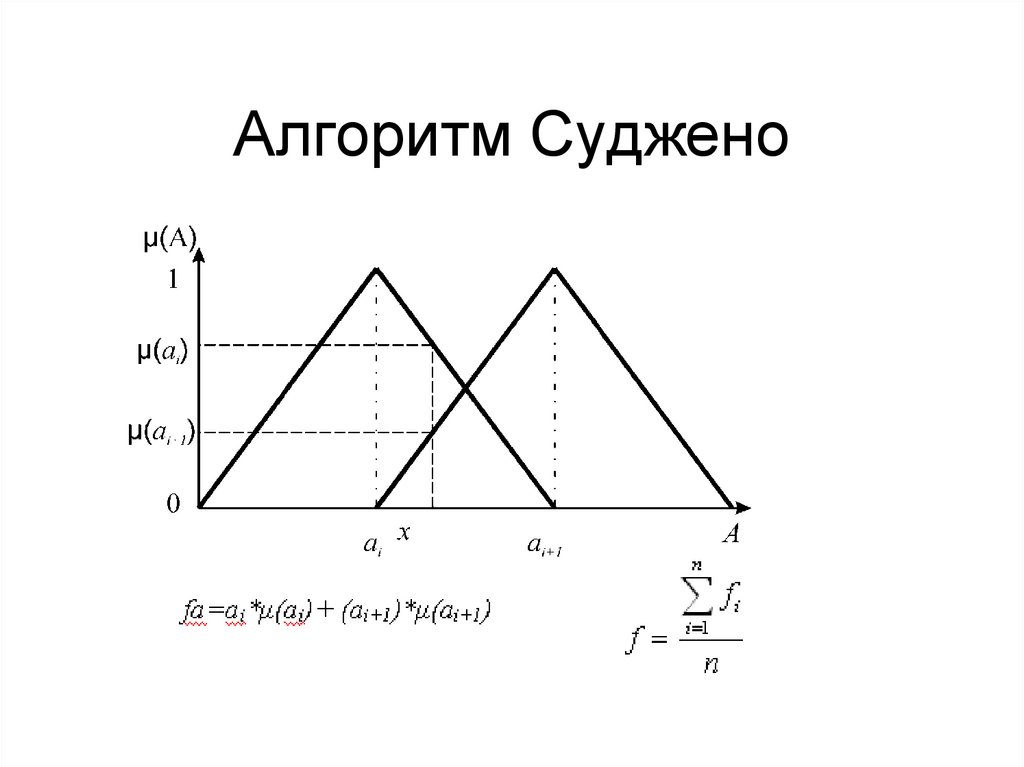
норма y 12,534. Алгоритм Суджено
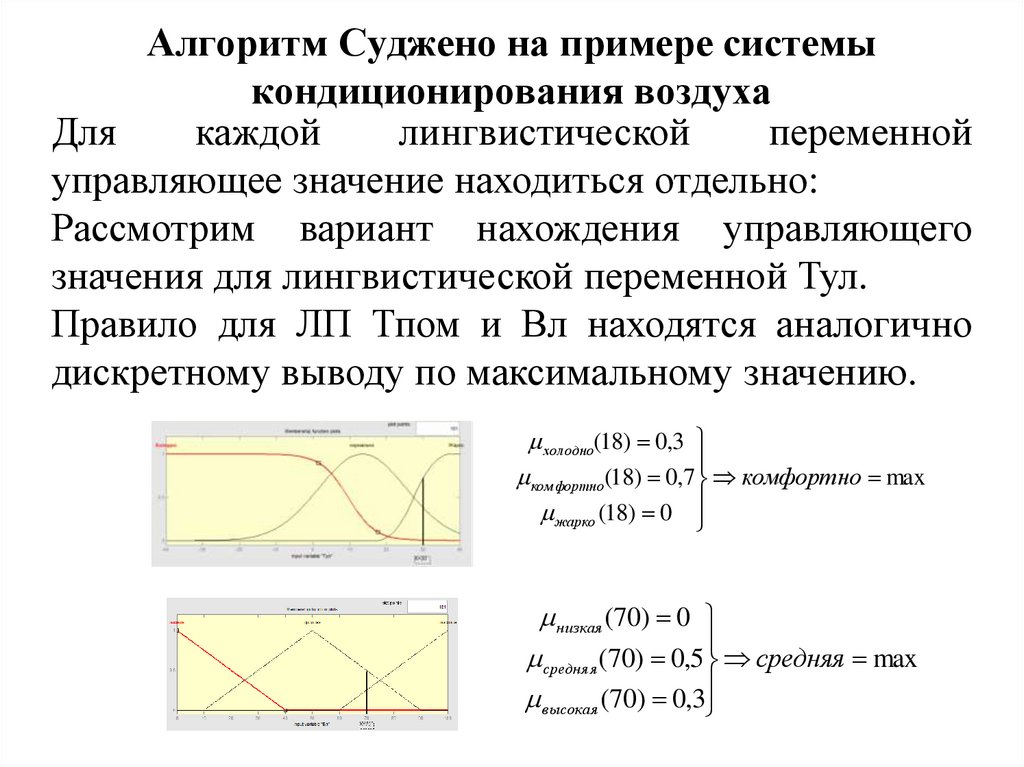
35. Алгоритм Суджено на примере системы кондиционирования воздуха
Длякаждой
лингвистической
переменной
управляющее значение находиться отдельно:
Рассмотрим вариант нахождения управляющего
значения для лингвистической переменной Тул.
Правило для ЛП Тпом и Вл находятся аналогично
дискретному выводу по максимальному значению.
хол одно(18) 0,3
ком фортно(18) 0,7 комфортно max
жарко (18) 0
низкая (70) 0
средняя (70) 0,5 средняя max
высокая (70) 0,3
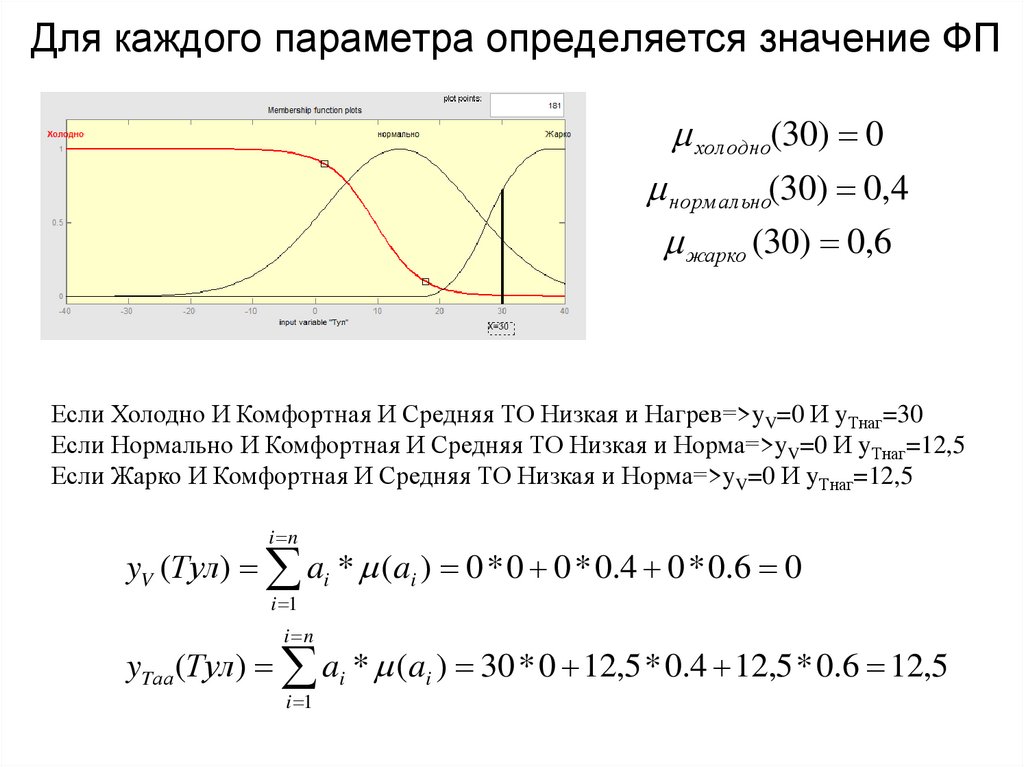
36. Для каждого параметра определяется значение ФП
холодно(30) 0норм ально(30) 0,4
жарко (30) 0,6
Если Холодно И Комфортная И Средняя ТО Низкая и Нагрев=>yV=0 И yТнаг=30
Если Нормально И Комфортная И Средняя ТО Низкая и Норма=>yV=0 И yТнаг=12,5
Если Жарко И Комфортная И Средняя ТО Низкая и Норма=>yV=0 И yТнаг=12,5
i n
yV (Тул) ai * (ai ) 0 * 0 0 * 0.4 0 * 0.6 0
i 1
i n
yTаа (Тул) ai * (ai ) 30 * 0 12,5 * 0.4 12,5 * 0.6 12,5
i 1
37.
Аналогичным способом находятся yV(Tпом), yV(Tвл),yнаг(Tпом), yнаг(Tвл). Управляющее значение y
определяется как среднеарифметическое между
соответствующими значениями:
i n
yV
y
Vi
i 1
i
yV (Тул) yV (Тпом) yV ( Вл )
3
i n
y
y Наг i 1
i
Наг i
y Наг (Тул) y Наг (Тпом) y Наг ( Вл )
3
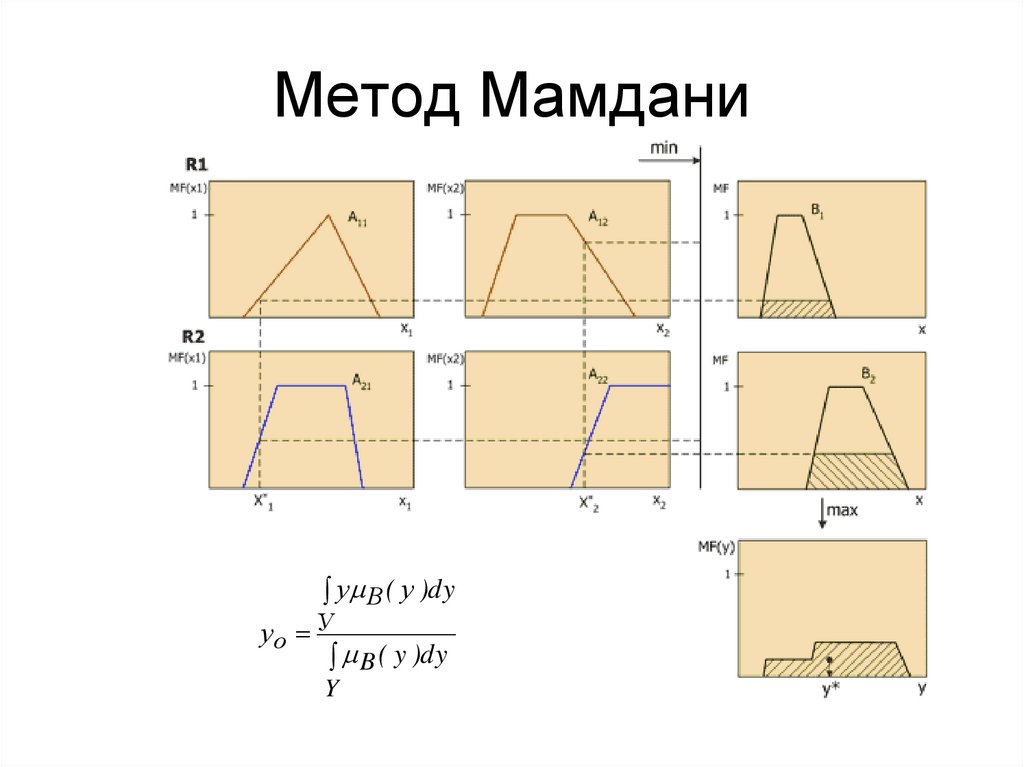
38. Метод Мамдани
у В ( у )dyуо У
B ( y )dy
Y






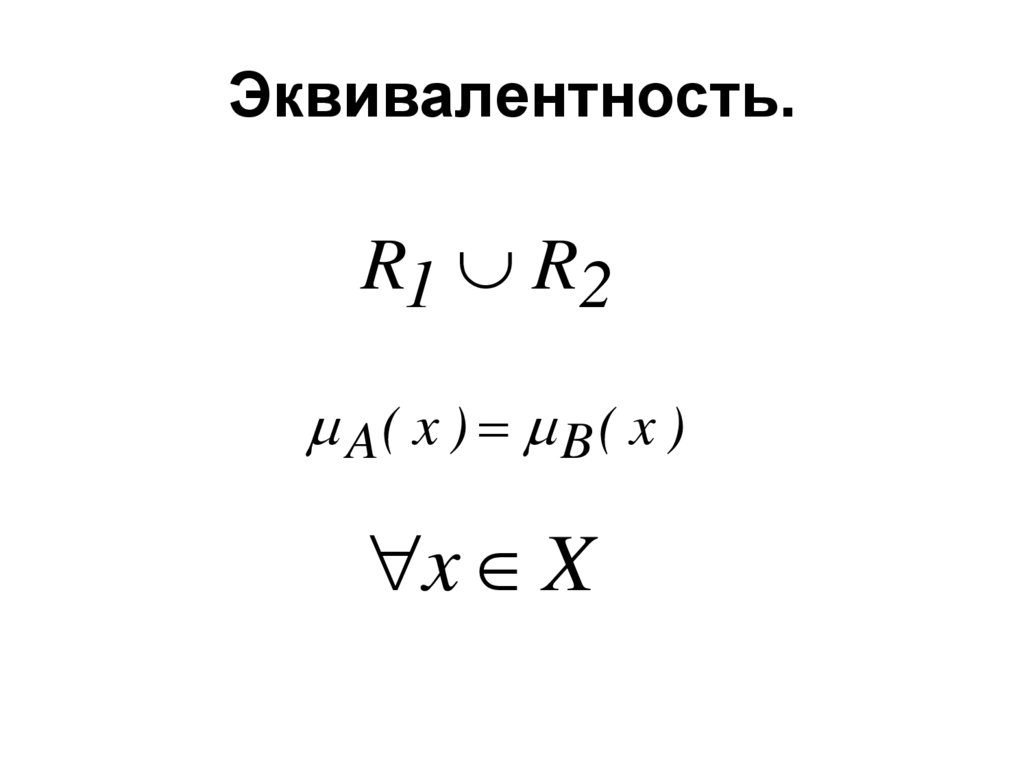
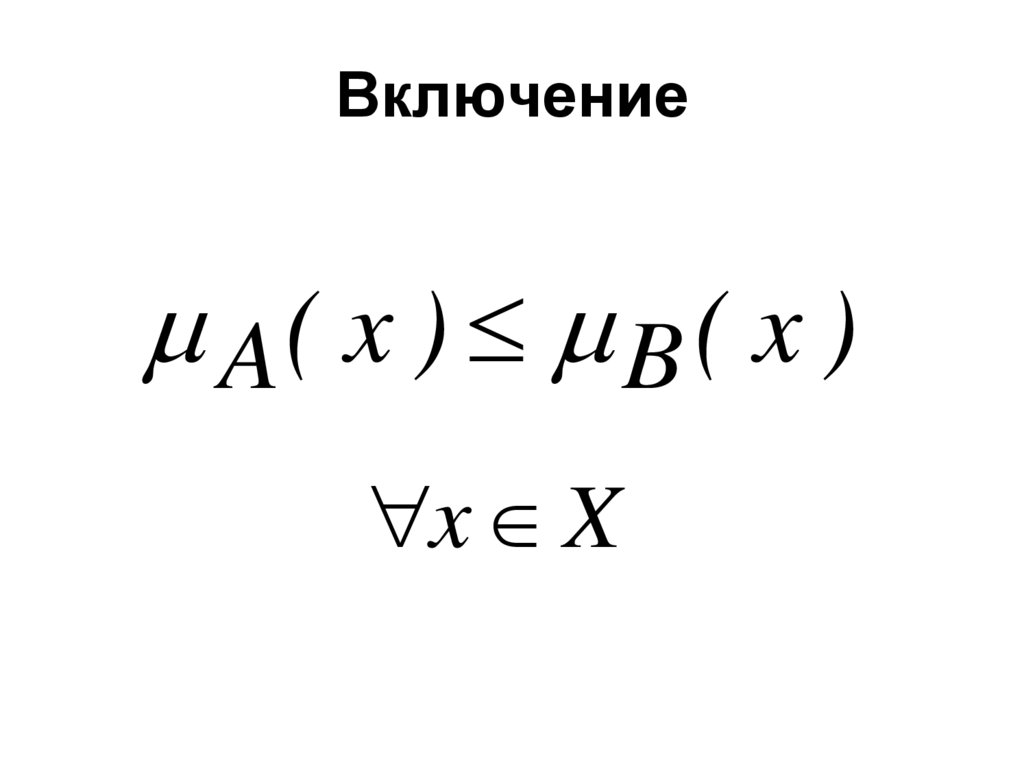









 Математика
Математика








