Случайная величина и распределение вероятностей

1.

Случайная величина и
распределение
вероятностей

2.

Случайные опыты, изучаемые в теории вероятностей,
связаны не только со случайными событиями, но и с
случайными величинами.
Случайная величина — это величина, значение которой
зависит от того, каким элементарным событием закончился
данный случайный опыт.
Значения случайной величины могут соответствовать
разным элементарным событиям.
Поэтому случайная величина является величиной,
значение которой зависит от случая.
В ходе случайного опыта или наблюдения случайная
величина принимает числовые значения.

3.

Пример:
Предположим, что имеется человек, который
бросает кубик.
Мы будем рассматривать случайную величину X,
которая представляет собой число выпавших очков.
Учитывая, что кубик имеет шесть граней, а на
каждой грани число очков может быть от одного до
шести, случайная величина X может принимать
значения из множества: {1;2;3;4;5;6}.

4.

Измерение веса случайно выбранного человека в килограммах
позволяет рассматривать его как случайную величину.
Случайная величина выигрыша в лотерее является результатом
фиксированной цены покупки билета.
Свойства случайной величины срока службы гаджета,
отсчитываемого в днях с момента выпуска или продажи, имеют
важное значение, например, при установлении гарантийного
периода на новый прибор.
Случайной величиной, которая является примером важности,
является число успехов в серии испытаний Бернулли.
В этой серии проводится 20 испытаний Бернулли, и число
успехов может быть любым целым числом от 0 до 20.
Также случайной величиной является число неудач.

5.

При проведении случайного опыта возникает случайная
величина. Величина X может иметь различные значения в ходе
этого опыта. Для полного описания случайной
величины X необходимо указать вероятности, с которыми она
принимает эти значения.
Вероятностное распределение, или
просто распределение случайной величины,
представляет собой закон, определяющий вероятность
принятия каждым значением этой величины.
(X=7),(X=−5) принято использовать для обозначения
событий, когда величина X может принимать определенные
значения, например, 7 или −5.
В таком случае, необходимо указать вероятность события,
когда X равно конкретному значению, такому как 7 или −5.

6.

Удобным способом задания распределения вероятностей
является таблица, график, диаграмма, формулы или даже
словесное описание.
Например, чтобы задать распределение случайной величины Y,
которая представляет собой число очков, выпавших при
однократном броске кубика, можно использовать таблицу.
Значение
1
2
3
4
5
6
Вероятность 1/6
1/6
1/6
1/6
1/6
1/6
В этом примере вероятности всех шести значений одинаковые.
Вероятность распределена поровну между шестью возможными
значениями.

7.

Сумма всех вероятностей в распределении равна единице,
так как она представляет собой сумму вероятностей всех
элементарных событий, которые представляют все
возможные значения случайной величины.
Пример:
В жизни много случайных величин, и их значения постоянно
меняются. Например, время безотказной работы гаджета
может быть любым числом, положительным или
отрицательным.
Такие случайные величины известны как непрерывные.
Функции используются для описания распределения
вероятностей между возможными
значениями непрерывных случайных величин.

8.

Задание № 1
Известно, что в классе учащихся — 22 чел.
Из них девочек — 10 чел.
Какое количество значений может принимать
случайная величина «число мальчиков,
присутствующих сегодня в классе»?

9.

Задание № 2
Задай с помощью таблицы распределение
вероятностей случайной величины X, равной
числу орлов, выпавших при двух бросках монеты.

10.

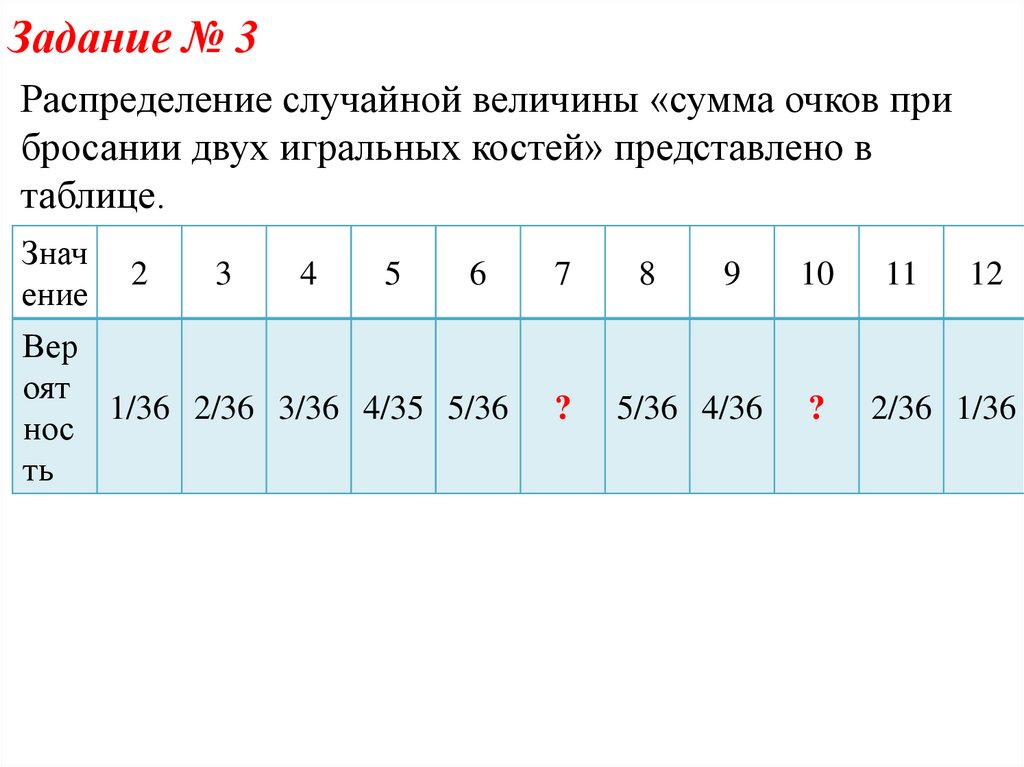
Задание № 3
Распределение случайной величины «сумма очков при
бросании двух игральных костей» представлено в
таблице.
Знач
ение
2
3
4
5
6
7
8
9
10
11
12
Вер
оят
1/36 2/36 3/36 4/35 5/36
нос
ть
?
5/36 4/36
?
2/36 1/36

11.

Задание № 4
По таблице, которая предоставлена, можно определить
вероятности для различных значений случайной
величины. Однако, среди данных вероятностей есть одно
значение, которое неизвестно. Найди её.
Значение
Вероятность
−2
−1
0
1
2
0,08
0,24
?
0,17
0,27

12.

Задание № 5
Случайная величина Z принимает все натуральные значения
от 1 до 10.
Вероятность события (Z=n) равна n/55.
Заполни четыре столбца в таблице распределения
вероятностей.

13.

Задание № 6
Распределение вероятностей случайной
величины X задано таблицей.
Значение X
0
0,5
1
1,5
2
Вероятность 0,17
0,24
0,18
0,27
0,14
Найди вероятность события «0,5<X<2».

14.

Задание № 7
В книге 123 стр.
Катя наугад открывает книгу в начале и смотрит
номер правой страницы.
Какие значения она может принимать?

15.

Задание № 8
Итоговый срез по статистике выполнили 26 чел.
Всем им были выставлены разные оценки — от «2» до
«5».
Сколько различных значений возможно у случайной
величины «средняя оценка за итоговый срез»?
Каким может быть это значение?

16.

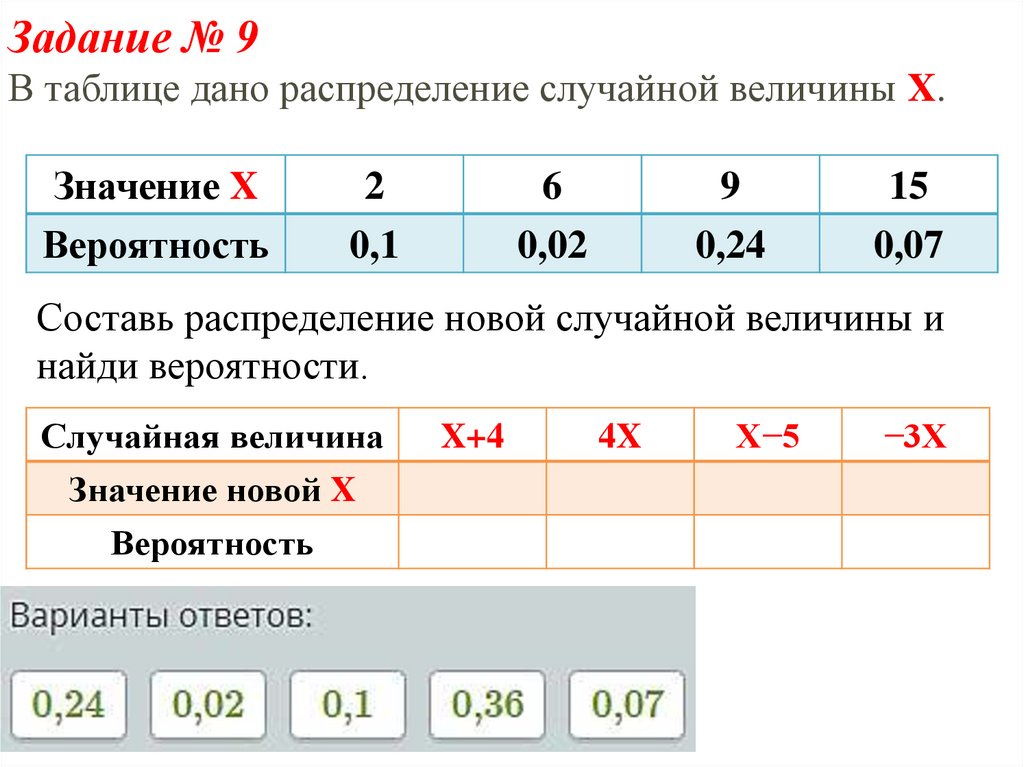
Задание № 9
В таблице дано распределение случайной величины X.
Значение X
Вероятность
2
0,1
6
0,02
9
0,24
15
0,07
Составь распределение новой случайной величины и
найди вероятности.
Случайная величина
Значение новой X
Вероятность
X+4
4X
X−5
−3X

17.

Домашнее задание
Задание № 1
Известно, что в классе учащихся — 30 чел.
Из них девочек — 14 чел.
Какое количество значений может принимать
случайная величина «число мальчиков,
присутствующих сегодня в классе»?

18.

Домашнее задание
Задание № 2
Задай с помощью таблицы распределение
вероятностей случайной величины X, равной
числу орлов, выпавших при двух бросках
монеты.

19.

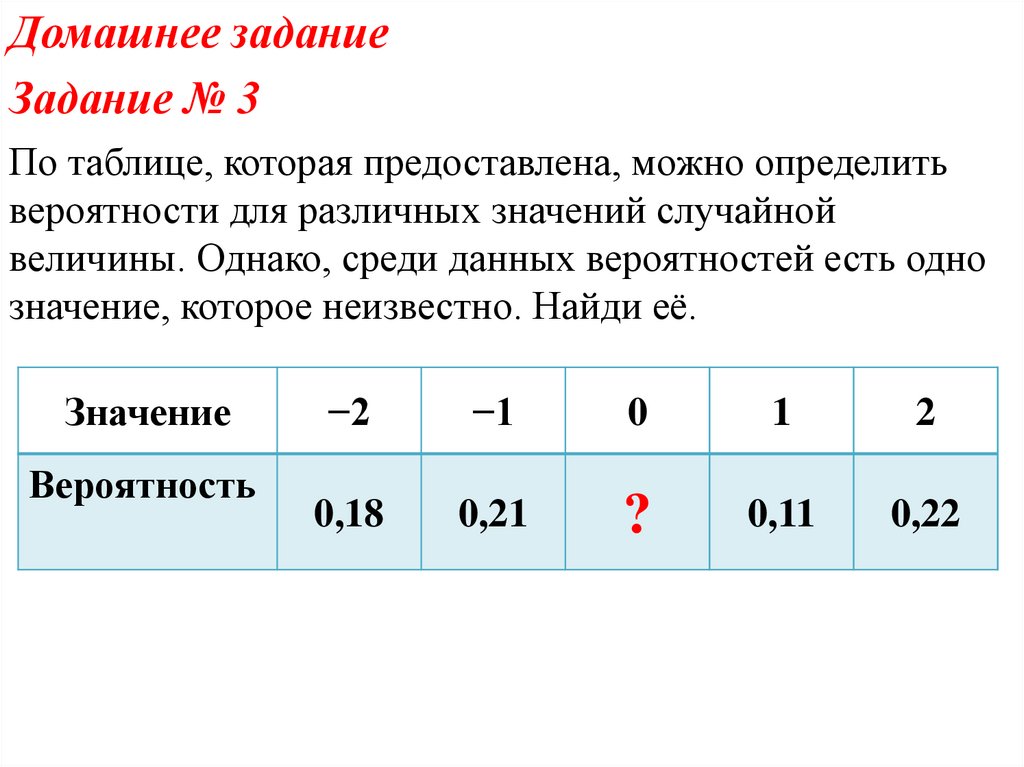
Домашнее задание
Задание № 3
По таблице, которая предоставлена, можно определить
вероятности для различных значений случайной
величины. Однако, среди данных вероятностей есть одно
значение, которое неизвестно. Найди её.
Значение
Вероятность
−2
−1
0
1
2
0,18
0,21
?
0,11
0,22

20.

Домашнее задание
Задание № 4
Распределение вероятностей случайной
величины X задано таблицей.
Значение X
0
0,5
1
1,5
2
Вероятность 0,18 0,22 0,09 0,07 0,44
Найди вероятность события «X>1».