Контекстно-свободные грамматики. Теория автоматов языков и трансляторов. Лекция 3

1. Теория автоматов языков и трансляторов Лекция 3 Контекстно-свободные грамматики

2 м/о
18.09.2024

2.

Доказать, что формальный язык L = {a(ba)n} регулярный
1-ый способ
G = ( {S, A},
{a, b},
{S aA, A bB, B aA, A bD, D a},
S)
Если n = 0, то добавим правило:
S a

3.

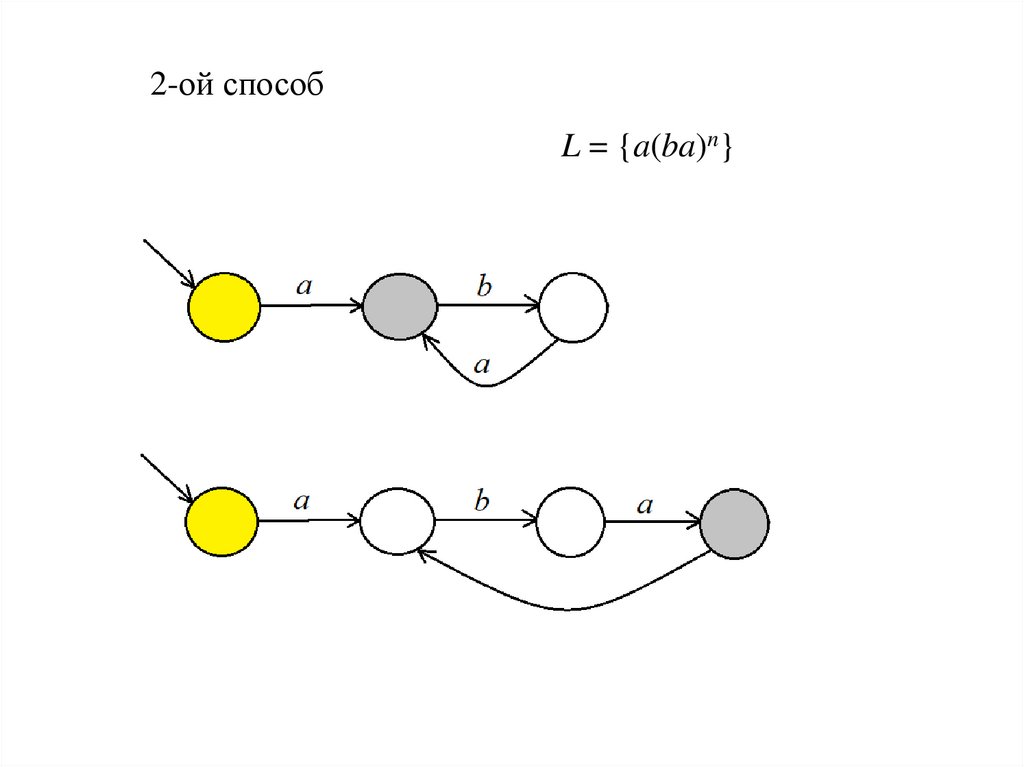
2-ой способ
L = {a(ba)n}

4.

Построить КС-грамматику для языка:
{0n1n | n 1}
S 0S1
S 01

5.

Язык типа 0:
Невозможно построить компилятор, который гарантированно
выполнял бы разбор предложений языка за ограниченное время
на основе ограниченных вычислительных ресурсов.
Все естественные языки относятся к этому типу,
поскольку структура и значение фразы естественного языка
может зависеть не только от контекста данной фразы,
но и от содержания того текста,
где эта фраза встречается,
поэтому существуют большие сложности в автоматизации
перевода текстов,
написанных на естественных языках и отсутствуют
компиляторы,
которые воспринимали бы программы на основе таких языков

6.

Тип 1
1А 2 1 2, где 1, 2 V*, А VN, V+
Или
, где , V*, | | | |
При построении компиляторов практического применения не
имеют.

7.

Язык типа 1
В общем случае время на распознавание предложений языка
экспоненциально зависит от длины исходной цепочки символов
Применяются в анализе и переводе текстов на естественных
языках;
распознаватели, построенные на их основе, позволяют
анализировать тексты с учетом контекстной зависимости в
предложениях входного языка
(но не учитывают содержание текста, поэтому в общем случае для точного
перевода с естественного языка все же требуется вмешательство человека);
также может выполняться автоматизированный перевод с одного естественного языка
на другой, могут использоваться сервисные функции проверки орфографии и
правописания в языковых процессорах.

8.

Тип 2
КС-грамматики:
А , где А VN , V+
И укорачивающие КС-грамматики:
А , где А VN , V*
используются при описании синтаксических конструкций языков
программирования

9.

Тип 2
КС-грамматики:
А , где А VN , V+
И укорачивающие КС-грамматики:
А , где А VN , V*
используются при описании синтаксических
конструкций языков программирования

10.

КС-грамматики
Приведенные грамматики – это КС-грамматики, которые не
содержат недостижимых и бесплодных символов, циклов и правил («пустых» правил)
Для преобразования произвольной КС-грамматики к
приведенному виду, необходимо удалить:
удалить все бесплодные символы;
удалить все недостижимые символы;
удалить -правила;
удалить цепные правила.
Шаги преобразования должны выполняться именно в указанном порядке, и
никак иначе.

11.

Язык типа 2
В общем случае время на распознавание предложений языка
полиномиально зависит от длины исходной строки
(в зависимости от класса языка это либо кубическая, либо
квадратичная зависимость, также существует много классов
языков, для которых эта зависимость линейна)
- лежат в основе синтаксических конструкций большинства современных языков
программирования, на их основе функционируют некоторые довольно сложные
командные процессоры, допускающие управляющие команды цикла и условия.

12.

Пример
Пусть задана КС-грамматика
G1 ( a, b , S , P, S)
где P состоит из правил:
(1) S aSbS
(2) S bSaS
(3) S ( пустое слово)
Грамматика G1 порождает множество всех слов в алфавите {a, b},
содержащих одинаковое число букв a и b.
Рассмотрим слово = babbaa
и процесс его вывода из аксиомы S:
S bSaS baSbSaS babSaS babSa babbSaSa babbaa L
Последовательность номеров правил грамматики, с помощью которой слово выводится
из аксиомы S , называется выводом слова.
Для = babbaa рассмотренный вывод имеет вид w( ) = 2133233.

13.

Левым (правым) выводом называется вывод, в котором
каждое правило применяется к самому левому (самому
правому) вхождению нетерминала в строке.
w( ) = 2132333 – левый вывод слова
w( ) = 2312333 – правый вывод слова
(1) S aSbS
(2) S bSaS
(3) S ( пустое слово)

14.

Для КС-грамматик существует удобный графический способ представления
вывода – дерево вывода.
Дерево строится следующим образом.
(1) Корень дерева помечается аксиомой грамматики.
(2) Если некоторая вершина дерева помечена нетерминалом A,
и в процессе вывода к этому нетерминалу применяется
правило A b1 b2 … bk,
то из вершины в следующий ярус проводится k ребер,
и полученные вершины следующего яруса помечаются
слева направо буквами b1 b2 … bk.
При применении правил вида A из вершины, помеченной нетерминалом
A, в следующий ярус проводится одно ребро и новая вершина помечается
символом пустого слова .
Для слова L(G1) листья дерева помечены символами терминального
алфавита либо символом .
Само слово получается обходом кроны дерева слева направо.

15.

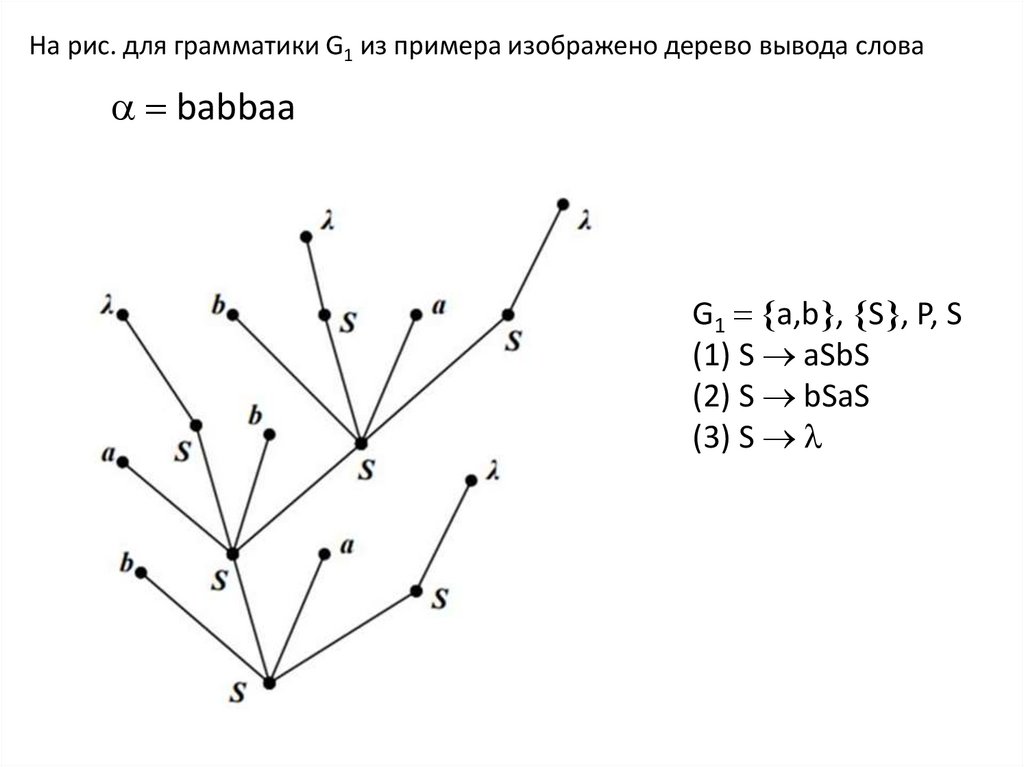
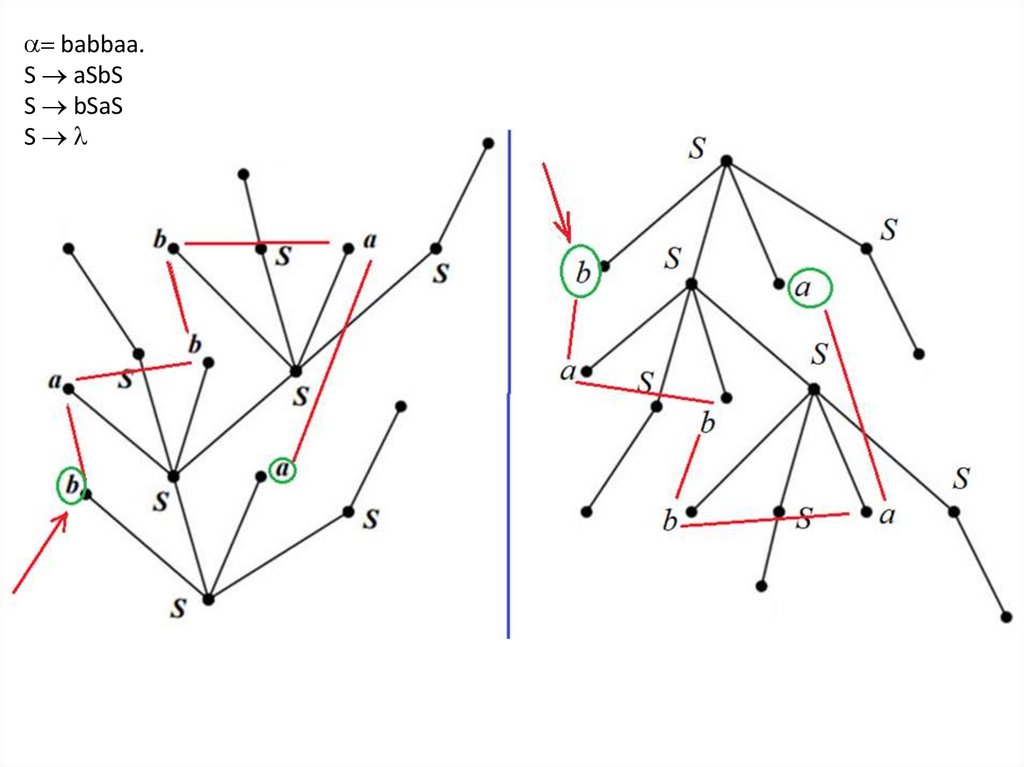
На рис. для грамматики G1 из примера изображено дерево вывода слова
babbaa
G1 a,b , S , P, S
(1) S aSbS
(2) S bSaS
(3) S

16.

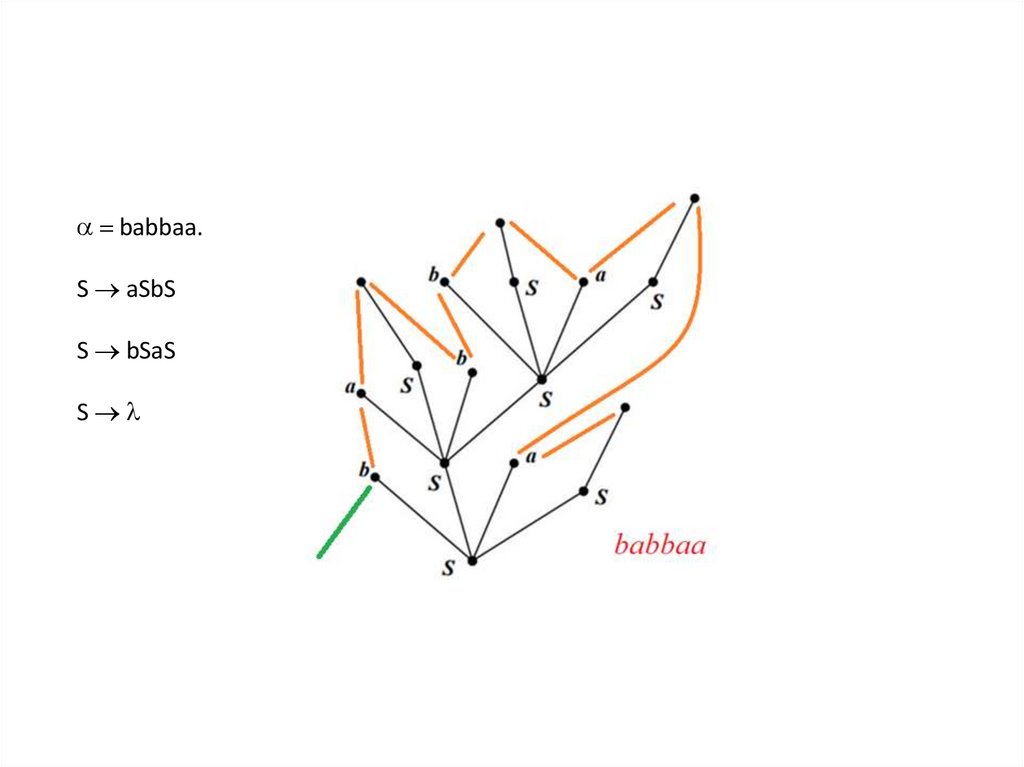
babbaa.
S aSbS
S bSaS
S

17.

babbaa.
S aSbS
S bSaS
S

18.

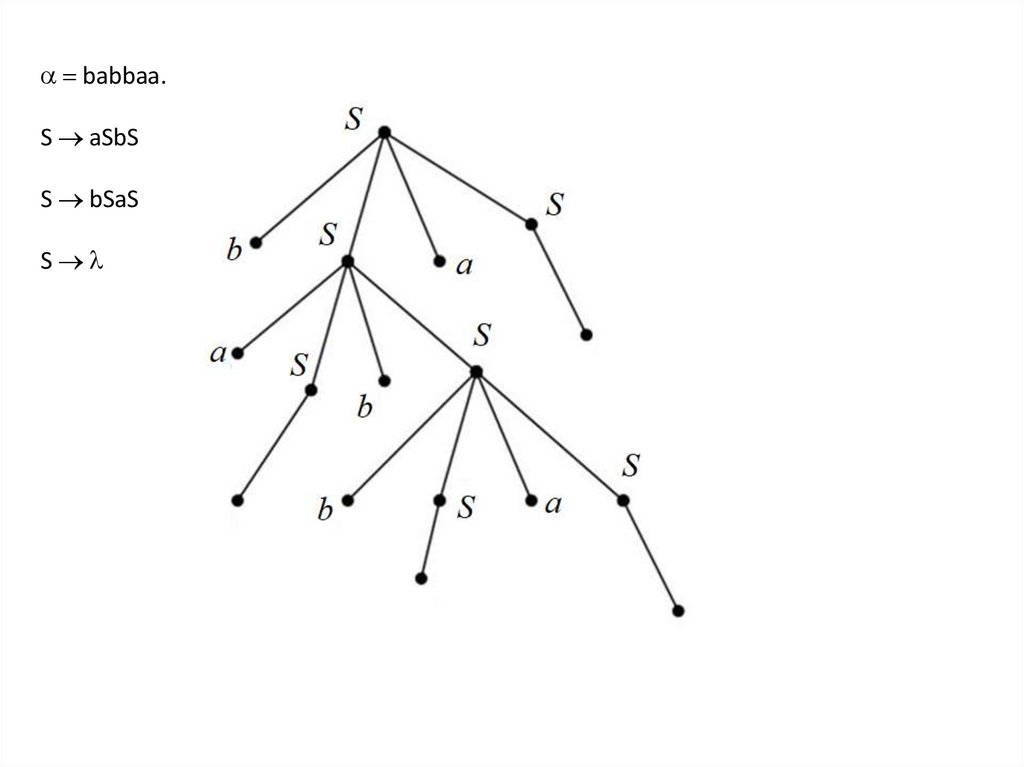
babbaa.
S aSbS
S bSaS
S

19.

КС-грамматика G называется грамматикой с однозначным выводом
(или однозначной грамматикой),
если каждое слово из L G имеет единственный левый вывод.
В противном случае КС-грамматика называется грамматикой с
неоднозначным выводом.

20.

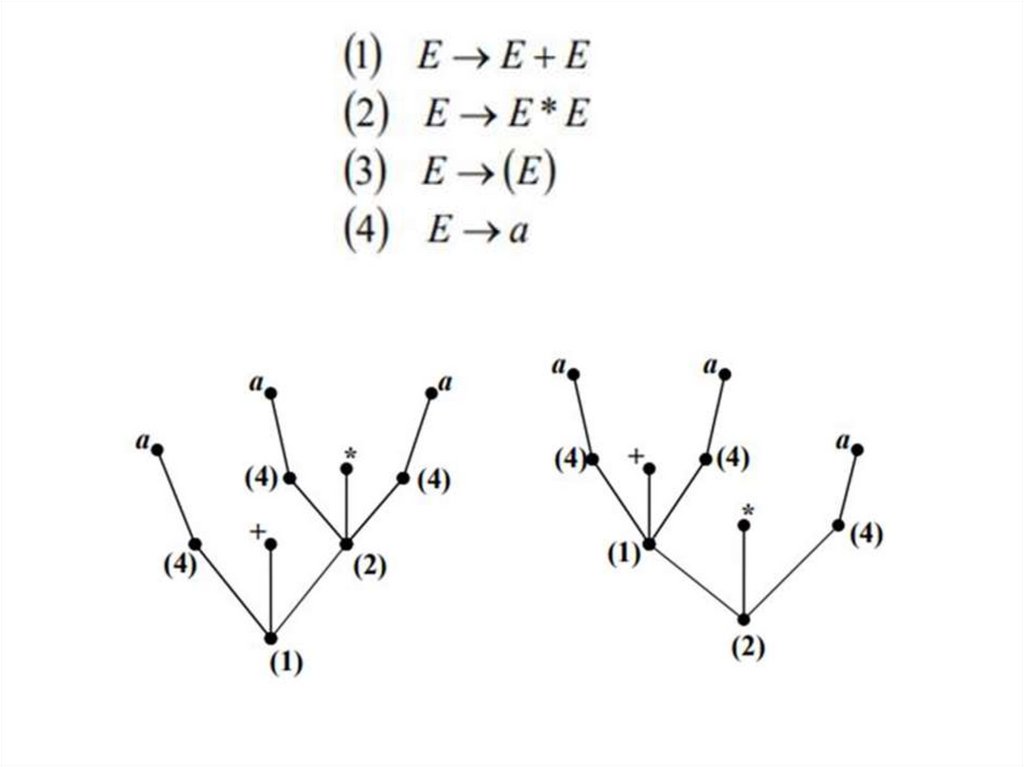
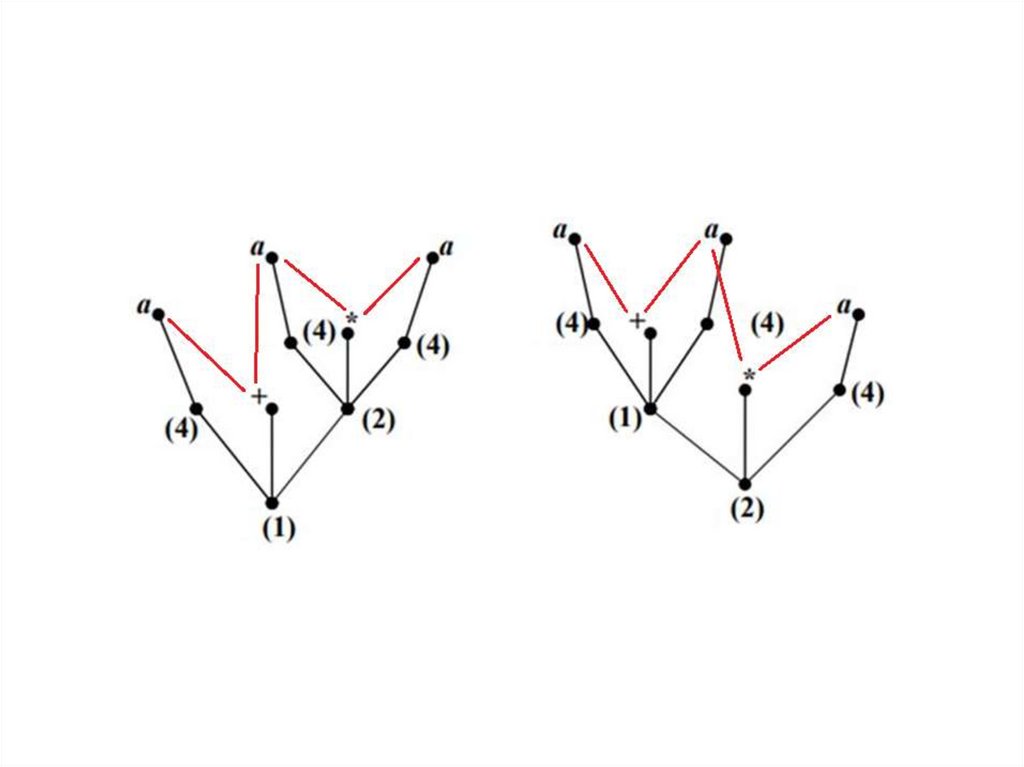
21.

22.

Для одного и того же КС-языка могут существовать
различные грамматики
(поэтому возникает проблема выбора грамматики, наиболее подходящей по тем
или иным свойствам, или проблема эквивалентного преобразования грамматики к
нужному виду)
Универсальных методов эквивалентных
преобразований КС-грамматик не существует из-за
неразрешимости алгоритмических проблем
распознавания эквивалентности КС-грамматик и
существенной неоднозначности КС-языков.

23. Некоторые преобразования (Рассмотрим несколько эквивалентных преобразований, которые с некоторой точки зрения улучшают

грамматику)

24.

Символ X VT VN называется полезным в КС-грамматике
G (VT, VN, P, S),
если X появляется в процессе вывода из аксиомы S
некоторого слова
w L G ,
т.е. S X w, где w VT*.
Если символ X не является полезным, то он называется
бесполезным.
Очевидно, что исключение бесполезных символов из
грамматики не изменяет порождаемого языка, поэтому все
бесполезные символы можно удалить.
Символ X VN называется порождающим, если X w для
некоторой терминальной цепочки w.
Символ X VT VN называется достижимым,
если существует вывод S X для некоторых и .

25.

Очевидно, что полезный нетерминальный символ грамматики
является одновременно и порождающим, и достижимым.
Можно доказать, что если
сначала удалить из грамматики непорождающие символы,
а затем недостижимые, то останутся только полезные.

26.

Алгоритм 1. Устранение непорождающих символов.
(Ni – множества)
Шаг 1.
Положить N0 и i 1.
Шаг 2.
Ni A | A P (VT Ni 1)*} Ni-1.
Шаг 3.
Если Ni Ni 1 , то положить i i 1 и перейти к шагу 2. В
противном случае положить Nе Ni – множество
порождающих символов.
Шаг 4.
Если Ne VN , т.е. имеются непорождающие символы, следует
перейти к грамматике G1 (VT, VN , P , S),
в которой VN Ne VN, и P состоит из правил множества P,
содержащих нетерминалы только из Ne.

27.

С помощью алгоритма 1. может быть решена
проблема пустоты для КС-языков.
Язык L(G) непустой тогда и только тогда,
когда S – порождающий символ,
т. е. когда имеется вывод S w
для некоторого слова w VT*.
Другими словами, язык L(G) непустой тогда и только тогда,
когда S Ne.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

Таким образом было
3 нетерминала
8 правил
Стало
11 нетерминалов
16 правил

61.

62. Нормальная форма Грейбах

Определение. Говорят, что контекстно-свободная
грамматика G = (VN, VT, P, S) представлена в нормальной
форме Грейбах, если каждое ее правило имеет вид
A a , где a VT, VN*.
Для доказательства того, что всякая контекстносвободная грамматика может быть приведена к
нормальной форме Грейбах, требуется обосновать
эквивалентность используемых при этом
преобразований.

63.

Лемма. Пусть G = (VN, VT, P, S) –
контекстно-свободная грамматика, A 1B 2 P,
{B i | B VN, i V+, i = 1, 2, ..., m} – множество
всех B-порождений, т. е. правил с нетерминалом B в
левой части.
Пусть грамматика G1 = (VN, VT, P1, S) получается из
грамматики G отбрасыванием правила
A 1B 2
и добавлением правил вида
A 1 i 2, i = 1, 2, ..., m.
Тогда L(G) = L(G1).

64. I

Очевидно, что L(G1) L(G).
Пусть в G1 S x, x VT*.
Использование в этом выводе правила
A 1 i 2 P1\P
равносильно двум шагам вывода в грамматике G:
A 1B 2 1 i 2.
Шаги вывода в грамматике G1, на которых
используются другие правила из множества правил P,
являются шагами вывода в грамматике G.
Поэтому в G
S x.

65. II

Очевидно, что L(G) L(G1).
Пусть в G
S x.
Если в этом выводе используется правило
A 1B 2 P\P1,
то рано или поздно для замены B будет использовано
правило вида B i P.
Эти два шага вывода в грамматике G равносильны
одному шагу вывода в грамматике G1: A 1 i 2.
Шаги вывода в грамматике G, на которых
используются другие правила из множества P,
являются шагами вывода в грамматике G1.
Поэтому в G1 S x.

66.

Лемма об устранении левой рекурсии.
Пусть G = (VN, VT, P, S) – контекстно-свободная
грамматика,
{A A i | A VN, i V*, i = 1,2, ..., m} – множество всех
леворекурсивных A-порождений,
{A j | j = 1,2, ..., n} – множество всех прочих Aпорождений.
Пусть G1 = (VN {Z}, VT, P1, S) – контекстно-свободная
грамматика, образованная добавлением нетерминала Z к
VN и заменой всех A-порождений правилами:
1) A j, A jZ, j = 1, 2, ..., n;
2) Z i, Z iZ, i = 1, 2, ..., m.
Тогда L(G1) = L(G).

67.

Доказательство.
Прежде всего заметим, что посредством левосторонних
выводов при использовании одних лишь A-порождений
порождаются регулярные множества вида
{ 1, 2, ..., n}{ 1, 2, ..., m}*,
и это является в точности множеством, порождаемым
правилами грамматики G1, имеющими A или Z в левых
частях.

68. I. Докажем, что L(G)  L(G1).

I. Докажем, что L(G) L(G1).
Пусть x L(G).
Левосторонний вывод в G S x можно перестроить в
вывод в G1 S x следующим образом:
каждый раз, когда в левостороннем выводе встречается
последовательность шагов:
tA tA i1 tA i2 i1 ... tA ip... i2 i1
t j ip... i2 i1 (t VT*, V*),
заменим их последовательностью:
tA jZ t j ipZ ... t j ip... i2Z t j ip... i2 i1 .
Полученный таким образом вывод является выводом x в
грамматике G1, хотя и не левосторонним.
Следовательно, x L(G1).

69. II. Докажем, что L(G1)  L(G).

II. Докажем, что L(G1) L(G).
Пусть x L(G1).
Рассмотрим левосторонний вывод в G1 S x, и перестроим его в
вывод в грамматике G следующим образом.
Всякий раз, как Z появляется в cентенциальной форме, мы
приостанавливаем левосторонний порядок вывода и вместо того,
чтобы производить замены в цепочке , предшествующей Z,
займемся замещением Z с помощью правил вида Z Z.
Далее, вместо того, чтобы производить подстановки в цепочке a,
продолжим использовать соответствующие правила для Z, пока,
наконец, Z не будет замещено цепочкой, его не содержащей.
После этого можно было бы заняться выводами терминальных
цепочек из и .
Результат этого, уже не левостороннего, вывода будет тем же
самым, что и при исходном левостороннем выводе в грамматике
G1.

70.

Теорема нормальная форма Грейбах.
Каждый контекстно-свободный язык может быть
порожден контекстно-свободной грамматикой в
нормальной форме Грейбах.
Доказательство.
Пусть G = (VN, VT, P, S) контекстно-свободная
грамматика в нормальной форме Хомского, порождающая
контекстно-свободный язык L.
Пусть VN = {A1, A2, ..., Am}.
Первый шаг построения состоит в том, чтобы в правилах
вида Ai Aj ,
где цепочка нетерминалов новой грамматики, всегда
было
j > i.
Этот шаг выполняется последовательно для i = 1, 2, ... , m
следующим образом.

71.

При i = 1 правило для A1 может иметь вид A1 a, a VT, и
тогда оно не нуждается в преобразованиях, либо оно имеет
вид A1 AjAk, Aj, Ak VN.
Если j > 1, то правило уже имеет требуемый вид.
В противном случае оно леворекурсивно, и в соответствии с
леммой может быть заменено правилами вида
A1 , A1 Z1, Z1 Ak, Z1 AkZ1,
= a, a VT , или = BC, причем B ≠ A1.
Предположим, что для i = 1, 2, ... , k правила вида Ai Aj
были преобразованы так, что j > i.
Если Ak+1 Aj есть правило, в котором j < k + 1, то мы
образуем новые правила, подставляя вместо Aj правую часть
каждого Aj-порождения согласно лемме.

72.

В результате, если в позиции Aj окажется нетерминал, то
его номер будет больше j .
Повторив этот процесс самое большее k – 1 раз, получим
порождения вида Ak+1 Ap , p k + 1.
Порождения с p = k + 1 затем преобразуются согласно
лемме введением новой переменной Zk+1.
Повторив описанный процесс для каждого нетерминала
исходной грамматики, мы получим правила только одного
из трех следующих видов:
Ak Ap , где p > k
Ak a , где a VT
Zk X , где X VT VN, (VN {Z1, Z2,..., Zm})*.

73.

Отметим, что крайний левый символ правой части правила
для Am по необходимости является терминалом, так как
нетерминала с большим номером не существует.
Крайний левый символ в правой части правила для
Am–1 может быть терминалом либо нетерминалом Am.
В последнем случае мы можем построить новые правила,
заменяя Am правыми частями Am-порождений согласно
лемме.
Эти новые правила будут иметь правые части,
начинающиеся с терминального символа.
Подобным же образом преобразуем правила для
Am–2, Am–3, ..., A1
до тех пор, пока правые части каждого из этих правил не
будут начинаться с терминала.

74.

Остается преобразовать правила для новых переменных
Z1, Z2, ..., Zm.
Правые части этих правил начинаются с терминального
символа либо с нетерминала исходной грамматики.
Пусть имеется правило вида
Zi Ak .
Достаточно еще раз применить к нему преобразования,
описанные в лемме, заменив Ak правыми частями Akпорождений, чтобы получить требуемую форму правил,
поскольку правые части правил для Ak уже начинаются с
терминалов.
На этом построение грамматики в нормальной форме
Грейбах, эквивалентной исходной грамматике G,
завершается.
Что и требовалось доказать.

75.

76.

77.

78.

79.

80.

81.

Таким образом было
5 правил
Стало
26 правил