Таблица производных

1.

f (х)
f /(х)
ех
lnx
ех
ах
ах lnа
logax
1
х lna
1
х

2.

3.

№ 47.5(а)
k = f ( хо )
1
3
f (х) = х е
х
2
1
1 3
1
х
х
х
е + х е = е х + х3
f ( х ) = х
3
3
2
1
1
1
4е
1
3
3
f (1) = е 1 +1 = е +1 =
3
3
3
1 3
3 3
4е
k=
3
1
3

4.

№ 47.6(а)
tgα = h ( хо )
h( х ) = е
х
h ( х ) = 1 е
х
1
= х
е
1
h (0) = 0 = 1
е
tgα = 1

5.

№ 47.7(а)
tgα = h ( хо )
1
5 х 1
5 х 1
е
5
е
=
h ( х) =
5
h (0,2) = е 5 0,2 1 е 0 = 1
tgα = 1
α = 45о

6.

26.02.2025
К л а с с н а я р а б о т а.
Производная показательной
и логарифмической функций.

7.

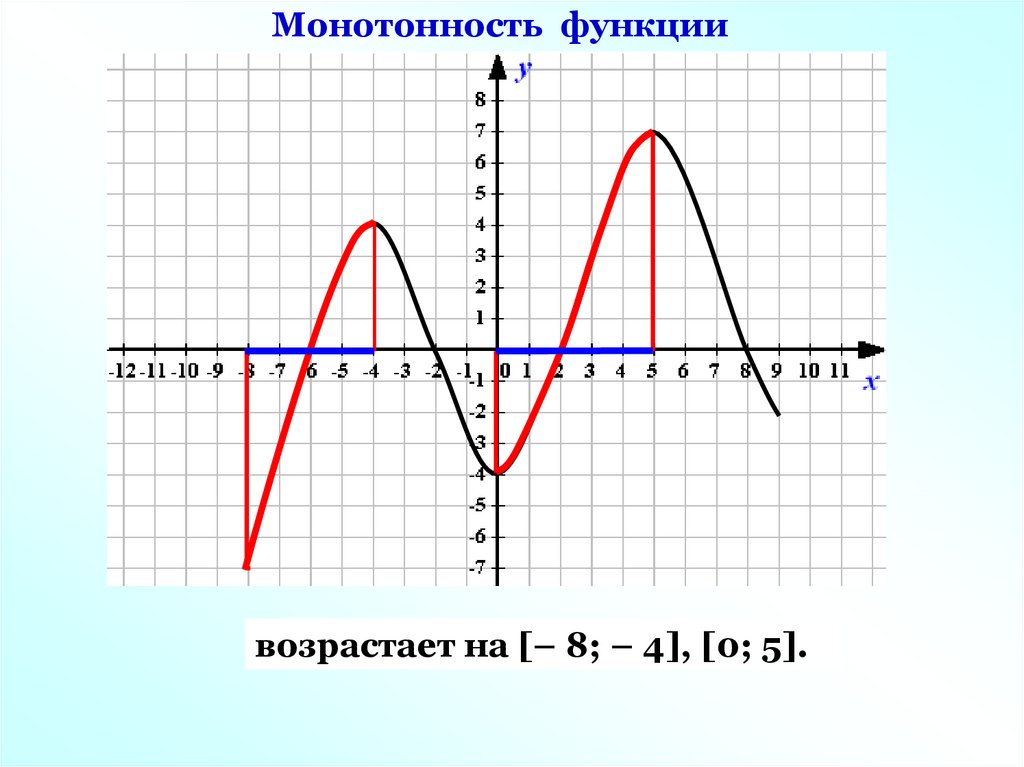
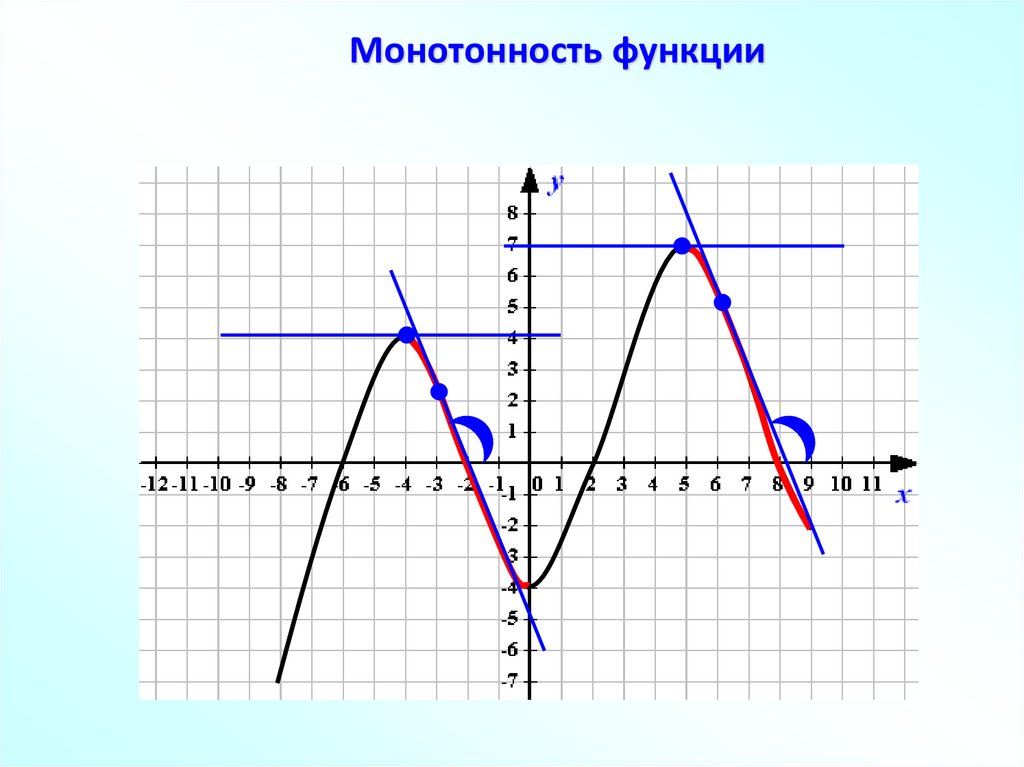
Монотонность функции
возрастает на [– 8; – 4], [0; 5].

8.

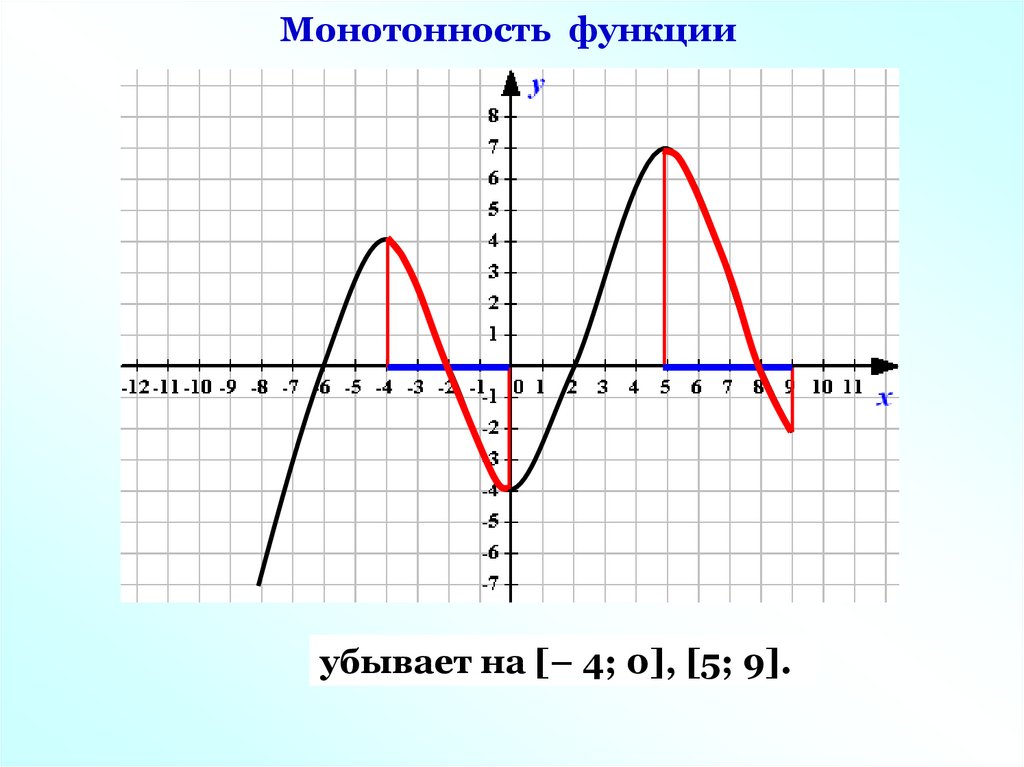
Монотонность функции
убывает на [– 4; 0], [5; 9].

9.

y
y2
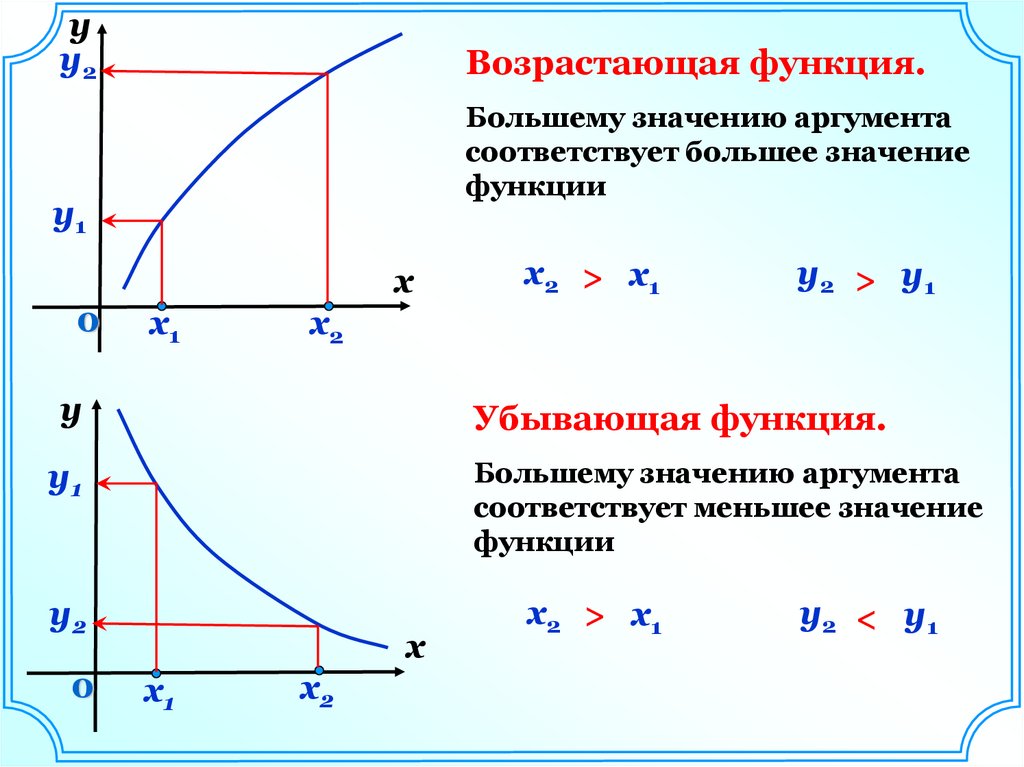
Возрастающая функция.
Большему значению аргумента
соответствует большее значение
функции
y1
0
x
x1
x2 > x1
y2 > y1
x2
y
Убывающая функция.
y1
Большему значению аргумента
соответствует меньшее значение
функции
y2
0
x
x1
x2
x2 > x 1
y2 < y 1

10.

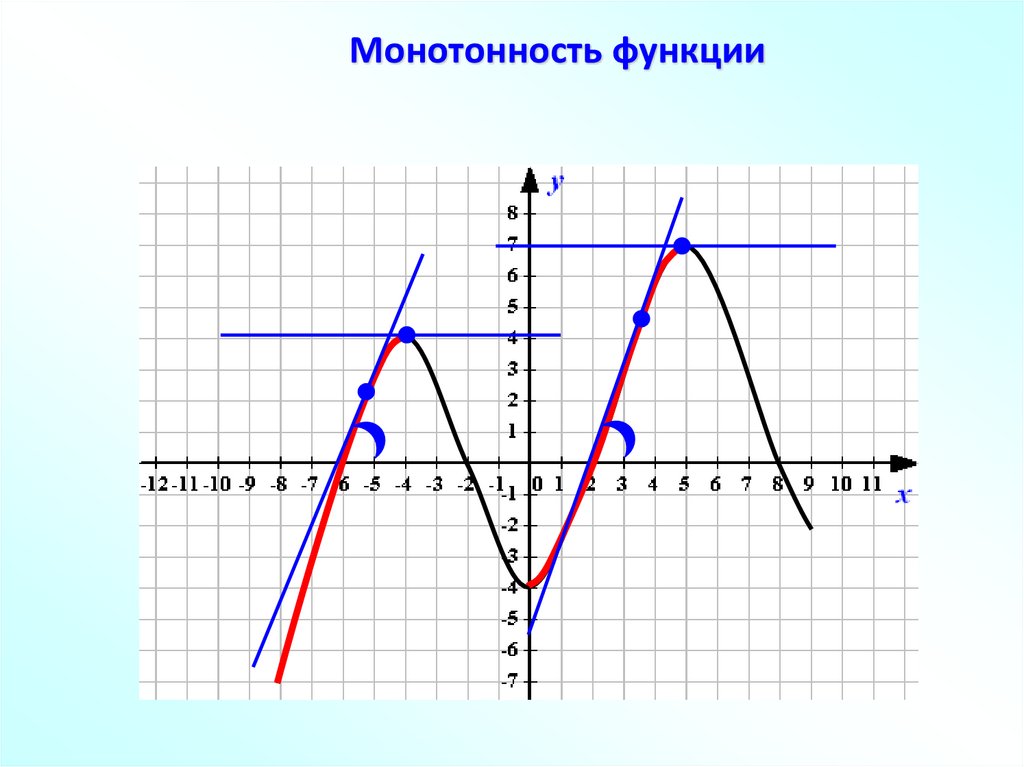
Монотонность функции

11.

Если во всех точках открытого
промежутка X выполняется неравенство f ′(x) ≥ 0, то функция y = f (x)
возрастает на промежутке X.
f ′(x) ≥ 0
y = f (x)
возрастает
на промежутке X.

12.

Монотонность функции

13.

Если во всех точках открытого
промежутка X выполняется неравенство f ′(x) ≤ 0, то функция y = f (x)
убывает на промежутке X.
f ′(x) ≤ 0
y = f (x)
убывает
на промежутке X.

14.

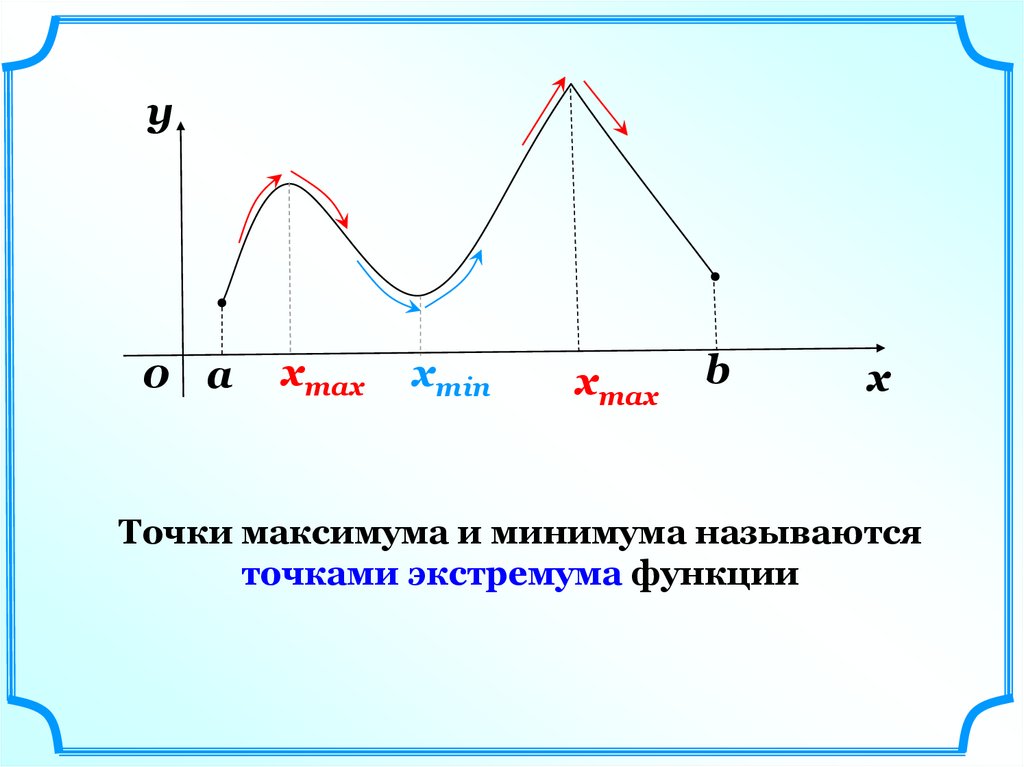
y
0 a
xmax
xmin
xmax
b
x
Точки максимума и минимума называются
точками экстремума функции

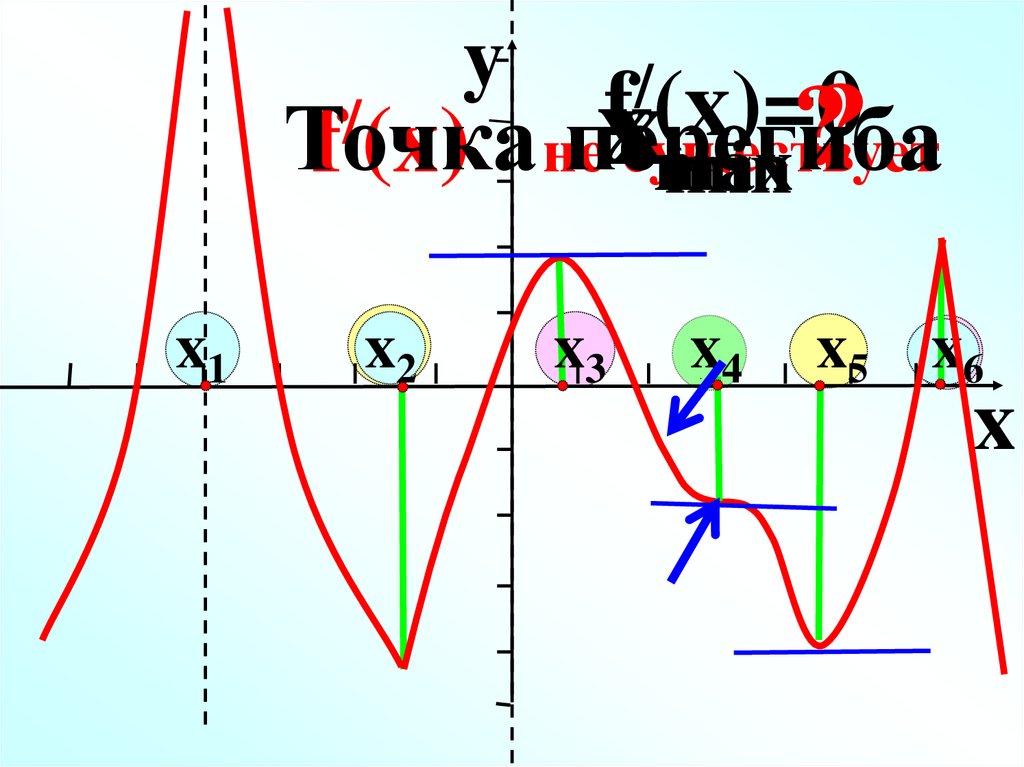
15.

y
/
f
(x)=0
/
Точка
f (x) неперегиба
существует
max
min
x1
x2
x
x3
??
x4
x5 x6
x

16.

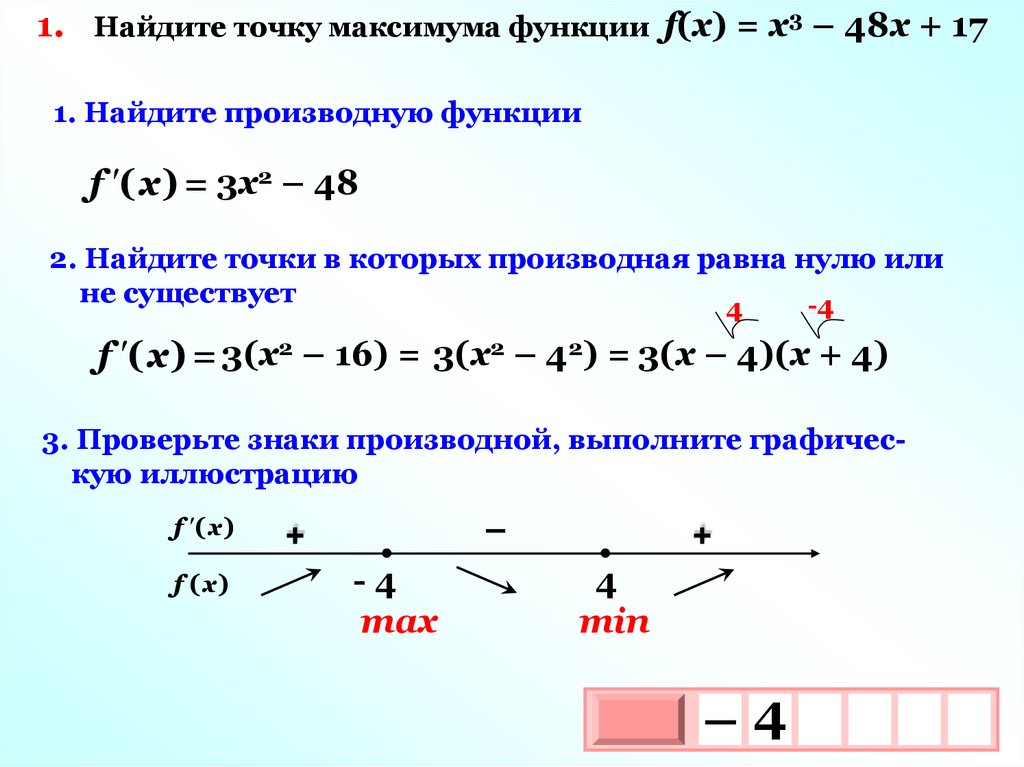
1. Найдите точку максимума функции f(х) = х3 – 48х + 17
1. Найдите производную функции
f ( х ) = 3х2 – 48
2. Найдите точки в которых производная равна нулю или
не существует
-4
4
f ( х ) = 3(х2 – 16) = 3(х2 – 42) = 3(х – 4)(х + 4)
3. Проверьте знаки производной, выполните графическую иллюстрацию
f ( х )
f (х)
–
+
-4
max
+
4
min
–4
3
10 х
х

17.

2. Найдите точку минимума функции у = (х – 10)2(х – 4) +
+2
у = (х2 – 20х + 100)(х – 4)+ 2 =
= х3 – 20х2 + 100х – 4х2 + 80х – 400 + 2 =
= х3 – 24х2 + 180х – 398
у ( х ) = 3х2 – 48х + 180 =3(х2 – 16х + 60) =
= 3(х – 6)(х – 10)
f ( х )
f (х)
–
+
6
max
+
10
min
10
3
10 х
х

18.

функция возрастает
Предположим, что
функция f не имеет на
отрезке [а; b] точек
экстремума.
наибольшее
значение
наименьшее
значение
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Тогда она возрастает
(рис. 1) или убывает
(рис. 2) на этом отрезке.
Значит,
наибольшее и наименьшее значения функции f
на отрезке [а; b] — это
значения в концах а и b.

19.

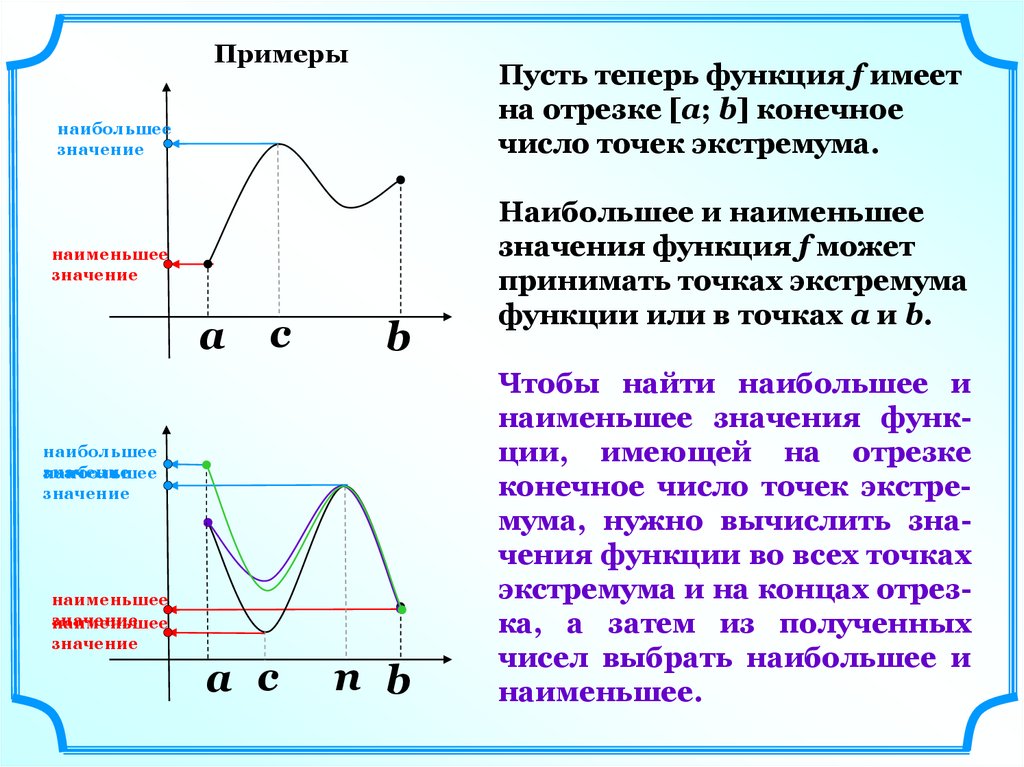
Примеры
Пусть теперь функция f имеет
на отрезке [а; b] конечное
число точек экстремума.
наибольшее
значение
наименьшее
значение
a
c
b
наибольшее
значение
наибольшее
значение
наименьшее
значение
наименьшее
значение
a c
n b
Наибольшее и наименьшее
значения функция f может
принимать точках экстремума
функции или в точках а и b.
Чтобы найти наибольшее и
наименьшее значения функции, имеющей на отрезке
конечное число точек экстремума, нужно вычислить значения функции во всех точках
экстремума и на концах отрезка, а затем из полученных
чисел выбрать наибольшее и
наименьшее.

20.

3.
Найдите наименьшее значение функции y = x3 –
– 27x на отрезке [0; 4].
1. Найдите производную функции
f ( х ) = 3х2 – 27
2. Найдите точки в которых производная равна нулю или
не существует
-3
3
f ( х ) = 3(х2 – 9) = 3(х2 – 32) = 3(х – 3)(х + 3)
3. Выберите точки, которые принадлежат заданному
отрезку
х=3
4. Вычислите значения функции на концах отрезка и в
выбранных точках
у(0) = 03 – 27 · 0 = 0
у(3) = 33 – 27 · 3 = – 54
у(4) =
43 – 27 · 4 = – 44
–5 4
3
10 х
х

21.

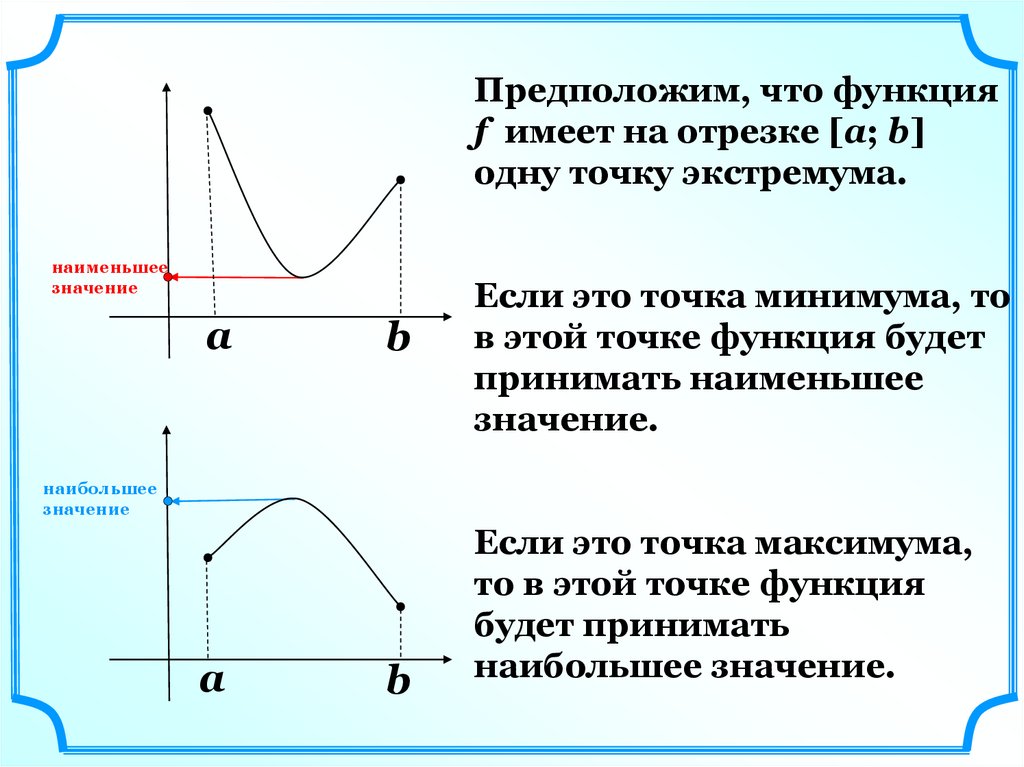
Предположим, что функция
f имеет на отрезке [а; b]
одну точку экстремума.
наименьшее
значение
a
b
Если это точка минимума, то
в этой точке функция будет
принимать наименьшее
значение.
наибольшее
значение
a
b
Если это точка максимума,
то в этой точке функция
будет принимать
наибольшее значение.

22.

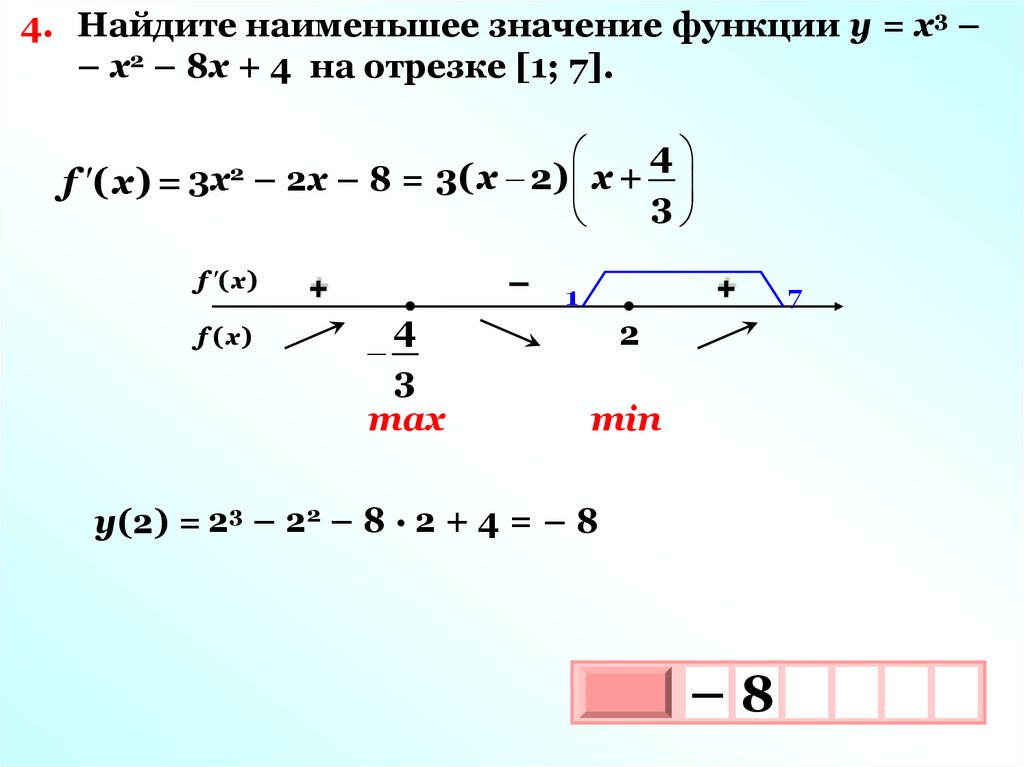
4. Найдите наименьшее значение функции y = x3 –
– x2 – 8х + 4 на отрезке [1; 7].
f ( х ) =
3х2 – 2х – 8 = 3( х 2)
f ( х )
f (х)
–
+
4
3
max
4
х+ 3
+
1
7
2
min
у(2) = 23 – 22 – 8 · 2 + 4 = – 8
–8
3
10 х
х

23.

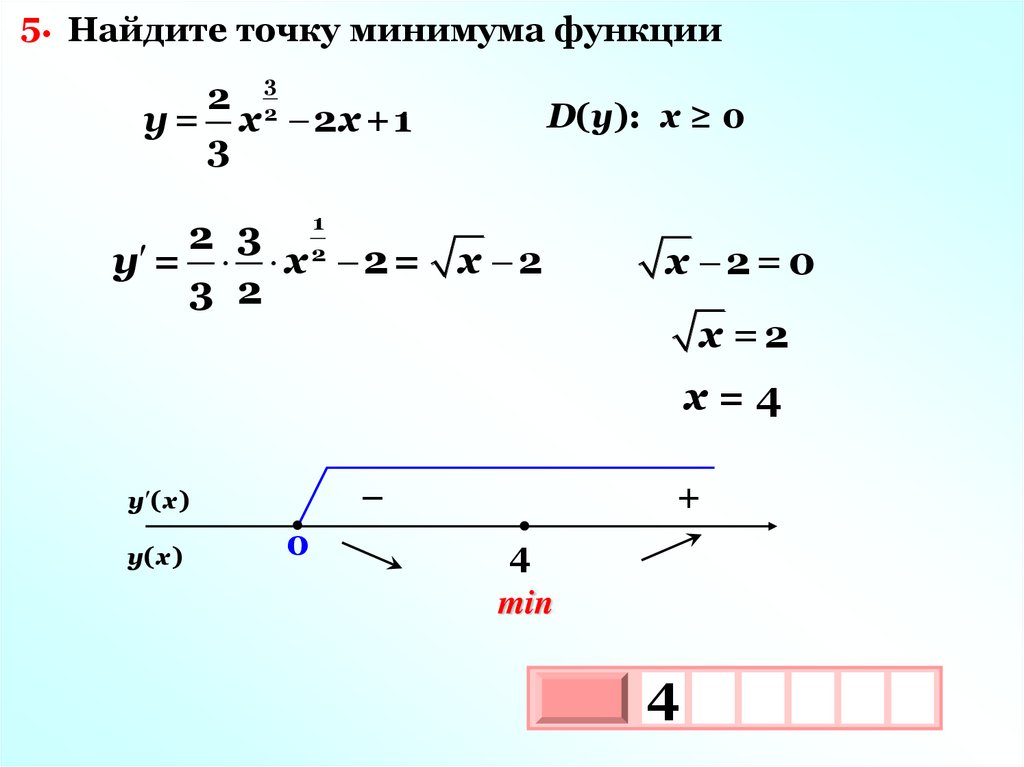
5. Найдите точку минимума функции
2 23
у = х 2x +1
3
D(у): х ≥ 0
2 3 21
у = х 2 = х 2
3 2
х 2=0
х =2
х=4
–
у ( х )
у( х )
0
+
4
min
4
3
10х
х

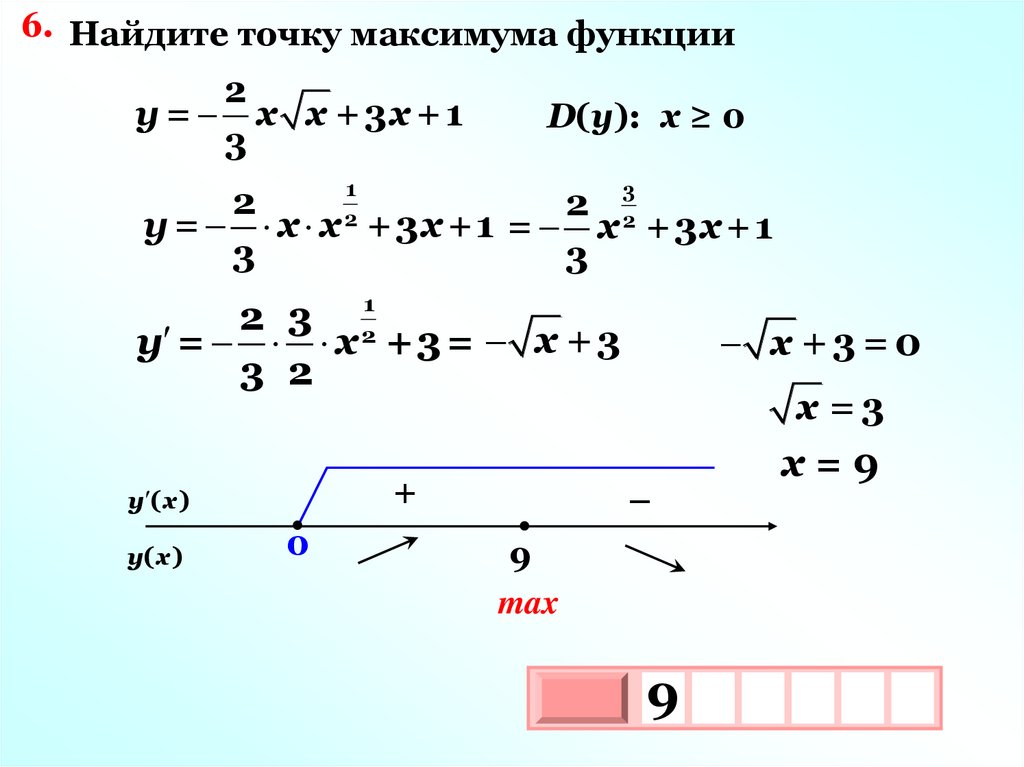
24.

6. Найдите точку максимума функции
2
у = х х +3 x +1
3
D(у): х ≥ 0
1
3
2
2
у = х х 2 +3x +1 = х 2 +3 x +1
3
3
1
2
2 3
у = х +3 = х + 3
3 2
+
у ( х )
у( х )
0
х +3=0
–
х =3
х=9
9
max
9
3
10х
х

25.

7. Найдите наименьшее значение функции у = х х 3 x +1
3
2
на отрезке [1; 9].
у = х 3x +1
3
3 21
х 3
1. y ′ = х 3 =
2
2
3
х 2=0
х 3=0
2. y ′ = 0
2
х = 4 1; 9
–
у ( х )
у( х )
1
+
4
min
9
3. y (4) = 4 4 3 4+1 = 8 – 12 + 1 = – 3
–3
3
10 х
х

26.

8.
Найдите точку максимума функции
х 2 +289
у=
х
/
1
1
÷ 2
х
х
289
у = х
х
D(у): х ≠ 0
1 289
у = 1 289 2 = 2 1 =
х
х
289 х 2 (17 х )(17 + х )
=
=
2
2
х
х
у ( х )
у( х )
–
+
– 17
min
+
0
–
17
max
1 7
3
10х
х

27.

х 2 + 25
9. Найдите наименьшее значение функции y=
х
на отрезке [– 10; 1].
Запишем функцию в удобном для дифференцирования
2
виде:
1
х
25
y=
+
х
х
y= х + 25
х
2
25
х
25 ( х 5)( х + 5)
1
1
=
=
1. y ′ = 1+25 2 =
2
2
2
х
х
х
х
2. y ′ = 0
x1 = 5 -10; 1
x2 = – 5 -10; 1
3. y (– 10) = – 12,5
y (1) = 26
y (– 5) = – 10
– 1 2 , 5
3
10х
х

28.

10. Найдите точку минимума функции
у = (х + 16)ех – 16
D(у): (– ∞; + ∞)
(uv) u/ v + uv/
/
у = 1 · ех – 16 + (х + 16) · 1 · ех – 16 =
= ех – 16 · (1 + х + 16) = ех – 16 · (х + 17)
у ( х )
у( х )
–
+
– 17
min
– 1 7
3
10х
х

29.

11. Найдите точку минимума функции
у = (х2 – 8х + 8)е6 – х
D(у): (– ∞; + ∞)
(uv) u/ v + uv/
/
у = (2х – 8)е6 – х + (х2 – 8х + 8)·(– 1)·е6 – х =
= (2х – 8)·е6 – х – (х2 – 8х + 8)·е6 – х =
= е6 – х · (2х – 8 – х2 + 8х – 8) =
= е6 – х · (– х2 + 10х – 16) = – е6 – х · (х2 – 10х + 16) =
= – е6 – х · (х – 2)(х – 8)
у ( х )
у( х )
–
–
+
2
min
8
max
2
3
10х
х

30.

12. Найдите точку минимума функции
у = (х + 3)2 е2 – х
D(у): (– ∞; + ∞)
у = (х2 + 6х + 9) · е2 – х
у = (2х + 6)е2 – х + (х2 + 6х + 9)·(– 1)·е2 – х =
= (2х + 6)·е2 – х – (х2 + 6х + 9)·е2 – х =
= е2 – х · (2х + 6 – х2 – 6х – 9) =
= е2 – х · (– х2 – 4х – 3) = – е2 – х · (х + 1)(х + 3)
у ( х )
у( х )
–
–
+
–3
min
–1
max
– 3
3
10х
х

31.

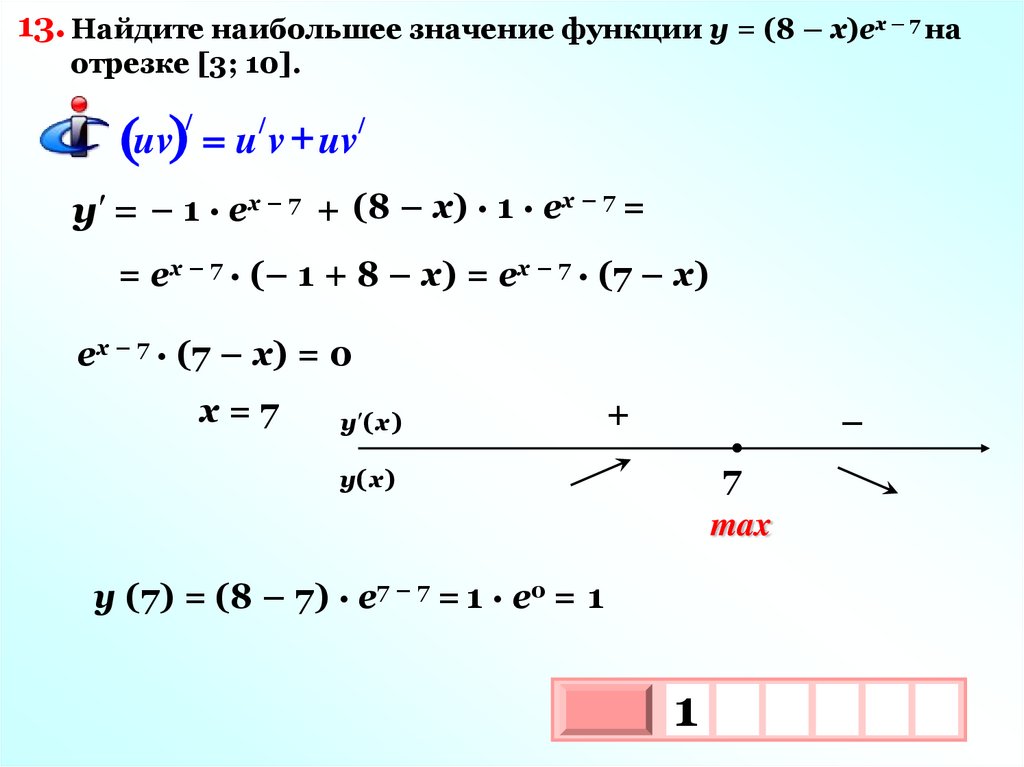
13. Найдите наибольшее значение функции у = (8 – х)ех – 7 на
отрезке [3; 10].
/
+
(uv) u v uv
/
/
у = – 1 · ех – 7 + (8 – х) · 1 · ех – 7 =
= ех – 7 · (– 1 + 8 – х) = ех – 7 · (7 – х)
ех – 7 · (7 – х) = 0
х=7
у ( х )
+
–
7
max
у( х )
y (7) = (8 – 7) · е7 – 7 = 1 · е0 = 1
1
3
10х
х

32.

14. Найдите наименьшее значение функции у = (х2 – 8х + 8)е2 – х
на отрезке [1; 7].
/
+
(uv) u v uv
/
/
у = (2х – 8) · е2 – х + (х2 – 8х + 8)·(– 1)·е2 – х =
= (2х – 8)·е2 – х – (х2 – 8х + 8)·е2 – х =
= е2 – х · (2х – 8 – х2 + 8х – 8) =
= е2 – х · (– х2 + 10х – 16) = – е2 – х · (х2 – 10х + 16) =
= – е2 – х · (х – 2)(х – 8)
у ( х )
у( х )
–
–
+
2
min
8
– 4
y (2) = (4 – 16 + 8) · е2 – 2 = – 4 · е0 = – 4
3
10х
х

33.

15. Найдите точку минимума функции
у = 2х – ln(х + 3) + 7
D(у): х + 3 > 0
х>–3
2( х +3) 1 2 х +5 2( х +2,5)
1
=
=
=
у = 2
х +3
х +3
х +3
х +3
–
у ( х )
у( х )
-3
+
2,5
min
–2 , 5
3
10х
х

34.

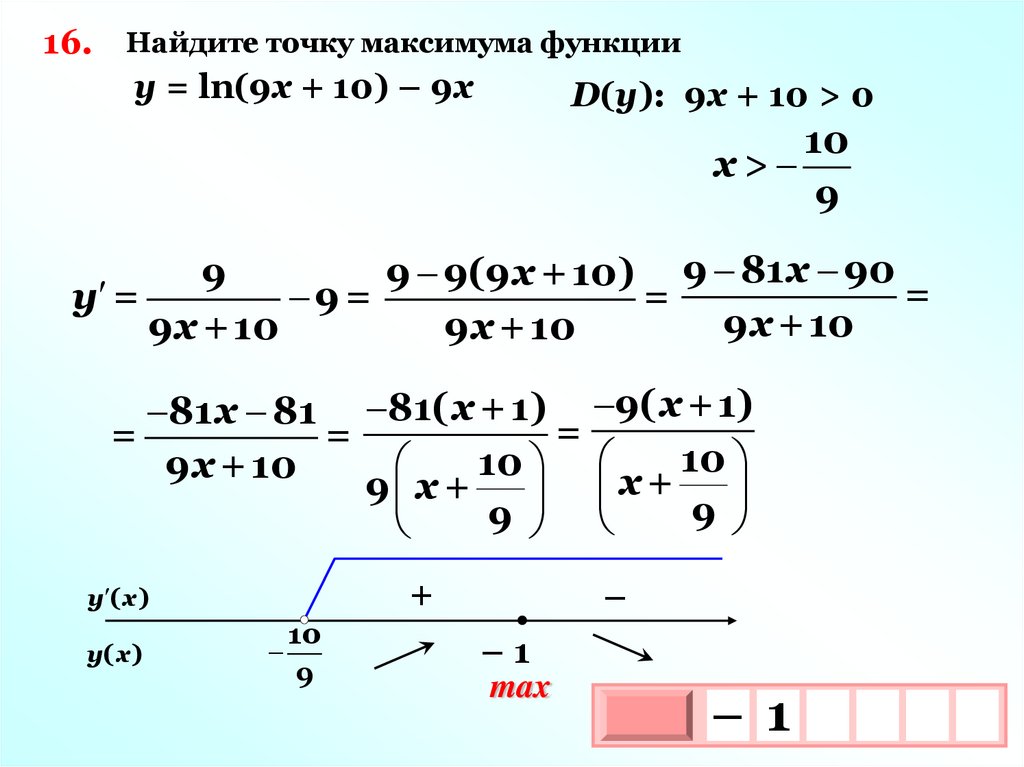
16. Найдите точку максимума функции
у = ln(9х + 10) – 9х
D(у): 9х + 10 > 0
10
x>
9
9
9 9(9 х +10) 9 81 х 90
=
у =
9=
=
9 х +10
9 х +10
9 х +10
81 х 81 81( х +1) 9( х +1)
=
=
=
10
10
9 х +10
9 х +
х+ 9
9
+
у ( х )
у( х )
10
9
–
–1
max
– 1
3
10х
х

35.

17.Найдите наибольшее значение функции у = ln(х + 5)5 – 5х на
отрезке [– 4,5; 0].
D(у):
у = ln(х + 5)5 – 5х
у = 5ln(х + 5) – 5х
х+5>0
х>–5
1
5 5( х + 5) 5 5 х 25
у = 5 1
5=
=
=
х +5
х +5
х +5
5 х 20 5( х + 4)
=
=
х +5
х +5
+
у ( х )
у( х )
–5
–
–4
max
y (– 4) = ln(– 4 + 5)5 – 5 · (– 4) = ln 1 + 20 = 20
20
3
10х
х

36.

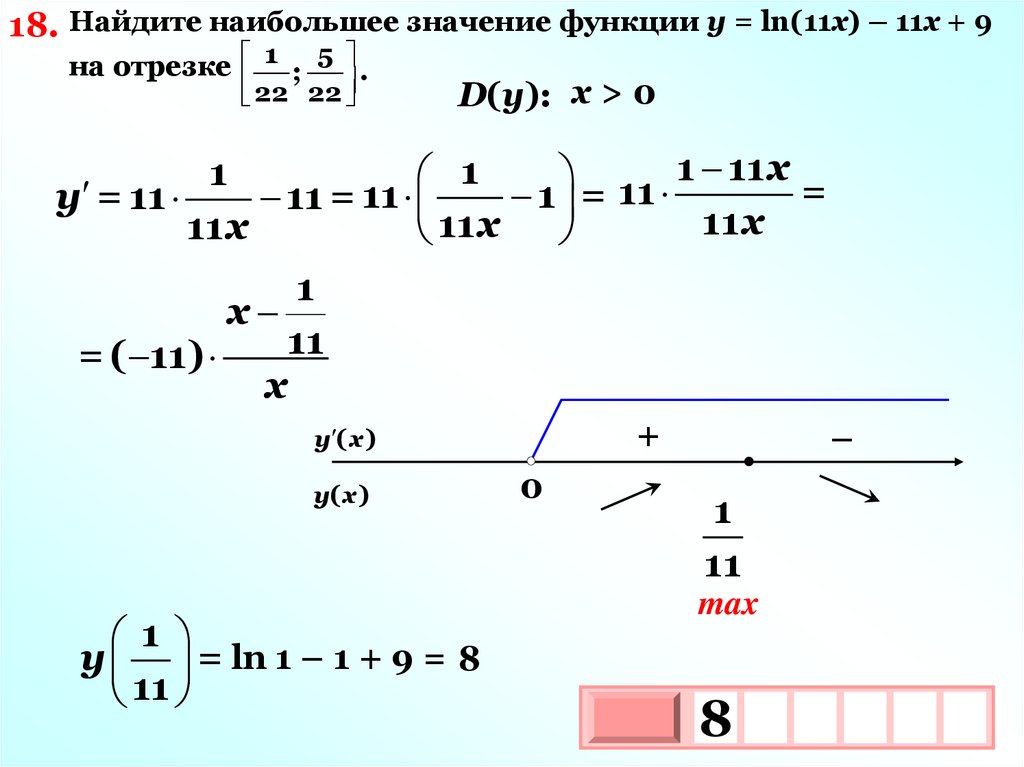
18. Найдите наибольшее значение функции у = ln(11х) – 11х + 9
на отрезке 1 ; 5 .
22 22
D(у): х > 0
1
1
11 1 11 х =
1 =
у = 11
11 = 11
11 х
11 х
11х
1
х
11
= ( 11)
х
+
у ( х )
у( х )
1
у = ln 1 – 1 + 9 = 8
11
0
–
1
11
max
8
3
10х
х

37.

19. Найдите наименьшее значение функции у = 2х2 – 5х + lnх – 3
5 7
на отрезке ; .
6 6
D(у): х > 0
1
4 ( х 1) х
2
4
1 4 х 5 х +1
у = 4 х 5+ =
=
х
х
х
+
у ( х )
у( х )
0
+
–
1
4
1
min
y (1) = 2 – 5 + ln 1 – 3 = – 6
– 6
3
10х
х

38.

20. Найдите наибольшее значение функции у = 7cosx +16x – 2 на
3π
отрезке
; 0 .
2
1 способ
у = – 7sinх + 16 > 0
Значит, функция у = 7соsх + 16х – 2 возрастает
на D(у), т.е. принимает наибольшее значение
на правом конце отрезка.
1
y (0) = 7 · соs0 + 16 · 0 – 2 = 5
5
3
10х
х

39.

20. Найдите наибольшее значение функции у = 7cosx +16x – 2 на
3π
отрезке
; 0 .
2
2 способ
у = – 7sinх + 16
у = 0, если – 7sinх + 16 = 0
– 7sinх = – 16
16
sinх =
>1
7
корней нет
0
3 π 7соs 3 π +16 3 π 2 = – 24π – 2
у
=
2
2
2
1
y (0) = 7 · соs0 + 16 · 0 – 2 = 5
5
3
10х
х

40.

21. Найдите наименьшее значение функции у = 5cosx – 6x + 4 на
3π
отрезке
; 0 .
2
1 способ
у = – 5sinх – 6 < 0
Значит, функция у = 5соsх – 6х + 4 убывает на
D(у), т.е. принимает наименьшее значение на
правом конце отрезка.
1
y (0) = 5 · соs0 – 6 · 0 + 4 = 9
9
3
10х
х

41.

21. Найдите наименьшее значение функции у = 5cosx – 6x + 4 на
3π
отрезке
; 0 .
2
2 способ
у = – 5sinх – 6
у = 0, если – 5sinх – 6 = 0
– 5sinх = 6
6
sinх = < 1
5
корней нет
0
3 π 5соs 3 π 6 3 π + 4 = 9π + 4
у
=
2
2
2
1
y (0) = 5 · соs0 – 6 · 0 + 4 = 9
9
3
10х
х

42.

22. Найдите наибольшее значение функции у = 10sinx 36 x +7
π
5π
на отрезке
; 0 .
6
1 способ
36
10cos
x
<0
у=
π
36
x +7 убывает на
Значит, функция у = 10sinx
π
D(у), т.е. принимает наибольшее значение на
левом конце отрезка.
5π 36 5π
5π
10sin
у
=
+7 =
6 π 6
6
1
= 10 + 30 +7 = 32
2
32
3
10х
х

43.

22. Найдите наибольшее значение функции у = 10sinx 36 x +7
5π
на отрезке
; 0 .
6
π
2 способ
36
10cos
x
у=
π
36
=0
π
18
cosx =
>1
5π
у = 0, если 10cosx
корней нет
5π 36 5π
5π
у
+7 =
= 10sin
6 π 6
6
1
= 10 + 30 +7 = 32
2
36
0+7 = 7
y (0) = 10sin0
π
32
3
10х
х

44.

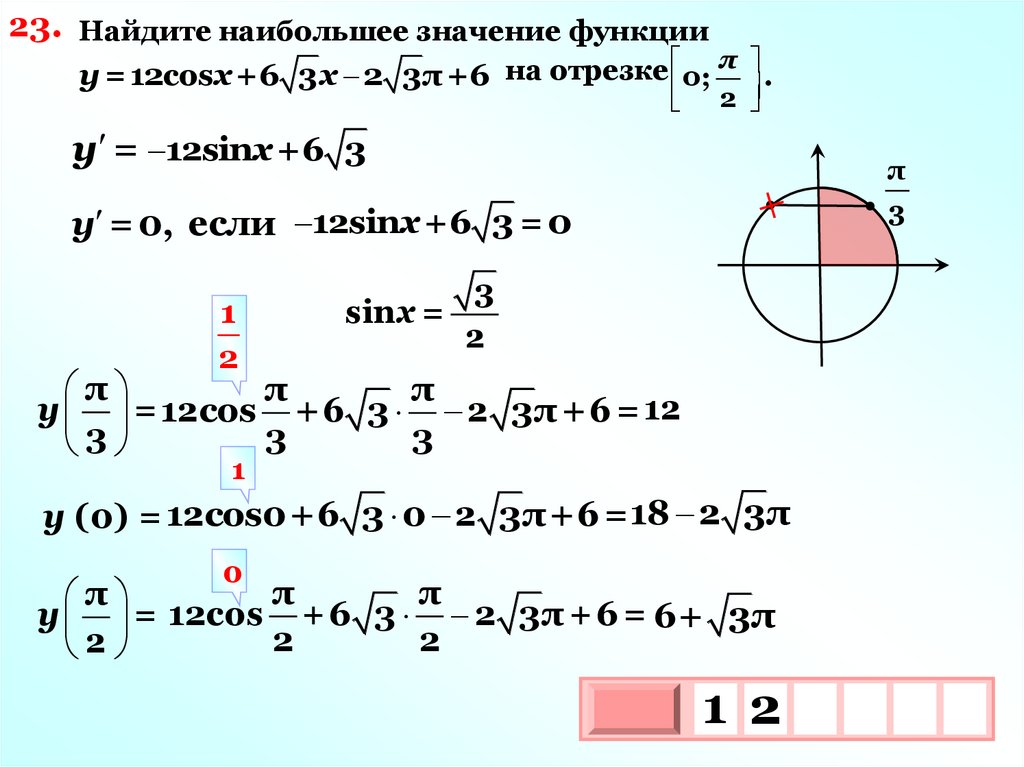
23. Найдите наибольшее значение функции
у =12cosx +6 3x 2 3π+6 на отрезке 0;
π
.
2
у = 12sinx +6 3
π
3
у = 0, если 12sinx +6 3 = 0
1
2
sinx =
3
2
π
π
π
у = 12cos +6 3 2 3π +6 = 12
3
3
3
1
y (0) = 12cos0+6 3 0 2 3π+6=18 2 3π
0
π
π
π
у = 12cos +6 3 2 3π +6 = 6+ 3π
2
2
2
1 2
3
10х
х

45.

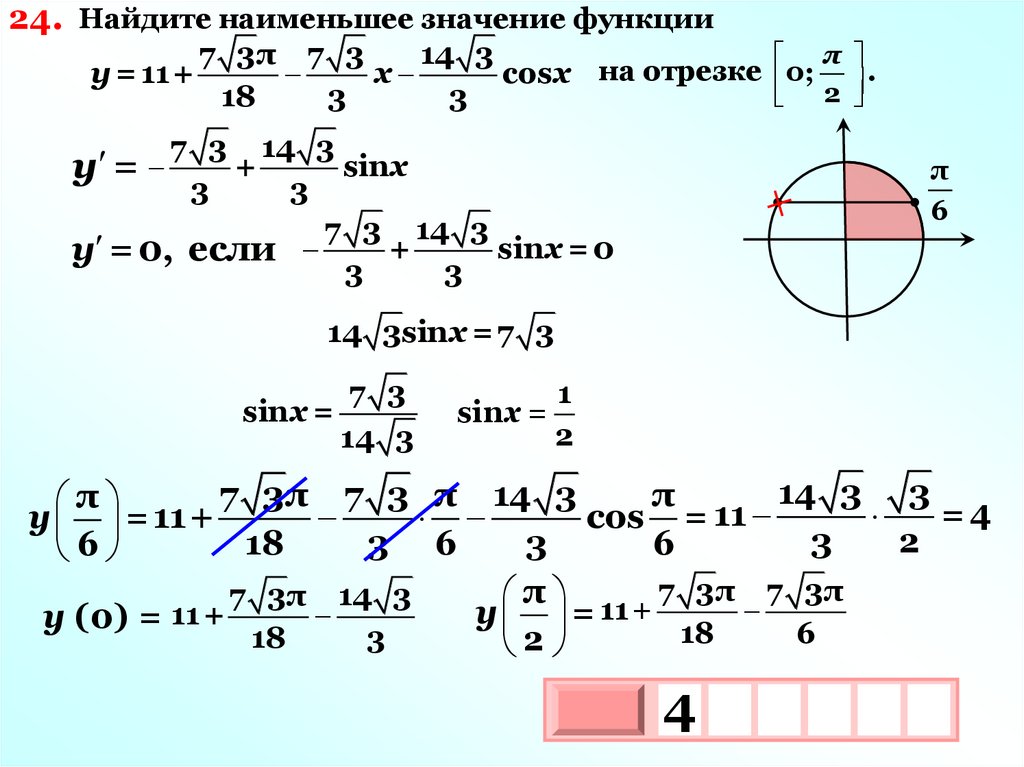
24. Найдите наименьшее значение функции
у = 11+
7 3π 7 3
14 3
π
x
cosx на отрезке 0; .
2
18
3
3
7 3 14 3
+
sinx
у =
3
3
7 3 14 3
+
sinx = 0
у = 0, если
3
3
π
6
14 3sinx = 7 3
sinx =
7 3
14 3
1
sinx =
2
14 3 3
7 3π 7 3 π 14 3
π
π
=4
cos = 11
у = 11+
3
2
18
3 6
3
6
6
π 11+ 7 3π 7 3π
7 3π 14 3
у =
y (0) = 11+
18
6
18
3
2
4
3
10х
х

46.

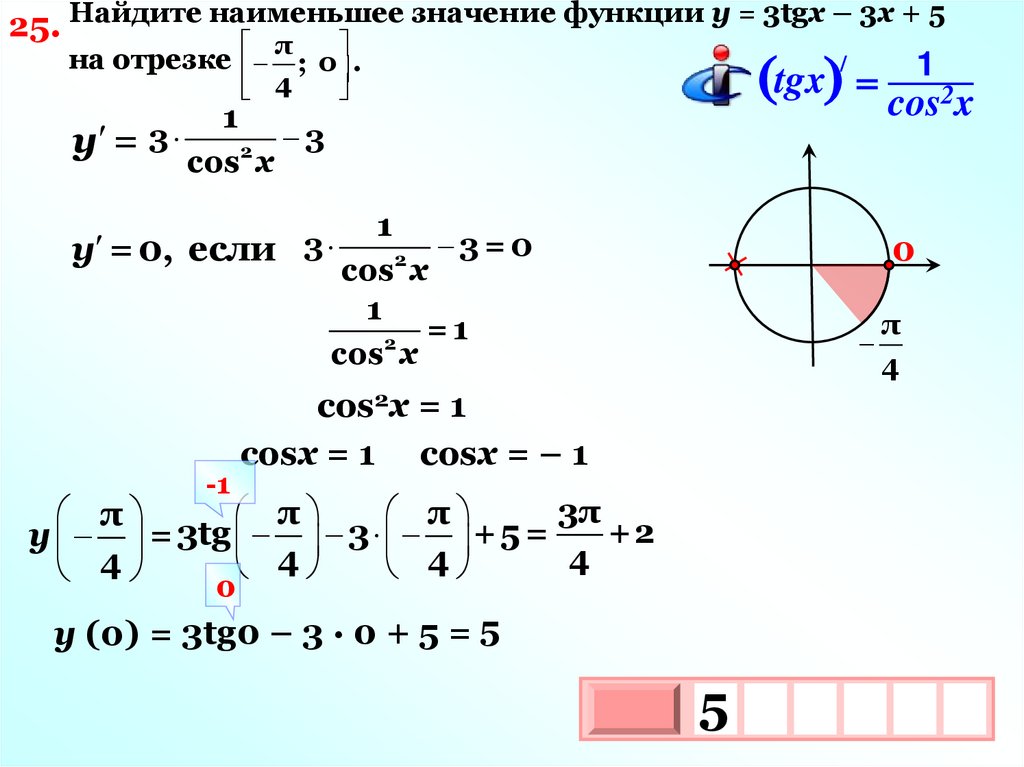
25. Найдите наименьшее значение функции у = 3tgx – 3x + 5
π
на отрезке ; 0 .
/
1
tgx
4
1
3
у = 3
2
cos x
( ) cos2x
1
3=0
у = 0, если 3
2
cos x
1
=1
2
cos x
-1
0
π
4
cos2x = 1
cosx = 1 cosx = – 1
3π
π
π
π
+2
у = 3tg 3 + 5 =
4
4
4
4
0
y (0) = 3tg0 – 3 · 0 + 5 = 5
5
3
10х
х

47.

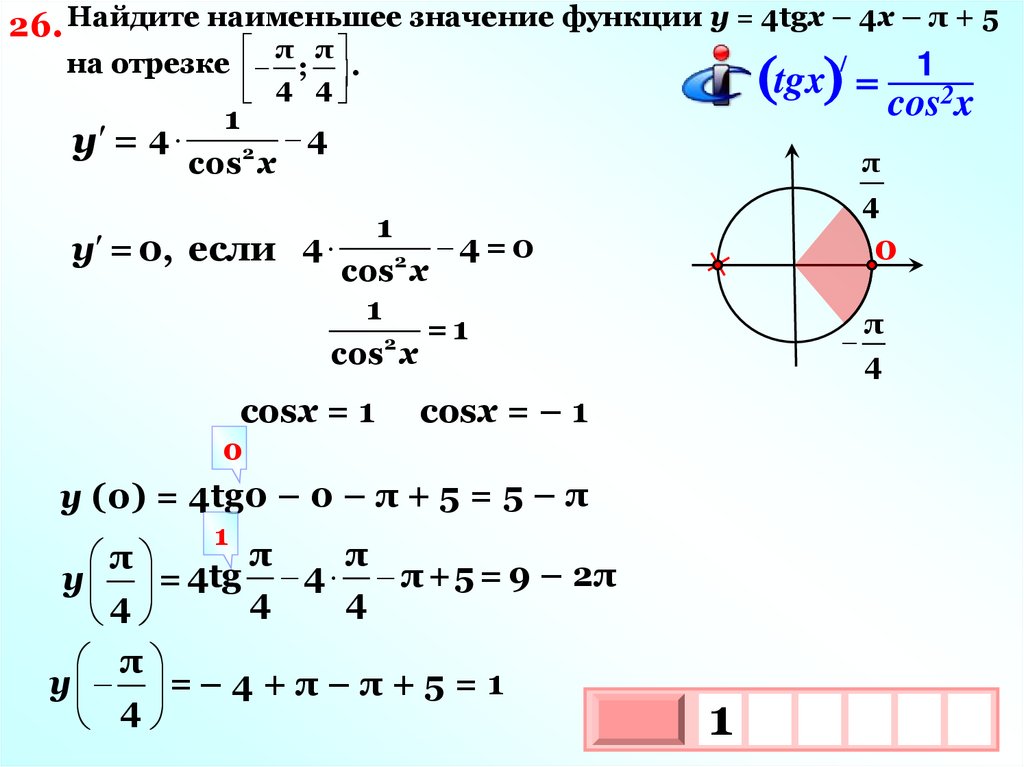
26. Найдите наименьшее значение функции у = 4tgx – 4x – π + 5
π π
/
на отрезке ; .
1
tgx
( ) cos2x
4 4
1
4
у = 4
2
cos x
π
4
1
4=0
у = 0, если 4
2
cos x
1
=1
2
cos x
cosx = 1
0
π
4
cosx = – 1
0
y (0) = 4tg0 – 0 – π + 5 = 5 – π
1
π
π
π
у = 4tg 4 π +5 = 9 – 2π
4
4
4
π
у = – 4 + π – π + 5 = 1
4
1
3
10 х
х

48.

49.

f (х) = х
g( х ) = 3 х 2
Найдите:
f (4) =
4= 2
g (2) = 3 · 2 – 2 = 4
f (t) = t
f (g(x)) = 3х 2
Функция, аргументом которой служит функция,
называется сложной.

50.

Алгоритм нахождения внешней функции:
1. Запишите формулу функции.
2. Представьте, что вам нужно вычислить значение функции при каком-то значении х. Для этого
вы подставляете это значение х в уравнение
функции и производите арифметические действия. То действие, которое вы делаете последним и
есть внешняя функция.
h( х) = 1 х
2
h(1) - ?

51.

Функция квадратного корня
у = 5 4х х2
Внутренняя функция – квадратичная функция
Показательная функция
у=2
х2 +2 х+5
Внутренняя функция – квадратичная функция
Логарифмическая функция
у = log5(4 – 2х – х2)
Внутренняя функция – квадратичная функция
Степенная функция
у = sin4 х
Внутренняя функция – тригонометрическая функция sinx

52.

При решении некоторых заданий на вычисление наибольшего и наименьшего значений
функции можно найти ответ и без вычисления производной.
Если внешняя функция является монотонно
возрастающей на всей области определения.
Значит, наибольшее значение она будет
иметь, когда внутренняя функция будет иметь
наибольшее значение.
А наименьшее значение она будет иметь, когда
внутренняя функция будет иметь наименьшее
значение.

53.

27. Найдите наибольшее значение функции у = 5 4 х х 2
Функция квадратного корня монотонно возрастает на
всей области определения. Значит, наибольшее значение она будет иметь, когда квадратичная функция будет
иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен
– 1 < 0, значит, ветви параболы направлены вниз. И
наибольшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
4
=– 2
хв = хmax =
2 ( 1)
yнаиб = у(– 2) = 5 4 ( 2) ( 2)2 =
5+8 4 = 3
3
3
10х
х

54.

28. Найдите наименьшее значение функции у = х 2 6 х +13
Функция квадратного корня монотонно возрастает на
всей области определения. Значит, наименьшее значение она будет иметь, когда квадратичная функция будет
иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен
+ 1 > 0, значит, ветви параболы направлены вверх. И
наименьшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
6
=3
хв = хmin =
2 1
yнаим = у(3) = 32 6 3+ 13 = 9 18+13 = 2
2
3
10х
х

55.

29. Найдите наименьшее значение функции у = 2
х2 +2 х+5
Показательная функция с основанием 2 > 1 монотонно
возрастает на всей области определения. Значит,
наименьшее
значение
она
будет
иметь,
когда
квадратичная функция будет иметь наименьшее
значение.
Старший коэффициент квадратного трехчлена равен
+ 1 > 0, значит, ветви параболы направлены вверх. И
наименьшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
2
=–1
хв = хmin =
2 1
( 1)2 +2 ( 1)+5
yнаим = у(– 1) = 2
= 21 2+5 = 24 = 16
1 6
3
10х
х

56.

7 6 х х2
30. Найдите наибольшее значение функции у = 3
Показательная функция с основанием 3 > 1 монотонно
возрастает на всей области определения. Значит,
наибольшее
значение
она
будет
иметь,
когда
квадратичная функция будет иметь наибольшее
значение.
Старший коэффициент квадратного трехчлена равен
– 1 < 0, значит, ветви параболы направлены вниз. И
наибольшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
6
=– 3
хв = хmax =
2 ( 1)
7 6 ( 3) ( 3)2
yнаиб = у(– 3) = 3
= 3 7+18 9 = 32 = 9
9
3
10х
х

57.

30. Найдите наибольшее значение функции
у = log5(4 – 2х – х2) + 3
Логарифмическая функция с основанием 5 > 1 монотонно возрастает на всей области определения. Значит,
наибольшее
значение
она
будет
иметь,
когда
квадратичная функция будет иметь наибольшее
значение.
Старший коэффициент квадратного трехчлена равен
– 1 < 0, значит, ветви параболы направлены вниз. И
наибольшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
2
=– 1
хв = хmах =
2 ( 1)
1
yнаиб = у(– 1) = log5(4 + 2 – 1) + 3 = log55 + 3 = 4
4
3
10х
х

58.

31. Найдите наименьшее значение функции
у = log3(х2 – 6х + 10) + 2
Логарифмическая функция с основанием 3 > 1 монотонно возрастает на всей области определения. Значит,
наименьшее
значение
она
будет
иметь,
когда
квадратичная функция будет иметь наименьшее
значение.
Старший коэффициент квадратного трехчлена равен
1 > 0, значит, ветви параболы направлены вверх. И
наименьшее значение квадратичная функция будет
иметь в вершине.
b
хв =
2a
6
=3
хв = хmin =
2 1
0
yнаим = у(3) = log3(9 – 18 + 10) + 2 = log31 + 2 = 2
2
3
10х
х

59.

У: стр. 313 § 47
З: §47 № 14(а), 21(а).